Определение положения центра тяжести тела в теоретической механике

Определение положения центра тяжести тела, составленного из тонких однородных стержней

Задача 122-23. Определить положение центра тяжести плоской фигуры (рис. 178), изогнутой из тонкой проволоки.

Решение.

1.    Фигура состоит из четырех прямых отрезков: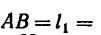

2.    Оси координат расположим так, чтобы они совпали с отрезками DE (ось х) и DB (ось у). Так как фигура плоская, третья ось здесь не нужна.

3.    Для центров тяжести 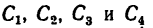каждого отрезка соответственно найдем, исходя из размеров фигуры, их координаты.

а    Обозначив 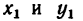координаты 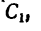найдем, что

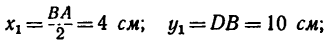
координаты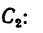

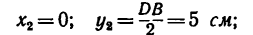
координаты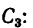

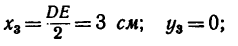
координаты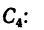

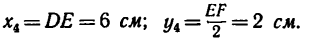
Для удобства, а также ввиду того, что координаты центров тяжести можно определить непосредственно по рисунку, данные для подстановки в формулы следует представлять в таком виде:

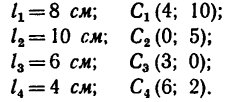
4. Подставим значения 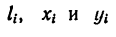в формулы (2) и сделаем вычисления:

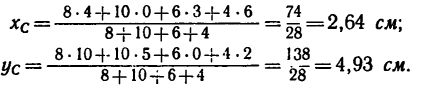
5. Отложив вдоль осей х и у найденные координаты, отметим на рис. 178 положение центра тяжести С данной фигуры.

Задача 123-23. Определить положение центра тяжести плоской фигуры ОАВ, изогнутой из тонкой проволоки в виде квадранта (рис. 179).

Решение 1.

1.    Фигура состоит из трех частей: двух прямолинейных отрезков 1 и 2 длиной r и дуги 3, равной четверти окружности.

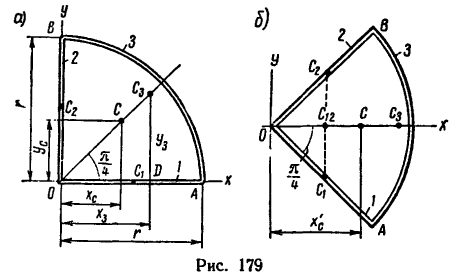
2.    Совместив оси координат с прямолинейными отрезками ОА и ОВ (рис. 179, а), приведем данные для подстановки в формулы:

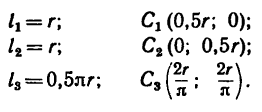
Координаты 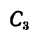находим из прямоугольного треугольника

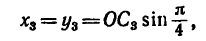
но по формуле (5)
поэтому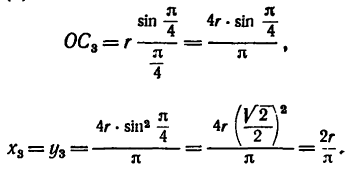
3.    Подставим значение 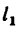и координат 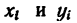в формулы (2) и сделаем вычисления:

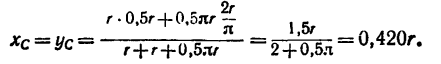
Решение 2.

1.    Так как фигура имеет одну ось симметрии, проходящую по биссектрисе прямого угла, одну из осей координат целесообразно совместить с осью симметрии (рис. 179, б)

В этом случае общий центр тяжести отрезков ОА и ОВ (точка 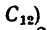находится на оси симметрии (оси х).

2.    Определим исходные данные для подстановки в формулы (2):

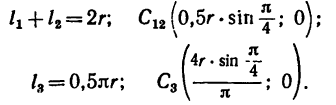
3. Найденные значения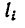и координат 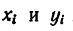подставим в формулы (2):

.
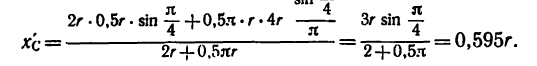Сравнивая из первого решения, видим, что (см. 2

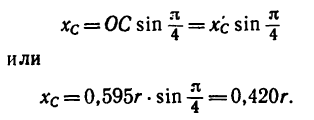
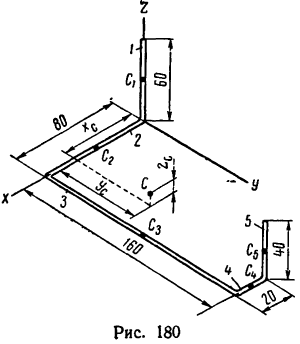
Задача 124-23. Определить положение центра тяжести пространственно изогнутой проволочной фигуры (рис. 180); размеры — в мм.

Решение.

1.    Расположив проволочную фигуру в осях координат как показано на рис. 180, разделим ее на пять прямолинейных участков 1, 2, 3, 4 и 5 и отметим точками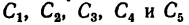центры тяжести каждого участка.

2.    Найдем исходные данные для подстановки в формулы — длины участков и координаты

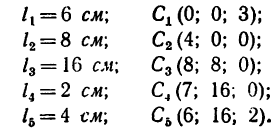
3.    Найденные исходные данные подставим в формулы (2) и вычислим координаты центра тяжести всей фигуры:

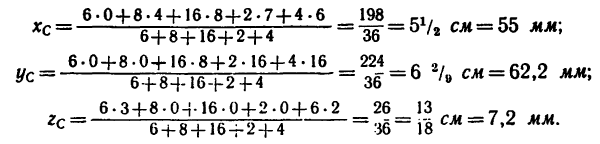
4.    Таким образом, центр тяжести фигуры расположен в точке С (55,0; 62,2; 7,2).

Следующую задачу рекомендуется решить самостоятельно.

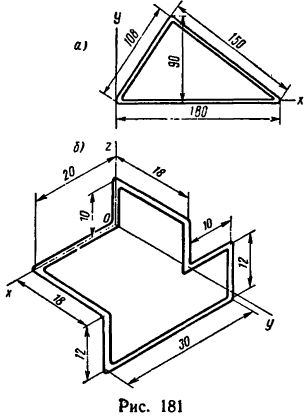
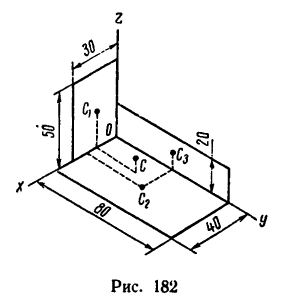
Задача 125-23. Определить положение центров тяжести плоской и пространственной проволочных фигур, показанных на рис 181
(размеры в мм).

Ответ (в осях, показанных на рис. 181);

а)    С (85,5; 26,5);

б)    С (6; 9,95; -2,19).

Определение положения центра тяжести фигур, составленных из пластинок

Задача 126-24. Определить положение центра тяжести фигуры, составленной из трех тонких плоских пластинок прямоугольной формы, пересекающихся друг с другом под прямыми углами (рис. 182); размеры —в мм.

Решение.

1.    Поместим начало координат в вершине трехгранного угла и расположим оси координат вдоль линий пересечения пластинок.

Фигура состоит из трех прямоугольников с центрами тяжести 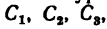расположенными на пересечении прямых, соединяющих середины противоположных сторон.

2. Исходя из размеров фигуры, определим необходимые данные для подстановки в формулы (3): 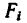— площади прямоугольников и координаты 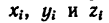их центров тяжести:

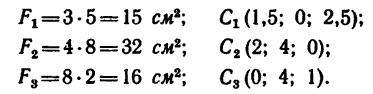
3. Подставим эти данные в формулы (4) и вычислим искомые координаты центра тяжести фигуры:

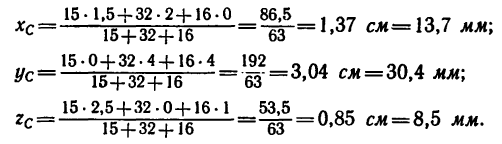
Центр тяжести фигуры расположен в точке С (13,7; 30,4; 8,5).

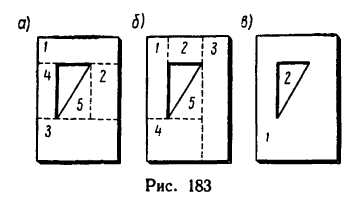
В последней задаче, а также в задачах, приведенных в предыдущем параграфе, расчленение фигур на составные части не вызывает особых затруднений. Но иногда фигура имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 — несколькими способами. Два варианта показаны на рис. 183, а к б.

Наиболее рациона.льным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.

Пластинка на рис. 183,в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.

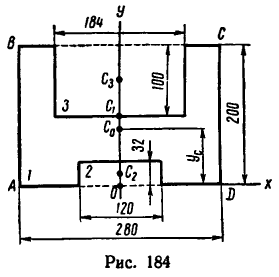
Задача 127-24. Определить положение центра тяжести тонкой однородной пластинки, имеющей ось симметрии. Формаш размеры пластинки показаны на рис. 184.

Решение.

1.    Пластинка имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось у, а ось х — с нижним краем пластинки.
2.    Дополнив пластинку до прямоугольника ABCD, разобьем ее тем самым на три части: 1, 2 и 3.

3.    Определим площади каждой части в и координаты их центров тяжести в см:

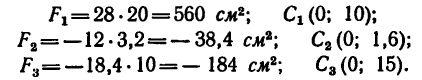
4.    Определим ординату центра тяжести пластинки, подставив найденные значения во вторую формулу системы (3):

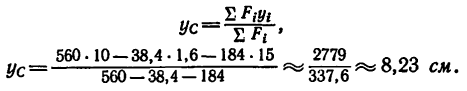
Таким образом, центр тяжести имеет ординату

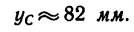
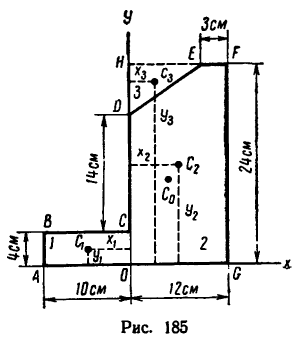
Задача 128-24. Определить положение центра тяжести плоской однородной пластинки ABCDEFG, размеры которой в см указаны на рис. 185.

Решение.

1.    Разбиваем пластинку на два прямоугольника АВСО и OHFG и на треугольник DHE, площадь которого считаем отрицательной.

2.    Начало координат помещаем в точке О, ось х совмещаем с прямой AG, ось у — с прямой CD.

3.    Определяем площади 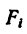составных частей и координаты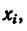 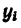их центров тяжести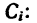

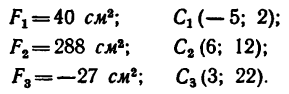
4.    Подставляем найденные значения площадей и координат в две первые формулы (3) и производим .вычисление:

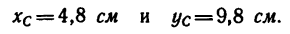
Таким образом, центр тяжести пластинки находится в точке (4,8; 9,8).

Следующую задачу рекомендуется решить самостоятельно.

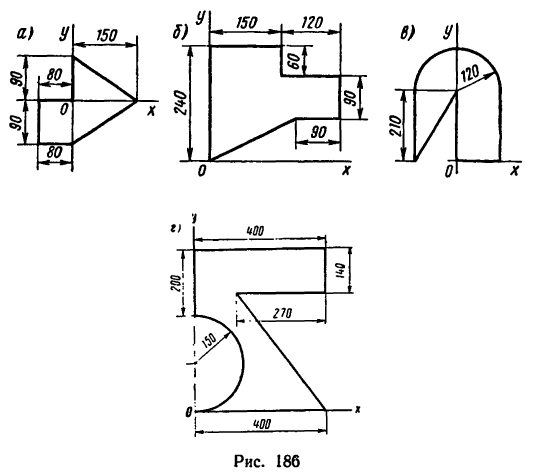
Задача 129-24. Определить положение центров тяжести тонких однородных пластинок, форма и размеры которых показаны на рис 186.

Ответ: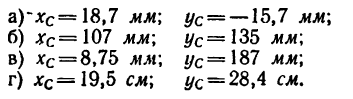

§ 28-8. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ СЕЧЕНИЙ, СОСТАВЛЕННЫХ ИЗ ПРОФИЛЕЙ СТАНДАРТНОГО ПРОКАТА
При решении задач, приведенных в этом параграфе, нужно пользоваться таблицами из ГОСТа на прокатную сталь (табл. 1—4).

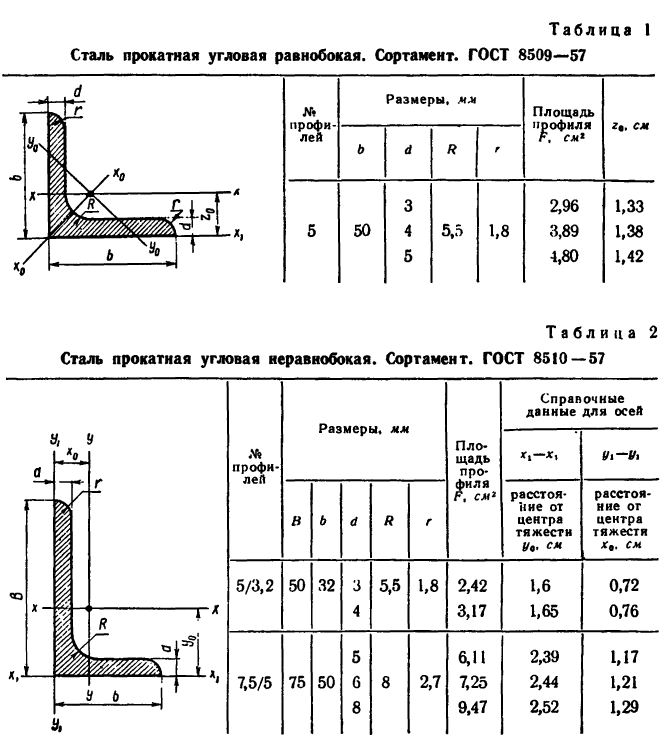
Эти таблицы для каждого профиля содержат их размеры и площадь, а для уголков и швеллера, кроме того, — координаты центров тяжести.

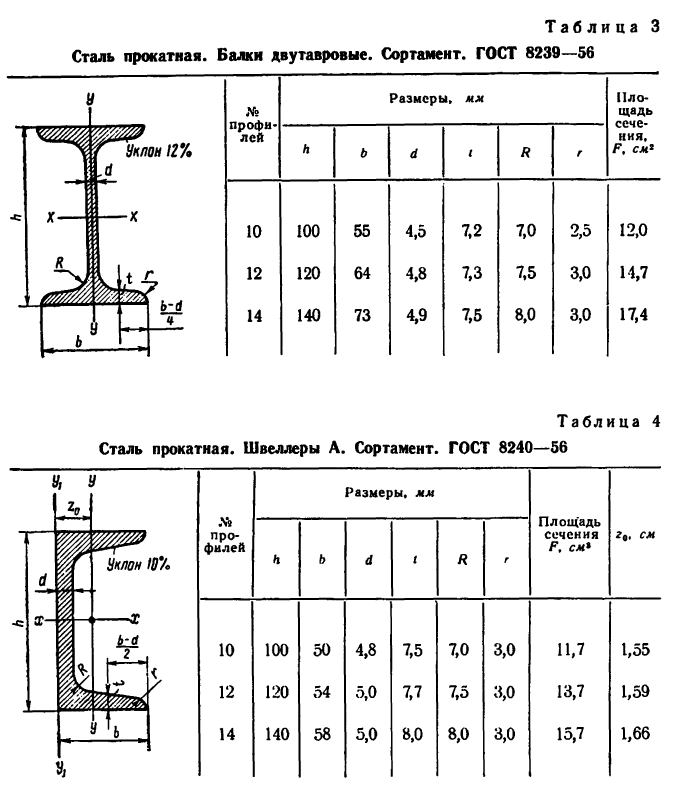
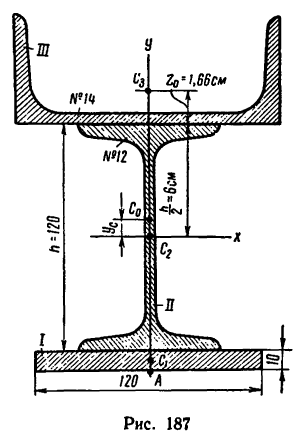
Задача 130-25. Определить положение центра тяжести симметричного сечения, составленного, как показано на рис. 187, из полосы размером 120x10 мм, двутавра № 12 (ГОСТ 8239—56) и швеллера 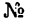14 (ГОСТ 8240—56).

Решение.

1.    Разбиваем сечение на три части: / — полоса, //—двутавр и /// — швеллер.

2.    Находим площади каждой части, выражая их в 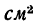. Площадь полосы определяем путем перемножения двух данных размеров, а площади двутавра и швеллера —по таблицам из ГОСТа.

Площадь сечения полосы

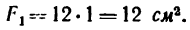
Площадь сечения двутавра № 12

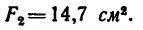
Площадь сечения швеллера № 14

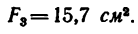
3.    Данное сечение имеет вертикальную ось симметрии. Совместим с этой осью ось у, а ось х проведем через середину двутавра через точку 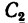— центр тяжести его сечения. Центр тяжести сечения полосы 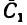расположен ниже точки 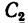, принятой в данном случае за начало координат, на расстоянии

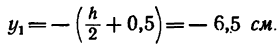
Центр тяжести швеллера 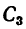находим при помощи тех же таблиц из ГОСТа Положение центра тяжести швеллеров в таблицах обозначено одной координатой 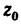; для швеллера № 14 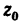= 1,66 см, следовательно,

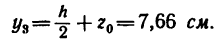
Таким образом,

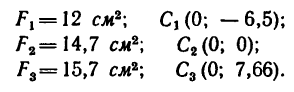
4.    Подставляем эти значения в расчетную формулу для ординаты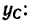

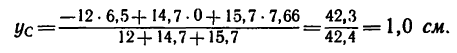
В выбранных осях положения центра тяжести сечения выражены координатами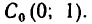

Это значит, что центр тяжести сечения находится от его нижнего края (от точки А) на расстоянии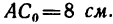

Задача 131-25. Определить положение центра тяжести сечения, составленного, как показано на рис 188, из трех профилен стандартного проката: швеллера 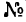10 (ГОСТ 8240—56), двутавра 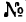12 (ГОСТ 8239—56) и неравпобокого уголка № 5/3,2 (размеры 50x32x4 мм ГОСТ 8510—57).

Решение.

1.    Разбиваем сечение на три части: / — швеллер, //-двутавр и ///—неравнобокий уголок.

2.    Начало координат поместим в вершине прямого угла неравнобокого уголка; ось х совместим с нижней полкой двутавра,

а ось у — с его вертикальной осью симметрии.

3 При помощи таблиц из ГОСТа находим:

площадь сечения швеллера  

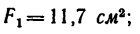
площадь сечения двутавра № 12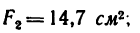

площадь сечения уголка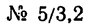  

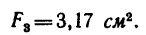
4.    В таблицах из ГОСТа положение центра тяжести швеллерапоказано одной координатой 1,55см, так' как швеллер имеет одну ось симметрии. Положение центра тяжести 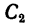двутавра в таблицах не показано, так как он имеет две оси симметрии и его центр тяжести расположен на их пересечении. Положение центра тяжести 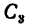неравнобокого уголка № 5/3,2 показано двумя координатами: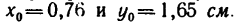

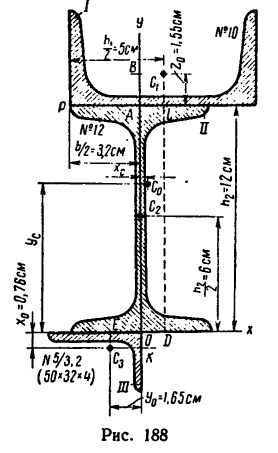
Располагаем центры тяжести 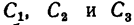на рисунке (см. рис. 188), а затем при помощи таблиц находим их координаты в выбранных осях, учитывая другие необходимые размеры профилей, которые также берутся из таблиц: координаты центра тяжести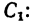

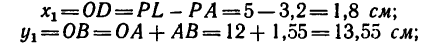
координаты центра тяжести

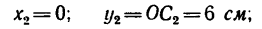
координаты центра тяжести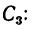

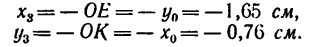
5.    Таким образом,

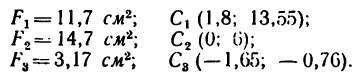
6.    Подставляем эти значения в расчетные формулы:

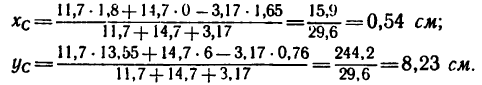
7.    Центр тяжести данного составного сечения имеет координаты (в мм) 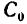(5,4; 82,3).

Следующую задачу рекомендуется решить самостоятельно.

Задача 132-25. Определить положение центра тяжести трех сечений, составленных из профилей стандартного проката, как показано на рис. 189.

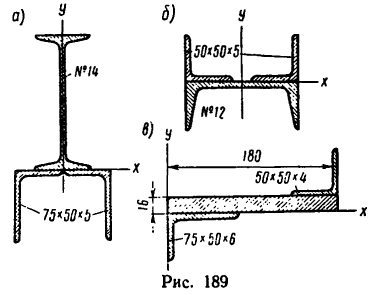
Ответ (в мм):

а)    С (0; 31,1);

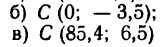
Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму

Чтобы решать задачи на определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму, необходимо иметь навыки определения координат

центра тяжести фигур, составленных из линий или площадей.

Задача 133-26. Определить положение центра тяжести тела, составленного из куба /, имеющего горизонтальную цилиндрическую канавку //, и прямоугольного параллелепипеда (рис. 190); размеры —в мм.

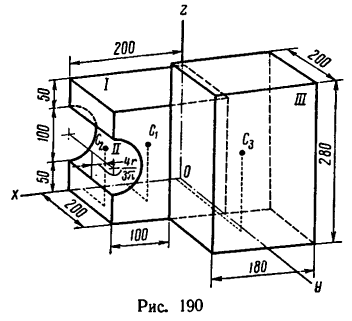
Решение.

1. Тело состоит из куба /, полуцилиндра //, объем которого считаем отрицательным, так как он вырезан из объема куба /, и прямоугольного параллелепипеда

2. Отметив на рисунке положение центра тяжести составных частей —центр тяжести куба, — центр тяжести полуцилиндра и 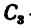—центр тяжести параллелепипеда), найдем исходные величины для подстановки их в формулы (4) - объемы 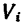- и координаты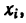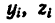их центров тяжести:

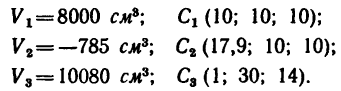
3.    После подстановки в расчетные формулы имеем:

Таким образом, центр тяжести данного тела находится в точке 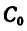(44; 216; 106).

Эту точку рекомендуется отметить на рис. 190 самостоятельно.

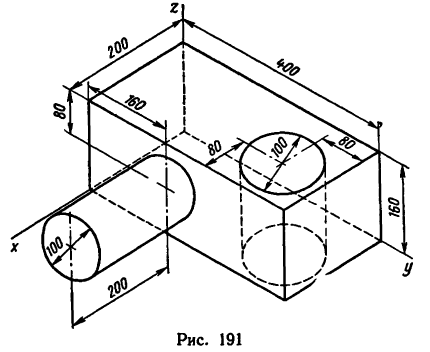
Задача 134-26 (для самостоятельного решения). Определить положение центра тяжести тела, форма и размеры (в мм) которого показаны на рис. 191.

Ответ. С (122; 184; 80).

РАЗДЕЛ ВТОРОЙ

КИНЕМАТИКА
В кинематике изучаются законы движения материальных точек и твердых тел с чисто геометрической стороны. Законом движения точки или тела можно назвать такую совокупность математических образов и уравнений, которая в любой момент времени позволяет установить, где находится точка или тело, куда и как они движутся. При этом в кинематике не рассматриваются вопросы, почему точка или тело двигается именно так, а не иначе. Эти вопросы изучаются в разделе «Динамика».

Прежде чем решить задачи но кинематике, необходимо выяснить следующее:

а)    можно ли данный в задаче движущийся предмет рассматривать как материальную точку или его нужно считать твердым телом;

б)    в какой форме закон движения задан в задаче.

Необходимость выяснения первого положения вызывается тем,

что законы движения материальных точек (предметов, формой и размерами которых можно пренебречь) и законы движения твердых тел (предметов, состоящих из множества материальных точек), как правило, отличаются друг от друга.

От способа задания закона движения зависит ход решения задачи.