
Определение площади и объема в физике с примером
Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
|
Рис. 6.1. |
Рис. 6.2. |
Рис. 6.3 |
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
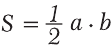 , (6.3)
, (6.3)
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R2, (6.4) .
Значение числа 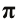 можно получить, если разделить длину круга L на его диаметр. Причем не имеет значения, каков размер круга и в каких единицах измерены длина и диаметр (нужно только, чтобы это были одни и те же единицы).
можно получить, если разделить длину круга L на его диаметр. Причем не имеет значения, каков размер круга и в каких единицах измерены длина и диаметр (нужно только, чтобы это были одни и те же единицы).
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
|
Рис. 6.4. |
Рис. 6.5. |
|
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a3 (6.6)
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR2 · h (6.7)
Объем шара (рис. 6.6)
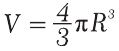 (6.8)
(6.8)
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
Куб с ребром 1 м имеет объем 1 м3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см3. Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
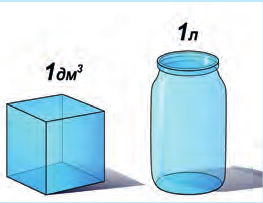
Рис. 6.7. Один литр – это 1дм3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м3 = 1 000 л | 1 м3 = 1 000 000 см3 |
| 1 л = 1 дм3 | 1 л = 1000 см3 |
| 1 дм3 = 1 000 см3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.

Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см3)
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R2.
- Объем шара равен
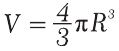 .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
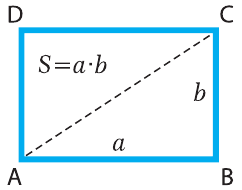
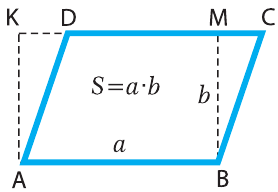
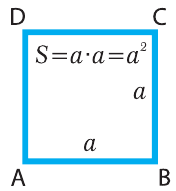
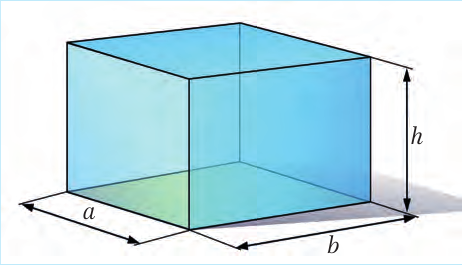
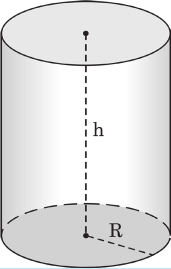
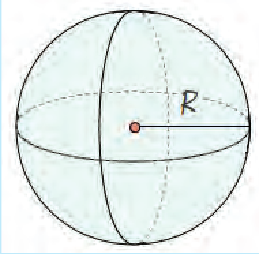 Рис. 6.6.
Рис. 6.6.