Операторный метод расчета переходных процессов

Содержание:

Операторный метод расчета переходных процессов:

Для решения линейных дифференциальных и интегродифференциальных уравнений в теории электрических цепей нашел широкое применение так называемый операторный метод, основанный на преобразованиях Лапласа.

Сущность этого метода заключается в том что функции вещественного переменного t преобразуются в функции комплексного переменного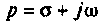

Переход от функции вещественного переменного t к функции комплексного переменного p  осуществляется с помощью прямого преобразования Лапласа

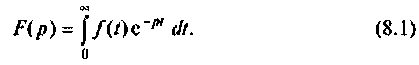
Обратный переход от функции комплексного переменного р к функциям вещественного переменного t осуществляется на основании обратного преобразования Лапласа

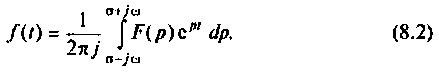
Функцию 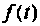 называют оригиналом, а функцию 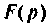— изображением оригинала по Лапласу или просто изображением.

Напомним, что для того чтобы функция 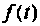имела изображение (8.1), необходимо, чтобы она:

1. удовлетворяла условиям Дирихле;
2. была равна нулю для отрицательных значений t, т. е. при
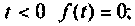
3. в интервале 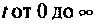не возрастала быстрее, чем некоторая показательная функция

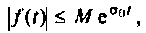
где 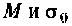- произвольные положительные числа, т.е. здесь не требуется абсолютная интегрируемость функции 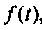как это требуется в интегралах Фурье. Поэтому преобразования Лапласа возможны для более широкого класса функций, чем преобразования Фурье.

Применение свойств преобразования Лапласа в сочетании с теоремой разложения дает возможность составить таблицы изображений и оригиналов, облетающие и ускоряющие нахождение оригиналов по изображениям [4, 26]. Применение операторного метода совместно с компьютерными математическими программными средами делает анализ и расчет электрических цепей доступным, быстрым и интересным.

Особенностью метода является необходимость выполнения трех этапов:

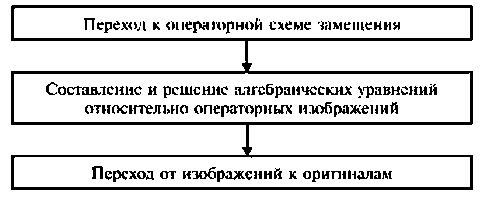
Эквивалентные операторные схемы замещения элементов

Активное сопротивление:

На рис. 8.1 изображена схема замещения в операторном виде участка цепи с активным сопротивлением. Для этого участка цепи связь между операторным напряжением и током записывается в виде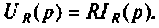 

Индуктивность:

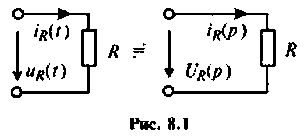
Для участка цепи с индуктивностью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.2.

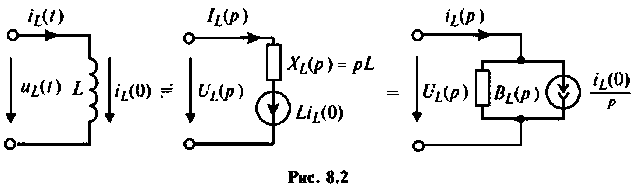
Связь между операторным напряжением и током записывается в виде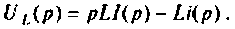

Емкость:

Для участка цепи с емкостью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.3.

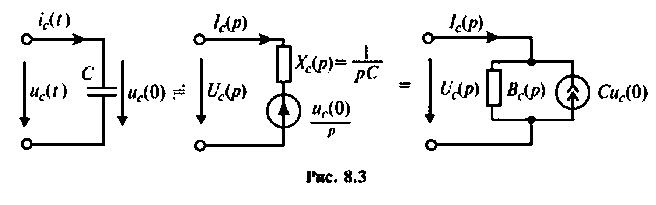
Связь между напряжением и током устанавливает соотношение

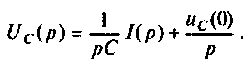
В эквивалентных операторных схемах для индуктивности и емкости с ненулевыми начальными условиями возникают дополнительные источники ЭДС 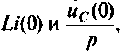которые называются внутренними. Они указывают на то, что в магнитном поле катушки и в электрическом поле конденсатора в момент коммутации была запасена энергия. Таким образом, начальные условия автоматически учитываются при переходе от интегрально-дифференциальных уравнений к алгебраическим (постоянную интегрирования вычислять не нужно).

Порядок расчета:

1. определяют независимые начальные условия;
2. составляют эквивалентную операторную схему замещения для послекоммутационной цепи;
3. составляют систему уравнений в операторной форме в соответствии с выбранным рациональным методом расчета эквивалентной схемы замещения и решают ее относительно изображений неизвестных величин;
4. для нахождения оригиналов неизвестных величин используют таблицы соответствия, формулы теоремы разложения, компьютерные программные среды и др.

Операторные функции электрических цепей

Основные операторные функции:

Операторной функцией цепи называется отношение изображения по Лапласу выходной величины к изображению входной 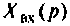при нулевых начальных условиях, т. е,

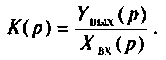
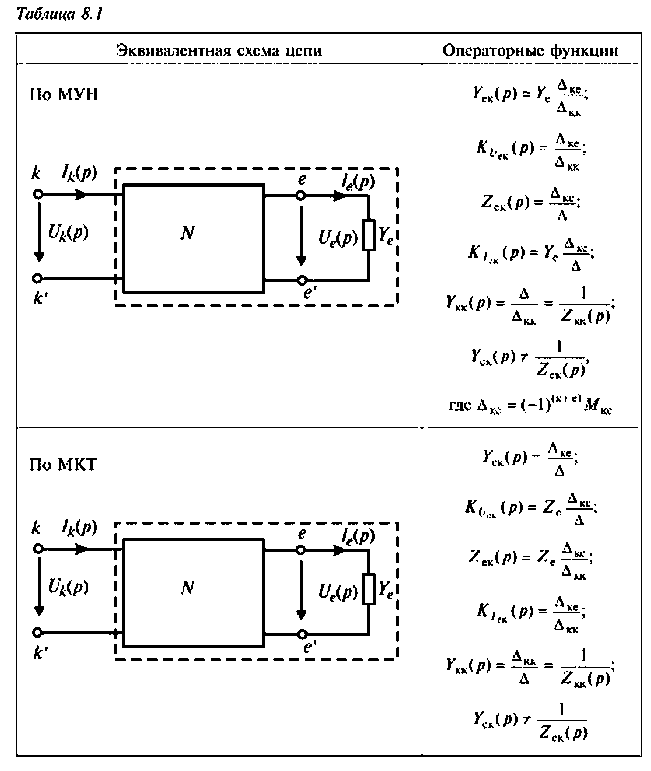
Операторная функция зависит только от параметров цепи и ее схемы. Различают входные и передаточные операторные функции. В табл. 8.1 приведены соотношения для расчета операторных функций сложных цепей.

Для расчета операторных функции можно применять все методы расчета комплексных функций

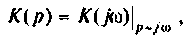
т. е. комплексная функция является частным случаем операторной при замене оператора 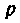на переменную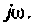

Анализ переходных процессов в цепях с помощью операторных функций

По известной операторной функции цепи и операторному изображению воздействия можно найти реакцию цепи на это воздействие

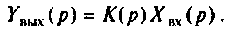
На рис. 8.4 (а—в) приведены временные диаграммы переходных процессов, а также полюсно-нулевое представление на комплексной плоскости.

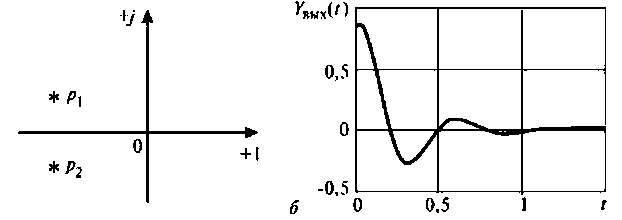
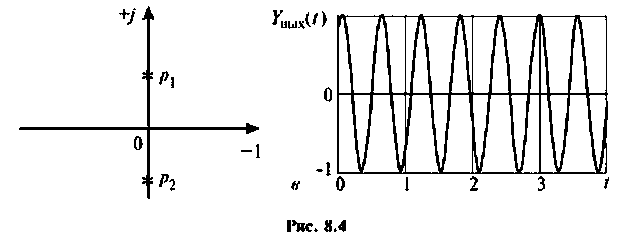
По расположению полюсов операторной функции можно судить о характере переходное процесса:

• если все полюсы расположены только на отрицательной вещественной полуоси, то переходный процесс в цепи носит апериодический характер;
• если имеются сопряженные полюсы в левой полуплоскости, то переходный процесс носит характер затухающих колебаний;
• если все полюсы расположены только на отрицательной мнимой оси, то переходный процесс в цепи носит характер незатухающих колебаний.

Примеры решения задач

Пример 8.4.1.

В интегродифференцирующем контуре постоянного тока (рис. 8.5), применяемом для коррекции ЭЦ и САУ. определить напряжение 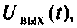построить его график, если 

Решение

Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало: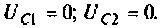

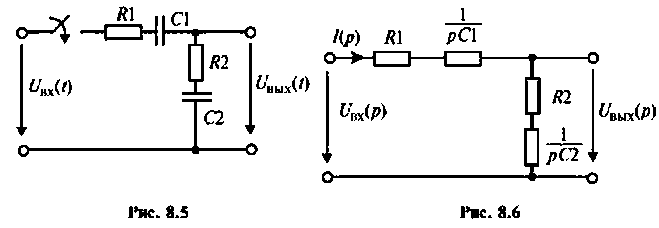
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.6).

Находят изображение напряжения 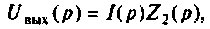где

 

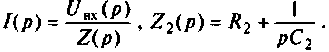
Сопротивление всей цепи определяется выражением

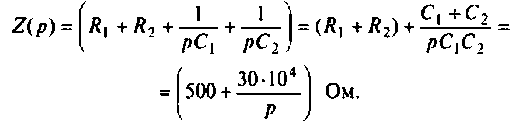
Тогда:

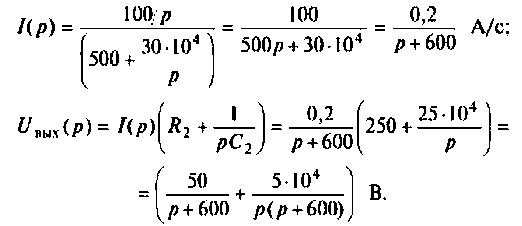
По данному изображению находят оригинал (рис. 8.7) напряжения 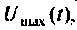 для этого пользуются таблицей преобразования Лапласа (см. табл. 8.2, п. 3.5) или преобразованиями в среде Mathcad (рис. 8.7).

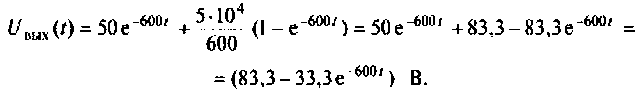
Пример 8.4.2.

К пассивному RС-фильтру нижних частот подключается нагрузка (рис. 8.8). Рассчитать и построить график, изменения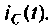

Дано: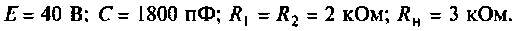

Решение

Определяют независимые начальные условия - напряжение на емкости

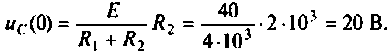
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.9).

Операторный ток 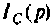 определяют методом наложения, т.е. как алгебраическую сумму двух частичных токов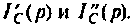

Операторные схемы, соответствующие частичным токам, изображены на рис. 8.10.

Искомый ток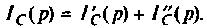

Определяют частичный ток

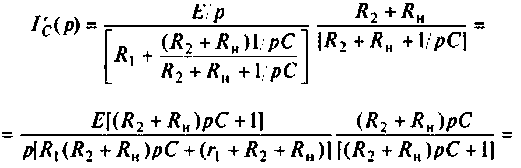
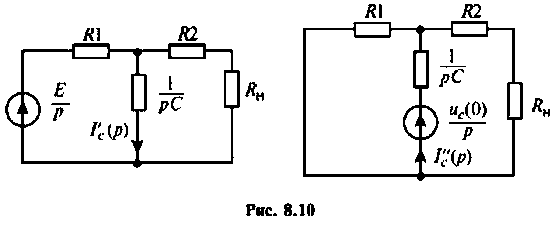
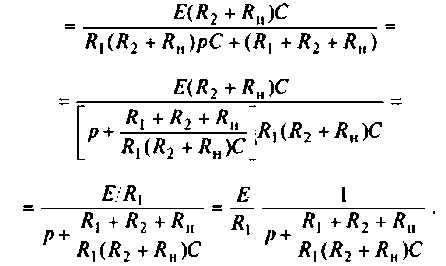
Аналогично определяют частичный ток

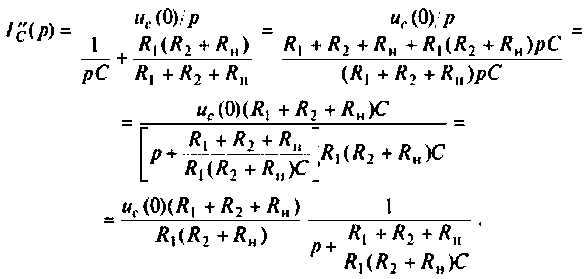
Искомый ток

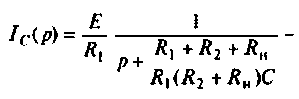
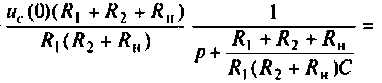
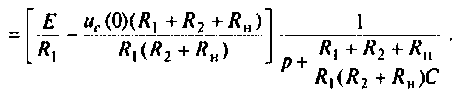
По данному изображению 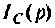находят оригинал

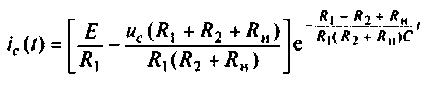
Подставляя числовые значения величин, получают

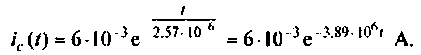
Строят график тока  в компьютерной программной среде (рис. 8.11).

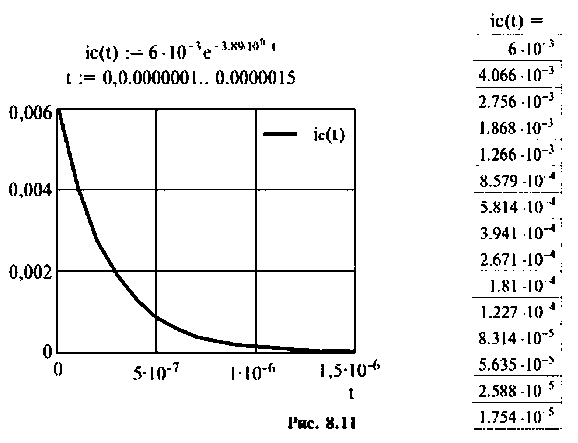
Выводы. До коммутации напряжение на емкости определялось падением напряжения на сопротивлении 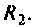Ток, проходящий через емкость, был равен нулю. После коммутации произошло перераспределение напряжения между сопротивлениями 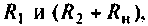вследствие чего напряжение на емкости повысилось и образовался зарядный ток. Когда конденсатор зарядится до напряжения, определяемого на сопротивлениях 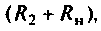прохождение тока через емкость прекратится.

Пример 8.4.3.

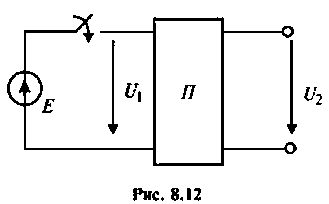
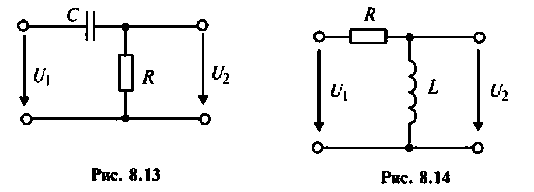
Рассчитать коэффициент передачи по напряжению пассивной цепи (рис. 8.12) и составить ее схему так, чтобы при подключении на вход источника постоянной ЭДС 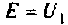получить на выходе напряжение вида: 

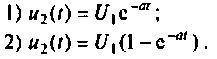
Решение

Применяя преобразования Лапласа, находят изображения

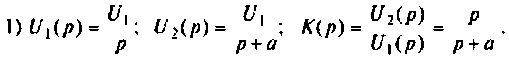
Из прямых преобразований Лапласа и Фурье следует, что

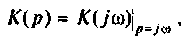
тогда

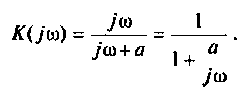
Если принять 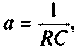тогда 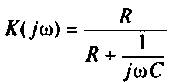  и схему можно составить из 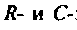элементов (рис. 8.13).

Если принять 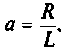тогда 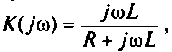 и схему можно составить из 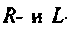элементов (рис. 8.14).

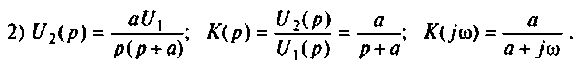
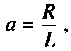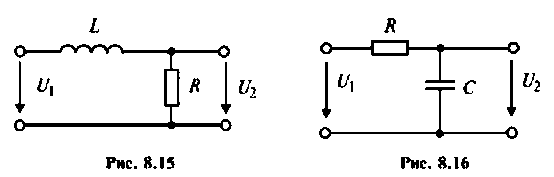
Если принять тогда 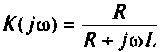 и схема будет иметь вид, изображенный на рис. 8.15.

Если принять 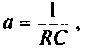тогда 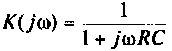и схема будет иметь вид, изображенный на рис. 8.16.

Пример 8.4.4.

Параллельный колебательный контур (рис. 8.17) включается на постоянное напряжение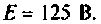

Определить напряжение на конденсаторе и построить его опюру, если:

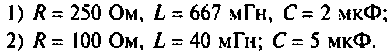
Решение

Определяют независимые начальные условия: напряжение на конденсаторе ток в катушке индуктивности

Строят эквивалентную операторную схему замещения после коммутации (рис. 8.18).

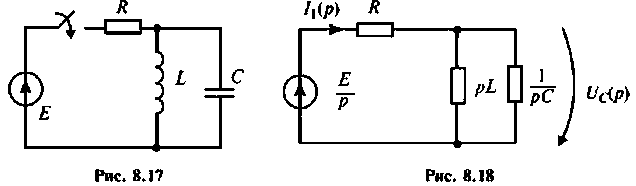
Находят изображение напряжения на конденсаторе

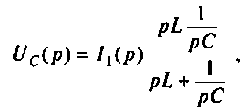
где             

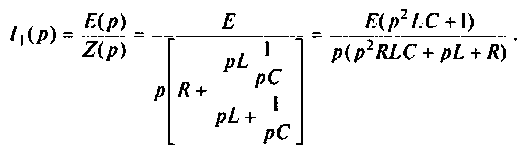
Тогда 

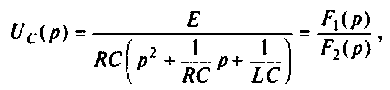
где   

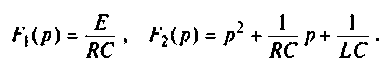
По данному изображению находят оригинал по теореме разложения дробно-рациональной функции

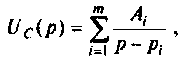
где 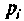— некратные полюсы изображения напряжения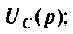 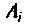— начальные значения компонент изображения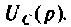

При простых (некратных) полюсах 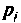начальные значения компонент определяются но выражению [4]

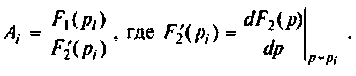
а) Для первого варианта значений:

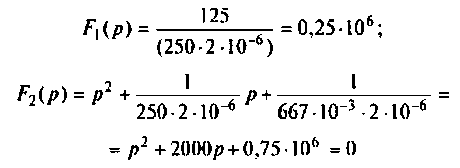
Полюсы изображения 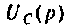после вычислений имеют значения:

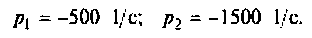
Вычисляют производную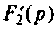 и ее значение при .

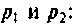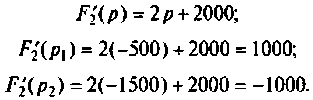
Вычисляют начальные значения компонент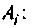

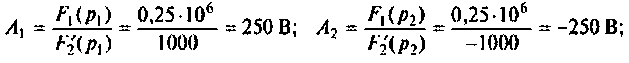
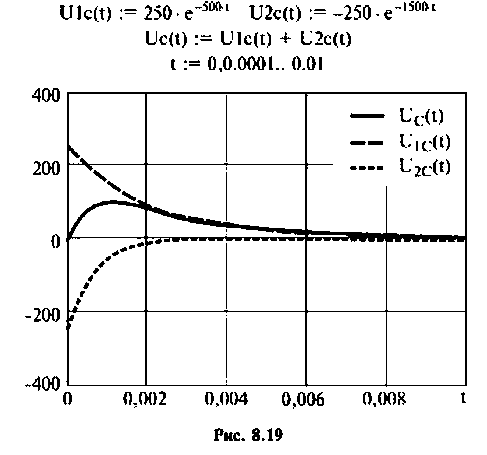
Следовательно,

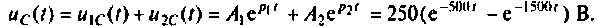
Графики напряжения на конденсаторе и его компонентов получены в среде Mathcad и показаны на рис. 8.19.

Тоn же результат может быть получен по таблице преобразования Лапласа (табл. 8.2, п. 8), если знаменатель изображения напряжения на конденсаторе представить в виде

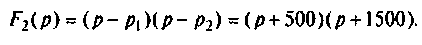
б) Для второго варианта числовых значений:

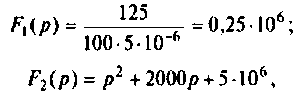
а полюсы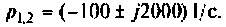

Находят производную от 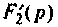и вычисляют ее значения при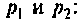

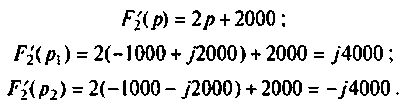
Следовательно,

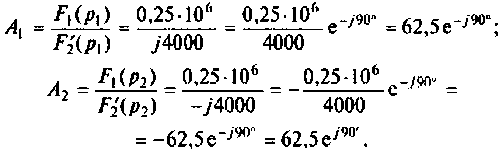
По теореме разложения определяют

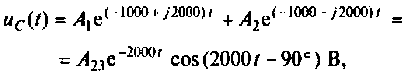
где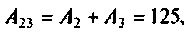      

или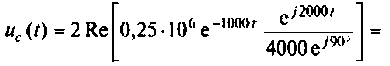    

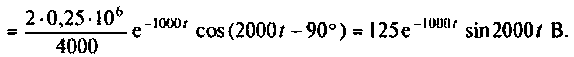
График изменения напряжения 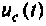 представлен на рис. 8.20. 

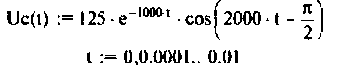
Тот же результат может быть получен по таблице преобразования Лапласа (см. табл. 8.2, п. 13), если знаменатель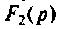 представить в виде

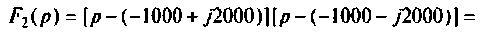
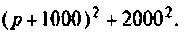
Примечание. Результаты этого примера сравните с результатами примера 6.3. Оцените достоинства и недостатки классического и операторного методов расчета переходных процессов.

Пример 8.4.5. 

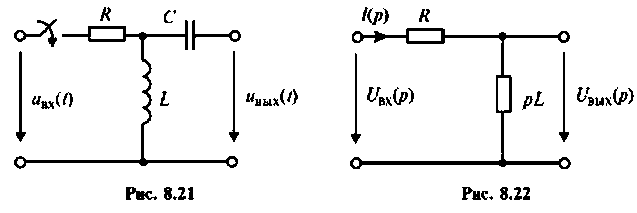
После замыкания ключа четырехполюсник (рис. 8.21) используется для работы на частоте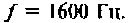

Определить:

а) коэффициент передачи по напряжению 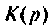в режиме холостого хода и при активной нагрузке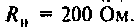

б) характер переходного процесса по кривой переходного процесса.
 

Дано: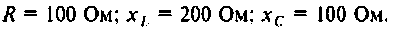

Решение

В режиме холостого хода

Изображают эквивалентную операторную схему замещения. На рис. 8.22 приведена операторная схема замещения при нулевых начальных условиях.

Находят изображение напряжения на выходе

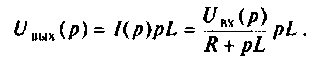
Откуда  

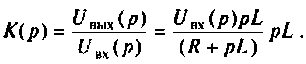
Определяют полюсы операторной функции из уравнения 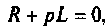тогда

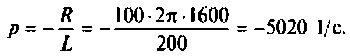
Переходной процесс в цепи имеет апериодический характер, что видно из расположения полюсов на комплексной плоскости (рис, 8.23).

В режиме нагрузки

Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.24).

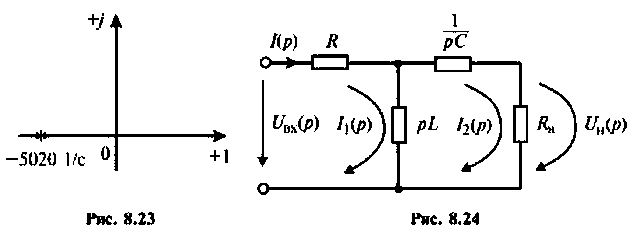
Определяют операторную функцию 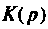по методу контурных токов, используя соотношение (см. табл. 8.1):

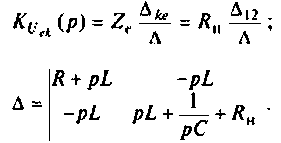
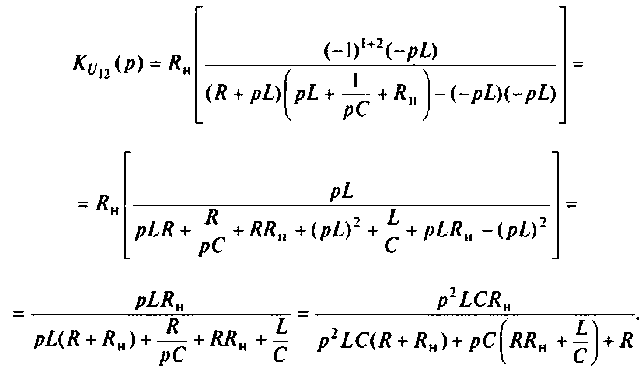
Определяют полюсы операторной функции из уравнения

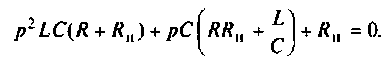
Для этога вначале вычисляют L и С.

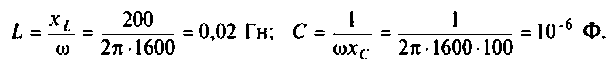
Находят корни уравнения:

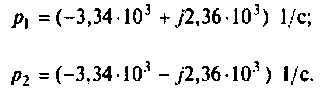
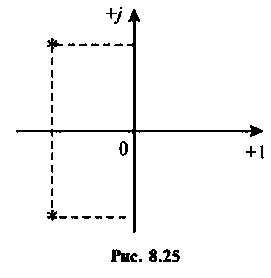
Переходный процесс в цепи имеет характер затухающих колебаний, что видно из расположения полюсов на комплексной плоскости (рис. 8.25).