
Однофазные электрические цепи переменного тока
Содержание:
Однофазные электрические цепи переменного тока:
Для получения, передачи и распределения электрической энергии применяются в основном устройства переменного тока: генераторы, трансформаторы, линии электропередачи и распределительные цепи переменного тока.
Постоянный ток, необходимый в некоторых областях народного хозяйства (транспорт, связь, электрохимия и др.), получают выпрямлением переменного тока.
Переменным электрическим током называют ток, периодически изменяющийся по величине и направлению.
Основное достоинство переменного тока заключается в возможности трансформировать напряжение. Кроме того, электрические машины переменного тока надежней в работе, проще по устройству и эксплуатации.
Говоря о переменном токе, обычно имеют в виду синусоидальный переменный ток, т. е. ток, изменяющийся по синусоидальному закону. При синусоидальном токе ЭДС электромагнитной индукции, самоиндукции и взаимоиндукции изменяются по синусоидальному закону.
Синусоидальный переменный ток проходит в замкнутой линейной электрической цепи под действием синусоидальной ЭДС.
Рассмотрим получение синусоидальной ЭДС. Если в однородном магнитном поле с индукцией В равномерно со скоростью V вращается рамка (рис. 10.1), то в каждой активной стороне этой рамки длиной 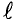
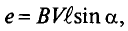
где а - угол, под которым активный проводник рамки пересекает магнитное поле (угол между 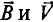 ), или угол поворота рамки относительно нейтральной плоскости
), или угол поворота рамки относительно нейтральной плоскости 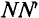 как углы со взаимно перпендикулярными сторонами.
как углы со взаимно перпендикулярными сторонами.
Плоскость  называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).
называется нейтральной, т. к. ЭДС в рамке, расположенной в этой плоскости, равна нулю (а = 0, следовательно, sin а = 0).
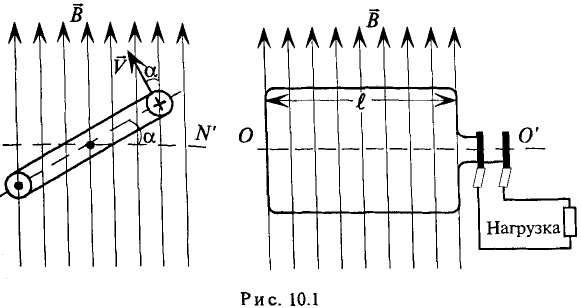
как 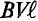 — величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.
— величина постоянная по условию, то е пропорциональна sin а, т. е. ЭДС в этой рамке, при вращении ее вокруг оси изменяется по синусоидальному закону. Если к этой рамке включить нагрузку (потребитель), то в замкнутой цепи (рис. 10.1) идет ток, который, как и ЭДС, изменяется по синусоидальному ну. Поэтому такой ток и называется синусоидальным.
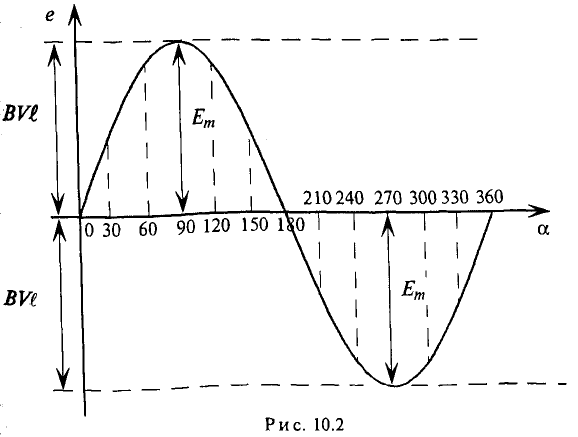
Синусоидальная ЭДС 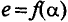 изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN". Как видно, синусоидальная ЭДС изменяется по величине и направлению.
изображена на графике рис. 10.2. график принято называть «волновая диаграмма». (Если изменяющаяся величина изображена в зависимости от времени то ее называют «временная диаграмма».) На этой диаграмме синусоида ограничивает величины ЭДС (ординаты) при раз-личных углах поворота рамки относительно нейтральной плоскости NN". Как видно, синусоидальная ЭДС изменяется по величине и направлению.
Величины, характеризующие синусоидальную ЭДС
Амплитуда — это максимальное значение периодически изменяющейся величины.
Обозначаются амплитуды прописными буквами с индексом m, т. е. 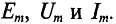
Нетрудно видеть (рис. 10.2), что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол а = 90° или на угол а = 270°, так как 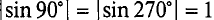 . Следовательно,
. Следовательно, 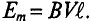
Тогда 
Период - это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения повторяются в той же последовательности.
Обозначается период буквой Т и измеряется в секундах, с (сек) т.е. 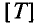 = с.
= с.
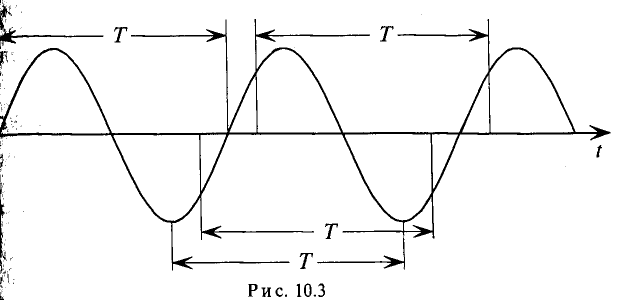
Значение ЭДС через каждый период определяется следующим равенством (рис. 10.3):
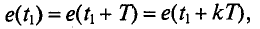
где к - целое число.
На рис. 10.3 изображена временная диаграмма синусоидальной ЭДС при вращении рамки в магнитном поле.
Частота - число периодов в единицу времени, т. е. величина, обратная периоду.
Обозначается частота буквой 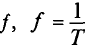 , и измеряется в герцах (Гц):
, и измеряется в герцах (Гц):
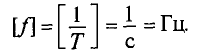
Стандартной частотой в электрических сетях России является частота 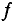 = 50 Гц. Для установок электронагрева пользуются частотами
= 50 Гц. Для установок электронагрева пользуются частотами 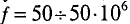 Гц (
Гц (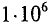 Гц = 1 МГц - мегагерц).
Гц = 1 МГц - мегагерц).
При частоте 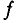 =50 Гц, т.е. 50 периодов в секунду, период
=50 Гц, т.е. 50 периодов в секунду, период
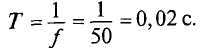
Угловая частота (угловая скорость) характеризуется углом поворотом рамки в единицу времени.
Обозначается угловая частота буквой 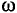 (омега):
(омега):

Измеряется угловая частота в единицах радиан в секунду, так как угол измеряется в радианах (рад).
Так, время одного периода Т рамка повернется на угол 360° = рад. Следовательно, угловую частоту можно выразить следующим образом:

Мгновенное значение — это значение переменной величины в й конкретный момент времени.
Мгновенные значения обозначаются строчными буквами..
Из выражения (10.2) следует, что угол поворота рамки 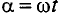 , мгновенные значения синусоидальных величин можно записать так:
, мгновенные значения синусоидальных величин можно записать так:
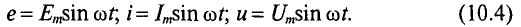
Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянными для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.
Фаза и сдвиг фаз
Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а), т.е. амплитуды ЭДС 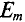 и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде
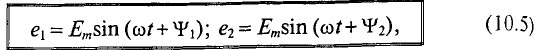
где 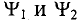 — углы, определяющие значения синусоидальных величин
— углы, определяющие значения синусоидальных величин 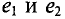 в начальный момент времени (t = 0), т.е.
в начальный момент времени (t = 0), т.е.
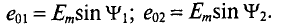
Поэтому эти углы 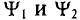 называют начальными фазами синусоид.
называют начальными фазами синусоид.
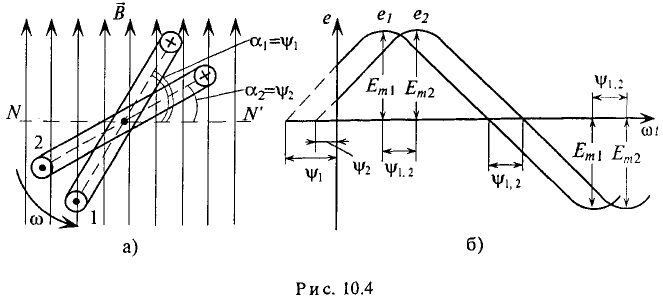
Начальные фазы 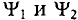 этих ЭДС различны.
этих ЭДС различны.
Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой 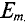 , угловой частотой со и начальной фазой
, угловой частотой со и начальной фазой  . Для каждой синусоиды эти величины
. Для каждой синусоиды эти величины 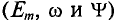 являются постоянными. В выражениях (10.4) начальные фазы
являются постоянными. В выражениях (10.4) начальные фазы  синусоид равны нулю (
синусоид равны нулю ( = 0).
= 0).
Величина 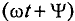 называется фазой синусоиды.
называется фазой синусоиды.
Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:

При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше, чем во второй, т. е. 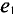 опережает по фазе
опережает по фазе 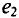 или
или 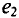 отстает по фазе
отстает по фазе 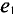 (рис. 10.46). Угол сдвига фаз
(рис. 10.46). Угол сдвига фаз  показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
показывает, на какой угол синусоидальная величина опережает или отстает от другой, достигает своих амплитудных и нулевых значений раньше позже).
Две синусоидальные величины одинаковой частоты, достигаю-одновременно своих амплитудных (одного знака) и нулевых сечений, считаются совпадающими по фазе (рис. 10.5а).
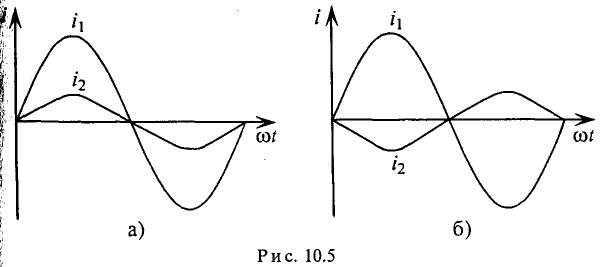
Если две синусоиды одинаковой частоты достигают одновременно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.
Время, на которое одна синусоидальная величина опережает и отстает от другой, характеризует время сдвига фаз 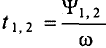 , которое можно выразить через период Т и частоту
, которое можно выразить через период Т и частоту 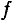 синусоиды следующим образом:
синусоиды следующим образом:
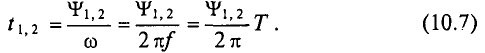
Среднее и действующее значения переменного тока
Кроме амплитудных и мгновенных значений переменный ток, напряжение, ЭДС характеризуются еще средними и действующими (эффективными) значениями.
Среднее значение переменного тока
Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение провод-проходит то же количество электричества Q, что и при переменном токе.
Таким образом, среднее значение переменного тока эквивалентно постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный промежуток времени.
Средние значения переменных величин обозначаются прописными буквами с индексом «с», т. е. 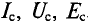 .
.
Если ток изменяется по синусоидальному закону, то за половину периода через поперечное сечение проводника проходит определенное количество электричества Q в определенном направлении, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. 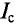 = 0.
= 0.
Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.
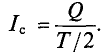
Из выражения (2.1) значение переменного тока 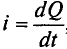 , откуда
, откуда 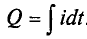 . Следовательно, среднее значение синусоидального тока
. Следовательно, среднее значение синусоидального тока 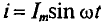 с начальной фазой
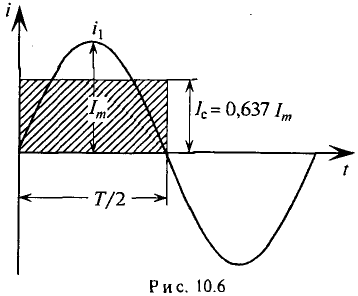
с начальной фазой 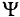 = 0 за полупериод определяется (рис. 10.6) выражением
= 0 за полупериод определяется (рис. 10.6) выражением
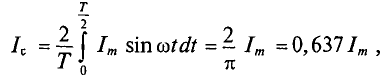
где 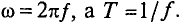
Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площади, ограниченной кривой тока и осью абсцисс за половину периода (рис. 10.6).
Под средним значением переменной величины понимают постоянную составляющую этой величины.
Средние значения синусоидального напряжения и ЭДС за полупериод можно определить по аналогии с током.
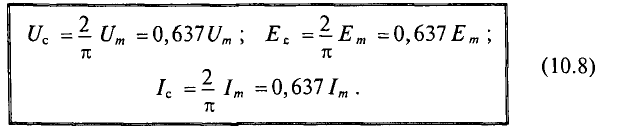
Действующее значение переменного тока
Действующее (или эффективное) значение переменного тока — значение переменного тока, эквивалентное постоянному току тепловому действию.
Действующее значения переменных величин обозначается прочими буквами без индексов: I, U, Е.
Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду первого тока Т, выделит в том же сопротивлении R такое же количество тепла, что и переменный ток i:
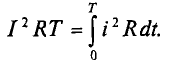
Откуда действующее значение переменного тока
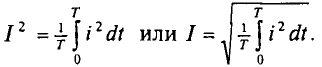
Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 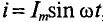 , то действующее сечение такого синусоидального тока будет равно
, то действующее сечение такого синусоидального тока будет равно
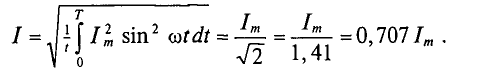
Действующее значение синусоидального тока в 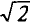 =1 ,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
=1 ,41 раза меньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.
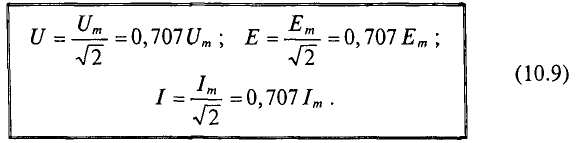
Номинальные значения тока и напряжения в электрических цепей и устройствах выражаются их действующими значениями.
Так, например, стандартные напряжения электрических сетей U= 127 В или U = 220 В выражают действующие значения этих напряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.
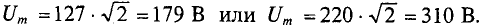
При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.
На шкалах измерительных приборов переменного тока указывается действующие значение переменного тока или напряжения.
Именно действующие значения тока, напряжения и ЭДС указываются в технической документации, если нет специальных оговорок.
Коэффициенты формы и амплитуды
Отклонения кривых тока, напряжения и ЭДС от синусоиды характеризуются коэффициентами формы 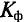 и амплитуды
и амплитуды 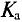 .
.
Коэффициент формы 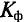 определяется отношением действующего значения переменной величины к ее среднему значению:
определяется отношением действующего значения переменной величины к ее среднему значению:

Коэффициент формы необходимо учитывать при проектировании и изучении выпрямительных устройств и электрических машин.
Для синусоидальных величин коэффициент формы будет равен
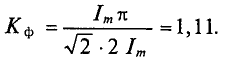
Коэффициент амплитуды 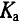 определяется отношением амплитудного значения переменной величины к ее действующему значению:
определяется отношением амплитудного значения переменной величины к ее действующему значению:

Для синусоидальных величин коэффициент амплитуды равен
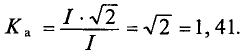
Чем больше коэффициент формы и коэффициент амплитуды отличается от значений 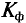 = 1,11 и
= 1,11 и 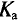 = 1,41, тем больше рассматриваемая кривая отличается от синусоиды. Так, например, если
= 1,41, тем больше рассматриваемая кривая отличается от синусоиды. Так, например, если 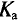 = 1,41, то исследуемая кривая имеет более острую форму, чем синусоида, а если
= 1,41, то исследуемая кривая имеет более острую форму, чем синусоида, а если 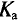 < 1,41, то более тупую.
< 1,41, то более тупую.
График прямоугольной формы имеет коэффициент амплитуды 1.
Векторные диаграммы
Для наглядности синусоидальные величины изображают векторами, вращающимися против часовой стрелки со скоростью, равной угловой частоте со этих синусоид. Так как эти векторы изображают синусоиды в начальный момент времени (t = 0), то они подвижны. Длина вектора в выбранном масштабе определяется амплитудой синусоиды, а угол поворота вектора против часовой стрелки относительно положительного направления оси абсцисс начальной фазе синусоиды. Таким образом, вектор учитывают все значения, характеризующие синусоидальную величину - амплитуду, угловую частоту и начальную фазу, пример, три синусоидальные ЭДС одинаковой частоты
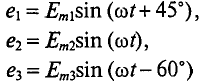
можно изобразить векторами (рис. 10.7).
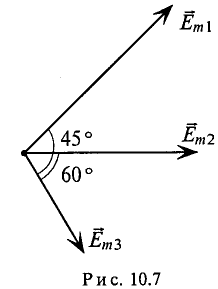
Совокупность нескольких векторов, изображающих синусоидальные величины одинаковой частоты в начальный момент времени, называется векторной диаграммой.
На векторной диаграмме (рис. 10.7) на-ю видны величины синусоид (ампли-), их начальные фазы и углы сдвига между ними. Очевидно, наибольшую амплитуду имеет ЭДС 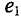 , а наименьшую ЭДС
, а наименьшую ЭДС 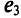 ЭДС
ЭДС 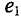 опережает по фазе
опережает по фазе 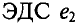 угол 45°, а ЭДС
угол 45°, а ЭДС 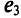 отстает от ЭДС
отстает от ЭДС 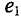 по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:
по фазе на угол 105° и т. д. Начало отсчета времени можно выбирать произвольно, т. е. один из векторов векторной диаграммы направляется произвольно, а остальные векторы (соответствующих длин) изображаются отношению к нему под углами, равными углам сдвига фаз между ними (рис. 10.8). При указанном ЭДС могут быть записаны так:

При этом амплитуды ЭДС и углы сдвига фаз остаются неизменными (как и угловая частота), а меняются только начальные фазы синусоид, изображенных на векторной диаграмме (рис. 10.7). В расчетах, если специально не оговорено, начальные фазы не играют роли.
Сложение синусоидальных величин
Сложение и вычитание синусоидальных величин одинаковой частоты можно осуществлять аналитически и графически. В результате такого сложения (вычисления) получается синусоида с той же частотой, с определенной амплитудой и определенной начальной фазой.
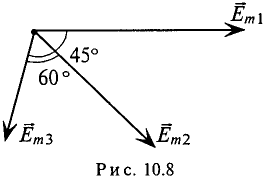
Аналитическое сложение предусматривает сложение мгновенных значений синусоидальных величин, выраженных аналитически, т. е.
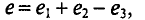
где 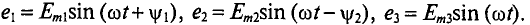
Тогда
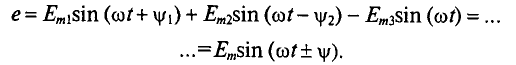
Математический анализ позволяет определить суммарную ЭДС е и ее аналитическое выражение.
Графическое сложение можно осуществлять по: 1) волновым (временном) диаграммам и 2) векторным диаграммам.
1. Графическое сложение по временным диаграммам (рис. 10.9) осуществляется следующим образом: ординаты суммарной синусоиды определяются сложением ординат слагаемых синусоид в различные моменты времени.
Как видно, в рассматриваемом примере амплитуда суммарной синусоиды не равна алгебраической сумме амплитуд слагаемых синусоид. Начальная фаза суммарной синусоиды также не является результатом арифметических действий, т.е. по временным диаграммам производятся только графические действия.
2. Графическое сложение по векторным диаграммам осуществляется в следующей последовательности. Прежде всего необходимо построить векторную диаграмму слагаемых синусоидальных величин (рис. 10.10а).
Определение вектора, изображающего суммарную синусоиду, осуществляется сложением векторов слагаемых синусоид по правилу многоугольника, т. е. из какой-либо точки О изображают вектор, соответствующий первой слагаемой синусоиде 10.106), из конца этого вектора изображают вектор, соответствующий второй слагаемой синусоиде, и т.д.
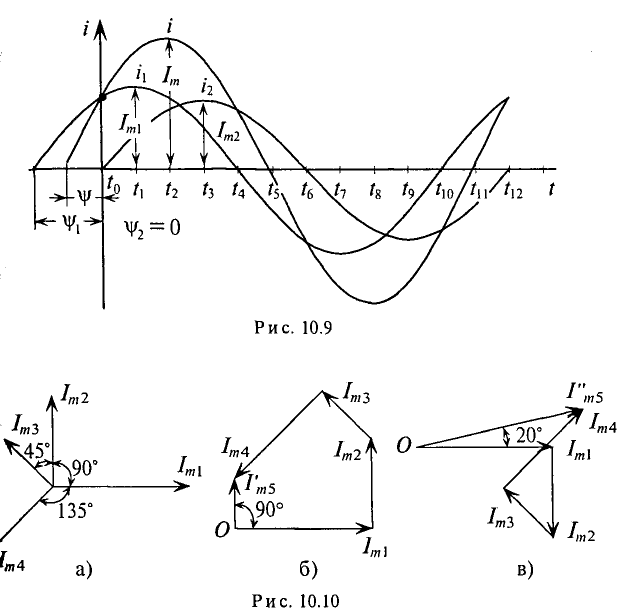
Вектор, соответствующий суммарной синусоиде, проводят из и О к концу последней слагаемой синусоиды.
Тот вектор (рис. 10.106), в масштабе изображения слагаемых синусоид, соответствует амплитуде суммарной синусоиды 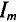 . Угол поворота этого вектора против часовой стрелки относительно положительного направления оси абсцисс соответствует положительному значению начальной фазы
. Угол поворота этого вектора против часовой стрелки относительно положительного направления оси абсцисс соответствует положительному значению начальной фазы 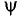 суммарной синусоиды, угловая частота суммарной синусоиды равна частоте слагаемых синусоид.
суммарной синусоиды, угловая частота суммарной синусоиды равна частоте слагаемых синусоид.
Вычитание синусоидальной величины равносильно умножение этой величины на отрицательную единицу (—1), что соответствует повороту вектора этой величины на 180" (рис. 10.10 в).
Сложение и вычитание синусоидальных величин по векторный диаграммам рассматривается в примере 10.1.
Пример 10.1
Заданы мгновенные значения четырех токов:

Определить:
1)суммарный ток при условии 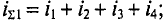
2)суммарный ток при условии 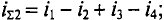
3)частоту f всех синусоид.
Решение
Для построения векторной диаграммы слагаемых токов задаются определенным масштабом токов 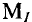 (например,
(например, 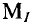 = 1 А/см). В этом масштабе построена векторная диаграмма токов на рис. 10.10а.
= 1 А/см). В этом масштабе построена векторная диаграмма токов на рис. 10.10а.
1. Для определения суммарного тока производится сложение векторов по правилу многоугольника (рис. 10.106). Суммарный ток в результате сложения будет равен 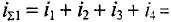
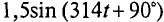 . Амплитуда суммарного тока
. Амплитуда суммарного тока 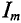 = 1,5 А определена из многоугольника в выбранном масштабе, а начальная фаза его измерена транспортиром
= 1,5 А определена из многоугольника в выбранном масштабе, а начальная фаза его измерена транспортиром 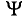 = 90°.
= 90°.
2. Построение многоугольника для заданного условия показано на рис. 10.10в. Из многоугольника определяется результирующий ток
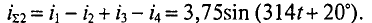
3. Частота слагаемых и результирующих токов будет равна
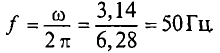
В заключение можно сделать вывод, что самым удобным и, следовательно, распространенным методом сложения синусоидальных величин является метод графического сложения по векторным диаграммам. Этот метод и будет использован при расчете электрических цепей однофазного и трехфазного тока, изменяющегося по синусоидальному закону.
Так как действующие значения синусоидальных величин пропорциональны их амплитудным значениям (см. (10.9)), то вектор, отражающий в определенном масштабе амплитудное значение, в этом масштабе представляет действующее значение той же вены. Исходя из этого, в дальнейшем на векторных диаграммах будут изображаться векторы, в определенном масштабе представляющие не амплитудное, а действующее значение синусоидальной вены, которое чаще всего используется при расчетах цепей переменного тока.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |