
Одночлены - определение и вычисление с примерами решения
Содержание:
Одночлены
Степень с натуральным показателем
Напомним, что произведение двух или трех одинаковых множителей, каждый из которых равен 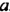
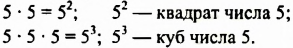
Квадрат числа 5 называют еще второй степенью этого числа, а куб — третьей степенью.
Соответственно произведение 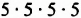 обозначают
обозначают 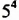 и называют четвертой степенью числа
и называют четвертой степенью числа 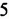 . В выражении
. В выражении 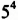 число
число 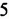 называют основанием степени, число
называют основанием степени, число 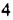 — показателем степени, а все выражение
— показателем степени, а все выражение 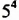 называют степенью.
называют степенью.
Определение:
Степенью числа  с натуральным показателем
с натуральным показателем 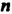 , большим 1, называют произведение
, большим 1, называют произведение 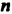 множителей, каждый из которых равен
множителей, каждый из которых равен  . Степенью числа
. Степенью числа  с показателем 1 называют само число
с показателем 1 называют само число  .
.
Степень с основанием  и показателем
и показателем 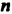 записывают так:
записывают так: 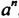 , читают: «
, читают: « в степени
в степени 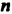 », или «
», или «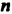 -ая степень числа
-ая степень числа  ».
».
Итак, по определению
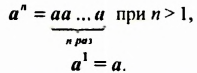
Выясним знак степени с натуральным показателем.
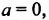 тогда
тогда 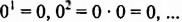 — любая натуральная степень числа 0 равна 0.
— любая натуральная степень числа 0 равна 0.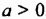 , тогда
, тогда 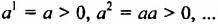 — любая натуральная степень положительного числа есть положительное число.
— любая натуральная степень положительного числа есть положительное число.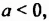 тогда
тогда  . Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.
. Степень отрицательного числа с четным показателем является положительным числом, поскольку произведение четного количества отрицательных чисел положительно. Степень отрицательного числа с нечетным показателем является отрицательным числом, поскольку произведение нечетного количества отрицательных чисел отрицательно.
Возводить числа в степень с натуральным показателем можно с помощью микрокалькулятора. Вычислить, например, значение 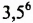 можно по схеме:
можно по схеме: 
или по более удобной схеме:

Получим значение степени: 1838,265625.
Возведение в степень — действие третьей ступени. Напомним, что если выражение без скобок содержит действия разных ступеней, то сначала выполняют действия высшей ступени, а потом — низшей. Так, чтобы найти значение выражения 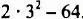 , действия нужно выполнять в такой последовательности: 1) возведение в степень; 2) умножение; 3) вычитание.
, действия нужно выполнять в такой последовательности: 1) возведение в степень; 2) умножение; 3) вычитание.
Примеры выполнения заданий:
Пример №110
Вычислить 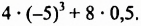
Решение:
Выполняя вычисления, можно:
а) записывать каждое действие в отдельности:

б) записывать вычисления в строчку:
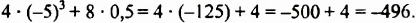
Ответ. 496.
Свойства степени с натуральным показателем
Умножение степеней с одинаковыми основаниями
Рассмотрим произведения двух степеней с основанием  . Учитывая, что
. Учитывая, что 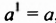 , получим:
, получим:
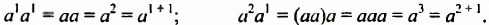
Следовательно, 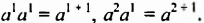 В этих примерах произведение степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, который равен сумме показателей степеней. Таким свойством обладает произведение любых степеней с одинаковыми основаниями.
В этих примерах произведение степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, который равен сумме показателей степеней. Таким свойством обладает произведение любых степеней с одинаковыми основаниями.
Свойство 1. Для любого числа  и произвольных натуральных чисел
и произвольных натуральных чисел  и
и 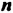 справедливо равенство
справедливо равенство 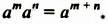 Доказательство. Учитывая определение степени, получаем:
Доказательство. Учитывая определение степени, получаем:
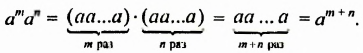
Из свойства 1, которое еще называют основным свойством степени, следует правило умножения степеней:
Чтобы умножить степени с одинаковыми основаниями, нужно основание оставить прежним, а показатели степеней сложить.
Например:
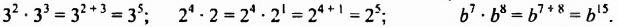
Правило умножения степеней распространяется на произведение трех и более степеней. Например:

Деление степеней с одинаковыми основаниями
Рассмотрим равенство 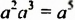 , где
, где 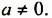 Из этого равенства по определению частного имеем:
Из этого равенства по определению частного имеем: 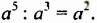 Равенство
Равенство 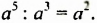 можно переписать так:
можно переписать так:
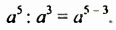
В этом примере частное степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, который равен разности показателя степени делимого и показателя степени делителя. Сформулируем и докажем соответствующее свойство в общем случае.
Свойство 2. Для любого числа 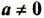 и произвольных натуральных чисел
и произвольных натуральных чисел 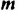 и
и 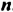 , где
, где 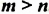 , справедливо равенство:
, справедливо равенство:
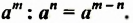
Доказательство. Поскольку 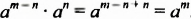 то есть
то есть 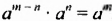 , то по определению частного имеем:
, то по определению частного имеем: 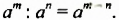
Из доказанного свойства следует правило деления степеней:
Чтобы разделить степени с одинаковыми основаниями, нужно основание оставить прежним, а из показателя степени делимого вычесть показатель степени делителя.
Например: 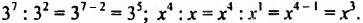
Возведение степени в степень
! Возведем степень 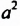 в куб:
в куб:
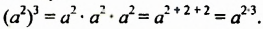
Итак, 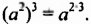 Из примера видно: чтобы возвести квадрат числа в куб, нужно оставить то же основание и взять показатель, равный произведению показателей. Сформулируем и докажем соответствующее свойство в общем случае.
Из примера видно: чтобы возвести квадрат числа в куб, нужно оставить то же основание и взять показатель, равный произведению показателей. Сформулируем и докажем соответствующее свойство в общем случае.
Свойство 3. Для любого числа  и произвольных натуральных чисел
и произвольных натуральных чисел 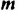 и
и 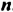 справедливо равенство
справедливо равенство
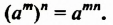
Доказательство.
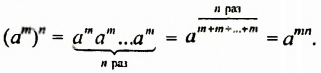
Из свойства 3 следует правило возведения степени в степень:
Чтобы возвести степень в степень, нужно основание оставить прежним, а показатели степеней перемножить.
Например: 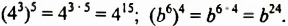
Возведение произведения в степень
Возведем произведение 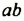 в куб:
в куб:
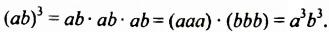
Итак, 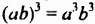 . Из примера видно: чтобы возвести в куб произведение, нужно возвести в куб каждый множитель и результаты перемножить. Сформулируем и докажем соответствующее свойство в общем случае.
. Из примера видно: чтобы возвести в куб произведение, нужно возвести в куб каждый множитель и результаты перемножить. Сформулируем и докажем соответствующее свойство в общем случае.
Свойство 4. Для любых чисел  и
и 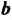 и произвольного натурального числа
и произвольного натурального числа 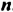 справедливо равенство
справедливо равенство
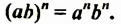
Доказательство.
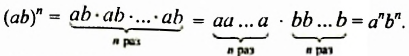
Имеем такое правило:
Чтобы возвести в степень произведение, нужно возвести в эту степень каждый множитель и результаты перемножить.
Это правило распространяется на произведение трех и более множителей. Например:
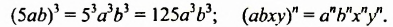
Примечание. Доказанные тождества 
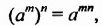
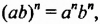 выражающие свойства степени, позволяют не только заменять выражения, которые стоят в их левых частях, выражениями, которые стоят в правых частях, но и наоборот:
выражающие свойства степени, позволяют не только заменять выражения, которые стоят в их левых частях, выражениями, которые стоят в правых частях, но и наоборот:
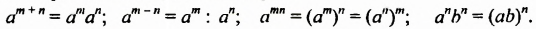
Примеры выполнения заданий:
Пример №111
Упростить выражение 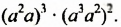
Решение:
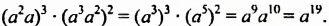
Пример №112
Вычислить:

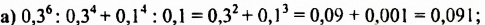
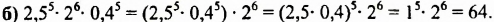
Пример №113
Представить 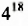 в виде степени с основанием
в виде степени с основанием 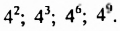
Решение:
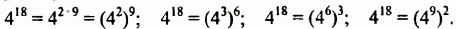
Пример №114
Представить в виде степени произведение 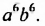
Решение:
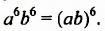
Одночлен и его стандартный вид
Рассмотрим две группы выражений:
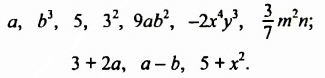
Какова особенность выражений первой группы? Чем они отличаются от выражений второй группы?
Выражения первой группы — это переменные, числа, их степени и произведения. Такие выражения называют одночленами. В общем виде одночлен — это произведение чисел, переменных и их степеней.
Выражения второй группы не являются одночленами, поскольку содержат действия сложения или вычитания.
Рассмотрим одночлен 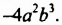 Он содержит только один числовой множитель, который стоит на первом месте, и степени разных переменных. Такой одночлен называют одночленом стандартного вида.
Он содержит только один числовой множитель, который стоит на первом месте, и степени разных переменных. Такой одночлен называют одночленом стандартного вида.
Одночленом стандартного вида называют такой одночлен, который содержит только один числовой множитель, находящийся на первом месте, ч степени разных переменных.
Числовой множитель одночлена стандартного вида называют коэффициентом одночлена. Коэффициент одночлена 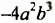 равен
равен 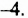 Считают, что коэффициенты одночленов
Считают, что коэффициенты одночленов 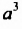 и
и 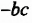 соответственно равны 1 и -1, поскольку
соответственно равны 1 и -1, поскольку  и
и 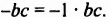
Одночлен 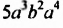 не является одночленом стандартного вида, поскольку содержит две степени с основанием
не является одночленом стандартного вида, поскольку содержит две степени с основанием 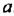 . Умножив
. Умножив 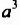 на
на 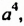 этот одночлен можно записать в виде одночлена стандартного вида:
этот одночлен можно записать в виде одночлена стандартного вида: 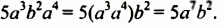
Умножение одночленов
Перемножим одночлены 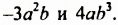 Используя свойства умножения и свойства степени, получим:
Используя свойства умножения и свойства степени, получим:
-3а2Ь • 4aby = (-3 • 4) • (а2а) • (ЬЬг) = -12аъЬ\
Итак, произведением одночленов -Ъа2Ь и 4аЬъ является одночлен -12а3Ь*. Вообще, произведением любых одночленов является одночлен.
Возведение одночлена в степень
Возведем одночлен -5а2Ь в куб. Используя свойства степени, получим:
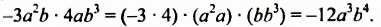
Итак, кубом одночлена 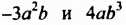 является одночлен
является одночлен 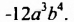 Вообще, натуральной степенью любого одночлена является одночлен.
Вообще, натуральной степенью любого одночлена является одночлен.
Степень одночлена
В одночлене 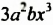 сумма показателей степеней вcex переменных равна
сумма показателей степеней вcex переменных равна 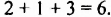 Эту сумму называют степенью одночленa, говорят, что
Эту сумму называют степенью одночленa, говорят, что 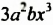 — одночлен шестой степени.
— одночлен шестой степени.
Степенью одночлена называют сумму показателей степеней всех переменных, которые в него входят. Если одночленом является число, отличное от нуля, то считают, что степень такого одночлена равна нулю.
Например: 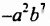 — одночлен девятой степени;
— одночлен девятой степени; 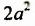 — одночлен второй степени;
— одночлен второй степени; 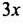 — одночлен первой степени;
— одночлен первой степени; 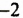 — одночлен нулевой степени.
— одночлен нулевой степени.
Примеры выполнения заданий:
Пример №115
Записать выражение в виде одночлена стандартного вида:
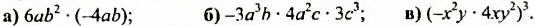
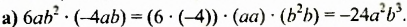
Сокращенная запись: 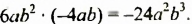
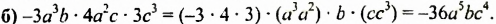
Сокращенная запись: 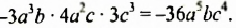
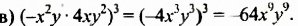
Пример №116
Представить одночлен 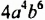 в виде:
в виде:
а) произведения двух одночленов стандартного вида;
б) произведения двух одночленов, одним из которых является 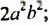
в) квадрата одночлена стандартного вида.
Решение:
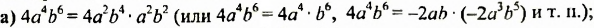
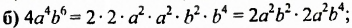
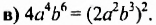
Интересно знать
Понятие степени с натуральным показателем возникло в античные времена в связи с вычислением площадей и объемов. Толкование степеней 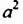 и
и 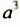 было геометрическим:
было геометрическим: 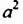 — это площадь квадрата со стороной
— это площадь квадрата со стороной 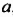 ,
, 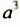 — объем куба с ребром
— объем куба с ребром 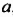 . Отсюда и названия «квадрат» и «куб» для степеней
. Отсюда и названия «квадрат» и «куб» для степеней 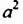 и
и 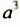 , которые используют и сейчас. К сожалению, такая геометрическая привязка в те времена стала тормозом для развития алгебры. Степени
, которые используют и сейчас. К сожалению, такая геометрическая привязка в те времена стала тормозом для развития алгебры. Степени 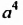 («квадрато-квадрат»),
(«квадрато-квадрат»), 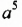 («кубо-квадрат») и т. д. остались как бы «вне закона», поскольку не имели соответствующей геометрической основы.
(«кубо-квадрат») и т. д. остались как бы «вне закона», поскольку не имели соответствующей геометрической основы.
Только в XVII в. французский математик Рене Декарт (1596-1650) дал геометрическое толкование произведения любого числа множителей после чего и произведение 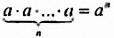 приняло «официальный статус».
приняло «официальный статус».
Декарт же ввел и современное обозначение степени с натуральным показателем в виде 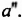
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |