
Общее уравнение плоскости с примерами решения
Содержание:
Общее уравнение плоскости
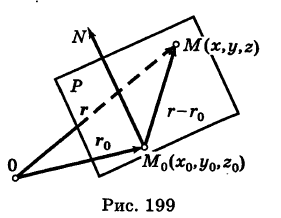
Плоскость Р в пространстве можно задать некоторой ее точкой 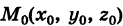

Это и есть уравнение плоскости в векторном виде. В координатной форме уравнение (1) имеет вид
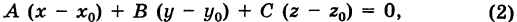
или
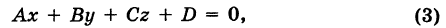
где
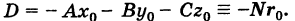
Уравнение (3) называется общим уравнением плоскости и представляет собой уравнение первой степени относительно текущих координат х, у, z. Таким образом, плоскость есть поверхность первого порядка.
Обратно, пусть дано невырожденное уравнение (3) 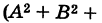
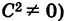 . Выберем некоторую точку
. Выберем некоторую точку 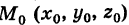 , лежащую на поверхности (3) (например, если
, лежащую на поверхности (3) (например, если 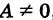 , то в качестве такой точки можно взять
, то в качестве такой точки можно взять 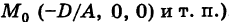 . Имеем
. Имеем
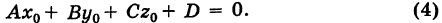
Вычитая из уравнения (3) уравнение (4), будем иметь
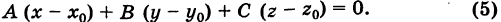
Отсюда, введя векторы 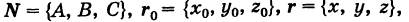 получим
получим
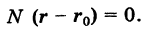
Следовательно, поверхность, заданная уравнением (3), является плоскостью, проходящей через точку 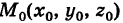 перпендикулярно вектору N.
перпендикулярно вектору N.
Пример:
Найти угол, образованный плоскостью 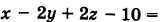
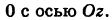
Решение:
Под углом между прямой и плоскостью понимается угол между данной прямой и ее проекцией на эту плоскость; этот угол является дополнительным к углу 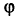 , образованному прямой и перпендикуляром (нормалью) к плоскости.
, образованному прямой и перпендикуляром (нормалью) к плоскости.
Нормальный вектор нашей плоскости есть 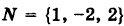 . Отсюда
. Отсюда
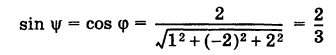
и, следовательно, 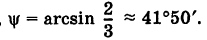
Если в уравнении (1) в качестве направляющего вектора плоскости взять единичный вектор 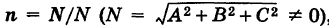 , то получим так называемое нормированное уравнение плоскости
, то получим так называемое нормированное уравнение плоскости

или, в координатах,
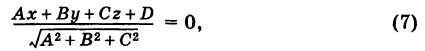
где 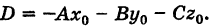 Уравнение (7) удобно при нахождении расстояния точки от плоскости.
Уравнение (7) удобно при нахождении расстояния точки от плоскости.
Пример:
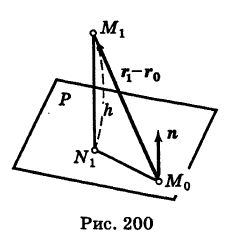
Найти расстояние h от точки 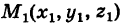 до плоскости Р, заданной уравнением (6) (рис. 200).
до плоскости Р, заданной уравнением (6) (рис. 200).
Пусть 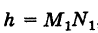 где
где 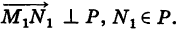
Рассмотрим вектор 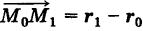 , где
, где 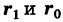 — радиус-векторы точек , учитывая, что
— радиус-векторы точек , учитывая, что 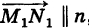 , находим
, находим 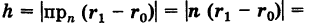
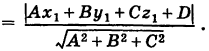 Следовательно, получаем правило: чтобы найти расстояние от точки до плоскости, нужно в левую часть нормированного уравнения плоскости подставить координаты данной точки и взять абсолютную величину полученного результата.
Следовательно, получаем правило: чтобы найти расстояние от точки до плоскости, нужно в левую часть нормированного уравнения плоскости подставить координаты данной точки и взять абсолютную величину полученного результата.
В частности, полагая 
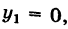
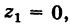 получаем растояние от начала координат до плоскости:
получаем растояние от начала координат до плоскости:
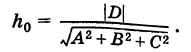
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |