
Образование проекций в начертательной геометрии с примерами
Содержание:
В любой отрасли промышленности для изготовления отдельных деталей и составных частей машин создаются их геометрические (идеальные) образы, которые называются чертежами. Под чертежами понимают плоское изображение геометрических очертаний и размеров технического объекта, выполненное таким образом, чтобы можно было представить его объёмные формы.
У будущего инженера важно выработать и развить пространственное (объемное) «видение» плоского изображения. Это позволяет не только правильно читать и понимать плоские чертежи, но и, используя целый ряд правил и положений, грамотно их выполнять. Все эти вопросы рассматриваются студентами вузов при изучении первой общепрофессиональной дисциплины «Инженерная графика».
Важнейшей составной частью является курс начертательной геометрии, который в силу его большой значимости во многих образовательных стандартах выделен в отдельную дисциплину.
Изучение этого курса преследует следующие основные цели:
- ознакомить студента с различными методами проецирования объекта на плоскость для получения изображения;
- развить пространственное представление об объёмных формах
- технических объектов и составляющих их частей по изображению этих объектов на плоскостях;
- сформировать и закрепить в сознании человека систему правил для решения графическими методами технических задач проектирования;
В отличие от других изданий лекционный курс минимизирован до объема, предусмотренного рабочей программой по начертательной геометрии для студентов специальности 190701 и 181400, достаточного для самостоятельной работы студента, выполнения им графических заданий.
Рекомендуется для студентов родственных специальностей, изучающих курс начертательной геометрии и обучаемых в ВУЗах министерства транспорта Российской Федерации.
При изучении курса приняты следующие обозначения:
1.1. Плоскости проекций: горизонтальная — 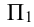
- фронтальная —
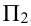
- профильная —
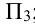 ;
; - дополнительная —
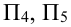
- аксонометрическая —
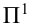 .
.
1.2. Точки: А, В, С, Д... или 1, 2, 3, 4 ...
1.3. Проекции точек на плоскость: 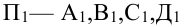 ... или
... или 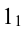 ,
, 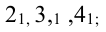
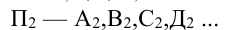 или
или  или
или 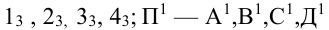 или
или 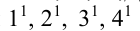
1.4. Точки на развертках: 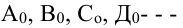 или
или 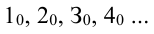
1.5. Последовательный ряд точек: 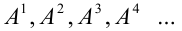
1.6. Линии: a, b, c, d...
1.7. Проекции линий на плоскость: 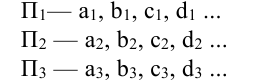
1.8. Линии уровня:
- горизонтальная (горизонталь) — h;
- фронтальная (фронталь) — f;
- профильная — р.
1.9. Координатные оси проекций:
- абсцисс — x;
- ординат — y;
- аппликат — z.
1.10. Новые оси абсцисс, полученные при замене плоскостей проекций: 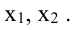
1.11. Аксонометрические оси координат: 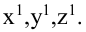
1.12. Последовательный ряд линий: 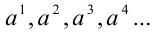
1.13. Прямая, проходящая через точки А и В: АВ.
1.14. Плоскости (поверхности): 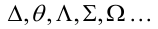
1.15. Знак принадлежности 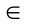
1.16. Знак совпадения ≡
Образование проекций и методы проецирования
Плоский чертеж какого-либо технического объекта может состоять из нескольких изображений, по которым и создается представление об объемных формах объекта. Такие плоские изображения называются проекциями рассматриваемого объекта.
Под проекцией любой точки понимают ее как бы «теневое» отображение на какой-либо плоскости. Так, если поместить материальную точку 1 между источниками света (световых лучей) 2 и какой-либо плоскостью 3 (рис. 2.1), на этой плоскости увидим тень 4 этой точки, которую и принято называть проекцией точки. 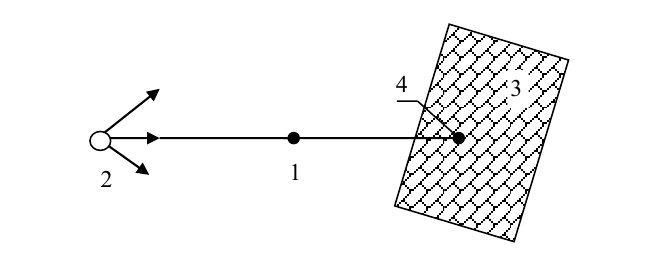
Рис. 2.1
Взаимное положение источника света и плоскости может быть произвольным. В зависимости от величины угла между лучом 2-1-4 и плоскостью 3 возможны два принципиально отличных варианта проекций точки:
- значение угла не равно 90°, тогда проекция точки называется косоугольной;
- значение угла равно 90° (прямой угол), тогда проекция называется прямоугольной, или ортогональной (от греч. orthogonios - прямоугольный).
Курс начертательной геометрии рассматривает два основных метода проецирования: центральный и параллельный.
Метод центрального проецирования
Суть метода заключается в следующем: пусть даны в пространстве треугольник ABC, плоскость 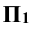 и произвольная точка S (рис. 2.2). Проведя из точки S прямые линии (лучи) через вершины треугольника ABC до пересечения их с плоскостью
и произвольная точка S (рис. 2.2). Проведя из точки S прямые линии (лучи) через вершины треугольника ABC до пересечения их с плоскостью 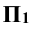 , получают точки
, получают точки 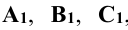 . Эти точки называют центральными проекциями точек А, В, С. Соединив прямыми линиями точки
. Эти точки называют центральными проекциями точек А, В, С. Соединив прямыми линиями точки 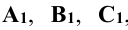 , получают центральную проекцию треугольника ABC. Точка S называется центром проецирования, плоскость
, получают центральную проекцию треугольника ABC. Точка S называется центром проецирования, плоскость  - плоскостью проекций, лучи
- плоскостью проекций, лучи 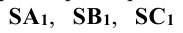 - проецирующими лучами.
- проецирующими лучами. 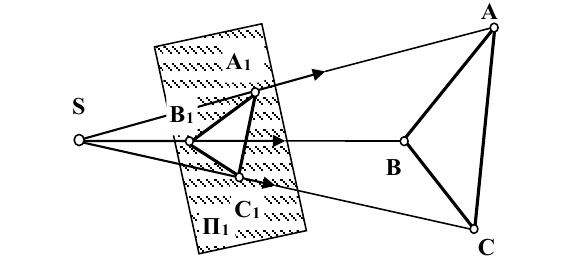 Рис. 2.2
Рис. 2.2
Метод параллельного проецирования
Если точку S удалить от плоскости  в бесконечность, проецирующие лучи будут практически параллельны между собой. Тогда они пересекутся с плоскостью проекций
в бесконечность, проецирующие лучи будут практически параллельны между собой. Тогда они пересекутся с плоскостью проекций  в точках
в точках 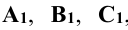 , которые называются параллельными проекциями точек А, В, С. Соединив, как и в предшествующем случае, точки
, которые называются параллельными проекциями точек А, В, С. Соединив, как и в предшествующем случае, точки 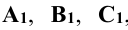 между собой, получают треугольник
между собой, получают треугольник 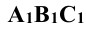 , который будет уже параллельной проекцией треугольника ABC. На рис. 2.3 стрелкой s обозначено направление проецирования. Если направление s перпендикулярно к плоскости
, который будет уже параллельной проекцией треугольника ABC. На рис. 2.3 стрелкой s обозначено направление проецирования. Если направление s перпендикулярно к плоскости  , то проекция треугольника
, то проекция треугольника 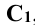 называется параллельной прямоугольной или ортогональной.
называется параллельной прямоугольной или ортогональной.
Если направление луча s не перпендикулярно к плоскости  , то проекция треугольника называется косоугольной.
, то проекция треугольника называется косоугольной. 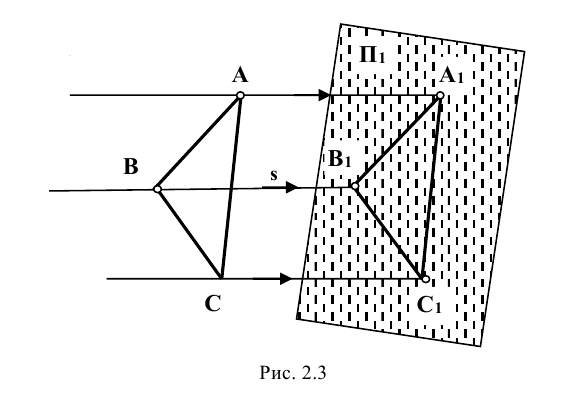
Система плоскостей проекций в практике решения инженерных задач
Наибольшее практическое применение нашёл метод параллельного ортогонального проецирования на две взаимно перпендикулярные плоскости проекций, одна из которых расположена горизонтально, а другая - вертикально.
Они соответственно получили обозначения: горизонтальная плоскость проекций –  , и фронтальная —
, и фронтальная — 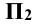 . Эти плоскости пересекаются между собой под прямым углом, образуя линию пересечения — ось х, и делят пространство на четыре четверти (квадранты), которые принято обозначать римскими цифрами I, II, III и IV (рис. 2.4).
. Эти плоскости пересекаются между собой под прямым углом, образуя линию пересечения — ось х, и делят пространство на четыре четверти (квадранты), которые принято обозначать римскими цифрами I, II, III и IV (рис. 2.4).
В случае недостаточной информативности об объекте по двум проекциям на указанные плоскости  и
и 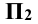 используют третью плоскость
используют третью плоскость 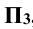 , перпендикулярную плоскостям
, перпендикулярную плоскостям  и
и 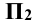 . Она называется профильной плоскостью проекций. Плоскость
. Она называется профильной плоскостью проекций. Плоскость 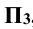 пересекается с плоскостью
пересекается с плоскостью  образуя ось у, и с плоскостью
образуя ось у, и с плоскостью 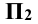 , образуя ось z.
, образуя ось z.
Указанные плоскости делят всё пространство вокруг уже на восемь частей, которые называются октантами и обозначаются римскими цифрами от I до VIII. 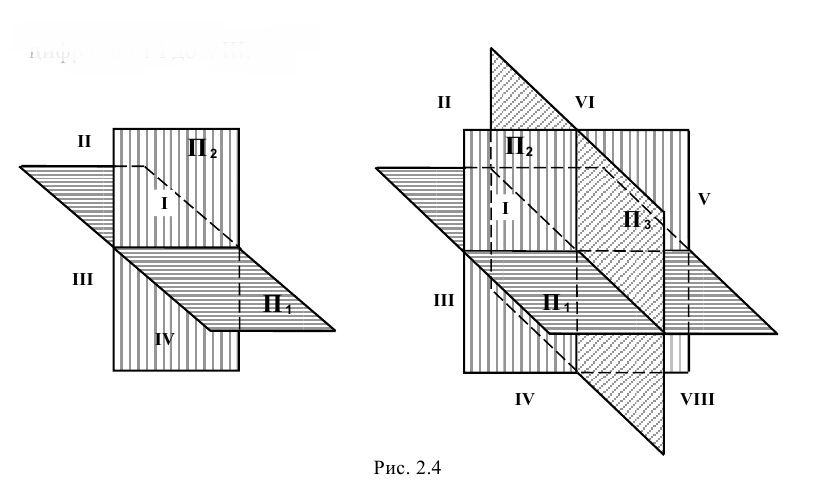
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |