
Образование и задание поверхности на чертеже с примерами
Содержание:
Образование и задание поверхности на чертеже:
В начертательной геометрии геометрические фигуры задаются графически, поэтому целесообразно поверхность рассматривать как совокупность последовательных положений линии  , перемещающейся в пространстве по определенному закону.
, перемещающейся в пространстве по определенному закону.
Закон перемещения линии 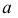
Подвижная линия 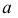 называется образующей, неподвижные линии
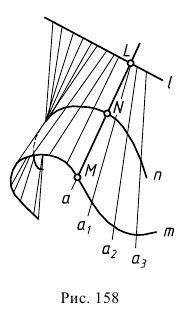
называется образующей, неподвижные линии 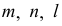 - направляющими (рис. 158).
- направляющими (рис. 158).
Рассмотренный способ образования поверхностей называется кинематическим.
Поверхность считается заданной на чертеже, если из множества точек пространства можно выделить те, которые принадлежат поверхности. При этом различают понятия каркаса, определителя и очерка поверхности.
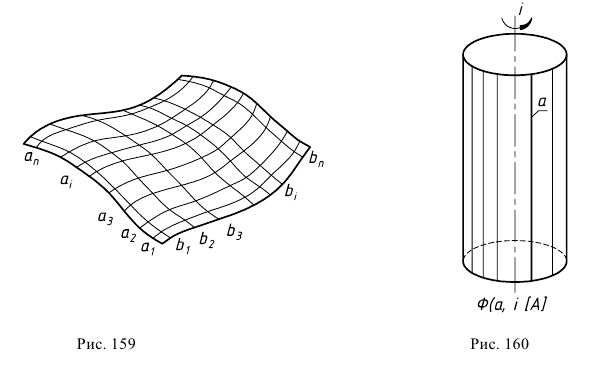
Каркас поверхности - множество точек или линий, определяющих поверхность. На рис. 159 показан каркас поверхности, состоящий из двух семейств линий 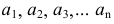 и
и 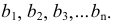
Определителем поверхности называется совокупность независимых условий, однозначно задающих поверхность. В определитель включаются геометрическая и алгоритмическая части.
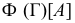 - форма записи определителя, где
- форма записи определителя, где 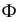 - обозначение поверхности;
- обозначение поверхности; 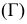 - геометрическая часть определителя, т.е. геометрические элементы, заданные на чертеже;
- геометрическая часть определителя, т.е. геометрические элементы, заданные на чертеже; 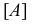 - алгоритмическая часть определителя, которая показывает характер изменения формы образующей
- алгоритмическая часть определителя, которая показывает характер изменения формы образующей 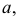 и закон ее перемещения.
и закон ее перемещения.
На рис. 160 показана поверхность прямого кругового цилиндра 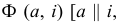 каждая точка прямой вращается вокруг оси
каждая точка прямой вращается вокруг оси 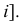 Длинную запись алгоритмической части иногда заменяют названием поверхности. Пишут: поверхность вращения
Длинную запись алгоритмической части иногда заменяют названием поверхности. Пишут: поверхность вращения 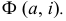
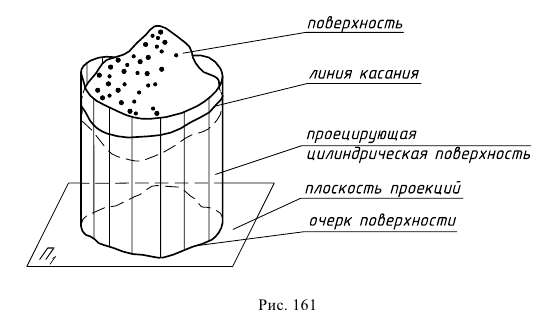
Очерком поверхности называется проекция проецирующей цилиндрической поверхности, которая огибает заданную поверхность.
Рис. 161 дает наглядное представление о том, как получается очерк произвольной замкнутой поверхности на горизонтальной плоскости проекций. Здесь множество проецирующих лучей, касательных к поверхности, образуют горизонтально-проецирующую поверхность. Проекцию этой поверхности на 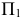 называют горизонтальным очерком заданной поверхности.
называют горизонтальным очерком заданной поверхности.
Классификация поверхностей
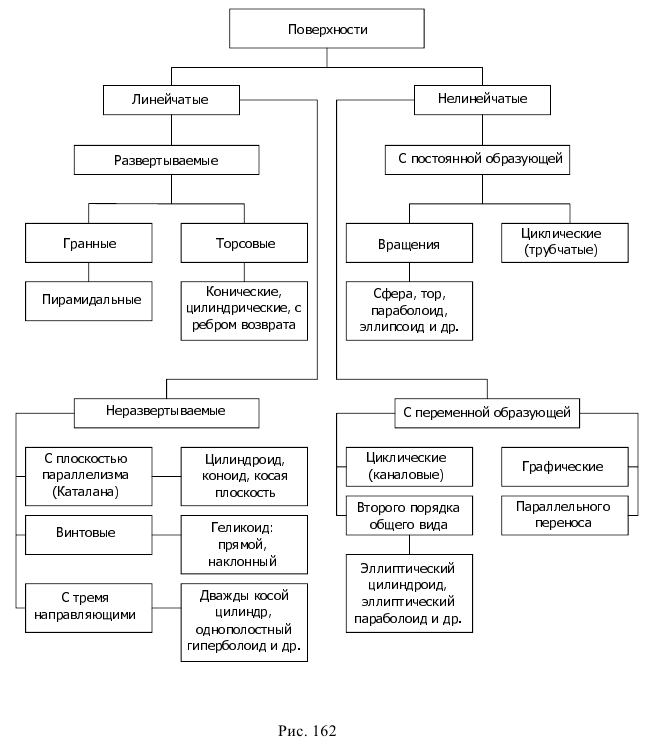
Большое многообразие поверхностей, различные способы их образования, сложности геометрических характеристик создают трудности в попытках классифицировать поверхности, объединить их в систему.
Основой классификации поверхностей могут служить их определители или геометрические особенности, связанные с кинематическим способом их образования.
Важными признаками формообразования поверхностей являются:
- - вид образующей и закон ее перемещения;
- - закон изменения образующей;
- - развертываемость куска поверхности.
На рис. 162 приведена ориентировочная классификация поверхностей.
Торсовые поверхности
Эти поверхности относятся к группе линейчатых развертываемых поверхностей с одной направляющей.
Характерным признаком торсовых поверхностей является то, что их прямолинейные образующие пересекаются. При этом пересечение может происходить как в собственной 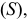 так и в несобственной
так и в несобственной 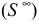 точках.
точках.
К рассматриваемой группе относятся:
- - поверхность с ребром возврата;
- - поверхность коническая;
- - поверхность цилиндрическая.
Поверхность с ребром возврата
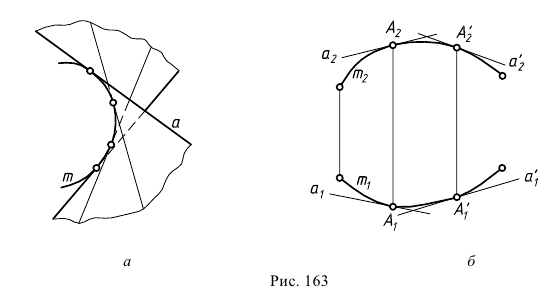
Поверхность с ребром возврата (торс) в общем случае образуется непрерывным перемещением прямолинейной образующей 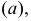 касающейся пространственной кривой
касающейся пространственной кривой 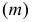 - направляющей (рис. 163, а). Кривая
- направляющей (рис. 163, а). Кривая 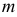 называется ребром возврата торса.
называется ребром возврата торса.
Торсовая поверхность состоит из двух полостей, линией раздела которых является ребро возврата. Ребро возврата полностью задает торс и является геометрической частью определителя поверхности. Алгоритмической частью служит условие касания образующих к ребру возврата.
Определитель имеет вид 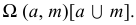
На эпюре Монжа любая неограниченная торсовая поверхность задается только проекциями ребра возврата 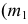 и
и 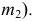 При этом каркас поверхности можно составить из семейства прямолинейных образующих, касательных к этому ребру. Так, на рис. 163, б проекциями образующей
При этом каркас поверхности можно составить из семейства прямолинейных образующих, касательных к этому ребру. Так, на рис. 163, б проекциями образующей 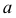 являются касательные
являются касательные 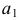 и
и 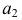 к проекциям
к проекциям 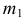 и
и 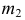 ребра возврата
ребра возврата 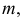 проведенные через проекции
проведенные через проекции 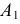 и
и 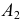 случайной точки
случайной точки 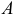 этого ребра.
этого ребра.
Наиболее широкое применение в инженерной практике нашел частный вид торсовой поверхности - винтовой торс, у которой ребром возврата служит цилиндрическая винтовая линия. Если ось винтовой линии расположить перпендикулярно к 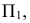 то образованная поверхность представит собой поверхность одинакового ската (по отношению к
то образованная поверхность представит собой поверхность одинакового ската (по отношению к 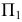 ), т.к. все касательные к винтовой линии пересекают плоскость
), т.к. все касательные к винтовой линии пересекают плоскость 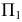 под одним и тем же углом. Чертеж отсека такой поверхности показан на рис. 164.
под одним и тем же углом. Чертеж отсека такой поверхности показан на рис. 164.
В процессе решения многих задач приходится задавать точки на поверхности изучаемых предметов.
В некоторых случаях, намечая проекции точки на поверхности, необходимо указывать видимость данной точки на той или иной проекции. Такое указание делают путем заключения в скобки невидимой проекции точки. На данной (как и любой торсовой) поверхности точки могут быть построены при помощи проходящих через них прямолинейных образующих.
Так, на рис. 165 показано построение фронтальной проекции 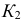 точки
точки 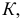 лежащей на поверхности с ребром возврата, по заданной горизонтальной
лежащей на поверхности с ребром возврата, по заданной горизонтальной 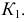 Для этого через точку
Для этого через точку 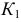 проведена касательная
проведена касательная 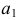 к проекции
к проекции 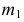 направляющей
направляющей 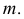 Далее через фронтальную проекцию
Далее через фронтальную проекцию 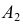 полученной точки
полученной точки 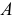 на ребре возврата
на ребре возврата 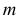 проведена фронтальная проекция
проведена фронтальная проекция 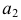 касательной
касательной 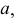 на которой расположена точка
на которой расположена точка 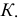 Линия связи, проведенная из
Линия связи, проведенная из 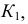 определяет искомую проекцию
определяет искомую проекцию 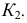
В некоторых случаях недостающую проекцию точки строят при помощи произвольной секущей плоскости, с расчетом, что точка должна быть в этой плоскости.
Коническая поверхность
Коническую поверхность можно считать частным случаем поверхности с ребром возврата - при вырождении ребра возврата 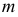 в точку -вершину
в точку -вершину 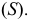 В этом случае все образующие поверхности будут пересекаться в собственной точке
В этом случае все образующие поверхности будут пересекаться в собственной точке 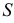 и поверхность определяется как коническая.
и поверхность определяется как коническая.
Для задания конической поверхности недостаточно иметь ребро возврата (точку) - поверхность останется еще неопределенной. В этом случае вводится дополнительная линия, заведомо принадлежащая задаваемой поверхности, и эта линия называется направляющей 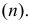
Таким образом, коническая поверхность образуется движением прямой 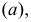 проходящей через неподвижную точку
проходящей через неподвижную точку 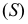 и пересекающей кривую
и пересекающей кривую  - направляющую (рис. 166).
- направляющую (рис. 166).
Если направляющая  - замкнутая линия, то поверхность называется замкнутой (рис. 167).
- замкнутая линия, то поверхность называется замкнутой (рис. 167).
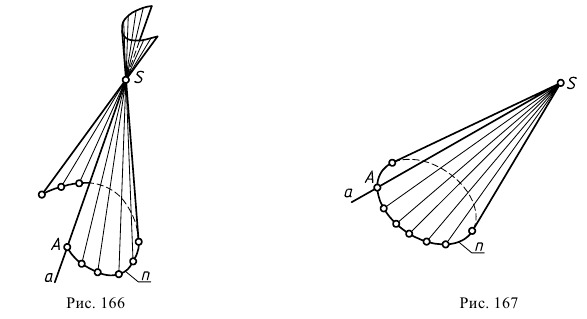
Коническая поверхность может иметь две полости (см. рис. 166), если образующие продолжены за вершину.
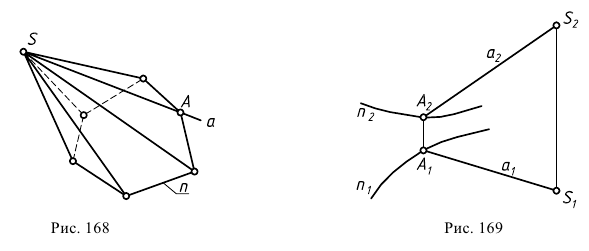
В случае замены кривой направляющей  ломаной линией поверхность называются пирамидальной (рис. 168). Поверхности с замкнутой ломаной направляющей называются еще многогранниками.
ломаной линией поверхность называются пирамидальной (рис. 168). Поверхности с замкнутой ломаной направляющей называются еще многогранниками.
Аналитически уравнение конической поверхности имеет вид
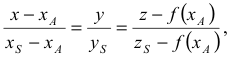
где 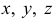 - текущие координаты точки
- текущие координаты точки 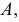 выбранной на направляющей кривой
выбранной на направляющей кривой 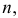 имеющей уравнение
имеющей уравнение 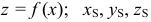 — координаты вершины
— координаты вершины 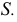 Определитель конической поверхности можно записать следующим образом:
Определитель конической поверхности можно записать следующим образом: 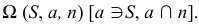
На эпюре Монжа коническая поверхность однозначно задается проекциями ее образующей 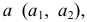 направляющей
направляющей 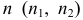 и вершины
и вершины 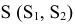 (рис. 169).
(рис. 169).
Для придания наглядности и выразительности изображению вычерчивают очерк поверхности и показывают наиболее важные линии и точки на поверхности.
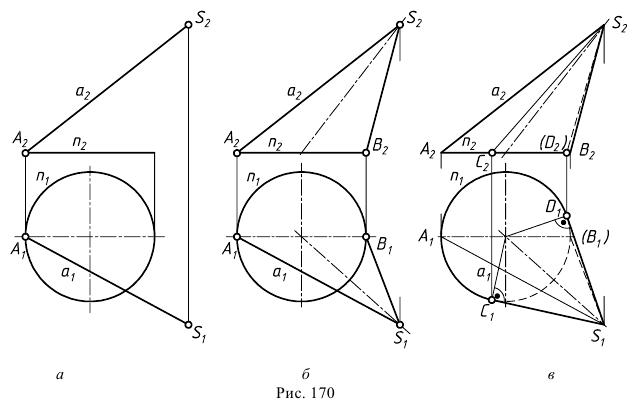
Чтобы построить очерк конической поверхности, следует на каждой плоскости проекций отметить граничные образующие, заключающие между собой область, внутри которой находится проекция поверхности. Пример построения очерка замкнутой конической поверхности, заданной определителем (рис. 170, а), показан на рис. 170, 6, в. Для построения фронтального очерка (см. рис. 170, б) на окружности 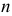 определяют крайние точки - правая
определяют крайние точки - правая 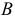 и левая
и левая 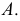 Проводят образующие
Проводят образующие 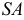 и
и 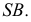 Проекции
Проекции 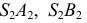 и
и 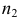 определяют фронтальный очерк поверхности. Проекции
определяют фронтальный очерк поверхности. Проекции 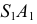 и
и 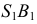 образующих
образующих 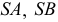 на
на 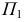 не являются очерковыми образующими.
не являются очерковыми образующими.
Для построения горизонтального очерка поверхности (см. рис.170, в) проводят касательные 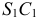 и
и 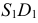 из точки
из точки 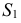 к окружности - основанию. Чтобы определить точки касания
к окружности - основанию. Чтобы определить точки касания 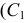 и
и 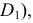 проводят радиусы окружности, перпендикулярные касательным образующим.
проводят радиусы окружности, перпендикулярные касательным образующим.
Для наглядности изображаемой поверхности невидимые элементы ее показывают штриховыми линиями.
Видимую часть поверхности на фронтальной плоскости проекции можно определить по горизонтальной проекции окружности 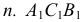 -обращенная к наблюдателю часть окружности, считается видимой на
-обращенная к наблюдателю часть окружности, считается видимой на 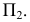 Таким образом, границей видимости поверхности на
Таким образом, границей видимости поверхности на 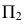 являются очерковые образующие
являются очерковые образующие 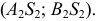
Видимую часть поверхности на 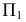 определяют часть окружности
определяют часть окружности 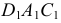 и очерковые образующие
и очерковые образующие 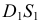 и
и 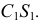
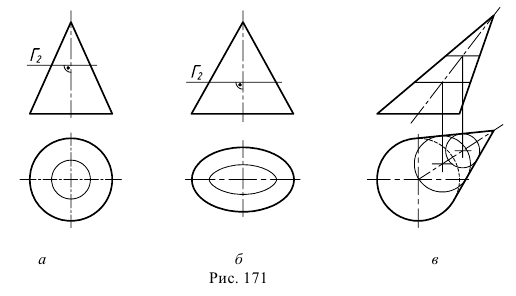
Конические поверхности различают по виду нормального сечения (нормальным сечением конической поверхности называется сечение, плоскость которого перпендикулярна оси поверхности). Конус общего вида - это коническая поверхность, у которой нормальным сечением является неопределенная кривая линия. Выделим случаи, когда нормальное сечение конической поверхности представляет собой замкнутую кривую второго порядка (конус второго порядка):
- - прямой круговой конус (рис. 171, а);
- - эллиптический конус (рис. 171, б);
- - эллиптический конус с круговым основанием (рис. 171, в) или наклонный круговой конус.
Точки на поверхности конуса могут быть построены при помощи проходящих через них образующих. На рис. 172 дан пример построения фронтальной проекции точки 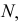 принадлежащей конической поверхности и заданной проекцией
принадлежащей конической поверхности и заданной проекцией 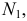 при условии, что эта точка видима на плоскости
при условии, что эта точка видима на плоскости 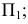 ход построений указан стрелками.
ход построений указан стрелками.
Пример построения очерка прямого кругового конуса, ось которого параллельна плоскости 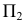 (но не
(но не 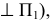 приведен на рис. 173.
приведен на рис. 173.
Фронтальный очерк задан, это равнобедренный треугольник 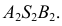 Горизонтальный очерк состоит из части эллипса и двух касательных к нему прямых. Эллипс можно построить по двум его осям: малой
Горизонтальный очерк состоит из части эллипса и двух касательных к нему прямых. Эллипс можно построить по двум его осям: малой 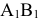 и большой, равной по своей величине диаметру окружности основания конуса. Для определения прямых
и большой, равной по своей величине диаметру окружности основания конуса. Для определения прямых 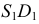 и
и 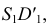 касательных к эллипсу, используется произвольная сфера, вписанная в конус.
касательных к эллипсу, используется произвольная сфера, вписанная в конус.
Построение начинают с отыскания точек 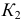 и
и 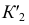 - фронтальных проекций случайных точек искомых касательных. Эти точки получаются при пересечении фронтальных проекций окружности касания конуса и сферы и экватора вписанной сферы. Далее находят проекции точек
- фронтальных проекций случайных точек искомых касательных. Эти точки получаются при пересечении фронтальных проекций окружности касания конуса и сферы и экватора вписанной сферы. Далее находят проекции точек 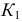 и
и 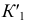 на горизонтальной проекции экватора. Соединяют полученные точки
на горизонтальной проекции экватора. Соединяют полученные точки 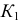 и
и 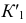 с точкой
с точкой 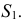 На этих прямых определяют и точки
На этих прямых определяют и точки 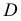 и
и 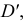 горизонтальные проекции которых
горизонтальные проекции которых 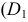 и
и 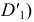 есть точки касания прямых с эллипсом.
есть точки касания прямых с эллипсом.
Цилиндрическая поверхность
Цилиндрическую поверхность можно считать производимой из поверхности с ребром возврата при условии, что ребро возврата представляет собой бесконечно удаленную точку. Тогда все образующие цилиндрической поверхности будут параллельны (пересекаться в несобственной точке).
Для того чтобы цилиндрическая поверхность была определена в пространстве, необходимо задать дополнительную линию, принадлежащую этой поверхности; эта линия будет называться направляющей поверхности.
Таким образом, цилиндрическую поверхность можно представить как поверхность, образованную движением прямой 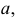 параллельной самой себе (или направлению
параллельной самой себе (или направлению 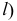 и пересекающей кривую
и пересекающей кривую 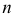 - направляющую (рис.174).
- направляющую (рис.174).
Если направляющая 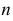 - замкнутая линия, то поверхность называется замкнутой. В случае замены кривой направляющей
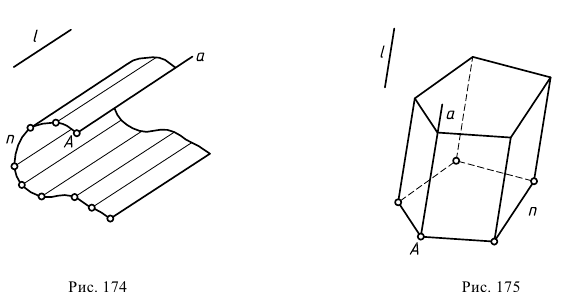
- замкнутая линия, то поверхность называется замкнутой. В случае замены кривой направляющей 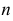 ломаной линией поверхность называется призматической (рис. 175).
ломаной линией поверхность называется призматической (рис. 175).
Аналитическое уравнение цилиндрической поверхности с направляющей кривой 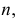 имеющей уравнение
имеющей уравнение 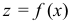 в координатной плоскости
в координатной плоскости 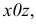 и с прямолинейной образующей
и с прямолинейной образующей 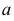 в виде вектора
в виде вектора 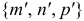 имеет вид
имеет вид
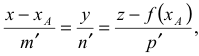
где 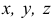 — текущие координаты точек поверхности; величина
— текущие координаты точек поверхности; величина 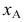 - параметр.
- параметр.
Исходя из принципа образования поверхности, определитель цилиндрической поверхности можно записать следующим образом:
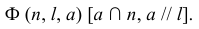
На эпюре Монжа цилиндрическая поверхность однозначно задается проекциями определителя: направляющей 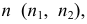 образующей
образующей 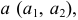 направлением переноса образующей
направлением переноса образующей 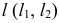 (рис. 176).
(рис. 176).
Для наглядности изображения цилиндрической поверхности на чертеже обычно строят очерки заданной поверхности. Рассмотрим пример построения очерка цилиндрической поверхности, заданной определителем (рис. 177, а).
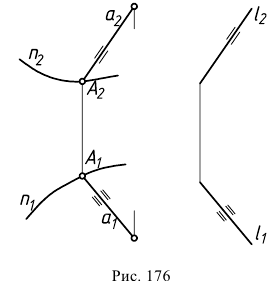
Для построения фронтального очерка поверхности (рис. 177, б) проводят крайние образующие 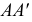 и
и 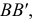 которые на
которые на 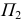 являются очерковыми образующими и служат границей видимости поверхности. Видимость проверяют по горизонтальной проекции окружности
являются очерковыми образующими и служат границей видимости поверхности. Видимость проверяют по горизонтальной проекции окружности 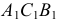 (видимость определяют после построения горизонтального очерка). Образующие
(видимость определяют после построения горизонтального очерка). Образующие 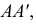
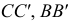 поверхности на
поверхности на 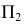 видны.
видны.
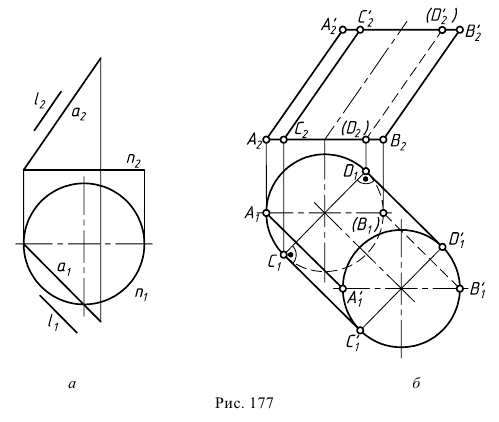
Для построения горизонтального очерка проводят две крайние на 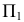 образующие
образующие 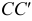 и
и 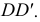 Точки касания
Точки касания 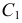 и
и 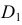 определяют, проводя радиусы окружности, перпендикулярные касательным. Образующие
определяют, проводя радиусы окружности, перпендикулярные касательным. Образующие 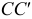 и
и 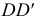 являются очерковыми на
являются очерковыми на 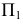 и служат границей видимости поверхности, а на
и служат границей видимости поверхности, а на 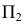 - это промежуточные образующие. Видимую часть поверхности на
- это промежуточные образующие. Видимую часть поверхности на 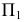 можно определить по фронтальным проекциям точек
можно определить по фронтальным проекциям точек 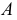 и
и 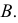 При взгляде сверху
При взгляде сверху 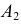 не закрыта, а
не закрыта, а 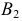 закрыта частью поверхности. Соответственно на
закрыта частью поверхности. Соответственно на 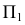 проекция
проекция 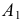 - видимая, а
- видимая, а 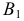 - невидимая. Следовательно, часть окружности
- невидимая. Следовательно, часть окружности 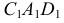 на
на 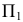 считается видимой и вместе с ней видима часть поверхности, образованная образующими, пересекающими эту часть окружности. Часть окружности
считается видимой и вместе с ней видима часть поверхности, образованная образующими, пересекающими эту часть окружности. Часть окружности 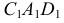 на
на 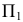 невидна.
невидна.
Цилиндрические поверхности, как и конические, различают по виду нормального сечения (нормальным сечением цилиндрической поверхности называют сечение, плоскость которого перпендикулярна образующим поверхности). Если нормальным сечением является неопределенная кривая линия, то это цилиндр общего вида.
Выделим случаи, когда нормальное сечение цилиндрической поверхности представляет собой кривую второго порядка. По виду полученной кривой цилиндр может быть эллиптическим (в частном случае круговым), параболическим, гиперболическим. Указанные цилиндрические поверхности относятся к числу поверхностей второго порядка. На рис. 178 показан эллиптический цилиндр, образующие которого перпендикулярны горизонтальной плоскости проекций.
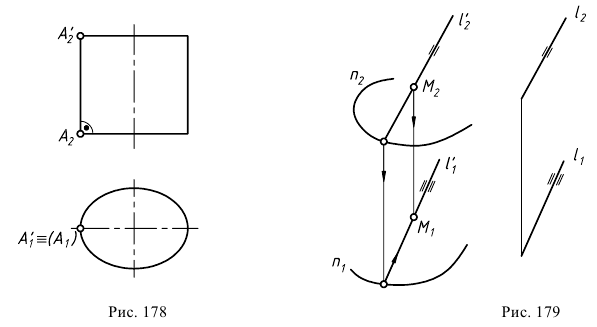
На цилиндрической поверхности точки строят при помощи проходящих через них прямолинейных образующих. Так, на рис. 179 показано построение горизонтальной проекции 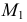 точки
точки 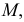 лежащей на цилиндрической поверхности, по заданной фронтальной
лежащей на цилиндрической поверхности, по заданной фронтальной 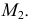 Построения показаны стрелками.
Построения показаны стрелками.
Проецирующие поверхности
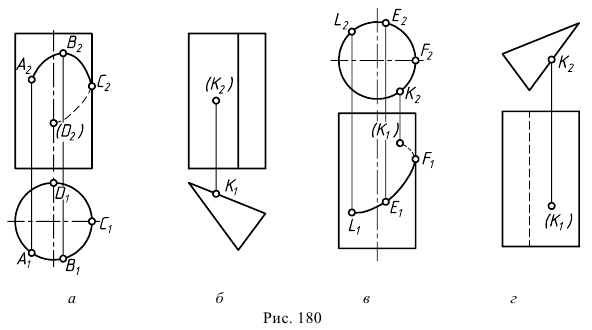
На комплексном чертеже задачи решаются проще, если цилиндрические и призматические поверхности занимают проецирующее положение, т.е. перпендикулярное одной из плоскостей проекций (см. рис. 178). При таком положении поверхности одна из проекций образующей вырождается в точку, а проекция поверхности - в линию. Вырожденная проекция поверхности, подобно проецирующей плоскости, обладает «собирательным свойством»: проекция любой линии, расположенной на поверхности, находится на вырожденной проекции поверхности. На рис. 180, а, б показаны случаи, когда горизонтальная проекция поверхности «собирает» на себя все горизонтальные проекции точек, расположенных на поверхности; на рис. 180, в, г - случаи, когда фронтальные проекции поверхностей «собирают» на себя все фронтальные проекции точек, расположенных на поверхности. Принадлежность точек поверхности определяется в этом случае принадлежностью проекций точек вырожденной проекции поверхности.
Поверхности с плоскостью параллелизма (поверхности Каталана)
Эти поверхности относятся к группе линейчатых неразвертываемых поверхностей с двумя направляющими. Характерным признаком поверхностей с плоскостью параллелизма является то, что их прямолинейные образующие являются скрещивающимися прямыми, так как при формировании этих поверхностей образующие, скользящие по двум направляющим, должны быть параллельны некоторой заданной плоскости. В этом случае все образующие будут пересекаться с плоскостью параллелизма в несобственных точках, множество которых определяют несобственную прямую; эту прямую следует рассматривать как третью направляющую линейчатой поверхности.
Часто поверхности с плоскостью параллелизма называют поверхностями Каталана (по имени бельгийского ученого-математика 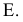 Каталана, исследовавшего свойства этих поверхностей). Определитель для группы поверхностей Каталана имеет вид:
Каталана, исследовавшего свойства этих поверхностей). Определитель для группы поверхностей Каталана имеет вид: 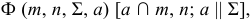 где
где 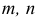 -направляющие линии;
-направляющие линии; 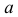 - образующая,
- образующая, 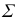 - плоскость параллелизма, в качестве которой можно выбрать любую произвольную плоскость или одну из плоскостей проекций. Для задания поверхности этой группы на эпюре Монжа достаточно указать проекции направляющих
- плоскость параллелизма, в качестве которой можно выбрать любую произвольную плоскость или одну из плоскостей проекций. Для задания поверхности этой группы на эпюре Монжа достаточно указать проекции направляющих 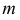 и
и 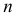 и положение плоскости параллелизма. В зависимости от формы направляющих и их расположения в пространстве можно получить различные поверхности этой группы.
и положение плоскости параллелизма. В зависимости от формы направляющих и их расположения в пространстве можно получить различные поверхности этой группы.
Рассмотрим отдельные виды линейчатых поверхностей с плоскостью параллелизма.
Цилиндроиды
Поверхность, называемая цилиндроидом, образуется в том случае, когда обе направляющие 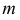 и
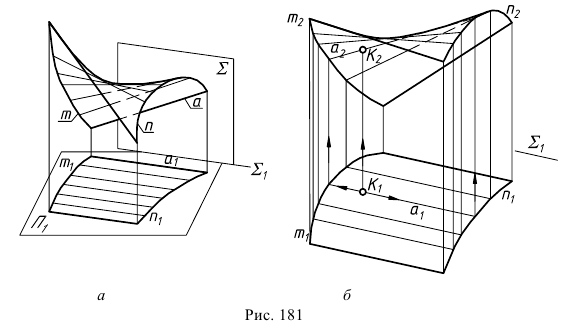
и 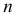 - кривые линии. На рис. 181, а дано наглядное изображение цилиндроида. Для получения проекционного чертежа, обладающего наглядностью, обычно указывают проекции нескольких прямолинейных образующих.
- кривые линии. На рис. 181, а дано наглядное изображение цилиндроида. Для получения проекционного чертежа, обладающего наглядностью, обычно указывают проекции нескольких прямолинейных образующих.
Так как заданная плоскость параллелизма является горизонтально-проецирующей плоскостью 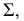 то построение проекций образующих (см. рис. 181, б) начинают с горизонтальной плоскости проекций, на которой горизонтальные проекции движущейся образующей
то построение проекций образующих (см. рис. 181, б) начинают с горизонтальной плоскости проекций, на которой горизонтальные проекции движущейся образующей 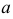 параллельны горизонтальному следу
параллельны горизонтальному следу 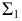 плоскости параллелизма
плоскости параллелизма 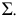 Фронтальные проекции образующих строят по двум точкам пересечения образующей с направляющими
Фронтальные проекции образующих строят по двум точкам пересечения образующей с направляющими 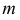 и
и 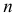 . Для построения точки, расположенной на поверхности, используют образующую (или произвольную линию поверхности, см. рис. 183).
. Для построения точки, расположенной на поверхности, используют образующую (или произвольную линию поверхности, см. рис. 183).
Коноиды
Отличие поверхности коноида от цилиндроида состоит только в том, что одна из направляющих линий коноида - прямая. На рис. 182 даны наглядное изображение и эпюр Монжа коноида. Здесь 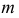 и
и 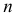 - направляющие, причем
- направляющие, причем 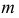 - прямая,
- прямая, 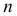 - кривая линии;
- кривая линии; 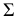 - горизонтально-проецирующая плоскость, которой параллельны все образующие коноида. Точка
- горизонтально-проецирующая плоскость, которой параллельны все образующие коноида. Точка 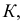 принадлежащая поверхности коноида, построена при помощи проходящей через нее прямолинейной образующей
принадлежащая поверхности коноида, построена при помощи проходящей через нее прямолинейной образующей 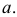
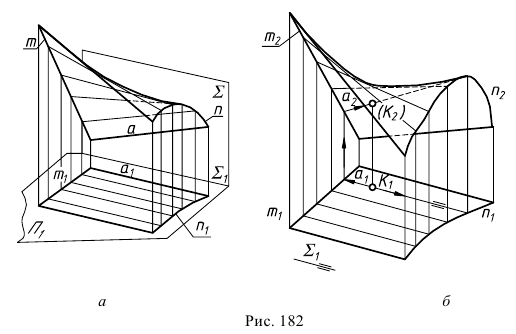
Косая плоскость (гиперболический параболоид)
Косая плоскость образуется непрерывным перемещением прямолинейной образующей а по двум направляющим - скрещивающимся прямым 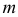 и
и 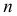 - параллельно некоторой плоскости параллелизма
- параллельно некоторой плоскости параллелизма 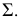 Эту же поверхность называют гиперболическим параболоидом, так как плоские сечения поверхности в одном из направлений дают гиперболы, а в другом - параболы (это положение доказано в аналитической геометрии).
Эту же поверхность называют гиперболическим параболоидом, так как плоские сечения поверхности в одном из направлений дают гиперболы, а в другом - параболы (это положение доказано в аналитической геометрии).
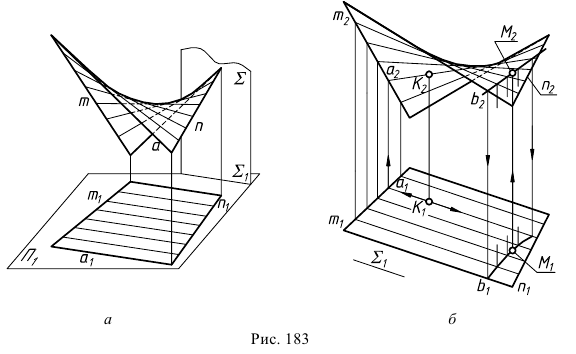
На рис. 183, а дан пример косой плоскости с плоскостью параллелизма 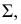 перпендикулярной
перпендикулярной 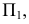 и направляющими прямыми
и направляющими прямыми 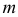 и
и 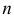 . На рис. 183, б приведен эпюр Монжа этой поверхности. Для наглядности проекционного чертежа построены проекции ряда образующих (аналогично рис.181, б и 182, б).
. На рис. 183, б приведен эпюр Монжа этой поверхности. Для наглядности проекционного чертежа построены проекции ряда образующих (аналогично рис.181, б и 182, б).
Для построения точки 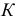 этой поверхности по заданной горизонтальной проекции
этой поверхности по заданной горизонтальной проекции 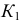 использована образующая прямая а (см. рис. 183, б). Для построения же точки
использована образующая прямая а (см. рис. 183, б). Для построения же точки 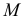 по заданной фронтальной ее проекции
по заданной фронтальной ее проекции 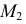 может быть использована произвольная линия на поверхности косой плоскости, например
может быть использована произвольная линия на поверхности косой плоскости, например 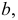 с расчетом, что точка
с расчетом, что точка 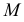 должна принадлежать этой линии. Фронтальная проекция
должна принадлежать этой линии. Фронтальная проекция 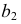 линии
линии 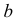 проходит через
проходит через 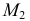 и пересекает ряд образующих поверхности в некоторых точках. По горизонтальным проекциям этих точек пересечения строится горизонтальная проекция
и пересекает ряд образующих поверхности в некоторых точках. По горизонтальным проекциям этих точек пересечения строится горизонтальная проекция 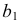 линии
линии 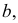 а на ней - искомая горизонтальная проекция
а на ней - искомая горизонтальная проекция 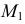 точки
точки 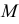 косой плоскости.
косой плоскости.
Винтовые линейчатые поверхности (геликоиды)
Винтовые поверхности образуются винтовым движением прямой линии 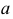 - образующей (винтовое перемещение характеризуется вращением вокруг оси и одновременным поступательным движением, параллельным этой оси). Каждая точка образующей перемещается по своей винтовой линии, причем все винтовые линии имеют общую ось, называемую осью винтовой поверхности
- образующей (винтовое перемещение характеризуется вращением вокруг оси и одновременным поступательным движением, параллельным этой оси). Каждая точка образующей перемещается по своей винтовой линии, причем все винтовые линии имеют общую ось, называемую осью винтовой поверхности 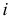 (рис. 184).
(рис. 184).
При перемещении образующей угол ее наклона к оси и перемещение вдоль оси (называемое шагом винтовой линии) могут меняться или оставаться постоянными.
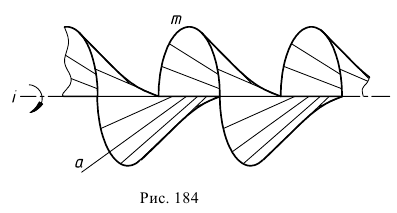
В практике чаще всего встречаются винтовые линейчатые поверхности с постоянным углом наклона образующей к оси и с постоянным шагом направляющей винтовой линии. Эти поверхности называют еще геликоидами (от слова «гелиса»-цилиндрическая винтовая линия постоянного шага).
В зависимости от величины угла наклона образующей к оси геликоиды бывают прямыми, если этот угол равен 90° (рис. 185, а), и косыми (наклонными), если угол - произвольный, отличный от 0 и 90° (рис.185, б).
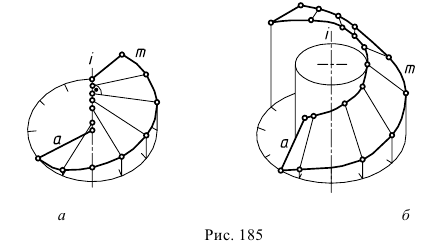
В свою очередь, прямые и косые геликоиды подразделяются на закрытые и открытые. Признаком для такого деления служит взаимное расположение оси геликоида и его образующей. Если образующая и ось пересекаются, геликоид называют закрытым, если скрещиваются - открытым.
Аналитическое уравнение винтовой поверхности постоянного шага можно представить в следующем виде:
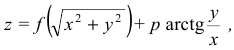
где 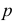 - винтовой параметр.
- винтовой параметр.
Определитель винтовой поверхности 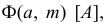 где
где 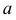 - образующая;
- образующая; 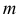 - направляющая винтовая линия;
- направляющая винтовая линия; 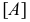 - дополнительные данные о характере движения образующей.
- дополнительные данные о характере движения образующей.
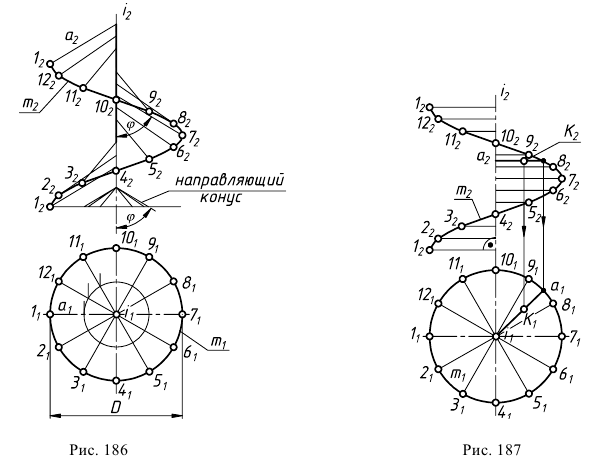
Как неоднократно отмечалось ранее, для получения наглядного изображения винтовой поверхности ее задание на эпюре Монжа проекциями геометрической части определителя следует расширить до задания каркасом, составленным из последовательных положений прямолинейной образующей.
Например, на рис. 186 показан косой геликоид. Он задан правой винтовой линией 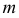 с диаметром
с диаметром 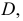 осью винтовой поверхности
осью винтовой поверхности 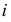 и образующей
и образующей 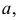 наклонной к оси под углом
наклонной к оси под углом 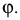 Предварительно построен один виток винтовой линии, начиная от точки 1, для чего окружность разделена на 12 частей. Точка 1, перемещаясь по винтовой линии, переходит последовательно в положения 2, 3, ... 12. Соответствующие образующие будут перемещаться параллельно образующим направляющего конуса вращения с углом
Предварительно построен один виток винтовой линии, начиная от точки 1, для чего окружность разделена на 12 частей. Точка 1, перемещаясь по винтовой линии, переходит последовательно в положения 2, 3, ... 12. Соответствующие образующие будут перемещаться параллельно образующим направляющего конуса вращения с углом 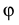 при вершине. Построив ряд образующих, получим дискретный каркас отсека винтовой поверхности.
при вершине. Построив ряд образующих, получим дискретный каркас отсека винтовой поверхности.
У прямого геликоида образующие всегда параллельны плоскости, перпендикулярной оси поверхности (рис. 187). По своему образованию прямой геликоид является коноидом. Действительно, образующая - прямая линия; она во всех положениях параллельна некоторой плоскости (в данном случае перпендикулярной к оси винтовой линии); образующая пересекает две направляющие линии, кривую и прямую (ось винтовой линии). Так как кривая направляющая представляет собой винтовую линию, то такая поверхность называется винтовым коноидом.
Для построения точки 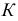 этой поверхности по заданной фронтальной проекции
этой поверхности по заданной фронтальной проекции 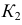 использована образующая прямая
использована образующая прямая 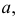 у которой сначала строится фронтальная проекция
у которой сначала строится фронтальная проекция 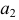 перпендикулярно к оси винтовой линии. По точке пересечения
перпендикулярно к оси винтовой линии. По точке пересечения  строится горизонтальная проекция
строится горизонтальная проекция 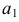 образующей и на ней точка
образующей и на ней точка 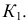
Поверхности вращения
Широкое применение поверхностей вращения в технике, машиностроении объясняется распространенностью вращательного движения и простотой обработки (образования) деталей на станках. Особенно распространены поверхности, имеющие в меридиональном сечении (см. ниже) кривые второго порядка или прямые.
Поверхности вращения общего вида
Поверхность, образованная вращением линии (плоской или пространственной кривой) вокруг неподвижной прямой - оси, называется поверхностью общего вида (рис. 188, а). Определитель поверхности может быть записан следующим образом: 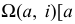 вращается вокруг
вращается вокруг 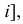 где
где 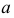 -образующая,
-образующая, 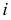 - прямая (ось вращения). При вращении каждая точка образующей описывает окружность с центром на оси
- прямая (ось вращения). При вращении каждая точка образующей описывает окружность с центром на оси 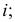 плоскость окружности перпендикулярна оси вращения.
плоскость окружности перпендикулярна оси вращения.
Окружности, описываемые точками образующей, называются параллелями, наибольшая из параллелей - экватором, наименьшая - горлом или горловиной.
Плоскости, проходящие через ось вращения, называются меридиональными, а линии, по которым плоскости пересекают поверхность, - меридианами. Меридиональная плоскость, параллельная плоскости проекций. называется главной, а линия пересечения ее с поверхностью - главным меридианом. Поверхность вращения считают закрытой, если меридиональное сечение поверхности является замкнутой кривой линией, пересекающей ось поверхности в двух точках.
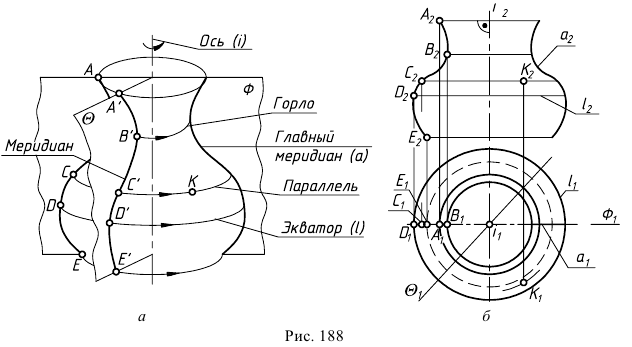
На эпюре Монжа поверхности вращения удобнее задавать очерками. Если ось поверхности занимает горизонтально-проецирующее положение, то горизонтальным очерком поверхности является горизонтальная проекция экватора 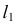 (рис. 188, б), а фронтальным очерком - фронтальная проекция главного меридиана
(рис. 188, б), а фронтальным очерком - фронтальная проекция главного меридиана 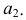 Для построения точек, расположенных на поверхности, рационально использовать параллели. Видимость точек на поверхности определяется очерковыми линиями, ограничивающими видимость самой поверхности относительно плоскостей проекций.
Для построения точек, расположенных на поверхности, рационально использовать параллели. Видимость точек на поверхности определяется очерковыми линиями, ограничивающими видимость самой поверхности относительно плоскостей проекций.
Поверхности вращения частного вида
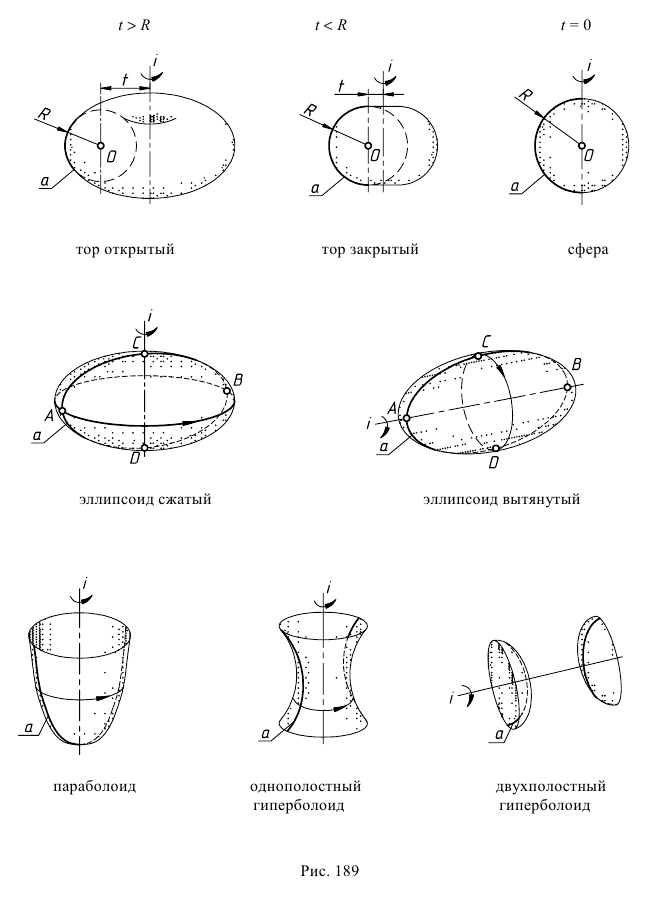
Такие поверхности имеют в меридиональном сечении кривую второго порядка или две прямые, на которые распадаются кривые второго порядка. По виду главного меридиана и расположению оси вращения поверхности вращения имеют разные названия. На рис. 189 представлена группа поверхностей, имеющих в качестве образующей кривую второго порядка 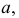 а в качестве оси вращения - проецирующую прямую
а в качестве оси вращения - проецирующую прямую 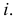
Рассмотрим подробнее эти поверхности.
Сфера. Это поверхность, образованная вращением окружности вокруг одного из своих диаметров. Ось вращения проходит через центр окружности. Уравнение поверхности: 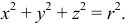
На рис. 190 дан чертеж сферы, заданной очерками. Пусть ось вращения - горизонтально-проецирующая прямая, тогда фронтальным очерком сферы будет фронтальная проекция главного меридиана 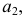 а горизонтальным очерком - горизонтальная проекция экватора
а горизонтальным очерком - горизонтальная проекция экватора 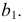 Для построения недостающих проекций
Для построения недостающих проекций 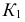 и
и 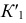 точек
точек 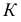 и
и 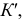 расположенных на поверхности, используют параллель. Видимость точек на поверхности определяют на фронтальной плоскости проекций
расположенных на поверхности, используют параллель. Видимость точек на поверхности определяют на фронтальной плоскости проекций 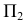 меридианом, а на
меридианом, а на 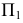 - экватором сферы. Невидимыми будут точки за меридианом и под экватором.
- экватором сферы. Невидимыми будут точки за меридианом и под экватором.
Тор открытый (или круговое кольцо). Ось вращения не пересекает образующую окружность, но лежит в ее плоскости. Уравнение поверхности:
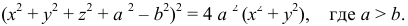
На рис. 191, а дана геометрическая часть определителя кругового кольца. Зная, что каждая точка линии 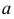 описывает окружность, плоскость которой перпендикулярна оси
описывает окружность, плоскость которой перпендикулярна оси 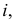 а центр расположен на оси, можно построить очерки поверхности. На рис. 191,б заданы очерки этой поверхности. По фронтальной проекции точки
а центр расположен на оси, можно построить очерки поверхности. На рис. 191,б заданы очерки этой поверхности. По фронтальной проекции точки 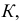 расположенной на поверхности, строят горизонтальные проекции ее. Если не известно, на видимой части поверхности расположена точка
расположенной на поверхности, строят горизонтальные проекции ее. Если не известно, на видимой части поверхности расположена точка 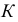 или на невидимой, то надо проводить все возможные параллели. В данном случае возможны две параллели, пересекающие образующую в двух точках 1 и 2, следовательно, при положении
или на невидимой, то надо проводить все возможные параллели. В данном случае возможны две параллели, пересекающие образующую в двух точках 1 и 2, следовательно, при положении 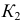 на поверхности возможны четыре положения точек
на поверхности возможны четыре положения точек 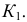
Тор закрытый. Ось вращения пересекает образующую окружность, но не проходит через ее центр (см. рис. 189). Уравнение поверхности:
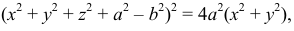 где
где 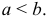
Эллипсоид вращения. Это поверхность, образованная вращением эллипса вокруг своей оси. Поверхность, образованная вращением вокруг малой оси, называется сжатым эллипсоидом вращения (рис. 192, а), а вращением вокруг большой оси - вытянутым эллипсоидом вращения (рис. 192, б).
Уравнение сжатого эллипсоида: 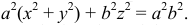
Уравнение вытянутого эллипсоида: 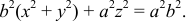
Параболоид вращения
Это поверхность, образованная вращение параболы вокруг ее оси (рис. 193). Уравнение поверхности: 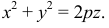
Гиперболоид вращения
Поверхность, образованная вращением гиперболы вокруг мнимой оси, называется однополостным гиперболоидом вращения (рис. 194, а). Поверхность, образованная вращением гиперболы вокруг ее действительной оси, называется двухполостным гиперболоидом вращения (рис. 194, б).
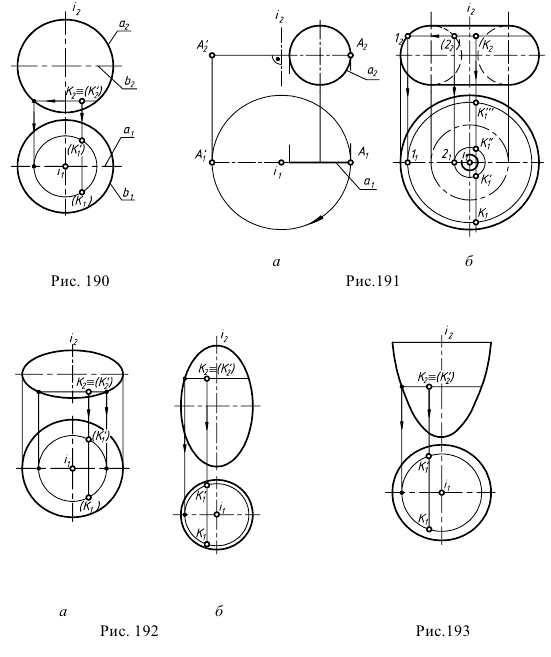
Уравнение двухполостного гиперболоида вращения: 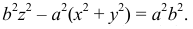 Уравнение однополостного гиперболоида вращения:
Уравнение однополостного гиперболоида вращения: 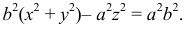
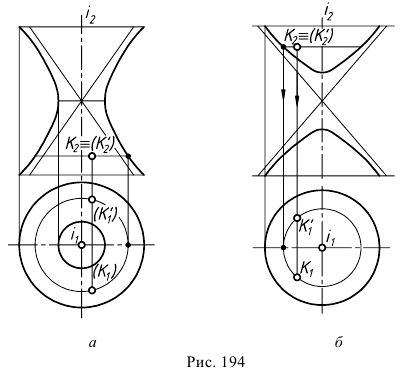
Линейчатые поверхности вращения
Поверхности, образованные вращением прямой линии вокруг оси, также являются поверхностями второго порядка. Возможны три случая взаимного расположения образующей 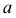 и оси
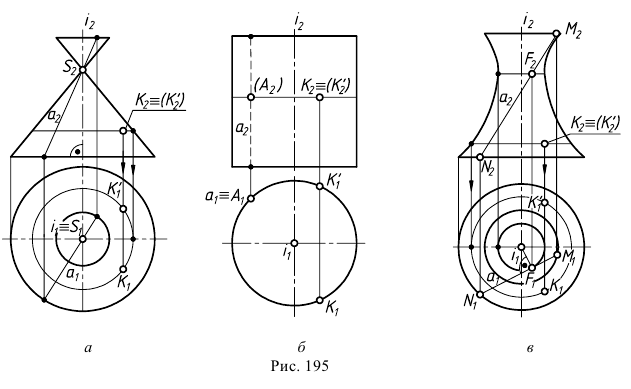
и оси 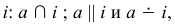 поэтому возможны три вида поверхностей (рис. 195).
поэтому возможны три вида поверхностей (рис. 195).
Коническая поверхность вращения
Образующая 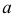 пересекает ось вращения
пересекает ось вращения 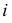 в точке
в точке 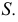 Если ось вращения
Если ось вращения 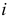 занимает проецирующее положение (см. рис. 195, а), то для построения точки, расположенной на поверхности, рационально построить параллель. Если ось поверхности занимает положение уровня (или общее), то для построения точки на поверхности удобно использовать образующую.
занимает проецирующее положение (см. рис. 195, а), то для построения точки, расположенной на поверхности, рационально построить параллель. Если ось поверхности занимает положение уровня (или общее), то для построения точки на поверхности удобно использовать образующую.
Уравнение конуса вращения: 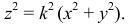
Цилиндрическая поверхность вращения
Образующая 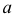 параллельна оси вращения
параллельна оси вращения 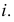 Если ось вращения - проецирующая прямая, то получаем проецирующую поверхность (см. рис. 195, б). Если ось занимает положение уровня, то для построения точки на поверхности необходимо использовать не параллель, которая на одной из плоскостей проекций изображается в виде эллипса, а образующую.
Если ось вращения - проецирующая прямая, то получаем проецирующую поверхность (см. рис. 195, б). Если ось занимает положение уровня, то для построения точки на поверхности необходимо использовать не параллель, которая на одной из плоскостей проекций изображается в виде эллипса, а образующую.
Уравнение цилиндра вращения: 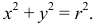
Однополостный гиперболоид вращения
Прямая 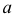 и ось вращения
и ось вращения 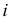 -скрещивающиеся прямые. На рис. 195, в показано построение параллелей, описываемых верхней точкой
-скрещивающиеся прямые. На рис. 195, в показано построение параллелей, описываемых верхней точкой 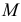 образующей
образующей 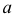 , нижней точкой
, нижней точкой 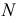 и точкой
и точкой 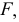 которая описывает горловину. Кратчайшее расстояние между скрещивающимися прямыми определяет точку
которая описывает горловину. Кратчайшее расстояние между скрещивающимися прямыми определяет точку 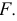 Для построения точки
Для построения точки 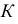 на поверхности используют параллель.
на поверхности используют параллель.
Линейчатые неразвертываемые поверхности с тремя направляющими
Определитель линейчатой поверхности с тремя направляющими имеет вид 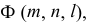 здесь
здесь 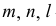 - направляющие.
- направляющие.
В зависимости от формы направляющих и их расположения в пространстве можно получить разнообразные поверхности. Некоторые из поверхностей этой группы представлены на рис. 196.
Поверхность косого цилиндра с тремя направляющими образуется при движении прямолинейной образующей по трем криволинейным направляющим (см. рис. 196, а). Такая поверхность может быть задана проекциями трех соответствующим образом подобранных направляющих.
Поверхность дважды косого цилиндра (см. рис. 158).
Поверхность дважды косого цилиндра образуется в том случае, когда две из трех направляющих кривые, а третья - прямая линия.
В инженерной практике находят применение частные случаи поверхности этого вида, например, поверхность косого клина. Эта поверхность получается в том случае, когда все три направляющие расположены в параллельных плоскостях, причем криволинейные направляющие -плавные кривые.
Поверхность косого клина используется при конструировании поверхности крыла летательного аппарата (см. рис. 196, б). При этом достигаются не только аэродинамические свойства крыла, но и обеспечиваются хорошие технологические условия изготовления его каркаса.
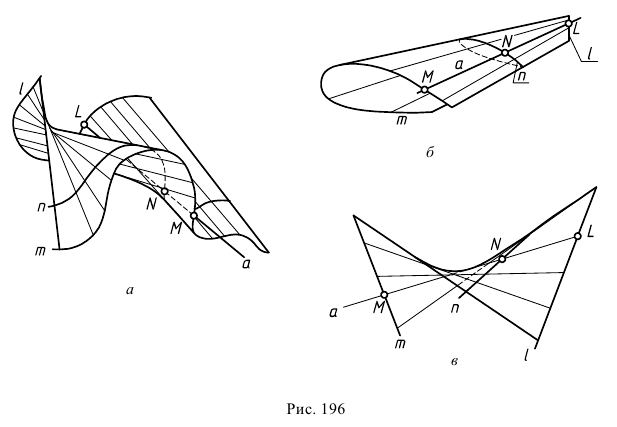
Поверхность однополостного гиперболоида может быть получена при движении прямолинейной образующей по трем скрещивающимся прямым, не параллельным одной плоскости.
На рис. 196, в поверхность однополостного гиперболоида задана прямыми направляющими 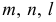 и показана образующая
и показана образующая 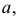 пересекающая направляющие в точках
пересекающая направляющие в точках 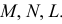
Нелинейчатые поверхности с образующей переменного вида
Эта группа поверхностей имеет определитель 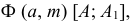
где 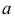 - образующая переменного вида,
- образующая переменного вида,
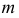 - направляющая,
- направляющая,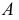 - закон перемещения образующей по направляющей,
- закон перемещения образующей по направляющей,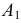 - закон изменения формы образующей.
- закон изменения формы образующей.
Из этой группы поверхностей можно выделить поверхность общего вида, образованную перемещением произвольной (плоской или пространственной) кривой 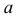 по криволинейной направляющей
по криволинейной направляющей  (см. рис. 159), и каналовую поверхность.
(см. рис. 159), и каналовую поверхность.
Каналовой (рис. 197) называют поверхность, образованную непрерывным каркасом замкнутых плоских сечений, определенным образом ориентированных в пространстве. Площади этих сечений монотонно изменяются в процессе их перемещения по направляющей 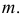 У поверхности, изображенной на рисунке, плоскости образующих ориентированы перпендикулярно направляющей.
У поверхности, изображенной на рисунке, плоскости образующих ориентированы перпендикулярно направляющей.
Нелинейчатые поверхности с образующей постоянного вида
Определитель такой поверхности имеет вид 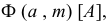 где
где
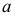 - образующая;
- образующая;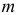 - направляющая;
- направляющая;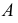 - закон перемещения образующей.
- закон перемещения образующей.
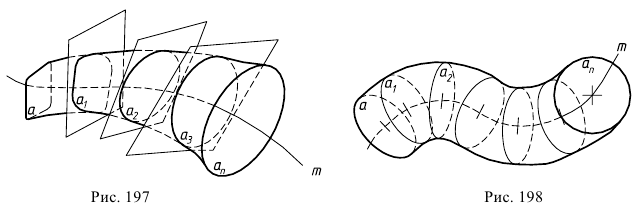
Характерным представителем этой группы поверхностей можно назвать трубчатую (циклическую) поверхность (рис. 198). Эту поверхность можно отнести также к каналовой поверхности, так как она содержит в себе свойства, присущие последней (см. рис. 197).
Поверхности параллельного переноса
Поверхностью параллельного переноса называют поверхность, образованную поступательным перемещением плоской линии. При этом образующие поверхность линии все время остаются параллельными между собой.
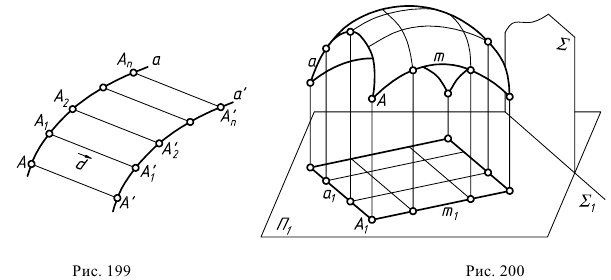
Под параллельными кривыми линиями подразумеваются линии, получаемые одна из другой путем параллельного переноса принадлежащих им точек на некоторое одинаковое расстояние. Например, на рис. 199 кривая 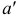 параллельна кривой
параллельна кривой 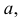 так как точки
так как точки 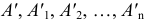 кривой
кривой 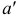 получены из точек
получены из точек 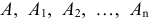 путем переноса их по параллельным прямым на величину вектора
путем переноса их по параллельным прямым на величину вектора 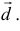
В общем виде поверхность переноса может быть задана производящей линией 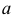 в начальном ее положении и направляющей (кривой линией
в начальном ее положении и направляющей (кривой линией 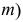 (рис. 200). Определитель такой поверхности имеет вид
(рис. 200). Определитель такой поверхности имеет вид 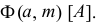
В геометрическую часть определителя входят образующая 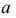 и направляющая
и направляющая 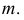 Алгоритмическая часть состоит из условия параллельного перемещения точек образующей
Алгоритмическая часть состоит из условия параллельного перемещения точек образующей 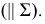
Графические и топографические поверхности
Нелинейчатая поверхность, кривая образующая 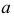 которой в процессе образования поверхности произвольно изменяет свой вид, называется графической (рис. 201).
которой в процессе образования поверхности произвольно изменяет свой вид, называется графической (рис. 201).
Форму графической поверхности имеют корпуса агрегатов, судов, двигательных аппаратов. Графическая поверхность задается некоторым числом линий, принадлежащих этой поверхности. К разряду графических относится топографическая (Topos (греч.) - местность, место) поверхность, т.е. земная поверхность с точки зрения ее изображений. Рельеф земной поверхности передается линиями - горизонталями 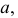 получаемыми при пересечении этой поверхности горизонтальными плоскостями (рис. 202).
получаемыми при пересечении этой поверхности горизонтальными плоскостями (рис. 202).
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |