Несинусоидальный ток

Содержание:

Несинусоидальный ток:

Периодическими несинусоидальными токами называют токи, изменяющиеся во времени по периодическому несинусоидальному закону.

Несинусоидальные токи

Несинусоидальные токи возникают при различных режимах работы электрических цепей. Таких режимов четыре.

1. Источник электрической энергии вырабатывает несинусоидальную ЭДС или несинусоидальный ток, а все элементы цепи (активные сопротивления, индуктивности и емкости) линейны, т. е. от величины тока не зависят. Такая цепь называется линейной.
2. Источник электрической энергии вырабатывает синусоидальную ЭДС, но один или несколько элементов цепи нелинейны, т.е. имеют нелинейные характеристики (катушка со стальным сердечником, выпрямители).
3. Источник электрической энергии вырабатывает несинусоидальную ЭДС, а в электрическую цепь входят одно или несколько нелинейных сопротивлений.
4. Источник электрической энергии вырабатывает постоянную или синусоидальную ЭДС, а один или несколько элементов цени в процессе работы изменяют свои параметры.

Таким образом, причиной несинусоидальности в электрической цепи может быть источник электрической энергии или потребитель, т. е. нагрузка, или оба одновременно.

В электрических генераторах (источниках электрической энергии) основной причиной несинусоидальной ЭДС (напряжений) является неравномерное распределение магнитного потока (по окружности) в зазоре между статором и ротором генератора.

Причиной появления несинусоидальных токов в нагрузке является, как указывалось выше, нелинейные вольт-амперные характеристики потребителей или преобразователей, например трансформаторов. В настоящей главе рассмотрен расчет и особенности работы линейных электрических цепей при воздействии на них несинусоидальных ЭДС, т. е. первый из перечисленных выше режимов работы. Остальные режимы рассматриваются в главе 19 и в специальной технической и справочной литературе.
 

Гармоники

Несинусоидальные колебания могут быть периодическими и непериодическими. При рассмотрении периодических несинусоидальных колебаний можно воспользоваться теоремой Фурье, Согласно которой любая периодически изменяющаяся величинa может быть представлена в виде суммы постоянной составляющей и ряда синусоидальных составляющих с кратными частотами.

Синусоидальные составляющие несинусоидальных колебаний называются гармониками.

Синусоидальная составляющая, частота которой равна частоте несинусоидальной периодической величины, называется основной, или первой, гармоникой. А синусоидальные составляющие, частоты которых в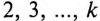

Аналитическое выражение несинусоидальной периодической функции можно записать так:

где 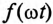— несинусоидальная величина, изменяющаяся с частотой 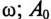— постоянная составляющая несинусоидальной величины; 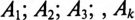- амплитуды соответственно 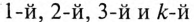гармоник, т. е. синусоидальных составляющих с частотой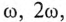 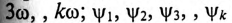 — начальные фазы соответственно 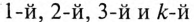гармоник.

Из выражения (18.1) следует, что сложение синусоидальных колебаний (гармоник) с различными частотами и разными начатыми фазами дает несинусоидальное колебание. Убедиться в этом можно при графическом сложении двух синусоидальных ЭДС 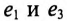(рис. 18.1).

На рис. 18.1а складываются две синусоиды 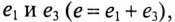где

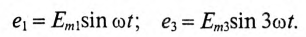
На рис. 18.1б складываются две синусоиды 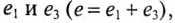где

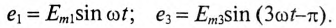
На рис. 18.1в складываются две синусоиды 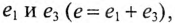где

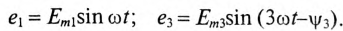
Как видно, суммарные колебания 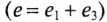в рассмотренных трех случаях (а,б и в) получились различными.

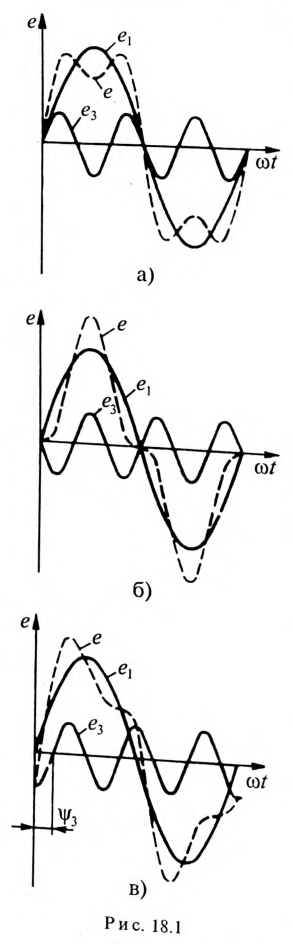
Из рис. 18.1 также видно, что не все несинусоидальные периодические колебания раскладываются в полный ряд Фурье. В данном случае складываются только 1-я и 3-я гармоники, и результирующие колебания 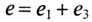могут быть записаны в виде:

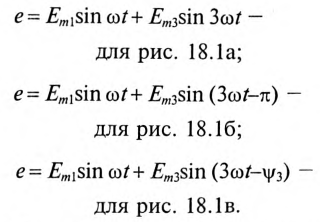
Таким образом, несинусоидальные кривые 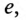изображенные на рис. 18.1, раскладываются в ряд Фурье только на нечетные гармоники 1-ю и 3-ю, т.е. в разложении отсутствуют постоянная составляющая, все четные гармоники и высшие нечетные гармоники (5-я, 7-я, 9-я и т.д.).

Гармоники можно преобразовать, применив из тригонометрии формулу синуса суммы двух углов. Из выражения (18.1) 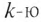гармонику можно представить в виде

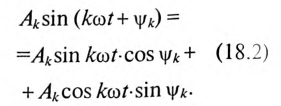
Обозначив постоянные величины выражения (18.2)

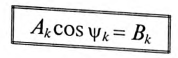
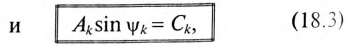
можно получить

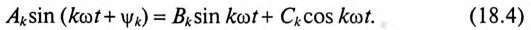
Тогда выражение (18.1), т.е. ряд Фурье для несинусоидальной периодической функции, примет вид

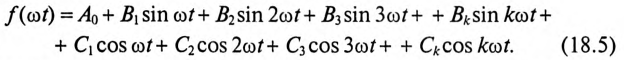
В отличие от амплитуды 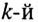гармоники 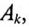постоянные величины 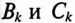могут быть положительными или отрицательными.

Такая запись (18.5) характерна тем, что гармоники составляют ряд синусов и ряд косинусов с начальными фазами, равными нулю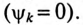
 

Свойства периодических кривых

Несинусоидальные периодические кривые, с которыми приходится встречаться в электротехнике, являются симметричными относительно оси абсцисс или ординат или начала координат.

Так как среднее за период Т значение синусоиды равно нулю (§ 10.3), то среднее за период значение несинусоидальных колебаний, состоящих из нескольких синусоид и не содержащих постоянной составляющей, также равно нулю.

Или иначе, если у несинусоидальной периодической кривой среднее за период значение (ордината) равна нулю, то постоянная составляющая такой кривой также равна нулю. Среднее значение периодической кривой, состоящей из постоянной составляющей и ряда гармоник, равно постоянной составляющей.

Так, например, пульсирующая кривая (рис. 18.2в) мгновенной мощности Р цепи переменного тока с активным сопротивлением может быть разложена на постоянную составляющую и синусоиду (гармонику), изменяющуюся с двойной частотой (см. выражение (11.3)), т.е. вторую гармонику. Среднее значение такой кривой равно постоянной составляющей, т. е. активной мощности 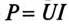 (см. (11.4)).

Периодическая кривая называется симметричной относительно оси абсцисс, если на расстоянии половины периода они имеют ординаты, одинаковые по величине, но обратные по знаку (рис. 18.2а), т.е. отрицательная полуволна такой кривой предоставляет собой зеркальное изображение положительной полуволны.

Кривые, симметричные относительно оси абсцисс, не содержат постоянной составляющей и четных гармоник (рис. 18.1). Такая кривая содержит только нечетные гармоники:

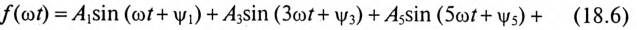
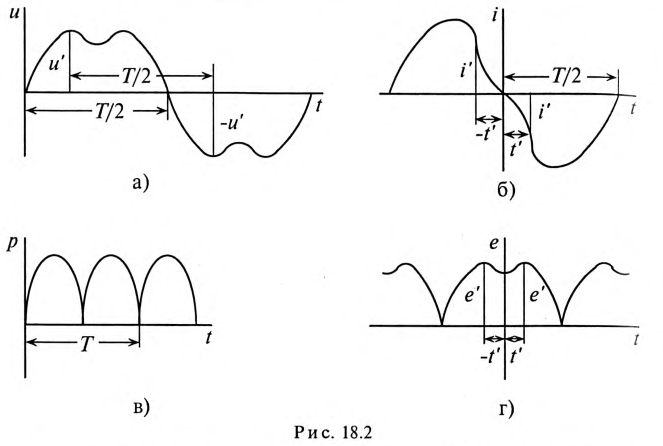
Кривые, симметричные относительно оси абсцисс, встречаются в электротехнике часто, например кривые тока в катушке со стальным сердечником, подключенной к сети с синусоидальным напряжением.

Периодическая кривая называется симметричной относительно начала координат, если любым двум абсциссам, имеющим одинаковое значение, но разные знаки, соответствуют ординаты, равные по величине и обратные по знаку (рис. 18.2б).

Кривые, симметричные относительно начала координат, не содержат постоянной составляющей и косинусоид. Такая кривая содержит только синусоиды:

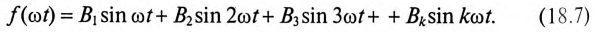
Часто встречаются кривые, симметричные относительно оси абсцисс и начала координат (кривые 1, 2, 3 и 4 таблицы 18.1). Такие кривые не содержат постоянной составляющей, четных гармоник и косинусоидальных составляющих, а содержат только нечетные синусоиды:

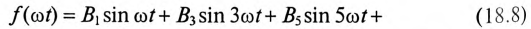
Кривая, симметричная относительно оси ординат, изображена на рис. 18.2г. Такая кривая не содержит синусоид. Она содержит постоянную составляющую и косинусоиды:

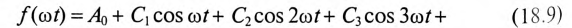
В таблице приведены несинусоидальные периодические кривые геометрически правильной формы и разложение их в ряд Фурье.

Таблица 18.1

 

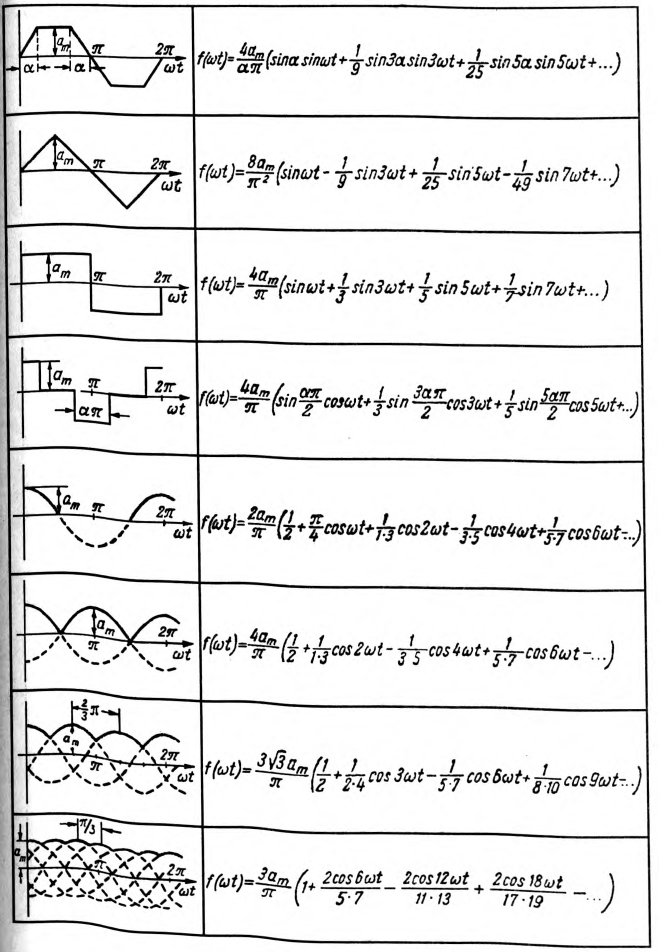
Несинусоидальный ток в линейных электрических цепях

Если к линейной цепи приложено несинусоидальное напряжение, которое раскладывается на ряд гармоник, то ток в этой цепи раскладывается на такое же количество тех же гармоник.

Если, например, к неразветвленной цепи, состоящей из R, L и С (рис. 18.3), приложено несинусоидальное напряжение

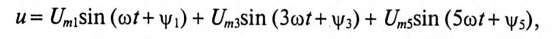
то сопротивление этой линейной цепи для различных гармоник имеет различные значения.

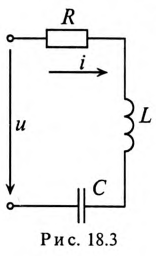
Активное сопротивление R для всех гармоник одинаковое, если пренебречь поверхностным эффектом.

Индуктивное сопротивление 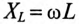с увеличением номера гармоники увеличивается, так как увеличивается частота 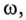и для любой гармоники может быть определено выражением

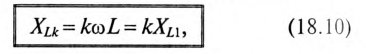
где 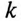— номер гармоники; 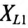- индуктивное сопротивление первой гармоники.

Емкостное сопротивление 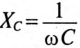увеличением номера гармоник уменьшается и для любой гармоники определяется выражением

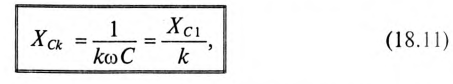
где 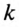— номер гармоники; 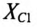— емкостное сопротивление первой гармоники.

Полное сопротивление неразветвленной линейной цепи для любой гармоники

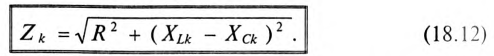
Угол сдвига фаз между током и напряжением для любой гармоники   

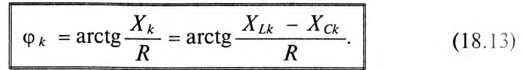
Очевидно, угол сдвига фаз 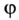может быть положительным или отрицательным в зависимости от характера цепи для определенной гармоники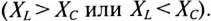

Амплитуды токов для каждой гармоники равны

Мгновенное значение несинусоидального тока в линейной цепи (рис. 18.3) с заданным несинусоидальным напряжением и определяется выражением

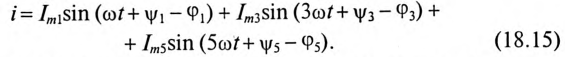
Если в неразветвленной цепи включен конденсатор, а в приложенном к этой цепи несинусоидальном напряжении имеется постоянная составляющая, то ток постоянной составляющей равен нулю, так как для постоянной составляющей конденсатор представляет разрыв цепи.

Если задан несинусоидальный ток в линейной цепи и 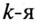гармоника тока записана

то напряжение в цепи, соответствующее этой гармонике, равно

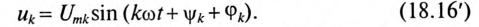
Для расчета всех параметров цепи используются выражения (18.10)—(18.14).

Пример 18.1

К линейной цепи (рис. 18.3) с параметрами 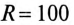,  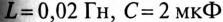приложено несинусоидальное напряжение

Определить и записать мгновенное значение тока 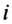в этой цепи.

Решение

Для определения полного сопротивления цепи вычисляются индуктивные и емкостные сопротивления для каждой гармоники (1-й, 3-й, 5-й и 7-й):

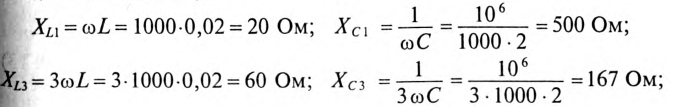
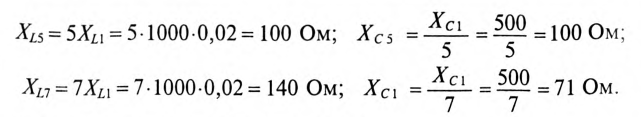
Тогда полные сопротивления Z гармоник:

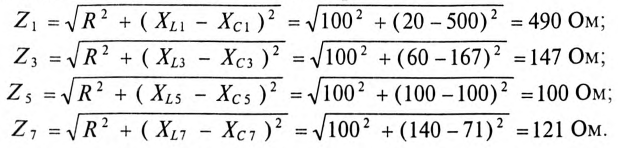
Амплитуды токов гармоник: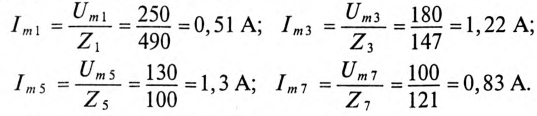                

Углы сдвига фаз для каждой гармоники: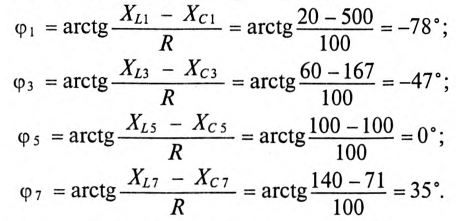

Тогда мгновенное значение тока в цепи равно

Из рассмотренного примера можно сделать следующий вывод. Если в линейной цепи включено только активное сопротивление R, то кривая тока будет подобна кривой напряжения. Если кроме активного в цепи имеются еще индуктивное и емкостное сопротивления, то кривая тока не будет подобна кривой напряжения. Такая цепь (рис. 18.3) для некоторых гармоник может иметь емкостной характер, например для первой и третьей гармоник в примере 18.1, так как ток опережает по фазе напряжение этих гармоник. Для некоторых гармоник — индуктивный характер, например для седьмой гармоники в примере 18.1, так как ток отстает от напряжения этой гармоники. Для одной из гармоник в разветвленной цепи с катушкой и конденсатором может быть резонанс напряжений, например для пятой гармоники в примере 18.1. Резонанс напряжений возник потому, что

В разветвленной цепи с несинусоидальным напряжением с параллельно соединенными катушкой и конденсатором для одной из гармоник может возникнуть резонанс токов при равенстве реактивных проводимостей, т. е.


Пример 18.2

В линейной цепи (рис. 18.3) протекает несинусоидальный ток 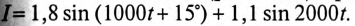Параметры цепи: 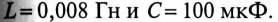Записать мгновенное значение напряжения 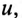приложенного к этой цепи.

Решение

Определяется индуктивное и емкостное сопротивления для 1-й и 2-й гармоник:

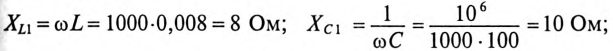
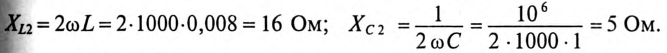
Полные сопротивления Z для 1-й и 2-й гармоник будет равны

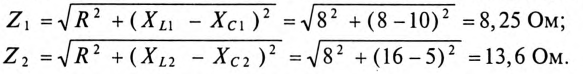
Амплитуды напряжений гармоник:

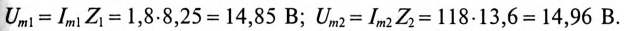
Углы сдвига фаз 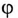 для 1-й и 2-й гармоник:

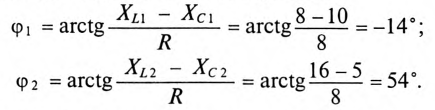
Мгновенное значение приложенного напряжения будет равно

 

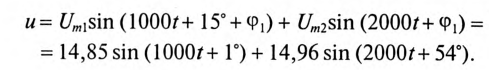
Действующее значение несинусоидальной величины

Действующим называют значение несинусоидального тока, эквивалентное постоянному току по тепловому действию.

При этом нужно учесть, что несинусоидальный ток складывается из постоянной составляющей и ряда гармоник:

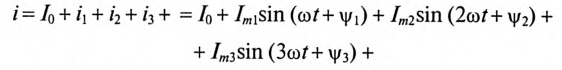
Каждая составляющая несинусоидального тока выделяет тепло в некотором элементе цепи с сопротивлением R. Воспользовавшись рассуждениями § 10.3 для определения действующих значений тока гармоник и постоянной составляющей несинусоидального тока, можно сделать вывод, что

где 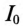— постоянная составляющая несинусоидального тока;  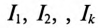 — действующее значение токов гармоник, т.е.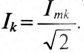

Таким образом, действующее значение несинусоидального тока является средней квадратичной величиной постоянной составляющей и действующих значений токов гармоник.

С учетом выражения (10.9) действующее значение несинусоидального тока можно определить по формуле

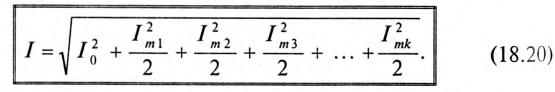
Аналогично действующее значение несинусоидального напряжения определяется выражением

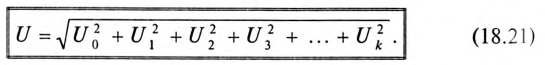
Действующее значение несинусоидального напряжения является средней квадратичной величиной постоянной составляющей и действующих значений напряжений гармоник.

Действующие значения несинусоидальных токов и напряжений измеряются амперметрами и вольтметрами электромагнитной, электродинамической и тепловой систем.

Кроме коэффициента формы 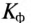и коэффициента амплитуды, определение которых дано в § 10.3 (выражение (10.10) и (10.11)), несинусоидальные периодические кривые характеризуйся коэффициентом искажений 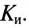Коэффициент искажений определяется отношением действующего значения основной (первой) гармоники тока или напряжения к действующему значению этих несинусоидальных величин. Такое определение аналогично для ЭДС, магнитного потока и т. д.

Коэффициент искажения тока

Коэффициент искажения напряжения

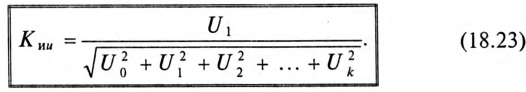
Для синусоиды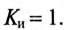

Чем меньше коэффициент искажения отличается от единицы, тем ближе к синусоиде данная кривая.

Так, например, для треугольной формы кривой (кривая 2 таблицы 18.1) - 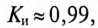, а для прямоугольной формы кривой (кривая 3 таблицы 18.1) -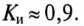

В электронике и радиотехнике несинусоидальность кривой характеризуют коэффициентом гармоник, показывающим удельный вес высших гармоник 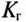относительно первой (основной) гармоники:

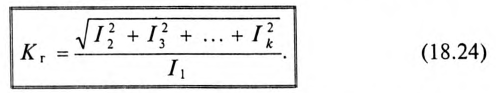
Чем меньше коэффициент гармоник, тем ближе к синусоиде несинусоидальная кривая.
 

Мощность несинусоидального тока

Под активной мощностью Р несинусоидального тока понимают среднее значение мгновенной мощности (§ ll.l) за период, т. е.

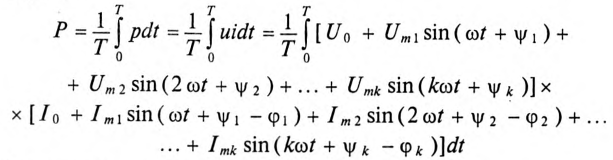
Проинтегрировав это выражение, получают

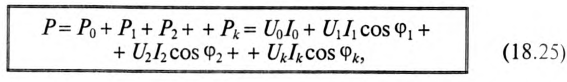
где 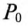— мощность постоянной составляющей несинусоидального тока; 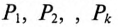— активные мощности гармоник несинусоидального тока.

Таким образом, потребляемая, т. е. активная, мощность в цепи несинусоидального тока определяется суммой постоянной мощности и активных мощностей гармоник.

Реактивная мощность в цепи несинусоидального тока, по аналогии, определяется выражением

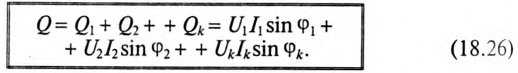
Реактивная мощность в цепи несинусоидального тока определяется суммой реактивных мощностей гармоник.

Постоянная составляющая реактивной мощности отсутствует, так как для постоянного тока колебание мощности (энергии) немыслимо.

Полная, или кажущаяся, мощность в цепях несинусоидального тока равна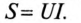

Следует иметь в виду, что несинусоидальный ток или напряжение не могут быть выражены при помощи векторов. Кривые несинусоидального тока и напряжения в общем случае даже не подобны. Так что невозможно применить понятие об угле сдвига фаз, принятое для синусоидальных токов.

Поэтому при изучении некоторых свойств цепей несинусоидального тока несинусоидальные токи и напряжения заменяют эквивалентными синусоидальными. Замена производится таким образом, что действующее значение синусоидального тока придется равным действующему значению заменяемого несинусоидального тока, а действующее значение синусоидального напряжения принимается равным действующему значению несинусоидального напряжения.

Тогда угол сдвига фаз 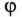между эквивалентными синусоидами ряжения и тока выбирается таким, чтобы активная мощность эквивалентного синусоидального тока была равна активной мощности несинусоидального тока, т.е.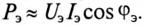

Откуда 

При этом 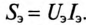Однако для цепи несинусоидального тока в общем случае

Равенство 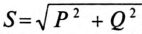(выражение (12.14)), выведенное из треугольника мощностей (рис. 12.2в), справедливо для синусоидального тока определенной частоты 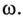Несинусоидальный ток складывается из нескольких синусоидальных составляющих с разными (кратными) частотами и разными углами сдвига фаз  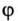между током и напряжением (определенными для каждой гармоники); т. е. для несинусоидального тока нельзя построить векторную диаграмму и прямоугольный треугольник мощностей. Поэтому выражение (12.14) для несинусоидального тока несправедливо и полная (кажущаяся) мощность не равна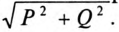

Пример 18.3

К линейной цепи (рис. 18.4) приложено несинусоидальное напряжение 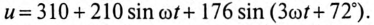Реактивные сопротивления для первой гармоники: 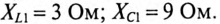Активов сопротивления: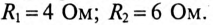

Требуется записать мгновенное значение тока цепи 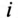и определить показания всех приборов, включенных в цепь, а также коэффициент мощности цепи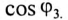

Решение

Так как в цепь включен конденсатор, то сопротивление цепи для постоянной составляющей несинусоидального напряжения равно бесконечности, а ток постоянной составляющей равен нулю, т. е.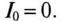

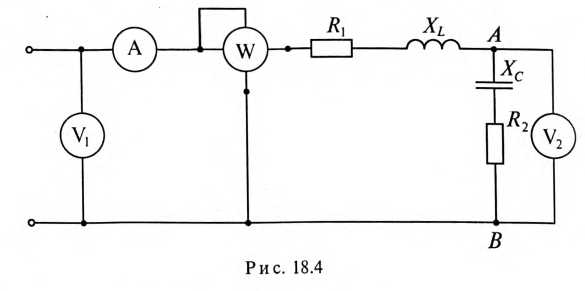
Сопротивление цепи для 1-й и 3-й гармоник:

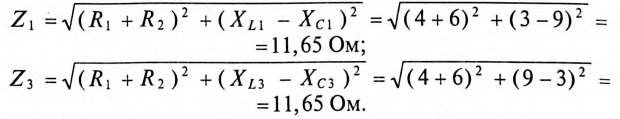
так как 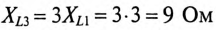и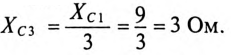

Амплитуды токов гармоник: 

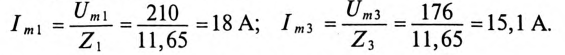
Углы сдвига фаз 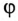для 1-й и 3-й гармоник:

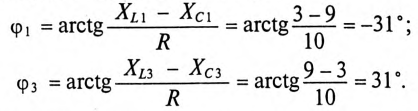
Тогда мгновенное значение несинусоидального тока цепи будет записано

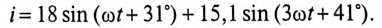
Показания вольтметра 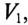т.е. действующее значение приложенного к цепи напряжения:

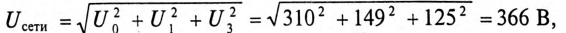
так как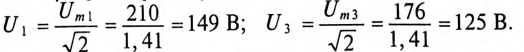

Таким образом, первый вольтметр 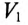показывает 366 В Амперметр А показывает действующее значение тока цепи

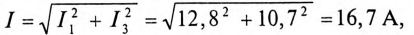
Так как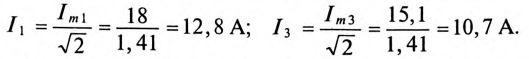

Таким образом, амперметр А показывает ток 16,7 А.

Для определения показаний второго вольтметра 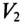вычисляют сопротивление участка АВ для 1-й и 3-й гармоник:

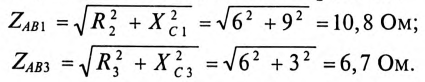
Тогда падение напряжения для 1-й и 3-й гармоник на участке АВ будет равно

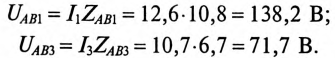
Кроме того, постоянная составляющая напряжения сети 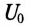 приложена к конденсатору. Следовательно, действующее значение напряжения на участке АВ:

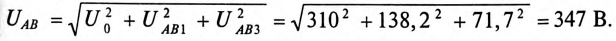
Таким образом, вольтметр 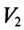показывает 347 В. Ваттметр 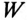измеряет активную мощность цепи, т. е.

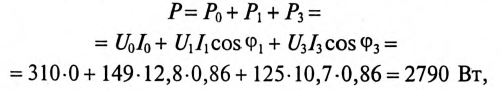
так как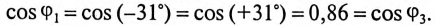

Ваттметр W показывает мощность P= 2790 Вт.

Для определения коэффициента мощности цепи 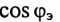вычисляется полная мощность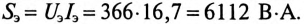

Тогда коэффициент мощности цепи

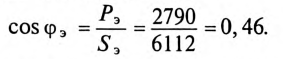
Эквивалентные синусоидальным величины .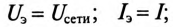

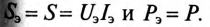Пример 18.4

Несинусоидальный ток в линейной цепи (рис. 18.5) 
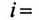
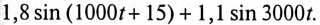Параметры цепи: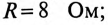

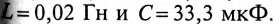
Требуется: записать мгновенное значение приложенного к цепи напряжения; определить показание всех включенных в цепь приборов; определить полную S, реактивную Q мощности и эквивалентный угол сдвига фаз между током и напряжением цепи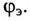

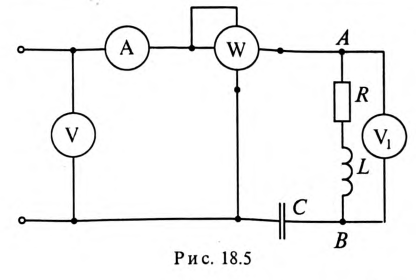
Решение

Определяются индуктивное 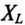и емкостное 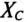сопротивления для 1-й и 3-й гармоник:

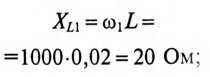
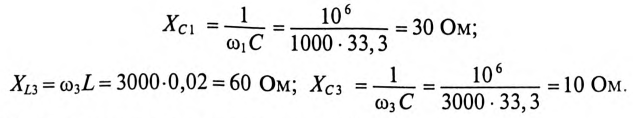
Сопротивление цепи для 1-й и 3-й гармоник:

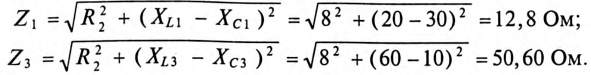
Амплитуды напряжений сети для 1-й и 3-й гармоник:

.

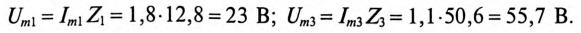Углы сдвига фаз для этих гармоник:

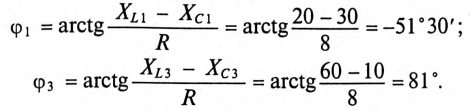
Тогда мгновенное значение приложенного к цепи напряжения записывается

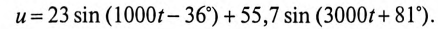
Действующее значение приложенного напряжения:

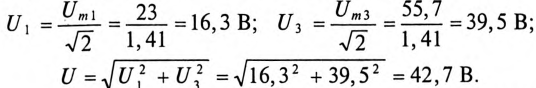
Вольтметр, включенный на входе цепи, показывает 42,7 В. Действующее значение тока:

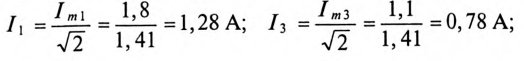
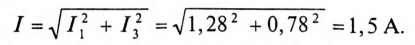
Амперметр показывает ток 1,5 A.

Ваттметр показывает активную мощность в цепи потребителей, определяемую значениями

Показания ваттметра:

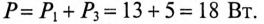
Вольтметр показывает падение напряжения на участке цепи АВ

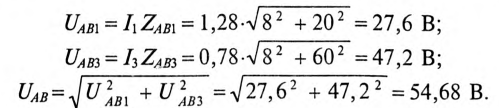
Вольтметр показывает напряжение 54,68 В.

Полная, или кажущаяся, мощность в цепи несинусоидального тока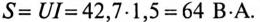

Реактивная мощность Q цепи равна

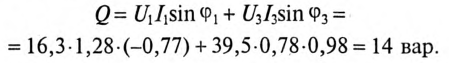
Эквивалентный угол сдвига фаз 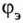между током и напряжением

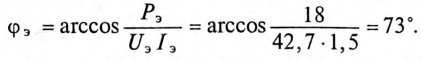
Эквивалентные синусоидальные величины соответственно равны

 

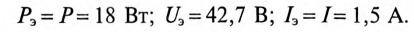
Электрические фильтры

Электрическая цепь, содержащая индуктивность и емкость, обладает различными сопротивлениями для различных гармоник, так как индуктивное сопротивление 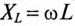с увеличением номера гармоники (увеличивается частота) увеличивается, а емкостное  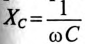уменьшается. Это дает возможность при заданной кривой напряжения изменять форму кривой тока путем включения электрического фильтра между источником и потребителем (рис. 18.6).

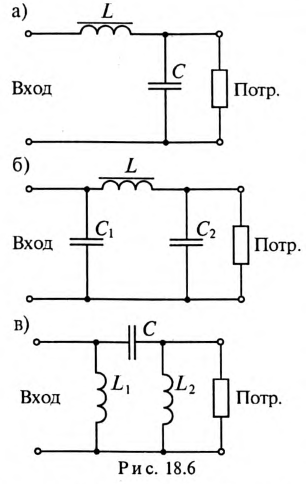
Для того чтобы отфильтровать высшие гармоники несинусоидального напряжения, т.е. не пропустить их к потребителю, последовательно с потребителем включается индуктивность, а параллельно емкость (рис. 18.6а, б). При этом чем выше номер гармоники, тем большим сопротивлением обладает индуктивность и тем большее напряжение этой гармоники падает на индуктивном сопротивлении и тем меньшее напряжение поступает на нагрузку. Кроме того, чем выше номер гармоники (частота), тем меньше сопротивление конденсатора, тем больший ток этой частоты проходит через конденсатор, отфильтровываясь от потребителя. На рис. 18.6 показаны Г-образный фильтр (рис. 18.6а) и П-образный фильтр (рис. 18.6б).

Если нужно отфильтровать постоянную составляющую несинусоидального напряжения или его низкие частоты (гармоники), то в фильтре (рис. 18.6а, б) меняют местами индуктивность и емкость (рис. 18.6в).

Если в напряжении, поступающем на вход фильтра, имеется 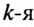гармоника, которую нужно отфильтровать, т. е. не пропустить к потребителю, то последовательно с потребителем можно включить параллельный резонансный контур (рис. 18.7а), настроенный в резонанс токов на частоту этой 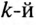гармоники. В результате чего на большом сопротивлении резонансного контура (близкого к бесконечности — при отсутствии активного сопротивления в контуре) напряжение 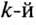гармоники падает на контуре, не попадая на нагрузку.

Такого же эффекта можно добиться, если параллельно с потребителем включить последовательный резонансный контур (рис. 18.7б), настроенный в резонанс напряжений на частоту 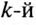гармоники.

При резонансе напряжений сопротивление последовательного контура мало, следовательно, уменьшается сопротивление участка АВ схемы и уменьшается напряжение 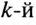гармоники на нем, а следовательно, и на потребителе.

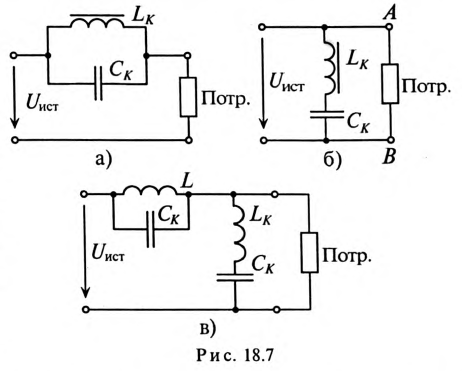
Одновременное включение обоих контуров (рис. 18.7в) обеспечивает значительно лучшую фильтрацию.

Однако резонансные фильтры хорошо отфильтровывают ту гармонику, на частоту которой они настроены в резонанс.

Фильтры, в которых резонансные контуры поменяли местами (рис. 18.8 по отношению к рис 18.7), называются полосовыми и служат для того, чтобы пропустить к приемнику 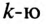гармонику, на которую они настроены в резонанс, и не пропустить другие гармоники.

Электрические фильтры широко используются в радиотехнике, в технике сильных токов, в выпрямительной технике, в технике Проводной связи, в вычислительной технике и др.

Определение несинусоидального тока

Расчет электрических цепей, выполненный ранее, проводился в предположении, что источники энергии были либо постоянными, либо синусоидальными и вызывали в элементах цепей постоянные или синусоидальные токи. В реальных условиях кривые ЭДС, напряжения и тока лишь в определенной мере могут считаться синусоидальными, при этом указанные параметры цепей могут иметь характер периодический, квазипериодический (почти периодический) и непериодический. Это происходит из-за наличия в электрических цепях нелинейных элементов: вентиля (диода), электрической дуги, катушки со стальным сердечником (дросселем), различного рода электрических помех и т.д., которые искажают синусоидальный сигнал, приводя к появлению несинусоидальных токов и напряжений. Кроме того, сам источник энергии может являться генератором несинусоидальной ЭДС. На рис. 7.1 представлены варианты данных сигналов.

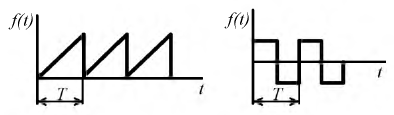
Рис. 7.1. Примеры несинусоидальных периодических сигналов

Так как рассматриваем линейные цепи, то появление несинусоидальных токов и напряжений обусловлено в этой главе наличием несинусоидальных источников напряжения.

Разложение периодической функции в тригонометрический ряд

Во всех задачах, где приходится иметь дело с периодическими несинусоидальными функциями токов, ЭДС и напряжений, необходимо свести их к более простому виду, для которого возможно применение известных методов расчета. Процессы, происходящие в линейных электрических цепях при несинусоидальных токах и напряжениях, удобнее всего рассчитывать, если воспользоваться тригонометрическим рядом Фурье. В общем случае выражение этого ряда имеет вид:

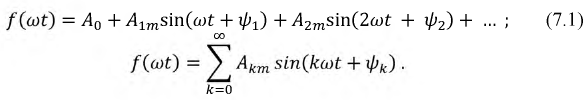
Первое слагаемое носит название нулевой гармоники или постоянной составляющей ряда При 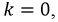где к - номер гармоник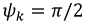и, и 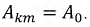Она присутствует в составе ряда не всегда. Если функция симметрична относительно оси времени, то нулевой составляющей нет.

Второе слагаемое - это первая или основная гармоника ряда. Она задает основной период несинусоидальной функции 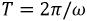(см. рис. 7.1).

Все остальные слагаемые носят название высших гармоник ряда. Период каждой из них кратен периоду основной гармоники. Сделаем преобразование ряда, раскрыв синус суммы:

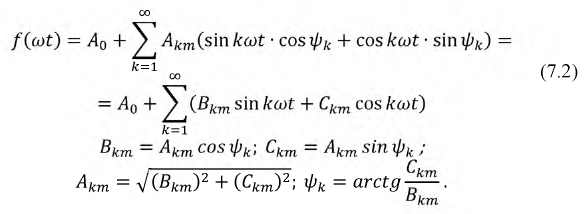
Коэффициенты ряда определяются по следующим формулам:

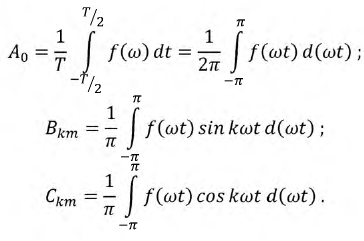
Выражения для коэффициентов ряда позволяют получить разложение в ряд любой периодической несинусоидальной функции, однако для большинства таких функций, которые используются в электрических цепях, эти разложения уже получены и могут быть взяты в соответствующей справочной литературе.

Состав элементов ряда может быть упрощен, если вид исходной функции обладает тем или иным видом симметрии, что иллюстрируется рис. 7.2.а).

a) 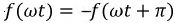- функция симметрична относительно оси абсцисс.

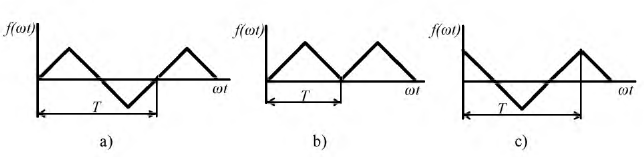
Рис. 7.2. Виды симметрии периодических функций

Разложение в ряд такой функции не содержит постоянной составляющей и четных гармоник:

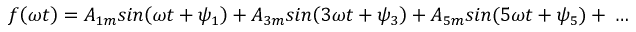
b) 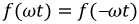 - функция симметрична относительно оси ординат.

В этом случае ряд не содержит синусных составляющих:

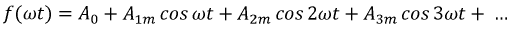
c) 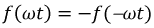- функция симметрична относительно начала координат.

Такая функция не содержит постоянной составляющей и косинусных составляющих:

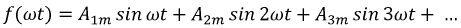
Амплитудное, среднее и действующее значения периодических несинусоидальных функций

Эти понятия аналогичны тем, которые были введены применительно к синусоидальным колебаниям, но в то же время они имеют свою специфику.

Амплитудное значение - это максимальное значение функции за период. На рис. 7.3 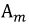- это максимальное значение функции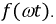 

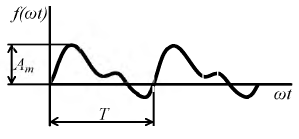
Рис. 7.3. График несинусоидальной функции

Среднее по модулю значение:

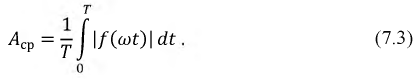
Действующее значение:

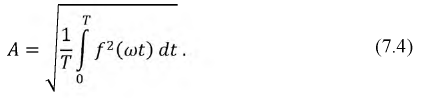
Последний из приведённых параметров относится к наиболее важным параметрам несинусоидальных периодических функций, поскольку именно эта величина измеряется приборами. Будем считать, что функция 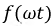 задана рядом (7.1), тогда:

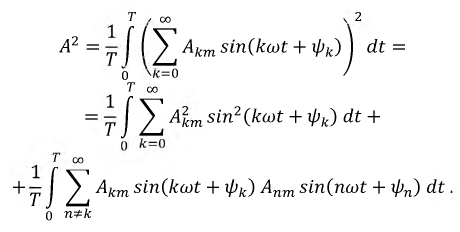
Второе слагаемое при интегрировании за полный период 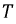обращается в ноль ввиду симметрии синусоидальных функций, таким образом:

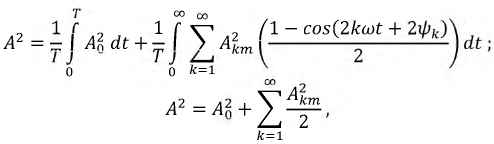
где 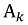- действующее значение каждой из гармоник.

Тогда:

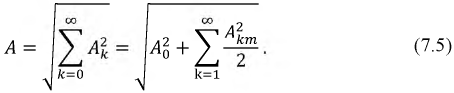
Например, действующие значения несинусоидального напряжения определятся выражением:

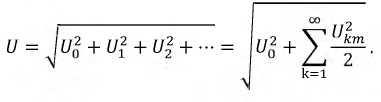
Коэффициенты, характеризующие форму несинусоидальных периодических функций

Для оценки несинусоидальных периодических функций в электроэнергетике вводят коэффициенты формы 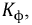амплитуды 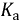и искажения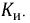

Коэффициент формы определяется как отношение действующего значения функции к ее среднему по модулю значению:

Для синусоиды:

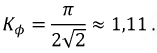
Коэффициент амплитуды равен отношению максимального значения функции к ее действующему значению:

Для синусоиды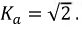 

Коэффициент искажений определяется отношением действующего значения первой гармоники к действующему значению всей кривой:

Для синусоиды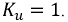

В электронике для оценки искажений пользуются коэффициентом гармоник, который определяется отношением действующего значения высших гармоник к действующему значению первой гармоники:

Для синусоиды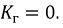 

В электроэнергетике вводят понятие практически синусоидальной кривой. Если действующее значение высших гармоник в напряжении промышленной сети не превышает 5% от действующего значения гармоники основной частоты, то такое напряжение считается практически синусоидальным.

Приборы электромагнитной, электродинамической и тепловой систем регистрируют действующее значение измеряемой величины. Приборы магнитоэлектрической системы реагируют на постоянную составляющую, а с выпрямителем - среднее по модулю значение.

При коэффициенте формы 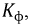сильно отличающимся от 1,11, погрешность приборов выпрямительной системы становится значительной.

Мощность периодических несинусоидальных токов

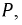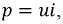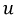Для определения активной мощности выделяемой на приемниках, воспользуемся формулой мгновенной мощности  где и 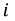заданы соответствующими рядами Фурье. Тогда 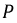определяется по выражению:

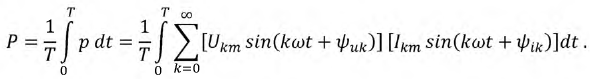
Используя известное тригонометрическое тождество:

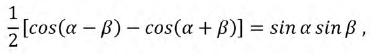
получим:

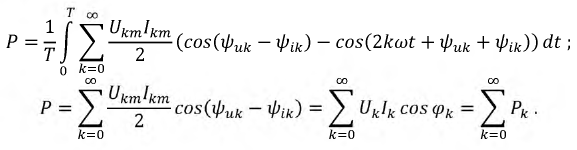
Искомая активная мощность:

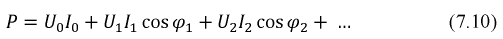
Аналогично определяется реактивная мощность:

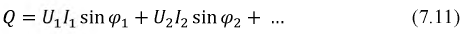
Полная мощность рассчитывается по формуле:

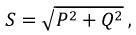
лишь в том случае, если спектры тока и напряжения совпадают. При несовпадении спектров этих функций:

где 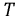- мощность искажения, обусловленная несовпадением спектров тока и напряжения.

Полную мощность целесообразно рассчитывать по формуле:

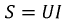
Для цепей с несинусоидальными источниками аналогично синусоидальным цепям вводят понятие коэффициента мощности:

где 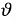некоторый фиктивный угол между эквивалентными синусоидами тока и напряжения, определяемый из соображения равенства активной мощности эквивалентного синусоидального тока и активной мощности несинусоидального тока.

Несинусоидальные функции времени с периодической огибающей

В отличие от периодических функций, рассмотренных выше, существуют несинусоидальные кривые с периодическими или почти периодическими огибающими. Для них характерно то, что они имеют конечное число слагаемых в разложении исходного ряда. Причем частоты огибающих и составляющих ряда несоизмеримы. Классическими примерами таких функций являются биения и модуляция.

Биения

Функция биения представляет собой сумму двух синусоидальных колебаний, имеющих одинаковые амплитуды и близкие, но не равные частоты.

причем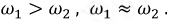 

Сумма этих функций:

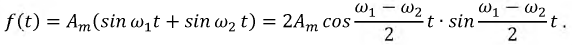
Обозначим:

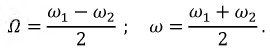
Тогда:

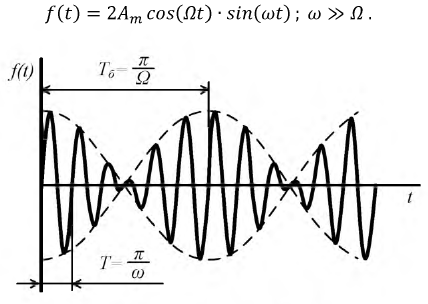
Рис. 7.4. График функции биения

В общем случае период биений 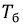не равен периоду кривой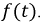 

Однако если отношение 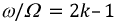составляет целое нечетное число, то период биений совпадает с периодом кривой  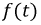и она является периодической.

Если отношение периодов биений и огибающей не равно целому числу, то результирующее колебание является квазипериодическим.

Модуляция

Синусоидальные колебания характеризуются тремя основными параметрами: амплитудой, частотой и начальной фазой. Если один из этих параметров медленно меняется во времени по некоторому периодическому закону, то говорят об амплитудной, частотной или фазовой модуляции. Рассмотрим данное явление на примере амплитудной модуляции, которая может быть представлена функцией вида:

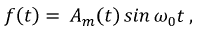
где 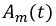- меняется по некоторому периодическому закону:

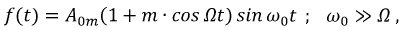
где 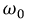 - несущая частота;  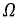- модулирующая частота; 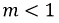- коэффициент (глубина) модуляции.

Параметр 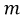показывает отклонение амплитуды модулирующего колебания от некоторого среднего значения. Выполним для рассматриваемой функции простейшие преобразования:

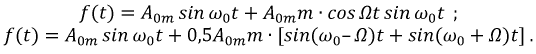
В результате модулированные по амплитуде колебания являются суммой трех колебательных составляющих. Одного с несущей частотой 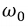и двух других с боковыми частотам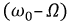и и 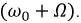График модулированного по амплитуде колебания приведен на рис. 7.5.

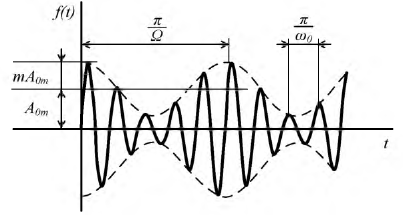
Рис. 7.5. График модулированных по амплитуде колебаний

Этот вид модуляции далеко не лучший, поскольку он в наибольшей степени подвержен помехам. Для повышения помехоустойчивости используются комбинированные методы модуляции.

Резонансные явления в цепях с несинусоидальными источниками

Рассматривая однофазные синусоидальные цепи, мы познакомились с явлением резонанса. Указанное явление имеет место и в цепях с несинусоидальными источниками, однако в этом случае оно имеет определенную специфику, связанную с тем, что резонанс может возникнуть как на основной частоте, так и на высших гармониках.

Для последовательного контура в цепях с несинусоидальным источником условие резонанса будет задано соотношением:

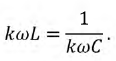
Ток в цепи на 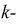ой гармонике можно рассчитать по формуле:

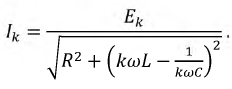
Меняя, например, индуктивность 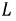 от 0 до  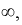для каждой из гармоник при некотором значении частоты и фиксированной 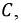можно получить резонансный режим. Пунктирной кривой показана результирующая зависимость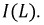

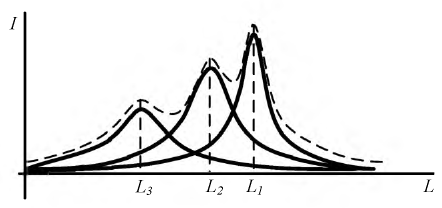
Рис. 7.6. Зависимость тока от индуктивности в цепи с несинусоидальным источником напряжения

Методика расчета цепей с несинусоидальными источниками

1. Заданную несинусоидальную функцию, питающую цепь, раскладывают в ряд Фурье и ограничиваются при этом несколькими гармониками, отбрасывая составляющие ряда, удельный вес которых незначителен.
2. Любым из известных методов расчета сложных электрических цепей производится расчет токов и напряжений заданной цепи. При этом используется комплексный метод расчета. Эта процедура выполняется для всех гармоник ряда, включая и постоянную составляющую, которая эквивалентна цепи с постоянным источником напряжения.

Комплексные решения, полученные для каждой из гармоник, складывать нельзя. Эту процедуру мешает выполнить то обстоятельство, что соответствующие полученным решениям векторы будут вращаться с различными угловыми частотами. Поэтому полученные комплексные решения должны быть переведены в реальные функции времени и лишь затем представлены в виде суммы (ряда Фурье) на основании принципа наложения.

Пример:

На цепь, схема которой изображена на рис. 7.7 b подаётся несинусоидальное напряжение 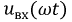(см. рис. 7.7а) амплитудой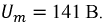 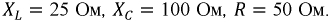Определить действующее значение напряжения на выходе, ограничиваясь первыми тремя членами ряда, в который можно разложить функцию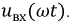

Примечание. Величины индуктивного и емкостного сопротивлений заданы для первой гармоники.

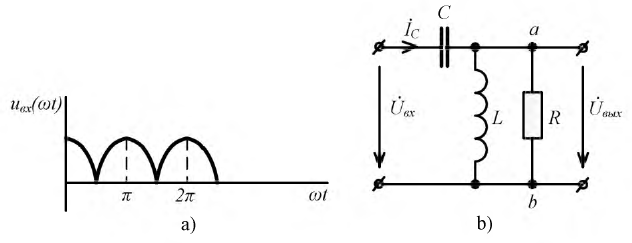
Рис. 7.7. Форма подводимого напряжения (а) и схема исследуемой цепи (b)

Используя известное разложение для заданного напряжения 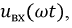получим:

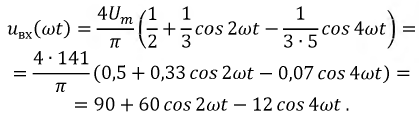
Для определения функции выходного напряжения составим передаточную функцию исходной цепи 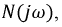которая связывает входное и выходное напряжения и является частотно-зависимой:

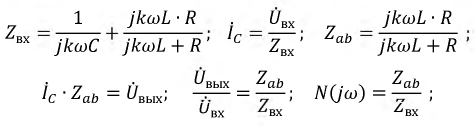
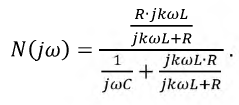
Определим 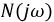для значений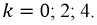 

При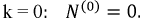 

При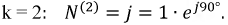 

Полученный результат показывает, что амплитуда выходного сигнала для второй гармоники равна амплитуде входного. Фаза выходного напряжения на этой же гармонике опережает фазу входного напряжения на 90°.

При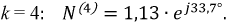 

Используя полученные значения функции 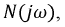представим выходное напряжение в виде ряда:

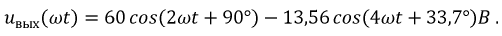
Итоговое действующее значение напряжения 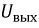 будет:

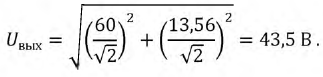
Высшие гармоники в трёхфазных цепях

Рассмотрим поведения высших гармоник в трёхфазных системах. При этом будем полагать, что фазные напряжения источника не содержат постоянных составляющих и четных гармоник, т.е. кривые напряжения симметричны относительно оси абсцисс, которые на практике встречаются наиболее часто.

Пусть напряжение фазы 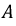источника, разложенное в ряд Фурье, имеет вид:

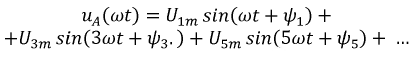
При записи напряжений фаз 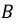и 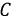учтем, что фаза 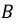отстает от фазы 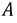на 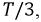 а фаза 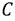опережает фазу 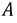на 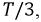тогда:

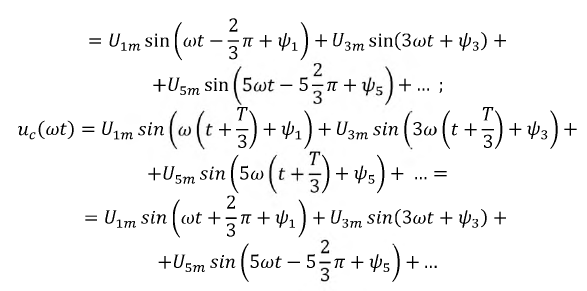
Для гармоник кратных трем 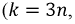 где 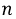 - целое число) напряжения во всех фазах совпадают по величине и направлению, т.е. они образуют нулевую последовательность фаз.

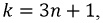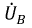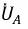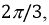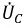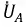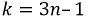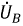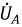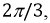Если номер гармоники  то напряжения образуют систему прямой последовательности фаз, когда напряжение отстает от на угол  а опережает на такой же угол. Для гармоник с номером напряжения образуют систему обратной последовательности фаз, когда опережает на a 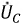отстает от 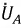на этот же угол.

На рис. 7.8 показаны симметричные составляющие соответствующих систем напряжений в трёхфазных цепях.

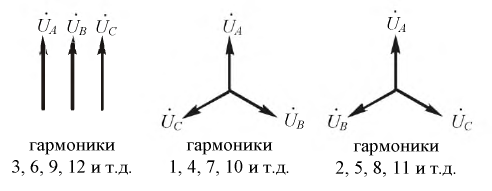
Рис. 7.8. Симметричные составляющие системы несинусоидальных напряжений в трёхфазных цепях

Способ соединения фаз генератора и нагрузки звездой

В линейных напряжениях, определяемых как разность соответствующих фазных напряжений, гармоники напряжений, кратные трем, отсутствуют, поэтому при несинусоидальных напряжениях:

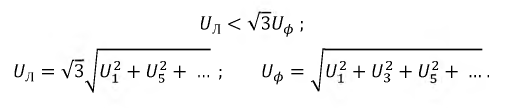
При наличии нулевого провода при симметричной нагрузке ток в нулевом проводе не равен нулю (гармоники тока кратные трем, образуют нулевую последовательность):

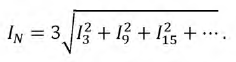
Гармоники тока, не кратные трем, в сумме дают нуль.

При отсутствии нулевого провода сумма фазных токов должна равняться нулю, поэтому в фазных токах гармоники, кратные трем, отсутствуют. Тогда между нулевыми точками источника и приемника возникает напряжение смещения, которое можно определить методом двух узлов:

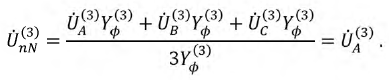
Для гармоник напряжений, не кратных трем, при симметричной нагрузке смещение нейтрали 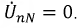Следовательно, вольтметр, включенный между нулевыми точками источника и приемника, покажет значение:

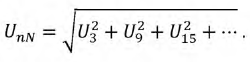
Способ соединения фаз генератора и нагрузки треугольником

При наличии в ЭДС гармоник, кратных трем, они образуют систему нулевой последовательности, поэтому результирующая ЭДС гармоник, кратных трем при соединении фаз треугольником, равна утроенной ЭДС одной фазы.

При этом вольтметр, включенный в разрыв обмоток (рис. 7.9), покажет напряжение:

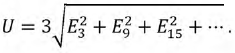
Если обмотки генератора соединить треугольником, то под действием ЭДС с номерами гармоник кратных трем возникают соответствующие гармоники тока. Результирующий ток в обмотках создает падения напряжения на сопротивлениях обмоток, которые, в свою очередь, уравновешивают ЭДС.

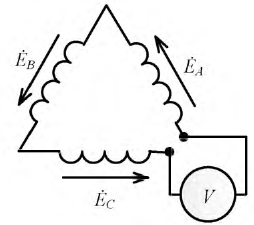
Рис. 7.9. Включение вольтметра в разрыв обмоток источника

Рассмотрим разность потенциалов на зажимах любой фазы источника, например, на фазе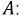 

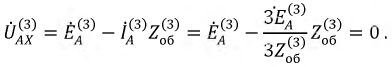
Таким образом, вольтметр, подключенный к любой фазе источника, образующего замкнутый треугольник, уже не будет содержать гармоник напряжения, кратных трем, и поэтому в нагрузке гармоники напряжения и тока, кратные трем, отсутствуют.

Уравнительный ток в обмотках генератора, вызванный гармониками тока кратными трем, вызывает дополнительный нагрев, поэтому фазы генератора обычно соединяют звездой.