
Неравномерное движение по окружности в физике - формулы и определение с примерами
Неравномерное движение по окружности:
Вы в 7 классе ознакомились с равномерным движением по окружности. В данной теме мы рассмотрим неравномерное движение по окружности. Вспомним физические величины, которые описывают равномерное движение по окружности (рис. 1.2).
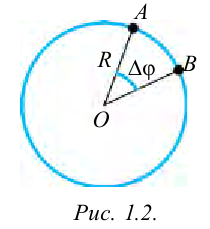
Величина, численно равная пути, пройденному за единицу времени равномерно двигающейся по дуге окружности материальной точкой, называется линейной скоростью и определяется следующим выражением:

2. Отношение угла поворота радиуса окружности при равномерном движении по окружности ко времени поворота называется угловой скоростью:

Угловая скорость, также как и линейная скорость, считается векторной величиной. Ее направление определяется по правилу правого винта. То есть, если головку винта вращать по направлению вращения тела, то поступательное движение его укажет направление вектора углового перемещения, или угловой скорости (рис. 1.3).
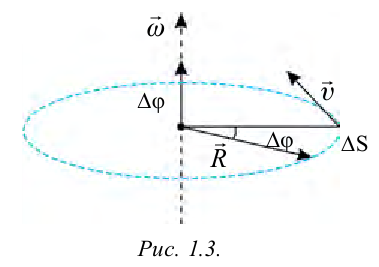
В большинстве случаев тела, совершающие вращательные движения, меняют скорость вращения. Например, в начале движения автомобиля до достижения им определенной скорости или в момент торможении до полной остановки, колеса автомобиля совершают вращательные движения с разной скоростью.
Движение, при котором угловая скорость предмета, совершающего вращательное движение, изменяется по времени называется переменным вращательным движением.
Среди переменных вращательных движений встречаются движения, в которых угловая скорость за любые равные промежутки времени меняется на равные значения. Например, колеса автобуса, который приближается к остановке или отъезжает от нее, совершают равнопеременное вращательное движение. В таких движениях ритм изменения угловой скорости описывается физической величиной, называемой угловым ускорением.
Величина, измеряемая отношением изменения угловой скорости ко времени, за которое произошло это изменение, называется угловым ускорением.

Угловое ускорение при равнопеременном движении с течением времени не меняется, так как угловая скорость такого движения тоже меняется за равные промежутки времени на равные значения. Если начальная угловая скорость двигающейся материальной точки равна 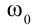 , угловая скорость через промежуток времени
, угловая скорость через промежуток времени 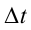 равна
равна 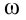 , то изменение угловой скорости будет:
, то изменение угловой скорости будет: 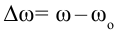 . Тогда уравнение (1.12) приобретает вид:
. Тогда уравнение (1.12) приобретает вид:

Исходя из этого, единица измерения углового ускорения будет равна 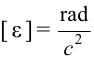 . Из выражения (1.13) можно вывести формулу для определения угловой скорости в любой момент времени:
. Из выражения (1.13) можно вывести формулу для определения угловой скорости в любой момент времени:

Если угловая скорость в ходе движения растет равномерно, вращательное движение будет равноускоренным 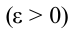 (рис. 1.4 а). Если угловая скорость вращательного движения в ходе вращения равномерно уменьшается, такое вращательное движение называется равномерно замедленным
(рис. 1.4 а). Если угловая скорость вращательного движения в ходе вращения равномерно уменьшается, такое вращательное движение называется равномерно замедленным 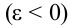 (рис. 1.4 б).
(рис. 1.4 б).
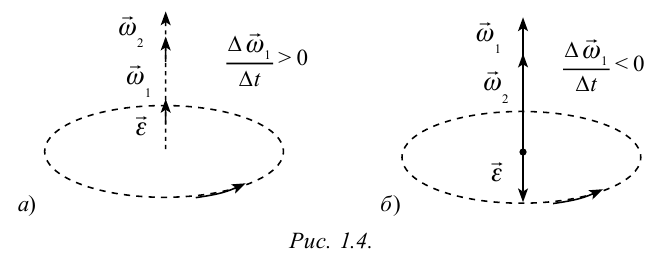
Из-за того, что при вращательном движении угловая скорость является векторной величиной, угловое ускорение тоже считается векторной величиной. Так как, в формуле (1.13) 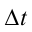 является скалярной величиной. В случае
является скалярной величиной. В случае 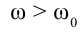 , вектор
, вектор 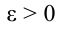 и угловое ускорение
и угловое ускорение 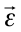 совпадает с направлением угловой скорости, а в случае
совпадает с направлением угловой скорости, а в случае 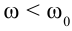 будет,
будет, 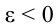 и вектор
и вектор 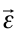 противонаправлен вектору
противонаправлен вектору 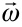 .
.
В уравнении равнопеременного прямолинейного движения достаточно заменить пройденный путь 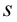 на угол поворота
на угол поворота 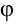 , скорость
, скорость 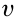 на угловую скорость
на угловую скорость 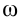 , ускорение
, ускорение 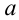 на угловое ускорение
на угловое ускорение 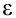 чтобы получить уравнение равномерно изменяющегося вращательного движения. Сопоставление этих уравнений для данных видов движения приводится в следующей таблице:
чтобы получить уравнение равномерно изменяющегося вращательного движения. Сопоставление этих уравнений для данных видов движения приводится в следующей таблице:

При вращательном движении встречаются случаи, когда меняется количественная величина линейной скорости материальной точки. В таких случаях в связи с изменением линейной скорости материальной точки возникает ускорение. Из-за того, что это ускорение появилось в результате изменения количественных величин скорости, его направление совпадает с направлением скорости. Поэтому оно называется касательным, т.е. тангенциальным ускорением и его можно выразить формулой:

Таким образом, если меняется линейная скорость материальной точки, совершающей вращательное движение, ее общее ускорение можно определить по формуле:
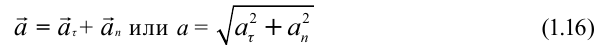
здесь 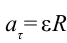 .
.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
- Движение горизонтально брошенного тела
- Движение тела, брошенного под углом к горизонту
- Электромагниты и их применение в физике
- Колебательный контур в физике
- Исследовательские методы в физике
- Вертикальное движение тел в физик