
Неравенство треугольника - определение и вычисление с примерами решения
Содержание:
Неравенство треугольника:
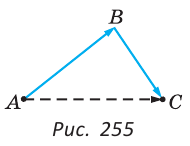
Опыт нам подсказывает, что путь из точки А в точку С по прямой АС короче, чем по ломаной ABC (рис. 255), т. е. АС <АВ + ВС. Докажем это.
Теорема (о неравенстве треугольника).
Любая сторона треугольника меньше суммы двух других его сторон.
Дано: 
Доказать: АС <АВ+ВС, АВ<АС+ВС, ВС < АВ+АС.
Доказательство:
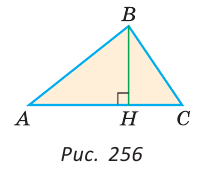
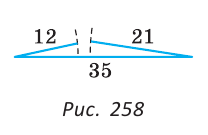
Пусть АС — наибольшая сторона Для сторон Следствие 1. Если для точек А, В и С верно, что АВ=АС+ВС, то эти точки лежат на одной прямой. При этом точка С лежит между точками А и В. Следствие 2. Длина отрезка, соединяющего концы незамкнутой ломаной, меньше длины ломаной. На рисунке 257 изображена незамкнутая ломаная ABCDE. Докажем, что АЕ<АВ+ВС+CD+DE. Соединим точку А с точками С и D отрезками. По неравенству треугольника АС<АВ+ВС и AD<АС+CD. Значит, AD<АВ+ВС+CD. Так как по неравенству треугольника АЕ Чтобы доказать, что данные три числа не могут быть длинами сторон треугольника, достаточно убедиться, что большее из этих чисел не меньше суммы двух других чисел. Например, треугольника со сторонами 21, 12, 35 не существует, так как не выполняется неравенство треугольника: 35>12+21 (рис. 258). Замечание. Из неравенств треугольника Пример: Внутри треугольника ABC взята точка М (рис. 259). Доказать, что периметр треугольника АМС меньше периметра треугольника ABC. Решение: Так как у треугольников ABC и АМС сторона АС — общая, то достаточно доказать, что AM + МС < АВ + ВС. Продлим сторону AM до пересечения со стороной ВС в точке К. Из Пример: Доказать, что медиана треугольника меньше полусуммы двух соседних сторон. Доказательство: Докажем, что для медианы ВМ треугольника ABC справедливо неравенство: ВМ < Продлим медиану ВМ на ее длину, MD = ВМ, BD = 2ВМ. Треугольники AMD и СМВ равны по первому признаку равенства треугольников ( Теорема 1. В треугольнике против большей стороны лежит больший угол. Доказательство. 1) Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что 2) Отложим на стороне АВ отрезок АF, равный стороне AC (рис. 108, б). 3) Так как АF < АВ, то точка F лежит между точками А и В. Отсюда следует, что 4) Угол 2 является внешним углом треугольника ВFС, следовательно, 5) Так как треугольник FАС является равнобедренным, то Таким образом, Отсюда получаем, что Теорема доказана. Теорема 2. В треугольнике против большего угла лежит большая сторона. Доказательство. 1) Пусть в треугольнике АBС 2) Предположим, что это не так. Тогда: либо АВ = АС, либо АВ < АС. 3) Если АВ = АС, то данный треугольник АBС является равнобедренным, а, значит, В каждом из этих случаев получаем противоречие с условием: Теорема доказана. Из данной теоремы следует утверждение: в прямоугольном треугольнике катет меньше гипотенузы. Действительно, гипотенуза лежит против прямого угла, а катет — против острого. Поскольку прямой угол больше острого, то по теореме 2 получаем, что гипотенуза больше катета. Теорема 3 (признак равнобедренного треугольника). Если два угла треугольника равны, то треугольник равнобедренный. Доказательство. Пусть в треугольнике два угла равны. Тогда равны стороны, лежащие против этих углов. В самом деле, если предположить, что одна из указанных сторон больше другой, то по теореме 1 угол, лежащий против этой стороны, будет больше угла, лежащего против другой стороны, что противоречит условию равенства углов. Значит, наше предположение неверно и в треугольнике две стороны равны, т. е. треугольник является равнобедренным. Теорема доказана. Докажем, что длина каждой стороны треугольника меньше суммы длин двух других сторон. Теорема 4. Длина каждой стороны треугольника меньше суммы длин двух других его сторон. Доказательство. 1) Пусть ABC — произвольный треугольник. Докажем, например, что выполняется неравенство АВ < АС + СВ (рис. 109, а). 2) Отложим на луче АС отрезок CF, равный стороне ВС (рис. 109, б). 3) В равнобедренном треугольнике ВСF угол 1 равен углу 2, а в треугольнике АВF 4) Так как в треугольнике против большего угла лежит большая сторона (теорема 2), то АВ < АF. Но так как АF = АС + СF, то АВ < АС + СВ. Теорема доказана. Следствие 1. Для любых трех точек А, В, С, не лежащих на одной прямой, справедливы следующие три неравенства, которые называются неравенствами треугольника: АВ < АС + СB; АС < АВ + ВС; АВ < ВА+АС. Следствие 2. Длина каждой стороны треугольника больше разности длин двух других его сторон. На основании первого и второго признаков равенства треугольников можно доказать следующие признаки равенства прямоугольных треугольников. Теорема 1 (о равенстве прямоугольных треугольников по двум катетам). Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны. Доказательство. Так как в прямоугольном треугольнике угол между катетами прямой, а любые два прямых угла равны, то по первому признаку равенства треугольников следует утверждение данной теоремы. Теорема доказана. Например, пусть ABCD — квадрат, а точки О и F — середины сторон АВ и AD соответственно (рис. 112, а). Тогда прямоугольные треугольники OAD и FAB равны. Действительно, поскольку каждый угол квадрата прямой, а его стороны равны, то АD =АВ и АО = АF, т. е. эти треугольники равны по двум катетам. Пусть точки О и F — середины ребер А1В1 и АВ соответственно прямоугольного параллелепипеда (рис. 112, б). Тогда равны прямоугольные треугольники АА1O и В1ВF, содержащиеся в грани АA1B1B прямоугольного параллелепипеда. Действительно, так как каждый угол прямоугольника АA1B1B прямой (рис. 112, в), а противоположные стороны равны, то верны равенства Теорема 2 (о равенстве прямоугольных треугольников по катету и прилежащему острому углу). Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны. Доказательство. Учитывая условие теоремы и тот факт, что прямые углы равны, получаем, что катет и два прилежащих к нему угла одного прямоугольного треугольника соответственно равны катету и двум прилежащим к нему углам второго прямоугольного треугольника. Следовательно, по второму признаку равенства треугольников эти треугольники равны. Теорема доказана. Докажем еще два признака равенства прямоугольных треугольников. Теорема 3 (о равенстве прямоугольных треугольников по гипотенузе и острому углу). Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны. Доказательство. 1) Пусть в прямоугольных треугольниках АBС и А1В1С1 равны гипотенузы АВ и А1В1, а также 2) Так как сумма градусных мер углов любого треугольника равна 180°, то в треугольнике ABC 3) Таким образом, гипотенуза AB и два прилежащих к ней угла треугольника ABC соответственно равны гипотенузе А1В1 и двум прилежащим к ней углам треугольника А1В1С1. Следовательно, на основании второго признака равенства треугольников получаем, что Теорема доказана. Например, пусть отрезки СО и AF — высоты равнобедренного треугольника ABC с основанием АС. Тогда Действительно, АС — общая гипотенуза этих треугольников, а Теорема 4 (о равенстве прямоугольных треугольников по гипотенузе и катету). Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны. Доказательство. 1) Пусть в прямоугольных треугольниках АСВ и А1С1 В1 2) На луче, противоположном лучу СB, отложим отрезок СF, равный отрезку С1В1. Тогда треугольники А1В1С1 и АСF равны по двум катетам. 3) Следовательно, АF =А1В1=АВ, т. е. треугольник АВF является равнобедренным и Теорема доказана. Например, пусть прямая l пересекает окружность, центром которой является точка А, в точках D и F (рис. 114, б). Отрезок АВ — перпендикуляр, проведенный из точки А к прямой l. Тогда треугольники ABF и ABD равны по гипотенузе и катету. Действительно, AF = AD как радиусы окружности, отрезок АВ — общий катет этих треугольников. АВС. Проведем высоту ВН. Из прямоугольного
АВС. Проведем высоту ВН. Из прямоугольного  АНВ следует АН<АВ (катет меньше гипотенузы). Аналогично из
АНВ следует АН<АВ (катет меньше гипотенузы). Аналогично из  СНВ НС<ВС. Сложив неравенства, получим АН+НС<АВ+ВС. Откуда АС<АВ+ВС. Два других неравенства АВ<АС+ВС и ВС
СНВ НС<ВС. Сложив неравенства, получим АН+НС<АВ+ВС. Откуда АС<АВ+ВС. Два других неравенства АВ<АС+ВС и ВС ,
,  и
и 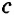 треугольника можно записать неравенства:
треугольника можно записать неравенства: 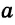 <
<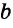 +
+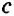 ,
, 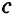 <
<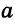 +
+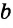 ,
,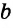 <
<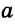 +
+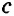 . Каждое из трех указанных неравенств называется неравенством треугольника.
. Каждое из трех указанных неравенств называется неравенством треугольника.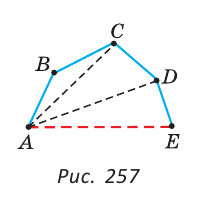
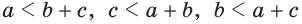 следует, что
следует, что 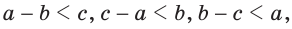 то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо
то есть любая сторона треугольника больше разности двух других его сторон. Так, для стороны а справедливо 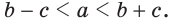
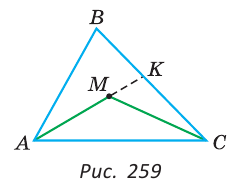
 МКС по неравенству треугольника МС<МК+КС. Тогда AM + МС<АК + КС (1). Из
МКС по неравенству треугольника МС<МК+КС. Тогда AM + МС<АК + КС (1). Из  АВК по неравенству треугольника АК < АВ + ВК, значит, АК + КС<АВ + ВС (2). Из неравенств (1) и (2) следует, что AM + МС < АВ + ВС. Утверждение доказано.
АВК по неравенству треугольника АК < АВ + ВК, значит, АК + КС<АВ + ВС (2). Из неравенств (1) и (2) следует, что AM + МС < АВ + ВС. Утверждение доказано.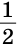 (АВ + ВС) (рис.260).
(АВ + ВС) (рис.260).
 AMD =
AMD =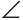 CMB как вертикальные), откуда AD = BC. В
CMB как вертикальные), откуда AD = BC. В  ABD по неравенству треугольника BD
ABD по неравенству треугольника BD Теоремы о соотношениях между сторонами и углами треугольника.
 C >
C >  B (рис. 108, а).
B (рис. 108, а).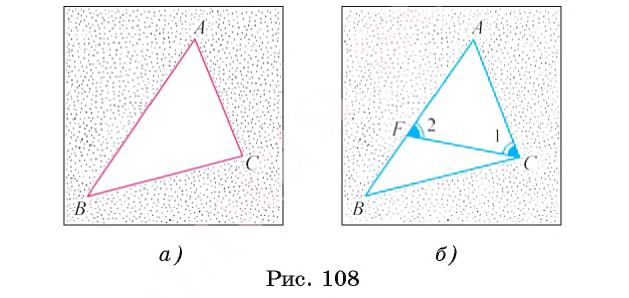
 l является частью угла ВСА, а, значит,
l является частью угла ВСА, а, значит,  ВСА >
ВСА >  1.
1. 2 >
2 >  B.
B. 1 =
1 =  2.
2. BСА >
BСА >  1,
1,  1 =
1 =  2 и
2 и  2 >
2 >  B.
B. ВСА >
ВСА >  B.
B. С >
С >  B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного.
B. Докажем, что АВ > АС (см. рис. 108, а). Доказательство проведем методом от противного. B =
B =  C. Если АВ < АС, то по теореме 1
C. Если АВ < АС, то по теореме 1  B >
B >  C.
C. C >
C >  B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.
B. Таким образом, сделанное предположение неверно и, значит, АВ > АС.Неравенство треугольника
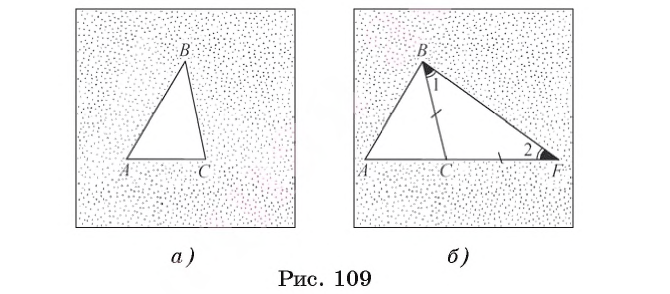
 АВF >
АВF >  l, следовательно, верно неравенство
l, следовательно, верно неравенство  АВF >
АВF >  2.
2.Признаки равенства прямоугольных треугольников
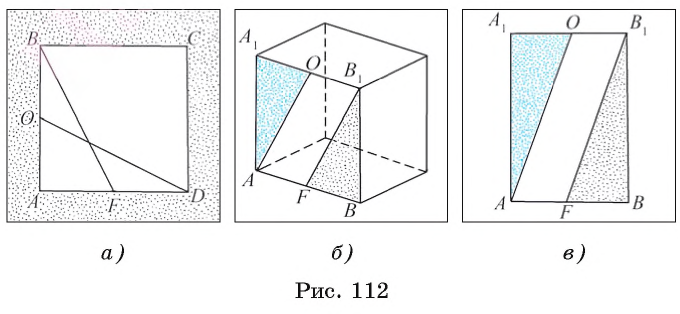
 АA1О =
АA1О = FBВ1= 90°, АА1=ВВ1 и А1O = ВF, т. е. треугольники равны по двум катетам.
FBВ1= 90°, АА1=ВВ1 и А1O = ВF, т. е. треугольники равны по двум катетам. А=
А= A1. Докажем, что треугольники ABC и А1В1С1 равны (рис. 113, а).
A1. Докажем, что треугольники ABC и А1В1С1 равны (рис. 113, а).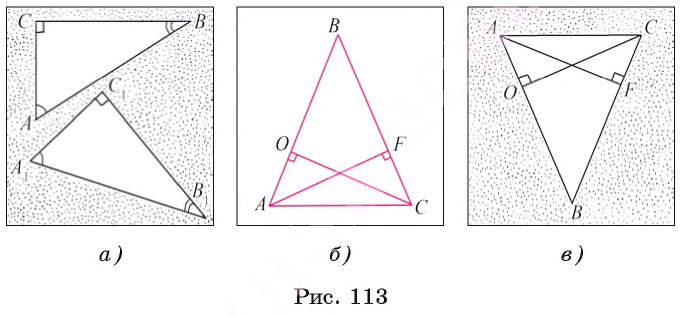
 B = 90° -
B = 90° -  A и в треугольнике А1В1С1
A и в треугольнике А1В1С1  B1 = 90° -
B1 = 90° -  A1. Так как
A1. Так как  A =
A =  A1, то
A1, то  B =
B =  B1.
B1. АВС =
АВС =  А1В1С1.
А1В1С1. АОС =
АОС =  CFA по гипотенузе и острому углу.
CFA по гипотенузе и острому углу. OAC =
OAC =  FCA, поскольку углы при основании равнобедренного треугольника ABC равны (рис. 113, б, в).
FCA, поскольку углы при основании равнобедренного треугольника ABC равны (рис. 113, б, в). C=
C= С1, AB=А1В1 и AC=А1C1 (рис. 114, a).
С1, AB=А1В1 и AC=А1C1 (рис. 114, a).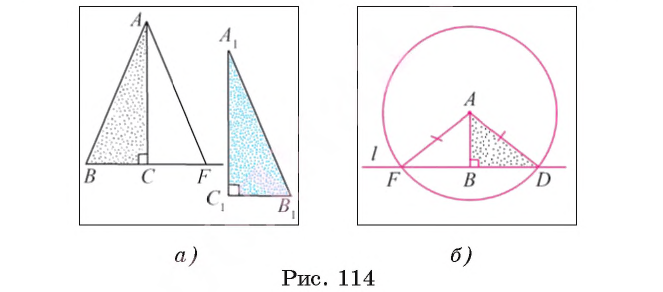
 B =
B =  F. Таким образом, прямоугольные треугольники АСВ и АСF равны по гипотенузе и острому углу. Кроме того, АCF = А1С1В1, значит, треугольник АСВ равен треугольнику А1С1В1.
F. Таким образом, прямоугольные треугольники АСВ и АСF равны по гипотенузе и острому углу. Кроме того, АCF = А1С1В1, значит, треугольник АСВ равен треугольнику А1С1В1.
Рекомендую подробно изучить предметы: Ещё лекции с примерами решения и объяснением: