
Непрерывные функции и их свойства с примерами решения
Содержание:
Непрерывные функции и их свойства
Определение непрерывной функции
Всюду далее будем считать, что вещественнозначная функция 
Определение 3.1. Функция 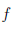 называется непрерывной в точке a из X, если для любой окрестности U
называется непрерывной в точке a из X, если для любой окрестности U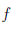 (a) найдется такая окрестность Ua точки a, что образ множества Ua
(a) найдется такая окрестность Ua точки a, что образ множества Ua  X при отображении
X при отображении 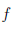 содержится в U
содержится в U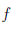 (a) .
(a) .
В логической символике это определение записывается так:
 : X →
: X → 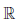 непрерывна в точке a ∈ X ⇔ ∀U
непрерывна в точке a ∈ X ⇔ ∀U (a) ∃ Ua :
(a) ∃ Ua :  (Ua X) ⊂ U
(Ua X) ⊂ U (a).
(a).
Поскольку под окрестностью конечной точки мы понимаем симметричную окрестность, то это определение равносильно следующему:
Определение 3.2 ( по Коши ). Функция  : X →
: X → 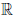 называется непрерывной в точке a ∈ X , если для любого числа ε > 0 найдется такое число δ = δ(ε) > 0, что для всех x ∈ X, удовлетворяющих условию |x - a|
называется непрерывной в точке a ∈ X , если для любого числа ε > 0 найдется такое число δ = δ(ε) > 0, что для всех x ∈ X, удовлетворяющих условию |x - a| 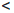 δ, выполняется неравенство |
δ, выполняется неравенство | (x) -
(x) -  (a)|
(a)|  ε.
ε.
В логической символике последнее определение можно записать так: функция  : X →
: X → 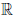 непрерывна в точке a ∈ X ⇔
непрерывна в точке a ∈ X ⇔
(∀ε > 0 ∃ δ = δ(ε) > 0 : ∀x ∈ X, |x - a|  δ ⇒ |
δ ⇒ | (x) -
(x) -  (a)|
(a)|  ε.)
ε.)
Замечание 1. Свойство непрерывности функции  изучается в любой точке a ∈ X , в то время как предел — в предельной точке a множества X , которая может не принадлежать X .
изучается в любой точке a ∈ X , в то время как предел — в предельной точке a множества X , которая может не принадлежать X .
Замечание 2. В определении непрерывной функции в точке a рассматриваются образы всех точек множества X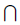 Ua , а в определении предела функции — образы точек из X
Ua , а в определении предела функции — образы точек из X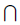 Ua , отличных от a.
Ua , отличных от a.
Если a ∈ X , но не является предельной точкой множества X , то ее называют изолированной точкой множества X . Ясно, что функция непрерывна в каждой изолированной точке области определения.
Поскольку  (a) принадлежит каждой окрестности U
(a) принадлежит каждой окрестности U (a) , то, учитывая определение предела функции
(a) , то, учитывая определение предела функции  в точке a, получаем следующее определение, равносильное предыдущим.
в точке a, получаем следующее определение, равносильное предыдущим.
Определение 3.3. Пусть  : X →
: X → 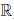 , a ∈ X , a — предельная точка множества X . Функция
, a ∈ X , a — предельная точка множества X . Функция  называется непрерывной в точке a, если существует предел функции в точке a и он равен значению функции f в точке a.
называется непрерывной в точке a, если существует предел функции в точке a и он равен значению функции f в точке a.
Учитывая представление функции, имеющей в точке конечный предел, получаем: непрерывность функции  в точке a означает, что
в точке a означает, что  имеет представление
имеет представление  (x) =
(x) =  (a) + o(1), x → a.
(a) + o(1), x → a.
Наконец, используя определение предела функции по Гейне, получаем определение, равносильное предыдущим
Определение 3.4 (по Гейне). Функция  : X →
: X → 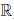 называется непрерывной в точке a ∈ X, если для любой последовательности {xn} элементов множества X, сходящейся к a, соответствующая последовательность {
называется непрерывной в точке a ∈ X, если для любой последовательности {xn} элементов множества X, сходящейся к a, соответствующая последовательность { (xn)} образов сходится к
(xn)} образов сходится к  (a).
(a).
Замечание. По сравнению с определением Гейне предела функции в определении 3.4 непрерывности функции снято требование, обязывающее все элементы последовательности {xn} быть отличными от a. (В случае, когда a — изолированная точка множества X , все элементы xn , начиная с некоторого, равны a.)
Определение 3.5. Функция  называется непрерывной на множестве X , если она непрерывна в каждой точке этого множества.
называется непрерывной на множестве X , если она непрерывна в каждой точке этого множества.
Совокупность вещественнозначных функций, непрерывных на множестве X , обычно обозначается символом C(X).
Рассмотрим некоторые примеры.
Пример 3.1. Функция  (x) = C, x ∈
(x) = C, x ∈ 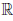 , непрерывна на
, непрерывна на 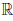 .
.
Действительно, для любой точки a ∈ 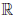 , для ∀x ∈
, для ∀x ∈ 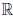 |
| (x) -
(x) -  (a)| = 0. Поэтому ∀ε > 0∀δ > 0 имеем:
(a)| = 0. Поэтому ∀ε > 0∀δ > 0 имеем:
|x - a| 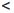 δ ⇒ |
δ ⇒ | (x) -
(x) -  (a)|
(a)| 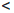 ε.
ε.
Последнее означает непрерывность функции в точке a, а значит и на множестве R.
Пример 3.2. Если  :
:  →
→  и
и  (x) = x, ∀x ∈
(x) = x, ∀x ∈  , то
, то  ∈ C (
∈ C (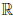 ).
).
Зафиксируем произвольную точку a ∈ 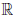 и число ε > 0. Так как
и число ε > 0. Так как
| (x) -
(x) -  (a)| = |x - a|, ∀x ∈
(a)| = |x - a|, ∀x ∈ 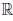 ,
,
то, полагая δ = ε, получим|x
- a| 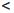 δ ⇒ |
δ ⇒ | (x) -
(x) -  (a)|
(a)|  ε.
ε.
Поэтому  непрерывна в точке a и непрерывна на
непрерывна в точке a и непрерывна на 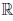 .
.
Пример 3.3. Функция  (x) = sinx непрерывна на
(x) = sinx непрерывна на 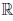 .
.
Для любых a ∈ 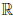 и x ∈
и x ∈ 
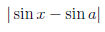 =
=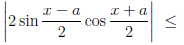
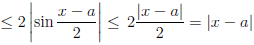 .
.
Поэтому для любого ε > 0 положим δ = ε и получим, что, как только |x-a| 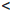 δ, так | sin x - sin a| ≤ |x - a|
δ, так | sin x - sin a| ≤ |x - a| 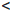 δ = ε.
δ = ε.
Аналогично доказывается непрерывность функции  (x) = cos x.
(x) = cos x.
Пример 3.4. Функция  (x) = |x| непрерывна на
(x) = |x| непрерывна на  .
.
Поскольку для любых a ∈  и x ∈
и x ∈ 
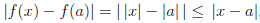 ,
,
то, как и в предыдущих примерах, достаточно положить δ = ε, чтобы доказать непрерывность функции в точке a, а значит на
в точке a, а значит на  .
.
К точкам разрыва функции  : X →
: X → 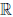 следует отнести те точки множества X , в которых функция
следует отнести те точки множества X , в которых функция  не является непрерывной. Однако такое определение целесообразно уточнить следующим образом.
не является непрерывной. Однако такое определение целесообразно уточнить следующим образом.
Определение 3.6. Точка a ∈ 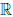 называется точкой разрыва функции
называется точкой разрыва функции  , если либо a ∈ X , но
, если либо a ∈ X , но  не является непрерывной в ней, либо a 6
не является непрерывной в ней, либо a 6 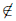 X , но является двусторонней предельной точкой множества X .
X , но является двусторонней предельной точкой множества X .
Заметим, что иногда к точкам разрыва функции  относят не только двусторонние, но и односторонние предельные точки множества X , которые не принадлежат X .
относят не только двусторонние, но и односторонние предельные точки множества X , которые не принадлежат X .
Учитывая определение 3.6 и определение непрерывной функции в точке a, заключаем, что a из X является точкой разрыва функции  , если
, если
∃U (a) :∀Ua ∃x∈X
(a) :∀Ua ∃x∈X Ua :
Ua : (x)
(x) 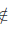 Uf(a)
Uf(a)
или
∃ε > 0 : ∀ δ > 0 ∃x ∈ X, |x - a| 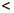 δ : |
δ : | (x) -
(x) -  (a)| ≥ ε.
(a)| ≥ ε.
Иными словами, предельная точка a множества X , принадлежащая X , является точкой разрыва функции , если либо не существует предела функции f в точке a, либо он существует, но отличен от значения
, если либо не существует предела функции f в точке a, либо он существует, но отличен от значения  (a) функции
(a) функции  в точке a.
в точке a.
Пример 3.5. Пусть  :
: 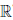 \{0} →
\{0} → 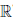 ,
,  (x) =
(x) = 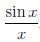 . Точка a = 0 не принадлежит области определения функции
. Точка a = 0 не принадлежит области определения функции  , но является для нее двусторонней предельной. Поэтому a = 0 — точка разрыва функции
, но является для нее двусторонней предельной. Поэтому a = 0 — точка разрыва функции  .
.
Пример 3.6. Рассмотрим функцию
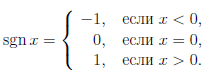
Поскольку каждая точка a  0 обладает окрестностью, в которой функция sgn x постоянна, то функция непрерывна в точке a
0 обладает окрестностью, в которой функция sgn x постоянна, то функция непрерывна в точке a 0. Далее, на последовательности {xn} : xn=
0. Далее, на последовательности {xn} : xn=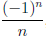 , n ∈
, n ∈  , функция принимает значения sgn xn = (-1)n, n ∈
, функция принимает значения sgn xn = (-1)n, n ∈  . Учитывая, что xn → 0 и не существует предел последовательности {sgn xn}, заключаем, что рассматриваемая функция терпит разрыв в точке a = 0.
. Учитывая, что xn → 0 и не существует предел последовательности {sgn xn}, заключаем, что рассматриваемая функция терпит разрыв в точке a = 0.
Определение 3.7. Пусть a — точка разрыва функции  , a – двусторонняя (или односторонняя) предельная точка множества X . Точку a называют точкой разрыва первого рода, если существуют конечные односторонние (или соответствующий односторонний) пределы функции
, a – двусторонняя (или односторонняя) предельная точка множества X . Точку a называют точкой разрыва первого рода, если существуют конечные односторонние (или соответствующий односторонний) пределы функции  в точке a.
в точке a.
Определение 3.8. Если a — точка разрыва первого рода функции  и в ней существует предел функции, то точку a называют точкой устранимого разрыва.
и в ней существует предел функции, то точку a называют точкой устранимого разрыва.
Если a — точка устранимого разрыва функции  и
и 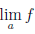 = A, то функция
= A, то функция
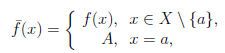
непрерывна в точке a.
Лемма 3.1. Если a — точка разрыва первого рода функции  и a — односторонняя предельная точка множества X , то она является точкой устранимого разрыва функции
и a — односторонняя предельная точка множества X , то она является точкой устранимого разрыва функции  .
.
Утверждение следует из предыдущего определения и теоремы о равносильности предела и одностороннего предела функции в односторонней предельной точке.
Определение 3.9. Если a — точка разрыва функции  и в этой точке не существует или бесконечен хоть один из односторонних пределов функции
и в этой точке не существует или бесконечен хоть один из односторонних пределов функции  , то a называется точкой разрыва второго рода.
, то a называется точкой разрыва второго рода.
Из определений 3.7 и 3.9 получаем, что каждая точка разрыва функции  , которая не является точкой разрыва первого рода, является точкой разрыва второго рода.
, которая не является точкой разрыва первого рода, является точкой разрыва второго рода.
Возвращаясь к примерам 5 и 6, замечаем, что, так как 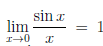 , то a = 0 является точкой устранимого разрыва функции
, то a = 0 является точкой устранимого разрыва функции  (x) = , а так как
(x) = , а так как 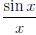 , а так как
, а так как 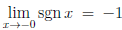 ,
, 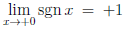 , поэтому a = 0 является точкой разрыва первого рода функции sgn x.
, поэтому a = 0 является точкой разрыва первого рода функции sgn x.
Пример 3.7. Функция Дирихле
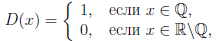
разрывна в каждой точке a ∈ 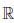 , поскольку не существует односторонних пределов
, поскольку не существует односторонних пределов  (a + 0),
(a + 0),  (a - 0), то есть любая точка a ∈
(a - 0), то есть любая точка a ∈ 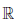 есть точка разрыва второго рода функции D(x).
есть точка разрыва второго рода функции D(x).
Теорема 3.1 (о точках разрыва монотонной функции). Монотонная на промежутке функция может иметь только точки разрыва первого рода.
Пусть для определенности функция  монотонна на (a, b]. Если x0 — точка разрыва функции
монотонна на (a, b]. Если x0 — точка разрыва функции  , то либо x0 ∈ (a, b), либо x0 = b. По следствию из теоремы о пределе монотонной функции существуют конечные односторонние пределы
, то либо x0 ∈ (a, b), либо x0 = b. По следствию из теоремы о пределе монотонной функции существуют конечные односторонние пределы  (x0 - 0),
(x0 - 0),  (x0 + 0), если x0 ∈ (a, b) и
(x0 + 0), если x0 ∈ (a, b) и  (x0 - 0) если x0 = b. Следовательно, x0 — точка разрыва первого рода.
(x0 - 0) если x0 = b. Следовательно, x0 — точка разрыва первого рода.
Часто бывает полезно понятие односторонней непрерывности функции в точке.
Определение 3.10. Пусть a — левосторонняя (правосторонняя) предельная точка множества X и a ∈ X . Говорят, что функция  , определенная на X, непрерывна в точке a слева (справа), если существует предел
, определенная на X, непрерывна в точке a слева (справа), если существует предел  (a - 0) (соответственно
(a - 0) (соответственно  (a + 0)) и он равен значению функции
(a + 0)) и он равен значению функции  в точке a.
в точке a.
Используя определения Коши и Гейне для одностороннего предела функции, можно получить соответствующие определения односторонней непрерывности функции в точке.
Например, если a — левосторонняя предельная точка X, a ∈ X , то функцию  : X ⊂
: X ⊂ 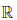 →
→ 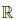 называют непрерывной в точке a слева, если ∀{xn} : xn ∈ X, xn
называют непрерывной в точке a слева, если ∀{xn} : xn ∈ X, xn 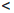 a, xn → a ⇒
a, xn → a ⇒  (xn) →
(xn) →  (a).
(a).
Замечание. В односторонней предельной точке, принадлежащей области определения функции, понятия односторонней непрерывности и непрерывности функции совпадают. Если же рассматриваемая точка является двусторонней предельной, то функция непрерывна в ней тогда и только тогда, когда она непрерывна и слева, и справа.
Пример 3.8. Пусть (x) = [x] ([x] — целая часть числа x). Фиксируем произвольную точку a из
(x) = [x] ([x] — целая часть числа x). Фиксируем произвольную точку a из  . Если a
. Если a 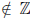 , то существует целое число n0 , такое, что n0
, то существует целое число n0 , такое, что n0 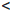 a
a 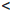 n0 + 1. Поэтому найдется окрестность Ua точки a такая, что Ua ⊂ (n0, n0 + 1). Следовательно, ∀ x ∈ Ua
n0 + 1. Поэтому найдется окрестность Ua точки a такая, что Ua ⊂ (n0, n0 + 1). Следовательно, ∀ x ∈ Ua  (x) = n0 =
(x) = n0 =  (a) и функция
(a) и функция непрерывна в точке a. Если же a = n0 ∈
непрерывна в точке a. Если же a = n0 ∈ 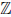 , то согласно примеру 17
, то согласно примеру 17  (n0 - 0) = n0 - 1
(n0 - 0) = n0 - 1 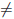
 (n0),
(n0),  (n0 + 0) = n0 =
(n0 + 0) = n0 =  (n0). Следовательно, функция f в точке n0 ∈ Z терпит разрыв первого рода и является непрерывной в ней справа.
(n0). Следовательно, функция f в точке n0 ∈ Z терпит разрыв первого рода и является непрерывной в ней справа.
Локальные свойства непрерывной функции
Теорема 3.2. Если функция  : X →
: X → 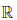 непрерывна в точке a, то она локально ограничена в ней. Если, кроме того,
непрерывна в точке a, то она локально ограничена в ней. Если, кроме того,  (a)
(a) 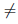 0, то найдется такая окрестность Ua точки a, что
0, то найдется такая окрестность Ua точки a, что
 (x)
(x) 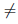 0, sgn
0, sgn  (x) = sgn
(x) = sgn  (a), ∀x ∈ X\Ua.
(a), ∀x ∈ X\Ua.
Если a — изолированная точка множества X , то утверждения очевидны. Если же a — предельная точка множества X , то утверждения следуют из соответствующих локальных свойств функции, имеющей в точке конечный предел .
.
Теорема 3.3. Если функции  и
и 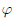 , определенные на множестве X, непрерывны в точке a, то функции
, определенные на множестве X, непрерывны в точке a, то функции  ±
± 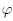 , f ·
, f · 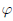 и, если (a) 6= 0, непрерывны в точке a.
и, если (a) 6= 0, непрерывны в точке a.
Доказательство этого утверждения аналогично доказательству теоремы 3.2.
Теорема 3.4. Пусть функция : X → Y имеет конечный предел в точке a, lim
: X → Y имеет конечный предел в точке a, lim  = b, b ∈ Y , функция
= b, b ∈ Y , функция 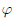 : Y →
: Y → 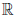 непрерывна в точке b. Тогда a существует предел суперпозиции функций
непрерывна в точке b. Тогда a существует предел суперпозиции функций 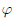 и
и  , при этом lim
, при этом lim 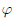 ◦
◦ =
= 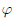 (b).
(b).
Фиксируем произвольную последовательность
{xn}: xn ∈ X, xn 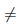 a, xn→ a.
a, xn→ a.
Поскольку  : X → Y и
: X → Y и 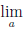
 = b, то
= b, то  (xn) ∈ Y, n ∈
(xn) ∈ Y, n ∈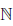 ,
,  (xn) → b. Обозначим a yn =
(xn) → b. Обозначим a yn =  (xn). Тогда последовательность {yn} обладает свойствами: yn ∈ Y, ∀n ∈
(xn). Тогда последовательность {yn} обладает свойствами: yn ∈ Y, ∀n ∈ 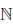 , yn → b. По условию функция
, yn → b. По условию функция 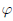 непрерывна в точке b, поэтому
непрерывна в точке b, поэтому 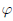 (yn) →
(yn) → 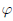 (b). Следовательно,
(b). Следовательно, 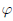 ◦ f (xn) →
◦ f (xn) → 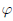 (b), и, по определению Гейне предела функции, существует предел
(b), и, по определению Гейне предела функции, существует предел 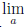
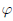 ◦ f =
◦ f = 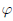 (b).
(b).
Cледствие. Если функция  : X → Y непрерывна в точке x0, а функция
: X → Y непрерывна в точке x0, а функция 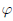 : Y → R непрерывна в точке y0 =
: Y → R непрерывна в точке y0 =  (x0), то функция
(x0), то функция 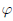 ◦
◦  непрерывна в точке x0 .
непрерывна в точке x0 .
Из теорем 3.3 и 3.4 и примеров 2, 3 следует, что многочлен
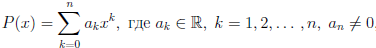 ,
,
является непрерывной на множестве  функцией, а рациональная функция
функцией, а рациональная функция 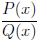 , где P (x) и Q(x) — многочлены, непрерывна в своей области определения.
, где P (x) и Q(x) — многочлены, непрерывна в своей области определения.
Глобальные свойства непрерывных функций
Описательно говоря, глобальными называются свойства, справедливые в области определения функции.
Теорема 3.5. Если функция  непрерывна на множестве X и X1 ⊂ X, то сужение
непрерывна на множестве X и X1 ⊂ X, то сужение  |х1 — непрерывная функция на X1.
|х1 — непрерывная функция на X1.
Пусть a — некоторая точка множества X1 . Так как  ∈ C(X), то
∈ C(X), то
∀ε > 0∃δ = δ(ε) > 0 : ∀x ∈ X  Ua(δ) ⇒ |
Ua(δ) ⇒ | (x) -
(x) -  (a)|
(a)|  ε.
ε.
Поэтому ∀x ∈ X1  Ua(δ) ⇒ |
Ua(δ) ⇒ | (x) -
(x) -  (a)|
(a)| 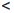 ε, то есть
ε, то есть
∀x ∈ X1 Ua(δ) ⇒ |
Ua(δ) ⇒ | |x1(x) -
|x1(x) -  |x1(a)|
|x1(a)| 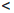 ε,
ε,
Это означает непрерывность  |х1 в точке a и то, что
|х1 в точке a и то, что  |х1 ∈ C(X1).
|х1 ∈ C(X1).
Замечание. Из того, что функция  |х1 непрерывна в точке x0, не следует непрерывность функции
|х1 непрерывна в точке x0, не следует непрерывность функции  в ней. Чтобы подтвердить это, рассмотрим пример.
в ней. Чтобы подтвердить это, рассмотрим пример.
Пример 3.9. Функция Дирихле, рассмотренная в примере 7, терпит разрыв в каждой точке x0 ∈ 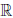 , однако, функции D |
, однако, функции D | , D |
, D |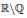 является непрерывными в каждой точке их области определения.
является непрерывными в каждой точке их области определения.
Теорема 3.6 (Больцано-Коши о промежуточном значении). Если функция  непрерывна на отрезке [a, b] и на концах его принимает различные значения, то есть
непрерывна на отрезке [a, b] и на концах его принимает различные значения, то есть  (a)
(a) 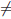
 (b), то для любого числа C, находящегося между
(b), то для любого числа C, находящегося между  (a) и
(a) и  (b), найдется такая точка γ ∈ (a, b), что
(b), найдется такая точка γ ∈ (a, b), что  (γ) = C.
(γ) = C.
Для определенности будем считать, что  (a)
(a) 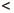
 (b). Фиксируем произвольное число C такое, что
(b). Фиксируем произвольное число C такое, что  (a)
(a) 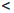 C
C 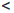
 (b).
(b).
Разделим отрезок [a, b] пополам точкой α1. Может случиться, что  (α1) = C. Тогда задача решена и в качестве γ возьмем α1 . Если же
(α1) = C. Тогда задача решена и в качестве γ возьмем α1 . Если же  (α1)
(α1) 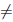 C, то из двух полученных отрезков выбираем тот, обозначим его [a1 , b1], на концах которого выполняются условия
C, то из двух полученных отрезков выбираем тот, обозначим его [a1 , b1], на концах которого выполняются условия  (a1)
(a1) 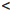 C
C 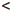
 (b1). Такой отрезок обязательно существует: [a1 , b1] = [α1 , b], если
(b1). Такой отрезок обязательно существует: [a1 , b1] = [α1 , b], если  (α1)
(α1) 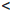 C, и [a1 , b1] = [a, α1], если
C, и [a1 , b1] = [a, α1], если  (α1) > C.
(α1) > C.
Разделим отрезок [a1, b1] пополам точкой α2. Если  (α2) = C, то γ = α2 и задача решена. Если
(α2) = C, то γ = α2 и задача решена. Если (α2)
(α2) 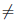 C, то из полученных отрезков возьмем тот, обозначим его [a2, b2], для которого
C, то из полученных отрезков возьмем тот, обозначим его [a2, b2], для которого  (a2)
(a2) 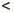 C
C 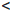
 (b2). Продолжая, в случае необходимости, этот процесс далее, либо на n0 шаге получим точку αn0 — середину [an0-1 , bn0-1], в которой
(b2). Продолжая, в случае необходимости, этот процесс далее, либо на n0 шаге получим точку αn0 — середину [an0-1 , bn0-1], в которой  (αn0) = C, либо получим систему вложенных отрезков [an, bn], n ∈
(αn0) = C, либо получим систему вложенных отрезков [an, bn], n ∈ 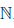 , таких, что bn - an=
, таких, что bn - an=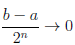 при n → ∞, и
при n → ∞, и
f(an)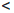 C
C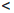
 (bn), n∈
(bn), n∈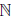 (3.1)
(3.1)
В первом случае полагаем γ = αn0 , что приводит к решению задачи. Во втором случае по лемме о вложенных отрезках существует единственная точка γ , принадлежащая всем отрезкам системы, такая что
lim an = lim bn = γ.
Поскольку γ ∈ [a, b], то  непрерывна в ней и
непрерывна в ней и
lim  (an) = lim
(an) = lim  (bn) =
(bn) =  (γ).ё
(γ).ё
Переходя к пределу в неравенствах (3.1), получим  (γ) = C. Так как γ ∈ [a, b] и
(γ) = C. Так как γ ∈ [a, b] и  (a)
(a) 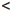 C
C 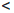
 (b), то γ ∈ (a, b).
(b), то γ ∈ (a, b).
Замечание 1. Доказательство теоремы дает алгоритм отыскания корня уравнения  (x) = C на отрезке [a, b], если функция
(x) = C на отрезке [a, b], если функция  непрерывна на отрезке [a, b] и число C находится между значениями
непрерывна на отрезке [a, b] и число C находится между значениями  (a) и
(a) и  (b) функции
(b) функции  на концах отрезка [a, b].
на концах отрезка [a, b].
Замечание 2. Теорема утверждает существование, но не единственность точки γ ∈ (a, b) такой, что  (γ) = C.
(γ) = C.
Замечание 3. В теореме 3.6 нельзя опустить требование непрерывности функции на отрезке [a, b]. (В подтверждение можно рассмотреть функцию sgn x на отрезке [-1,1].)
на отрезке [a, b]. (В подтверждение можно рассмотреть функцию sgn x на отрезке [-1,1].)
Cледствие 1. Если функция  непрерывна на отрезке [a, b] и на концах его принимает значения разных знаков, тo еcть
непрерывна на отрезке [a, b] и на концах его принимает значения разных знаков, тo еcть  (a) ·
(a) ·  (b)
(b) 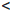 0, то найдется такая точка γ ∈ (a, b), что
0, то найдется такая точка γ ∈ (a, b), что  (γ) = 0.
(γ) = 0.
Cледствие 2. Многочлен нечетной степени с действительными коэффициентами P (x) = 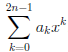 ,
,
ak ∈ 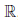 , k = 0, 1, 2, .., 2n - 1, a2n-1
, k = 0, 1, 2, .., 2n - 1, a2n-1 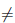 0, n ∈
0, n ∈ 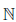 ,
,
имеет по меньшей мере один действительный корень.
Без ограничения общности можно считать a2n-1 = 1. Тогда
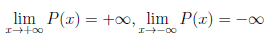
В силу определения бесконечно большой функции определенного знака, найдутся точки a и b из 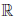 , такие что a
, такие что a 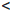 b и P (a)
b и P (a) 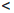 0, P (b) > 0. Поскольку P (x) ∈ C(
0, P (b) > 0. Поскольку P (x) ∈ C(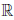 ), то P (x) ∈ C ([a, b]) и по следствию 1 теоремы 3.6 получаем нужное.
), то P (x) ∈ C ([a, b]) и по следствию 1 теоремы 3.6 получаем нужное.
Теорема 3.7 (1–ая теорема Вейерштрасса). Если функция непрерывна на отрезке [a, b], то она ограничена на нем.
Предположим, что  ∈ C ([a, b]), но
∈ C ([a, b]), но  не является ограниченной на отрезке [a, b]. Тогда
не является ограниченной на отрезке [a, b]. Тогда
∀ n ∈ 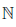 ∃ xn ∈ [a, b] : |
∃ xn ∈ [a, b] : | (xn)| > n.
(xn)| > n.
По лемме Больцано-Вейерштрасса из полученной последовательности {xn} можно выделить сходящуюся подпоследовательность {xnk }. Пусть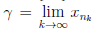 .
.
Тогда γ ∈ [a, b] и по определению Гейне непрерывной функции
f(xnk) → f(γ) при k → ∞.
С другой стороны,
 (xnk)| > nk, ∀ k ∈
(xnk)| > nk, ∀ k ∈ 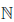
Следовательно, | (xnk)| → +∞ при k → ∞. Полученное противоречие завершает доказательство.
(xnk)| → +∞ при k → ∞. Полученное противоречие завершает доказательство.
Замечание 1. На промежутке, отличном от отрезка, утверждение теоремы 3.7, вообще говоря, неверно. Например, функция (x) = 1/x непрерывна на промежутке (0, 1], но не ограничена на нем, поскольку
(x) = 1/x непрерывна на промежутке (0, 1], но не ограничена на нем, поскольку 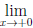 1/x = +∞. x→+0
1/x = +∞. x→+0
Замечание 2. С помощью теоремы 3.7 иногда удается доказать ограни
ченность функции, непрерывной на промежутке, отличном от отрезка. Например, рассмотрим функцию f(x) = e-1/x, ∀ x ∈ (0, 1]. Так как  ∈ C((0, 1]) и
∈ C((0, 1]) и 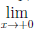 f(x) = 0, то функция
f(x) = 0, то функция
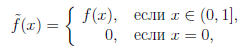
Теорема 3.9 (Дарбу об образе отрезка при непрерывном отображении). Если функция  непрерывна на отрезке [a, b], то образ отрезка [a, b] при отображении
непрерывна на отрезке [a, b], то образ отрезка [a, b] при отображении  совпадает с отрезком [m
совпадает с отрезком [m , M
, M ], где
], где
m = inf {
= inf { (x) | x ∈ [a, b]}, M
(x) | x ∈ [a, b]}, M = sup{
= sup{ (x) | x ∈ [a, b]}.
(x) | x ∈ [a, b]}.
По второй теореме Вейерштрасса существуют точки p, q ∈ [a, b] такие, что f (p) = M ,
,  (q) = mf . Пусть p
(q) = mf . Пусть p  q и m
q и m
 M
M . Поскольку
. Поскольку  ∈ C ([p, q]), то, применяя к функции
∈ C ([p, q]), то, применяя к функции  на отрезке [p, q] теорему Больцано-Коши о промежуточном значении, получаем, что [m
на отрезке [p, q] теорему Больцано-Коши о промежуточном значении, получаем, что [m , M
, M ] ⊂
] ⊂  ([a, b]). С другой стороны, по определениям точных верхней и нижней границ числового множества
([a, b]). С другой стороны, по определениям точных верхней и нижней границ числового множества  ([a, b]) ⊂ [m
([a, b]) ⊂ [m , M
, M ]. Следовательно,
]. Следовательно,  ([a, b]) = [m
([a, b]) = [m , M
, M ]. Если же m
]. Если же m = M
= M = M , то
= M , то  (x) = M, ∀x ∈ [a, b], а поэтому
(x) = M, ∀x ∈ [a, b], а поэтому  ([a, b]) = {M}.
([a, b]) = {M}.
Cледствие. Если функция  непрерывна и не убывает (не возрастает) на отрезке [a, b], то
непрерывна и не убывает (не возрастает) на отрезке [a, b], то  ([a, b]) = [
([a, b]) = [ (a),
(a),  (b)] (соответственно,
(b)] (соответственно,  ([a, b]) = [
([a, b]) = [ (b), f (a)]).
(b), f (a)]).
Замечание 1. Если образом отрезка [a, b] при отображении  является отрезок
является отрезок  ([a, b]), то отсюда, вообще говоря, не следует, что функция
([a, b]), то отсюда, вообще говоря, не следует, что функция  является непрерывной. Подтверждением служит функция
является непрерывной. Подтверждением служит функция
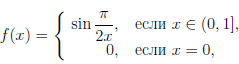
которая терпит разрыв в точке x = 0, однако  ([0, 1]) = [-1, 1].
([0, 1]) = [-1, 1].
Замечание 2. Можно доказать, что если функция  непрерывна и не убывает (не возрастает) на интервале (a, b), то
непрерывна и не убывает (не возрастает) на интервале (a, b), то  ((a, b)) = (A, B) (соответственно,
((a, b)) = (A, B) (соответственно,  ((a, b)) = (B, A)), где
((a, b)) = (B, A)), где
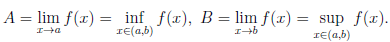
Если функция  непрерывна и не убывает (не возрастает) на промежутке [a, b), то
непрерывна и не убывает (не возрастает) на промежутке [a, b), то  ([a, b)) = [
([a, b)) = [ (a), B) (соответственно,
(a), B) (соответственно,  ([a, b)) = (B,
([a, b)) = (B,  (a)]).
(a)]).
Предлагаем читателю доказать эти утверждения самостоятельно.
Теорема 3.10 (o непрерывности монотонной функции). Если функция f монотонна на промежутке X и множество  (X) — промежуток, то функция
(X) — промежуток, то функция  непрерывна на X .
непрерывна на X .
Для определенности считаем, что функция  не убывает и X = (a, b). Прежде всего, заметим, что в силу теоремы о пределе монотонной функции, в каждой точке x ∈ (a, b)
не убывает и X = (a, b). Прежде всего, заметим, что в силу теоремы о пределе монотонной функции, в каждой точке x ∈ (a, b)  (x - 0) ≤
(x - 0) ≤  (x) ≤
(x) ≤  (x + 0).
(x + 0).
Доказательство теоремы проведём методом «от противного». Предположим, что существует точка c ∈ (a, b), в которой функция f терпит разрыв. Тогда выполняется хотя бы одно из двух неравенств
 (c-0)
(c-0) 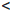
 (c),
(c),  (c)
(c) 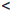
 (c+0).
(c+0).
Пусть, например, (c - 0)
(c - 0) 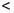
 (c). Поскольку
(c). Поскольку
 (c-0) = sup
(c-0) = sup (x),
(x),  (c+0) = inf
(c+0) = inf  (x), x∈(a,c) x∈(c,b)
(x), x∈(a,c) x∈(c,b)
то на интервале (a, c) и (c, b) функция  не принимает значений, принадлежащих интервалу (
не принимает значений, принадлежащих интервалу ( (c - 0),
(c - 0),  (c)). Но этого не может быть, так как множество
(c)). Но этого не может быть, так как множество  ((a, b)) — промежуток. Следовательно, предположение неверно, то есть, функция f непрерывна на промежутке (a, b).
((a, b)) — промежуток. Следовательно, предположение неверно, то есть, функция f непрерывна на промежутке (a, b).
Cледствие. Если функция f монотонна на промежутке X , то следующие условия эквивалентны:
1) функция непрерывна на промежутке X ,
непрерывна на промежутке X ,
2)  (X) — промежуток.
(X) — промежуток.
Теорема 3.11 (о непрерывности функции, обратной к монотонной). Если функция  возрастает (убывает) на отрезке [a, b] и непрерывна на нем, то ее обратная функция
возрастает (убывает) на отрезке [a, b] и непрерывна на нем, то ее обратная функция  -1 : [
-1 : [ (a),
(a),  (b)] → [a, b] (соответственно,
(b)] → [a, b] (соответственно,  -1 : [
-1 : [ (b),
(b),  (a)] → [a, b] ) непрерывна.
(a)] → [a, b] ) непрерывна.
Будем считать для определенности, что функция  возрастает на отрезке [a, b]. В силу следствия из теоремы 3.9,
возрастает на отрезке [a, b]. В силу следствия из теоремы 3.9,  ([a, b]) = [
([a, b]) = [ (a),
(a),  (b)]. По теореме о существовании обратной функции к монотонной существует функция
(b)]. По теореме о существовании обратной функции к монотонной существует функция  -1 : [
-1 : [ (a),
(a),  (b)] → [a, b], которая возрастает.
(b)] → [a, b], которая возрастает.
Наконец, по определению обратной функции  -1 ([
-1 ([ (a),
(a),  (b)]) = [a, b]. Тогда по теореме 3.10 функция
(b)]) = [a, b]. Тогда по теореме 3.10 функция  -1 непрерывна на [
-1 непрерывна на [ (a),
(a),  (b)].
(b)].
Замечание. Аналогично, с учетом замечания 2 к теореме 3.9 можно доказать, что если функция  возрастает (убывает) на промежутке X и непрерывна на нём, то обратная функция
возрастает (убывает) на промежутке X и непрерывна на нём, то обратная функция  -1 возрастает (убывает) и непрерывна на промежутке f (X).
-1 возрастает (убывает) и непрерывна на промежутке f (X).
Рассмотрим некоторые примеры.
Пример 3.10. Пусть  (x) = xn, n ∈
(x) = xn, n ∈ 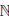 , n ≥ 2, x ∈ [0, +∞). В этом случае степенная функция
, n ≥ 2, x ∈ [0, +∞). В этом случае степенная функция  (x) = xn возрастает на промежутке [0, +∞) и непрерывна на нем. Поскольку
(x) = xn возрастает на промежутке [0, +∞) и непрерывна на нем. Поскольку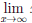 xn = +∞,
xn = +∞,  (0) = 0, то по замечанию 2) к теореме 3.9 и x→∞
(0) = 0, то по замечанию 2) к теореме 3.9 и x→∞
по теоремам 1.1, 3.11 существует обратная функция  -1 : [0, +∞) → [0, +∞), которая также возрастает и непрерывна. Её называют арифметическим корнем n–ой степени и обозначают x =
-1 : [0, +∞) → [0, +∞), которая также возрастает и непрерывна. Её называют арифметическим корнем n–ой степени и обозначают x = 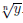 .
.
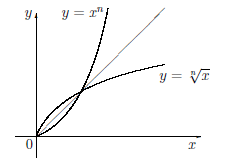
Графики (см.рисунок выше) функций y = xn и y = 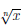 симметричны относительно биссектрисы 1-го и 3-го квадрантов.
симметричны относительно биссектрисы 1-го и 3-го квадрантов.
Пример 3.11. Функция  (x) = sin x, x ∈ [-π/2, π/2] возрастает и непрерывна. Поскольку
(x) = sin x, x ∈ [-π/2, π/2] возрастает и непрерывна. Поскольку  (±π/2) = ±1, то по теоремам 1.1, 3.9, 3.11 существует обратная функция
(±π/2) = ±1, то по теоремам 1.1, 3.9, 3.11 существует обратная функция  -1 : [-1, 1] → [-π/2, π/2], которая возрастает и непрерывна. Её называют функцией "арксинус"и обозначают arcsin. Следовательно, функция arcsin каждому числу x ∈ [-1, 1] ставит в соответствие такое число из отрезка
-1 : [-1, 1] → [-π/2, π/2], которая возрастает и непрерывна. Её называют функцией "арксинус"и обозначают arcsin. Следовательно, функция arcsin каждому числу x ∈ [-1, 1] ставит в соответствие такое число из отрезка 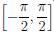 синус которого равен x.
синус которого равен x.
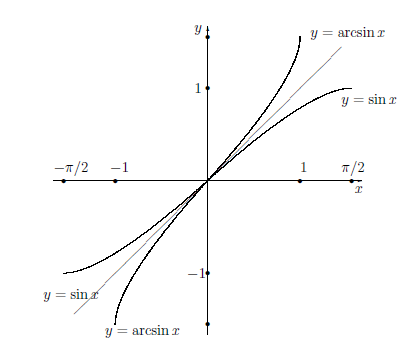
Графики (см. рисунок) функций y = sin x, x ∈ 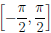 и y = arcsin x, x ∈ [-1, 1] симметричны относительно биссектрисы 1-го и 3-го квадрантов.
и y = arcsin x, x ∈ [-1, 1] симметричны относительно биссектрисы 1-го и 3-го квадрантов.
Замечание. Аналогично вводятся и рассматриваются непрерывная убывающая функция y = arccos x, которая действует из [-1, 1] в [0, π], и непрерывная возрастающая функция y = arctg x, которая действует из  в (-π/2, π/2).
в (-π/2, π/2).
Показательная, логарифмическая и степенная функции
В школьном курсе алгебры и начал анализа определена степень ar числа a > 0 с рациональным показателем r, то есть на множестве Q рациональных чисел определена показательная функция  (r) = ar, выяснены некоторые ее свойства:
(r) = ar, выяснены некоторые ее свойства:
1) ar > 0, ∀r ∈ Q,
2)  возрастает на Q, если a > 1;
возрастает на Q, если a > 1;  убывает на Q, если a ∈ (0, 1),
убывает на Q, если a ∈ (0, 1),
3) ap · aq = ap+q, ∀p, q ∈ Q,
4) (ap)q = ap·q, ∀p,q ∈ Q,
5) (a·b)p=ap·bp, ∀p∈ Q,∀a > 0∀b> 0.
Докажем следующие утверждения.
Лемма 3.2. Если  : Q →
: Q → 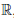 ,
,  (r) = ar, то
(r) = ar, то 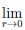
 (r) = 1.
(r) = 1.
Для определенности будем считать a > 1. Так как
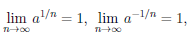
то ∀ε > 0 ∃N = N(ε) ∈ 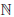 : ∀n > N
: ∀n > N
|a1/n - 1| 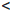 ε, |a-1/n - 1|
ε, |a-1/n - 1| 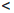 ε.
ε.
Пусть n0 ∈ 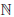 и n0 > N . Тогда
и n0 > N . Тогда
1 - ε 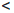 a-1/n0
a-1/n0 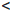 a1/n0
a1/n0 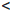 1 + ε.
1 + ε.
Следовательно, если δ = 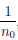 , то ∀ r ∈ (-δ, δ)
, то ∀ r ∈ (-δ, δ)  Q
Q
1-ε 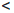 a-1/n0
a-1/n0 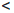 ar
ar 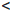 a1/n0
a1/n0 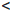 1+ε.
1+ε.
Иными словами, ∀ ε > 0 ∃δ =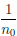 > 0 : ∀r ∈ (-δ, δ)
> 0 : ∀r ∈ (-δ, δ)  Q справедливо неравенство |ar - 1|
Q справедливо неравенство |ar - 1| 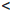 ε, что завершает доказательство.
ε, что завершает доказательство.
Случай a ∈ (0, 1) рассматривается аналогично.
Лемма 3.3. Пусть a > 0, {rn} — сходящаяся последовательность рациональных чисел. Тогда последовательность {arn} сходится.
Для определенности будем считать, что a > 1.
Покажем, что числовая последовательность {arn} является фундаментальной. Заметим, что ∀n, m ∈ 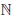
|arn -arm| =arm|arn-rm - 1|.
Так как последовательность {rn} сходится, то существует такое рациональное число A, что rn ≤ A, ∀n ∈  . Следовательно, ∀n ∈
. Следовательно, ∀n ∈ 
arn ≤ aA = B.
По лемме 3.2 ∀ ε > 0 ∃δ = δ(ε) > 0 : ∀r ∈ (-δ, δ)  выполняется неравенство |ar-1|
выполняется неравенство |ar-1|
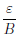 .
.
Из фундаментальности последовательности {rn} получаем:
∃N = N(δ) ∈ 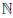 : ∀n > N, ∀m > N |rn -rm|
: ∀n > N, ∀m > N |rn -rm| 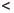 δ.
δ.
Отсюда ∀n > N, ∀m > N
|arn -arm| =arm|arn-rm - 1|  B·
B·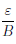 =ε,
=ε,
B что означает фундаментальность последовательности {arn}.
Определение 3.12. Пусть a > 0, x0 ∈ 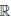 , {rn} — последовательность рациональных чисел, сходящаяся к x0 . Положим
, {rn} — последовательность рациональных чисел, сходящаяся к x0 . Положим
ax0 = 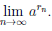
Лемма 3.4. Определение 3.12 корректно в том смысле, что величина предела 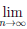 arn не зависит от выбора последовательности рациональных чисел {rn}, сходящейся к x0.
arn не зависит от выбора последовательности рациональных чисел {rn}, сходящейся к x0.
Пусть {rn/}, {rn//} — произвольные последовательности рациональных чисел, сходящиеся к x0. Согласно лемме 3.3 соответствующие последовательности {arn0}, {arn00} сходятся. Докажем, что 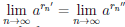 .
.
Составим новую последовательность {rn} такую, что
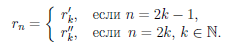
Ясно, что она сходится к числу x0. По лемме 3.3 последовательность {arn} сходится. Учитывая, что последовательности {arn/}, {arn//} являются подпоследовательностями последовательности {arn }, получим
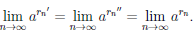
Замечание. Если x0 = 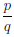 — рациональное число, то величина степени ax0, найденная по определению 3.12, совпадает со значением ap/q в ранее известном из школьного курса алгебры смысле, поскольку среди последовательностей рациональных чисел, сходящихся к x0 =
— рациональное число, то величина степени ax0, найденная по определению 3.12, совпадает со значением ap/q в ранее известном из школьного курса алгебры смысле, поскольку среди последовательностей рациональных чисел, сходящихся к x0 = 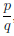 , есть последовательность
, есть последовательность
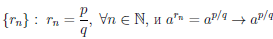
Определение 3.13. Пусть a — некоторое положительное число и a 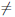 1.
1.
Функцию, определенную законом
∀x ∈  → ax ,
→ ax ,
называют показательной с основанием a.
Изучим некоторые свойства показательной функции.
Теорема 3.12. Если a > 1, то функция 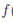 (x) = ax возрастает на
(x) = ax возрастает на 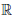 . Если же a ∈ (0, 1), то функция
. Если же a ∈ (0, 1), то функция 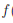 (x) = ax убывает на
(x) = ax убывает на 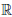 .
.
Докажем первую часть утверждения.
Фиксируем произвольные числа x1 , x2 ∈  такие, что x1
такие, что x1 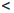 x2 . По принципу
x2 . По принципу
Архимеда существуют рациональные числа r1 , r2 такие, что x1 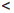 r1
r1 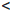 r2
r2 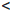 x2 .
x2 .
Пусть {rn/}, {rn//} — последовательности рациональных чисел, сходящиеся соответственно к x1 и x2 , причем
rn/ 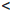 r1
r1 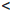 r2
r2 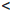 {rn// , ∀n ∈
{rn// , ∀n ∈  .
.
По свойству 2 показательной функции, определенной на множестве Q рациональных чисел,
arn/ 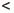 ar1
ar1 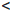 ar2
ar2 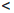 arn// , ∀n ∈
arn// , ∀n ∈  .
.
Переходя в крайних неравенствах к пределу при n → ∞ и учитывая определение 3.12, получим
ax1 ≤ ar1 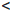 ar2 ≤ ax2 .
ar2 ≤ ax2 .
Итак,
∀x1 , x2 ∈  : x1
: x1 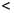 x2 ⇒ ax1
x2 ⇒ ax1 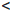 ax2 ,
ax2 ,
что доказывает возрастание функции f(x) = ax на множестве  , если a > 1.
, если a > 1.
Случай a ∈ (0, 1) рассматривается аналогично.
Теорема 3.13. Показательная функция  (x) = ax на
(x) = ax на  принимает только положительные значения.
принимает только положительные значения.
Для определенности рассмотрим показательную функцию с основанием a > 1.
Пусть x0 — произвольное действительное число. По принципу Архимеда найдется целое число n0 такое, что n0 ≤ x0 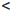 n0 + 1. В силу возрастания функции
n0 + 1. В силу возрастания функции  (x) = ax, имеем:
(x) = ax, имеем:
an0 ≤ ax0
Но по свойству 1 показательной функции, определенной на множестве Q рациональных чисел, an0 > 0. Поэтому ax0 > 0.
Теорема 3.14. Показательная функция (x) = ax непрерывна на множестве R действительных чисел.
(x) = ax непрерывна на множестве R действительных чисел.
Функция f монотонна на множестве  , поэтому имеет конечные односторонние пределы в точке x = 0. Поскольку
, поэтому имеет конечные односторонние пределы в точке x = 0. Поскольку
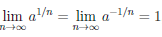 ,
,
то  (+0) =
(+0) = (-0) = 1. Следовательно, существует предел
(-0) = 1. Следовательно, существует предел
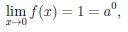
что означает непрерывность функции  в точке x = 0.
в точке x = 0.
Фиксируем теперь произвольную точку x0 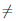 0 и произвольное число ε > 0. Заметим, что
0 и произвольное число ε > 0. Заметим, что
| (x) -
(x) - (x0)| = |ax-ax0| = ax0|ax-x0 -1|.
(x0)| = |ax-ax0| = ax0|ax-x0 -1|.
Так как функция  непрерывна в точке x = 0, то
непрерывна в точке x = 0, то
∃ δ = δ(ε) > 0 : ∀x ∈  , |x - xo|
, |x - xo| 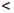 δ ⇒ |ax - 1|
δ ⇒ |ax - 1| 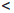
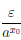
Поэтому ∀x ∈ 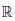 : |x — x0|
: |x — x0| 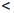 δ ⇒ |ax — ax0|
δ ⇒ |ax — ax0|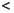 ax0 .
ax0 . 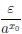 = ε, что доказывает непрерывность функции
= ε, что доказывает непрерывность функции  в произвольной точке x0 ∈ a
в произвольной точке x0 ∈ a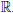 .
.
Теорема 3.15. Если  (x) = ax, то
(x) = ax, то  (
(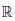 ) = (0, +∞).
) = (0, +∞).
Для определённости будем считать, что a > 1. В силу теоремы 3.12 функция y = ax возрастает на 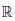 . Далее, существуют следующие пределы
. Далее, существуют следующие пределы
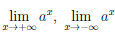
Но, как мы знаем, 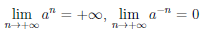 . Поэтому по теореме Гейне о пределе функции
. Поэтому по теореме Гейне о пределе функции
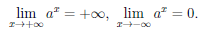
По замечанию 2 к теореме 3.9 f (-∞, +∞) = (0, +∞).
Согласно теореме 3.11 о непрерывности обратной функции к монотонной на интервале, показательная функция  (x) = ax имеет обратную
(x) = ax имеет обратную  -1 : (0, +∞) → R, которая непрерывна, возрастает, если a > 1, и убывает, если a ∈ (0, 1). Её называют логарифмической с основанием a (a > 0, a
-1 : (0, +∞) → R, которая непрерывна, возрастает, если a > 1, и убывает, если a ∈ (0, 1). Её называют логарифмической с основанием a (a > 0, a 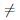 1) и обозначают loga : (0, +∞) →
1) и обозначают loga : (0, +∞) →  . В случае, если a = e, логарифм называют натуральным и обозначают символом ln.
. В случае, если a = e, логарифм называют натуральным и обозначают символом ln.
Определение 3.14. Пусть α — некоторое действительное число, отличное от нуля. Функция, которая каждому положительному x ставит в соответствие xα, называется степенной, α — её показателем.
Теорема 3.16. Степенная функция  (x) = xα непрерывна на интервале (0, +∞).
(x) = xα непрерывна на интервале (0, +∞).
Утверждение следует из теоремы 3.4 о непрерывности суперпозиции функций, так как  (x) = eαlnx.
(x) = eαlnx.
При α > 0 полагают 0α = 0 и доопределяют степенную функцию в точке x = 0, то есть при α > 0 считают, что степенная функция определена на множестве [0, +∞). При этом
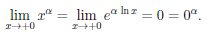
Следовательно, функция xα, α > 0, непрерывна на множестве [0, +∞).
Теорема 3.17. Пусть функции u(x) и v(x) определены и непрерывны на множестве X. Если u(x) > 0 для всех x ∈ X, то функция (u(x))v(x) непрерывна на X .
Утверждение, так как (u(x))v(x) = ev(x)lnu(x), ∀x ∈ X.
Некоторые замечательные пределы
Лемма 3.5. Если a > 0, a 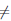 1, то
1, то 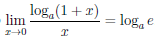
Пусть  : X = (-1, 0)∪(0, +∞) →
: X = (-1, 0)∪(0, +∞) → 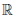 ,
,  (x) =
(x) = 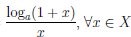
Поскольку  (x) = loga(1 + x)1/x, ∀x ∈ X, (1 + x)1/x → e при x → 0 и функция loga x непрерывна в точке x = e, то
(x) = loga(1 + x)1/x, ∀x ∈ X, (1 + x)1/x → e при x → 0 и функция loga x непрерывна в точке x = e, то
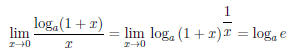
Следствие 1. Если а > 0, 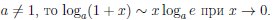
Следствие 2. 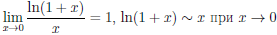
Лемма 3.6. Если a > 0, a 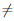 1, то
1, то 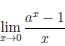 = ln a.
= ln a.
Положим ax -1 = t, ∀x ∈ 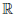 . Тогда x = loga(1 + t) — непрерывная на множестве (-1, +∞) функция. Поэтому при t → 0, x(t) → 0 и
. Тогда x = loga(1 + t) — непрерывная на множестве (-1, +∞) функция. Поэтому при t → 0, x(t) → 0 и
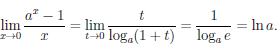
Следствие. Если а > 0, а  1, то ax -1 ~ x ln а при x → 0
1, то ax -1 ~ x ln а при x → 0
В частности, ex — 1 ~ x при x → 0.
Лемма 3.7. Если μ ∈ 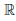 ∖{0}, то
∖{0}, то 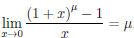 .
.
Утверждение верно, так как (1 + x)μ = eμ ln(1+x)
Следствие. Если μ ∈  ∖{0}, то (1 + x)μ - 1 ~ μx при x → 0.
∖{0}, то (1 + x)μ - 1 ~ μx при x → 0.
3.7 Равномерная непрерывность функции
Определение 3.15. Функция  : X → R называется равномерно непрерывной на множестве X , если для любого числа ε > 0 найдется такое δ = δ (ε) > 0, что для любых точек x/ и x// из X таких, что |x/ - x// |
: X → R называется равномерно непрерывной на множестве X , если для любого числа ε > 0 найдется такое δ = δ (ε) > 0, что для любых точек x/ и x// из X таких, что |x/ - x// | 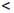 δ, выполняется неравенство |
δ, выполняется неравенство |  x/ ) -
x/ ) -  (x// )|
(x// )| 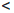 ε.
ε.
С помощью символики это определение записывается так:
функция  : X → R равномерно непрерывна на X ⇔
: X → R равномерно непрерывна на X ⇔
(∀ε > 0 ∃ δ = δ(ε) > 0 : ∀x/ , x// ∈ X, |x/ - x// | 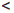 δ ⇒ |
δ ⇒ | (x/ ) -
(x/ ) -  (x//)|
(x//)| 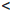 ε.)
ε.)
Очевидно, что если функция  равномерно непрерывна на множестве X , то она непрерывна на нем, то есть непрерывность — необходимое условие равномерной непрерывности. Однако непрерывность функции на множестве, вообще говоря, не влечет ее равномерной непрерывности на этом множестве, поскольку
равномерно непрерывна на множестве X , то она непрерывна на нем, то есть непрерывность — необходимое условие равномерной непрерывности. Однако непрерывность функции на множестве, вообще говоря, не влечет ее равномерной непрерывности на этом множестве, поскольку
 ∈ C(X) ⇔ ∀x0 ∈ X, ∀ε > 0∃δ= δ(x0,ε) > 0 :
∈ C(X) ⇔ ∀x0 ∈ X, ∀ε > 0∃δ= δ(x0,ε) > 0 :
| (x) -
(x) -  (x0)|
(x0)| 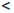 ε, ∀x ∈ X : |x - x0|
ε, ∀x ∈ X : |x - x0| 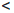 δ.
δ.
В этом определении число δ зависит не только от ε, но и от точки x0 ∈ X .
Рассмотрим несколько примеров.
Пример 3.12. Покажем, что функция  (x) =
(x) = 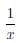 равномерно непрерывна на множестве [1, +∞), но не является равномерно непрерывной на множестве (0, 1].
равномерно непрерывна на множестве [1, +∞), но не является равномерно непрерывной на множестве (0, 1].
1) Пусть X = [1, +∞). Для любых двух точек x/ и x// из [1, +∞)
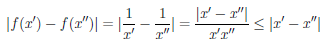 .
.
Зафиксируем ε > 0 и положим δ = ε. Тогда
∀x/, x// ∈ [1, +∞) |x/ - x// | 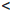 δ ⇒ || (x/ ) -
δ ⇒ || (x/ ) - 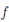 (x// )| ≤ | x/ - x//|
(x// )| ≤ | x/ - x//| 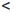 δ = ε.
δ = ε.
Поэтому функция | равномерно непрерывна на множестве [1, +∞).
2) Теперь покажем, что функция 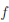 (x) = — не является равномерно непрерывной на промежутке (0, 1], хотя и непрерывна на нём. В связи с этим запишем отрицание свойства равномерной непрерывности функции:
(x) = — не является равномерно непрерывной на промежутке (0, 1], хотя и непрерывна на нём. В связи с этим запишем отрицание свойства равномерной непрерывности функции:
функция | : X → R не является равномерно непрерывной на X  |
|
∃ ε > 0 : ∀δ > 0 ∃ x/δ, x//δ ∈ X : |x/δ - x//δ | 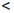 δ, но |
δ, но |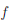 (x/δ) - f(x//δ) |≥ ε.
(x/δ) - f(x//δ) |≥ ε.
Зафиксируем произвольно δ ∈ (0, 1). Пусть x/δ — произвольная точка из интервала (0, δ) ⊂ (0,1), а 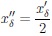 . Тогда x/δ - x//δ∈ (0,1],
. Тогда x/δ - x//δ∈ (0,1],
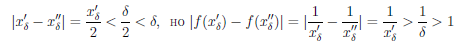
Следовательно, для числа ε = 1 и для любого - > 0 ∃ x/δ, x//δ ∈ (0, 1] :
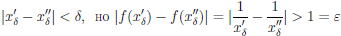 ,
,
то есть  не является равномерно непрерывной на промежутке (0, 1].
не является равномерно непрерывной на промежутке (0, 1].
Пример 3.13. Покажем, что функция  (x) = sin — не является равномерно непрерывной на интервале (0, 1), хотя является ограниченной и непрерывной на нем.
(x) = sin — не является равномерно непрерывной на интервале (0, 1), хотя является ограниченной и непрерывной на нем.
Для доказательства рассмотрим последовательность точек
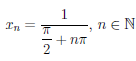
Очевидно, что xn ∈ (0,1), ∀n ∈  , и xn → 0 при n → +∞. Поэтому
, и xn → 0 при n → +∞. Поэтому
∀δ ∈ (0, 1), ∃n0 ∈  : |xn|
: |xn| 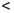 δ, ∀n > n0.
δ, ∀n > n0.
Учитывая, что (xn) = sin 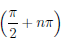 = (—1)n, получим, что
= (—1)n, получим, что 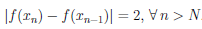
Следовательно, ∃ ε0 = 2 : ∀ δ ∈ (0, 1), ∃ x/δ = xn, x//δ = xn+1 , n > n0 :
|x/δ- x//δ |= |xn- χn+1| δ, но |
δ, но | (x/δ)-
(x/δ)-  (x//δ )|≥ εo.
(x//δ )|≥ εo.
Это означает, что рассматриваемая функция не является равномерно непрерывной на интервале (0, 1).
Пример 3.14. Докажем, что функция (x) = x2 не является равномерно непрерывной на множестве [1, +∞).
(x) = x2 не является равномерно непрерывной на множестве [1, +∞).
Рассмотрим последовательность точек xn = 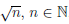 . Очевидно, что xn ∈ [1, +∞), и
. Очевидно, что xn ∈ [1, +∞), и
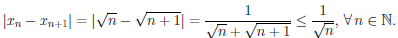
В то же время, |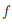 (xn) -
(xn) - 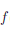 (xn+1 )| = |n -(n+1) | = 1.
(xn+1 )| = |n -(n+1) | = 1.
Так как 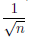 → 0 при n → +∞, то n
→ 0 при n → +∞, то n
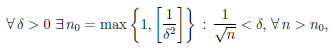
значит, ∣xn — xn+1 ∣ 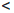
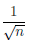 =
= 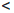 δ для n > n0. Пусть ε = 1, δ — произвольное положительное число. Положим x/δ =
δ для n > n0. Пусть ε = 1, δ — произвольное положительное число. Положим x/δ = 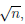 , x//δ =
, x//δ = 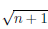 , n > n0. Тогда
, n > n0. Тогда
∀δ > 0∃x/δ,x//δ ∈ [1, +∞) : |x/δ - x//δ| 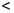 δ, |
δ, |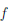 (x/δ) - f(x//δ)| = 1 = ε.
(x/δ) - f(x//δ)| = 1 = ε.
Следовательно, функция 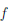 (x) = x2 не является равномерно непрерывной на [1, +∞).
(x) = x2 не является равномерно непрерывной на [1, +∞).
Теорема 3.18 (Кантора). Если функция непрерывна на отрезке, то она равномерно непрерывна на нем.
Предположим, что 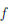 ∈ C ([a, b]), но не является равномерно непрерывной на отрезке [a,b]. Тогда cуществует ε0 > 0 такое, что для любого δ > 0 найдутся точки x/δ, x//δ ∈ [a, b], ∣x/δ — x//δ|
∈ C ([a, b]), но не является равномерно непрерывной на отрезке [a,b]. Тогда cуществует ε0 > 0 такое, что для любого δ > 0 найдутся точки x/δ, x//δ ∈ [a, b], ∣x/δ — x//δ| 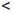 δ, но |f (x/δ) — f (x//δ)| ≥ ε0. Возьмем, например, последовательность чисел δn =
δ, но |f (x/δ) — f (x//δ)| ≥ ε0. Возьмем, например, последовательность чисел δn =  , ∀ n ∈
, ∀ n ∈  . Тогда найдутся последовательности {x/n}, {x//n} ∈ [a, b] такие, что
. Тогда найдутся последовательности {x/n}, {x//n} ∈ [a, b] такие, что
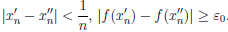
Поскольку последовательность {x/n} ограничена, по лемме Больцано-Вейершт-расса она имеет сходящуюся подпоследовательность {x/nk }. Пусть 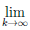 x/nk = γ.
x/nk = γ.
Очевидно, что γ ∈ [a, b]. Далее, в силу выбора последовательностей,
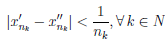
Поскольку lim nk = +∞, то подпоследовательность {x//nk } сходится к той же точке γ. Далее, 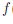 (x/nk) →
(x/nk) →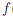 (γ) ,
(γ) ,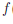 (x//nk) →
(x//nk) →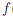 (γ)→ при k → ∞, поэтому разность
(γ)→ при k → ∞, поэтому разность 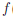 (x/nk ) —
(x/nk ) — 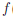 (x//nk) обязана быть бесконечно малой. С другой стороны, в силу выбора элементов x/nk, x//nk, |
(x//nk) обязана быть бесконечно малой. С другой стороны, в силу выбора элементов x/nk, x//nk, |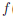 (x/nk ) —
(x/nk ) — 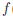 (x//nk)| ≥ ε0, ∀ k ∈
(x//nk)| ≥ ε0, ∀ k ∈ 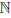 . Следовательно, число 0 не является пределом последовательности {
. Следовательно, число 0 не является пределом последовательности {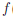 (x/nk ) —
(x/nk ) — 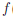 (x//nk )}. Полученное противоречие завершает доказательство теоремы.
(x//nk )}. Полученное противоречие завершает доказательство теоремы.
Замечание 1. Приведенные примеры показывают, что в условиях теоремы Кантора нельзя заменить отрезок на промежуток другого вида.
Замечание 2. Из доказательства теоремы Кантора следует, что она остаётся в силе на ограниченном множестве X , содержащем все свои предельные точки.
0----------------
Свойства непрерывных функций
Определение 11.1. Пусть 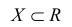 подмножество во множестве действительных чисел R. Х называется ограниченным сверху (снизу), если
подмножество во множестве действительных чисел R. Х называется ограниченным сверху (снизу), если  такое число М(m), что выполняется неравенство
такое число М(m), что выполняется неравенство 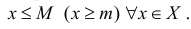
При этом M(m) называется верхней (нижней) гранью множества Х. Наименьшая из всех возможных верхних граней множества Х называется точной верхней гранью множества Х и обозначается sup X (латинское supremum (супремум) – наивысшее). Наибольшая из всех возможных нижних граней множества Х называется точной нижней гранью множества Х и обозначается inf X (латинское infimum (инфимум) – наинизшее).
П р и м е р 11.1
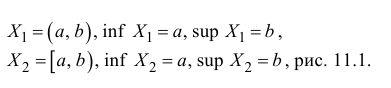
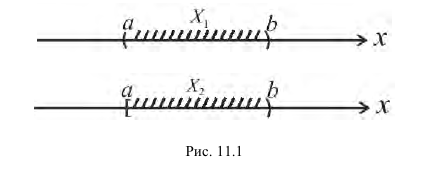
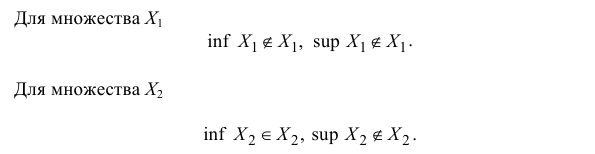
Аксиома Вейерштрасса. Всякое непустое ограниченное множество 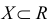 имеет конечные точные верхние и нижние грани sup X и inf X .
имеет конечные точные верхние и нижние грани sup X и inf X .
Для функции 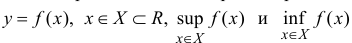 определяются, как sup f( X) и inf f(X ) – множества значений f(X ) функции y=f(x) при
определяются, как sup f( X) и inf f(X ) – множества значений f(X ) функции y=f(x) при 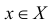 .
.
П р и м е р 11.2
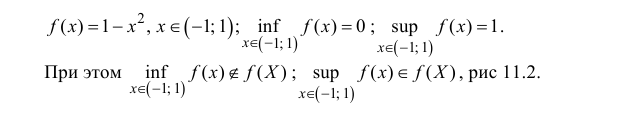
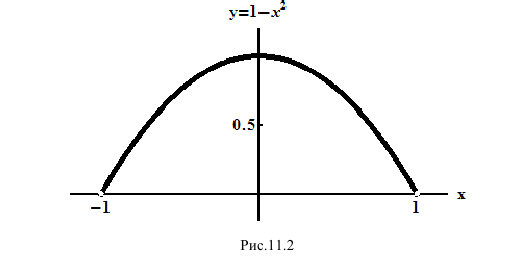
Теорема 11.1 . (теорема Вейерштрасса). Если функция y=f(x) непрерывна на отрезке 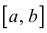 , то она достигает на этом отрезке своих точных верхней и нижней граней, то есть
, то она достигает на этом отрезке своих точных верхней и нижней граней, то есть 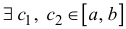 такие, что
такие, что 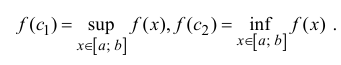
При этом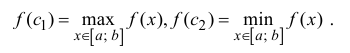
Если в условии теоремы 10.1 рассматривать не отрезок, а интервал ( a,b ) или полуинтервал, то она не выполняется.
Например, для y=f(x) из примера 11.2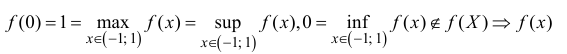
не имеет минимума на множестве ( -1,1).
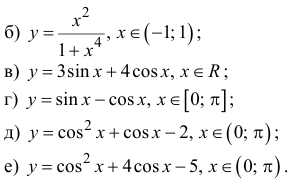
Найти 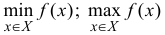 на этих множествах.
на этих множествах.
Теорема 11.2. (теорема Больцано–Коши). Если функция y=f(x) непрерывна на отрезке 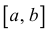 и принимает на его концах значения разных знаков, то
и принимает на его концах значения разных знаков, то 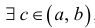 , такая, что f(c)=0.
, такая, что f(c)=0.
П р и м е р 11.3
Проверить, что уравнение cosx= x имеет корень на интервале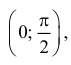 рис. 11.3.
рис. 11.3.
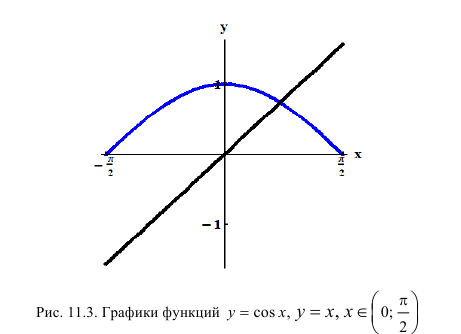
Р е ш е н и е
Функция y=cos x - x непрерывна . 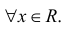
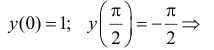
по теореме 2 0; 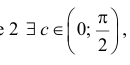 такая что f(c)=0.
такая что f(c)=0.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |