Непрерывность функций и точки разрыва с примерами решения

Содержание:

Непрерывность функций и точки разрыва

Непрерывность функции

Определение: Функция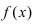

• - она определена в этой точке и ее некоторой 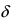-окрестности;
• - существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.

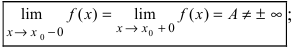
- предел функции в точке 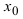равен значению функции в исследуемой точке, т.е.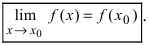

Пример:

Найти область непрерывности функции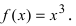

Решение:

Данная функция непрерывна так как в каждой точке указанного интервала функция определена, в каждой точке существуют конечные и равные лево- и правосторонние пределы, а предел функции в каждой точке равен значению функции в этой точке.

Замечание: Всякая элементарная функция непрерывна в области своего определения.

Точки разрыва

Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.

Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.

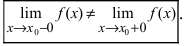
Пример:

Доказать, что функция 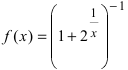в точке 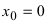имеет разрыв первого рода.

Решение:

Нарисуем график функции в окрестности нуля (Рис. 64): 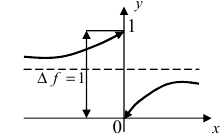Рис. 64. График функции 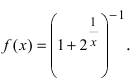Область определения функции: 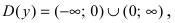т.е. точка 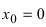является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 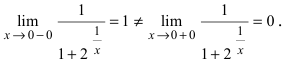Следовательно, в изучаемой точке данная функция терпит разрыв первого рода.

Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).

Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.

Пример:

Доказать, что функция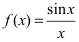 имеет в точке 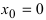устранимый разрыв.

Решение:

В точке 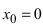функция имеет неопределенность 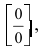поэтому эта точка является точкой, подозрительной на разрыв. Вычислив в этой точке лево- и правосторонний пределы 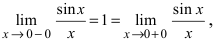убеждаемся, что данная точка является точкой устранимого разрыва.

Определение: Все остальные точки разрыва называются точками разрыва II рода.

Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы

один из односторонних пределов равен 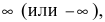т.е. в такой точке функция терпит бесконечный разрыв.

Пример:

Исследовать на непрерывность функцию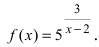

Решение:

Найдем область определения этой функции: 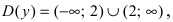т.е. точка

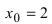является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 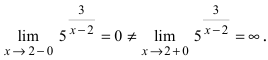Так как левосторонний предел конечен, а правосторонний предел бесконечен, то в изучаемой точке данная функция терпит разрыв II рода.

Пример:

Исследовать на непрерывность функцию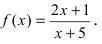

Решение:

Найдем область определения этой функции: 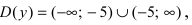т.е. точка 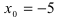является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: 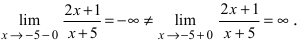Так как левосторонний и правосторонний пределы бесконечены, то в изучаемой точке данная функция терпит разрыв II рода.

Операции над непрерывными функциями

Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.

Доказательство: Докажем приведенную теорему для суммы двух функций 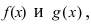которые определены в некоторой 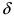-окрестности точки 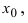в которой лево- и правосторонние пределы равны между собой. Так как функции 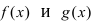непрерывны в некоторой 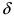-окрестности точки 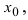то выполняются равенства: 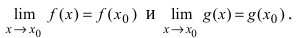В силу того, что существуют конечные пределы обеих функций, то по теореме о пределе суммы двух функций имеем, что 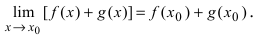Аналогично теорема доказывается для суммы (разности) любого конечного числа непрерывных функций. Нижеприведенные теоремы доказываются так же, как и теорема.

Теорема: Произведение непрерывных функций есть непрерывная функция.

Теорема: Частное двух непрерывных функций 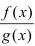при условии, что во всех точках общей области определения функция 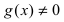, есть непрерывная функция.

Теорема: Сложная функция от непрерывных функций есть непрерывная функция.

• Заказать решение задач по высшей математике

Схема исследования функции на непрерывность

Исследование функции на непрерывность проводят по следующей схеме:

• находят область определения функции; точки, в которых функция не определена, являются точками подозрительными на разрыв: если функция задана словесным образом, т.е. описывается разными формулами на разных интервалах, то точками подозрительными на разрыв являются точки, определяющие границы интервалов;
• исследуют подозрительные на разрыв точки, для чего вычисляют лево- и правосторонние пределы; классифицируют точки разрыва;
• при наличии точек разрыва строят график функции в малой 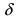-окрестности точки .

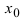Пример:

Исследовать на непрерывность функцию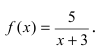

Решение:

Согласно схеме исследования функции на непрерывность имеем:

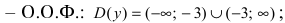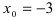• точка является точкой подозрительной на разрыв.
• вычислим левосторонний 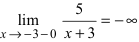и правосторонний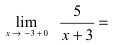 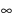пределы; так как пределы бесконечные, то точка 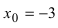является точкой разрыва второго рода;
• построим график функции в небольшой окрестности точки разрыва (Рис. 65).

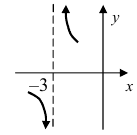
Рис. 65. Поведение графика функции 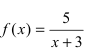в малой окрестности точки разрыва второго рода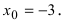

Из рисунка видно, что график функции 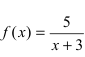—неограниченно приближается к вертикальной прямой 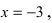нигде не пересекая эту прямую.

Свойства непрерывных функций на отрезке (a; b)

Свойства непрерывных функций на отрезке .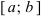

Определение: Замкнутый интервал 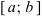будем называть сегментом.

Приведем без доказательства свойства непрерывных функций на сегменте .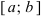

Теорема: Если функция 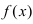непрерывна на сегменте 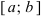, то она достигает своего наименьшего (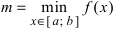) и наибольшего (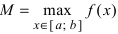) значения либо во внутренних точках сегмента, либо на его концах.

Пример:

Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).

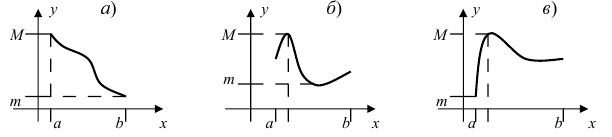
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.

Решение:

На графике а) функция достигает своего наименьшего и наибольшего значений на концах сегмента На графике б) функция достигает своего наименьшего 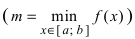и наибольшего значения 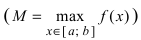во внутренних точках сегмента На графике в) функция достигает своего наименьшего значения 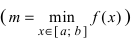на левом конце сегмента 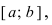а наибольшего значения 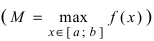во внутренней точке сегмента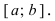

Тб. Если функция 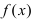непрерывна на сегменте 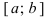и достигает своего наименьшего (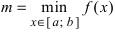) и наибольшего (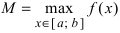) значений, то для любого вещественного числа С, удовлетворяющего неравенству 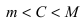, найдется хотя бы одна точка 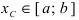такая, что .

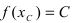Пример:

Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).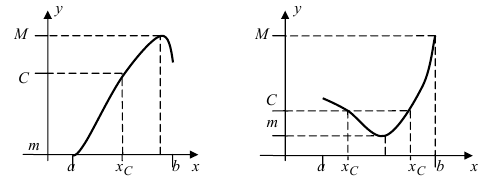

Рис. 67. Графики функций, удовлетворяющих условиям Тб.

Теорема: Если функция 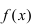непрерывна на сегменте 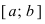и на его концах принимает значения разных знаков, то найдется хотя бы одна точка 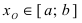такая, что.

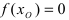Пример:

Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).

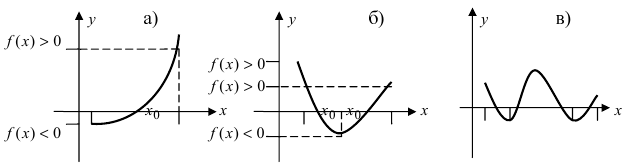
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.

На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.