
Непрерывность функции - определение с примерами решения
Содержание:
Непрерывность функции
Пусть х есть некоторое значение данной переменной величины. Наряду с х рассмотрим другое значение х1 этой переменной величины. Введем следующее определение.
Определение: Приращением переменной величины называется разность между новым значением этой величины и ее прежним значением, т. е. в нашем случае приращение переменной величины равно 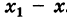
Для обозначения приращения используется греческая буква 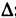
Прибавляя к значению переменной величины ее приращение, получаем приращенное значение этой величины. Например, 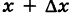 есть приращенное значение величины х.
есть приращенное значение величины х.
Предположим, что у есть некоторая функция от аргумента х, т. е.

Дадим аргументу х приращение 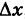 ; тогда у получит соответствующее приращение
; тогда у получит соответствующее приращение 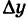 . Этот факт, очевидно, можно записать так:
. Этот факт, очевидно, можно записать так:
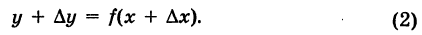
Из равенств (1) и (2) следует
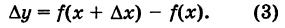
Пример:
Определить приращение аргумента х и приращение функции у = х2, если аргумент х изменился от -1 до 2.
Решение:
Здесь, очевидно, 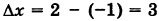 и
и 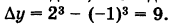
Понятие приращения функции поясним геометрически. Пусть кривая АВ есть график функции у = f(x) (рис. 93).
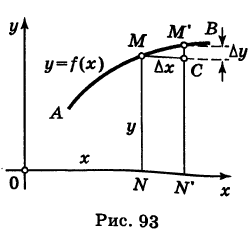
Рассмотрим на этой кривой точку М с текущими координатами х и у. Дадим абсциссе х точки М(х, у) приращение 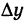 , тогда ордината ее у получит приращение
, тогда ордината ее у получит приращение 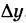 . Точка М(х, у) займет при этом положение
. Точка М(х, у) займет при этом положение 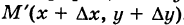 . Пусть С есть точка пересечения прямой, проходящей через точку М и параллельной оси Ох, и перпендикуляра M'N опущенного из точки М' на ось Ох. Очевидно, что
. Пусть С есть точка пересечения прямой, проходящей через точку М и параллельной оси Ох, и перпендикуляра M'N опущенного из точки М' на ось Ох. Очевидно, что
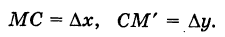
Может случиться, что для некоторого х при стремлении Ах к нулю точка М' неограниченно приближается к точке М и, следовательно, 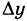 также стремится к нулю. В таком случае функция у = f(x) называется непрерывной при данном значении х. Более точно:
также стремится к нулю. В таком случае функция у = f(x) называется непрерывной при данном значении х. Более точно:
Определение: Функция f(x), определенная на множестве X, называется непрерывной при х = х1 (или непрерывной в точке х1)у если:
1)функция определена при 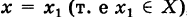 ;
;
2)приращение функции в точке х1 стремится к нулю, когда приращение аргумента 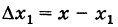 стремится к нулю, т. е.
стремится к нулю, т. е.
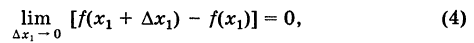
где бесконечно малое приращение 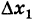 пробегает лишь те значения, для которых
пробегает лишь те значения, для которых 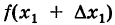 имеет смысл. При этом мы, как всегда, предполагаем, что
имеет смысл. При этом мы, как всегда, предполагаем, что 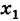 является предельной точкой множества X и, таким образом, в любой окрестности
является предельной точкой множества X и, таким образом, в любой окрестности 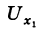 найдутся точки
найдутся точки 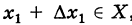 , отличные от
, отличные от 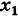
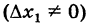 , для которых функция f(x) определена.
, для которых функция f(x) определена.
Короче говоря, функция называется непрерывной в данной точке, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Используя понятие предела функции, получаем развернутое определение непрерывности функции в точке: функция f(x) непрерывна в точке х1 тогда и только тогда, когда 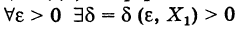 такое, что
такое, что
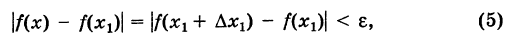
если 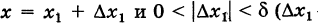 — любое допустимое приращение). Заметим, что неравенство (5), очевидно, выполнено и при
— любое допустимое приращение). Заметим, что неравенство (5), очевидно, выполнено и при 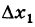 = 0, т. е. здесь
= 0, т. е. здесь 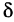 -окрестность точки хх можно трактовать как полную:
-окрестность точки хх можно трактовать как полную: 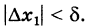
Определение: Функция fix) называется не прерывной на данном множестве X, если: 1) она определена на этом множестве 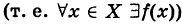 непрерывна в каждой точке этого множества, т. e.
непрерывна в каждой точке этого множества, т. e.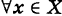 справедливо равенство
справедливо равенство
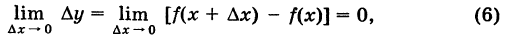
где 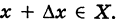
Замечание. Множество X здесь трактуется как область определения функции, т. е. точки 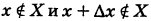 не рассматриваются.
не рассматриваются.
Например, функция fix) непрерывна на отрезке 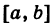 , если:
, если:
1)эта функция определена в каждой точке этого отрезка,
2)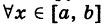 справедливо равенство (6), где
справедливо равенство (6), где 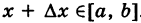 .
.
Пример:
Функция
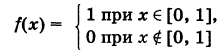
непрерывна на отрезке X = [0, 1], хотя она не является непрерывной на оси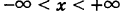 .
.
Пример:
Исследовать на непрерывность функцию  .
.
Решение:
Давая аргументу х приращение 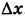 , получим
, получим
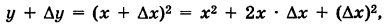
где 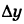 — приращение функции у. Отсюда
— приращение функции у. Отсюда
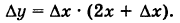
Очевидно, каково бы ни было фиксированное значение х, если 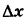 бесконечно мало, то
бесконечно мало, то 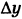 также будет бесконечно малым. Следовательно, функция х2 непрерывна при любом значении аргумента х. Иными словами, х2 является непрерывной функцией в бесконечном интервале
также будет бесконечно малым. Следовательно, функция х2 непрерывна при любом значении аргумента х. Иными словами, х2 является непрерывной функцией в бесконечном интервале
Легко также доказать непрерывность степенной функции 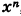 , где
, где 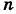 — натуральное постоянное число.
— натуральное постоянное число.
Определение: Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции.
Если х = х0 — точка разрыва функции у = f(x), то возможны два случая:
1)функция f(x} определена при х = х0, причем
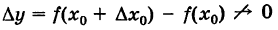
2)функция f(x) не определена при х = х0 и говорить о приращении функции в точке х0 не имеет смысла. В этом случае условимся х = х0 называть точкой разрыва функции f(x) только тогда, когда функция fix) определена в непосредственной близости значения х0
То есть при любом 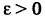 в интервале
в интервале 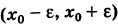 найдутся точки, где функция f(x) определена.
найдутся точки, где функция f(x) определена.
Если можно изменить или дополнительно определить функцию f(x) в точке х0 (т. е. выбрать число f(x0)) так, что измененная или пополненная функция f(x) будет непрерывна при х = х0, то эта точка называется устранимой точкой разрыва функции f(x). В противном случае, т. е. когда функция f(x) остается разрывной при х = х0 при любом выборе числа f(x0), значение х0 называется неустранимой точкой разрыва функции f(x).
Пример:
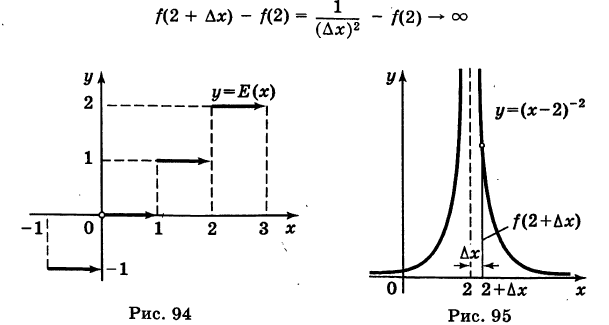
Рассмотрим функцию Е(х), равную целой части числа х, т. е. если 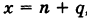 , где
, где 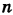 — целое число и
— целое число и 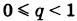 , то Е(х) =
, то Е(х) = 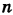 (рис. 94).
(рис. 94).
Например, E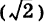 = 1, Е(
= 1, Е(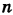 ) = 3, Е(-1,5) = -2 и т. д.
) = 3, Е(-1,5) = -2 и т. д.
Функция Е(х) разрывна при каждом целочисленном значении аргумента х. В самом деле, например, при х = 1 и достаточно малом 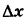 имеем
имеем
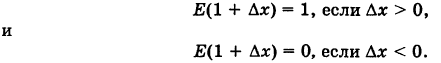
Отсюда, приняв во внимание, что Е(1) = 1, получим
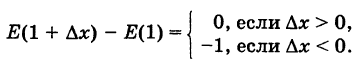
Следовательно, приращение функции 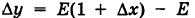 (1) не стремится к нулю при
(1) не стремится к нулю при 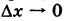 , поэтому функция разрывна при х = 1.
, поэтому функция разрывна при х = 1.
Аналогичное рассуждение можно провести для каждого из значений х = kt где k — целое число. Итак, точки х = k (k = 0, ±1, ±2,...) — неустранимые точки разрыва функции Е(х).
Пример:
Пусть 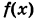 = 1/(х — 2)2.
= 1/(х — 2)2.
Эта функция не определена при х = 2, но имеет смысл для всех значений х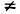 2 (рис. 95). Какое бы значение мы ни приписали числу f(2), всегда будем иметь
2 (рис. 95). Какое бы значение мы ни приписали числу f(2), всегда будем иметь
при 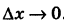 . Таким образом, здесь при х = 2 при любом выборе значения f(2) бесконечно малому приращению
. Таким образом, здесь при х = 2 при любом выборе значения f(2) бесконечно малому приращению 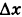 аргумента соответствует бесконечно большое приращение
аргумента соответствует бесконечно большое приращение 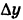 функции. Следовательно, эта функция имеет неустранимую точку разрыва при х = 2.
функции. Следовательно, эта функция имеет неустранимую точку разрыва при х = 2.
Другое определение непрерывности функции
Ввиду важности понятия непрерывности функции дадим другое определение непрерывности в точке, эквивалентное приведенному выше.
Определение: Функция f(x) называется непрерывной при 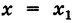 , если: 1) эта функция определена при
, если: 1) эта функция определена при 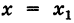 ; 2) имеет место равенство
; 2) имеет место равенство

т. е. функция непрерывна в данной точке 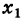 тогда и только тогда, когда предел функции при
тогда и только тогда, когда предел функции при 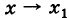 равен значению функции в предельной точке (рис. 96). Здесь, понятно, предполагается, что переменная х принимает лишь те значения, для которых f(x) имеет смысл. Иными словами, для функции f(x), непрерывной при значении х„ из того обстоятельства, что
равен значению функции в предельной точке (рис. 96). Здесь, понятно, предполагается, что переменная х принимает лишь те значения, для которых f(x) имеет смысл. Иными словами, для функции f(x), непрерывной при значении х„ из того обстоятельства, что 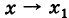 вытекает предельное соотношение
вытекает предельное соотношение

Легко видеть, что:
1)если функция f(x) непрерывна при 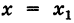 в указанном ранее смысле, т. е. если ,
в указанном ранее смысле, т. е. если ,
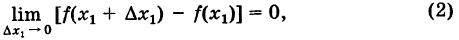
то, полагая х, + 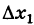 = х, где, очевидно,
= х, где, очевидно, 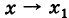 , при
, при  , и пользуясь теоремой о пределе алгебраической суммы, получаем
, и пользуясь теоремой о пределе алгебраической суммы, получаем

Следовательно, функция f(x) непрерывна также при 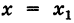 и в нашем новом смысле;
и в нашем новом смысле;
Здесь, как обычно, предполагается, что 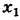 есть предельная точка области определения функции f(x).
есть предельная точка области определения функции f(x).
2)очевидно, что, и обратно, из равенства (3) вытекает равенство (2).
Таким образом, эквивалентность двух определений полностью доказана.
Для функции, непрерывной на множестве X, в силу формулы (1) для каждого значения 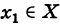 выполнено равенство
выполнено равенство
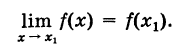
Так как 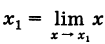 , то отсюда получаем
, то отсюда получаем
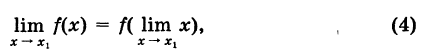
т. е. если функция непрерывна, то знаки предела и функции перестановочны.
В подробных курсах анализа доказывается, что формула (4) остается верной для любой непрерывной функции 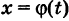 такой, что
такой, что 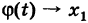 при
при 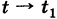 . Таким образом, имеем усиленное свойство перестановочности функции и предела:
. Таким образом, имеем усиленное свойство перестановочности функции и предела:
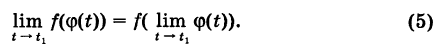
Из определения 3 вытекает, что функция разрывна в данной точке тогда и только тогда, когда: или 1) не существует предела функции в этой точке, или же 2) предел функции в данной точке существует, но не совпадает со значением функции в этой точке.
Непрерывность основных элементарных функций
1)Степенная функция
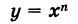
(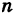 — натуральное (см. рис. 60)) непрерывна при любом значении х.
— натуральное (см. рис. 60)) непрерывна при любом значении х.
2)Показательная функция
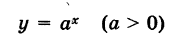
(см. рис. 63) непрерывна при любом значении х. 138
3)Тригонометрическая функция
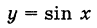
(см. рис. 65) непрерывна при каждом значении х.
В самом деле, давая аргументу х приращение 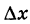 и обозначая через
и обозначая через 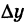 соответствующее приращение функции у, будем иметь
соответствующее приращение функции у, будем иметь 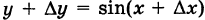 ; отсюда
; отсюда
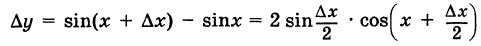
В силу замечания к теореме при 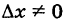 имеем
имеем
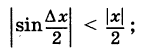
кроме того,
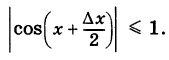
Поэтому
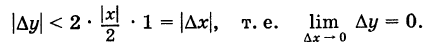
Следовательно, функция sin х непрерывна в интервале 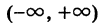 .
.
Совершенно так же доказывается, что
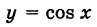
есть непрерывная функция в интервале 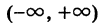 (см. рис. 65).
(см. рис. 65).
Основные теоремы о непрерывных функциях
Теорема: Сумма конечного числа непрерывных функций есть функция непрерывная.
Доказательство: В самом деле, если 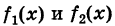 — функции, непрерывные на некотором множестве
— функции, непрерывные на некотором множестве 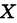 , а
, а 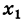 — любое значение из этого множества, то
— любое значение из этого множества, то
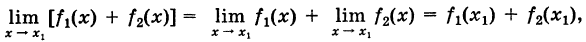
Предполагается, что все рассматриваемые функции определены и непрерывны на некотором общем множестве X (например, на интервале (а, b) или отрезке [а, b] и т. п.).
т. е. предел суммы при 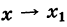 равен значению этой суммы при
равен значению этой суммы при 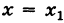
Следовательно, функция 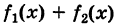 также непрерывна на множестве X.
также непрерывна на множестве X.
Теорема: Произведение конечного числа непрерывных функций есть функция непрерывная.
Доказательство аналогичное.
Следствие. Целый полином
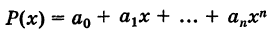
есть функция непрерывная.
Теорема: Частное от деления двух непрерывных функций есть функция, непрерывная во всех точках, в которых делитель отличен от нуля.
Доказательство аналогичное.
Следствие. Дробная рациональная функция
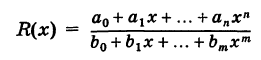
непрерывна всюду, за исключением тех значений х, где знаменатель обращается в нуль.
Теорема: Непрерывная функция от непрерывной функции есть функция также непрерывная; иначе говоря, сложная функция, состоящая из непрерывных функций, непрерывна.
Доказательство: Пусть 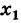 — произвольная точка области определения сложной функции
— произвольная точка области определения сложной функции 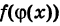 , причем функция
, причем функция 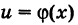 непрерывна в точке
непрерывна в точке 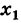 , а функция f(u) непрерывна в точке
, а функция f(u) непрерывна в точке 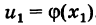 . На основании усиленного свойства перестановочности непрерывной функции и предела имеем
. На основании усиленного свойства перестановочности непрерывной функции и предела имеем
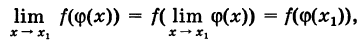
т. е. сложная функция 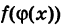 непрерывна в точке
непрерывна в точке 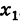 .
.
В силу теоремы 4, например, функции 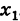 непрерывны вследствие непрерывности функций
непрерывны вследствие непрерывности функций 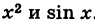 .
.
Функции, которые мы будем рассматривать в дальнейшем, непрерывны всюду, кроме, быть может, отдельных значений аргумента.
Например, функция
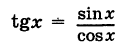
(см. рис. 66) в силу теоремы 3 настоящего параграфа непрерывна для всех значений аргумента х, кроме тех, для которых cos х = О, т. е. кроме значений 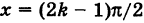 , где k — любое целое число. Аналогично, функция
, где k — любое целое число. Аналогично, функция
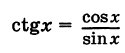
(см. рис. 66) непрерывна при 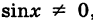 , т. е. при
, т. е. при 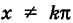 (k — целое).
(k — целое).
Справедлива теорема о непрерывности обратной функции, которую мы приводим без доказательства.
Теорема: Если функция у = f(x) непрерывна и строго монотоннана промежутке 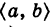 , то существует однозначная обратная функция
, то существует однозначная обратная функция 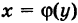 , определенная на промежутке
, определенная на промежутке 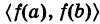 , причем последняя также непрерывна и монотонна в том же смысле.
, причем последняя также непрерывна и монотонна в том же смысле.
В силу этой теоремы радикал 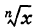 (
(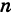 — натуральное) (см. рис 62), логарифмическая функция
— натуральное) (см. рис 62), логарифмическая функция 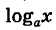 (а > 0,
(а > 0, 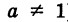 ) (см. рис. 64), главные значения обратных тригонометрических функций arcsin х, arccos х, arctg х, arcctg х (см. рис. 67—70) непрерывны при всяком значении аргумента х, при котором эти функции определены.
) (см. рис. 64), главные значения обратных тригонометрических функций arcsin х, arccos х, arctg х, arcctg х (см. рис. 67—70) непрерывны при всяком значении аргумента х, при котором эти функции определены.
Раскрытие неопределенностей
Может случиться, что функция f(x) определена и непрерывна всюду, за исключением некоторого значения 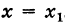 при котором функция f(x) теряет смысл (становится неопределенной). Возникает вопрос: нельзя ли так выбрать число f(x), чтобы дополненная функция f(x) была непрерывна при
при котором функция f(x) теряет смысл (становится неопределенной). Возникает вопрос: нельзя ли так выбрать число f(x), чтобы дополненная функция f(x) была непрерывна при 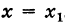 ?
?
В силу предыдущего для этого необходимо и достаточно выполнение равенства
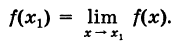
Операция нахождения предела функции f(x) при 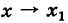 в этом случае называется раскрытием неопределенности, а сам предел
в этом случае называется раскрытием неопределенности, а сам предел 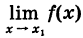 если он существует, носит не совсем удачное название истинного значения функции f(x) при
если он существует, носит не совсем удачное название истинного значения функции f(x) при 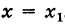 .
.
То есть f(x) или строго возрастает, или строго убывает на 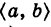 .
.
Пример:
Пусть
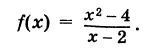
Эта функция теряет смысл при х = 2. Полагая дополнительно
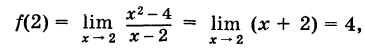
получим функцию, непрерывную всюду, в том числе и при х = 2. Если же положить 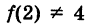 , то соответствующая функция будет разрывна при х = 2 (рис. 97).
, то соответствующая функция будет разрывна при х = 2 (рис. 97).
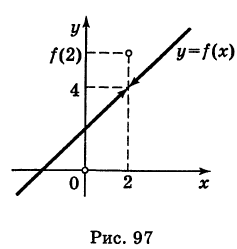
Пример:
Функция
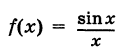
не определена при х = 0. Полагая дополнительно
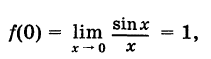
мы получим функцию, определенную и непрерывную для всех значений аргумента х.
Классификация точек разрыва функции
Точка х0 разрыва функции f(x) называется точкой разрыва первого рода, если существуют конечные односторонние пределы функции (рис. 87):
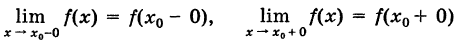
(при этом функция f(x) не обязательно должна быть определена в точке х0, т. е. f(x0) может не существовать). Величина
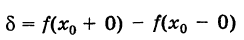
называется скачком функции f(x) в точке х0.
Все прочие точки разрыва хх функции f(x) называются ее точками разрыва второго рода. Среди них важное значение имеют точки бесконечного разрыва х1, для которых существуют (конечные или бесконечные) односторонние пределы
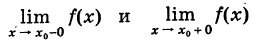
и хотя бы один из них является бесконечным (см., например, рис. 98).
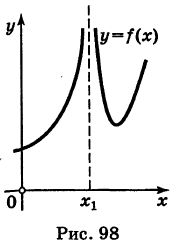
В этом случае прямая 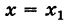 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции
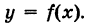
Функция, допускающая на данном промежутке лишь точки разрыва первого рода в конечном числе, называется кусочно-непрерывной на этом промежутке. Заметим, что в точках разрыва кусочно-непрерывная функция может быть не определена. Отметим, что для непрерывности функции f(x) в точке х0 необходимо и достаточно равенства трех чисел:
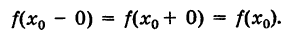
Пример:
Определить характер точки разрыва х0 = 0 функции
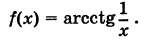
Решение:
Здесь мы имеем
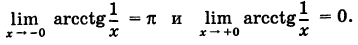
Следовательно, х0 = 0 есть точка разрыва первого рода.
Непрерывность функции
Определение 5.1. Пусть функция y=f(x) определена в некоторой окрестности
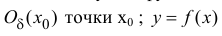 непрерывна в точке
непрерывна в точке 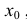 , если
, если
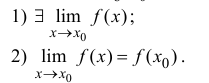
Функция y=f(x) непрерывна на множестве Х , если она непрерывна в каждой точке этого множества.
Точка, в которой функция не является непрерывной, называется точкой
разрыва.
П р и м е р 5.1
Функция 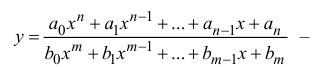 дробно-рациональная функция, непрерывная во всех точках из области определения (кроме точек, где знаменатель равен 0).
дробно-рациональная функция, непрерывная во всех точках из области определения (кроме точек, где знаменатель равен 0).
П р и м е р 5.2
Функции 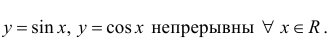
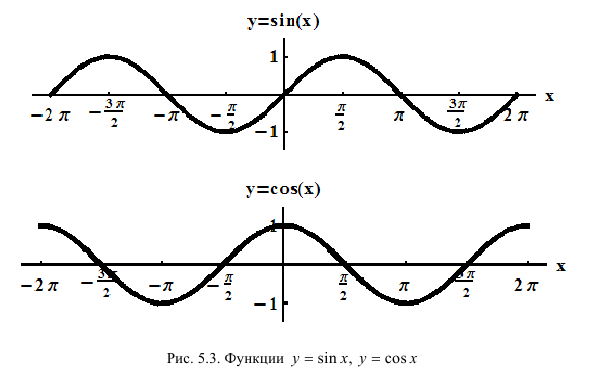

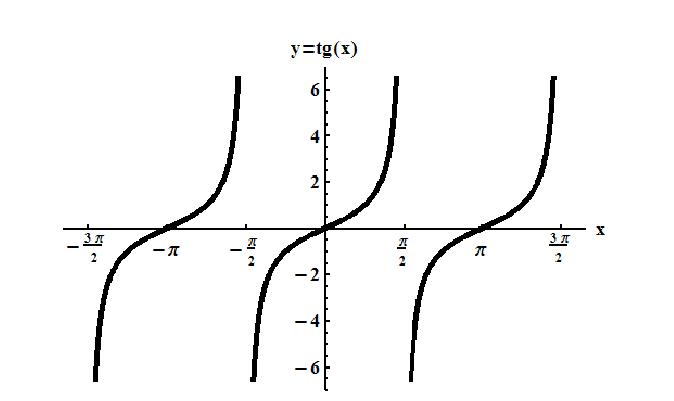
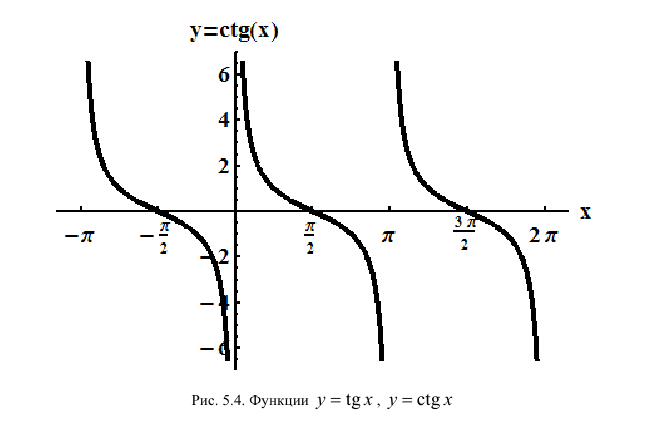
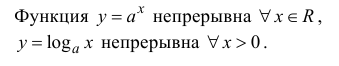
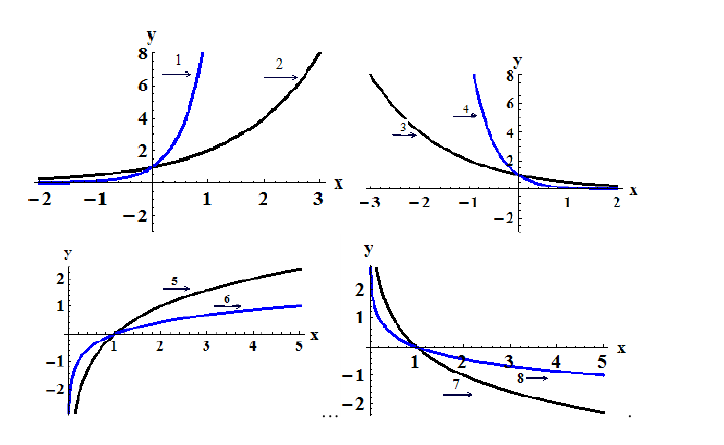
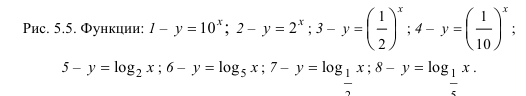
Функция 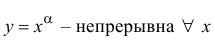 из области ее определения.
из области ее определения.
П р и м е р 5.3
Рассмотрим функцию Дирихле:
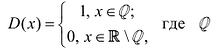 – множество рациональных чисел. Она разрывна
– множество рациональных чисел. Она разрывна 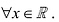
Определение 5.2. Функция y=f(x) называется непрерывной слева (справа) в точке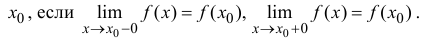
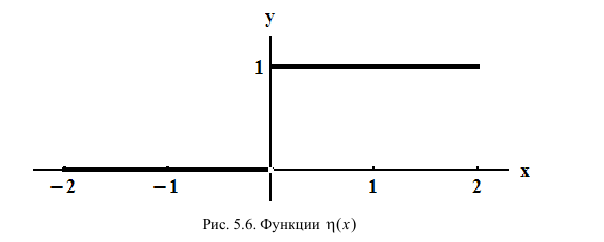
П р и м е р 5.4
Единичная функция Хевисайда: 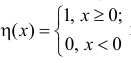 непрерывна справа в точке
непрерывна справа в точке 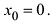
Теорема 5.1. Пусть функции 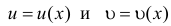 непрерывны в точке
непрерывны в точке 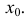 .
.
Тогда и функции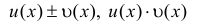 непрерывны в точке
непрерывны в точке 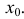 . Если
. Если 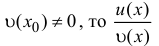 , – также непрерывны в точке
, – также непрерывны в точке 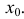 .
.
Доказательство следует из теоремы 3.3 и определения 5.1.
Определение 5.3. Пусть функция u=u(x ) определена на множестве Х со
значениями во множестве U и функция y=f(u ) определена на множестве U
со значениями во множестве Y. Тогда функцию 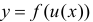 будем называть
будем называть
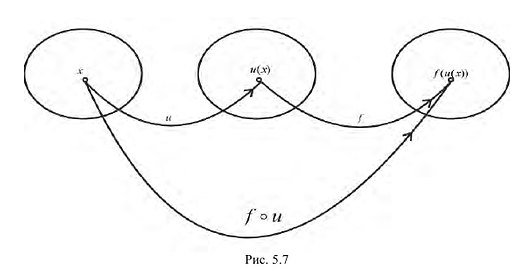
сложной функцией 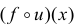 (композицией функций f и u), рис. 5.7.
(композицией функций f и u), рис. 5.7.
Теорема 5.2. Пусть функция 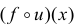 непрерывна в точке
непрерывна в точке 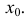 и функция
и функция
u=u(x ) непрерывна в точке 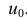 Тогда сложная функция
Тогда сложная функция 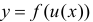
непрерывна в точке 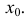 .
.
Доказательство следует из определения 3.2 и определения 5.1.
П р и м е р 5.5
Исследовать на непрерывность функцию 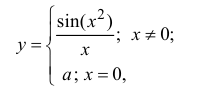
в зависимости от значений а .
Р е ш е н и е
Функция 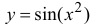 непрерывна
непрерывна 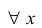 (как композиция двух непрерывных функций
(как композиция двух непрерывных функций
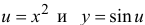 (см. теорему 5.2)).
(см. теорему 5.2)).
По теореме 5.1 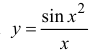 непрерывна
непрерывна 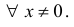 . Найдем
. Найдем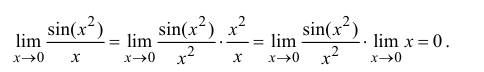
Поэтому при 0 =a функция непрерывна 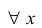 . При 0≠ a разрывна в точке 0 =x и непрерывна
. При 0≠ a разрывна в точке 0 =x и непрерывна 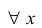 ≠0.
≠0.
Определение 5.4. Пусть функция y=f(x) определена в некоторой окрестности
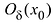 точки
точки 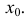 , кроме, может быть, самой точки
, кроме, может быть, самой точки 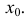 . Пусть
. Пусть 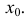 – точка разрыва функции y=f(x) и при этом существуют конечные пределы
– точка разрыва функции y=f(x) и при этом существуют конечные пределы 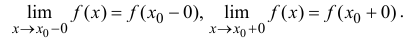 Тогда точка
Тогда точка 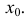 называется точкой разрыва 1-го рода функции y=f(x). При этом
называется точкой разрыва 1-го рода функции y=f(x). При этом 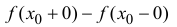 называется скачком функции. Если скачок равен 0, то разрыв называется устранимым.
называется скачком функции. Если скачок равен 0, то разрыв называется устранимым.
П р и м е р 5.6
Для функции 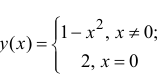
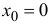 – точка устранимого разрыва.
– точка устранимого разрыва.
Для функции 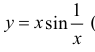 (см. упражнение 3.4)
(см. упражнение 3.4) 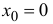 – точка устранимого
– точка устранимого

Для функции s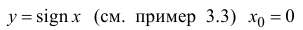 – точка разрыва 1-го рода. Разрыв – неустранимый. Скачок функции в точке
– точка разрыва 1-го рода. Разрыв – неустранимый. Скачок функции в точке 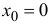 равен 2.
равен 2.
Для единичной функции Хевисайда 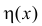 (см. пример 5.4)
(см. пример 5.4) 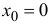 – точка
– точка
разрыва 1-го рода. Разрыв – неустранимый. Скачок функции в точке 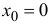 равен 1.
равен 1.
Определение 5.5. Пусть функция y=f(x) определена в некоторой окрестности
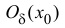 , кроме, может быть, самой точки
, кроме, может быть, самой точки 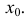 . Точка
. Точка 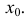 называется точкой разрыва 2-го рода функции y=f(x), если хотя бы один из односторонних пределов
называется точкой разрыва 2-го рода функции y=f(x), если хотя бы один из односторонних пределов
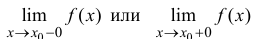 равен
равен 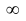 или не существует.
или не существует.
П р и м е р 5.7
Для функций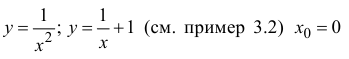 – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
Для функции 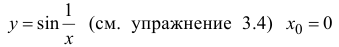 – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
Для функций 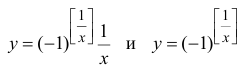 (см. упражнения 3.7, 3.8)
(см. упражнения 3.7, 3.8) 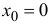 – точка разрыва 2-го рода. Точки
– точка разрыва 2-го рода. Точки 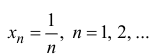 – точки разрыва 1-го рода. Разрывы неустранимые.
– точки разрыва 1-го рода. Разрывы неустранимые.
Для функции 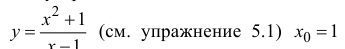 – точка разрыва 2-го рода. Для функции Дирихле D ( x ) (см. пример 5.3) любая точка
– точка разрыва 2-го рода. Для функции Дирихле D ( x ) (см. пример 5.3) любая точка 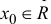 – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
П р и м е р 5.8
Исследовать на непрерывность и найти точки разрыва функции 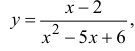 ,рис. 5.8.
,рис. 5.8.
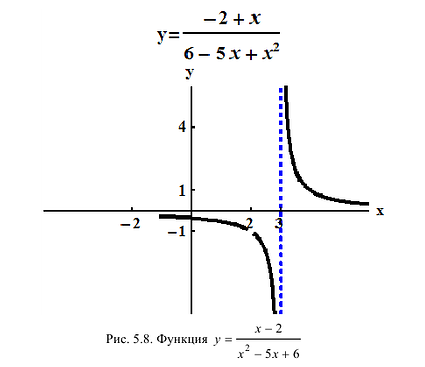
Р е ш е н и е
Функция – дробно-рациональная. Непрерывна везде, кроме точек, где знаменатель обращается в ноль: 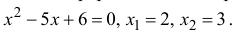
Рассмотрим точку 2= x.
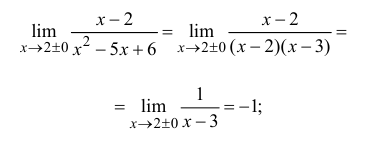
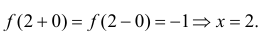 – точка устранимого разрыва.
– точка устранимого разрыва.
Рассмотрим точку x=3.
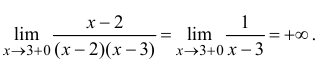
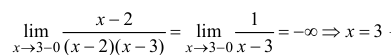 – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
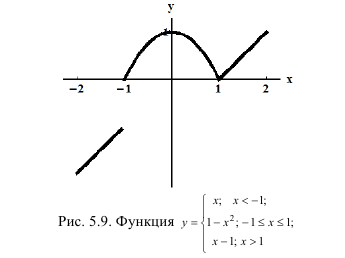
П р и м е р 5.9
Исследовать на непрерывность и определить тип точек разрыва для
функции:
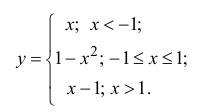
Р е ш е н и е
Функции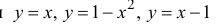 непрерывны
непрерывны 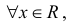 поэтому и наша функция непрерывна везде, кроме, может быть, точек ч=-1 и х=1. Слева
поэтому и наша функция непрерывна везде, кроме, может быть, точек ч=-1 и х=1. Слева
и справа от точек x=±1 функция задается различными аналитическими
выражениями.
Пусть x=1
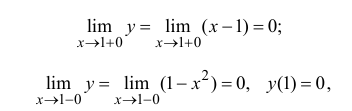
то есть 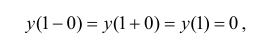 поэтому функция непрерывна в точке x=1.
поэтому функция непрерывна в точке x=1.
Пусть x=-1
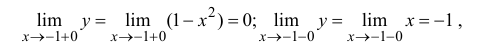
то есть 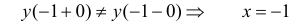 – точка разрыва 1-го рода (см. определение 5.3). Разрыв – неустранимый, скачок функции равен 1.
– точка разрыва 1-го рода (см. определение 5.3). Разрыв – неустранимый, скачок функции равен 1.
П р и м е р 5.10
Исследовать на непрерывность функцию 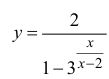 (рис. 5.10) х=0, х=2 – точки разрыва функции.
(рис. 5.10) х=0, х=2 – точки разрыва функции.
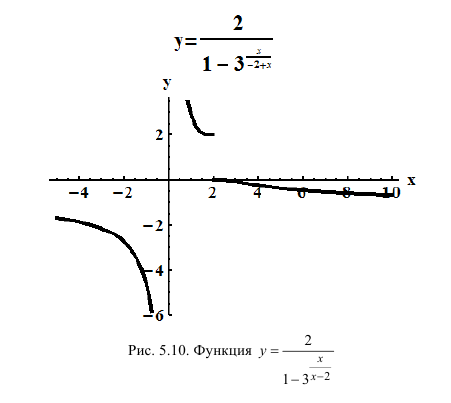
Р е ш е н и е
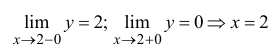 – точка разрыва 1-го рода. Разрыв неустранимый, скачок функции равен –2.
– точка разрыва 1-го рода. Разрыв неустранимый, скачок функции равен –2.
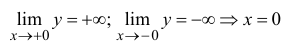 – точка разрыва 2-го рода.
– точка разрыва 2-го рода.
П р и м е р 5.11
Определить тип точек разрыва функции 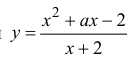 в зависимости от значений параметра а .
в зависимости от значений параметра а .
Р е ш е н и е
x =-2 – точка разрыва функции. Найдем 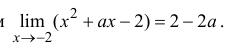
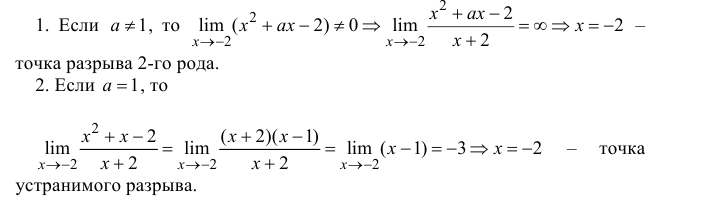
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |