
Нелинейные цепи переменного тока
Содержание:
Нелинейные цепи переменного тока:
Нелинейные электрические и магнитные цепи переменного тока широко применяются для создания разнообразной аппаратуры. К ней относятся электронные, ионные, ферромагнитные и полупроводниковые приборы, используемые для генерирования, усиления, модуляции, прямого и обратного преобразования временного тока в постоянный, умножения и деления частоты, а также многие другие устройства. В ряде случаев нелинейность цепей не используется, но должна быть учтена при расчетах.
Для электрических нелинейных цепей переменного тока остаются справедливыми законы Кирхгофа в их первой форме для мгновенных значений токов и напряжений (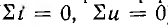
В цепях переменного тока для всех нелинейных элементов основной интерес представляет зависимость между напряжением и током, лричем она различна для мгновенных и действующих значений этих величин.
При переменном токе необходимо учитывать инерционность некоторых нелинейных элементов. Например, из-за тепловой инерции температура, а следовательно, и сопротивление лампы накаливания, даже при сравнительно низкой частоте (например, 50 гц), з течение каждого периода тока остаются практически постоянными. Поэтому зависимость u(i) между мгновенными значениями напряжения и тока лампы линейна. Вместе с тем зависимость U (I) между действующими значениями напряжения и тока резко нелинейна — сопротивление накаленной лампы больше, чем холодной, примерно в 10 раз. Ввиду линейной зависимости u(i) при синусоидальном напряжении ток будет также синусоидальным, и в этом случае для действующих значений могут быть, с учетом связи U (I), применены векторные диаграммы и символический метод, что крайне упрощает расчеты.
Однако большинство нелинейных элементов при не слишком высоких частотах безынерционны и зависимость u (i) оказывается нелинейной. Поэтому при периодических процессах кривые напряжения и тока них по форме различны, например при синусоидальном напряжении ток оказывается несинусоидальным, и наоборот. В этом случае следует оперировать непосредственно с мгновенными значениями, но когда несинусондальность формы кривой имеет для данной задачи второе пенное значение, в качестве первого приближения применяют векторные диаграммы и символический метод для эквивалентных синусо или для первых гармоник, учитывая нелинейную связь U (I) и oперируя с некоторыми усредненными значениями параметров цепи. В этих случаях расчет подобен расчету цепей с инерционными элементами.
В некоторых устройствах применяются нелинейные элемент находящиеся под одновременным воздействием постоянного и переменного тока или напряжения. При этом расчеты усложняются, но и зде оперируют с мгновенными значениями, если форма кривых существенна, в противном же случае ограничиваются соотношениям между действующими значениями.
Далее рассматриваются зависимости между мгновенными значениями и между действующими значениями напряжения и тока для индуктивных и емкостных нелинейных безынерционных элементов, а также некоторые явления и устройства, основанные на свойствах подобны) элементов. Попутно на этих примерах рассматриваются приемы и методы анализа и расчета нелинейных цепей.
Методы анализа нелинейных цепей на примере катушки индуктивности со стальным сердечником
Основой большинства электрических машин и аппаратов, применяемых в электротехнике низких и повышенных частот, является катушка со стальным сердечником.
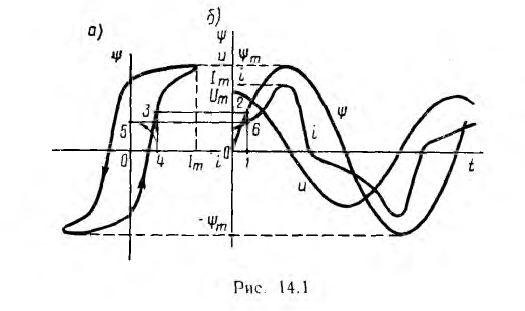
Если пренебречь активным сопротивлением обмотки катушки, при напряжении
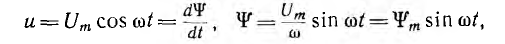
сцепление ψ изменяется по закону синуса с амплитудой 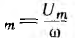 (рис. 14.1, б).
(рис. 14.1, б).
Кривую тока i (t) легко построить графическим методом, определяя для ряда ординат синусоиды ψ соответствующие знания i по кривой ψ(i) (рис. 14.1, построение 1—2—3—4—5—6). Так как кривая тока симметрична относительно оси абсцисс, она содержит только нечетные гармоники; чем больше насыщение, тем резче выражены в кривой i(t) высшие гармоники, в основном третья и пятая.
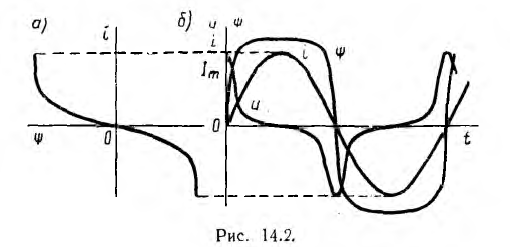
Кривую тока можно также рассчитывать аналитическим методом математической аппроксимации зависимости i (ψ). Если пренебречь гистерезисом и вихревыми токами, зависимость i (ψ) совпадает с основной кривой намагничивания (рис. 14.2, а). Эту кривую можно приближенно представить, например, следующим выражением:
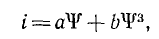
которое при напряжении 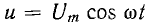 и, следовательно, синусоидальном потокосцеплении
и, следовательно, синусоидальном потокосцеплении 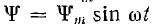 получает вид:
получает вид:
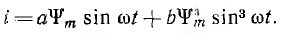
После подстановки
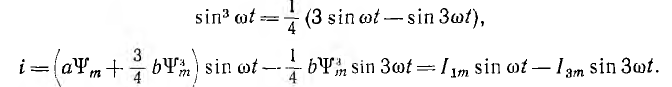
Таким образом, кривая тока содержит первую и третью гармоники так как их максимальные значения суммируются, кривая i (t) имеет заостренную форму с амплитудой 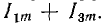
Более точная аппроксимация кривой i (ψ) многочленом с большим шелом членов
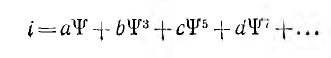
привела бы к появлению в кривой тока также и высших гармоник -пятой, седьмой и т. д., что и имеет место в действительности.
Если катушка питается синусоидальным током 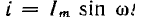 удобней пользоваться зависимостью ψ(i), например представив е аналитически на исследуемом участке выражением
удобней пользоваться зависимостью ψ(i), например представив е аналитически на исследуемом участке выражением
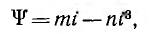
после аналогичных преобразований получающим вид:
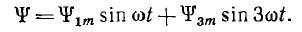
Так как максимальные значения гармоник потокосцепления вычитаются, кривая ψ(t) имеет тупую форму (рис. 14.2, б). Напряжение катушки
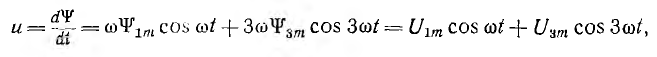
т. е. кривая u(t) заострена (см. рис. 14.2, б), причем отношение максимального значения третьей гармоники к первой для кривой напряжения в три раза больше, чем для кривой потокосцепления.
По формулам для действующих значений синусоидального напряжения U и тока I может быть определена эквивалентная индуктивность Lэ при пренебрежении активным сопротивлением катушки
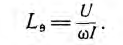
Например, для синусоидального напряжения 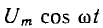 при пренебрежении гистерезисом и при принятой выше зависимости i = аψ + bψ3 эта эквивалентная индуктивность
при пренебрежении гистерезисом и при принятой выше зависимости i = аψ + bψ3 эта эквивалентная индуктивность
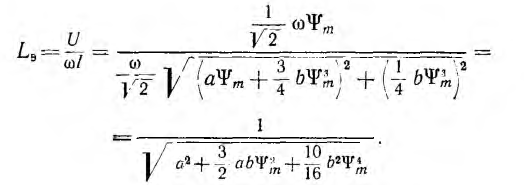
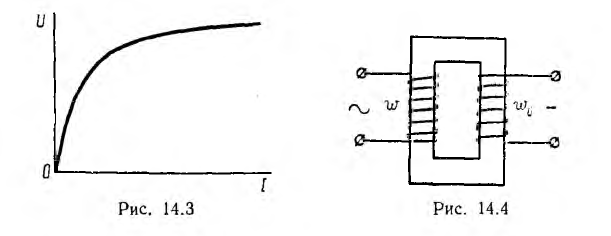
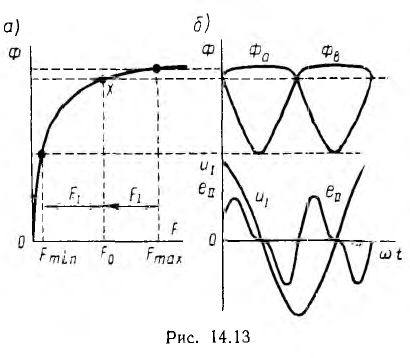
Отсюда видно, что с ростом U, а следовательно, и ψm индуктивность Lэ уменьшается, ток 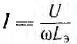 растет быстрее напряжения и вольт-амперная характеристика U (I) вначале почти прямолинейна, а затем угол, образуемый ею с осью тока, уменьшается (рис. 14.3).
растет быстрее напряжения и вольт-амперная характеристика U (I) вначале почти прямолинейна, а затем угол, образуемый ею с осью тока, уменьшается (рис. 14.3).
Характеристика U (I), снятая при синусоидальном токе, будет несколько отличаться от характеристики U (I) при синусоидального напряжении, но вид ее сохранится.
Если сердечник имеет обмотку из ω витков, обтекаемую постоянным током I0, и обмотку из w витков, присоединенную к источнику синусоидального напряжения 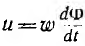 (рис. 14.4), зависимость от времени магнитного потока Ф, создаваемого обеими обмотками, должна иметь вид:
(рис. 14.4), зависимость от времени магнитного потока Ф, создаваемого обеими обмотками, должна иметь вид:
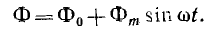
Если мысленно заменить обмотку ω0 постоянного тока эквивалентной, с числом витков ω, приняв постоянный ток равным 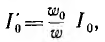 потокосцепления обеих обмоток будут одинаковыми и равными:
потокосцепления обеих обмоток будут одинаковыми и равными:
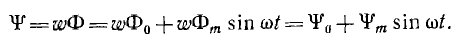
Тогда, приняв ту же зависимость i (ψ), можно получить выражение для мгновенного значения суммы i токов обеих обмоток:
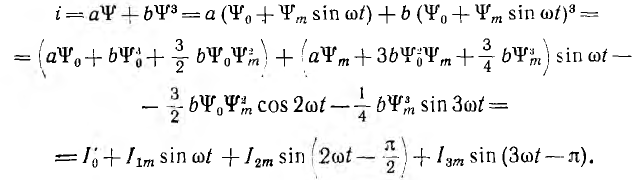
Если считать, что в цепь постоянного тока включен фильтр, не пропускающий переменный ток, первый постоянный член полученного выражения будет током I0 этой обмотки, а три остальных члена — первой, второй и третьей гармониками тока обмотки ω. Более точная аппроксимация дала бы также гармоники более высокого порядка.
Отсюда можно сделать следующие выводы:
- в цепи переменного тока, помимо нечетных, появились четные гармоники;
- так как ток
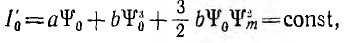 , постоянная составляющая ψ0 потокосцеплений уменьшается с ростом переменной составляющей ψm что объясняется насыщением сердечника намагничивающей силой обмотки ω переменного тока.
, постоянная составляющая ψ0 потокосцеплений уменьшается с ростом переменной составляющей ψm что объясняется насыщением сердечника намагничивающей силой обмотки ω переменного тока.
Эквивалентная индуктивность обмотки переменного тока
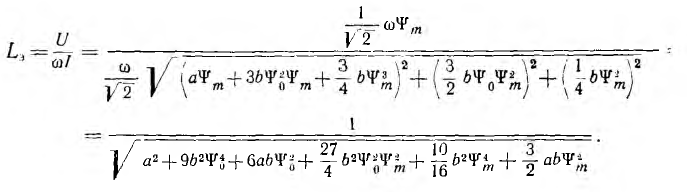
Отсюда видно, что:
- характеристики
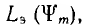 а следовательно, и вольтамперны-характеристики U (I) для цепи переменного тока имеют тот же вид что и без подмагничивания постоянным током, но чем больше ψо, т. е. I0, тем ниже лежит вольтамперная характеристика (рис. 14.5);
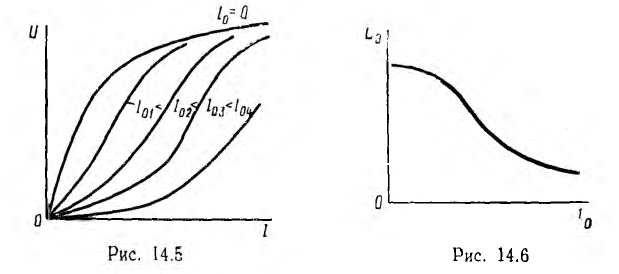
а следовательно, и вольтамперны-характеристики U (I) для цепи переменного тока имеют тот же вид что и без подмагничивания постоянным током, но чем больше ψо, т. е. I0, тем ниже лежит вольтамперная характеристика (рис. 14.5); - величиной индуктивности Lэ цепи переменного тока можно управлять, изменяя ψ0 т. е. величину постоянного тока I0 (рис. 14.6).
Если задаться синусоидальным током обмотки w, а не напряжением, можно, пользуясь, например, аппроксимацией вида ψ = mi — ni3, аналогичным образом показать, что кривая потокосцепления ψ (t) будет содержать постоянную составляющую, нечетные и четные гармоники. Очевидно также, что в общем случае напряжению и потокосцеплению любой другой сложной формы будет соответствовать ток i (t) также сложной формы, содержащий четные и нечетные гармоники, и наоборот.
Если активным сопротивлением r обмотки катушки пренебречь нельзя, нелинейное уравнение получает вид:
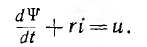 (14.1)
(14.1)
Для его приближенного решения может быть применен метод гармонического баланса в сочетании с аналитической аппроксимацией ψ (i).
Пусть приложенное напряжение 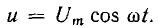 . Так как кривая ψ(i) симметрична относительно осей координат и r = const, кривая i (t) будет симметричной относительно оси абсцисс, т. е. она может содержать только нечетные гармоники, причем в общем случае ряд Фурье будет бесконечным. Так как приходится ограничиваться несколькими гармониками (обычно двумя-тремя), метод и по этой причине является приближенным. Пусть, например,
. Так как кривая ψ(i) симметрична относительно осей координат и r = const, кривая i (t) будет симметричной относительно оси абсцисс, т. е. она может содержать только нечетные гармоники, причем в общем случае ряд Фурье будет бесконечным. Так как приходится ограничиваться несколькими гармониками (обычно двумя-тремя), метод и по этой причине является приближенным. Пусть, например,
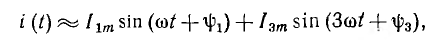
тогда неизвестными будут две амплитуды (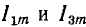 ) и две начальные фазы (
) и две начальные фазы (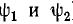 ).
).
Подставив аппроксимацию
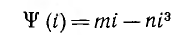 mi — ni3
mi — ni3
исходное уравнение (14.1), после элементарных тригонометрических преобразований, аналогичных выполненным выше, исходное уравнение можно привести к виду:
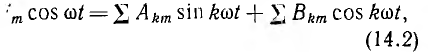
где k — номер гармоники, а Аkm и Bkm— алгебраические суммы коэффициенте, соответственно, при всех sin kωt и cos kωt, являющиеся функциями всех четырex неизвестных.
На основе гармонического баланса теперь можно приравнять слева и справа коэффициенты при sinωt, cos ωt, sin Зωt и cos 3ωt, т. е.
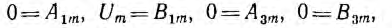
Из этих четырех уравнений определить неизвестные 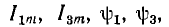 ходящие в выражения для Aкm и Bкm, а следовательно, и в окончательное выражение для i (t).
ходящие в выражения для Aкm и Bкm, а следовательно, и в окончательное выражение для i (t).
Необходимо заметить, что в уравнение (14.2) войдут гармоники высшего порядка, которые в дальнейшем не учитываются, что является ще одной причиной приближенности результата.
Очевидно, что метод гармонического баланса может быть применен для случая, когда u (t) представляет собой несинусоидальную периодическую кривую, т. е. сумму гармоник.
Эта же задача может быть приближенно решена методом кусочно-линейной аппроксимации нелинейной зависимости ψ(|i) , соответствующей основной кривой намагничивания. Кривая ψ(i) заменяется ломаной прямой (рис. 14.7), и подстановка линейных равнений для ее прямых участков в исходное уравнение

приводит к замене этого нелинейного уравнения системой линейных уравнений, число которых равно числу использованных прямых участков. Затем их общие решения припасовываются: величина потокосцепления ψ для конца предыдущего участка приравнивается потокосцеплению для начала следующего участка, откуда определяются постоянные интегрирования этих линейных уравнений.
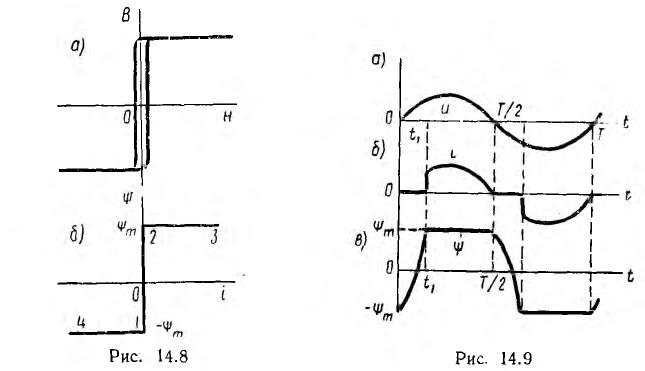
Все эти расчеты весьма упрощаются, если прямые участки кусочно- линейной аппроксимации могут быть взяты совпадающими с осью координат. Далее эта задача решается для тороидальной катушки с сердечником из магнитномягкого материала, имеющего почти пря угольную кривую намагничивания B (H) с узкой петлей гистерезиса (рис. 14.8, а). В первом приближении ей соответствует прямоугольная зависимость 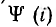 с вертикальным 1-2 и двумя горизонтальными и 4-1 участками (рис. 14.8, б).
с вертикальным 1-2 и двумя горизонтальными и 4-1 участками (рис. 14.8, б).
На рис. 14.9, а показано заданное напряжение 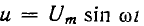 Пусть при t = 0 потокосцепление равно
Пусть при t = 0 потокосцепление равно 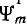 (рис. 14.9, в). За время t его роста на участке 1-2 рис. 14.8, 6 до значения +
(рис. 14.9, в). За время t его роста на участке 1-2 рис. 14.8, 6 до значения +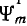 ток i = 0 (рис. 14.9, б); при этом уравнение (14.3) и его решение имеют вид
ток i = 0 (рис. 14.9, б); при этом уравнение (14.3) и его решение имеют вид
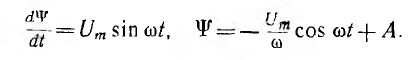
Постоянная интегрирования А определяется припасовкой при t= 0
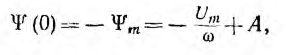
откуда 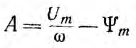 и окончательно
и окончательно
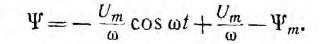
Это выражение определяет закон изменения 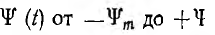 (см. рис. 14.9, в). Тогда продолжительность t1 этого процесса может быть определена из зависимости:
(см. рис. 14.9, в). Тогда продолжительность t1 этого процесса может быть определена из зависимости:
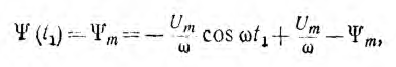
Откуда
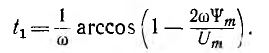
Позже t1 до конца полупериода в соответствии с участком 2-3 ис. 14.8, 6) 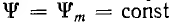 и уравнение (14.3) получает вид:
и уравнение (14.3) получает вид:
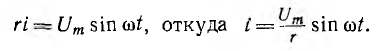
График изменения тока показан на рис. 14.9, б. Из-за прямоугольной аппроксимации кривой намагничивания (см. рис. 14.8, б) в момент времени t1 получился скачок тока; в действительности будет иметь место быстрое, но плавное нарастание тока, соответствующее реальной кривой намагничивания (см. рис. 14.8, а).
Во втором полупериоде процесс повторяется с изменением знака.
Сегнетоэлектрический конденсатор
Зависимость заряда q сегнетоконденсатора от напряжения u подобна зависимости смещения D от напряженности поля E и изображается гистерезисной петлей (рис. 14.10, а). При синусоидальном токе
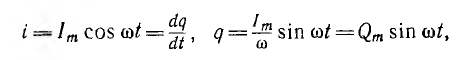
т.е. заряд q изменяется по закону синуса с амплитудой 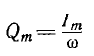 (рис. 14.10, б).
(рис. 14.10, б).
Кривая напряжения может быть построена графически путем определения для ряда ординат синусоиды q соответствующих значений и по кривой q (и) (см. рис. 14.10, б построение 1— 2—3—4—5—6). В кривой напряжения, симметричной относительно оси абсцисс, содержатся только нечетные гармоники.
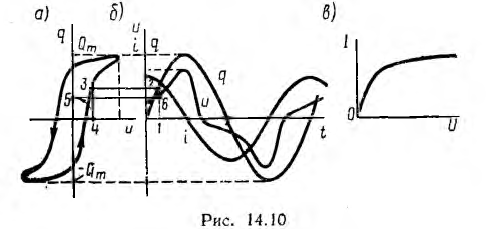
Из сравнения кривых рис. 14.1, б и 14. 10, б видно, что кривая i (t) катушки с сердечником подобна кривой u(t) сегнетоконденсатора, если подобны кривые u(t) катушки и i (t) конденсатора. Отсюда вытекает подобие вольтамперной характеристики I (I) катушки (см. рис. 14.3) и ампервольтной характериcтики I (U) конденсатора (рис. 14.10, в). Следовательно, рассмотренные цепи с нелинейной индуктивностью и с нелинейной емкостью дуальны как и линейные цепи с L и С , что может послужить основанием для построения сегнетоэлектрической аппаратуры, аналогичной ферромагнитной. В соответствии с табл. 7.1 для этого нужно заменить индуктивности емкостями, и наоборот, последовательные соединения — параллельными, и наоборот, источники напряжения источниками тока, и наоборот, активные сопротивления остаются б изменений. В таком дуальном сегнетоэлектрическом аппарате будет вести себя заданным образом величина, дуальная аналогичной величине ферромагнитного аппарата; например, ферромагнитный стабилизатор напряжения превратится в сегнетоэлектрический стабилизатор тока.
Устройства, основанные на нелинейной зависимости мгновенных значений напряжения и тона
Ферромагнитный и сегнетоэлектрический утроители частоты:
Наличие высших гармоник в кривой тока катушек со стальным сердечником при синусоидальном напряжении используется для умножения частоты. В схемах, осуществляющих преобразование трехфазной системы напряжений основной частоты в однофазное напряжение утроенной частоты, применяют три одинаковые катушки, соединенные звездой (рис. 14.11).
При включенном нулевом проводе и пренебрежении его сопротивлением и сопротивлениями всех проводов фазные напряжения на катушках будут равны синусоидальным напряжениям фаз генератора, и форма кривой тока в каждой фазе будет такой же, как показано на рис. 14.1, б. Ток iN нулевого провода, равный сумме линейных токов, будет содержать лишь гармоники, кратные трем:
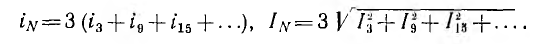
При размыкании нулевого провода из кривых линейных токов будут исключены гармоники, кратные трем, и форма кривой ток; изменится; из-за этого э. д. е., а следовательно, и фазные напряжения 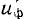 на катушках перестанут быть синусоидальными, и в них появятся высшие гармоники, которые не скажутся на синусоидальном законе линейного напряжения, т. е. гармоники, кратные трем, действующее значение напряжений на катушках будет:
на катушках перестанут быть синусоидальными, и в них появятся высшие гармоники, которые не скажутся на синусоидальном законе линейного напряжения, т. е. гармоники, кратные трем, действующее значение напряжений на катушках будет:
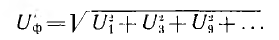
несмотря на симметрию цепи, появится узловое напряжение
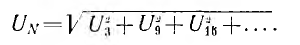
Если в нулевой провод будет включена нагрузка (см. рис. 14.11), формы кривых узлового напряжения и тока несколько изменятся по сравнению с вычисленными выше, но по-прежнему они будут содержать только гармоники, кратные трем.
Если в фазы схемы рис. 14.11 взамен катушек включить сегнетоконденсаторы, ток нагрузки, включенной в нулевой провод, будет также состоять из гармоник, кратных трем, т. е. и эта схема будет утроителем частоты.
Ферромагнитный удвоитель частоты
Ферромагнитный удвоитель частоты состоит из двух одинаковых однофазных трансформаторов со стальными сердечниками, работающих с подмагничиванием постоянным током (а и b на рис. 14.12). Каждый трансформатор имеет по три обмотки с числом витков ω1, ωu, ω0. Одинаковые обмотки обоих трансформаторов соединены последовательно. Обмотки ω1 образуют первичную цепь удвоителя и питаются переменным гоком частоты f от сети, обмотки являются вторичной цепью удвоителя, в которую включается нагрузка; обмотки ωu, обтекаемые постоянным током служат для подмагничивания.
Обмотки ω1 и ω0 трансформаторов соединены таким образом, что если в данный момент времени в первом трансформаторе переменная н. с. первичной обмотки ω1 и постоянная н. с. обмотки ω0 действуют огласно, то во втором трансформаторе они действуют встречно. Н. с. каждом трансформаторе изменяется oт 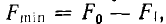 т. е. разности н. с. обмотки ω0 и максимального значения н. с. F1 обмотки ω1, до их суммы
т. е. разности н. с. обмотки ω0 и максимального значения н. с. F1 обмотки ω1, до их суммы 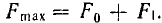 . Соответствующие этим н. с. магнитные потоки а и Фb обоих трансформаторов могут быть определены графически кривой Ф (F), аналогичной основной кривой намагничивания рис. 14.13). Из-за несимметрии этой кривой относительно точки х, соответствующей среднему значению н. с. F0, при синусоидальном токе обмоток ω1, а следовательно, и их н. е., определяемые по этим н. кривые
. Соответствующие этим н. с. магнитные потоки а и Фb обоих трансформаторов могут быть определены графически кривой Ф (F), аналогичной основной кривой намагничивания рис. 14.13). Из-за несимметрии этой кривой относительно точки х, соответствующей среднему значению н. с. F0, при синусоидальном токе обмоток ω1, а следовательно, и их н. е., определяемые по этим н. кривые 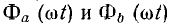 относительно их среднего значения несимметричны. Поэтому кривая Фa(ωt) потока трансформатора а, кроме постоянной составляющей Ф0 и нечетных гармоник, должна содержать четные гармоники:
относительно их среднего значения несимметричны. Поэтому кривая Фa(ωt) потока трансформатора а, кроме постоянной составляющей Ф0 и нечетных гармоник, должна содержать четные гармоники:
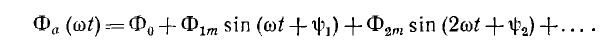
Ввиду обратного включения обмотки ω1 в трансформаторе b ее переменная составляющая потока сдвинута по фазе на половит периода, т. е. на угол π для первой гармоники, откуда
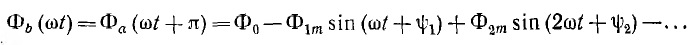
Суммарное потокосцепление вторичной цепи ω11
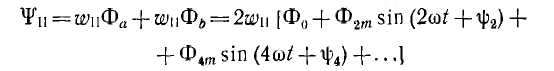
и э. д. с. вторичной цепи
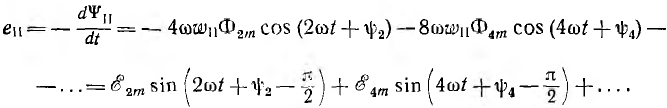
Следовательно, частота основной гармоники этой э. д. с. в два раза больше частоты напряжения, приложенного к зажимам первичной цепи, т. е. рассмотренное устройство является удвоителем частоты. Потокосцепление первичной цепи
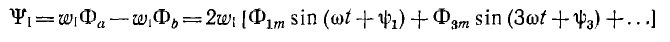
и ее напряжение
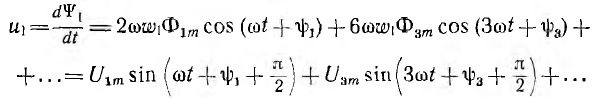
содержит только нечетные гармоники.
Обычно заданным является синусоидальное напряжение u1, а не ток, но это не отразится на рассмотренном явлении удвоения частоты. Кривые первичного напряжения 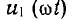 и вторичной э. д. с.
и вторичной э. д. с. 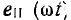 также показаны на рис. 14.13, б.
также показаны на рис. 14.13, б.
Выпрямление переменных токов
Для выпрямления, т. е. для получения из переменног тока — постоянного, должны применяться нелинейные резистор с несимметричной вольтамперной характеристикой, имеющие одноcтороннюю проводимость (см. рис. 1.11). Таким свойст-зом обладают меднозакисные, селеновые, германиевые, кремниевые а другие полупроводниковые вентили, ртутные вентили, газотроны и электронные лампы.
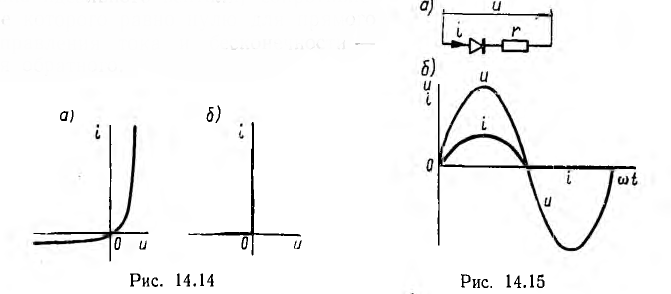
На рис. 14.14, а изображена типичная ампервольтная характериcтика полупроводникового вентиля, на рис. 14.14, б—характеристика идеального вентиля, сопротивление наличие которого равно нулю для прямого направления тока и бесконечности — для обратного.
Такую характеристику вентиля можно рассматривать, как кусочно-линейную аппроксимацию характеристики реального вентиля, что позволит применить приближенный аналитический метод для определения зависимости i (t).
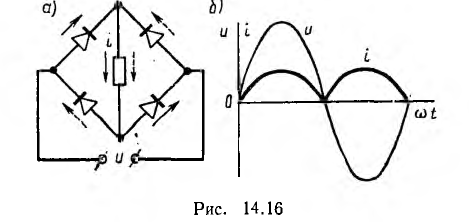
При включении идеального вентиля последовательно с нагрузкой, имеющей активное сопротивление r (на рис. 14.15, а показано условное изображение вентиля), для прямого полупериода напряжения u=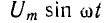 ток
ток
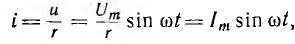
для обратного i = 0 (рис. 14.15, б), т. е. по цепи идет ток одного направления. Рассмотренное выпрямление называется однополупериодным.
Мостовая схема из четырех вентилей (рис. 14.16, а) осуществляет двухполупериодное выпрямление, так как через нагрузку, включенную в диагональ моста, протекает ток одного направления; в течение одного полупериода ток идет через одну пару выпрямителей, включенных в противоположные плечи, во время второго полупериода — через вторую пару (рис. 14.16, а). Следовательно, полученное выражена для тока одного полупериода будет действительно и для второго полупериода.
Разложение кривой i (t) (рис. 14.16, б) в ряд Фурье (см. приложение 3) дает:
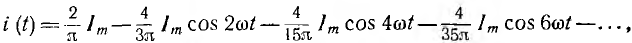
т. е. помимо постоянной составляющей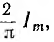 равной среднему значению кривая тока содержит четные гармоники. Эти гармоники обычно стремятся удалить или уменьшить с помощью фильтров. При однополу-периодном выпрямлении среднее значение тока, очевидно, будет вдвое меньше, т. е. равно
равной среднему значению кривая тока содержит четные гармоники. Эти гармоники обычно стремятся удалить или уменьшить с помощью фильтров. При однополу-периодном выпрямлении среднее значение тока, очевидно, будет вдвое меньше, т. е. равно 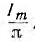
Ферромагнитные элементы вычислительных машин
Основой ферромагнитных запоминающих элементов электронных вычислительных машин является тороидальный сердечник, выполненный из магнитных материалов, обладающих почти прямоугольной предельной (т. е. при очень больших ±Hmах) петлей гистерезиса В (H).
Эта же петля в других масштабах дает зависимость магнитного потока Ф от н. с. F (рис. 14. 17, а). При F = 0 в намагниченном ранее сердечнике будет остаточный магнитный поток +Фr или —Фr.
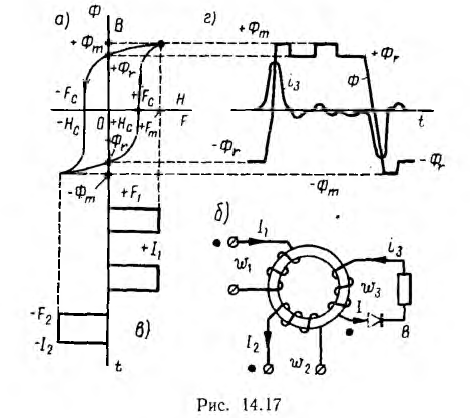
В вычислительной технике одному из этих состояний, например +Фr, приписывают значение цифры 1, а —Фr — значение 0, т.е. такой элемент может «запомнить» одну из этих цифр. С помощью набора подобных элементов можно в двоичном исчислении запомнить заданное число в виде ряда из цифр 1 и 0.
На сердечник наложены равномерно распределенные по нему обмотки, образующие тороидальную магнитную цепь, поток во всех сечениях которой одинаков. Одна из обмоток может представлять собой провод, расположенный по оси тороида, так как его н. с. также обеспечивает равенство магнитного потока во всех сечениях сердечника.
Пусть на тороид наложены две входные обмотки с одинаковым числом витков ω1 =ω2 и одна выходная ω3, включенная на исполнительную цепь, причем в нее может быть включен вентиль (рис. 14.17, б). На схеме точками показаны одноименные зажимы этих обмоток. Входные обмотки ω1 и ω2 питаются равными по величине и продолжительности импульсами тока +I1 и —I2, т. е. противоположного направления, в необходимой последовательности, например показанной на рис. 14.17, в. Эти токи создают пропорциональные им импульсы н. с. +F1 и —F2, которые должны быть больше ±FC, соответствующих коэрцитивным силам ±НС.
Пусть под действием предыдущего импульса —/\> сердечник намагнитился в отрицательном направлении. Тогда его магнитный поток характеризуется точкой —Фr на предельной петле гистерезиса. Следующий затем импульс -F1 перемагнитит сердечник до максимального значения +Фm (рис. 14.17, г); при этом в выходной обмотке проиндуктируется импульс э. д. с. 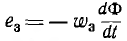 , посылающей в исполнительную цепь рабочий импульс тока i3. Средние значения е3 и i3 пропорциональны изменению потока
, посылающей в исполнительную цепь рабочий импульс тока i3. Средние значения е3 и i3 пропорциональны изменению потока 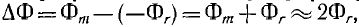 , так как из-за прямоугольного характера предельной петли гистерезиса Фr, лишь немногим меньше Фm.
, так как из-за прямоугольного характера предельной петли гистерезиса Фr, лишь немногим меньше Фm.
После окончания импульса F1 произойдет незначительное уменьшение потока Фm до значения Фr, проиндуктированные при этом импульс э. д. с. е3 и импульс тока i3, являющийся в этом режиме помехой, будут незначительными.
Так как следующим импульсом является опять импульс +Fl сопровождающее его возрастание потока от +Фr, до +Фm, и затем убывание до + Фг создает также незначительные помехи разных знаков. Следующий импульс —F2 вызывает процесс, аналогичный рассмотренному при импульсе +F1 но импульсы рабочего тока и помех изменят знаки.
Из изложенного видно, что магнитный элемент работает в режиме трансформатора. Поэтому н. с. первичных обмоток ω1 и ω2 должна быть рассчитана не только на перемагничивание сердечника, но и на компенсацию размагничивающего действия тока i3 в рабочей цепи, т. е. согласно закону полного тока
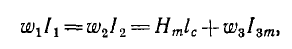
где Нm — максимальное значение напряженности поля;
1С — средняя длина сердечника;
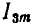 — максимальное значение рабочего тока.
— максимальное значение рабочего тока.
Импульсы рабочего тока разного знака, соответствующие цифрам 1 и 0, воздействуют на последующие элементы вычислительной машины. Если в рабочую цепь включить вентиль В (см. рис. 14.17, б), по ней будет проходить ток только одного направления, соответствующий например, цифре 1. Тогда элемент работает в режиме нагруженной трансформатора. Цифре 0 будет соответствовать отсутствие рабочей тока, т. е. режим холостого хода трансформатора. Это приведет к возможности облегчения выходной и одной из входных обмоток и уменьшению средней мощности, потребляемой элементом, что позволит уменьшить его габариты. Кроме того, устранение тока обратного напрапвления необходимо в тех случаях, когда его н. с. создает помехи в других элементах.
Явление и устройства, основанные на нелинейной зависимости действующих значений напряжения и тока
Резонанс в нелинейных цепях:
Резонанс в цепи, содержащей катушку индуктивности со стальным сердечником и линейный конденсатор, называется феррорезонансом. Для его качественного исследования можно пренебречь активным сопротивлением цепи, а кривые напряжения и тока сложной формы заменить эквивалентными синусоидами.
Вольтамперная характеристика U' (I) цепи с последовательным соединением катушки со стальным сердечником и линейного конденсатора (рис. 14.18, а) может быть построена на основе кривой UL (I) для катушки и прямой Uc (I) для конденсатора (рис. 14.18,6). Так как напряжения UL и Uc находятся в противофазе, то
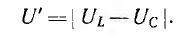
Феррорезонанс напряжений будет при UL = Uc при этом U'=0. Из-за наличия потерь в цепи и высших гармоник действительная вольтамперная характеристика U (I) расположена выше теоретической U' (I) и точка феррорезонанса будет вблизи точки A, соответствующей минимальному напряжению U0 и значению тока I0. При токе, меньшем, чем I0, в цепи преобладает индуктивное напряжение, при большем — емкостное.
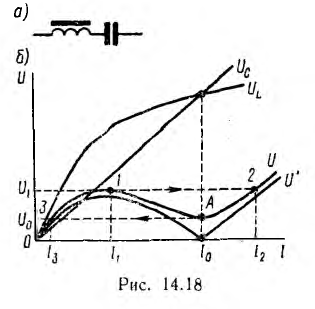
Плавному повышению напряжения до значения U1 соответствует плавное увеличение тока до значения I1 (точка I.) Дальнейшее увеличение напряжения будет сопровождаться скачком тока до значения I2 (точка 2). Последующее повышение напряжения сопровождается плавным увеличением тока. При плавном понижении напряжения до значения U0 ток снижается до значения I0 (точка А), после чего следует скачкообразное уменьшение его до значения I3, отвечающего переходу из точки А в точку 3. Очевидно, что скачки тока сопровождаются изменением знака угла сдвига фаз в цепи. Если же плавно изменять ток, можно получить все точки характеристики, в том числе и на ее падающем участке.
Таким образом, исследуемая линейная цепь в отличие от резонансной цепи с постоянными параметрами имеет следующие особенности: I) резонанс в ней может быть достигнут изменением величины приложенного напряжения, что объясняется происходящим при этом изменением индуктивности; 2) при одном и том же напряжении на зажимах цепи ток в цепи может иметь три различных значения.
Однако режимы, соответствующие падающему участку 1-А характеристики, будут неустойчивыми: при случайном увеличении тока падение напряжения в цепи станет меньше приложенного напряжения, ток будет возрастать до значения, соответствующего этому напряжению на правой поднимающейся части характеристики; при случайном уменьшении тока приложенное напряжение окажется недостаточным, и спад тока будет продолжаться до аналогичной точки на левой части характеристики.
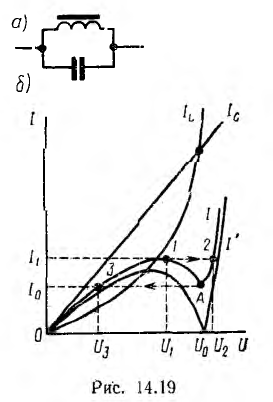
Для цепи с параллельным соединением катушки индуктивности со стальным сердечником и линейного конденсатора (рис. 14.19, а) надо построить ампервольтную характеристику 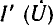 тока в неразветвленной части цепи по кривой
тока в неразветвленной части цепи по кривой 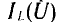 катушки и прямой
катушки и прямой 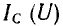 конденсатора (рис. 14.19,6); ток
конденсатора (рис. 14.19,6); ток
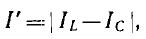
так как токи в катушке и в конденсаторе находятся в противофазе. Точка, в которой кривая касается оси абсцисс (I' = 0), соответствует феррорезонансу токов 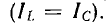
Действительная кривая I(U) пройдет выше теоретической I' (U) из-за потерь в цепи и высших гармоник. Точка феррорезонанса токов близка к точке А минимального значения тока /0 при напряжении U0. При напряжении U < U0 в цепи преобладает ток емкости, при напряжении U > U0 — индуктивности.
Плавному увеличению тока до значения соответствует плавное повышение напряжения на зажимах цепи до значения (точка I). Дальнейшее увеличение тока будет сопровождаться скачком напряжения ДО значения U2 соответствующего точке 2. В последующем с ростом тока напряжение будет увеличиваться плавно. Если теперь уменьшать ток в цепи, то изменение напряжения будет следовать за изменением тока до значения U2 соответствующего точке 4, после чего происходит скачкообразное уменьшение напряжения до значения U3, соответствующего точке 3.
Из рис. 14.19, б видно, что при одном и том же токе на зажимах цепи могут быть три различных напряжения, из которых при неизменном токе цепи устойчивыми будут только режимы на поднимающихся участках ампервольтной характеристики. Если же плавно изменять величину питающего цепь напряжения, можно получить также все точки на падающем участке характеристики, так как тогда обе ветви цепи будут независимыми друг от друга.
Необходимо подчеркнуть, что упомянутые скачки имеют место на диаграммах для действующих значений, в действительности же происходит быстрое, но плавное изменение мгновенных значений этих величин.
Впервые явление феррорезонанса было исследовано П.Л. Калантаровым.
Аналогичные явления происходят при сегнеторезонансе в цепях с сегнетоконденсатором и линейной катушкой, дуальных ферро-резонансным. Дуальными будут схемы феррорезонанса напряжений и сегнеторезонанса токов и схемы феррорезонанса токов и сегнето-резонанса напряжений.
Ферромагнитный стабилизатор напряжения
В ряде электрических установок при изменении напряжения питающей сети напряжение на приемнике необходимо поддерживать неизменным. Для этой цели служат различные по своему принципу действия стабилизаторы напряжения.
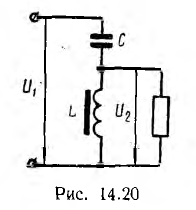
В простейшем ферромагнитном стабилизаторе напряжения (рис. 14.20) стабилизированное напряжение U2 снимается с зажимов катушки индуктивности со стальным сердечником, стабилизируемое напряжение U1 подается на зажимы всей схемы, состоящей из последовательного соединения конденсатора и параллельного разветвления катушки и цепи нагрузки.
При отключенной нагрузке цепь представляет собой схему феррорезонанса напряжений, процессы в которой поясняет рис. 14.21, аналогичный рис. 14.18. Ввиду различного наклона кривых 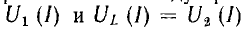 для токов, больших резонансного, одному и тому же изменению тока
для токов, больших резонансного, одному и тому же изменению тока 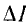 соответствует большое изменение
соответствует большое изменение 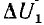 напряжения и малое изменение
напряжения и малое изменение 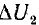 напряжения
напряжения 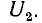
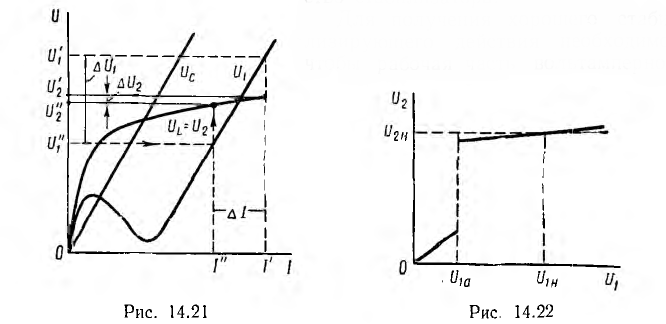
По точкам кривых рис. 14.21 можно построить характеристику стабилизатора 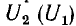 , определяя значения
, определяя значения 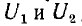 для одних и тех же значений тока (рис. 14.22). Из этой кривой видно, что стабилизирующее действие схемы имеет место лишь при напряжениях сети, больших некоторого критического напряжения Ula, соответствующего точке 2 рис. 14.18, б. При уменьшении напряжения U1 ниже критического происходит скачкообразное понижение напряжения U2, и оно уже не стабилизируется.
для одних и тех же значений тока (рис. 14.22). Из этой кривой видно, что стабилизирующее действие схемы имеет место лишь при напряжениях сети, больших некоторого критического напряжения Ula, соответствующего точке 2 рис. 14.18, б. При уменьшении напряжения U1 ниже критического происходит скачкообразное понижение напряжения U2, и оно уже не стабилизируется.
Показателем качества работы стабилизатора является коэффициент стабилизации
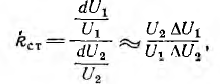
пределяемый из характеристики стабилизатора для номинального апряжения; чем больше коэффициент стабилизации, тем выше качество стабилизатора.
Для получения хорошего стабилизирующего действия необходимо, чтобы рабочая часть вольтамперной характеристики катушки с ферромагнитным сердечником была возможно более пологой, другими словами, надо работать при большом напряжении, т. е. при значительном токе в обмотке катушки.
В схеме рис. 14.20 большой реактивный ток полностью берется из сети, что нежелательно. Этот недостаток может быть устранен при использовании в схеме резонанса токов (рис. 14.23). Здесь L1 — катушка с ненасыщенным ферромагнитным сердечником, сопротивление которой линейно, L2 — катушка с насыщенным сердечником, образующая с линейным конденсатором С2 нелинейный участок схемы. В этой цепи ток I, потребляемый из сети, при холостом ходе стабилизатора значительно меньше тока нелинейной индуктивности L2.
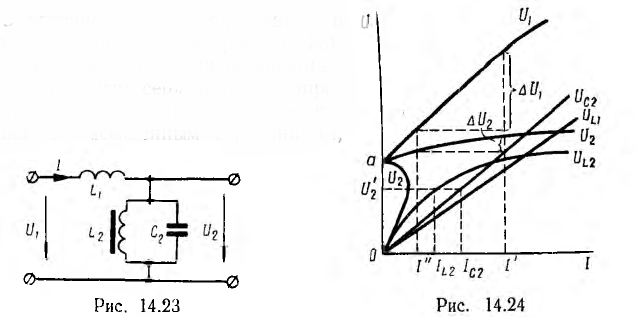
Построение кривых для этого стабилизатора при режиме холостого ода ведется в следующем порядке (рис. 14.24). Из характеристик 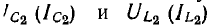 определяются токи, соответствующие одному и тому же значению напряжения U2, например U'2 (показано пунктиром), а по ним — ток I в неразветвленном участке цепи, т. е. в катушкe L1
определяются токи, соответствующие одному и тому же значению напряжения U2, например U'2 (показано пунктиром), а по ним — ток I в неразветвленном участке цепи, т. е. в катушкe L1
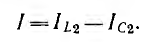
Определив ток I для различных значений напряжения Иъ строя кривую U2 (I). Точка а на этой кривой соответствует резонансу токов для меньшего напряжения преобладает емкостный ток, для большего -индуктивный. Этот последний участок и используется для стабили зации напряжения; ниже точки а происходит срыв стабилизации.
Первичное напряжение
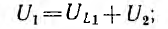
на графике оно показано для зоны стабилизации. Как видно из рис. 14.24, при увеличении тока от I" до I' значительному изменению 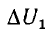 напряжения соответствует малое изменение
напряжения соответствует малое изменение 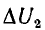 напряжения U2.
напряжения U2.
Из кривых U1 (I) и U2 (I) можно вычислить коэффициент стабилизации и получить характеристику стабилизатора так, как это было показано выше. Все изложенное соответствует холостому ходу стабилизатора, нагрузка уменьшает стабилизирующее действие.
Общими недостатками всех ферромагнитных стабилизаторов является зависимость их работы от частоты, а также наличие высших гармоник в выходном напряжении.
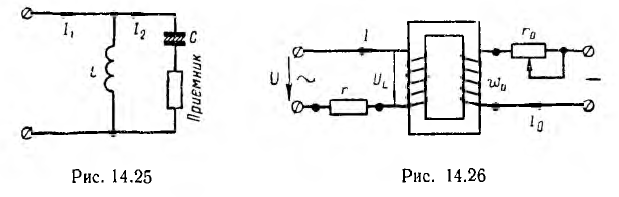
Аналогичные стабилизаторы можно построить, используя линейные катушки и нелинейные сегнетоконденсаторы. Например, цепь рис. 14.25, дуальная схеме рис. 14.20 стабилизатора напряжения, будет стабилизировать ток I2 цепи нагрузки при изменениях входного тока I1.
Ферромагнитный усилитель мощности
Под усилителем мощности подразумевают устройство, позволяющее управлять большой мощностью в рабочей цепи, расходуя малую мощность в управляющей цепи. В ферромагнитном усилителе цепь управления питается постоянным током.
Принципиальная схема простейшего ферромагнитного усилителя показана на рис. 14.26. Катушка индуктивности с ферромагнитным сердечником включена в сеть переменного ток. последовательно с приемником — активным сопротивлением r. На том же сердечнике помещена управляющая обмотка ω0, питаемая постоянным током.
Если пренебречь высшими гармониками и активным сопротивле-ием катушки, ток в рабочей цепи при напряжении U
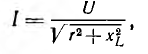
де xL — реактивное сопротивление катушки.
При включении постоянного тока в управляющую обмотку создается дополнительное подмагничивание сердечника, уменьшающее величину эквивалентной индуктивности 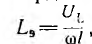 , а следовательно, и величину реактивного сопротивления
, а следовательно, и величину реактивного сопротивления 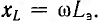 Таким образом, включение постоянного тока вызовет при неизменном напряжении U увеличение переменного тока и перераспределение напряжения между сопротивлением г приемника и сопротивлением xL катушки. При определенных соотношениях параметров нагрузки и усилителя мощность
Таким образом, включение постоянного тока вызовет при неизменном напряжении U увеличение переменного тока и перераспределение напряжения между сопротивлением г приемника и сопротивлением xL катушки. При определенных соотношениях параметров нагрузки и усилителя мощность 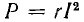 в рабочей цепи может значительно превышать мощность
в рабочей цепи может значительно превышать мощность 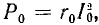 расходуемую в цепи управления.
расходуемую в цепи управления.
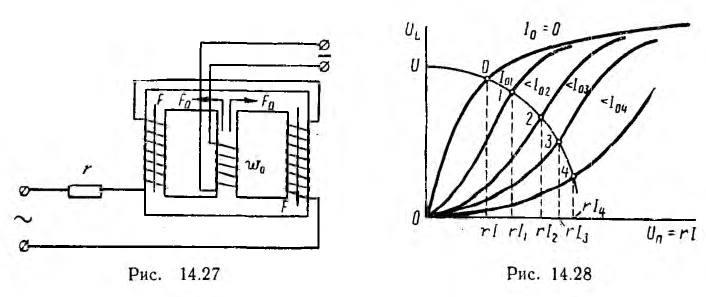
При воздействии на ферромагнитный магнитопровод переменной и постоянной н. с. в кривой переменного тока появляются четные гармоники, а переменный поток, создаваемый рабочим током, будет индуктировать переменную э. д. с. в цепи управления. Для устранения этих нежелательных явлений ферромагнитный усилитель выполняют по схеме рис. 14.27.
Обмотка управления, обтекаемая постоянным током, расположена на среднем стержне; ее н. с. F0 направлена в боковые стержни. Рабочая обмотка разделена на две одинаковые последовательно соединенные секции, расположенные на боковых стержнях; обе секции включаются в сеть так, что когда в одном стержне н. е., создаваемые обмотками постоянного и переменного токов, складываются, в другом — вычитаются. Поэтому симметрия кривой потокосцепления 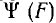 обмотки Переменного тока не нарушается, а четные гармоники в кривой тока че появляются. Такая схема устраняет также наведение переменной э. д. с. в управляющую обмотку током рабочей цепи, так как н. с. в среднем стержне рабочей цепи, создаваемая переменным током, равна нулю.
обмотки Переменного тока не нарушается, а четные гармоники в кривой тока че появляются. Такая схема устраняет также наведение переменной э. д. с. в управляющую обмотку током рабочей цепи, так как н. с. в среднем стержне рабочей цепи, создаваемая переменным током, равна нулю.
Семейство характеристик усилителя UL (I) при различной величине постоянного тока I0 в управляющей обмотке показано на рис. 14.28, где по оси ординат отложено напряжение на рабочей об мотке усилителя, а по оси абсцисс, в том же масштабе — произведение тока I на сопротивление r, т. е. напряжение на приемнике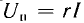 . Чем больше постоянный ток в цепи управления, тем характеристик будет более пологой, что соответствует меньшей величине магнитно-проницаемости сердечника. Связь между реактивным напряжением U: на рабочей обмотке усилителя, активным напряжением Uп на приемнике и напряжением U сети переменного тока определяется уравнением
. Чем больше постоянный ток в цепи управления, тем характеристик будет более пологой, что соответствует меньшей величине магнитно-проницаемости сердечника. Связь между реактивным напряжением U: на рабочей обмотке усилителя, активным напряжением Uп на приемнике и напряжением U сети переменного тока определяется уравнением
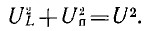
Это уравнение является уравнением окружности радиуса U с центром в начале координат. Точки пересечения этой окружности с характеристиками усилителя дают связь между постоянным током I0 в обмотке управления и переменным током I в рабочей обмотке (рис. 14.29)
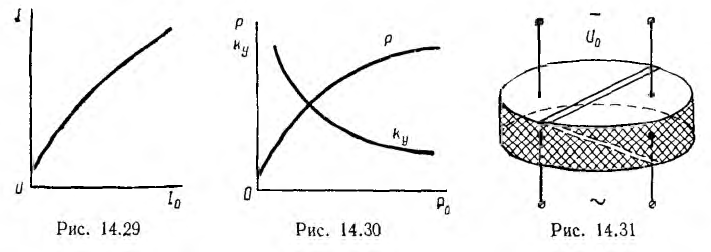
На рис. 14.30 показана зависимость Р (Р0), где 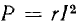 — полезная мощность рабочей цепи, а
— полезная мощность рабочей цепи, а 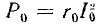 — мощность цепи управления (масштаб Р во много раз превышает масштаб P0). Отношение
— мощность цепи управления (масштаб Р во много раз превышает масштаб P0). Отношение 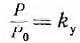 называется коэффициентом усиления по мощности; величина его обычно тем меньше, чем больше полезная мощность Р. При мощностях порядка долей ватта и сердечниках усилителя, выполненных из сплавов типа пермаллой, можно получить усиление, доходящее до 103 раз; если сердечник выполнен из обычной трансформаторной стали, то при мощностях порядка нескольких десятков ватт коэффициент усиления не превышает 100.
называется коэффициентом усиления по мощности; величина его обычно тем меньше, чем больше полезная мощность Р. При мощностях порядка долей ватта и сердечниках усилителя, выполненных из сплавов типа пермаллой, можно получить усиление, доходящее до 103 раз; если сердечник выполнен из обычной трансформаторной стали, то при мощностях порядка нескольких десятков ватт коэффициент усиления не превышает 100.
В принципе возможно также построить сегнетоэлектрический усилитель, например такой, как на рис. 14.31. Здесь верхний и нижний электроды сегнетоконденсатора разрезаны пополам, причем разрезы взаимно перпендикулярны. К верхним полудискам приложено управляющее постоянное напряжение U0, нижние полудиски включаются в регулируемую цепь переменного тока. В сегнетоэлектрике происходит наложение постоянного электрического поля на переменное, благодаря чему диэлектрическая проницаемость и емкость конденсатора для цепи переменного тока изменяются.
Нелинейные цепи переменного тока
В цепях постоянного и переменного токов широко применяют элементы с нелинейной вольт-амперной характеристикой u(t). Их активное сопротивление R зависит от тока и напряжения.
При переменном токе можно использовать и нелинейные реактивные элементы. К таким элементам относятся катушки и трансформаторы с ферромагнитными сердечниками, имеющие нелинейную зависимость магнитного потока от тока Ф(i), конденсаторы с сегнетодиэлектриками, у которых заряд нелинейно связан с напряжением Q(u).
С помощью нелинейных активных сопротивлений с несимметричной вольт-амперной характеристикой можно осуществлять выпрямление напряжения и тока, так как в кривых напряжений и токов цепи появляются постоянные составляющие, которые можно выделить.
В цепи с синусоидальным источником питания нелинейные реактивные элементы, имеющие, как правило, симметричную вольт-амперную характеристику, вносят искажение в форму кривых напряжений и токов, т. е. вызывают появление высших гармоник, из которых наиболее резко выделяется третья. Можно отфильтровать одну из высших гармоник и таким образом осуществить умножение частоты.
Совместное применение активных и реактивных нелинейных элементов, а также неоднородных источников питания (э. д. с. разной частоты, постоянных э. д. с. вместе с переменными) значительно увеличивает число практических задач, успешно решаемых в различных отраслях техники (радиоэлектронике, автоматике и др.).
Кроме уже отмеченных задач решаются, например, такие, как усиление напряжения и мощности, генерирование колебаний различной формы, модулирование колебаний и т. д.
Токи в цепи с вентилями
Вентилем называют элемент цепи, обладающий односторонней проводимостью (полупроводниковые диоды, ртутные вентили, газотроны, тиратроны и электровакуумные лампы).
Вольт-амперные характеристики и схемы замещения вентиля
У идеального вентиля при одной полярности напряжения сопротивление равно нулю, а при другой (обратной) — бесконечности. Его вольт-амперная характеристика состоит из двух участков (рис. 24.1, а). Один из них совпадает с отрицательной осью u, другой — с положительной осью i.
Характеристика реального вентиля (рис. 24.1, б) указывает на то, что его сопротивление в одном направлении мало, а в другом велико, но в обоих случаях оценивается конечными величинами.
Реальную характеристику вентильного сопротивления можно, приближенно представить в виде ломаной линии, как на рис. 24.1, в или г.
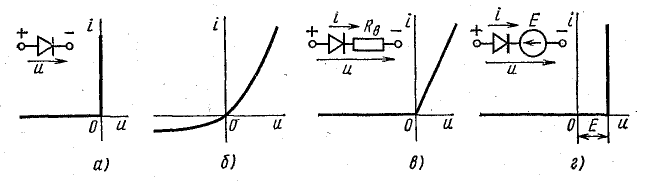
Рис. 24.1. Вольт-амперные характеристики и схемы замещения вентиля
Для полупроводниковых диодов и электронных ламп более подходит характеристика рис. 24.1, в, а для ртутных вентилей и газотронов — характеристика рис. 24.1, г. Такая замена реальных вольт-амперных характеристик позволяет составить простую электрическую схему замещения вентиля.
Цепь из последовательно соединенных идеального вентиля и элемента с активным сопротивлением имеет вольт-амперную характеристику рис. 21.1, в, характеристика рис. 24.1, г соответствует цепи из идеального вентиля и источника постоянной э. д .с.
Ток в цепи с вентилем
На рис. 24.2 показана кривая тока в цепи с нелинейной вольт-амперной характеристикой (для примера взята цепь с полупроводниковым диодом) при синусоидальной форме действующего в ней напряжения.
Каждому мгновенному напряжению u соответствует по характеристике i(u) ток i. Определяя эти величины, как показано на рисунке, и откладывая их в координатах i, t, можно построить кривую тока в функции времени i(t).
В данном случае кривая тока имеет положительные и отрицательные полуволны, но положительные во много раз больше отрицательных.
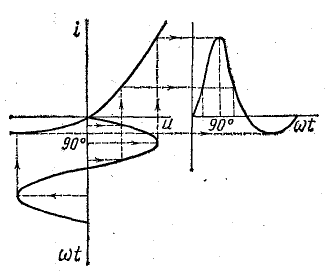
Рис. 24.2. Построение кривой тока в цепи с полупроводниковым диодом
Построим кривую тока в цепи последовательно соединенных реального вентиля и элемента с линейным сопротивлением R при синусоидальном напряжении источника питания 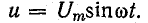
На рис. 24.3 изображены вольт-амперные характеристики вентиля и элемента цепи с сопротивлением R.
Для этой схемы справедливо уравнение напряжений
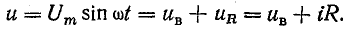
На основании этого уравнения построена вольт-амперная характеристика всей цепи i(u) путем суммирования падений напряжения на вентиле (uв) и постоянном сопротивлении (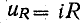 ) при различных величинах тока.
) при различных величинах тока.
На том же чертеже в координатах u, t построена кривая напряжения в функции времени u(t).
Чем больше амплитуда напряжения источника, тем сильнее отличаются положительная и отрицательная полуволны тока в цепи с вентилем.
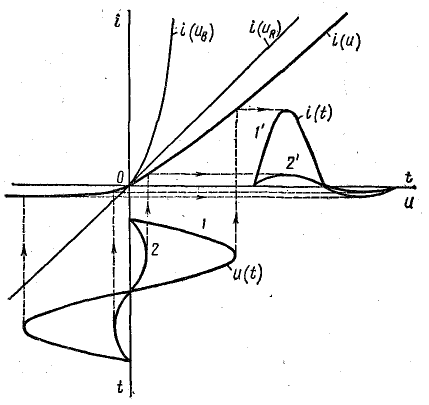
Рис. 24.3. Построение кривой тока неразветвленной цепи с вентилем
При достаточно больших значениях u отрицательную полуволну тока можно не принимать во внимание и считать, что кривая тока состоит только из положительных полуволн (кривые 1 и 1' на рис. 24.3).
Кривая тока такого вида наряду с гармоническими имеет постоянную составляющую тем большей величины, чем больше напряжение источника и чем больше вольт-амперная характеристика приближается к идеальной.
При малой амплитуде напряжения источника прямая и обратная полуволны тока могут оказаться близкими по величине (кривые 2 и 2'). В этом случае выпрямляющее действие вентильного сопротивления незначительно.
Электрический вентиль в цепи с неоднородными источниками питания
Включение вентиля в цепь с неоднородными источниками питания открывает новые возможности технического применения нелинейных цепей.
В цепи рис. 24.4, а при наличии вентиля действуют две э. д. с.: переменная 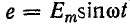 и постоянная Е0.
и постоянная Е0.
На рис. 24.4, б представлена вольт-амперная характеристика, показанная на рис. 24.1, в, и там же в координатах 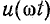 построена зависимость напряжения от времени.
построена зависимость напряжения от времени.
При Е0 = О напряжение u2 совпадает с синусоидальной э. д. с. е2 (кривая 2); это напряжение вызывает в цепи ток (кривая 2').
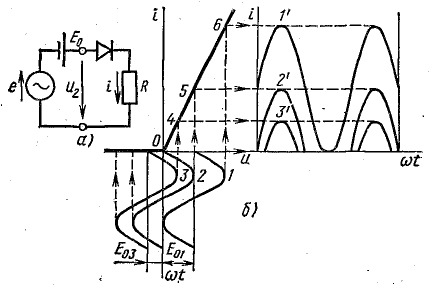
Рис. 24.4. Построение кривых тока в неразветвленной цепи с вентилем, постоянной и переменной э. д. с.
При включении в сеть отрицательной постоянной э. д. с. 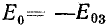 напряжение в цепи
напряжение в цепи 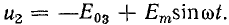
На графике это отражается перенесением оси ωt влево на величину Е03. Введение постоянной э. д. с. изменило форму тока (кривая 3'); следовательно, изменились (уменьшились) постоянная и переменная составляющие тока.
Если в цепь включить постоянную э. д. с. Е01 такой величины, чтобы результирующее напряжение оставалось все время положительным, то кривая тока по форме совпадает с кривой напряжения (кривые 1 и 1').
Таким образом, можно, изменяя постоянную э. д. с., управлять переменной составляющей тока.
Задача 24.1.
Построить график зависимости постоянной составляющей тока от величины постоянной э. д .с. Е0 в цепи, схема которой изображена на рис. 24.5, а.
Переменная э. д. с. e выражается уравнением 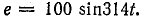
Нагрузочное сопротивление 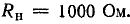
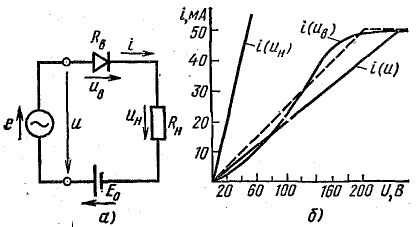
Рис. 24.5. К задаче 24.1
Вольт-амперная характеристика выпрямительного элемента представлена на рис. 24.5, б кривой i(uв).
Решение. Для упрощения решения задачи реальная вольт-амперная характеристика на рис. 24.5, б заменена идеальной (штриховая прямая). На том же чертеже нанесена вольт-амперная характеристика нагрузочного сопротивления — прямая i(uн) и построена вольт-амперная характеристика цепи i(u). Из этой характеристики следует, что общее сопротивление цепи 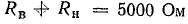
На рис. 24.6 по общей вольт-амперной характеристике цепи построены кривые тока при двух величинах постоянной э. д. с.: 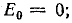

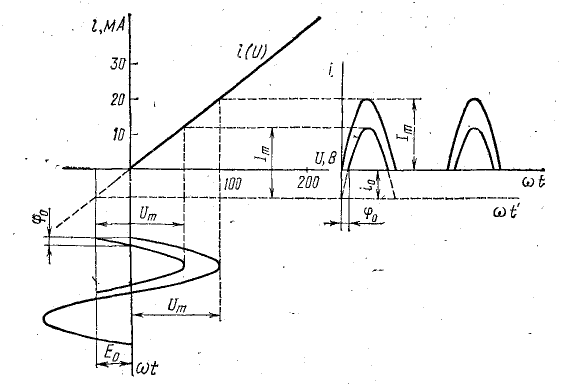
Рис. 24.6. К задаче 24.1
Из построения видно, что при Е = 0 в течение первого полупериода кривая тока представляет собой синусоидальную функцию 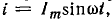 а во вторую половину периода ток равен нулю.
а во вторую половину периода ток равен нулю.
При 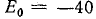 кривая тока в течение части периода (от φ0 до 180° — φ0) также представляет собой синусоидальную функцию, но относительно другой оси абсцисс ωt', отстоящей от первоначальной оси на
кривая тока в течение части периода (от φ0 до 180° — φ0) также представляет собой синусоидальную функцию, но относительно другой оси абсцисс ωt', отстоящей от первоначальной оси на 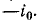
Величина 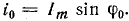
Угол φ0, который назовем углом отсечки, зависит от величины Е0.
Из графиков напряжений следует, что
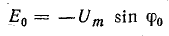
и
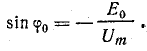
Найдем выражение постоянной составляющей тока в общем виде. В первоначальных осях координат уравнение тока можно записать так:
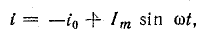
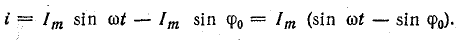
Постоянная составляющая тока определяется выражением (23.4)
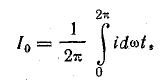
Ток i — положительный при изменении фазового угла от φ0 до π — φ0. При всех других фазовых углах в пределах периода ток равен нулю. Поэтому
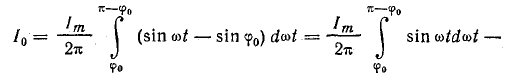
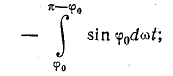
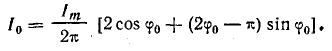
В последнем выражении Im — амплитуда синусоидального тока при одно-полупериодном выпрямлении, т. е. при Е0 = 0 и φ0 = 0
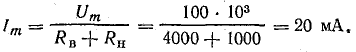
В этом случае
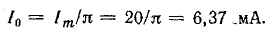
При φ0 = π/2 I0 = 0.
Для построения графика I0(Е0) вычислите I0 и Е0 при различных углах отсечки φ0:
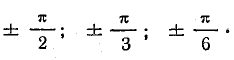
График I0(Е0) построен на рис. 24.7.
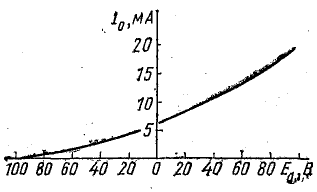
Рис. 24ю7. К задаче 24.1
Э. Д. С. Магнитный поток и ток в цепи с нелинейной индуктивностью
Магнитный поток и намагничивающий ток катушки с ферромагнитным сердечником связаны между собой нелинейной характеристикой Ф(i) [магнитная проницаемость ферромагнитных материалов не постоянна (см. рис. 8.31)], поэтому индуктивность катушки с сердечником изменяется в зависимости от тока. Это является причиной различия по форме кривой намагничивающего тока и кривой напряжения.
Идеализированная катушка с ферромагнитным сердечником
Рассмотрим электромагнитные процессы в идеализированной катушке, пренебрегая активным сопротивлением ее обмотки и не учитывая потери энергии в сердечнике (рис. 24.8); напряжение, приложенное к такой катушке, уравновешивается только э. д. с. самоиндукции: 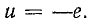
При синусоидальном напряжении источника э. д .с. в катушке может быть только синусоидальной. Но синусоидальная э. д. с. может наводиться магнитным потоком синусоидальной формы, что следует из формулы (10.2). Если
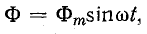
то
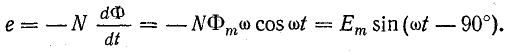
Амплитуда э.д.с.
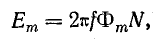
а действующее значение
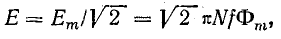
или

Кривая циклического намагничивания сердечника Ф(i) без потерь от гистерезиса и вихревых токов изображена на рис. 24.9. Эта кривая подобна основной кривой намагничивания материала сердечника В(Н), так как магнитный поток 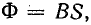 а ток в катушке
а ток в катушке 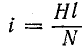 согласно закону полного тока. На рис. 24.9 для ряда мгновенных величин синусоидального потока определены соответствующие намагничивающие токи; затем проведена кривая i(ωt), которая, будучи периодической, сильно отличается от синусоиды.
согласно закону полного тока. На рис. 24.9 для ряда мгновенных величин синусоидального потока определены соответствующие намагничивающие токи; затем проведена кривая i(ωt), которая, будучи периодической, сильно отличается от синусоиды.
Рассматривая кривую i(ωt), легко убедиться в том, что в составе гармоник тока особенно выделяется третья гармоника (ср. кривую тока с кривой э. д .с. на рис. 23.1, б).
Рис. 24.8. Схема катушки с ферромагнитным сердечником
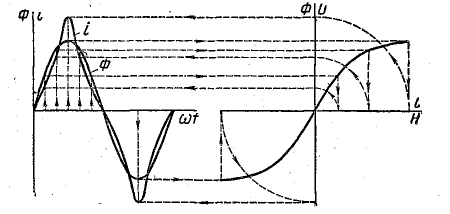
Рис. 24.9. Построение кривой тока в катушке с ферромагнитным сердечником по основной кривой намагничивания
Векторная диаграмма идеализированной катушки
Действующий ток I определяется формулой (23.25) или с использованием поправочного коэффициента формулой

где 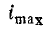 — амплитуда основной кривой тока.
— амплитуда основной кривой тока.
Для катушек с сердечником из электротехнической (трансформаторной) стали коэффициент 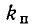 находится по кривой рис. 24.10, на котором показана его зависимость от максимальной величины магнитной индукции; при
находится по кривой рис. 24.10, на котором показана его зависимость от максимальной величины магнитной индукции; при 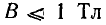 коэффициент
коэффициент 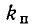 близок к единице, а при
близок к единице, а при 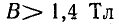 быстро увеличивается.
быстро увеличивается.
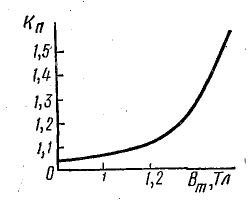
Рис. 24.10. Зависимость поправочного коэффициента от магнитной индукции
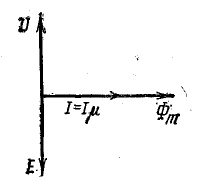
Рис. 24.11. Векторная диаграмма идеализированной катушки с ферромагнитным сердечником
Таким образом, не учитывая магнитных потерь в сердечнике и потерь в обмотке, получим совпадение начальных фаз синусоидального магнитного потока и несинусоидального тока. Заменив реальный ток катушки его первой гармоникой i1 (или эквивалентным синусоидальным током iэк с такой же действующей величиной, как и несинусоидальный ток), можно построить векторную диаграмму катушки с ферромагнитным сердечником (рис. 24.11). Векторы тока I и потока Фm совпадают по фазе; э. д. с. самоиндукции Е отстает, а напряжение U на катушке опережает магнитный поток на 90°. Ток в идеализированной катушке является реактивным. Он не сопровождается преобразованием электрической энергии в другой вид энергии (активная составляющая тока Iа = 0), но создает магнитное поле в сердечнике. Поэтому его называют, намагничивающим током 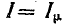 .
.
Магнитный поток и э. д .с. самоиндукции при синусоидальном токе в идеализированной катушке
При увеличении амплитуды напряжения на катушке амплитуда и действующая величина тока в ней будут возрастать быстрее. В результате вольтамперная характеристика катушки с ферромагнитным сердечником оказывается нелинейной; по форме она повторяет кривую намагничивания сердечника (см. рис. 24.9).
При синусоидальном токе в обмотке катушки магнитный поток, э. д .с. и напряжение несинусоидальны, что показывает построение кривой на рис. 24.12. График магнитного потока имеет притуплённую форму, близкую к трапеции.
Э. д. с. и напряжение на катушке имеют более заостренную форму, чем синусоида (рис. 24.13).

Рис. 24.12. Построение кривой магнитного потока в ферромагнитном сердечнике
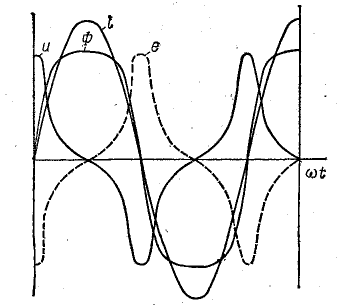
Рис. 24.13. Графики Ф, u, e в катушке с ферромагнитным сердечником
Задача 24.4.
Катушка с числом витков N = 400 намотана на сердечник из электротехнической стали марки 1311. Размеры сердечника даны на рис. 24.14. Пренебрегая потерями энергии в сердечнике, а также активным сопротивлением и потоком рассеяния, построить кривую тока в катушке, если напряжение на ее зажимах выражается уравнением u = 169 sin314t.
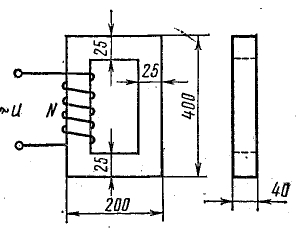
Рис. 24.14. К задаче 24.4
Решение. Согласно условию задачи, активное сопротивление обмотки и магнитный поток рассеяния можно считать равными нулю. При этих условиях напряжение на зажимах катушки равно э. д. с., наводимой основным магнитным потоком в сердечнике: u = —e.
Для определения амплитуды магнитного потока воспользуемся формулой (24.1):
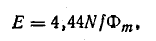
Из уравнения напряжения известны
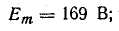
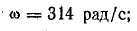
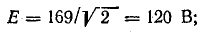
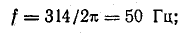
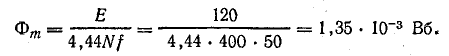
Графические построения выполните самостоятельно в следующем порядке.
1. По кривой В(Н) приложения 4 постройте кривую Ф(i) сердечника заданных размеров, используя формулы
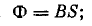
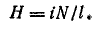
2. Кривую тока постройте так, как это показано на рис. 24.9.
3. Определите по чертежу максимальную величину тока и его действующую величину по формуле (24.2).
4. Постройте векторную диаграмму катушки со стальным сердечником.
Влияние гистерезиса и вихревых токов на ток катушки с ферромагнитным сердечником
Магнитный гистерезис вносит дополнительные изменения в форму кривой намагничивающего тока. Эти изменения обусловлены тем, что при увеличении магнитного потока ход кривой тока определяется восходящей, а при уменьшении потока — нисходящей ветвью петли гистерезиса.
Ток в катушке с учетом магнитного гистерезиса
На рис. 24.15 изображен график Ф(i) зависимости магнитного потока от намагничивающего тока катушки с ферромагнитным сердечником (петля магнитного гистерезиса). Петля гистерезиса, полученная при медленном циклическом изменении намагничивающего тока, называется статической.
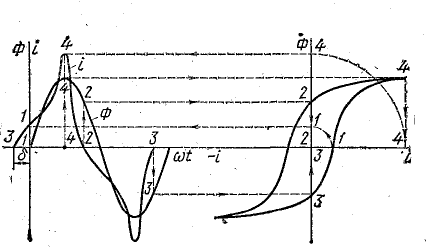
Рис. 24.15. Построение кривой тока в катушке с ферромагнитным сердечником с учетом магнитного гистерезиса
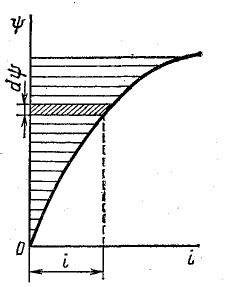
Рис. 24.16. К определению энергии магнитного поля катушки с ферромагнитным сердечником
На том же рисунке дана кривая тока i(ωt), показывающая, что при увеличении магнитного потока кривая тока идет выше, а при уменьшении потока — ниже кривой, построенной при тех же условиях на рис. 24.9 по основной кривой намагничивания. Кроме того, начальные фазы потока и тока не совпадают (угол сдвига δ), в связи с чем первая гармоника тока (или эквивалентный ток) отстает от приложенного напряжения на угол 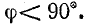
Энергия магнитного поля катушки
Наличие сдвига по фазе между током и напряжением, меньшего 90°, указывает на то, что активная мощность в цепи не равна нулю даже в том случае, если активное сопротивление обмотки катушки R = 0.
Следовательно, ток катушки из-за потерь на гистерезис имеет активную составляющую, а средняя мощность за период не равна нулю.
В данном случае активная мощность характеризует расход энергии на перемагничивание ферромагнитного сердечника.
Изменение энергии магнитного поля 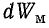 выражается площадью элементарного прямоугольника со сторонами i и
выражается площадью элементарного прямоугольника со сторонами i и 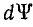 [см. формулу (11.12) и графическое определение энергии магнитного поля катушки без сердечника. Следовательно,
[см. формулу (11.12) и графическое определение энергии магнитного поля катушки без сердечника. Следовательно,
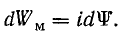
Энергия магнитного поля, запасенная при увеличении тока в катушке, определяется площадью, ограниченной кривой 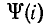 и осью ординат (рис. 24.16):
и осью ординат (рис. 24.16):
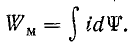
Рассмотрим цикл перемагничивания сердечника, начиная с точки 1, когда i = 0 и 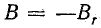 (рис. 24.17, а).
(рис. 24.17, а).
Для размагничивания сердечника от 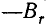 до 0 и последующего намагничивания до
до 0 и последующего намагничивания до 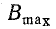 затрачивается энергия, которая определяется площадью, ограниченной контуром 1-2-3-4-0-1. Эта площадь непосредственно определяет величину
затрачивается энергия, которая определяется площадью, ограниченной контуром 1-2-3-4-0-1. Эта площадь непосредственно определяет величину 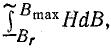 но
но 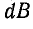 пропорционально
пропорционально 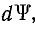 а Н пропорционально i.
а Н пропорционально i.
На всем протяжении рассматриваемой части петли магнитного гистерезиса (1-2-3) напряженность поля Н и приращения магнитного потокосцепления 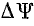 положительны.
положительны.
При размагничивании от 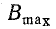 до
до 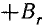 (участок 3-5) напряженность поля по-прежнему положительна, а приращения потокосцепления отрицательны. Площадь, ограниченную контуром 3-4-5-3, нужно считать отрицательной. Энергия, пропорциональная этой площади, возвращается источнику. На участке 5-6-7 петли гистерезиса напряженность поля и приращения потокосцепления отрицательны. Площадь, ограниченная контуром 5-6-7-8-1-0-5, положительна. Это означает, что энергия опять потребляется от источника. Размагничивание на участке 7-1 сопровождается возвращением энергии источнику в количестве, пропорциональном площади 7-8-1-7.
(участок 3-5) напряженность поля по-прежнему положительна, а приращения потокосцепления отрицательны. Площадь, ограниченную контуром 3-4-5-3, нужно считать отрицательной. Энергия, пропорциональная этой площади, возвращается источнику. На участке 5-6-7 петли гистерезиса напряженность поля и приращения потокосцепления отрицательны. Площадь, ограниченная контуром 5-6-7-8-1-0-5, положительна. Это означает, что энергия опять потребляется от источника. Размагничивание на участке 7-1 сопровождается возвращением энергии источнику в количестве, пропорциональном площади 7-8-1-7.
Таким образом, энергия, израсходованная в единице объема ферромагнитного сердечника за один цикл перемагничивания, определяется площадью, ограниченной петлей магнитного гистерезиса.
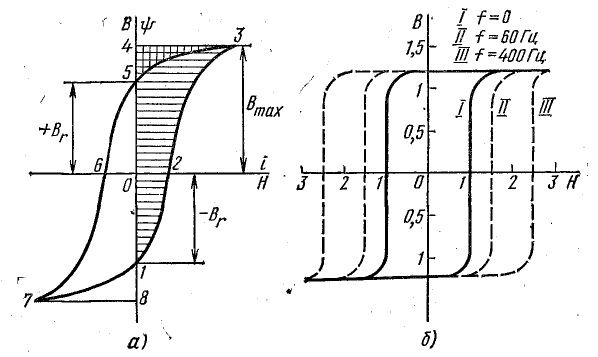
Рис. 24.17. К вопросу об определении потерь энергии в ферромагнитном сердечнике
Потери энергии в ферромагнитном сердечнике катушки
При достаточно быстром изменении намагничивающего тока в ферромагнитном сердечнике возникают вихревые токи.
Вихревые токи создают намагничивающую силу, направленную навстречу намагничивающей силе обмотки с током i, поэтому изменения магнитной индукции и магнитного потока в сердечнике как бы задерживаются: те же величины магнитной индукции и потока получатся при большем намагничивающем токе в обмотке. Это значит, что при переменном токе в обмотке петля магнитного гистерезиса шире статической петли в связи с действием вихревых токов. Петля магнитного гистерезиса, соответствующая переменному намагничивающему току, называется динамической.
На рис. 24.17, б показаны динамические кривые намагничивания сплава железо —никель при различных частотах тока. Вихревые токи увеличиваются с ростом частоты перемагничивания, удельной проводимости и магнитной проницаемости материала сердечника, при этом динамическая петля расширяется.
Возникновение вихревых токов вызывает дополнительный расход энергии в сердечнике. Энергия, израсходованная на перемагничивание сердечника и поддержание в нем вихревых токов, преобразуется в тепло. Эту энергию называют магнитными потерями или потерями в стали по названию наиболее применяемого ферромагнитного материала.
Мощность магнитных потерь Рм пропорциональна площади динамической петли магнитного гистерезиса. Ее обычно определяют по формуле
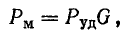
где G — масса ферромагнитного сердечника, кГ; Pуд — удельная мощность потерь в стали, Вт/кГ.
Зависимости Pуд от магнитной индукции В при данной частоте для различных ферромагнитных материалов приводятся в справочных таблицах.
Векторная диаграмма катушки с учетом потерь энергии в сердечнике
Зная магнитные потери, найдем активную составляющую эквивалентного тока катушки:

Упрощенная векторная диаграмма катушки с ферромагнитным сердечником (без учета активного сопротивления обмотки и магнитного рассеяния) дана на рис. 24.18. При построении диаграммы в произвольном направлении отложен вектор напряжения U. Под прямым углом к нему откладывается вектор магнитного потока Фm, который отстает по фазе от напряжения на 90°. От потока на 90° отстает э. д. с., величина которой Е равна величине U.
Активная составляющая тока совпадает по фазе с напряжением, а полный ток катушки отстает от напряжения на угол φ:
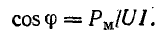
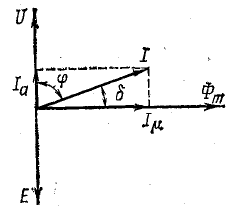
Рис. 24.18. Векторная диаграмма катушки с ферромагнитным сердечником без учета активного сопротивления обмотки и магнитного рассеяния
Реактивная составляющая тока катушки Iμ, совпадающая по фазе с магнитным потоком, называется намагничивающим током:
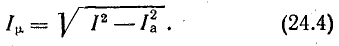
Угол δ между векторами полного тока катушки и магнитного потока называется углом потерь:
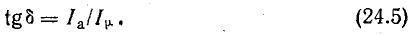
Задача 24.5.
Определить действующий ток и коэффициент мощности катушки задачи 24.4 при наличии в сердечнике воздушных зазоров в стыках, общая (эквивалентная) длина которых δ = 0,5 мм. Сопротивление обмотки и магнитное рассеяние не учитывать. Толщина листов сердечника 0,5 мм. Удельные потери в стали Руд = 7,9 Вт/кг.
Решение. Наибольшая величина магнитного потока определена при решении задачи 24.4:
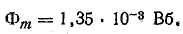
Наибольшая магнитная индукция
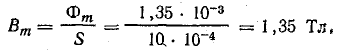
Магнитная цепь катушки состоит из двух участков: стального сердечника, длина которого по средней линии lст = 110 см, и воздушного зазора δ = 0,5 мм.
Согласно закону полного тока,
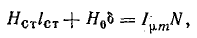
где Hст, H0 — напряженность магнитного поля в стали и воздушном зазоре; Iμm — амплитуда намагничивающей составляющей тока катушки.
По приложению 4 при В = 1,35 Тл
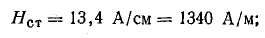
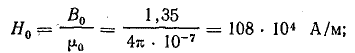
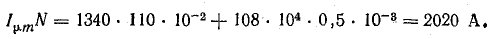
Действующую величину намагничивающего тока определяем по формуле (24.2):
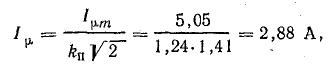
где
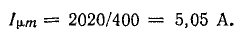
Для определения активной составляющей тока Iа нужно найти потери в стали. Масса сердечника
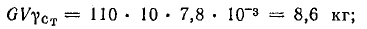
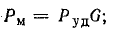
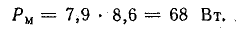
Активная составляющая тока
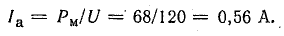
Ток в обмотке
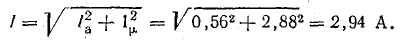
Коэффициент мощности катушки
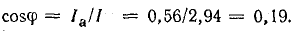
Полная векторная диаграмма и схемы замещения катушки с ферромагнитным сердечником
При построении упрощенной векторной диаграммы (см. рис. 24.18) не учитывались активное сопротивление обмотки и магнитное рассеяние.
Однако в практике расчетов и эксплуатации электромагнитных устройств (электрических машин, трансформаторов, электроаппаратуры и т. д.) эти факторы имеют существенное значение и ими во многих случаях пренебрегать нельзя.
Потери энергии в обмотке катушки
Энергия, потребляемая катушкой, расходуется на покрытие не только магнитных потерь (потерь в ферромагнитном сердечнике), но и электрических (потерь в обмотке).
Мощность электрических потерь — их часто называют потерями в меди — пропорциональна квадрату тока и активному сопротивлению обмотки R:

Таким образом, активная мощность катушки

а активная составляющая тока

Магнитное рассеяние
Когда не учитывается магнитное рассеяние, предполагается, что магнитный поток катушки полностью замыкается по ферромагнитному сердечнику. Действительно, большая часть линий магнитной индукции замыкается по сердечнику, образуя основной магнитный поток Ф.
Но магнитное поле существует и в пространстве, окружающем сердечник, что можно изобразить линиями магнитной индукции проведенными полностью или частично вне сердечника, в воздухе (рис. 24.19).
Эти линии характеризуют другой магнитный поток Фs, который называется потоком рассеяния.
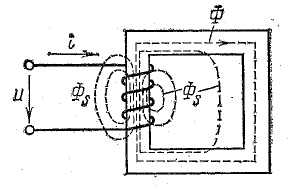
Рис. 24.19. Магнитный поток рассеяния в катушке с ферромагнитным сердечником
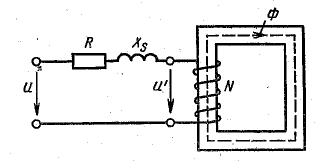
Рис. 24.20. Схема реальной катушки с ферромагнитным сердечником
Оба магнитных потока создаются одним и тем же током катушки, но из-за различия сред рассматриваются и определяются отдельно.
Основной магнитный поток Ф не пропорционален току, так как связан с ним нелинейной кривой намагничивания ферромагнитного сердечника. Поэтому э. д. с. в катушке, наводимая основным потоком, определяется по формуле (24.1): Е = 4,44 NfФm.
Магнитный поток рассеяния Фs пропорционален току, так как магнитная проницаемость воздуха постоянна. Э. д. с. Еs, наводимая в катушке потоком рассеяния, пропорциональна скорости изменения тока:
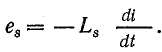
Поэтому
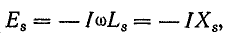
где Хs —индуктивное сопротивление рассеяния.
Полная векторная диаграмма катушки с ферромагнитным сердечником
Напряжение 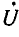 , приложенное к катушке, состоит из трех составляющих: первая (
, приложенное к катушке, состоит из трех составляющих: первая (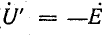 ) уравновешивает э. д. с. основного потока; вторая (
) уравновешивает э. д. с. основного потока; вторая (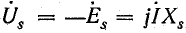 ) уравновешивает э. д. с. потока рассеяния, т. е. является падением напряжения в индуктивном сопротивлении рассеяния; третья (
) уравновешивает э. д. с. потока рассеяния, т. е. является падением напряжения в индуктивном сопротивлении рассеяния; третья ( ) есть падение напряжения в активном сопротивлении обмотки:
) есть падение напряжения в активном сопротивлении обмотки:
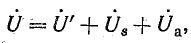
или
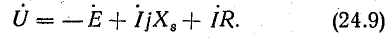
Этому уравнению соответствует электрическая схема рис. 24.20, на которой активное сопротивление R и индуктивное сопротивление рассеяния Хs как бы отделены от катушки, которая после отделения может рассматриваться без активного сопротивления и без рассеяния при напряжении на ее зажимах U'.
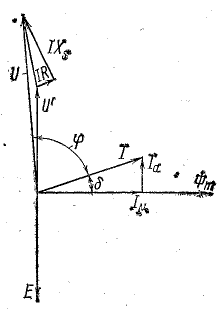
Рис. 24.21. Векторная диаграмма реальной катушки с ферромагнитным сердечником
Уравнениям (24.9) соответствует также векторная диаграмма рис. 24.21, которая отличается от диаграммы рис. 24.18 наличием векторов падения напряжения в активном и реактивном сопротивлениях катушки.
Таким образом, реальную катушку можно заменить цепью последовательного соединения идеализированной катушки (без активного сопротивления и без рассеяния), к которой приложено напряжение U', и двух линейных сопротивлений: активного R и индуктивного Хs.
Схемы замещения катушки с ферромагнитным сердечником
При решении практических задач для идеализированной катушки можно составить схему замещения с постоянными (при данном напряжении на катушке) величинами сопротивлений: активного Rм и индуктивного Хм, соединенными последовательно (рис. 24.22, а).
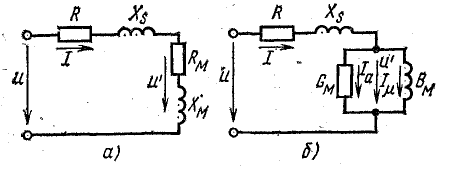
Рис. 24.22. Схемы замещения катушки с ферромагнитным сердечником
При этом потери в ферромагнитном сердечнике Рм заменяют равными электрическими потерями в активном сопротивлении:
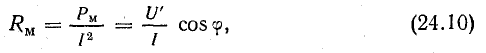
а Хм определяют из уравнения

Вместо последовательного соединения Rм, Хм можно включить параллельно две ветви (рис. 23.22, б).
В первой ветви, содержащей активную проводимость Gм, ток равен активной составляющей тока катушки Iа:
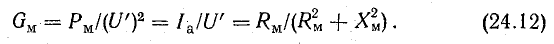
Вторая ветвь содержит реактивную проводимость Вм и намагничивающий ток Iμ:
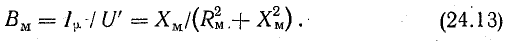
Нетрудно заметить, что обе схемы замещения полностью соответствуют уравнению (24.9) и векторной диаграмме рис. 24.21.
Величины сопротивления Rм и Хм, постоянные при одном действующем напряжении U на катушке, должны быть изменены, если это напряжение изменится.
Задача 24.7.
Катушка, имеющая N = 300 витков, включается в сеть переменного тока с напряжением U = 220 В и частотой f = 50 Гц. Катушку можно надеть на стальной сердечник или снять. При отсутствии стального сердечника активная мощность катушки P1 = 500 Вт, а ток I1 = 12 А. При наличии стального сердечника установлено, что активная мощность и ток уменьшаются до Р2 = 300 Вт, I2 = 5 А.
Определить э. д. с. Е, амплитуду магнитного потока Фm, коэффициент мощности cosφ, мощность потерь в обмотке Рэ, мощность потерь в сердечнике Рм, намагничивающую составляющую тока и построить векторную диаграмму в двух случаях: при отсутствии и наличии сердечника внутри катушки.
Примечание. Магнитным потоком рассеяния при наличии стального сердечника пренебречь.
Решение. При отсутствии стального сердечника коэффициент мощности
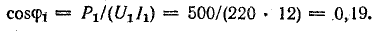
Активное сопротивление
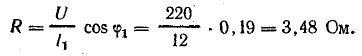
Падение напряжения в активном сопротивлении
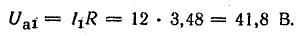
Напряжение U1', уравновешивающее э. д. с. в катушке Е1 определяется на основании векторной диаграммы из треугольника напряжений (рис. 24.23):
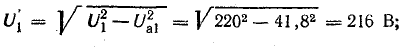
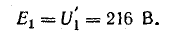
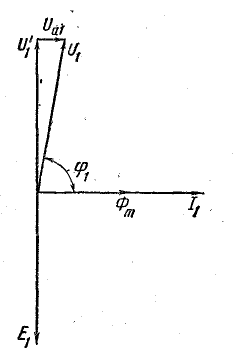
Рис. 24.23. К задаче 24.7
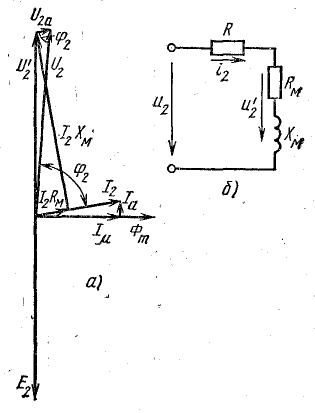
Рис. 24.24. К задаче 24.7
Амплитуда магнитного потока
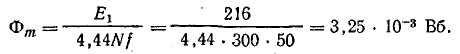
При отсутствии стального сердечника мощность магнитных потерь Рм = 0, а мощность потерь в меди равна общей активной мощности катушки: Рэ = Р1 = 500 Вт.
Составляющая тока, обусловленная потерями в стали, Iа = 0, а намагничивающая составляющая тока совпадает с полным током катушки Iμ = I1 = 12А.
При наличии стального сердечника
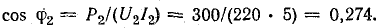
Мощность потерь в меди
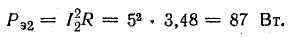
Мощность потерь в стали
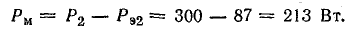
Падение напряжения в активном сопротивлении
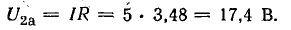
Э. д. с. катушки и составляющая общего напряжения, уравновешивающая эту э. д. с., из треугольника напряжений (см. векторную диаграмму рис. 24. 24, а), по теореме косинусов,
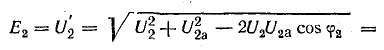
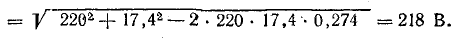
Составляющая тока, обусловленная потерями в стали,
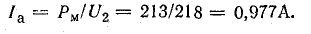
Намагничивающая составляющая тока
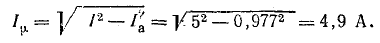
Амплитуда магнитного потока
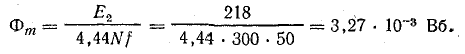
Векторная диаграмма построена в следующем порядке.
В произвольном направлении отложен вектор напряжения на катушке U2 и под углом φ2 к нему — вектор тока с учетом, что ток отстает от напряжения. Параллельно вектору тока из конца вектора напряжения отложен отрезок, выражающий величину падения напряжения U2а в активном сопротивлении обмотки. Разность векторов U2 — U2а = U2' дает вектор напряжения, уравновешивающего э. д. с. катушки.
В сторону, противоположную направлению вектора U2', отложен равный ему вектор э. д. с. Е2.
Перпендикулярно вектору Е2 проведены опережающий его по фазе вектор магнитного потока Фm и совпадающий по фазе с потоком вектор намагничивающего тока Iμ.
Перпендикулярно вектору тока Iμ из конца его отложен вектор тока Ia, конец которого совпадает с концом вектора общего тока I2, так как I2 = Ia + Iμ.
Напряжение U2' и э. д. с. Е2 можно определить при помощи схемы замещения катушки со стальным сердечником при последовательном соединении элементов (рис. 24.24, б).
На этой схеме напряжение U2' приложено к участку последовательно соединенных активного сопротивления Rм и индуктивного сопротивления Xм.
Активное сопротивление должно быть взято такой величины, чтобы при заданном токе в катушке мощность в этом сопротивлении была равна мощности потерь в стальном сердечнике:
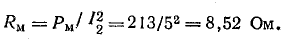
Индуктивное сопротивление Хм должно быть взято таким, чтобы векторная сумма падений напряжения в сопротивлениях Хм и Rм была равна напряжению U2'.
Из схемы замещения следует
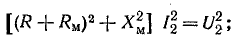
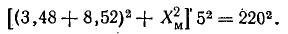
Отсюда Хм = 42,3 Ом, тогда
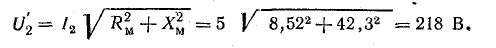
Применение катушек с ферромагнитным сердечником
В практике широко применяются элементы с нелинейной зависимостью магнитного потока от тока Ф(i).
Рассмотренные ранее вопросы, относящиеся к катушкам с ферромагнитным сердечником, имеют общий характер независимо от назначения и условий их работы в электрических цепях.
Дополнительно рассмотрим некоторые явления, лежащие в основе практического применения катушек с ферромагнитным сердечником.
Феррорезонанс
В цепи с линейными элементами при постоянной частоте источника питания резонанс достигается непосредственным изменением индуктивности или емкости.
Если индуктивность или емкость нелинейны, то резонанс может наступать при изменении тока в цепи или приложенного напряжения без какой-либо регулировки катушки и конденсатора.
Индуктивность или емкость такой нелинейной цепи изменяется в связи с изменением тока или напряжения, что ведет к изменению ее собственной частоты, которая может принять величину, равную частоте вынужденных колебаний источника.
В цепях, содержащих катушку со стальным сердечником и конденсатор, резонансные явления, связанные с нелинейным характером индуктивности, называют феррорезонансом.
Рассмотрим это явление, пренебрегая потерями в ферромагнитном сердечнике и считая ток синусоидальным.
При последовательном соединении конденсатора и катушки с сердечником (рис. 24.25) ток в цепи отстает от индуктивного напряжения на 90° и опережает емкостное напряжение тоже на 90°. Таким образом, векторы напряжения 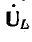 и
и 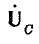 находятся в противофазе.
находятся в противофазе.
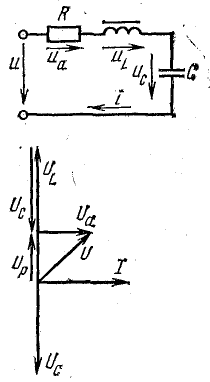
Рис. 24.25. Схема и векторная диаграмма неразветвленной цепи, в которой возможен феррорезонанс напряжений
Напряжение источника питания уравновешивается суммой активного и реактивных падений напряжения:
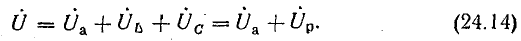
В этой сумме общее реактивное напряжение 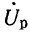 цепи по абсолютной величине равно разности реактивных напряжений катушки и конденсатора:
цепи по абсолютной величине равно разности реактивных напряжений катушки и конденсатора: 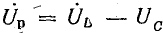 .
.
Невыразим графически зависимость между напряжением цепи U и током I, пользуясь уравнением (24.14).
Было отмечено, что вольт-амперная характеристика катушки по форме повторяет кривую намагничивания (рис. 24.26). Вольт-амперная характеристика конденсатора — это прямая, проходящая через начало координат:
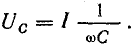
Величину емкости можно подобрать так, что прямая Uс(I) пересечет кривую UL(I).
Точка пересечения А является точкой резонанса, который при последовательном соединении катушки и конденсатора называется феррорезонансом напряжений. В этой точке величины UL и UC одинаковы, а их разность Uр равна нулю.
На рис. 24.26 построена также вольт-амперная характеристика цепи с учетом активного напряжения Uа = IR.
Общее напряжение определяется выражением
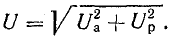
Из графика U(I) видно, что с ростом тока напряжение сначала растет (участок 0-2), затем падает, достигая минимума в точке резонанса 3, а далее снова растет (участок 3-4).
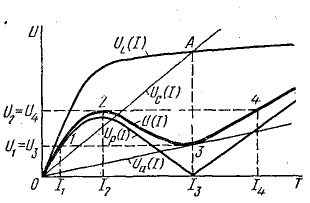
Рис. 24.26. Вольт-амперные характеристики цепи, в которой возможен феррорезонанс напряжений
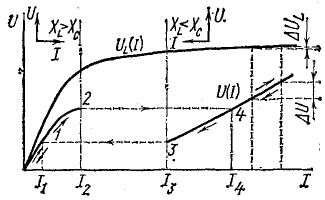
Рис. 24.27. Изменение тока в цепи при феррорезонансе напряжений
Практически такую кривую можно получить опытным путем, если имеется возможность непрерывного увеличения тока при постоянном напряжении источника, т. е. когда в цепи кроме катушки и конденсатора последовательно включен резистор с большим регулируемым сопротивлением.
При непрерывном увеличении напряжения источника в цепи рис. 24.25 ток плавно растет до I2 (рис. 24.27), а затем скачком увеличивается до I4 и далее плавно растет.
При уменьшении напряжения ток плавно уменьшается до I3, а затем скачком до I1 и снова падает плавно.
Скачкообразное изменение тока сопровождается изменением на 180° фазы тока по отношению к напряжению (опрокидывание фазы).
После точки резонанса, т. е. при напряжениях источника, больших напряжения опрокидывания фазы, Напряжение на катушке изменяется мало, что связано с переходом по характеристике намагничивания в область магнитного насыщения. Это используется в практике для стабилизации напряжения.
Пусть входное напряжение U изменилось на 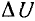 (рис. 24.27). При этом напряжение на катушке изменилось лишь незначительно (на
(рис. 24.27). При этом напряжение на катушке изменилось лишь незначительно (на 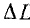 ). Таким образом, на нагрузке, подключенной параллельно катушке, напряжение остается практически постоянным.
). Таким образом, на нагрузке, подключенной параллельно катушке, напряжение остается практически постоянным.
Стабилизаторы напряжения, работающие по такому принципу, называются феррорезонансными.
При параллельном соединении конденсатора и катушки со стальным сердечником в цепи может возникнуть феррорезонанс токов.
Катушка с ферромагнитным сердечником при одновременном намагничивании постоянным и переменным током
Возможности практического использования нелинейной зависимости Ф(i) между магнитным потоком и намагничивающим током катушки с ферромагнитным сердечником значительно расширяются, если сердечник намагничивается одновременно переменным и постоянным током. Такое намагничивание можно осуществить, если на сердечнике кроме основной обмотки N1, включенной в цепь переменного тока, имеется дополнительная обмотка N0 с постоянным током I0 (рис. 24.28, d).
Предположим, что к обмотке N1 приложено синусоидальное напряжение. В этом случае при малом активном сопротивлении обмотки переменная составляющая магнитного потока может быть только синусоидальной.
Кроме синусоидальной составляющей магнитного потока, обусловленной намагничивающей силой I1N1 основной обмотки, намагничивающей силой I0N0 обмотки постоянного подмагничивания в сердечнике создается постоянный поток Ф01.
Таким образом, магнитный поток в сердечнике выражается суммой:
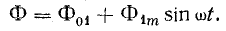
Построение на рис. 24.28, б показывает, что при наличии подмагничивания сердечника постоянным током переменный ток в обмотке значительно больше, чем при отсутствии подмагничивания (ср. кривые 2 и 1). Изменяя постоянный ток в обмотке подмагничивания N0 (управляющая цепь), можно изменять ток в основной обмотке N1 (управляемая цепь).
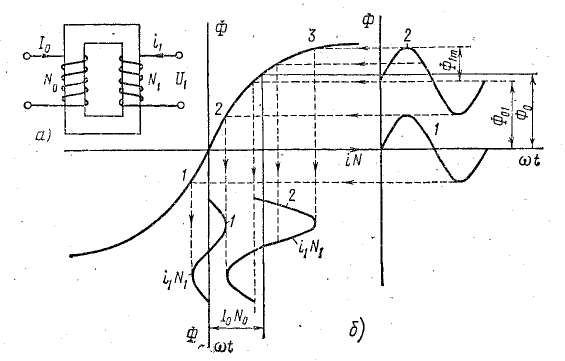
Рис. 24.28. Кривые тока и магнитного потока в катушке с ферромагнитным сердечником при намагничивании постоянным и переменным током
Нужно отметить, что постоянная составляющая магнитного потока Ф01 оказывается меньше того потока Ф0, который создается в сердечнике намагничивающей силой I0N0 при отсутствии переменного тока в обмотке. Обмотка переменного тока оказывает некоторое размагничивающее действие.
Общая намагничивающая сила в сердечнике определяется суммой:
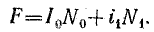
При отсутствии постоянной составляющей намагничивающей силы I0N0 и синусоидальном напряжении на зажимах обмотки N1 график тока в ней по форме близок к синусоиде, так как изменение тока i1 находится в пределах прямолинейной части кривой намагничивания, т. е. не захватывает области магнитного насыщения.
При подмагничивании постоянным током переменный ток в обмотке N1 при том же напряжении на ее зажимах увеличивается и по форме отличается от синусоиды тем больше, чем больше намагничивающая сила I0N0. Изменение тока в управляемой цепи (обмотка N1) в зависимости от постоянного тока в управляющей цепи (обмотка N0) объясняется тем, что рабочий участок по кривой намагничивания перемещается в область магнитного насыщения (на рис. 24.28, б этот участок находится между точками 2 и 3).
Дроссели насыщения
Катушка с ферромагнитным сердечником, предназначенным для работы в цепи переменного тока при дополнительном подмагничивании постоянным током, называется дросселем насыщения.
Использование таких дросселей для управления и регулирования в электрических цепях переменного тока основано на изменении индуктивного сопротивления катушки подмагничиванием постоянным током.
Схема дросселя насыщения, изображенная на рис. 24.28, а, имеет большой недостаток. Переменный магнитный поток наводит в управляющей обмотке N0 переменную э. д, с., что является причиной переменного тока, искажающего рассмотренную картину процесса.
Для устранения этого недостатка дроссель насыщения выполняют на двух одинаковых сердечниках (рис. 24.29).
Обмотки управления N0 соединяют между собой последовательно встречно, обмотки переменного тока N1 — последовательно согласно. При таком соединении одинаковых обмоток переменные э. д. с., наводимые в управляющих обмотках, направлены противоположно, а результирующая э. д .с. в управляющей цепи равна нулю.
Аналогичный результат достигается в дросселе с трехстержневым сердечником (рис. 24.30). Управляющая обмотка N0 расположена на среднем стержне, а обмотка переменного тока N1 разделена на две одинаковые части, которые расположены на крайних стержнях и соединены последовательно согласно. При таком включении переменные составляющие магнитного потока в среднем стержне направлены противоположно, поэтому результирующий переменный поток в нем равен нулю и переменная э. д. с. в управляющей обмотке не наводится.
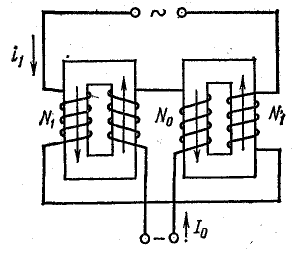
Рис. 24.29. Схема дросселя насыщения с двумя сердечниками
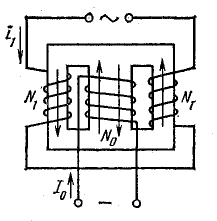
Рис. 24.30. Схема дросселя насыщения с трехстержневым сердечником
В дросселях насыщения нет движущихся частей, они позволяют плавно регулировать ток или напряжение в электрической цепи переменного тока, мощность которой значительно больше мощности цепи управления.
Принцип работы магнитного усилителя
Дроссели насыщения применяются в различных схемах магнитных усилителей мощности, тока или напряжения.
На рис. 24.31 изображена простейшая схема магнитного усилителя с трехстержневым дросселем насыщения. В цепи переменного тока усилителя последовательно включены рабочая обмотка N1 и нагрузка с сопротивлением Rн.
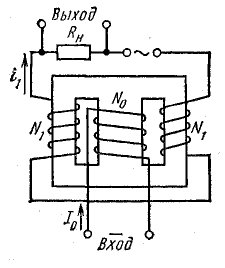
Рис. 24.31. Схема магнитного усилителя
Основной характеристикой магнитного усилителя является коэффициент усиления Ку — отношение приращения выходной мощности к вызвавшему его приращению входной мощности:
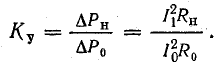
При отсутствии постоянного тока в управляющей цепи ферромагнитный сердечник магнитно не насыщен, поэтому индуктивное сопротивление рабочей обмотки N1 велико, а ток i1 относительно мал. При подаче сигнала на управляющую обмотку сердечник насыщается, магнитная проницаемость материала сердечника уменьшается, в результате чего индуктивное сопротивление обмотки N1 уменьшается, а ток в рабочей цепи увеличивается.
Благодаря этому увеличиваются мощность и напряжение на нагрузке.
Дроссели насыщения, предназначенные для магнитных усилителей, выполняются на сердечниках из ферромагнитных сплавов, которые характеризуются большой магнитной проницаемостью в слабом магнитном поле и насыщаются при небольшом увеличении напряженности магнитного поля (см., например, кривую намагничивания на рис. 24.17, б).
Благодаря большой величине магнитной проницаемости при отсутствии постоянного подмагничивания (при холостом ходе) усилитель имеет малый ток холостого хода в рабочей обмотке и малые потери энергии. Переход сердечника в состояние магнитного насыщения при подаче слабого сигнала позволяет получить большой коэффициент усиления (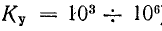 ).
).
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |