
Нелинейные резистивные цепи
Содержание:
Нелинейные резистивные цепи:
Процессы, протекающие в нелинейных электрических цепях, намного сложнее и разнообразнее, чем процессы в линейных цепях и в то же время они менее исследованы. В нелинейных цепях могут иметь место явления, которые не наблюдаются в цепях, содержащих только линейные элементы. Например, реакция нелинейной цепи на внешнее воздействие может содержать гармонические колебания таких частот, которые отсутствуют во внешнем воздействии; при приложении к нелинейной цепи только постоянных токов и напряжений в ней при определенных условиях могут возникать незатухающие колебания, так называемые автоколебания; интенсивность реакции нелинейной цепи на определенное воздействие, как правило, нелинейно зависит от интенсивности воздействия, причем плавные изменения частоты или интенсивности внешнего воздействия могут приводить к скачкообразным изменениям частоты и интенсивности реакции; во многих случаях реакция нелинейной цепи на заданное воздействие не определяется однозначно; при одних и тех же воздействиях нелинейная цепь может иметь несколько установившихся режимов, называемых состоянием равновесия, причем некоторые из этих состояний могут оказаться неустойчивыми. Явления, имеющие место в нелинейных элементах, положены в основу функционирования большинства радиоэлектронных устройств, причем важнейшие для радиоэлектроники процессы генерирования колебаний, модуляции, детектирования, выпрямления, ограничения, умножения и преобразования частоты и многие другие в принципе не могут быть реализованы с помощью линейных цепей с постоянными параметрами.
Как отмечалось ранее, характеристики большинства реальных элементов в той или иной степени нелинейны. В одних случаях нелинейность характеристик невелика и при построении упрощенной модели ею можно пренебречь, в других — нелинейностью характеристик реальных элементов пренебречь нельзя и при построении упрощенных моделей таких цепей приходится использовать идеализированные элементы с нелинейными характеристиками. Нелинейность характеристик реальных элементов обычно считается несущественной, если ее наличие не является принципиальным для функционирования устройства, т. е. приводит лишь к появлению некоторых второстепенных эффектов, которыми в рамках решаемой задачи можно пренебречь. На практике нелинейностью характеристик реального элемента, как правило, можно пренебречь, если характеристика элемента практически линейна в рабочем, диапазоне токов и напряжений, а функционирование устройства не построено на использовании нелинейности соответствующей характеристики. Следует, однако, иметь в виду, что окончательное решение о том, является ли нелинейность несущественной, не может быть произведено в рамках линейного приближения, а требует решения задачи с учетом нелинейности характеристик.
Рассмотрим лишь основные особенности и методы расчета цепей, содержащих нелинейные резистивные элементы (нелинейные резисторы, транзисторы, диоды и т. п.). Более детально процессы в нелинейных цепях, в том числе и в цепях, содержащих нелинейные энергоемкие элементы (нелинейные конденсаторы и индуктивные катушки), рассматриваются в курсе «Радиотехнические цепи и сигналы».
Нелинейные резистивные элементы
В соответствии с основным методом теории цепей при изучении нелинейных резистивных цепей не будем рассматривать физические процессы, имеющие место в реальных элементах, а ограничимся лишь представлением этих элементов с помощью упрощенных моделей, заменяющих каждый из элементов в рамках решаемой задачи. В частности, будем пренебрегать эффектами, связанными с запасанием энергии электрического и магнитного полей, имеющими место во всех реальных элементах, и считать, что свойства нелинейных резистивных элементов полностью определяются их статическими вольт-амперными характеристиками (ВАХ). Для каждого реального элемента зависимость между мгновенными значениями токов и напряжений будет совпадать с ВАХ только в том случае, если частота изменения токов и напряжений на внешних зажимах элемента не превышает некоторого предельного значения. В этом случае нелинейный резистивный элемент можно рассматривать как безынерционнный. Если рабочая частота элемента близка к предельной или превышает ее, то статические ВАХ не отражают зависимости между мгновенными значениями токов и напряжений на зажимах элемента. При таких условиях нелинейный элемент следует рассматривать как инерционный.
В зависимости от числа внешних выводов различают нелинейные двухполюсные элементы (резисторы с нелинейным сопротивлением, электровакуумные и полупроводниковые диоды) и нелинейные многополюсные элементы (транзисторы различных типов, электровакуумные триоды и пентоды). При принятых ранее положительных направлениях токов и напряжений ВАХ нелинейных пассивных двухполюсных элементов должны располагаться в первом и третьем квадрантах координатной плоскости u— i и проходить через начало координат.
Если ВАХ нелинейного резистивного элемента хотя бы частично располагается во втором или четвертом квадрантах либо не проходит через начало координат, то потребляемая таким элементом мощность может быть отрицательной и, следовательно, такой элемент не является пассивным.
Вольт-амперная характеристика нелинейного двухполюсного элемента может быть симметричной (см. рис. 1.3, а) или несимметричной (см. рис. 1.3, б, в) относительно начала координат. Для двухполюсника с симметричной характеристикой выполняется условие
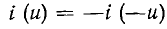
или
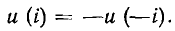
Очевидно, что режим работы нелинейной цепи не изменится, если выводы нелинейного резистивного элемента с симметричной характеристикой поменять местами. Если условие (5.1) не выполняется, то ВАХ нелинейного резистивного двухполюсника не является симметричной.
Различают нелинейные резистивные элементы с монотонной и немонотонной ВАХ. У элементов с монотонной ВАХ увеличение приложенного к элементу напряжения приводит к увеличению (или хотя бы не уменьшению) тбка и, наоборот, увеличение тока приводит к возрастанию падения напряжения на элементе. Напряжение и ток на зажимах такого элемента связаны между собой однозначной зависимостью, причем производные 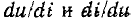 во всех точках ВАХ принимают только неотрицательные значения. Если хотя бы в ограниченном диапазоне изменения токов и напряжений увеличение напряжения на зажимах элемента приводит к уменьшению тока или, наоборот, увеличение тока приводит к уменьшению напряжения, то ВАХ такого элемента — немонотонна. Ток и напряжение нелинейного резистивного элемента с немонотонной ВАХ не связаны между собой взаимно однозначной зависимостью.
во всех точках ВАХ принимают только неотрицательные значения. Если хотя бы в ограниченном диапазоне изменения токов и напряжений увеличение напряжения на зажимах элемента приводит к уменьшению тока или, наоборот, увеличение тока приводит к уменьшению напряжения, то ВАХ такого элемента — немонотонна. Ток и напряжение нелинейного резистивного элемента с немонотонной ВАХ не связаны между собой взаимно однозначной зависимостью.
Различают немонотонные вольт-амперные характеристики N- и S-типов. У элементов с N-oбразной ВАХ (см. рис. 1.3, б) каждому значению напряжения на зажимах элемента соответствует вполне определенное значение тока, однако в определенном диапазоне изменения токов одному и тому же значению тока может соответствовать несколько различных значений напряжения. Элементы с S-oбразной ВАХ отличаются тем, что в некотором диапазоне изменения напряжений заданому значению напряжения соответствует несколько различных значений тока (см. рис. 1.3, в).
Вольт-амперная характеристика безынерционного нелинейного резистивного двухполюсного элемента может рассматриваться как зависимость мгновенного значения реакции данного элемента у = у (t) на некоторое воздействие от мгновенного значения воздействия х = х (t). Для однозначного определения этой зависимости ВАХ N-типа должна быть представлена в виде функции i = i (u), а ВАХ S=типа — в виде u = u (i). При таком представлении ВАХ рассматриваемых элементов содержат как восходящие, так и падающие участки. На восходящих участках dy/dx положительна, на падающих — отрицательна. В связи с тем что дифференциальные сопротивления нелинейных резистивных элементов на падающих участках ВАХ отрицательны, нелинейные двухполюсные элементы с немонотонной ВАХ обычно называют элементами с отрицательным сопротивлением.
Зависимость между токами и напряжениями элементов с монотонной ВАХ может быть представлена как в виде u = u (i), так и в виде i = i (u). Дифференциальное сопротивление элементов с монотонной ВАХ не принимает отрицательных значений.
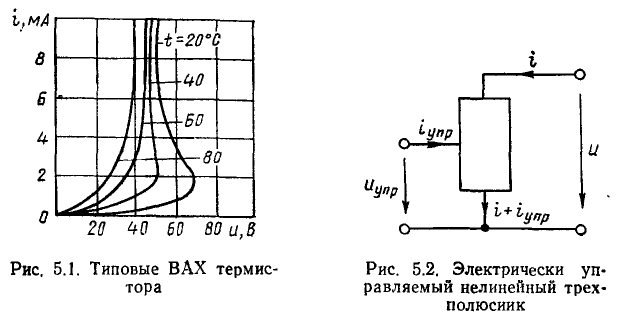
Вид ВАХ нелинейного резистивного двухполюсника может зависеть от некоторой величины, не связанной непосредственно с токами или напряжениями цепи, в которую включен данный элемент, в частности от температуры, освещенности, давления и др. Такие элементы относятся к неэлектрически управляемым двухполюсникам. Так как каждому значению управляющей величины соответствует своя кривая, характеризующая зависимость между током и напряжением на зажимах неэлектрически управляемого резистивного двухполюсника, то такие двухполюсники характеризуются семейством ВАХ (рис. 5.1).
Важнейший класс нелинейных резистивных элементов составляют электрически управляемые элементы (транзисторы различных типов, вакуумные и газоразрядные трехэлектродные и многоэлектродные приборы). Элементы этого типа содержат два основных электрода (катод и анод у электронных ламп, эмиттер и коллектор у биполярных транзисторов, сток и исток у полевых транзисторов), сопротивление между которыми изменяется под действием тока или напряжения одного или нескольких управляющих электродов (сетки у электронных ламп, базы у биполярных транзисторов, затвора или подложки у полевых транзисторов). В частности, ток i нелинейного резистивного трехполюсника (рис. 5.2), имеющего два основных и один управляющий электроды, является функцией напряжения между основными электродами и u тока 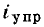 или напряжения
или напряжения 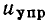 управляющего электрода:
управляющего электрода:
Как видно из рис 5.2, выводы нелинейного управляемого трехполюсника образуют с остальной частью цепи два контура — основной (выходной) и управляющий (входной), причем один из выводов является общим для обоих контуров.
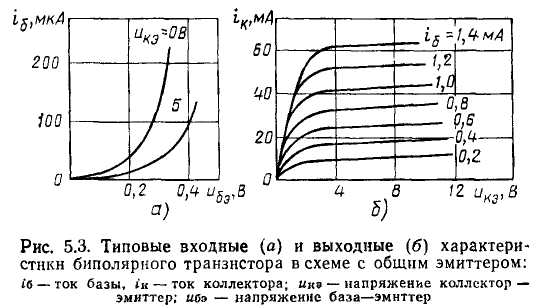
Электрически управляемые нелинейные резистивные элементы могут быть охарактеризованы различными семействами ВАХ. Выходные ВАХ отображают зависимость между выходным током i и выходным напряжением u при различных значениях входного тока 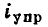 или напряжения
или напряжения 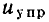 (рис. 5.3, б; 5.4, а), входные ВАХ — зависимость между входным током и входным напряжением при различных значениях выходного напряжения (рис. 5.3, а), проходные ВАХ — зависимость выходного тока от входного тока или напряжения при различных значениях выходного напряжения (рис. 5.4, б).
(рис. 5.3, б; 5.4, а), входные ВАХ — зависимость между входным током и входным напряжением при различных значениях выходного напряжения (рис. 5.3, а), проходные ВАХ — зависимость выходного тока от входного тока или напряжения при различных значениях выходного напряжения (рис. 5.4, б).
Вид ВАХ нелинейного управляемого резистивного элемента существенным образом зависит от схемы включения элемента, т. е. от того, какой из электродов является общим для основного и управляющего контуров.
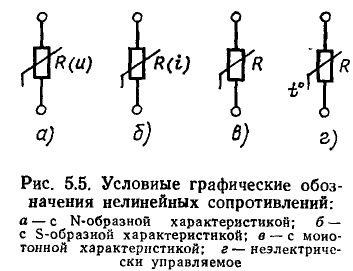
На принципиальных электрических схемах реальные нелинейные резистивные элементы изображают с помощью установленных стандартами ЕСКД условных графических обозначений. При построении эквивалентных схем цепей нелинейные резистивные элементы либо изображают в виде двухполюсников или многоплюсников (см. рис. 5.2), либо представляют схемами замещения, содержащими наряду с другими элементами идеализированные нелинейные сопротивления (рис. 5.5). Для неэлектрически управляемых сопротивлений рядом с «полочкой» на условном графическом обозначении сопротивления указывают буквенное обозначение соответствующей управляющей величины (рис. 5.5, г).
Уравнения электрического равновесия нелинейных резистивных цепей
Как и в случае линейных электрических цепей, задача анализа нелинейной резистивной цепи заключается в общем случае в определении токов и напряжений всех или части ветвей при заданных параметрах независимых источников энергии. Если нелинейная цепь включает в себя р ветвей, из которых 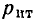 ветвей содержат независимые источники тока, а
ветвей содержат независимые источники тока, а 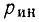 состоят только из независимых источников напряжения, то для определения
состоят только из независимых источников напряжения, то для определения 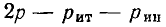 неизвестных токов и напряжений можно воспользоваться р уравнениями, составленными на основании законов Кирхгофа, и
неизвестных токов и напряжений можно воспользоваться р уравнениями, составленными на основании законов Кирхгофа, и 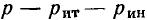 уравнениями ветвей.
уравнениями ветвей.
В связи с тем что токи ветвей дерева любой электрической цепи однозначно выражаются через токи главных ветвей, а напряжения главных ветвей — через напряжения ветвей дерева, при выборе дерева графа нелинейной резистивной электрической цепи в качестве ветвей дерева необходимо использовать ветви цепи, содержащие нелинейные элементы с S-образной характеристикой, и ветви с независимыми источниками напряжения, а в качестве главных ветвей следует выбирать ветви с источниками тока и ветви, содержащие нелинейные резистивные элементы с N-образной характеристикой. Нелинейные резистивные элементы с монотонной ВАХ могут входить как в состав ветвей дерева, так и в состав главных ветвей. Очевидно, что все уравнения основной системы уравнений электрического равновесия нелинейной резистивной цепи будут алгебраическими, причем, по крайнем мере, одно из компонентных уравнений будет нелинейным.
Аналитически разрешить такие уравнения можно только в исклюительных случаях, при некоторых специально подобранных видах нелинейности. Как правило, эти уравнения решают приближенными численными, графическими или графо-аналитическими методами. В ряде случаев исследование процессов в простейших нелинейных резистивных цепях удается провести без составления уравнений электрического равновесия — путем выполнения различных преобразований исходной цепи.
Графические методы анализа нелинейных резистивных цепей
Простейшие преобразования нелинейных резистивных цепей:
Рассмотрим простейшие эквивалентные преобразования, которые можно применять как при анализе нелинейных резистивных цепей постоянного тока, так и при анализе нелинейных цепей, находящихся под произвольным внешним воздействием.
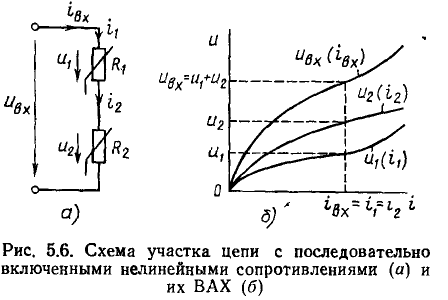
Пусть участок цепи (рис. 5.6, а) содержит два последовательно включенных нелинейных сопротивления и 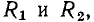 вольт-амперные характеристики которых представлены на рис. 5.6, б. Очевидно, что при любом значении тока
вольт-амперные характеристики которых представлены на рис. 5.6, б. Очевидно, что при любом значении тока 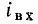
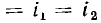 напряжение
напряжение 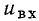 на зажимах данного участка цепи равно сумме напряжений на каждом из нелинейных сопротивлений:
на зажимах данного участка цепи равно сумме напряжений на каждом из нелинейных сопротивлений: 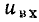
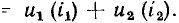
Суммируя ординаты зависимостей 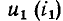 и
и 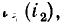 получаем зависиость между напряжением
получаем зависиость между напряжением 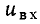 и током
и током 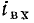 на зажимах рассматриваемого участка цепи (рис. 5.6, б). Таким образом, участок цепи, содержащий два последовательно включенных нелинейных сопротивления, может быть заменен одим нелинейным сопротивлением, ВАХ
на зажимах рассматриваемого участка цепи (рис. 5.6, б). Таким образом, участок цепи, содержащий два последовательно включенных нелинейных сопротивления, может быть заменен одим нелинейным сопротивлением, ВАХ 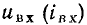 которого получается путем суммирования ординат ВАХ
которого получается путем суммирования ординат ВАХ 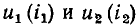 сопротивлений. Аналогичным образом можно заменить участок цепи, содержащий последовательно включенные линейное и нелинейное сопротивления, а также участок цепи, представляющий собой последовательное соединение произвольного количества линейных и нелинейных сопротивлений.
сопротивлений. Аналогичным образом можно заменить участок цепи, содержащий последовательно включенные линейное и нелинейное сопротивления, а также участок цепи, представляющий собой последовательное соединение произвольного количества линейных и нелинейных сопротивлений.
Пример 5.1.
Найдем, зависимость между током и напряжением участка цепи (рис. 5 7, а), представляющего собой последовательное соединение линейного 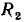 и нелинейного
и нелинейного 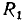 сопротивлений, ВАХ
сопротивлений, ВАХ 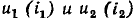 которых приведены на рис. 5.7, б. Определим изменение напряжения
которых приведены на рис. 5.7, б. Определим изменение напряжения 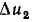 на линейном сопротивлении
на линейном сопротивлении 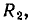 соответствующее приращению напряжения на зажимах цепи
соответствующее приращению напряжения на зажимах цепи 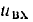 на
на 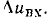
Вольт-амперную характеристику 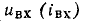 рассматриваемого участка цепи получаем, суммируя ординаты ВАХ
рассматриваемого участка цепи получаем, суммируя ординаты ВАХ 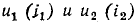 последовательно включенных элементов. Используя эту характеристику (рис. 5.7, б), можно найти приращение тока цепи
последовательно включенных элементов. Используя эту характеристику (рис. 5.7, б), можно найти приращение тока цепи 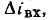 соответствующее изменению входного напряжения на
соответствующее изменению входного напряжения на 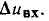 Далее, используя зависимость
Далее, используя зависимость 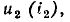 определяем соответствующее
определяем соответствующее
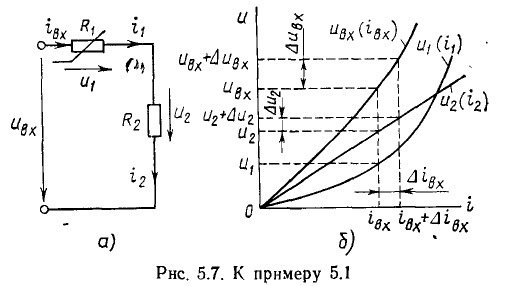
данному приращению тока приращение напряжения 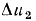 на линейном сопротивлении. Как видно из рис. 5.7, б, приращение напряжения на линейном сопротивлении оказалось значительно меньше вызвавшего его изменение входного напряже ния
на линейном сопротивлении. Как видно из рис. 5.7, б, приращение напряжения на линейном сопротивлении оказалось значительно меньше вызвавшего его изменение входного напряже ния 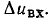
Рассмотрим участок цепи (рис. 5.8, а), представляющий собой параллельное включение двух нелинейных сопротивлений 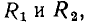 ВАХ
ВАХ 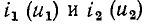 которых приведены на рис. 5.8, б. Как следует из первого закона Кирхгофа, входной ток
которых приведены на рис. 5.8, б. Как следует из первого закона Кирхгофа, входной ток 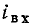 рассматриваемого участка цепи при любом напряжении
рассматриваемого участка цепи при любом напряжении 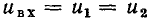 равен сумме токов нелинейных сопротивлений:
равен сумме токов нелинейных сопротивлений: 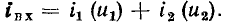

Суммируя ординаты зависимостей 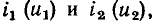 получаем ВАХ
получаем ВАХ 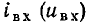 нелинейного сопротивления, которым можно заменить рассматриваемый участок цепи. Используя аналогичный прием, можно определить ВАХ участка цепи, содержащего произвольное количество параллельно включенных линейных и нелинейных сопротивлений.
нелинейного сопротивления, которым можно заменить рассматриваемый участок цепи. Используя аналогичный прием, можно определить ВАХ участка цепи, содержащего произвольное количество параллельно включенных линейных и нелинейных сопротивлений.
Поочередное применение правил эквивалентного преобразования участков с последовательным и параллельным соединением элементов позволяет постепенно «свертывать» участки цепей со смешанным соединением линейных и нелинейных сопротивлений с монотонными ВАХ.
Пример 5.2.
Найдем зависимость между током и напряжением на входе участка цепи со смешанным соединением элементов (рис. 5.9, а). Вольт-амперные характеристики 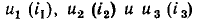 сопротивлений
сопротивлений 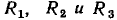 приведены на рис. 5.9, б. Определим приращение напряжения на сопротивлении
приведены на рис. 5.9, б. Определим приращение напряжения на сопротивлении 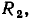 соответствующее изменению входного напряжения на
соответствующее изменению входного напряжения на 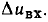
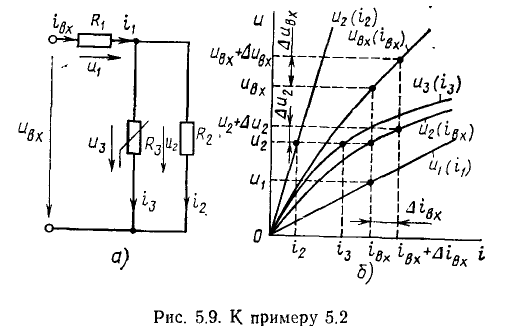
Суммируя абсциссы кривых 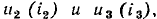 получаем ВАХ
получаем ВАХ 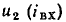
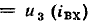 участка цепи, представляющего собой параллельное соединение сопротивлений
участка цепи, представляющего собой параллельное соединение сопротивлений 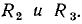 Далее, суммируя ординаты кривых
Далее, суммируя ординаты кривых 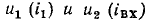
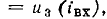 находим зависимость
находим зависимость 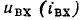 на входе рассматриваемого участка цепи.
на входе рассматриваемого участка цепи.
Пусть напряжение на входе цепи изменилось на 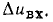 Используя зависимость
Используя зависимость 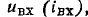 находим приращение тока
находим приращение тока 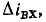 соответствующее этому изменению входного напряжения, и далее с помощью кривой
соответствующее этому изменению входного напряжения, и далее с помощью кривой  определяем приращение напряжения на линейном сопротивлении
определяем приращение напряжения на линейном сопротивлении 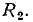 Как и для цепи, рассмотренной в примере 5.1, приращение напряжения
Как и для цепи, рассмотренной в примере 5.1, приращение напряжения 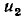 оказывается значительно меньшим, чем вызвавшее его изменение входного напряжения
оказывается значительно меньшим, чем вызвавшее его изменение входного напряжения 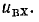
Цепи, рассмотренные в примерах 5.1 и 5.2, можно использовать для стабилизации напряжения. Отношение относительного приращения напряжения на входе таких цепей к относительному приращению выходного напряжения называется коэффициентом стабилизации
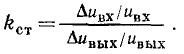
Очевидно, что для цепи, схема которой приведена на рис. 5.7, а, 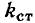 >1, если ВАХ нелинейного элемента вогнутая
>1, если ВАХ нелинейного элемента вогнутая 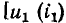 на рис. 5.7, б], а для цепи, схема которой приведена на рис. 5.9, а,— только когда ВАХ нелинейного элемента выпуклая
на рис. 5.7, б], а для цепи, схема которой приведена на рис. 5.9, а,— только когда ВАХ нелинейного элемента выпуклая 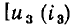 на рис. 5.9, б]. Следует подчеркнуть, что эффект стабилизации напряжения в принципе не может иметь места в цепях, составленных из элементов с линейными ВАХ.
на рис. 5.9, б]. Следует подчеркнуть, что эффект стабилизации напряжения в принципе не может иметь места в цепях, составленных из элементов с линейными ВАХ.
Преобразования активных нелинейных резистивных двухполюсников
Рассмотрим участок цепи с последовательно соединенными нелинейным сопротивлением R и источником постоянного напряжения Е_ (рис. 5.10, а). Вольт-амперная характеристика 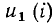 нелинейного сопротивления и внешняя характеристика Е_ (i) идеализированного источника напряжения приведены на рис. 5.10, б, в. Очевидно, что напряжение на входе такого участка цепи при любом токе равно сумме падения напряжения на сопротивлении и напряжения на зажимах идеализированного источника:
нелинейного сопротивления и внешняя характеристика Е_ (i) идеализированного источника напряжения приведены на рис. 5.10, б, в. Очевидно, что напряжение на входе такого участка цепи при любом токе равно сумме падения напряжения на сопротивлении и напряжения на зажимах идеализированного источника:

Из выражения (5.3) следует, что ВАХ рассматриваемого участка цепи может быть получена путем суммирования ординат кривых 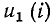 и Е_ (i), т. е. путем смещения ВАХ
и Е_ (i), т. е. путем смещения ВАХ 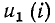 сопротивления на Е_ вверх по ординате при Е_ > 0 (рис. 5.10, б) или вниз — при E_ < 0
сопротивления на Е_ вверх по ординате при Е_ > 0 (рис. 5.10, б) или вниз — при E_ < 0
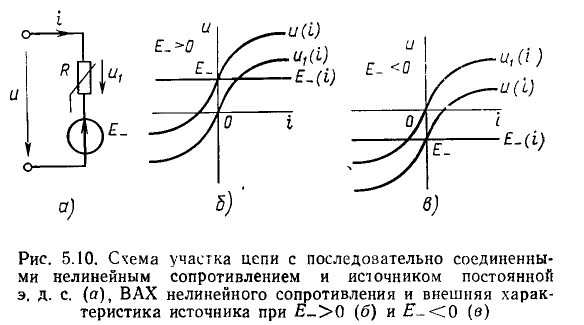
(рис. 5.10, в). Из рис. 5.10, б, в видно, что ВАХ u (i) не проходит через начало координат и частично располагается во втором или четвертом квадрантах координатной плоскости u—i.
Аналогично ВАХ активного двухполюсника, представляющего собой параллельное соединение нелинейного сопротивления R и источника постоянного тока J_ (рис. 5.11, а), получается путем смещения ВАХ  сопротивления вдоль оси токов на
сопротивления вдоль оси токов на  (рис. 5.11, б, в). Как и в предыдущем случае, ВАХ нелинейного двухполюсника, содержащего источник тока, не проходит через начало координат.
(рис. 5.11, б, в). Как и в предыдущем случае, ВАХ нелинейного двухполюсника, содержащего источник тока, не проходит через начало координат.
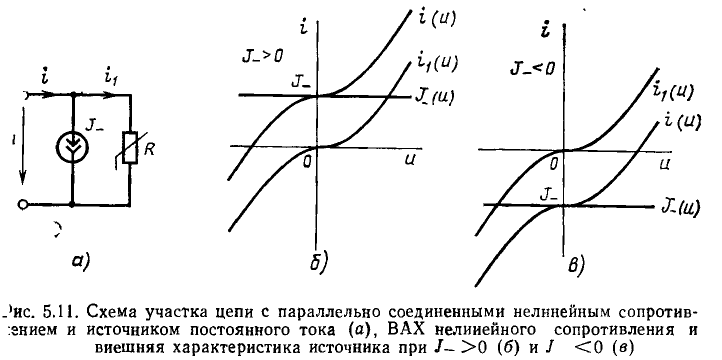
Графические построения можно использовать и при решении обратной задачи: заменить нелинейный двухполюсник, ВАХ которого не проходит через начало координат, нелинейным сопротивлением и идеализированным источником постоянного тока или напряжения.
Пример 5.3.
Найдем последовательную и параллельную схемы замещения источника энергии (рис. 5.12, а), внешняя характеристика u(i) которого приведена на рис. 5.12, б (штриховая линия).
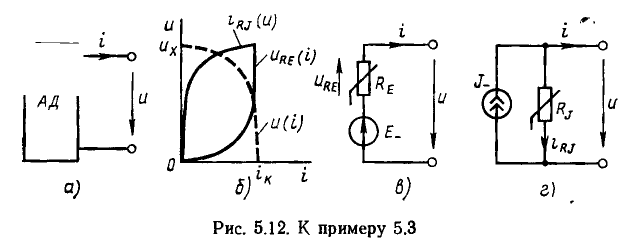
Последовательная схема замещения рассматриваемого двухполюсника (рис. 5.12, в) содержит независимый источник постоянного напряжения и нелинейное сопротивление 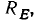 ВАХ которого
ВАХ которого 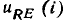 (рис. 5.12, б) собирается из условия
(рис. 5.12, б) собирается из условия
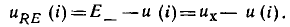
Параллельная схема замещения источника энергии содержит независимый источник постоянного тока 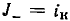 (рис. 5.12, г) и нелинейное сопротивление
(рис. 5.12, г) и нелинейное сопротивление 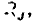 ВАХ которого (рис. 5.12, б) определяется из соотношения
ВАХ которого (рис. 5.12, б) определяется из соотношения
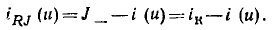
Следует обратить внимание на то, что направление тока на зажимах активного двухполюсника (рис. 5.12, а) выбрано противоположным направлению тока, принятого для пассивных двухполюсников, поэтому ВАХ данного двухполюсника переместилась из второго в первый квадрант координатной плоскости u — i.
Определение рабочих точек нелинейных резистивных элементов
Задача анализа нелинейной цепи постоянного тока обычно сводится к определению рабочих точек нелинейных резистивных элементов, т. е. к определению токов и напряжений на зажимах этих элементов, соответствующих заданным значениям э. д. с. независимых источников постоянного напряжения и токов независимых источников постоянного тока. Эту задачу во многих случаях удобнее решать графически.
Рассмотрим простейшую цепь, состоящую из идеального источника постоянного напряжения E_ и нелинейных сопротивлений 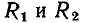 (рис. 5.13, а), вольт-амперные характеристики которых приведены на рис. 5.13, б [кривые
(рис. 5.13, а), вольт-амперные характеристики которых приведены на рис. 5.13, б [кривые 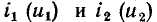 соответственно]. Для нахождения рабочих точек сопротивлений
соответственно]. Для нахождения рабочих точек сопротивлений 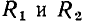 воспользуемся методикой преобразования участка цепи с последовательным соединением нелинейных элементов. Суммируя абсциссы кривых
воспользуемся методикой преобразования участка цепи с последовательным соединением нелинейных элементов. Суммируя абсциссы кривых 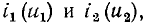 получаем
получаем
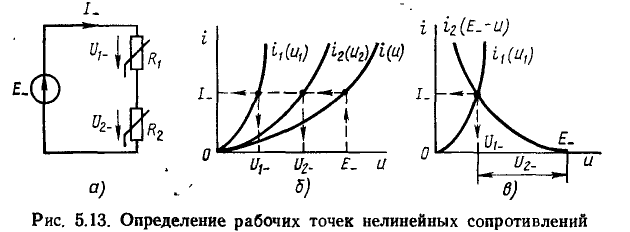
ВАХ участка цепи, представляющего собой последовательное соединение сопротивлений 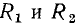 [кривая i (u)]. Используя эту зависимость, находим постоянный ток I_, протекающий через данный участок цепи, а следовательно, и через каждое из сопротивлений, если напряжение на зажимах этого участка цепи равно напряжению независимого источника E_. Далее, используя ВАХ
[кривая i (u)]. Используя эту зависимость, находим постоянный ток I_, протекающий через данный участок цепи, а следовательно, и через каждое из сопротивлений, если напряжение на зажимах этого участка цепи равно напряжению независимого источника E_. Далее, используя ВАХ 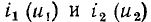 каждого из сопротивлений, определяем падения напряжения на этих сопротивлениях
каждого из сопротивлений, определяем падения напряжения на этих сопротивлениях 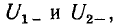 вызванное током I_. Аналогично можно найти рабочие точки произвольного числа последовательно включенных нелинейных и линейных сопротивлений, соответствующие различным значениям э. д. с. независимого источника постоянного напряжения.
вызванное током I_. Аналогично можно найти рабочие точки произвольного числа последовательно включенных нелинейных и линейных сопротивлений, соответствующие различным значениям э. д. с. независимого источника постоянного напряжения.
В простейшем случае, когда рассматриваемая цепь содержит только два последовательно включенных сопротивления, а э.д.с. независимого источника имеет одно фиксированное значение Е_, для определения рабочих точек сопротивлений можно воспользоваться более простым
приемом, позволяющим обойтись без построения суммарной ВАХ сопротивлений. С этой целью на оси напряжений (рис. 5.13, в) откладывают отрезок, соответствующий заданному значению э.д. с. источника напряжения, и из конца этого отрезка строят зеркальное отображение ВАХ одного из элементов, например сопротивления 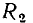 [кривая на рис. 5.13, в]. В точке пересечения
[кривая на рис. 5.13, в]. В точке пересечения 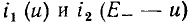
выполняются условия электрического равновесия цепи 
 следовательно, точка пересечения
следовательно, точка пересечения 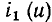 и
и 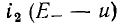 и есть искомая рабочая точка нелинейных сопротивлений
и есть искомая рабочая точка нелинейных сопротивлений 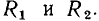 Сопротивление
Сопротивление  ВАХ которого представляется в виде
ВАХ которого представляется в виде 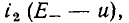 обычно рассматривается как сопротивление нагрузки нелинейного элемента
обычно рассматривается как сопротивление нагрузки нелинейного элемента 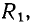 а кривая
а кривая 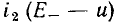 называется нагрузочной кривой.
называется нагрузочной кривой.
Если одно из сопротивлений, например 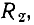 является линейным (рис. 5.14, а), то задача определения рабочей точки нелинейной цепи с последовательным юединением двух сопротивлений упрощается. В этом случае для определения рабочей точки нелинейного сопротивления
является линейным (рис. 5.14, а), то задача определения рабочей точки нелинейной цепи с последовательным юединением двух сопротивлений упрощается. В этом случае для определения рабочей точки нелинейного сопротивления 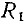 необходимо найти точку пересечения ВАХ
необходимо найти точку пересечения ВАХ 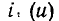 этого сопротивления с нагрузочной прямой
этого сопротивления с нагрузочной прямой 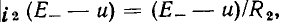 проведенной через точку u = Е_ на оси напряжений и точку
проведенной через точку u = Е_ на оси напряжений и точку 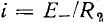 на оси токов (рис. 5.14, б). Аналогичным образом находят рабочие точки управляемых нелинейных резистивных элементов.
на оси токов (рис. 5.14, б). Аналогичным образом находят рабочие точки управляемых нелинейных резистивных элементов.
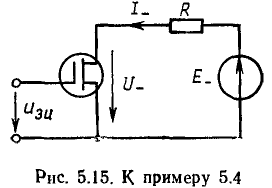
Пример 5.4.
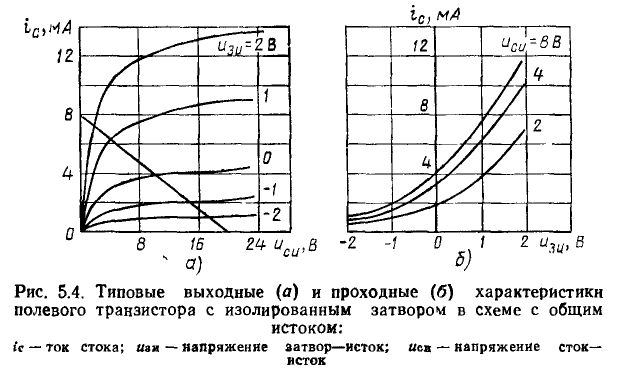
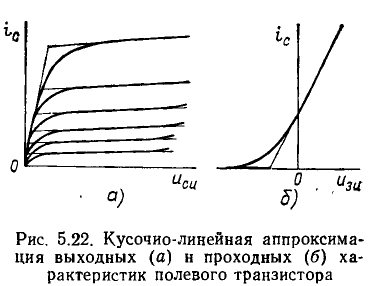
Определим ток стока I_ и напряжение сток—исток U_ полевого транзистора с изолированным затвором, входящего в состав электричеcкой цепи, схема которой приведена на рис. 5.15 (R = 2,5 кОм, Е_ = 20 В, 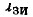 = 1 В). Выходные ВАХ транзистора приведены на рис. 5.4, а.
= 1 В). Выходные ВАХ транзистора приведены на рис. 5.4, а.
Рабочая точка транзистора определяется пересечением ВАХ транзистора, соответствующей заданному значению напряжения затвор—исток 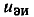 = 1 В, и нагрузочной прямой, проведенной через точки Е_=20 В на оси напряжения
= 1 В, и нагрузочной прямой, проведенной через точки Е_=20 В на оси напряжения 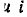 = E_/R = 8 мА на оси токов (см. рис. 5.4, а). Искомые значения тока стока и напряжения сток—исток I_ = 6,4 мА, U_ = 4 В.
= E_/R = 8 мА на оси токов (см. рис. 5.4, а). Искомые значения тока стока и напряжения сток—исток I_ = 6,4 мА, U_ = 4 В.
Используя графический метод, можно убедиться, что когда ВАХ нелинейного резистивного элемента монотонна, при каждом значении напряжения источника питания ВАХ элемента пересекается с нагру. зочной прямой только в одной точке, т. е. имеется единственная рабочая точка (единственное состояние равновесия).
Немонотонная ВАХ может пересекаться с нагрузочной прямой в нескольких точках (рис. 5.16), и, следовательно, нелинейный резистивный элемент с немонотонной ВАХ может иметь несколько рабочих точек (несколько состояний равновесия) (Более подробно вопросы, связанные с определением рабочих точек элементов с немонотонной ВАХ, в том числе с исследованием устойчивости состояний равновесия цепей с такими элементами, будут рассмотрены в курсе «Радиотехнические цепи и сигналы»).
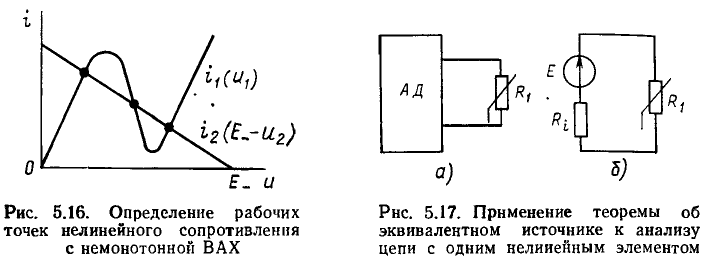
Если в состав сложной цепи, содержащей произвольное количество источников энергии и линейных сопротивлений, входит только один нелинейный элемент, то для определения рабочей точки этого элемента удобно воспользоваться теоремой об эквивалентном источнике. С этой целью нелинейный элемент выделяют из рассматриваемой цепи, а оставшуюся часть цепи представляют в виде линейного автономного двухполюсника АД (рис. 5.17, а). Заменяя этот двухполюсник последовательной схемой замещения (рис. 5.17, б), сводят задачу анализа сложной цепи к рассмотренной ранее задаче определения рабочей точки нелинейного элемента с линейной нагрузкой (см. рис. 5.14, а).
Определение реакции безынерционного нелинейного резистивного элемента на произвольное внешнее воздействие
Графические методы позволяют определить реакцию произвольного безынерционного нелинейного элемента на заданное внешнее воздействие. Пусть у (х) — ВАХ некоторого нелинейного сопротивления (рис. 5.18, а), причем х—величина, принятая в качестве внешнего воздействия, а у— величина, рассматриваемая как реакция нелинейного сопротивления на это воздействие. Построим на этом же рисунке зависимости внешнего воздействия х = х (t) и реакции у = у (t) от времени. График х (t) расположим в нижней части рисунка так, чтобы
ось x(t) была параллельна оси х ВАХ, а ось времени — направлена вниз. Зависимость у = у (t) построим в правой части рисунка так, чтобы ось времени была направлена вправо, а ось у (t) расположена параллельно оси у ВАХ.
Для определения реакции цепи на заданное внешнее воздействие необходимо для каждого момента времени 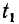 выполнить следующие графические построения: по графику функции х (t) найти мгновенное значение внешнего воздействия
выполнить следующие графические построения: по графику функции х (t) найти мгновенное значение внешнего воздействия  затем по ВАХ определить соответствующее этому внешнему воздействию мгновенное значение реакции
затем по ВАХ определить соответствующее этому внешнему воздействию мгновенное значение реакции  и построить точку с ординатой
и построить точку с ординатой 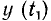 на графике у = у (t). Очевидно, что при увеличении количества точек на временной оси, для которых выполняются такие построения, точность определения реакции элемента на заданное внешнее воздействие возрастает.
на графике у = у (t). Очевидно, что при увеличении количества точек на временной оси, для которых выполняются такие построения, точность определения реакции элемента на заданное внешнее воздействие возрастает.
Недостатком рассмотренного приема является то, что графики х (t) и у (t) построены в разных местах чертежа, а это неудобно при определении взаимно соответствующих точек на временных осях и затрудняет сравнение формы кривых х (t) и у (t).
Этот недостаток может быть устранен, если график х (t) построить непосредственно под графиком у (t) (рис. 5.18). В этом случае линии, проектирующие точки графика х = х (t) на ВАХ у (х), перегнутся под углом 90", причем точки перегиба расположатся на некоторой вспомогательной прямой, проведенной под углом 45° к координатным осям через точку пересечения оси у ВАХ и оси времени зависимости х = х (t).

Как видно из рисунка, реакция нелинейной цепи на гармоническое воздействие в общем случае не является гармонической функцией времени.
Графические построения, приведенные на рис. 5.18, б, можно использовать и для решения обратной задачи — определения вида ВАХ безынерционного нелинейного резистивного элемента по известной реакции этого элемента на заданное внешнее воздействие.
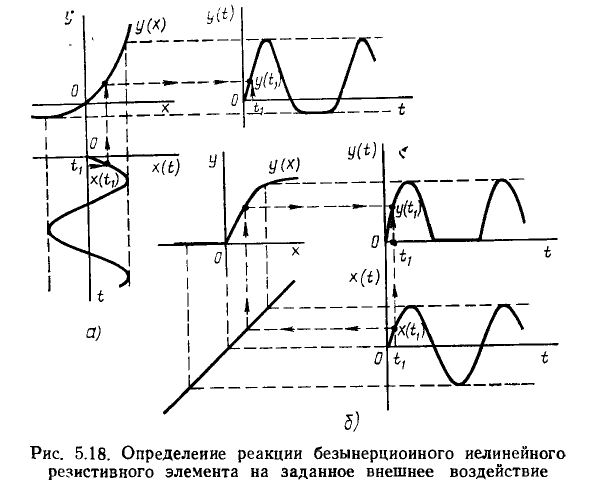
Например, на рис. 5.19 показано, как, используя описанные графические построения, определить вид ВАХ нелинейных резистивных элементов, обеспечивающих двустороннее ограничение гармонических колебаний (рис. 5.19, а), однополупериодное (рис. 5.19, б) и двухполупериодное (рис. 5.19, в) выпрямление переменного тока.
Аппроксимация характеристик нелинейных резистивных элементов
Задача аппроксимации:
Вольт-амперные характеристики реальных элементов электрических цепей обычно имеют сложный вид, их представляют в виде графиков или таблиц экспериментальных данных. В ряде случаев непосредственное применение ВАХ, задаваемых в такой форме, оказывается неудобным и их стремятся представить в виде достаточно простых аналитических соотношений, хотя бы качественно отражающих характер рассматриваемых зависимостей. Замена сложных функций приближенными аналитическими выражениями называется аппроксимацией (от лат. approximare — приближаться).
Аналитические выражения, аппроксимирующие ВАХ нелинейных резистивных элементов, с одной стороны (для повышения точности и достоверности анализа) должны как можно более точно описывать ход реальных характеристик, а с другой — повышение точности аппроксимации приводит, как правило, к усложнению аппроксимирующих выражений, что затрудняет как определение значений входящих в эти выражения коэффициентов, так и применение этих выражений для анализа цепи. В связи с тем что характеристики однотипных нелинейных резистивных элементов от экземпляра к экземпляру отличаются За счет производственного разброса параметров и погрешности измерений, нецелесообразно стремиться получить аппроксимирующие выражения, точность которых превышает точность определения характеристик отдельных элементов. Таким образом, при решении задачи аппроксимации так же, как и при решении любой задачи, связанной с выбором расчетной модели, необходимо идти на компромисс между точностью и сложностью модели.
Успешное решение задачи аппроксимации в значительной степени зависит от ширины аппроксимируемой области ВАХ, т. е. от диапазона, в котором могут изменяться токи и напряжения исследуемого элемента. Как правило, чем уже область аппроксимации, тем более простой функцией может быть описана соответствующая ВАХ.
Задача аппроксимации ВАХ включает в себя две самостоятельные задачи: выбор аппроксимирующей функции и определение значений, входящих в эту функцию постоянных коэффициентов.
Выбор аппроксимирующей функции
Функцию, аппроксимирующую ВАХ какого-либо нелинейного резистивного элемента, выбирают либо исходя из физических представлений о работе данного элемента, либо чисто формально, основываясь на внешнем сходстве ВАХ с графическим изображением той или иной функции. Для аппроксимации ВАХ используют как элементарные, так и различные трансцендентные функции, а также степенные, экспоненциальные и тригонометрические полиномы и кусочно-линейные функции.
Так как внешнее сходство ВАХ с графическим изображением функции, выбранной в качестве аппроксимирующей, может оказаться обманчивым, перед тем, как перейти к определению значений коэффициентов соответствующей функции, желательно проверить возможность ее применения, используя метод выравнивания. Сущность этого метода заключается в том, что для проверки гипотезы о виде функциональной зависимости у = у (х), заданной множеством значений 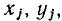 переменные х и у заменяют некоторыми новыми переменными
переменные х и у заменяют некоторыми новыми переменными 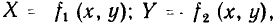 которые выбирают таким образом, чтобы при сделанных допущениях о виде функции у = у (х) переменные У и X были связаны между собой линейной зависимостью
которые выбирают таким образом, чтобы при сделанных допущениях о виде функции у = у (х) переменные У и X были связаны между собой линейной зависимостью

Таким образом, если проверяемая гипотеза о виде функции у = у (х) справедлива, то точки 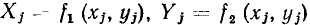 должны располагаться на одной прямой.
должны располагаться на одной прямой.
Если предполагается, что заданная зависимость описывается степенной функцией

то, логарифмируя левую и правую части выражения (5.5) lg у = lg а + b lg х, нетрудно прийти к выводу о том, что зависимость между вспомогательными переменными Y=lg у и X=lg х должна иметь линейный характер:

Если зависимость между величинами у и х аппроксимируется показательной функцией

то линейной зависимостью

будут связаны между собой переменные 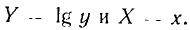 Для степенного полинома второй степени
Для степенного полинома второй степени

линейный вид должна иметь зависимость 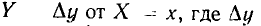 =
=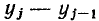 — разность значений функции у (х), соответствующих двум соседним значениям аргумента
— разность значений функции у (х), соответствующих двум соседним значениям аргумента 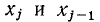 (предполагается, что значения аргумента образуют арифметическую прогрессию с шагом h). Если заданная зависимость у = у (х) аппроксимируется экспоненциальным полиномом вида
(предполагается, что значения аргумента образуют арифметическую прогрессию с шагом h). Если заданная зависимость у = у (х) аппроксимируется экспоненциальным полиномом вида

то линейной зависимостью

должны быть связаны вспомогательные функции Y = lg (у — с) и X = х. Для определения с выбирают три значения аргумента 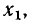
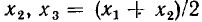 и соответствующие им три значения функции
и соответствующие им три значения функции 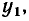
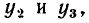 которые затем подставляют в выражение
которые затем подставляют в выражение
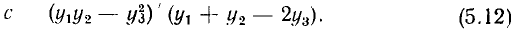
Если при проверке гипотезы о виде аппроксимирующей функции методом выравнивания окажется, что зависимость между вспомогательными переменными X и Y имеет линейный характер только в определенном диапазоне изменения X, то, следовательно, данная гипотеза справедлива только в соответствующем диапазоне изменения аргумента исследуемой функции 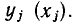
Пример 5.5.
На рис. 5.20, а изображена прямая ветвь ВАХ кремниевого диода. Проверим, можно ли аппроксимировать эту характеристику полиномом второй степени (5.9).
Выбираем шаг изменения аргумента h = 0,2 В и рассчитываем значения вспомогательной переменной У =-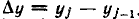 — соответствующие выбранным значениям аргумента (рис. 5.20, б). Как видно из рисунка, зависимость У
— соответствующие выбранным значениям аргумента (рис. 5.20, б). Как видно из рисунка, зависимость У
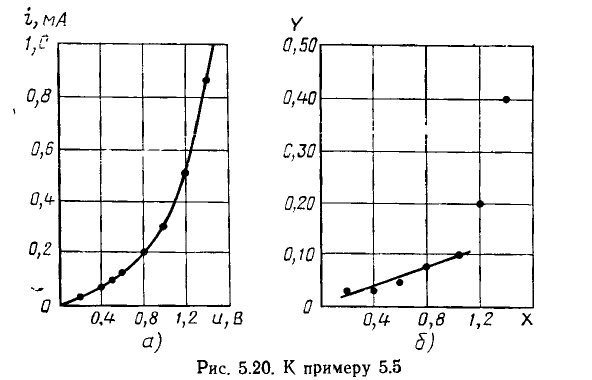
от X практически совпадает с линейной при изменении X - х в пределах от 0 до 1 В, следовательно, в этой области рассматриваемая ВАX может быть аппроксимирована полиномом второй степени.
Пример 5.6.
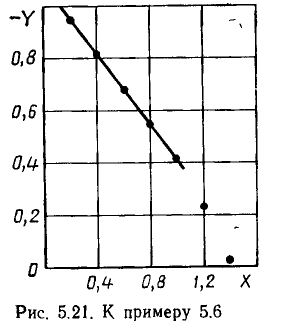
Проверим, можно ли ВАХ диода аппроксимировать (см рис. 5 20, а) с помощью экспоненциального полинома вида (5.10).
Для определения константы с выберем три значения аргумента 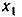 =0,
=0, 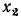 = 1,
= 1, 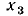 = 0,5 и найдем соответствующие им значения функции
= 0,5 и найдем соответствующие им значения функции 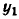 =0,
=0, 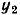 =0.3 и
=0.3 и 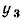 = 0,095. Подставляя эти значения в выражение (5.12), получаем с = —0,082. Далее строим зависимость вспомогательной функции Y = lg (у — — с) от X=х (рис. 5.21). Как видно из рисунка, в пределах от X = 0 до X = 1 зависимость Y (X) практически совпадает с линейной, следовательно, в этой области рассматриваемая ВАХ может быть аппроксимирована экспоненциальным полиномом рассматриваемого типа.
= 0,095. Подставляя эти значения в выражение (5.12), получаем с = —0,082. Далее строим зависимость вспомогательной функции Y = lg (у — — с) от X=х (рис. 5.21). Как видно из рисунка, в пределах от X = 0 до X = 1 зависимость Y (X) практически совпадает с линейной, следовательно, в этой области рассматриваемая ВАХ может быть аппроксимирована экспоненциальным полиномом рассматриваемого типа.
Из приведенных примеров следует, что задача выбора аппроксимирующей функции не имеет единственного решения. Выбор той или иной функции во многом зависит от опыта и интуиции исследователя и в значительной степени определяется простотой нахождения значений коэффициентов функции и удобством ее применения для анализа.
Определение коэффициентов аппроксимирующей функции
Рассмотрим кратко основные методы определения коэффициентов аппроксимирующей функции. Наиболее часто для этой цели используют метод выбранных точек, в соответствии с которым значения коэффициентов аппроксимирующей функции определяют исходя из совпадения значений этой функции со значениями аппроксимируй мой функции в ряде заранее выбранных точек, называемых узлами интерполяции (от лат. interpolate — подновлять). Если для аппроксимации ВАХ, задаваемой множеством точек 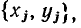 выбрана функция
выбрана функция
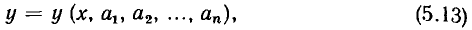
имеющая п неизвестных постоянных коэффициентов 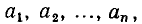 то для определения этих коэффициентов выбирают n наиболее характерных точек ВАХ, лежащих в пределах рабочей области. Подставляя значения
то для определения этих коэффициентов выбирают n наиболее характерных точек ВАХ, лежащих в пределах рабочей области. Подставляя значения 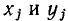 в каждой из выбранных точек в выражение (5.13), получают систему из п уравнений
в каждой из выбранных точек в выражение (5.13), получают систему из п уравнений 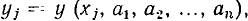 решая которую, находят значения всех неизвестных коэффициентов. Очевидно, что такой выбор коэффициентов действительно обеспечивает совпадение значений аппроксимируемой и аппроксимирующей функций в узлах интерполяции, однако в промежутках между ними погрешность аппроксимации может быть весьма существенной (информация о ходе аппроксимирующей функции в них не учитывается), что является недостатком этого метода.
решая которую, находят значения всех неизвестных коэффициентов. Очевидно, что такой выбор коэффициентов действительно обеспечивает совпадение значений аппроксимируемой и аппроксимирующей функций в узлах интерполяции, однако в промежутках между ними погрешность аппроксимации может быть весьма существенной (информация о ходе аппроксимирующей функции в них не учитывается), что является недостатком этого метода.
В отличие от метода выбранных точек метод наименьших квадратов обеспечивает наименьшую сумму квадратов отклонений  значений аппроксимирующей функции
значений аппроксимирующей функции 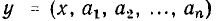 от значений исходной функции
от значений исходной функции 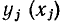 в произвольном числе точек m, не связанном с числом неизвестных коэффициентов n:
в произвольном числе точек m, не связанном с числом неизвестных коэффициентов n:
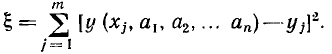
Приравнивая нулю первые производные 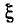 по каждому из коэффициентов, получаем систему из n уравнений для определения n неизвестных числовых значений коэффициентов:
по каждому из коэффициентов, получаем систему из n уравнений для определения n неизвестных числовых значений коэффициентов:
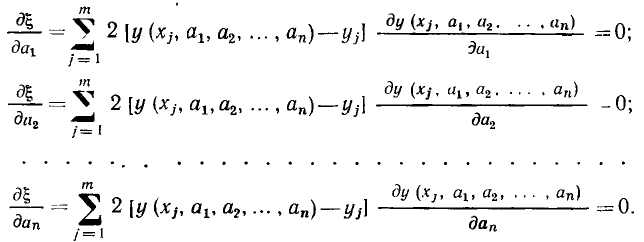
Метод наименьших квадратов требует весьма громоздких вычислений и применяется обычно только в тех случаях, когда необходима высокая точность аппроксимации.
Если гипотеза о характере аппроксимирующей функции проверялась методом выравнивания, то неизвестные значения коэффициентов аппроксимирующей функции могут быть определены по известным значениям коэффициентов 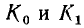 линейного уравнения (5,4), связывающего между собой значения вспомогательных переменных X и Y. Составляя уравнение прямой линии, вдоль которой располагаются точки
линейного уравнения (5,4), связывающего между собой значения вспомогательных переменных X и Y. Составляя уравнение прямой линии, вдоль которой располагаются точки 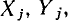 и сравнивая его с уравнением, описывающим зависимость между вспомогательными переменными, которое соответствует проверяемой гипотезе о виде функции у (х) [например, с уравнениями (5.6), (5.8) или (5.11)], находим значения искомых коэффициентов.
и сравнивая его с уравнением, описывающим зависимость между вспомогательными переменными, которое соответствует проверяемой гипотезе о виде функции у (х) [например, с уравнениями (5.6), (5.8) или (5.11)], находим значения искомых коэффициентов.
Пример 5.7.
Определим значения коэффициентов экспоненциального полинома 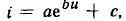 аппроксимирующего ВАХ. кремниевого диода (см. рис. 5.20, а) в диапазоне напряжений от 0 до 1 В.
аппроксимирующего ВАХ. кремниевого диода (см. рис. 5.20, а) в диапазоне напряжений от 0 до 1 В.
Возможность аппроксимации ВАХ, приведенной на рис. 5.20, экспоненциальным полиномом указанного типа была показана в примере 5.6. Там же было найдено числовое значение коэффициента с. Составим уравнение прямой (рис. 5.21), на которой в рассматриваемом диапазоне изменения аргумента располагаются точки 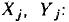
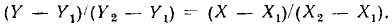
Здесь 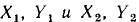 —координаты двух любых точек, через которые проходит данная прямая. Выбирая
—координаты двух любых точек, через которые проходит данная прямая. Выбирая 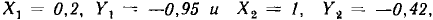 получаем уравнение прямой в следующей форме:
получаем уравнение прямой в следующей форме:
У = 0,66Х — 1,08.
Сравнивая это выражение с выражением (5.11), получаем соотношения для определения неизвестных значений коэффициентов а и b:
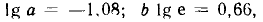
откуда а = 0,082, b = 1,52.
Таким образом, в диапазоне от 0 до 1 В рассматриваемая ВАХ может быть аппроксимирована выражением, мА,
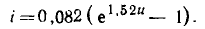
На практике для аппроксимации характеристик нелинейных элементов в основном используют степенные полиномы
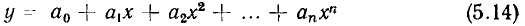
и кусочно-линейные функции. Аппроксимация с помощью степенного полинома универсальна и позволяет повышать точность расчета путем увеличения степени полинома.
Любые аппроксимирующие функции могут быть разложены в степенные ряды и приведены к виду (5.14). Поскольку сложность определения значений коэффициентов аппроксимирующей функции возрастает с увеличением числа членов полинома. для аппроксимации ВАХ обычно используют полиномы низких степеней. Часто для аппроксимации ВАХ применяют неполные (укороченные) полиномы, т. е. полиномы, не содержащие членов некоторых степеней. Так, если ВАХ нелинейного элемента проходит через начало координат, то в полиноме (5.14) отсутствует член нулевой степени  = 0). Симметричные ВАХ описываются нечетными полиномами, т. е. полиномами, содержащими члены только нечетных степеней.
= 0). Симметричные ВАХ описываются нечетными полиномами, т. е. полиномами, содержащими члены только нечетных степеней.
Аппроксимация с помощью кусочно-линейных функций заключается в разбиении рабочей области аппроксимируемой функции на несколько участков (интервалов) и замене функции на каждом из них отрезком прямой. С увеличением количества интервалов точность аппроксимации возрастает, однако для упрощения анализа цепи желательно использовать кусочно-линейные функции с минимальным числом интервалов. Примеры кусочно-линейной аппроксимации ВАХ представлены на рис. 5.22.
Аппроксимация вольт-амперных характеристик в окрестности рабочей точки
На практике часто приходится иметь дело с рабочей областью ВАХ настолько узкой, что можно считать, что изменение токов и напряжений происходит только в окрестности некоторой рабочей точки. В таких случаях нет необходимости аппроксимировать ВАХ в широком диапазоне токов и напряжений, а достаточно ограничиться аппроксимацией лишь в окрестности выбранной рабочей точки.
Пусть ток и напряжение некоторого нелинейного резистивного элемента в рабочей точке равны 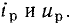 Значение тока i этого элемента, соответствующее некоторому новому значению напряжения
Значение тока i этого элемента, соответствующее некоторому новому значению напряжения 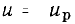
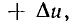 можно представить в виде ряда Тейлора
можно представить в виде ряда Тейлора
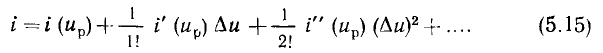
Здесь 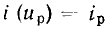 — значение тока в рабочей точке,
— значение тока в рабочей точке, 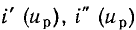 — значения производных тока по напряжению в рабочей точке, определяемые либо по заданной функции i = i (u), аппроксимирующей ВАХ в широком диапазоне токов и напряжений, либо по табличным значениям, функции
— значения производных тока по напряжению в рабочей точке, определяемые либо по заданной функции i = i (u), аппроксимирующей ВАХ в широком диапазоне токов и напряжений, либо по табличным значениям, функции 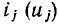 с помощью формул численного дифференцирования:
с помощью формул численного дифференцирования:
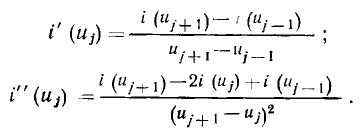
Вводя обозначения 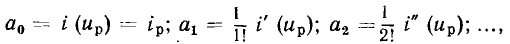 выражение (5.15) можно представить в виде полинома относительно приращений напряжения
выражение (5.15) можно представить в виде полинома относительно приращений напряжения
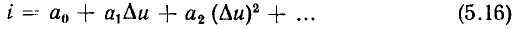
Как правило, при аппроксимации ВАХ нелинейных резистивных элементов в окрестности рабочей точки используются полиномы низких степеней, причем в большинстве случаев, когда приращения напряжения 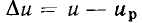 и тока
и тока 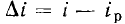 весьма малы, можно ограничиться полиномом первой степени
весьма малы, можно ограничиться полиномом первой степени

Таким образом, вольт-амперные характеристики нелинейных резистивных элементов могут быть линеаризованы в окрестности выбранной рабочей точки.
Нелинейные резистивные элементы при гармоническом внешнем воздействии
Нелинейное сопротивление при гармоническом воздействии:
Ранее, при рассмотрении графических методов анализа нелинейных цепей, было показано, что реакция нелинейного резистивного элемента на гармоническое внешнее воздействие в общем случае не является гармонической функцией времени. Так как графические методы анализа позволяют установить только качественное соответствие между видом ВАХ нелинейного резистивного элемента и реакций этого элемента на заданное гармоническое воздействие, то для получения количественных соотношений необходимо воспользоваться аналитическими методами.
Пусть ВАХ некоторого нелинейного сопротивления может быть аппроксимирована полиномом n-й степени
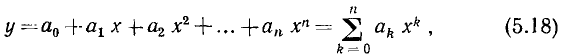
а внешнее воздействие х = x(t) является гармонической функцией времени

Подставляя (5.19) в (5.18) и выражая слагаемые вида 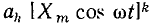 через гармонические функции кратных частот
через гармонические функции кратных частот
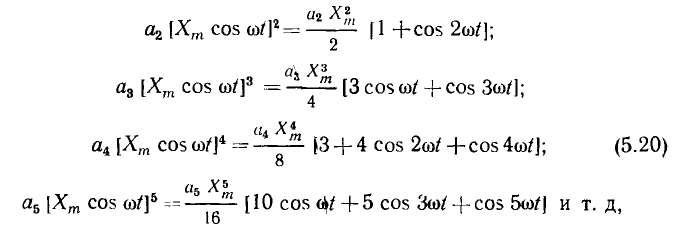
получаем
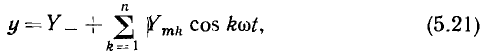
где
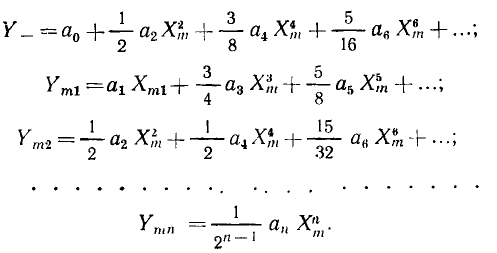
Как видно из выражения (5.21), реакция нелинейного сопротивления на гармоническое внешнее воздействие определенной частоты и представляет собой сумму постоянной составляющей Y_ и гармонических составляющих (гармоник) с частотами, кратными частоте внешнего воздействия. Гармоническая составляющая, частота которой равна частоте внешнего воздействия (k = 1), называется первой гармоникой, гармоническая составляющая, частота которой в два раза превышает частоту внешнего воздействия (k = 2), — второй гармоникой ит.д. Номер высшей гармонической составляющей (k = n) равен степени полинома n, аппроксимирующего ВАХ рассматриваемого нелинейного сопротивления. Амплитуда k-й гармоники 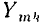 зависит только от членов полинома k-й и более высоких степеней, причем амплитуды четных гармоник и постоянная составляющая определяются только членами полинома четных степеней, а амплитуды нечетных гармоник — членами полинома нечетных степеней. Следовательно, если ВАХ нелинейного сопротивления аппроксимируется четным полиномом, то реакция нелинейного сопротивления не будет содержать нечетных гармоник, а если ВАХ аппроксимируется нечетным полиномом, то реакция нелинейного сопротивления на гармоническое воздействие не будет содержать постоянной составляющей и четных гармоник. Выражение (5.21) описывает важнейшее свойство нелинейных цепей, заключающееся в том, что их реакция на гармоническое воздействие содержит колебания различных частот (в том числе и нулевой), т. е. нелинейная цепь выступает в роли генератора колебаний, частота которых отличается от частоты внешнего воздействия.
зависит только от членов полинома k-й и более высоких степеней, причем амплитуды четных гармоник и постоянная составляющая определяются только членами полинома четных степеней, а амплитуды нечетных гармоник — членами полинома нечетных степеней. Следовательно, если ВАХ нелинейного сопротивления аппроксимируется четным полиномом, то реакция нелинейного сопротивления не будет содержать нечетных гармоник, а если ВАХ аппроксимируется нечетным полиномом, то реакция нелинейного сопротивления на гармоническое воздействие не будет содержать постоянной составляющей и четных гармоник. Выражение (5.21) описывает важнейшее свойство нелинейных цепей, заключающееся в том, что их реакция на гармоническое воздействие содержит колебания различных частот (в том числе и нулевой), т. е. нелинейная цепь выступает в роли генератора колебаний, частота которых отличается от частоты внешнего воздействия.
Понятие о режимах малого и большого сигнала
Как следует из изложенного ранее, реакция безынерционного нелинейного резистивного элемента на гармоническое внешнее воздействие полностью определяется видом полинома, аппроксимирующего ВАХ рассматриваемого элемента. В свою очередь, степень аппроксимирующего полинома и значения его коэффициентов зависят от формы ВАХ элемента, а также от ширины и местоположения рабочей области ВАХ. На практике для выбора местоположения рабочей области ВАХ нелинейного резистивного элемента, находящегося под гармоническим внешним воздействием, к зажимам этого элемента наряду с источником гармонического воздействия прикладывают некоторое постоянное напряжение или постоянный ток, так называемые напряжение или ток смещения.
Пусть напряжение u на зажимах некоторого нелинейного сопротивления R (u) содержит постоянную составляющую U_ (напряжение смещения) и переменную составляющую, изменяющуюся во времени по гармоническому закону

Для определения тока сопротивления i воспользуемся выражением (5.16), аппроксимирующим ВАХ сопротивления в окрестности рабочей точки 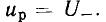 Подставляя (5.22) в (5.16) и используя формулы (5.20), (5.21), получаем
Подставляя (5.22) в (5.16) и используя формулы (5.20), (5.21), получаем
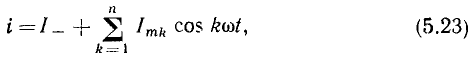
где I_ — постоянная составляющая тока сопротивления; 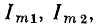
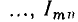 — амплитуды 1, 2, ..., n-й гармоник, определяемые выражениями:
— амплитуды 1, 2, ..., n-й гармоник, определяемые выражениями:
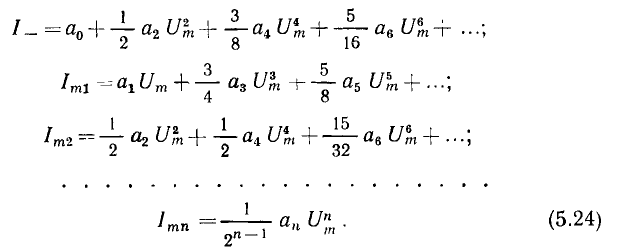
Рассмотрим случай, когда амплитуда переменной составляющей напряжения 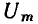 = 0. Тогда через сопротивление течет постоянный ток
= 0. Тогда через сопротивление течет постоянный ток

называемый током покоя.
Из определения статического сопротивления (см. § 1.2) следует, что ток покоя и напряжение смещения 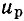 = U_ связаны между собой соотношением
= U_ связаны между собой соотношением
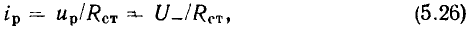
т.е. статическое сопротивление можно рассматривать как сопротивление нелинейного элемента постоянному току в выбранной рабочей точке.
Обратимся к так называемому режиму малого сигнала, при котором амплитуда переменной составляющей настолько ма
ла, что в пределах рабочей области ВАХможетбыть приближенно заменена отрезком прямой линии. Это означает, что в разложении (5 16) можно пренебречь всеми членами, содержащими 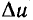 в степенях первой. Как следует из выражений (5.23), (5.24), ток нелинейного сопротивления в нерассматриваемом режиме содержит две составляющие: постоянную I_, равную току покоя, и переменную
в степенях первой. Как следует из выражений (5.23), (5.24), ток нелинейного сопротивления в нерассматриваемом режиме содержит две составляющие: постоянную I_, равную току покоя, и переменную 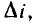 частота которой совпадает с частотой переменной составляющей приложенного напряжения:
частота которой совпадает с частотой переменной составляющей приложенного напряжения:
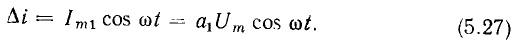
Подставляя выражение (5.22) в (5.27) и используя определение дифференциального сопротивления (см. § 1.2), находим, что переменные составляющие тока и напряжения сопротивления связаны между 2 обои соотношением
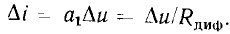
Таким образом, дифференциальное сопротивление нелинейного резистивного двухполюсного элемента можно рассматривать как сопротивление этого элемента для малых приращений, или, другими словами, как сопротивление переменному току в режиме малого сигнала.
Из выражении (5.25), (5.27) следует, что в режиме малого сигнала постоянная составляющая тока нелинейного сопротивления зависит только от постоянной составляющей приложенного напряжения а амплитуда переменной составляющей тока прямо пропорциональна амплитуде переменной составляющей напряжения.
Следовательно, в режиме малого сигнала рассматриваемое сопротивление ведет себя подобно линейному, а нелинейность его проявляется только в том, что значения  зависят от выбора рабочей точки.
зависят от выбора рабочей точки.
Анализ нелинейных резистивных цепей в режиме малого сигнала обычно выполняют в два этапа. На первом этапе анализируют нелинейную цепь по постоянному току, при этом все нелинейные резистивные элементы представляют схемами замещения по постоянному току в частности, двухполюсные нелинейные резистивные элементы представляют статическими сопротивлениями). На втором этапе выолняют анализ цепи по переменному току и все элементы цепи предгавляют схемами замещения по переменному току (двухполюсные нелинейные резистивные элементы представляются дифференциальными сопротивлениями). Окончательно реакцию цепи находят как суперпозицию решений, полученных в процессе анализа по постоянному переменному току.
В режиме большого сигнала ВАХ нелинейного резистивного элемента в пределах рабочей области не может быть заменена отрезком прямой и в полиноме (5.16), аппроксимирующем ВАХ окрестности рабочей точки, приходится учитывать члены, содержаще  в степенях выше первой. В этом случае, как видно из выражений (5.24), переменная составляющая тока включает в себя гармонические составляющие, частота которых кратна частоте переменной составляющей приложенного напряжения, постоянная составляющая тока отличается от тока покоя:
в степенях выше первой. В этом случае, как видно из выражений (5.24), переменная составляющая тока включает в себя гармонические составляющие, частота которых кратна частоте переменной составляющей приложенного напряжения, постоянная составляющая тока отличается от тока покоя:
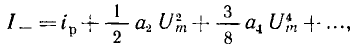
а амплитуда первой гармоники 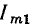 не прямо пропорциональна амплитуде переменной составляющей напряжения
не прямо пропорциональна амплитуде переменной составляющей напряжения 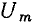 .
.
Таким образом, в режиме большого сигнала постоянная составляющая тока и амплитуды всех гармоник зависят как от напряжения смещения, так и от амплитуды переменной составляющей напряжения 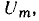 поэтому раздельное исследование цепи по постоянному и переменному току становится невозможным.
поэтому раздельное исследование цепи по постоянному и переменному току становится невозможным.
Нелинейное сопротивление при одновременном воздействии двух гармонических колебаний
Найдем реакцию нелинейного сопротивления на внешнее воздействие х (t), представляющее собой сумму двух гармонических колебаний различных частот:
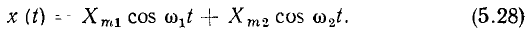
Пусть BAX нелинейного сопротивления аппроксимирована полиномом второй степени

Подставляя (5.28) в (5.29) и выполняя преобразования, получаем
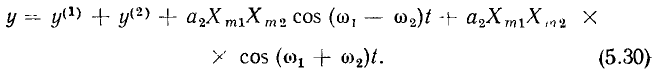
Здесь 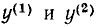 — реакции рассматриваемого нелинейного сопротивления на воздействие каждой из составляющих х (t) в отдельности:
— реакции рассматриваемого нелинейного сопротивления на воздействие каждой из составляющих х (t) в отдельности:
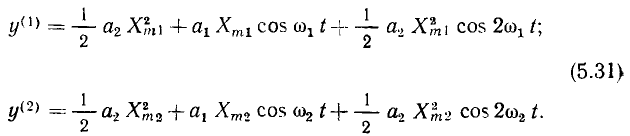
Из выражений (5.30), (5.31) видно, что реакция нелинейного сопротивления на одновременное воздействие двух гармонических колебаний различных частот не равна сумме реакций на воздействие каждого из гармонических колебаний в отдельности и содержит помимо постоянной составляющей и гармонических составляющих с частотами 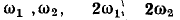 колебания суммарной
колебания суммарной 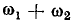 и разностной
и разностной  частот, которое называются колебаниями комбинационных частот.
частот, которое называются колебаниями комбинационных частот.
Способность нелинейных резистивных элементов преобразовывать частоту воздействующих колебаний с образованием постоянной составляющей и колебаний кратных и комбинационных частот широко используется на практике для построения различных радиотехнических устройств, таких, как преобразователи частоты, смесители, модуляторы и демодуляторы.
Если функционирование устройства не связано с использованием нелинейных преобразований воздействующих колебаний, то нелинейность ВАХ реальных элементов приводит к искажению формы воздействующих колебаний. Такие искажения называются нелинейными. Количественно они оцениваются с помощью коэффициента нелинейных искажений
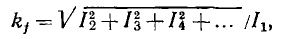
где 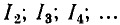 — действующие значения всех гармонических составляющих, кроме первой (основной)
— действующие значения всех гармонических составляющих, кроме первой (основной) 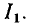
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Преобразование схем электрических цепей
- Установившиеся процессы в линейных электрических цепях
- Методы расчета простых электрических цепей
- Метод сигнальных графов
- Идеализированные активные элементы
- Топологии электрических цепей
- Уравнения электрического равновесия цепей
- Линейные цепи при гармоническом воздействии