Наклонная плоскость в физике - виды, формулы и определения с примерами

Наклонная плоскость:

Перечень простых механизмов не ограничивается рычагами и блоками. Простым механизмом является также устройство, которое называют наклонной плоскостью. Это может быть любая плоскость, наклоненная под некоторым углом к горизонту. Использование наклонной плоскости дает возможность получить выигрыш в силе. В этом легко убедиться, проделав простой опыт.

К крючку динамометра прицепим брус массой 200 г и начнем равномерно поднимать вертикально вверх. Динамометр покажет силу примерно 2 Н.

Закрепим в штативе гладкую дощечку так, чтобы она была наклонена под некоторым углом к горизонту. Положим на нее брус и начнем равномерно его двигать по доске вверх. Показания динамометра будут заметно меньше, чем в первом случае. Поскольку такая доска может быть произвольной длины, то с ее помощью можно поднять груз на любую высоту. При этом действующая на тело сила будет меньшей, чем вес тела.

Наклонная плоскость дает возможность получить выигрыш в силе, зависящий от угла ее наклона.

Чем меньше высота наклонной плоскости по сравнению с ее длиной, тем большим будет выигрыш в силе. Если длину наклонной плоскости обозначить

Для идеальной наклонной плоскости эти отношения равны:

Из формулы видно, что для выигрыша в силе нужно сделать более длинной наклонную плоскость при той же самой высоте подъема.

Свойства наклонной плоскости используются во многих сферах производственной деятельности человека. Так, когда вывозят руду с глубоких карьеров, дорогу, по которой движутся автомобили - рудовозы, прокладывают по склону котлована, постепенно поднимая ее вверх.

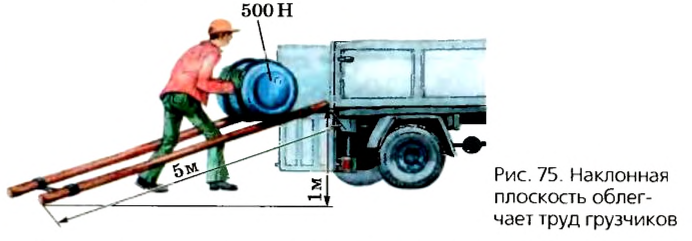
Наклонную плоскость используют и для работ по погрузке транспорта (рис. 75).

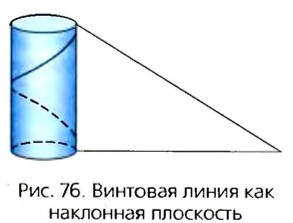
Отдельным видом наклонной плоскости является винт. Резьба, нанесенная на боковую поверхность цилиндра, образует определенный угол с его продольной осью (рис. 76), и это дает возможность получать выигрыш в силе.

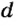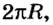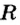За один оборот винта гайка перемещается на расстояние, равное расстоянию между двумя соседними витками. Но каждая точка гайки перемещается на длину одного витка, что значительно больше шага винта. Если шаг винта обозначить буквой , а длину одного витка -  где - радиус витка, то получим соотношение

Винты, как правило, дают значительный выигрыш в силе, поэтому их используют в различных технических устройствах для надежного соединения деталей.

• Заказать решение задач по физике

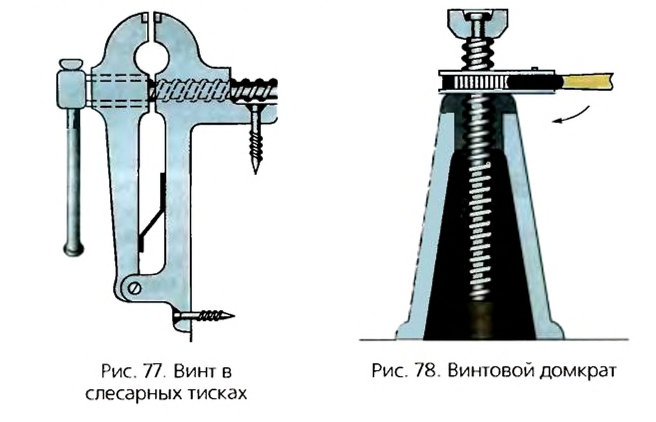
Как пример использования винта могут быть слесарные тиски. Для прокручивания винта тисков прикладывается небольшая сила, а губки тисков будут действовать на тело со значительной силой (рис. 77).

Подобным образом действует и винтовой домкрат (рис. 78).