
Наибольшее и наименьшее значения функции с примерами решения
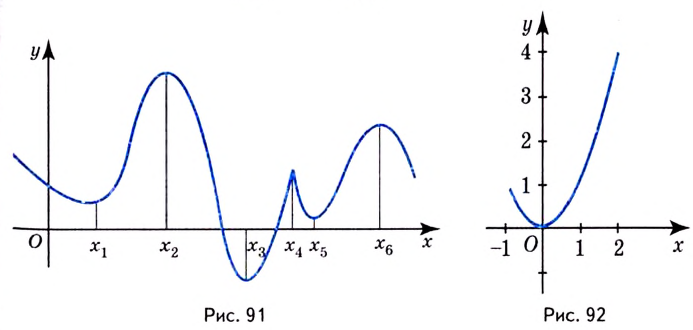
От максимумов и минимумов функции следует отличать её наибольшее и наименьшее значения на промежутке. Функция может иметь несколько максимумов (минимумов) на некотором промежутке (рис. 91), но не более одного наибольшего (наименьшего) значения. Функция может не иметь максимума (минимума) на промежутке, но иметь наибольшее (наименьшее) значение.
Например функция, график которой изображён на рисунке 91, наибольшее значение имеет в точке 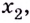
Наибольшее и наименьшее значения функции тесно связаны с её областью значений. Если область значений непрерывной функции — промежуток 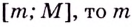 наименьшее значение данной функции,
наименьшее значение данной функции, 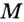 — наибольшее её значение.
— наибольшее её значение.
Поскольку непрерывная функция наибольшее и наименьшее значения может иметь только в точках экстремума или на концах отрезка, то для нахождения этих значений пользуются таким правилом.
Чтобы найти наибольшее и наименьшее значения непрерывной функции 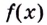 на промежутке
на промежутке 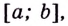 нужно вычислить её значения
нужно вычислить её значения 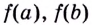 на концах данного промежутка и в критических точках, принадлежащих этому промежутку, а потом выбрать из них наибольшее и наименьшее.
на концах данного промежутка и в критических точках, принадлежащих этому промежутку, а потом выбрать из них наибольшее и наименьшее.
Записывают так: 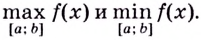
Пример №1
Найдите наибольшее и наименьшее значения функции 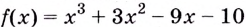 на промежутке
на промежутке 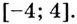
Решение:
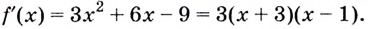 Критические точки:
Критические точки: 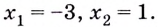
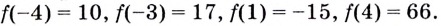
Из этих четырёх значений функции наименьшим является -15, а наибольшим — 66.
Ответ, 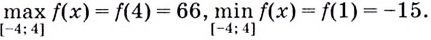
Пример №2
Найдите наибольшее и наименьшее значения функции 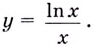
Решение:
Областью определения функции является промежуток 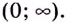
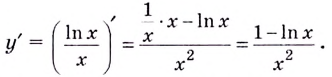
Если 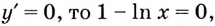 отсюда
отсюда 
Если 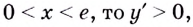 а если
а если 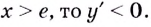 Следовательно,
Следовательно,  — точка максимума.
— точка максимума.
Поскольку на промежутке 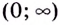 функция имеет только одну критическую точку
функция имеет только одну критическую точку 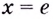 и эта точка является точкой максимума, то наибольшее значение функция принимает именно в этой точке и оно равно
и эта точка является точкой максимума, то наибольшее значение функция принимает именно в этой точке и оно равно 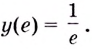 Наименьшего значения функция не имеет.
Наименьшего значения функция не имеет.
Ответ, 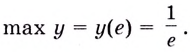 Наименьшего значения функция не имеет.
Наименьшего значения функция не имеет.
К нахождению наибольшего или наименьшего значений функции сводится решение многих прикладных задач.
Пример №3
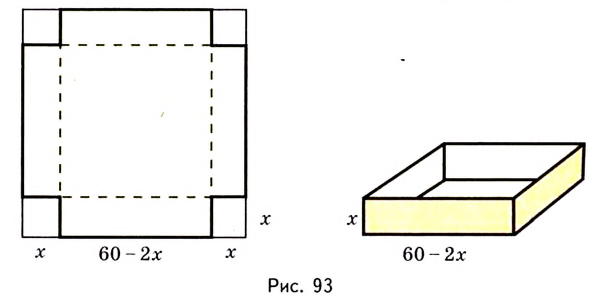
Есть квадратный лист жести со стороной 60 см. Найдите размеры квадратов, которые надо вырезать в углах данного листа, чтобы из полученной заготовки сделать коробку наибольшего объёма {рис. 93).
Решение:
Чтобы получить коробку (в форме прямоугольного параллелепипеда), надо вырезать равные квадраты в углах листа. Пусть 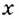 — длина стороны такого квадрата. Тогда высота коробки равна
— длина стороны такого квадрата. Тогда высота коробки равна 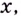 а сторона основания
а сторона основания 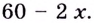 Объём коробки
Объём коробки 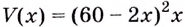 — функция от
— функция от 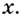
Надо исследовать математическую модель задачи: при каком значении 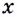 : функция
: функция 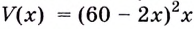 на промежутке
на промежутке 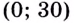 принимает наибольшее значение.
принимает наибольшее значение.
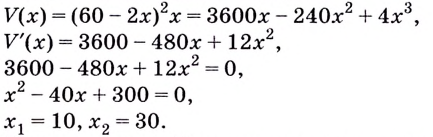
Значение  не принадлежит промежутку
не принадлежит промежутку 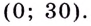 Поэтому
Поэтому 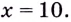
Поскольку при 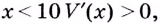 а при
а при 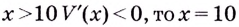 — точка максимума. Итак, в этой точке функция
— точка максимума. Итак, в этой точке функция 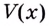 принимает наибольшее значение.
принимает наибольшее значение.
Ответ. Надо вырезать квадраты, стороны которых равны 10 см.
Пример №4
Найдите область значений функции 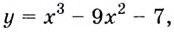 если
если 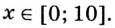
Решение:
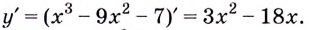 Найдём критические точки:
Найдём критические точки: 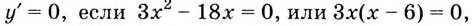 отсюда
отсюда 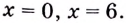
Найдём значение функции на концах промежутка 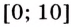 и в критических точках:
и в критических точках: 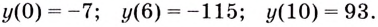
Заданная функция непрерывна, её наибольшее значение 93, а наименьшее -115, значит, область её значений — отрезок 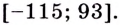
Ответ. 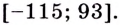
Пример №5
Найдите кратчайшее расстояние от точки 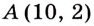 до графика функции
до графика функции 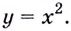
Решение:
Пусть ближайшая к 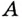 точка
точка 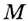 графика функции имеет абсциссу
графика функции имеет абсциссу 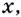 её ордината равна
её ордината равна 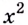 (рис. 94). Найдём квадрат расстояния между точками
(рис. 94). Найдём квадрат расстояния между точками 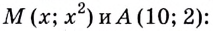
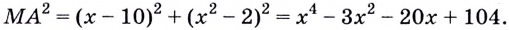 Длина расстояния
Длина расстояния 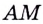 наименьшая, когда её квадрат наименьший. Итак, найдём наименьшее значение функции
наименьшая, когда её квадрат наименьший. Итак, найдём наименьшее значение функции 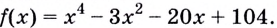
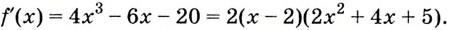
Уравнение 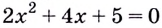 действительных корней не имеет, поэтому функция
действительных корней не имеет, поэтому функция 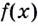 имеет одну критическую точку
имеет одну критическую точку 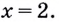 Если
Если 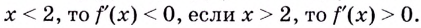 Следовательно,
Следовательно, 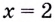 — точка минимума. В этой точке функция
— точка минимума. В этой точке функция 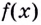 принимает наименьшее значение.
принимает наименьшее значение.
Наименьшее значение квадрата расстояния
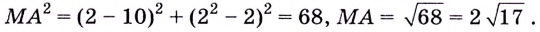
Ответ. 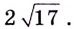
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |