Момент силы относительно точки и относительно оси в теоретической механике

Содержание:

Момент силы относительно точки и относительно оси:

Пусть дана сила Р, направленная как угодно в пространстве, и произвольная точка О (рис. 100).

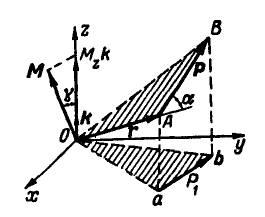
Рис. 100.

Опустим из точки О перпендикуляр на силу Р (на чертеже перпендикуляр не показан) и обозначим плечо силы Р относительно точки О через р. Тогда моментом силы Р относительно точки О (или линейным моментом силы) Называется вектор М, численно равный произведению Р на плечо р и отложенный от точки О перпендикулярно плоскости, проходящей через Р и О в такую сторону, чтобы, смотря с конца стрелки вектора М, сила Р вращала плоскость ОАВ вокруг точки О против часовой стрелки.

Если из центра моментов О провести радиус-вектор

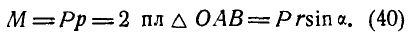
Из сказанного следует, что, линейный момент силы может быть представлен, как векторное произведение радиуса-вектора на силу Р, т. е.:

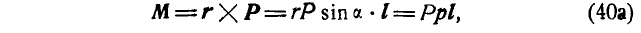
где 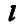— единичный вектор направления М.

Наряду с линейным моментом силы введем в рассмотрение еще одно важное понятие момента силы относительно оси.

Пусть требуется найти момент силы Р относительно какой-либо оси, например z (рис. 100). Для этого силу Р спроектируем на любую плоскость, перпендикулярную к оси z, например на координатную плоскость хОу; обозначим эту проекцию через 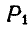. Затем из точки О пересечения оси z с плоскостью хОу опускаем перпендикуляр 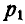на направление найденной проекции 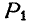силы Р. Тогда произведение 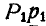, взятое со знаком 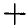или , и будет искомым моментом силы Р относительно оси z, т. е:

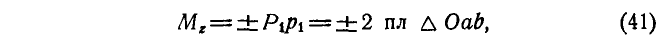
где знак 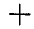берется, если, смотря с положительного направления оси z, проекция силы Р представляется вращающей плоскость хОу вокруг оси z против часовой стрелки, и знак минус, если по часовой стрелке. В нашем случае (рис. 100) в правой части равенства (41) следует взять знак плюс.

Следует заметить, что момент силы относительно оси обращается в нуль, когда сила параллельна оси или пересекает ось, т. е. когда вообще сила и ось расположены в одной плоскости.

 

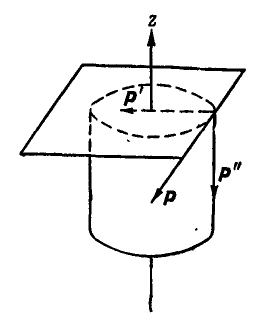
Рис 101.

С понятием момента силы относительно оси часто придется встречаться в дальнейшем. Если представить себе цилиндр (рис. 101), который может вращаться вокруг неподвижной оси z, то сила Р, действующая на цилиндр, не будет его вращать в двух случаях:  когда она пересекает ось z (положение 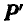) и когда она параллельна оси (положение 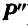), т. е. когда сила Р и ось z лежат в одной плоскости и, следовательно, момент силы Р относительно оси z обращается в нуль.

Найдем зависимость между моментом силы Р относительно оси, например z (рис. 100), и моментом силы Р относительно точки О, взятой на этой оси.

Обозначим линейный момент силы через М, а момент силы относительно оси z представим в виде вектора 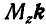, отложенного от точки О в положительном направлении оси z. Обозначим угол между М и 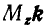через 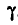. Из рисунка 100 видно, что 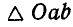представляет собой проекцию 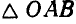на плоскость хОу, а поэтому, по известной теореме геометрии, имеем:

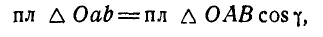
где 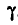— угол между плоскостями треугольников, или, что то же, — между векторами М и .

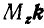Умножив обе части последнего равенства на 2, получим:

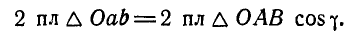
Тогда на основании равенств (40) и (41) будем иметь:

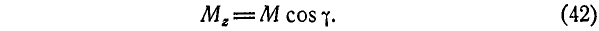
Из равенства (42) следует, что проекции линейного момента силы 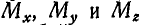на координатные оси х, у и z представляют собой момент силы Р относительно осей х, у и z.

Линейный момент М может быть выражен по формуле (4) через компоненты:

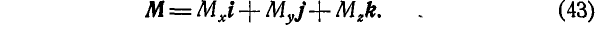
Величины 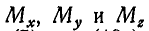можно определить, пользуясь равенствами (42) и (5) или (40а) и (11):

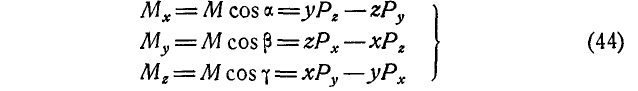
где 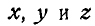— проекции радиуса вектора 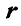на координатные оси, или, что все равно, координаты точки приложения силы;

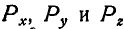— проекции силы Р на координатные оси;

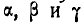— углы, которые образует вектор М с координатными осями.

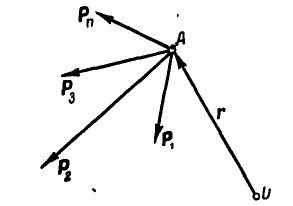
Рис. 102.

Если на точку А (рис. 102) действуют силы 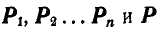— их равнодействующая, то

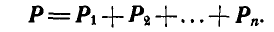
Умножая векторно обе части равенства на радиус-вектор 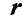, проведенный из любой точки О в точку приложения сил А, имеем:

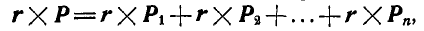
или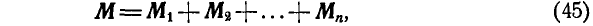  

т. е. момент равнодействующей сил, линии действия которых пересекаются в точке, относительно любой точки равен геометрической сумме моментов сил составляющих относительно той же точки.

Проектируя векторное равенство (45) на координатные оси, согласно (42) получаем:

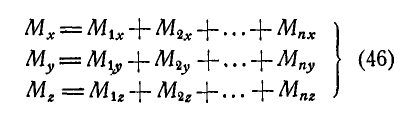
т. е. момент равнодействующей сил, линии действия которых пересекаются в одной точке, относительно какой-либо оси равен алгебраической сумме моментов сил составляющих относительной той же оси.

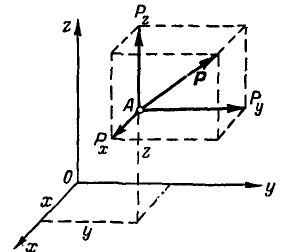
Рис. 103.

На основании последних равенств формулы (44) могут быть получены непосредственно из чертежа. Для этого представим силу Р (рис. 103), приложенную в точке А, определяемой координатами х, у и z в виде трех составляющих 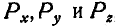, параллельных координатным осям. Тогда на основании равенств (46) моменты 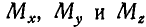силы Р относительно координатных осей найдутся непосредственно из чертежа:

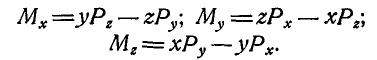
Задача:

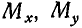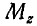Найти моменты и силы 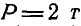относительно осей х, у и z (рис. 104), если сила Р параллельна оси Оу и OA совпадает с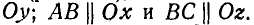

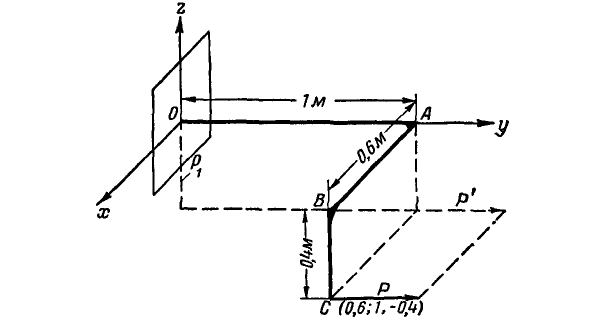
Рис. 104.

Решение. Момент силы Р относительно оси у равен нулю, так как сила Р параллельна оси Оу, т. е. .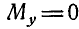

Для нахождения момента силы Р относительно оси Ох проектируем силу Р на плоскость yOz, перпендикулярную к оси Ох (проекция Р). Опустив далее из точки О пересечения оси Ох с плоскостью yOz перпендикуляр 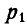на направление проекции 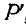, имеем:

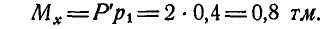
Аналогично находим, что 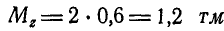. Моменты 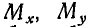и 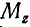силы Р относительно осей х, у и z можно было бы найти также по формулам (44):

 

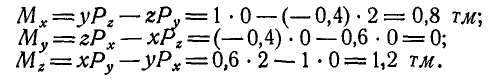
Задача:

Найти линейный момент М силы 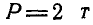относительно точки О, если сила Р направлена по диагонали куба (рис. 106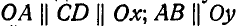) и и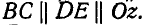

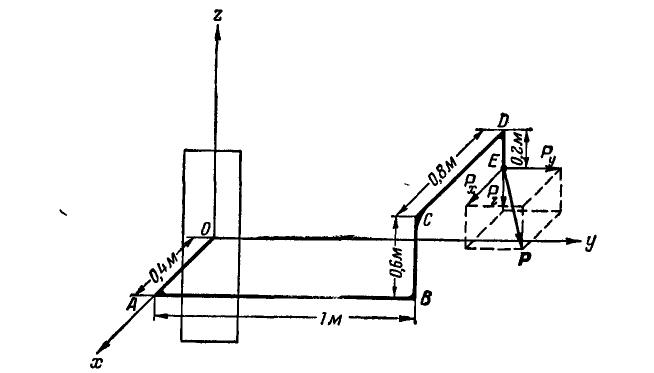
Рис. 106.

Решение. Проекции силы Р на координатные оси будут:

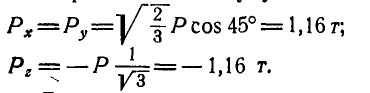
Так как точка приложения силы 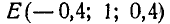нам известна, то проекции линейного момента М на координатные оси найдутся по формулам (44):

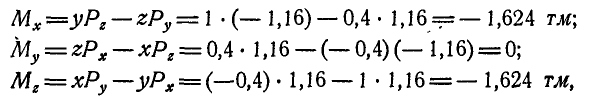
откуда по формуле (43) находим:

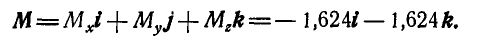
Момент силы относительно точки

Для равновесия рычага необходимо и достаточно, чтобы сумма моментов действующих на него сил относительно точки опоры равнялась нулю

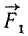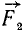Условие равновесия рычага. Твердое тело, имеющее возможность поворачиваться вокруг неподвижной оси под воздействием сил, линии действия которых расположены в плоскостях, перпендикулярных оси вращения, называют рычагом. Пусть рычаг (рис. 27) представляет собой невесомый жесткий стержень. На него действуют только две силы и , перпендикулярные к рычагу в точках А и В.

Если точка опоры С, т. е. точка пересечения оси вращения с плоскостью чертежа, лежит между линиями действия сил (рис. 27, а), то рычаг называют рычагом первого рода. Рычагом второго рода называют рычаг, в котором точка опоры находится по одну сторону от линий действия сил (рис. 27, б).

Для равновесия рычага необходимо и достаточно, чтобы равнодействующая активных сил 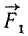и 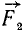 была уравновешена реакцией в точке опоры. Таким образом, равнодействующая сил 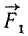и 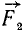должна проходить через точку С, т. е. должно существовать равенство

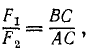
или

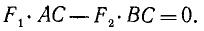
Будем называть расстояние от точки опоры до линии действия силы плечом силы, а произведение модуля силы на плечо—моментом силы относительно точки опоры С. Момент .мы считаем положительным, если сила стремится повернуть рычаг против вращения стрелок часов, и отрицательным, если сила стремится повернуть плечо в ту же сторону, в какую поворачиваются стрелки часов. Момент силы 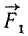относительно опоры на левом чертеже положительный, а момент силы  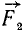- отрицательный.

Таким образом, условие равновесия рычага выразим так: для равновесия рычага необходимо и достатнчно, чтобы сумма моментов сил относительно точки опоры равнялась нулю:

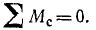        (13)

Задача:

Груз G (рис. 28, а) поднимают тросом, перекинутым через блок и намотанным на барабан l лебедки. Барабан лебедки жестко скреплен с зубчатым колесом ll, которое находится в зацеплении с зубчатым колесом lll, жестко скрепленным с рукояткой O₃A. Определить силу F, прикладываемую к точке А рукоятки лебедки для равномерного поднятия груза G, в положении, изображенном на чертеже. Даны диаметры: D₁, D₂, D₃. Длина рукоятки O₃A=l.

Решение. Лебедку можно рассматривать как состоящую из двух рычагов. Один рычаг (назовем его первым) представляет собой твердое тело, состоящее из барабана l и шестерни ll и имеющее неподвижную ось O₁. Другой рычаг—твердое тело, состоящее из шестерни  lll и рукоятки O₃A и имеющее неподвижную ось O₃. Для решения задачи из условия равновесия первого рычага определим давление P_3,2 между зубцами шестерен, а зная его, найдем F из условия равновесия второго рычага.

На первый рычаг действуют следующие силы (рис. 28, б): 1) сила натяжения троса, равная весу груза, направленная вверх и стремящаяся повернуть рычаг по ходу часовой стрелки; 2) давление P_3,2 зубцов колеса lll на зубцы колеса ll, направленное вверх и поворачивающее первый рычаг против хода часов, и 3) реакция в оси O₁.

Момент силы T относительно точки опоры O₁ равен — 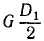. Момент силы P_3,2 равен 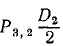. Момент реакции в оси относительно точки O₁ равен нулю. Из условия равновесия рычага находим

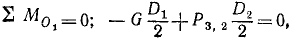
откуда

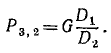
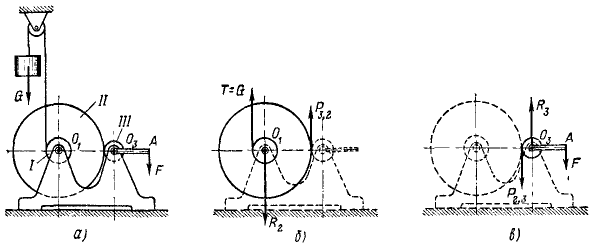
Рис. 28

Ко второму рычагу (рис. 28, в) приложены: I) сила давления зубцов колеса II, равная (по принципу равенства действия и противодействия) P_3,2, но направленная вниз и стремящаяся повернуть второй рычаг против хода часов; 2) давление F руки человека, направленное вниз и поворачивающее рычаг по ходу часов, и 3) реакция в оси O₃, момент которой относительно O3 равен нулю.

Момент силы P_3,2 относительно точки опоры O₃ равен 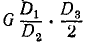. Момент искомой силы F равен —F∙l. Пo условию равновесия рычага

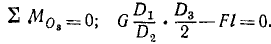
Ответ. 

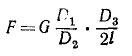
Мы выясни ли, что момент силы относительно точки опоры рычага  зависит не только от величины силы, но и от ее положения по отношению к точке опоры рычага. Чем дальше от точки опоры лежит линия действия силы, тем больше момент. Если сила не перпендикулярна рычагу (рис. 29), то способность ее поворачивать рычаг вокруг точки опоры мы и в этом случае будем измерять моментом силы, а под плечом будем понимать кратчайшее расстояние от точки опоры до линии действия силы. Пусть сила F приложена к рычагу в точке А и составляет с ним некоторый угол а. Разложим силу на две составляющие, из которых одна (F sin a) перпендикулярна к рычагу, а другая (F cos a) направлена вдоль рычага. Эта вторая составляющая не может повернуть рычаг, а поворачивать его будет только первая составляющая (F sin a)  или, как говорят, только эта составляющая создает вращающий момент.

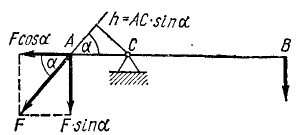
Рис. 29

Следовательно, момент силы F относительно опоры C 

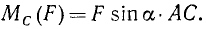
Но, как видно из чертежа, АC sin a= h. Называя плечом силы относительно точки длину перпендикуляра, опущенного из точки на линию действия силы, мы находим, что и в этом случае момент равен произведению модуля силы на плечо:

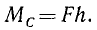   (14)

Момент силы относительно точки выражается произведением модуля силы на плечо, взятым со знаком плюс или минус

Момент силы относительно точки. Понятие момента применимо не только к силам, действующим на рычаг, но и к силам, приложенным ко всякому твердому телу. Момент силы может быть определен не только относительно опоры, но и относительно всякой точки. Точку, относительно которой определен момент  силы, называют центром момента.

Таким образом, опуская из точки О перпендикуляр на линию действия силы 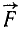и умножая модуль силы на длину этого перпендикуляра, получим момент силы F относительно точки О. Знак момента будем определять, руководствуясь следующим правилом: если мысленно, закрепив центр момента и действуя на плечо в направлении силы, будем поворачивать плечо против хода часовой стрелки, то момент силы относительно данного центра положителен, если же по ходу часовой стрелки, то ‘.момент отрицателен.

Так (рис. 30), моменты сил 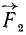, 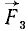и 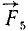относительно точки О положительны, а моменты сил 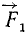и 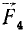относительно той же точки отрицательны.

Одна и та же сила может иметь положительный момент относительно одной точки и отрицательный —относительно другой. Так, момент силы 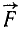(рис. 31) относительно точки О положителен, а относительно точки C отрицателен.

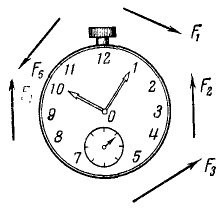
Рис. 30

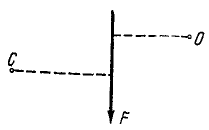
Рис. 31

Момент силы относительно начала координат связан с проекциями X и Y силы на оси и с координатами х и у точки ее приложения соотношением M₀=xY-yX.

• Заказать решение задач по теоретической механике

Аналитическое выражение момента силы.

Пусть дана сила 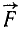(рис. 32), направление которой составляет с осями координат углы α_F и β_F. Направляющие косинусы этой силы

;

.

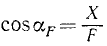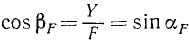Проведем вектор 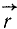из начала координат в точку приложения силы. Этот вектор называют радиусом-вектором. Если координаты точки приложения силы обозначить через х и у, то, как видно из чертежа,

;

.

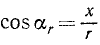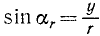Плечо силы h относительно точки О определим из △OAN:

h = r sin  δ.

И для определения величины момента силы получаем следующую формулу:

M₀= r Fsin  δ.    (15)

Угол δ как внутренний угол ΔOAK равен внешнему a_F без другого внутреннего, с ним не смежного—a_r, поэтому

sin δ = sin (a_F -a_r) = sina_Fcosa_r-cos a_F sin a_r.

Подставляя сюда, а затем в (15) найденные выше значения тригонометрических величин, получим

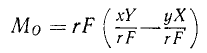
и окончательно 

M₀= хY - yX¹.    (16)

Определяя момент силы по формуле (16), нет надобности определять его знак, сообразуясь с ходом часовой стрелки, т. к. знак получается непосредственно из формулы в зависимости от знаков χ, y, X, Y. В нашем курсе формуле (16) уделена значительная роль.

Момент силы относительно точки выражается векторным произведением радиуса-вектора точки приложения силы на вектор силы: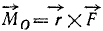 

Момент силы относительно точки как вектор

Напомним, что векторным произведением 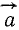на 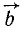называют вектор  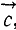направленный перпендикулярно к a и b согласно «правилу буравчика», а по модулю равный произведению модулей a и b на синус угла между направлениями этих векторов.

Следовательно, как видно из (15), величина момента силы равна модулю векторного произведения радиуса-вектора 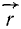на вектор силы  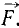 Момент силы относительно точки О как вектор можно представить:

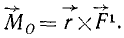    (17)

Вектор 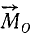не изображен на рис. 32, потому что он направлен перпендикулярно к плоскости, в которой лежат векторы 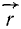и 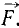, т. е. в данном случае перпендикулярно плоскости чертежа. Если же изобразить силу 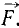не в плоскости чертежа, а в трехмерном пространстве, то момент 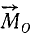силы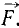 относительно точки О надо отложить от точки О перпендикулярно к плоскости, составляемой радиусом-вектором и вектором силы. Удобна следующая геометрическая интерпретация (рис. 33). Обозначив буквами А и В начало и конец вектора силы, получим треугольник OAB, площадь которого равна половине произведения основания AB на высоту h = OA sin δ.

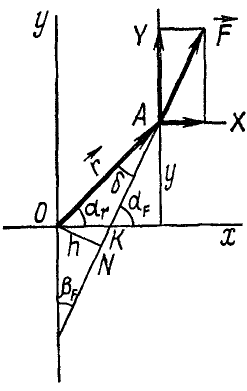
Рис. 32

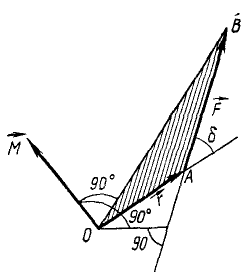
Рис. 33

Сравнивая это равенство с (14), найдем, что момент 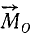силы 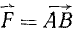 относительно точки О численно равен удвоенной площади треугольника OAB. Напомним, что отрезок AB выражен в единицах силы, а потому площадь треугольника OAB выражается не в единицах площади, а в единицах момента силы (ед. силы × ед. длины):

M₀ = 2 пл. ΔOAB¹

Вектор момента направлен от точки О перпендикулярно к плоскости OAB в такую сторону, с которой вектор силы AB представляется поворачивающим треугольник OAB вокруг точки О против хода часов. По модулю он равен (в некотором выбранном масштабе) удвоенной площади треугольника OAB.

Если вектор силы AB переместить вдоль линии действия силы в пределах абсолютно твердого тела, к которому сила AB приложена, оставив точку О неизменной, то вектор момента не изменится, так как не изменятся плоскость и площадь треугольника OAB. Сила является вектором скользящим, и действие силы, а следовательно, и ее момент не изменяются при перенесении силы вдоль линии действия. Напротив, если мы переменим точку О, то положение и площадь треугольника OAB, вообще говоря, изменятся, а следовательно, изменится и момент силы. Поэтому момент силы относительно какой-либо точки О является вектором прикрепленным, он приложен к точке О и переносить его в какое-либо другое место тела нельзя.
Выражение момента силы относительно точки в виде вектора вполне соответствует физической сущности этого понятия, и если силы расположены в различных плоскостях, то моменты сил относительно точки складывают по правилу параллелограмма. Только при рассмотрении системы сил, расположенных в одной плоскости, можно игнорировать направление вектора момента, а учитывать его величину и знак, т. е. определять момент по формулам (14), (15) или (16). В такой системе, когда все силы и центр моментов расположены в одной плоскости, векторы моментов различных сил относительно какой-либо точки О направлены от точки О перпендикулярно к этой плоскости в ту или другую сторону, и в этом случае их складывают алгебраически.

Момент равнодействующей равен сумме моментов составляющих

Теорема Вариньона

Пусть даны пространственный пучок сил 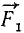, , 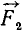..., 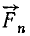(рис. 34) и равнодействующая 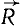этого пучка. Возьмем где-либо совершенно произвольно точку О, проведем радиус вектор  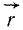из точки О в точку приложения сил пучка, определим момент каждой силы относительно точки О и сложим эти моменты:

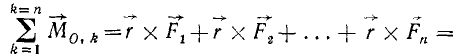
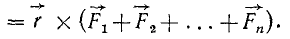
Заменяя согласно (1) геометрическую сумму всех сил сходящейся системы их равнодействующей, получим

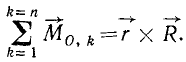      (18)

Словами это равенство можно прочитать так: момент равнодействующей системы сходящихся сил относительно какой-либо точки равен сумме моментов всех сил относительно той же точки. Момент
силы относительно точки есть вектор, поэтому сумма является геометрической. В частном случае, если все силы и центр моментов лежат в одной плоскости, то все векторы моментов направлены по одной прямой, перпендикулярной к этой плоскости, и геометрическое сложение моментов сил заменяется алгебраическим.

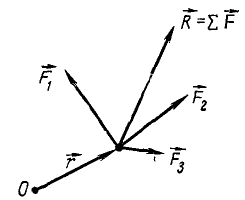Рис. 34

Рис. 35

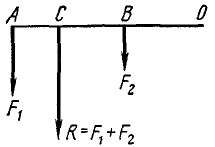
Таким образом, момент равнодействующей плоской системы сходящихся сил равен алгебраической сумме моментов составляющих. Теорема Вариньона о моменте равнодействующей справедлива не только для пучка сил, ио для всякой системы сил, имеющей равнодействующую. Так, например, момент равнодействующей R двух параллельных сил F₁ и F₂ относительно произвольной точки О (рис. 35) равен:

R ^. CO = (F₁ + F₂)CO = F₁(OA-AC) + F₂ (СВ + ВО) = F₁AO + F₂BO.

что и требовалось доказать. Методом от n к n+1 нетрудно показать справедливость теоремы Вариньона для любого числа сил.

Момент силы относительно оси

Чтобы определить момент силы относительно оси, нужно спроецировать силу на плоскость, перпендикулярную к оси, и затем определить момент проекции силы относительно точки пересечения оси и плоскости

Момент силы относительно оси. Ознакомление с понятием момента силы относительно оси, имеющим большое значение, начнем с конкретного примера. Дверь (рис. 36) может поворачиваться вокруг оси. Механическое воздействие силы 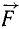, поворачивающей дверь, зависит не только от величины, но и от положения вектора силы по отношению к оси. Разложим силу 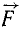на две составляющие, из которых одну 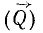направим параллельно осн, а другую (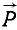) расположим в плоскости, перпендикулярной к оси. Очевидно, что составляющая, параллельная оси, поворачивать дверь не будет, действие же составляющей, расположенной в плоскости, перпендикулярной к оси, зависит не только от ее величины Р, но и от кратчайшего расстояния между линией действия этой составляющей и осью. Иначе говоря, действие силы 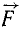на закрепленную на оси дверь характеризуется моментом составляющей 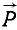(расположенной в плоскости, перпендикулярной к оси) относительно точки пересечения оси и плоскости.

Установим теперь общее правило определения момента силы относительно оси.

Чтобы определить момент силы относительно оси, нужно эту силу спроецировать на перпендикулярную к оси плоскость и определить момент проекции силы относительно точки пересечения оси и плоскости. Момент силы относительно оси — скалярная величина, потому что у него нет собственного направления, а «направлен» он по оси в ту или иную сторону, т. е. определяется величиной и знаком и, конечно, направлением оси.

Где именно проведена перпендикулярная к оси плоскость, не имеет значения, так как проекции силы на параллельные плоскости и плечи проекций силы во всех случаях одни и те же.

Если сила параллельна оси или пересекает ось, то момент силы относительно  оси равен нулю. Эти два случая можно объединить в один: момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости.

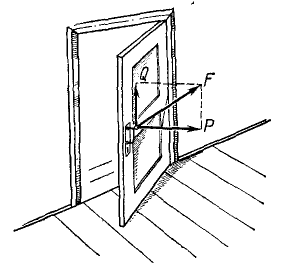
Рис. 36

Момент силы относительно оси равен проекции на эту ось момента силы относительно какой-либо точки, взятой на оси

Покажем, что момент силы относительно оси равен проекции на данную ось вектора момента силы относительно какой-либо точки той же оси.

Возьмем на оси zz' произвольную точку О (рис. 37) и определим момент силы 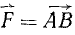относительно этой точки. Момент 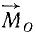силы 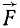 относительно точки О выражается вектором, по модулю равным удвоенной площади треугольника OAB и приложенным в точке О перпендикулярно к плоскости Δ OAB.

Проведем через точку О плоскость, перпендикулярную к оси. Чтобы определить момент M_z силы относительно оси, спроецируем силу на эту плоскость и определим момент проекции 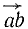относительно точки пересечения оси и плоскости, т. е. относительно точки О. Этот момент численно равен удвоенной площади треугольника Oab и направлен перпендикулярно к Oab, т. е. по оси zz'.

Но Δ Oab является проекцией Δ OAB на плоскость, перпендикулярную к оси. Площадь проекции равна площади проецируемой фигуры, умноженной на косинус двугранного угла между плоскостями, измеряемого линейным углом между перпендикулярами к этим плоскостям, т. е.

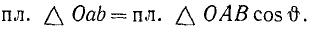
Спроецировав на ось момент силы относительно точки О и принимая во внимание это равенство, найдем, что численно 

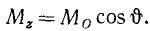      (19)

При решении задач особенно часто приходится определять моменты сил относительно координатных осей. Согласно только что доказанному момент силы относительно какой-либо из осей координат равен проекции на эту ось момента сил относительно любой точки этой оси, в частности относительно точки О начала координат:

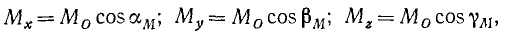      (20)

где cosa_M, cosβ_M и Cosγ_M-направляющие косинусы вектора момента силы относительно начала координат.

Если момент относительно оси умножим на единичный вектор этой оси, то получим не проекцию, а составляющую момента относительно точки, не скалярную, а векторную величину:

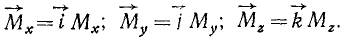      (21)

Из равенств (20) и (21) непосредственно получаем

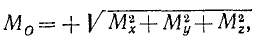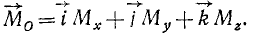      (22)

      (22^/)

Аналитические выражения моментов силы относительно осей координат. Выразим моменты силы относительно осей координат через координаты точки приложения силы и проекции силы на координатные оси.

На чертеже (рис. 38) изображены оси координат и составляющие силы, приложенной к точке А (xyz) (сама сила на чертеже не показана). Чтобы определить моменты силы относительно оси Ох, нужно сначала спроецировать силу 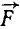на плоскость yОz. Проекция равнодействующей равна сумме проекций составляющих, и вместо того, чтобы спроецировать силу 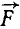, мы можем спроецировать ее составляющие. Проекция составляющей 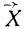равна нулю, проекции же составляющих  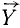и 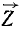равны этим составляющим.

Теперь нам остается определить алгебраическую сумму моментов этих проекций относительно точки О, которая по теореме Вариньона равна моменту проекции равнодействующей на плоскость yОz, или, что то же, моменту силы 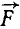относительно оси Ох. Так мы получаем первую из формул (23). Аналогично можно доказать две другие формулы (23), выражающие моменты силы относительно осей Oy и Oz:

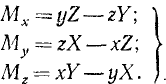      (23)

Для вывода формул (23) мы выбрали точку приложения силы в первом октанте (х, у и z положительны) и направили силу от начала координат (X, Y и Z положительны). Если координаты или проекции силы отрицательны, то в формулы (23) надо, конечно, подставить отрицательные значения.

Достаточно запомнить одну из формул (23), а следующую можно получить из предыдущей, применив круговую подстановку, т. е. заменив всюду икс на игрек, игрек на зет и зет на икс. Случаи, когда формулы можно получить одну из другой такой подстановкой, мы будем отмечать символом:

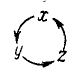
Выражение (23) можно получить непосредственно из свойств векторного произведения, если представить векторное произведение определителем третьего порядка:

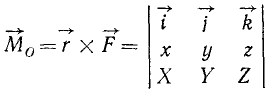      (17^/)

Раскладывая этот определитель по элементам первой строки, найдем:

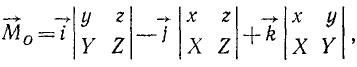
или

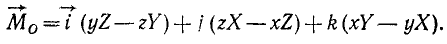
Сравнив это равенство с (22'), получим формулы (23).

Обратим внимание на то, что правая часть третьей из формул (23) тождественна выражению (16) момента силы, лежащей в плоскости хОу, относительно начала координат. Объяснение заключается в том, что при выводе формулы (23) для определения Мz силу сначала спроецировали на плоскость хОу и затем определили момент проекции относительно начала координат. Формула же (16) выражает момент относительно начала координат силы, лежащей в плоскости хОу. Моменты этой силы относительно осей, расположенных с ней в одной плоскости, равны нулю (M_x= 0, M_y= 0), а момент относительно оси O_z численно равен величине момента относительно начала координат (M_z = M₀).