Моделирование поверхностей на эпюре Монжа с примерами

Содержание:

Моделирование поверхностей на эпюре Монжа:

В начертательной геометрии при моделировании поверхностей преимущественно используют кинематический и каркасный способы их образования.

При кинематическом способе поверхность рассматривается как совокупность всех последовательных положений некоторой линии — образующей, перемещающейся в пространстве по определенному закону. Линия, которую пересекают все образующие поверхности, называется направляющей.

Упорядоченное множество линий, принадлежащих поверхности, называется ее каркасом. Обычно в качестве линий каркаса используют семейство образующих или семейство направляющих.

При каркасном способе поверхность рассматривается как совокупность некоторого числа линий, образующих каркас. Основное отличие каркасных поверхностей от кинематических состоит в том, что для первых задается определенное число линий каркаса — дискретный каркас, а у вторых в любой точке поверхности может быть построена линия каркаса, т. е. поверхность имеет непрерывный каркас.

При моделировании поверхности важную роль играет ее определитель.

Определитель поверхности

Совокупность условий, задающих поверхность, называется определителем поверхности. Определитель состоит из двух частей: геометрической и алгоритмической.

Геометрическая часть определителя включает в себя геометрические элементы, участвующие в образовании поверхности. Такой набор элементов называется репером (от французского слова repere — метка, ориентир).

Алгоритмическая часть определителя содержит перечень операций, позволяющих реализовать переход от репера к остальным точкам поверхности.

При моделировании поверхности необходимо:

1. промоделировать репер;
2. реализовать алгоритм, посредством которого осуществляется переход от модели репера к модели произвольной точки, принадлежащей данной поверхности.

На эпюре Монжа поверхность задается проекциями ее репера.

Построение произвольной точки, принадлежащей поверхности, осуществляется с помощью простейших линий каркаса поверхности, проходящих через эту точку.

При моделировании поверхности возникает понятие очерка поверхности.

Очерк поверхности

Совокупность точек касания проецирующих прямых поверхности образует контурную линию k (рис. 32). Очерк k1 — проекция контурной линии на плоскость проекций. Контурная линия делит поверхность на две части — видимую и невидимую.

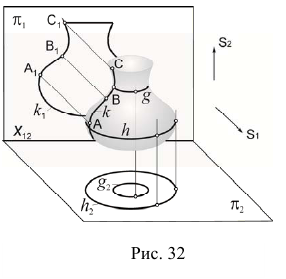
При моделировании поверхности по методу Монжа различают фронтальный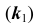

Моделирование линейчатых поверхностей

Линейчатая поверхность образуется движением прямой линии (образующей), которая в общем случае пересекает три направляющие, в частном случае — две или одну направляющую.

Линейчатые поверхности с одной направляющей

Линейчатые поверхности с одной направляющей образуются движением прямой линии, которая пересекает направляющую (кривую или ломаную линию) и вершину (собственную или несобственную точку). В табл. 1 представлены различные формы поверхности с одной направляющей в зависимости от вида направляющей и вершины.

Таблица 1

Моделирование конической поверхности

Для построения модели конической поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей (кривая линия) и вершины (собственная точка), а также решить задачу построения произвольной точки поверхности.

Задача 1.

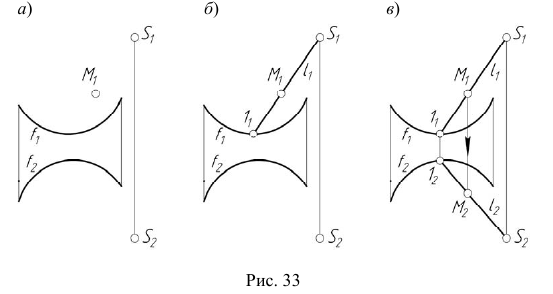
На эпюре Монжа построить произвольную точку M, принадлежащую конической поверхности 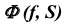(рис. 33).

Алгоритм решения

1. Отмечаем произвольно проекцию 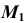точки M (см.рис. 33, а).
2. Через проекцию 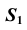вершины 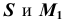проводим проекцию 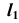образующей 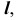принадлежащей поверхности 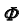(см. рис. 33, б),
3. Отмечаем проекцию 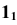точки пересечения образующей 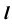с направляющей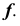
4. Находим проекцию 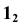из условия принадлежности точки 1 линии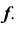
5. Строим вторую проекцию 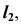соединяя точки 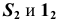(см. рис. 33, в).

6. Через точку 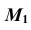проводим линию проекционной связи и, при пересечении ее с прямой 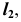отмечаем искомую проекцию 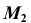точки M, принадлежащей образующей 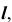а следовательно, и поверхности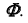

Моделирование цилиндрической поверхности

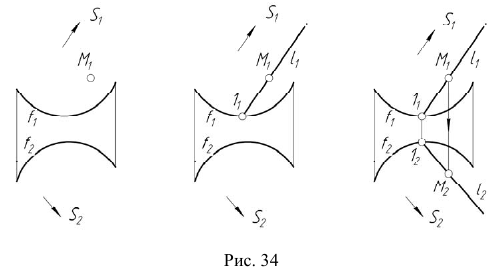
Для построения модели цилиндрической поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей 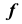(кривая линия) и вершины S (несобственная точка), а также решить задачу построения произвольной точки поверхности. Задача построения произвольной точки цилиндрической поверхности будет решаться аналогично задаче 4 (рис. 34).

Моделирование пирамидальной поверхности

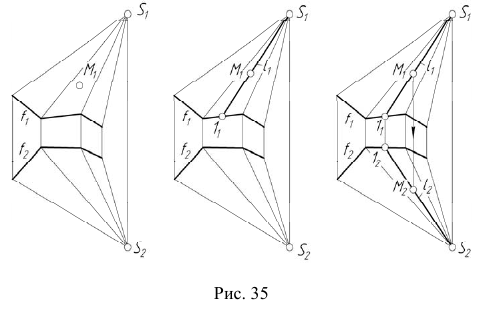
Для построения модели пирамидальной поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей (ломаная линия) и вершины S (собственная точка), а также решить задачу построения произвольной точки поверхности. Задача построения произвольной точки пирамидальной поверхности будет решаться аналогично задаче 4 (рис. 35).

Моделирование призматической поверхности

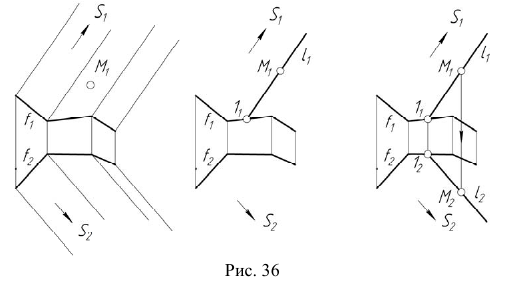
Для построения модели призматической поверхности необходимо задать на эпюре Монжа проекции ее репера — направляющей (ломаная линия) и вершины S (несобственная точка), а также решить задачу построения произвольной точки поверхности. Задача построения произвольной точки призматической поверхности будет решаться аналогично задаче 4 (рис. 36). Следует отметить, что, умея строить одну точку поверхности, можно построить проекции любой линии, принадлежащей заданной поверхности, рассматривая эту линию как совокупность отдельных точек.

Пример:

Построение линии принадлежащей цилиндрической поверхности 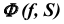(рис. 37, а).

Порядок построения

1. Построение очерковых линий и определение видимости направляющей (рис. 37, б).

Для определения видимости линии 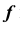используются конкурирующие точки M и N. По расположению фронтальных проекций этих точек можно сделать вывод, что точка N, принадлежащая направляющей 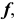находится под точкой M, принадлежащей образующей m. Следовательно, участок линии 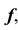содержащий точку N при проецировании на плоскость 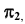будет невидимым. На проекции 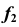этот участок отмечен штриховой линией.

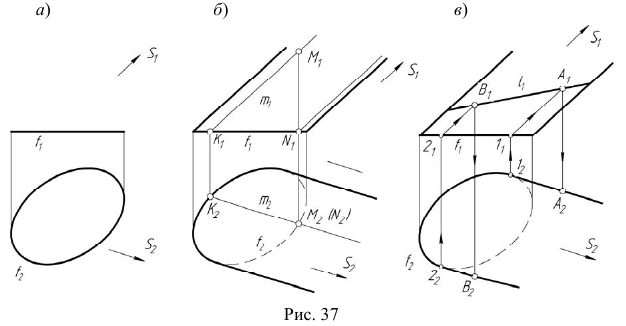
2. Определение проекций точек изменения видимости линии 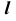при проецировании на плоскость 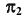(рис. 37, в). Проекция 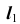проведена произвольно.

Построение начинается с горизонтальной проекции — с точек касания 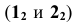очерковых прямых с кривой 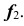Стрелками показана последовательность действий определения искомых проекций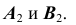

3. Построение точек С и D (рис. 38, а). Построение начинается с фронтальных проекций 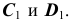Проекции 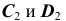определяются по алгоритму решения задачи 4.

4. Построение проекций точек 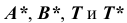(рис. 38, б). Построение начинается с фронтальной проекции: точка 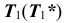отмечается произвольно на 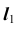, проекция 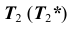определяется по алгоритму решения задачи 4.

Аналогично строятся остальные точки заданной линии.

5. Определение видимости линии 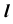при проецировании на горизонтальную плоскость проекций.

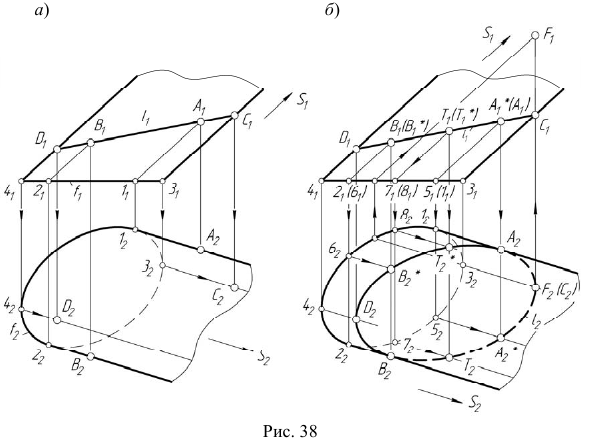
Видимость линии 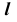определяется по конкурирующим точкам C и F цилиндрической поверхности. По расположению фронтальных проекций этих точек можно сделать вывод, что точка F выше точки C. Следовательно, часть линии 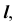содержащая точку C, будет невидимой от точки A до точки B.

Линейчатые поверхности с двумя направляющими и плоскостью параллелизма

Такие поверхности образуются движением прямой, которая движется параллельно некоторой плоскости 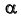и пересекает при этом две направляющие m и n.

В табл. 2 представлены различные формы поверхности с двумя направляющими в зависимости от вида направляющих.

Таблица 2

Наибольшее применение из приведенных (см. Табл. 2) поверхностей в инженерной практике нашла косая плоскость. Косую плоскость также называют гиперболическим параболоидом, так как ее каркас состоит не только из прямых линий, но также из семейств кривых второго порядка — гипербол и парабол.

Моделирование косой плоскости

Для построения модели косой плоскости необходимо задать на эпюре Монжа проекции направляющих m и n, а также проекции плоскости параллелизма 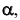и решить задачу построения произвольной точки поверхности.

Задача 2.

На эпюре Монжа построить недостающую проекцию 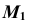точки M, принадлежащей косой плоскости 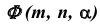(рис. 39). Проекция 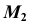выбрана произвольно.

Плоскостью параллелизма в данной задаче является горизонтально-проецирующая плоскость .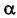

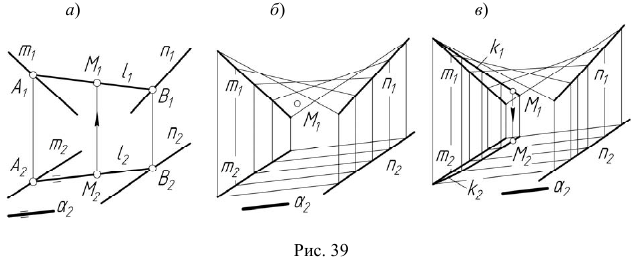
Алгоритм решения

1. Через 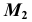параллельно проекции 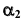плоскости параллелизма проводим горизонтальную проекцию 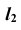образующей 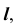принадлежащей поверхности 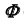(см. рис. 39, а).
2. Строим фронтальную проекцию 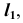используя для построения проекции точек пересечения A и B образующей 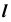с направляющими m и n.
3. Через точку 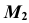проводим линию проекционной связи и, при пересечении ее с прямой 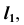отмечаем искомую проекцию 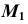точки M, принадлежащей образующей 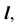а следовательно, и поверхности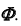

На рис. 39, б, в показано построение недостающей проекции 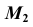точки M, принадлежащей косой плоскости.

Проекция 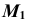выбирается произвольно (см. рис. 39, б). Далее строятся проекции линий каркаса поверхности аналогично построению проекций прямой 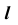(см. рис. 39, а). Через 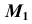проводится произвольно проекция 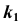кривой 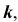принадлежащей поверхности 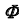. При построении 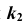используются точки пересечения линии 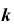с линиями каркаса. Искомая проекция 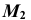определяется на пересечении линии проекционной связи с горизонтальной проекцией линии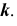

Линейчатые проецирующие поверхности

Цилиндрическая и призматическая поверхности могут занимать проецирующее положение в том случае, если направление на вершину (несобственную точку) будет совпадать с направлением проецирования на одну из плоскостей проекций. Другими словами, образующие проецирующей поверхности будут перпендикулярны одной из плоскостей проекций.

На рис. 40 приведен пример фронтально-проецирующей цилиндрической поверхности.

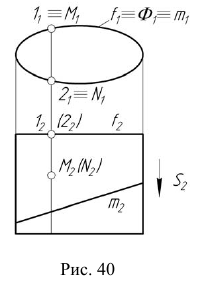
Фронтальная проекция любой точки, принадлежащей поверхности 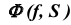будет находиться на вырожденной проекции 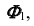которая совпадает с проекцией 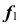направляющей линии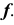

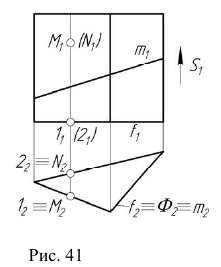
На рис. 40 также показано положение проекций точек M, N и линии m, принадлежащих цилиндрической поверхности. На рис. 41 приведен пример горизонтально-проецирующей призматической поверхности.

Горизонтальная проекция любой точки, принадлежащей поверхности 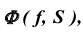будет находиться на вырожденной проекции 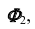которая совпадает с проекцией 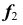направляющей линии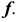

На рис. 41 также показано положение проекций точек M, N и линии m, принадлежащих призматической поверхности.

• Заказать чертежи

Моделирование поверхностей вращения

Поверхность вращения образуется вращением какой-либо линии (образующей) вокруг неподвижной оси (рис. 42). Как правило, ось вращения располагается перпендикулярно одной из плоскостей проекций.

Если образующая поверхности вращения — прямая линия, то образуется линейчатая поверхность. Если образующая — кривая, поверхность вращения будет относиться к классу нелинейчатых поверхностей.

Репер поверхности вращения включает в себя ось вращения i и образующую линию f. Каждая точка образующей линии вращается по окружности, которая называется параллелью. Плоскость этой параллели перпендикулярна оси вращения, а центр принадлежит оси вращения.

Параллель наибольшего радиуса называется экватором, а параллель наименьшего радиуса — горлом.

Меридиан — линия на поверхности, расположенная в одной плоскости с осью вращения. Главный меридиан — меридиан, плоскость которого параллельна плоскости проекций. Если ось вращения перпендикулярна плоскости 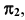то главный меридиан параллелен 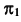Если же ось вращения перпендикулярна плоскости 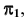то главный меридиан параллелен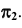

Один из очерков поверхности вращения определяется главным меридианом, а второй — экватором или экватором и горлом.

Моделирование поверхности вращения общего вида

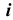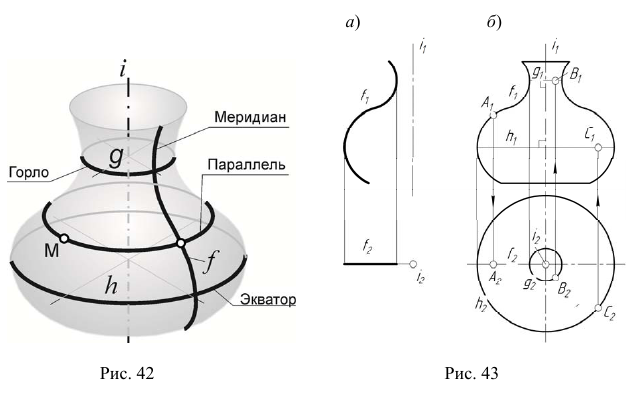
Для построения модели поверхности вращения необходимо задать на эпюре Монжа проекции ее репера: оси вращения и образующей линии 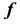(рис. 43, а), а также решить задачу построения произвольной точки поверхности. Дополним эпюр фронтальным и горизонтальным очерками поверхности. На рис. 43, б основной линией изображены очерки поверхности, а также отмечены проекции точек A, B и C, принадлежащих главному меридиану, горлу и экватору соответственно.

Задача 3.

На эпюре Монжа построить произвольную точку 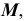принадлежащую поверхности вращения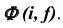

Алгоритм решения 1

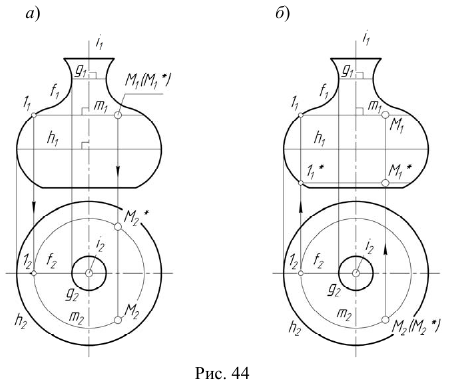
1. Отмечаем произвольно проекцию 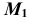точки M (рис. 44, а).
2. Через 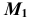перпендикулярно 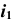проводим проекцию 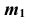параллели 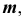принадлежащей поверхности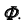
3. Находим проекцию 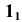точки пересечения параллели m с образующей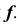
4. Строим горизонтальную проекцию параллели m — окружность, проходящую через точку 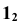и с центром в точке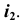
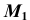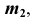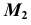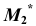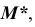5. Через точку проводим линию проекционной связи и, при пересечении ее с окружностью отмечаем две точки — проекцию точки M видимой части поверхности и точки принадлежащей невидимой части поверхности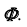

Алгоритм решения 2

1. Отмечаем произвольно проекцию 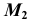точки M (рис. 44, б).

2. Через 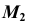строим окружность 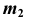с центром в точке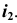

3. Находим проекцию 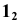точки пересечения параллели m с образующей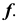

4. Строим проекции 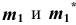— прямые, перпендикулярные 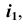проходящие через точки 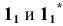соответственно.

5. Через точку 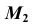проводим линию проекционной связи и, при пересечении ее с прямыми 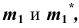отмечаем точки 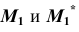— проекции точек 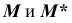видимой и невидимой частей поверхности 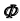соответственно.

Приведенные алгоритмы решения подобной задачи применимы для любой поверхности вращения.

В зависимости от формы образующей линии 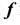могут получаться различные виды поверхности вращения.

Моделирование сферы

Сфера образуется вращением окружности вокруг одного из ее диаметров (рис. 45, а). Один из реперов сферы — ось вращения 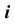и образующая окружность 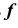(рис. 45, б). Сфера также может быть задана экватором h и главным меридианом 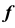(рис. 45, в).

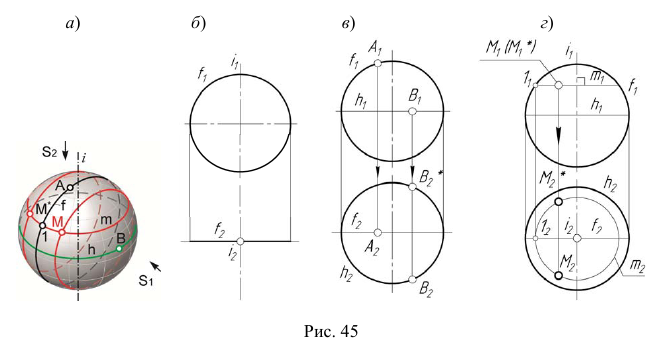
На рис. 45, г показано построение точки M, принадлежащей сфере 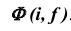. Построение выполнено по первому алгоритму задачи 5.

Моделирование торовой поверхности

Торовая поверхность образуется вращением окружности вокруг оси, которая расположена в плоскости окружности, но не проходит через ее центр (рис. 46).

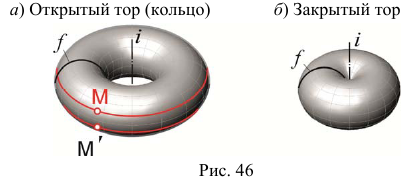
Репером торовой поверхности будут ось вращения 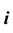и образующая окружность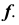

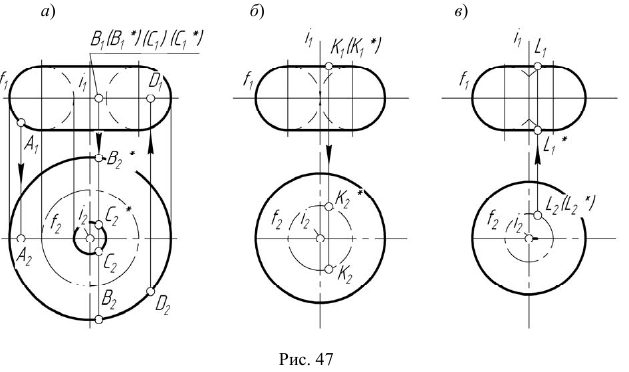
На рис. 47 изображены три модели торовой поверхности в зависимости от взаимного положения оси вращения и образующей окружности, а также модели точек, принадлежащих контурным линиям торовой поверхности. Если ось вращения 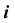не пересекает образующую окружность 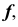то образуется открытый тор (кольцо) (см. рис. 47, а). Если же ось вращения 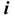касается образующей окружности 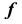или пересекает ее, то образуется закрытая торовая поверхность (см. рис. 47, б, в).

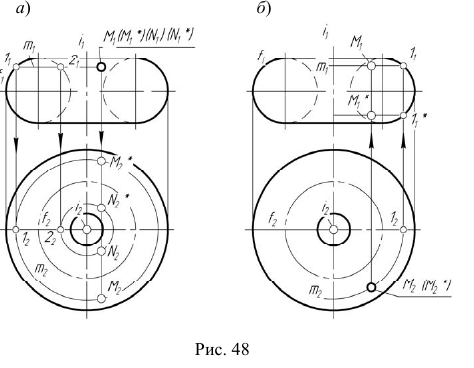
На рис. 48, а показано построение произвольной точки M, принадлежащей торовой поверхности 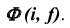Построение выполняется по первому алгоритму задачи 5. На рис. 48, б показано построение точки M по второму алгоритму задачи 5.

Линейчатые поверхности вращения

При вращении прямой линии, которая пересекает ось вращения в собственной или несобственной точке, образуются, соответственно, коническая или цилиндрическая поверхности. Если прямая линия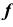 скрещивается с осью вращения 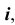образуется поверхность, называемая однополостным гиперболоидом вращения.

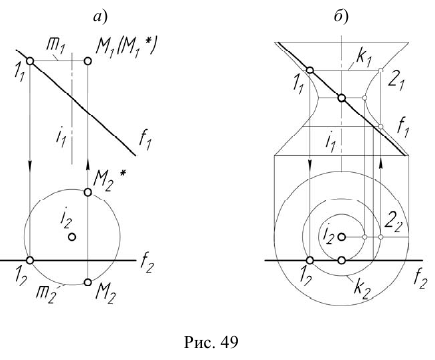
Эта поверхность также может быть получена путем вращения гиперболы вокруг ее мнимой оси. На рис. 49, а показано построение произвольной точки M, принадлежащей поверхности однополостного гиперболоида вращения 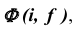а на рис. 49, б — построение фронтального очерка заданной поверхности. Через точку 1, принадлежащую образующей прямой 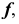проводится параллель 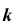поверхности вращения, после чего определяется точка 2, принадлежащая главному меридиану. Аналогично строятся все остальные точки гиперболы.