
Моделирование плоскости на эпюре Монжа с примерами
Содержание:
Моделирование плоскости на эпюре Монжа:
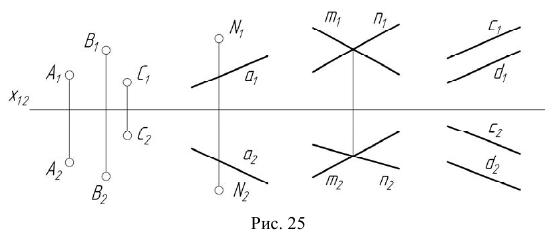
Плоскость является простейшей поверхностью. Способы задания плоскости общего положения (произвольно расположенной относительно плоскостей проекций) представлены на рис. 25:
- три точки, не лежащие на одной прямой, —
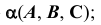
- прямая и точка, не принадлежащая этой прямой, —
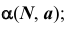
- две пересекающиеся или две параллельные прямые —
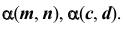
Задача 1.
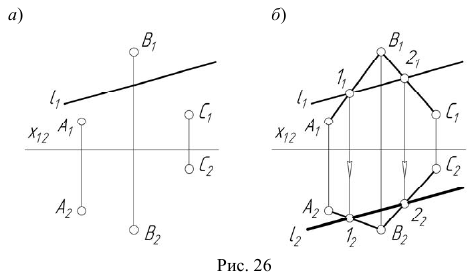
На эпюре Монжа построить модель какой-либо прямой, принадлежащей плоскости 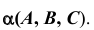
Предпосылка для решения задачи: прямая принадлежит плоскости, если она проходит через две точки этой плоскости.
Алгоритм решения
- Проводим произвольно проекцию
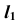 прямой
прямой 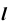 (рис. 26, а).
(рис. 26, а). - Соединяем между собой соответствующие проекции точек A и B, B и C (рис. 26, б).
- Отмечаем точки
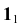 и
и 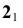 пересечения проекции прямой
пересечения проекции прямой 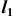 с проекциями прямых
с проекциями прямых 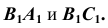
- Находим горизонтальные проекции точек
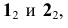 проводим через них проекцию
проводим через них проекцию  прямой
прямой 
Задача 2.
На эпюре Монжа построить модель точки, принадлежащей плоскости 
Построение недостающей проекции точки, принадлежащей плоскости, основано на условии принадлежности этой точки прямой, лежащей в плоскости.
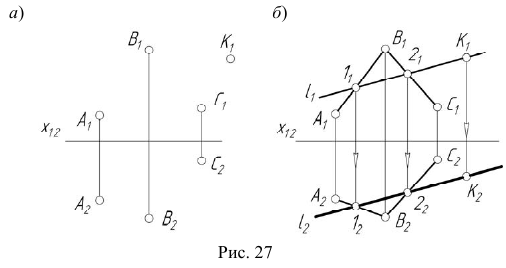
Алгоритм решения
- Отмечаем произвольно проекцию
 точки
точки  (рис. 27, а).
(рис. 27, а). - Через
 проводим первую проекцию
проводим первую проекцию 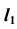 прямой
прямой 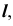 принадлежащей плоскости
принадлежащей плоскости 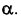
- Строим вторую проекцию
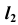 прямой
прямой 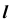 (см. задачу 2).
(см. задачу 2). - Через точку
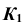 проводим линию проекционной связи и, при пересечении ее с прямой
проводим линию проекционной связи и, при пересечении ее с прямой 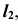 отмечаем искомую проекцию
отмечаем искомую проекцию 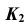 точки
точки 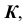 принадлежащей прямой
принадлежащей прямой 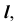 а следовательно и плоскости
а следовательно и плоскости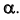
Плоскости частного положения. Проецирующие плоскости
Плоскость, проходящая через проецирующую прямую, называется проецирующей плоскостью.
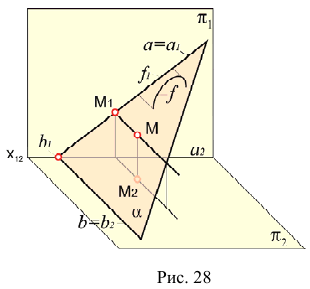
Очевидно, что фронтально-проецирующая плоскость перпендикулярна плоскости проекций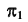 (рис. 28), а горизонтально-проецирующая плоскость — плоскости проекций
(рис. 28), а горизонтально-проецирующая плоскость — плоскости проекций 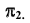
Одна из проекций проецирующей плоскости вырождается в прямую. Эта прямая обладает собирательным свойством. Видно (см. рис. 28, что фронтальные проекции всех элементов плоскости 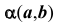 расположены (собраны) на одной прямой
расположены (собраны) на одной прямой 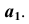
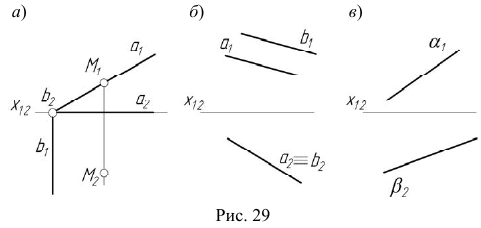
На рис. 29, а , б представлены проекции фронтально-проецирующей плоскости 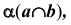 перпендикулярной
перпендикулярной 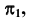 и горизонтальнопроецирующей плоскости
и горизонтальнопроецирующей плоскости 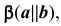 перпендикулярной
перпендикулярной 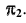 Чаще всего проецирующие плоскости задаются на эпюре Монжа своими вырожденными проекциями (рис. 29, в).
Чаще всего проецирующие плоскости задаются на эпюре Монжа своими вырожденными проекциями (рис. 29, в).
Плоскости уровня
Плоскость уровня —плоскость, параллельная одной из плоскостей проекций. На рис. 30 изображена плоскость 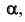 параллельная горизонтальной плоскости проекций. Треугольник ABC, принадлежащий плоскости
параллельная горизонтальной плоскости проекций. Треугольник ABC, принадлежащий плоскости 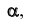 будет проецироваться на плоскость
будет проецироваться на плоскость 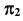 без искажения, т. е. по горизонтальной проекции треугольника можно судить о его истинных размерах.
без искажения, т. е. по горизонтальной проекции треугольника можно судить о его истинных размерах.
На рис. 31, а представлены проекции плоскости уровня 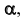 параллельной плоскости
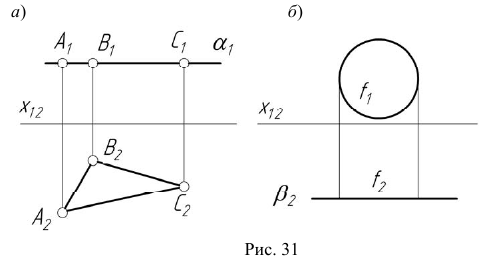
параллельной плоскости 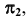 а на рис. 31, б — плоскости
а на рис. 31, б — плоскости 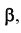 параллельной плоскости
параллельной плоскости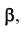
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |