
Моделирование линии на эпюре Монжа с примерами
Содержание:
Моделирование линии на эпюре Монжа:
В этом разделе рассмотрим моделирование прямой и кривой линии, способы их задания на чертеже и свойство инцидентности точек и линий.
Моделирование прямой линии
Прямая в общем случае моделируется двумя парами точек (рис. 12, а) или парой прямых (рис. 12, б). Прямую линию, не параллельную и не перпендикулярную плоскостям проекций, будем называть прямой общего положения.
Задача 1
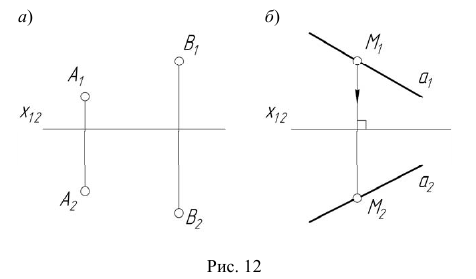
На эпюре Монжа построить модель произвольной точки М, принадлежащей прямой a.
Алгоритм решения
1. Отметим произвольно на 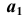
Прямые частного положения
Различают две группы прямых частного положения:
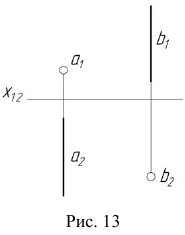
1. Проецирующие прямые — прямые, проходящие через один из центров проецирования. Одна из проекций проецирующей прямой вырождается в точку (рис. 13).
Прямая a — фронтально-проецирующая прямая.
Прямая b — горизонтально-проецирующая прямая.
Две точки, лежащие на одной проецирующей прямой, называются конкурирующими. На эпюре Монжа с помощью проекций конкурирующих точек можно определять взаимную видимость геометрических объектов.
На рис. 14, а представлены две пары конкурирующих точек A, B 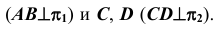 Стрелками показано направление взгляда наблюдателя из центров проецирования на плоскости проекций. Видимой считают ту точку, которая находится ближе к центру проецирования. При проецировании на плоскость
Стрелками показано направление взгляда наблюдателя из центров проецирования на плоскости проекций. Видимой считают ту точку, которая находится ближе к центру проецирования. При проецировании на плоскость 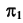 видимой будет точка A, а при проецировании на плоскость
видимой будет точка A, а при проецировании на плоскость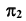 — точка С. На рис. 14, б представлены модели конкурирующих точек на эпюре Монжа. В скобках указаны проекции невидимых точек при проецировании на соответствующую плоскость проекций.
— точка С. На рис. 14, б представлены модели конкурирующих точек на эпюре Монжа. В скобках указаны проекции невидимых точек при проецировании на соответствующую плоскость проекций.
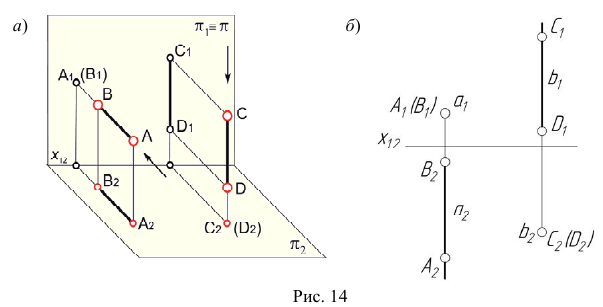
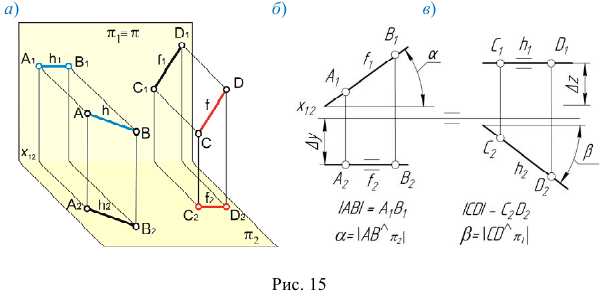
2. Линии уровня — прямые, параллельные одной из плоскостей проекций (рис. 15, а).
Прямая 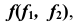 параллельная плоскости проекций
параллельная плоскости проекций 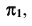 называется фронталью. Вторая проекция фронтали параллельна оси проекций
называется фронталью. Вторая проекция фронтали параллельна оси проекций 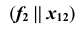 (рис. 15, б).
(рис. 15, б).
Прямая 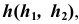 параллельная плоскости проекций
параллельная плоскости проекций 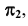 , называется горизонталью. Первая проекция горизонтали параллельна оси проекций
, называется горизонталью. Первая проекция горизонтали параллельна оси проекций 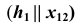 (рис. 15, в).
(рис. 15, в).
Прямая d, параллельная плоскости проекций 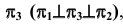 называется профильной прямой (рис. 16, а). Обе проекции этой прямой лежат на линии проекционной связи, перпендикулярной
называется профильной прямой (рис. 16, а). Обе проекции этой прямой лежат на линии проекционной связи, перпендикулярной 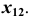 Наличие проекций двух точек С и D, принадлежащих этой прямой, делает ее модель однозначной. Для построения произвольной точки M, принадлежащей профильной прямой d, можно воспользоваться проекцией прямой на плоскость
Наличие проекций двух точек С и D, принадлежащих этой прямой, делает ее модель однозначной. Для построения произвольной точки M, принадлежащей профильной прямой d, можно воспользоваться проекцией прямой на плоскость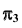 (рис. 16, б) или пятым свойством параллельного проецирования — свойством пропорциональности (рис. 16, в).
(рис. 16, б) или пятым свойством параллельного проецирования — свойством пропорциональности (рис. 16, в).
Взаимное положение прямых
Рассмотрим три варианта взаимного положения прямых в пространстве.
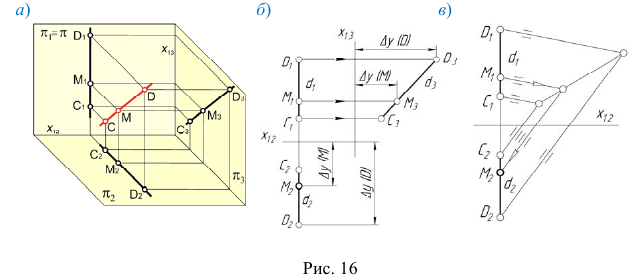
1) Пересекающиеся прямые (рис. 17, а).
Проекции пересекающихся между собой прямых пересекаются в точке, которая является проекцией точки пересечения этих прямых, т. е., если 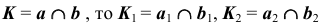 (рис. 17, б).
(рис. 17, б).
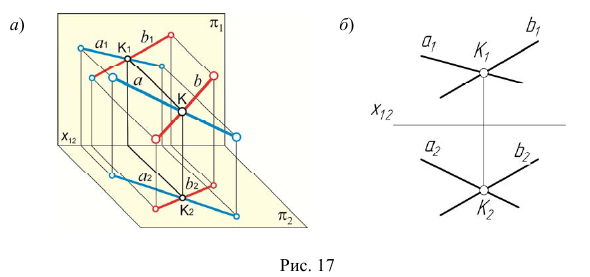
2) Параллельные прямые (рис. 18, а). Проекции параллельных прямых параллельны между собой, т. е., если 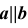 , то
, то 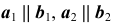 (рис. 18, б).
(рис. 18, б).
3) Скрещивающиеся прямые (рис. 19, а) Проекции скрещивающихся между собой прямых пересекаются в точке, которая является проекцией конкурирующих точек, принадлежащих этим прямым (рис. 19, б).
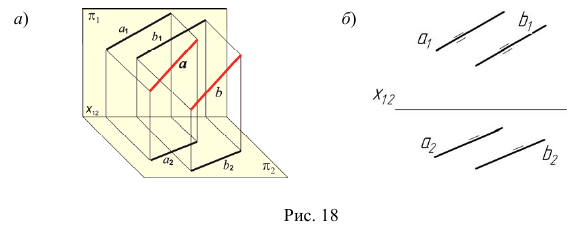
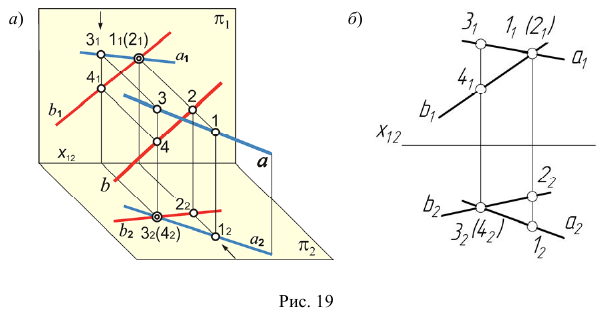
По расположению горизонтальных проекций 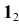 и
и 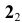 конкурирующих точек 1 и 2 можно сделать вывод, что прямая b находится за прямой a, а по расположению фронтальных проекций
конкурирующих точек 1 и 2 можно сделать вывод, что прямая b находится за прямой a, а по расположению фронтальных проекций 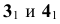 конкурирующих точек 3 и 4 можно сделать вывод, что прямая b находится под прямой a.
конкурирующих точек 3 и 4 можно сделать вывод, что прямая b находится под прямой a.
Моделирование кривой линии
Кривую линию можно рассматривать как траекторию движущейся точки или как совокупность точек, обладающих каким-либо общим для них свойством. Кривая линия может являться результатом взаимного пересечения поверхностей.
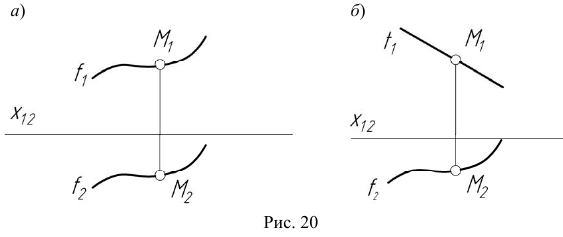
Кривая линия может быть плоской или пространственной. Если все точки кривой расположены в одной плоскости, то такая линия называется плоской. Кривая линия, которая не может быть совмещена с плоскостью всеми своими точками, называется пространственной, например винтовая линия. Моделью кривой линии в общем случае является пара кривых линий 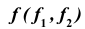 (рис. 20, а).
(рис. 20, а).
В частном случае, когда плоская кривая принадлежит проецирующей плоскости, она моделируется прямой и кривой линиями (рис. 20, б).
Построение произвольной точки M, принадлежащей кривой линии 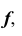 выполняется по тем же правилам, как и для прямой линии (см. рис. 20).
выполняется по тем же правилам, как и для прямой линии (см. рис. 20).
Моделирование замкнутой кривой
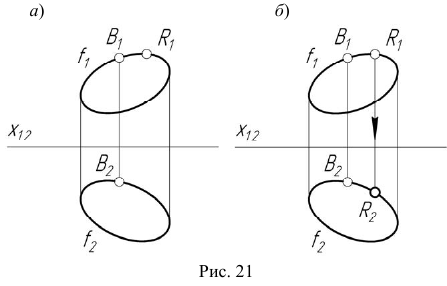
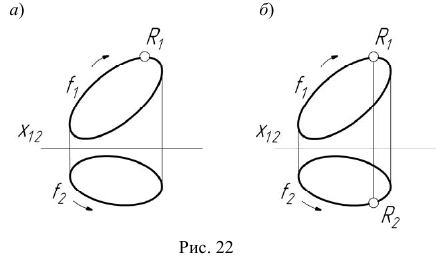
При моделировании замкнутой кривой линии нужно учитывать то, что порядок следования точек на проекциях сохраняется. Кривая на эпюре Монжа задается двумя проекциями и точкой B (рис. 21, а) или двумя проекциями и направлением обхода (рис. 22, а).
На рис. 21, б и 22, б показано построение произвольной точки R, принадлежащей замкнутой кривой линии 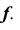
Порядок кривой линии
Наибольшее число точек пересечения плоской кривой с прямой линией определяет порядок плоской кривой. Наибольшее число точек пересечения пространственной кривой линии с плоскостью определяет порядок пространственной кривой. В общем случае порядок проекции кривой равен порядку самой кривой. В частном случае проекция может иметь меньший порядок, как, например, для плоской кривой, лежащей в проецирующей плоскости (рис. 20, б).
Рассмотрим некоторые кривые линии, наиболее широко применяемые на практике.
Кривые второго порядка
Кривые второго порядка называются коническими сечениями, так как они могут быть получены при пересечении поверхности прямого кругового конуса плоскостью. В зависимости от положения секущей плоскости 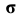 по отношению
по отношению
к образующим конуса получаются различные кривые второго порядка:
- эллипс или окружность, когда плоскость пересекает все образующие (рис. 23, а);
- парабола, когда секущая плоскость параллельна одной образующей (рис. 23, б);
- гипербола, когда плоскость параллельна двум образующим (рис. 23, в).
Когда плоскость проходит через вершину конуса, кривая распадается на пару прямых.
При параллельном проецировании проекцией эллипса и окружности является эллипс или, в частном случае, окружность, проекцией параболы является парабола, проекцией гиперболы — гипербола.
Винтовая линия
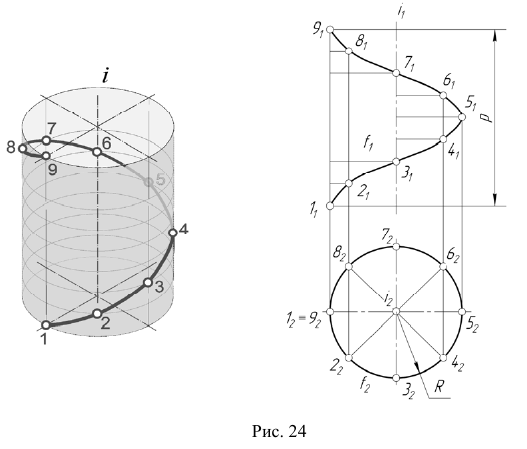
Из пространственных кривых линий широкое применение в инженерной практике получила цилиндрическая винтовая линия, представляющая собой траекторию движения точки, которая равномерно вращается вокруг некоторой оси  и одновременно перемещается вдоль этой оси с постоянной скоростью (рис. 24). Величина перемещения точки в направлении оси
и одновременно перемещается вдоль этой оси с постоянной скоростью (рис. 24). Величина перемещения точки в направлении оси 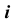 , соответствующая одному полному обороту вокруг оси, называется шагом винтовой линии.
, соответствующая одному полному обороту вокруг оси, называется шагом винтовой линии.
Репер винтовой линии состоит из величины шага p и радиуса R. Рассмотрим пример построения модели винтовой линии 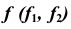 на эпюре Монжа.
на эпюре Монжа.
Пример
Построение модели винтовой линии 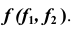
Порядок построения
- Проведем ось вращения
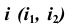 перпендикулярно плоскости проекций
перпендикулярно плоскости проекций 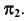
- В первом поле на
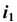 отложим величину шага p, а во втором поле из центра — проекции оси
отложим величину шага p, а во втором поле из центра — проекции оси 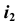 — проведем окружность радиуса R, которая является второй проекцией
— проведем окружность радиуса R, которая является второй проекцией 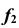 винтовой линии
винтовой линии 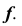
- Разделим окружность
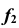 на одинаковое количество равных частей (в данном случае — на 8); интервал шага p также разделим на 8 равных частей.
на одинаковое количество равных частей (в данном случае — на 8); интервал шага p также разделим на 8 равных частей. - Через точки деления окружности
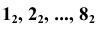 проводим линии проекционной связи.
проводим линии проекционной связи. - Находим первые проекции точек деления окружности
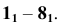
- Соединяем последовательно точки
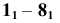 и получаем первую проекцию винтовой линии
и получаем первую проекцию винтовой линии 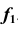
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |