
Многочлены - определение и вычисление с примерами решения
Содержание:
Многочлены
Многочлен
Выражение 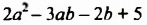
Определение: Многочленом называют сумму нескольких одночленов.
Одночлены, составляющие многочлен, называют членами этого многочлена.
Например, членами многочлена 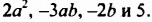 являются одночлены
являются одночлены 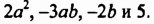
Многочлен, состоящий из двух членов, называют двучленом, многочлен, состоящий из трех членов, — трехчленом и т. д. Так,
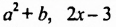 — двучлены;
— двучлены;
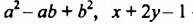 — трехчлены.
— трехчлены.
Считают, что каждый одночлен является многочленом, который состоит из одного члена.
Многочлен стандартного вида
Рассмотрим многочлен 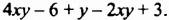 Два его члена
Два его члена 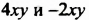 являются подобными слагаемыми, поскольку отличаются только числовыми множителями. Члены -6 и 3 не содержат переменных. Они также являются подобными слагаемыми. Подобные слагаемые многочлена называют подобными членами многочлена.
являются подобными слагаемыми, поскольку отличаются только числовыми множителями. Члены -6 и 3 не содержат переменных. Они также являются подобными слагаемыми. Подобные слагаемые многочлена называют подобными членами многочлена.
Приведем в многочлене 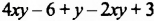 его подобные члены:
его подобные члены:
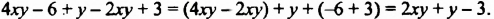
Многочлен 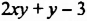 уже не имеет подобных членов, и каждый его член является одночленом стандартного вида. Такой многочлен называют многочленом стандартного вида.
уже не имеет подобных членов, и каждый его член является одночленом стандартного вида. Такой многочлен называют многочленом стандартного вида.
Определение:
Многочлен, являющийся суммой одночленов стандартного вида, среди которых нет подобных членов, называют многочленом стандартного вида.
Среди многочленов
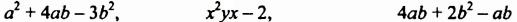
только первый является многочленом стандартного вида, а два другие — нет, поскольку во втором многочлене первый член не является одночленом стандартного вида, а третий многочлен имеет подобные члены.
Степень многочлена
Многочлен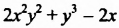 имеет стандартный вид, и его членами являются одночлены соответственно четвертой, третьей и первой степени. Наибольшую из этих степеней называют степенью данного многочлена. Итак,
имеет стандартный вид, и его членами являются одночлены соответственно четвертой, третьей и первой степени. Наибольшую из этих степеней называют степенью данного многочлена. Итак, 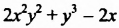 — многочлен четвертой степени.
— многочлен четвертой степени.
Определение:
Степенью многочлена стандартного вида называют наибольшую степень одночленов, образующих данный многочлен.
По этому определению  — многочлены первой степени;
— многочлены первой степени; 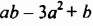 — многочлен второй степени;
— многочлен второй степени; 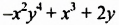 — многочлен шестой степени.
— многочлен шестой степени.
Члены многочлена можно записывать в произвольном порядке. Для многочленов стандартного вида, содержащих одну переменную, члены, как правило, записывают в порядке убывания или возрастания показателей степеней. Например:

Каждый многочлен является целым выражением. Однако не каждое целое выражение является многочленом. Например, целые выражения 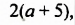
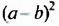 - не многочлены, поскольку они не являются суммами одночленов.
- не многочлены, поскольку они не являются суммами одночленов.
Примеры выполнения заданий:
Пример №117
Записать в стандартному виде многочлен:

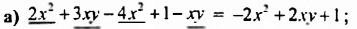
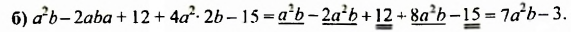
Сложение и вычитание многочленов
Сложение многочленов
Сложим многочлены 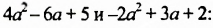
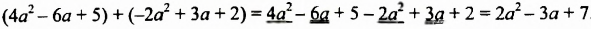 .
.
Раскрыв скобки и приведя подобные слагаемые, мы записали сумму данных многочленов в виде многочлена. Итак, суммой многочленов 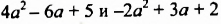 является многочлен
является многочлен 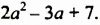
Таким же образом находят сумму трех и более многочленов. Сумму любых многочленов всегда можно записать в виде многочлена.
Вычитание многочленов
Вычтем из многочлена 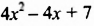 многочлен
многочлен 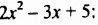
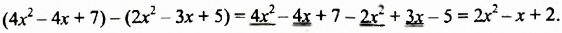
Раскрыв скобки и приведя подобные слагаемые, мы записали разность данных многочленов в виде многочлена. Итак, разностью многочленов 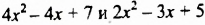 является многочлен
является многочлен 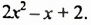
Разность любых многочленов всегда можно записать в виде многочлена.
Примеры выполнения заданий:
Пример №118
Найти сумму многочленов:
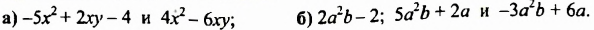
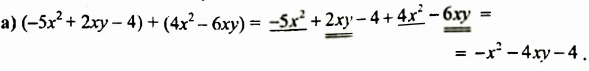
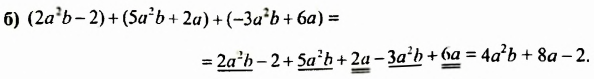
Пример №119
Найти разность многочленов 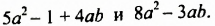
Решение:
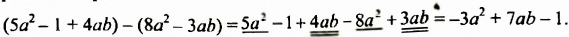
Пример №120
Решить уравнение 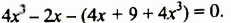
Решение:
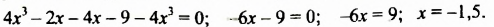
Ответ.-1,5.
Пример №121
Доказать, что сумма трех последовательных нечетных чисел делится на 3.
Решение:
Пусть из трех последовательных нечетных чисел наименьшим является 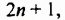 где
где 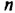 — некоторое целое число. Тогда следующие нечетные числа —
— некоторое целое число. Тогда следующие нечетные числа — 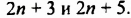 Сумма этих трех чисел
Сумма этих трех чисел
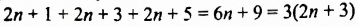
делится на 3, поскольку имеет делитель 3.
Умножение одночлена на многочлен
Умножим одночлен 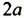 на многочлен
на многочлен 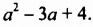 Используя распределительное свойство умножения, получим:
Используя распределительное свойство умножения, получим:
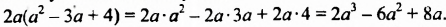
Итак, произведением одночлена 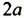 и многочлена
и многочлена 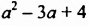 является многочлен
является многочлен 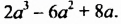 Чтобы найти произведение, мы умножили одночлен на каждый член многочлена и полученные результаты сложили.
Чтобы найти произведение, мы умножили одночлен на каждый член многочлена и полученные результаты сложили.
Чтобы умножить одночлен на многочлен, нужно одночлен умножить на каждый член многочлена и полученные произведения сложить.
По этому правилу можно умножать и многочлен на одночлен. Например:
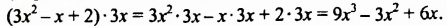
Произведение любого одночлена и любого многочлена всегда можно :ать в виде многочлена.
Примеры выполнения заданий:
Пример №122
Выполнить умножение:

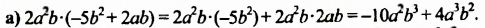
Сокращенная запись: 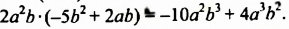
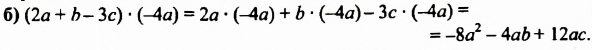
Сокращенная запись: 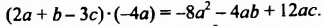
Пример №123
Упростить выражение 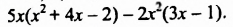
Решение:
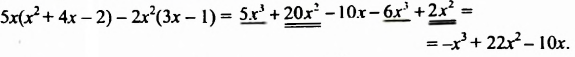
Пример №124
Решить уравнение 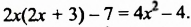
Решение:
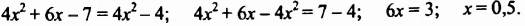
Ответ. 0,5.
Умножение многочлена на многочлен
Умножим многочлен 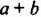 на многочлен
на многочлен 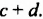 Сведем умножение этих многочленов к умножению многочлена на одночлен. Для этого обозначим многочлен
Сведем умножение этих многочленов к умножению многочлена на одночлен. Для этого обозначим многочлен 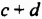 через
через 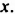 Тогда:
Тогда:
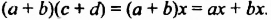
Возвращаясь к замене 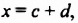 получаем:
получаем:
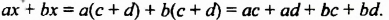
Итак, произведением многочлена 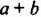 и многочлена
и многочлена 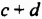 является многочлен
является многочлен 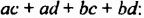
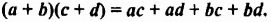
Выражение 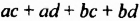 мы получили бы сразу, если бы умножили
мы получили бы сразу, если бы умножили 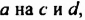 , потом
, потом 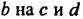 и полученные произведения сложили. Можно сказать и так: произведение
и полученные произведения сложили. Можно сказать и так: произведение 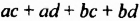 можно получить, если умножить каждый член многочлена
можно получить, если умножить каждый член многочлена 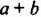 на каждый член многочлена
на каждый член многочлена 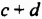 и полученные произведения сложить.
и полученные произведения сложить.
Приходим к такому правилу:
Чтобы умножить многочлен на многочлен, достаточно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Умножим по этому правилу многочлен 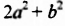 на многочлен
на многочлен 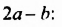
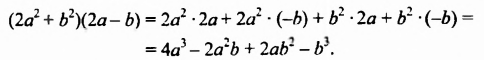
Выполняя умножение многочленов, промежуточные результаты можно не записывать:
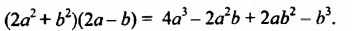
В каждом из рассмотренных примеров произведение двух многочленов мы записывали в виде многочлена. Вообще, произведение любых многочленов всегда можно записать в виде многочлена.
Примеры выполнения заданий:
Пример №125
Выполнить умножение:

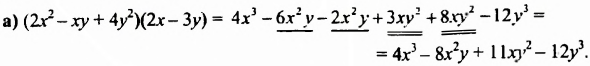
б) Найдем произведение первых двух многочленов, а потом полученное произведение умножим на третий многочлен:
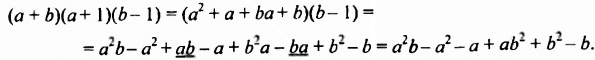
Пример №126
Решить уравнение 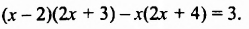
Решение:
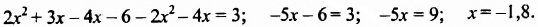
Ответ.-1,8.
Разложение многочленов на множители способом вынесения общего множителя за скобки
1. В шестом классе мы изучали разложение чисел на множители. Например, число 60 можно записать в виде произведения двух чисел 12 и 5:
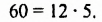
Говорят, что число 60 разложили на два множителя 12 и 5.
На множители можно разложить и многочлены. Например,
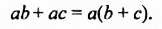
Записав многочлен 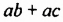 в виде произведения
в виде произведения 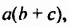 говорят, что многочлен
говорят, что многочлен 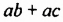 разложили на два множителя
разложили на два множителя 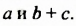 Каждый из этих множителей — многочлен (первый многочлен состоит только из одного члена).
Каждый из этих множителей — многочлен (первый многочлен состоит только из одного члена).
Разложить многочлен на множители значит представить его в виде произведения нескольких многочленов.
Сравните

2. Рассмотрим один из способов разложения многочленов на множители. Выполним умножение одночлена на многочлен:
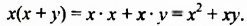
Перепишем эти равенства в обратном порядке:
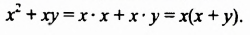
Многочлен 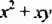 разложили на два множителя
разложили на два множителя 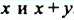 Чтобы разложить многочлен
Чтобы разложить многочлен 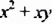 на множители, достаточно в его членах
на множители, достаточно в его членах 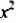 и
и 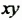 выделить общий множитель
выделить общий множитель 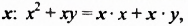 а потом на основании распределительного свойства умножения записать полученное выражение в виде произведения многочленов
а потом на основании распределительного свойства умножения записать полученное выражение в виде произведения многочленов 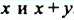
Такой способ разложения многочленов на множители называют способом вынесения общего множителя за скобки.
Примеры выполнения заданий:
Пример №127
Разложить на множителя многочлен 12х3у - 18х2у2.
Решение:
Сначала найдем общий числовой множитель для коэффициентов 12 и -18. Если коэффициентами являются целые числа, то в качестве общего числового множителя берут, как правило, наибольший общий делитель модулей этих коэффициентов. В нашем случае это число 6. Степени с основанием 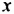 входят в оба члена многочлена. Поскольку первый член содержит
входят в оба члена многочлена. Поскольку первый член содержит 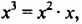 а второй —
а второй — 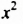 , то общим множителем для степеней с основанием
, то общим множителем для степеней с основанием 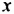 является
является 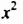 (за скобки выносят переменную с меньшим показателем). В члены многочлена входят соответственно множители
(за скобки выносят переменную с меньшим показателем). В члены многочлена входят соответственно множители 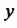 и
и 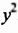 , за скобки можно вынести
, за скобки можно вынести 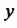 . Таким образом, за скобки можно вынести одночлен
. Таким образом, за скобки можно вынести одночлен 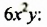
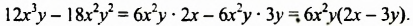
Пример №128
Разложить на множители многочлен 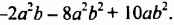
Решение:
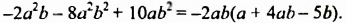
Пример №129
Разложить на множители: 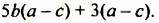
Решение:
Данное выражение является суммой двух слагаемых, для которых общим множителем является выражение 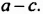 Вынесем этот множитель за скобки:
Вынесем этот множитель за скобки:
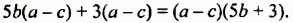
Пример №130
Разложить на множители: 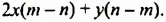
Решение:
Слагаемые имеют множители 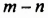 и
и 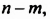 которые отличаются только знаками. В выражении
которые отличаются только знаками. В выражении 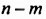 вынесем за скобки -1, тогда второе слагаемое будет иметь вид
вынесем за скобки -1, тогда второе слагаемое будет иметь вид 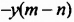 и оба слагаемых будут иметь общий множитель
и оба слагаемых будут иметь общий множитель 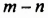 .
.
Следовательно,
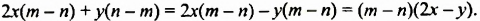
Пример №131
Найти значение выражения 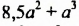 при
при 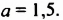
Решение:
Разложим сначала многочлен 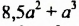 на множители:
на множители:
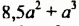
При 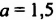 получим:
получим:
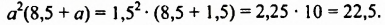
Пример №132
Решить уравнение 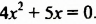
Решение:
Разложим левую часть уравнения на множители:
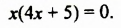
Произведение 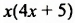 равно нулю только тогда, когда хотя бы один из множителей равен нулю:
равно нулю только тогда, когда хотя бы один из множителей равен нулю:
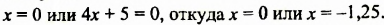
Ответ. 0; -1,25.
Разложение многочленов на множители способом группировки
Изучение этого способа разложения многочленов на множители начнем с рассмотрения примера умножения многочленов. Выполним умножение двучлена 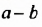 на двучлен
на двучлен 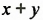 следующим образом:
следующим образом:
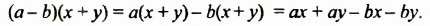
Выполняя преобразования в обратном порядке, многочлен 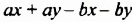 можно разложить на два множителя
можно разложить на два множителя 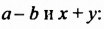
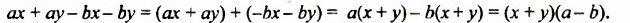
Проанализируем последние преобразования. Имеем многочлен, члены которого можно группировать так, чтобы каждая группа имела общий множитель: для группы 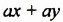 — общий множитель
— общий множитель 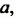 для группы
для группы 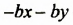 — общий множитель
— общий множитель 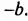 В каждой группе выносим общий множитель за скобки. В образованной разности
В каждой группе выносим общий множитель за скобки. В образованной разности 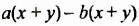 имеем общий множитель
имеем общий множитель 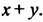 Выносим его за скобки и получаем
Выносим его за скобки и получаем 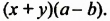
Рассмотренный способ разложения многочленов на множители называют способом группировки. При применении этого способа нужно образовывать такие группы членов, чтобы они имели общий множитель. После вынесения в каждой группе общего множителя за скобки должен образоваться общин множитель для всех групп, который также нужно вынести за скобки.
Многочлен 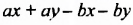 можно разложить на множители, группируя его члены иначе:
можно разложить на множители, группируя его члены иначе:
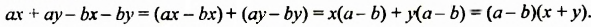
Сравните

Примеры выполнения заданий:
Пример №133
Разложить на множители многочлен 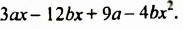
Решение:
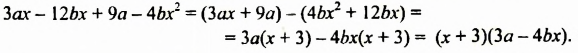
Пример №134
Разложить на множители трехчлен 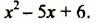
Решение:
Представим второй член 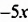 в виде
в виде 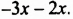 Тогда:
Тогда:
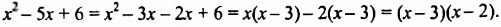
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |