
Мгновенный центр ускорений в теоретической механике
Содержание:
Мгновенный центр ускорений:
В каждый момент движения плоской фигуры в своей плоскости, если 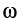 Эту точку называют мгновенным центром ускорений. Обозначим ее через
Эту точку называют мгновенным центром ускорений. Обозначим ее через 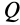 . Для доказательства этой теоремы предположим, что известны по модулю и направлению ускорение какой-либо точки плоской фигуры, угловая скорость и угловое ускорение этой фигуры. Пусть
. Для доказательства этой теоремы предположим, что известны по модулю и направлению ускорение какой-либо точки плоской фигуры, угловая скорость и угловое ускорение этой фигуры. Пусть 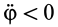 (рис. 56). Мгновенный центр ускорений лежит на линии, проведенной под углом
(рис. 56). Мгновенный центр ускорений лежит на линии, проведенной под углом 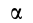 к ускорению точки, тангенс которого вычисляем по формуле
к ускорению точки, тангенс которого вычисляем по формуле
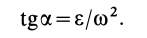
Рис. 56
При этом угол 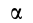 надо отложить от ускорения
надо отложить от ускорения 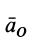 в направлении дуговой стрелки углового ускорения
в направлении дуговой стрелки углового ускорения 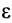 , т. е. в рассматриваемом случае по часовой стрелке. Только в точках этой прямой ускорение
, т. е. в рассматриваемом случае по часовой стрелке. Только в точках этой прямой ускорение 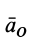 и ускорение от вращения
и ускорение от вращения 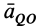 могут иметь противоположные направления и одинаковые значения, т. е.
могут иметь противоположные направления и одинаковые значения, т. е.
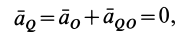
и тогда
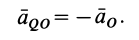
Но
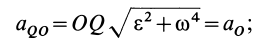
следовательно,
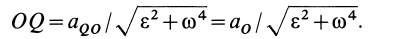
Из приведенного доказательства следует, что мгновенный центр ускорений является единственной точкой плоской фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.
Если мгновенный центр ускорений известен, то, выбрав его за полюс, для ускорения точки  плоской фигуры по формуле (10) получаем
плоской фигуры по формуле (10) получаем
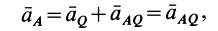
так как
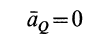
и, следовательно,
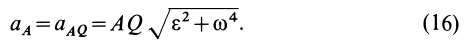
Ускорение 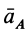 направлено под углом
направлено под углом 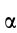 к отрезку
к отрезку 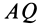 , соединяющему точку
, соединяющему точку 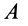 с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения
с мгновенным центром ускорений в сторону дуговой стрелки углового ускорения 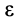 (рис. 57).
(рис. 57).
Для точки 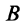 , аналогично,
, аналогично,

и ускорение 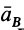 также направлено под углом
также направлено под углом 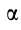 к отрезку
к отрезку 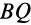 .
.
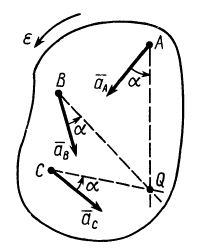
Рис. 57
Из формул (16) и (17) имеем
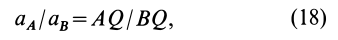
т. е. ускорения точек плоской фигуры при плоском движении пропорциональны расстояниям от этих точек до мгновенного центра ускорений.
Итак, суммируя результаты, получаем, что ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью 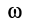 и угловым ускорением
и угловым ускорением 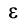 .
.
Для вычисления скоростей точек плоской фигуры при плоском движении принимают, что плоская фигура вращается вокруг мгновенного центра скоростей, а для вычисления ускорения следует считать, что она вращается вокруг мгновенного центра ускорений.
При качении без скольжения колеса по прямой (см. пример в § 7) получается, что ускорение мгновенного центра скоростей не равно нулю; следовательно, в общем случае мгновенные центры скоростей и ускорений являются различными точками плоской фигуры.
Ускорения точек плоской фигуры при плоском движении, подобно скоростям точек, можно определять двумя способами: по формуле (10), выражающей зависимость ускорений двух точек плоской фигуры, и по формуле (16), используя мгновенный центр ускорений. Обычно мгновенный центр ускорений, кроме частных случаев, когда угловая скорость или угловое ускорение равны нулю, располагается на плоской фигуре так, что трудно определить расстояние от него до рассматриваемых точек фигуры. Поэтому определение ускорения точек рекомендуется вычислять по формуле (10).
Рассмотрим способы нахождения мгновенного центра ускорений как в частных, так и в общем случаях.
1. Пусть известно, что угловое ускорение 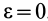 , а угловая скорость
, а угловая скорость 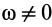 . Очевидно, это возможно в случае, когда плоская фигура вращается в своей плоскости с постоянной угловой скоростью или когда угловая скорость достигает относительно наибольшего или наименьшего значения. В этом случае для угла
. Очевидно, это возможно в случае, когда плоская фигура вращается в своей плоскости с постоянной угловой скоростью или когда угловая скорость достигает относительно наибольшего или наименьшего значения. В этом случае для угла 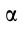
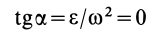
и, следовательно, угол 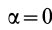 .
.
Мгновенный центр ускорений лежит на прямой линии, по которой направлено ускорение какой-либо точки плоской фигуры (рис. 58). Так как это справедливо для любой точки фигуры, то, следовательно, мгновенный центр ускорений лежит в точке пересечения прямых линий, по которым направлены ускорения точек плоской фигуры. Ускорения точек плоской фигуры в этом случае направлены к мгновенному центру ускорений, так как они состоят только из одной относительной нормальной составляющей от вращения вокруг мгновенного центра ускорений.
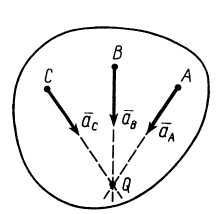
Рис. 58
Если известно ускорение, например точки 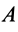 , то мгновенный центр ускорений можно найти по расстоянию
, то мгновенный центр ускорений можно найти по расстоянию 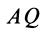 :
:
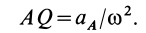
Эта формула получается из (16) в том случае, когда угловое ускорение равно нулю.
2. Пусть угловая скорость 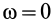 , а угловое ускорение
, а угловое ускорение 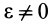 . Это возможно при мгновенном поступательном движении.
. Это возможно при мгновенном поступательном движении.
Тогда
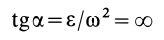
и, следовательно, угол 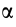 — прямой. Его надо откладывать от ускорения точки в направлении дуговой стрелки углового ускорения. Мгновенный центр ускорений лежит на пересечении перпендикуляров к ускорениям точек плоской фигуры, проведенных из этих точек (рис. 59). Если известно числовое значение ускорения какой-либо точки
— прямой. Его надо откладывать от ускорения точки в направлении дуговой стрелки углового ускорения. Мгновенный центр ускорений лежит на пересечении перпендикуляров к ускорениям точек плоской фигуры, проведенных из этих точек (рис. 59). Если известно числовое значение ускорения какой-либо точки 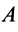 , то расстояние от
, то расстояние от 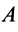 до мгновенного центра ускорений можно вычислить по формуле
до мгновенного центра ускорений можно вычислить по формуле 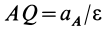 , которая получается из формулы (16) при
, которая получается из формулы (16) при 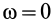 .
.
3. В общем случае, когда угловая скорость 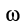 и угловое ускорение
и угловое ускорение 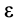 известны и не равны нулю, для угла
известны и не равны нулю, для угла 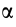 имеем
имеем
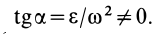
Мгновенный центр ускорений лежит на пересечении прямых линий, проведенных к ускорениям точек фигуры под одним и тем же углом 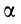 , причем угол а нужно откладывать от ускорений точек в направлении дуговой стрелки углового ускорения независимо от направления угловой скорости плоской фигуры (см. рис. 57). Если известно ускорение, например точки
, причем угол а нужно откладывать от ускорений точек в направлении дуговой стрелки углового ускорения независимо от направления угловой скорости плоской фигуры (см. рис. 57). Если известно ускорение, например точки  , то расстояние от точки
, то расстояние от точки  до мгновенного центра ускорений можно найти по формуле (16), т. е.
до мгновенного центра ускорений можно найти по формуле (16), т. е.
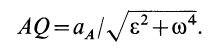
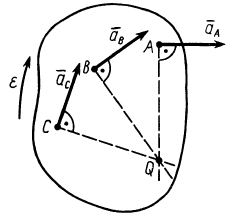
Рис. 59
4. Пусть в данный момент времени известны ускорения двух точек плоской фигуры:  и
и  (рис. 60). Укажем способ нахождения мгновенного центра ускорений в этом случае. По формулам (10)... (13), приняв за полюс точку
(рис. 60). Укажем способ нахождения мгновенного центра ускорений в этом случае. По формулам (10)... (13), приняв за полюс точку 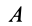 , имеем
, имеем
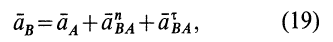
где
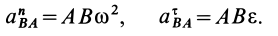
Проецируя левую и правую части векторной формулы (19) на две взаимно перпендикулярные оси 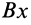 и
и 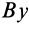 , получаем
, получаем
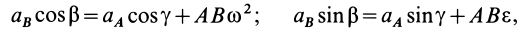
где 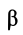 и
и 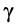 — известные углы соответственно между ускорениями
— известные углы соответственно между ускорениями 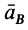 и
и 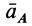 и положительным направлением оси
и положительным направлением оси 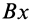 .
.
При принятом направлении оси 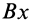 проекцию
проекцию 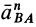 на эту ось надо взять со знаком плюс, так как
на эту ось надо взять со знаком плюс, так как 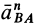 направлена всегда от точки
направлена всегда от точки  к полюсу
к полюсу  . Проекцию ускорения
. Проекцию ускорения 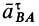 на ось
на ось 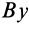 предположительно возьмем с плюсом, считая дуговую стрелку
предположительно возьмем с плюсом, считая дуговую стрелку 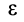 в рассматриваемом случае направленной против часовой стрелки. Определяя
в рассматриваемом случае направленной против часовой стрелки. Определяя 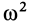 и
и 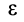 , легко находим
, легко находим
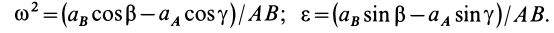
Естественно, что в реальных случаях величина 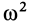 , найденная из полученной формулы, должна оказаться положительной. Знак же углового ускорения
, найденная из полученной формулы, должна оказаться положительной. Знак же углового ускорения 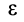 определяется знаком правой части формулы для
определяется знаком правой части формулы для 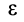 .
.
После того как найдены 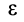 и
и 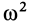 , задача нахождения мгновенного центра ускорений сводится к уже рассмотренному случаю 3.
, задача нахождения мгновенного центра ускорений сводится к уже рассмотренному случаю 3.
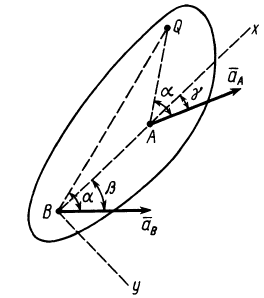
Рис. 60
Основные способы вычисления углового ускорения при плоском движении
При вычислении ускорений точек фигуры при плоском движении необходимо знать угловое ускорение. Рассмотрим некоторые приемы его определения.
1. Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение е определяем путем дифференцирования их по времени, т. е.
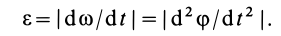
2. Обычно требуется определить угловое ускорение в какой-либо момент времени по другим величинам, известным в этот же момент времени. В этом случае угловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени, считая ее для вывода формулы известной функцией времени. Угловую скорость можно найти по формуле (7):
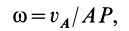
где 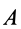 — точка плоской фигуры;
— точка плоской фигуры; 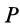 — мгновенный центр скоростей.
— мгновенный центр скоростей.
Дифференцируя 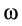 по времени, получаем
по времени, получаем
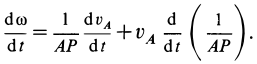
В тех случаях, когда 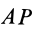 постоянно,
постоянно,

так как
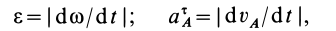
где 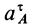 — касательное ускорение точки
— касательное ускорение точки 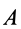 .
.
Так, например, при качении колеса без скольжения по неподвижной прямой линии (см. рис. 55), если за точку 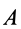 взять центр колеса
взять центр колеса  , то, учитывая, что он движется прямолинейно, получим
, то, учитывая, что он движется прямолинейно, получим
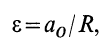
так как в этом случае
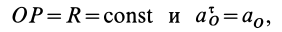
где 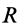 — радиус колеса.
— радиус колеса.
При качении без скольжения одного колеса по неподвижному другому колесу сначала установим зависимость между угловой скоростью 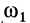 подвижного колеса и угловой скоростью со кривошипа
подвижного колеса и угловой скоростью со кривошипа 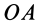 (рис. 61). Учитывая, что мгновенный центр скоростей подвижного колеса лежит в точке соприкосновения колес, получаем
(рис. 61). Учитывая, что мгновенный центр скоростей подвижного колеса лежит в точке соприкосновения колес, получаем
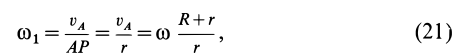
где 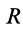 — радиус неподвижного колеса;
— радиус неподвижного колеса; 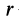 — радиус подвижного колеса.
— радиус подвижного колеса.
Дифференцируя по времени (21), имеем
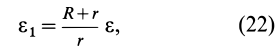
так как
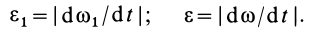
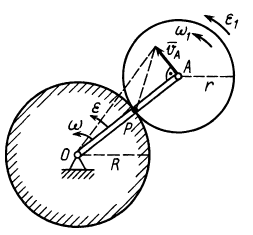
Рис. 61
Из сравнения (21) и (22) видно, что связь между угловыми скоростями и угловыми ускорениями колес полностью аналогична. Это справедливо и для углов поворота колес, если нулевые их значения выбрать в один и тот же момент времени.
При внешнем зацеплении дуговые стрелки угловой скорости и углового ускорения подвижного колеса совпадают с дуговыми стрелками соответственно угловой скорости и углового ускорения кривошипа  .
.
Рис. 62
При внутреннем зацеплении колес дуговые стрелки  и
и  колеса и кривошипа имеют противоположные направления.
колеса и кривошипа имеют противоположные направления.
3. Иногда угловое ускорение  можно найти путем проецирования на оси координат известного по направлению ускорения, например точки
можно найти путем проецирования на оси координат известного по направлению ускорения, например точки 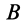 , если ускорение какой-либо другой точки
, если ускорение какой-либо другой точки 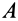 и угловая скорость фигуры
и угловая скорость фигуры 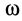 известны или их можно вычислить предварительно.
известны или их можно вычислить предварительно.
Так, если ускорение точки 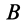

то, проецируя обе части (23) на ось 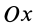 , перпендикулярную ускорению
, перпендикулярную ускорению 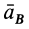 , получаем соотношение, из которого можно определить угловое ускорение, если другие величины, входящие в это соотношение, известны.
, получаем соотношение, из которого можно определить угловое ускорение, если другие величины, входящие в это соотношение, известны.
Определим этим способом угловое ускорение линейки эллипсографа 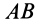 (рис. 62). Эллипсографом называют механизм, в котором одна точка
(рис. 62). Эллипсографом называют механизм, в котором одна точка 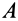 его линейки движется только по оси
его линейки движется только по оси 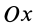 , а другая
, а другая 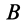 — по оси
— по оси 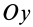 . Линейка эллипсографа обычно приводится в движение вращением кривошипа
. Линейка эллипсографа обычно приводится в движение вращением кривошипа 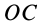 вокруг оси
вокруг оси 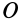 , причем точка
, причем точка 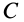 лежит на середине линейки и описывает окружность с центром в точке
лежит на середине линейки и описывает окружность с центром в точке 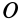 , а точки части линейки
, а точки части линейки 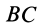 описывают всевозможные эллипсы, заключенные между окружностью и прямой
описывают всевозможные эллипсы, заключенные между окружностью и прямой  . Точки части линейки
. Точки части линейки  соответственно могут описать набор эллипсов, заключенных между окружностью и прямой
соответственно могут описать набор эллипсов, заключенных между окружностью и прямой  .
.
В эллипсографе, когда ускорения точек  и
и 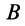 направлены соответственно по осям
направлены соответственно по осям 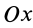 и
и 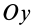 , проецируя (23) на
, проецируя (23) на 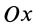 , получаем
, получаем
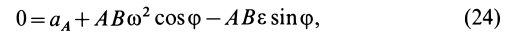
так как
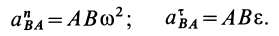
Соотношение (24) и служит для определения углового ускорения линейки эллипсографа 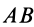 , если все другие величины в этом соотношении известны или их можно предварительно определить.
, если все другие величины в этом соотношении известны или их можно предварительно определить.
Описанным выше приемом удобно определять угловое ускорение шатунов в различных кривошипно-шатунных механизмах, когда у шатуна есть точка, движущаяся прямолинейно.
Если известны ускорения двух точек 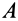 и
и 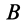 плоской фигуры по модулю и направлению в какой-либо момент времени, то путем проецирования соотношения (23) на два взаимно перпендикулярных направления, одно из которых удобно направить по
плоской фигуры по модулю и направлению в какой-либо момент времени, то путем проецирования соотношения (23) на два взаимно перпендикулярных направления, одно из которых удобно направить по 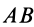 , получим два уравнения для определения угловой скорости и углового ускорения (см. п. 4 § 8).
, получим два уравнения для определения угловой скорости и углового ускорения (см. п. 4 § 8).
Наоборот, по угловой скорости и угловому ускорению из этих уравнений можно найти числовые значения ускорений точек 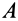 и
и 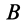 , если известны направления ускорений этих точек.
, если известны направления ускорений этих точек.
4. В задачах (см. § 6, рис. 53), где зависимость между угловыми скоростями различных тел можно установить путем дифференцирования по времени тождественных соотношений между углами поворота, зависимость между угловыми ускорениями часто можно получить путем двукратного дифференцирования по времени этих тождеств. Так, после первого дифференцирования в рассматриваемом случае
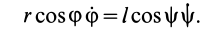
Дифференцируя вторично, имеем
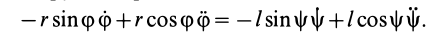
Так как 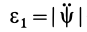 — угловое ускорение шатуна
— угловое ускорение шатуна  и
и  — угловое ускорение кривошипа
— угловое ускорение кривошипа 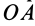 , то
, то
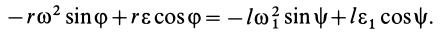
Если дополнительно известно, что угловая скорость 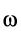 кривошипа
кривошипа 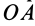 постоянна, т. е.
постоянна, т. е. 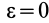 , то
, то
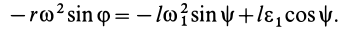
Отсюда можно определить угловое ускорение шатуна в зависимости от углов 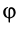 и
и 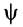 и угловых скоростей
и угловых скоростей 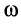 и
и 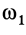 .
.
Пример:
Диск радиусом 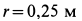 приводится в движение от кривошипа
приводится в движение от кривошипа 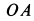 и вертикальной рейки (рис. 63). От кривошипа движение диску передается при помощи шатуна
и вертикальной рейки (рис. 63). От кривошипа движение диску передается при помощи шатуна 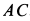 . Рейка движется поступательно по закону
. Рейка движется поступательно по закону 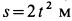 ; кривошип вращается согласно уравнению
; кривошип вращается согласно уравнению 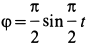 . Угол
. Угол 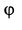 отсчитывается от горизонтального направления.
отсчитывается от горизонтального направления.
Определить угловые скорость и ускорение диска и шатуна, а также скорости и ускорения точек 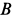 ,
, 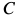 ,
, 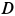 , мгновенные центры скоростей и ускорений диска в момент времени
, мгновенные центры скоростей и ускорений диска в момент времени 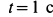 , если
, если 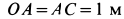 и точки
и точки 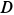 диска и
диска и 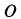 кривошипа расположены на одной горизонтальной прямой.
кривошипа расположены на одной горизонтальной прямой.
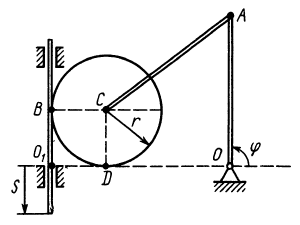
Рис. 63
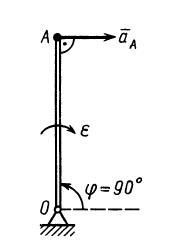
Рис. 64
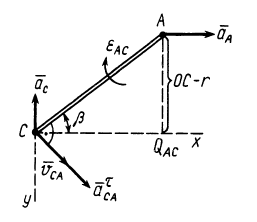
Рис. 65
Решение. Положение кривошипа в момент времени 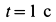 определяется
определяется 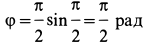 . Кривошип в этот момент занимает вертикальное положение, параллельное рейке.
. Кривошип в этот момент занимает вертикальное положение, параллельное рейке.
Для алгебраических угловой скорости и углового ускорения кривошипа имеем
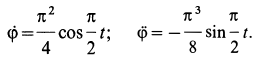
При 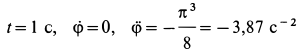 . Таким образом угловые скорость и ускорение кривошипа
. Таким образом угловые скорость и ускорение кривошипа 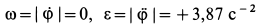 . Дуговую стрелку для
. Дуговую стрелку для 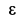 следует направить против положительного направления угла
следует направить против положительного направления угла 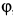 , так как
, так как 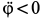 .
.
Для скорости и ускорения точки 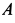 кривошипа, вращающегося вокруг неподвижной оси, имеем:
кривошипа, вращающегося вокруг неподвижной оси, имеем:
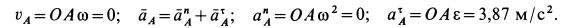
Ускорение 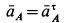 изображено на рис.64 с учетом дуговой стрелки для
изображено на рис.64 с учетом дуговой стрелки для 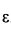 .
.
У точки 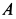 шатуна такие же скорость и ускорение, как и у точки
шатуна такие же скорость и ускорение, как и у точки 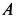 кривошипа. Приняв точку
кривошипа. Приняв точку 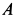 за полюс (рис. 65), определяем скорость точки
за полюс (рис. 65), определяем скорость точки 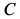 шатуна по формуле
шатуна по формуле

Но 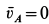 ; следовательно,
; следовательно, 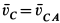 , причем
, причем 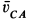 перпендикулярна
перпендикулярна 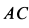 . В проекциях на выбранные оси координат из (а) получаем
. В проекциях на выбранные оси координат из (а) получаем
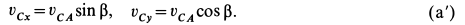
Траекторией точки 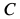 является вертикальная прямая. Поэтому
является вертикальная прямая. Поэтому 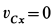 ,
, 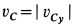 . С учетом этого из (а') имеем, что
. С учетом этого из (а') имеем, что 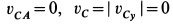 и угловая скорость шатуна
и угловая скорость шатуна 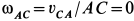 .
.
Вычисляем скорость и ускорение точки 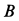 рейки по формулам
рейки по формулам 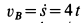 ,
, 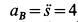 . При
. При 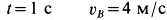 ,
, 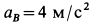 . Производные
. Производные 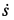 и
и 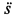 положительны, поэтому
положительны, поэтому 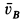 и
и 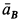 следует направить в сторону возрастания
следует направить в сторону возрастания 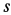 .
.
При отсутствии скольжения у точки 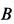 диска будут такие же скорость и составляющая ускорения в вертикальном направлении
диска будут такие же скорость и составляющая ускорения в вертикальном направлении 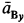 , как и у точки
, как и у точки 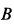 рейки (рис. 66).
рейки (рис. 66).
Приняв за полюс точку 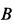 диска, определяем скорость его точки
диска, определяем скорость его точки 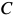 по формуле
по формуле
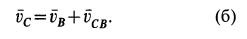
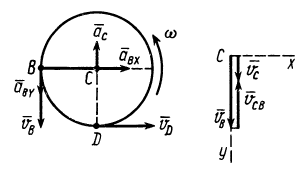
Рис. 66
Предположив, что диск вращается против часовой стрелки, строим треугольник скоростей для точки  в соответствии с (б). Он выродился в отрезок прямой (рис. 66).
в соответствии с (б). Он выродился в отрезок прямой (рис. 66).
В проекциях на оси координат из (б) имеем 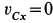 ,
, 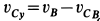 . Но
. Но 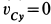 ; следовательно,
; следовательно, 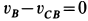 и
и 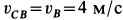 . Скорость
. Скорость 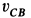 получилась положительной; следовательно, предположение о направлении вращения диска подтвердилось. Угловую скорость диска определяем по формуле
получилась положительной; следовательно, предположение о направлении вращения диска подтвердилось. Угловую скорость диска определяем по формуле
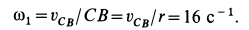
Мгновенным центром скоростей диска является его точка  , так как
, так как 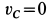 . Используя эту точку как
. Используя эту точку как  , для точки
, для точки  имеем
имеем
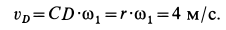
Перейдем к определению ускорений точек и углового ускорения диска 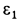 . Приняв за полюс точку
. Приняв за полюс точку 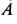 шатуна, ускорение его точки
шатуна, ускорение его точки  определим по формуле
определим по формуле

где 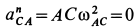 ,
, 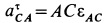 и
и 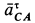 перпендикулярно
перпендикулярно 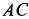 . На основании (в) строим многоугольник ускорений для точки
. На основании (в) строим многоугольник ускорений для точки  (рис. 67, а), предполагая, что
(рис. 67, а), предполагая, что 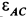 направлено против часовой стрелки.
направлено против часовой стрелки.
В проекциях на оси координат из (в) (см. рис. 65 и 67, а) имеем
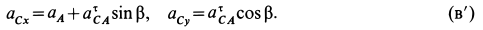
Ускорение точки  направлено параллельно оси
направлено параллельно оси 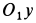 вследствие ее прямолинейного движения в этом направлении. Следовательно,
вследствие ее прямолинейного движения в этом направлении. Следовательно, 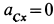 ,
, 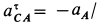 ,
, 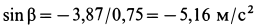 ,
, 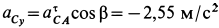 так как
так как
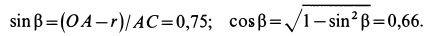
Так как 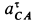 получили со знаком минус, то направление для дуговой стрелки
получили со знаком минус, то направление для дуговой стрелки 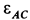 противоположно предположенному (см. рис. 65).
противоположно предположенному (см. рис. 65).
Угловое ускорение шатуна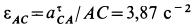 . Ускорение
. Ускорение 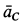 направлено вверх, т.е.
направлено вверх, т.е. 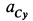 отрицательно, и
отрицательно, и 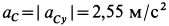 . Для определения углового ускорения диска
. Для определения углового ускорения диска 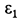 вычислим ускорение точки
вычислим ускорение точки  , приняв за полюс точку
, приняв за полюс точку 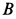 . Имеем
. Имеем

где
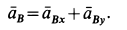
В соответствии с (г) строим многоугольник ускорений для точки  , приняв
, приняв 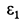 направленным против часовой стрелки (рис. 67, б).
направленным против часовой стрелки (рис. 67, б).
В проекциях на выбранные оси координат из (г) с учетом рис. 67, б получаем
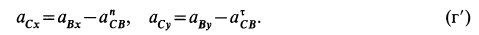
Но
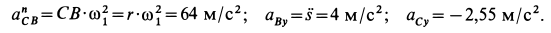
С учетом полученных значений из (г') имеем:
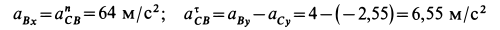
и
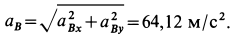
Ускорение 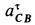 получилось положительным, что подтверждает правильность выбора направления для
получилось положительным, что подтверждает правильность выбора направления для 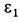 . Угловое ускорение диска
. Угловое ускорение диска
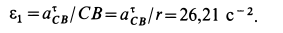
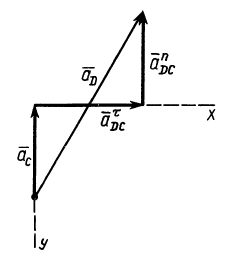
Рис. 68
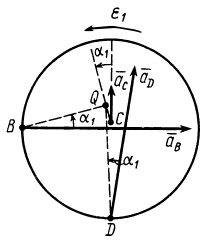
Рис. 69
Приняв за полюс точку  , для ускорения точки
, для ускорения точки 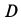 получим
получим

где
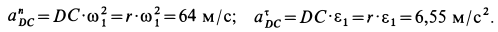
На рис. 68 приведен многоугольник ускорений для точки 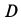 . В проекциях на оси координат из (д) имеем
. В проекциях на оси координат из (д) имеем
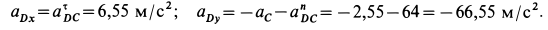
Определим ускорение точки 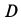 :
:
Для определения мгновенного центра ускорений 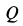 диска вычисляем
диска вычисляем
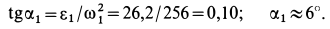
Угол 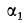 откладываем от ускорения
откладываем от ускорения 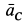 в направлении дуговой стрелки
в направлении дуговой стрелки 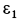 . На линии, проходящей через точку
. На линии, проходящей через точку  под углом
под углом 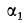 находится точка
находится точка 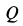 . Расстояние до нее от точки
. Расстояние до нее от точки  определяем по формуле
определяем по формуле
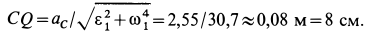
Точка 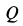 находится вблизи точки
находится вблизи точки  . На рис. 69 указаны в примерном масштабе значения ускорений точек диска и положение
. На рис. 69 указаны в примерном масштабе значения ускорений точек диска и положение 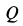 . Ускорения
. Ускорения 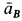 и
и 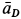 тоже образуют такие же углы
тоже образуют такие же углы 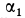 с отрезками прямых, соединяющих эти точки с точкой
с отрезками прямых, соединяющих эти точки с точкой 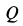 .
.
Мгновенный центр ускорений шатуна 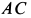 находится в точке
находится в точке 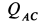 (см. рис. 65), так как для шатуна
(см. рис. 65), так как для шатуна
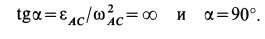
Теорема о конечном перемещении плоской фигуры
Понятие мгновенного центра скоростей плоской фигуры при плоском движении можно ввести используя теорему о конечном перемещении плоской фигуры. Фигуру в ее плоскости из заданного положения I в любое другое положение II (рис. 70) можно перевести одним поворотом в этой плоскости вокруг точки 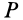 , называемой центром конечного вращения.
, называемой центром конечного вращения.
Пусть в положении I плоская фигура характеризуется отрезком 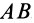 , скрепленным с фигурой, а в положении II этот отрезок займет положение
, скрепленным с фигурой, а в положении II этот отрезок займет положение 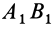 .
.
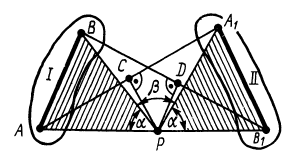
Рис. 70
Рассмотрим случай, когда 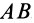 и
и 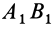 не параллельны. Можно доказать, что центр конечного вращения
не параллельны. Можно доказать, что центр конечного вращения 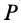 находится на пересечении перпендикуляров
находится на пересечении перпендикуляров 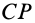 и
и 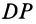 , восставленных из середин отрезков
, восставленных из середин отрезков 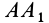 и
и 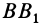 . Для этого докажем, что заштрихованные треугольники
. Для этого докажем, что заштрихованные треугольники 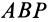 и
и 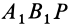 равны по трем сторонам;
равны по трем сторонам; 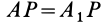 как гипотенузы в равных прямоугольных треугольниках
как гипотенузы в равных прямоугольных треугольниках 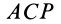 и
и 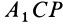 , так как по построению точка
, так как по построению точка 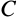 есть середина отрезка
есть середина отрезка 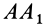 , a
, a 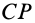 — общий катет треугольников. Аналогично, рассматривая равные треугольники
— общий катет треугольников. Аналогично, рассматривая равные треугольники 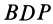 и
и 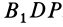 , получаем
, получаем 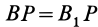 ;
; 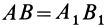 — по условию.
— по условию.
Для перевода плоской фигуры из положения I в положение II достаточно совместить между собой равные треугольники 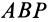 и
и 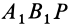 . Это можно осуществить одним поворотом треугольника
. Это можно осуществить одним поворотом треугольника 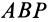 в его плоскости вокруг вершины
в его плоскости вокруг вершины 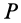 . При этом если сторону
. При этом если сторону 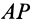 до совмещения со стороной
до совмещения со стороной 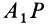 повернуть на угол
повернуть на угол 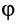 , то сторону
, то сторону 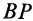 до совмещения со стороной
до совмещения со стороной 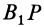 следует повернуть на угол
следует повернуть на угол 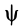 , равный углу ф, так как углы
, равный углу ф, так как углы 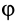 и
и 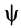 состоят из общего для них угла
состоят из общего для них угла 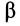 и одинаковых углов
и одинаковых углов 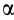 , лежащих в равных заштрихованных треугольниках против равных сторон.
, лежащих в равных заштрихованных треугольниках против равных сторон.
Итак, если отрезок 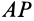 повернуть вокруг
повернуть вокруг 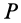 на угол
на угол 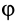 , то отрезок
, то отрезок 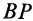 при этом повернется на тот же угол и в том же направлении, что и отрезок
при этом повернется на тот же угол и в том же направлении, что и отрезок 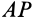 , и, следовательно, точка
, и, следовательно, точка 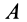 совпадает с точкой
совпадает с точкой 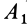 , а точка
, а точка 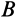 —с точкой
—с точкой 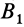 , т. е. отрезок
, т. е. отрезок 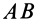 совпадет всеми своими точками с отрезком
совпадет всеми своими точками с отрезком 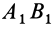 .
.
В том случае, когда отрезок 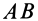 параллелен отрезку
параллелен отрезку 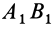 , перпендикуляры
, перпендикуляры 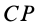 к
к 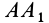 и
и 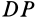 к
к 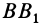 параллельны и, следовательно, пересекаются в бесконечности. В этом случае
параллельны и, следовательно, пересекаются в бесконечности. В этом случае 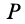 следует считать находящимся в бесконечности и плоскую фигуру из положения I в положение II можно перевести поступательным перемещением, что соответствует повороту фигуры вокруг бесконечно удаленной точки.
следует считать находящимся в бесконечности и плоскую фигуру из положения I в положение II можно перевести поступательным перемещением, что соответствует повороту фигуры вокруг бесконечно удаленной точки.
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |