Методы расчета простых электрических цепей

Методы расчета простых электрических цепей:

Простыми обычно называют электрические цепи, которые образованы последовательным, параллельным или смешанным соединением пассивных элементов. Наиболее часто простые цели содержат один источник энергии. При расчете путем эквивалентных преобразований схемы такие цепи можно свести к одноконтурной цепи, состоящей из источника и одного эквивалентного пассивного элемента.

Сложными называют электрические цепи, в которых кроме простых (последовательное* параллельное), имеются сложные соединения пассивных элементов (например, звезда, треугольник). Они обычно содержат несколько источников энергии. Такие цепи не удается свести к одноконтурным с помощью эквивалентных преобразований.

Эквивалентным называется такое преобразование схемы электрической цепи (или ее отдельного участка), при котором напряжение и ток на входе преобразованной цепи (участка цепи) остаются такими же, как и в исходной схеме.

Эквивалентные преобразования схемы цепи основаны на преобразовании законов электрического равновесии — первого и второго законов Кирхгофа. Поэтому они справедливы как для пассивных, так и для активных элементов цени. Главной целью преобразования схемы является упрощение расчета токов и напряжений за счет упрощения структуры цепи.

Основным смыслом эквивалентных преобразований является замена нескольких элементов в исходной цепи одним эквивалентным элементом. Эквивалентное преобразование источников наиболее часто состоит в замене источника тока эквивалентным источником напряжения и наоборот.

Очевидные правила преобразования, которые следуют из законов Ома и Кирхгофа, сведены в табл. 2.1. Кроме преобразования простых соединений, в таблице приведены формулы для преобразования треугольника элементов  и  эквивалентную звезду элементов и наоборот.

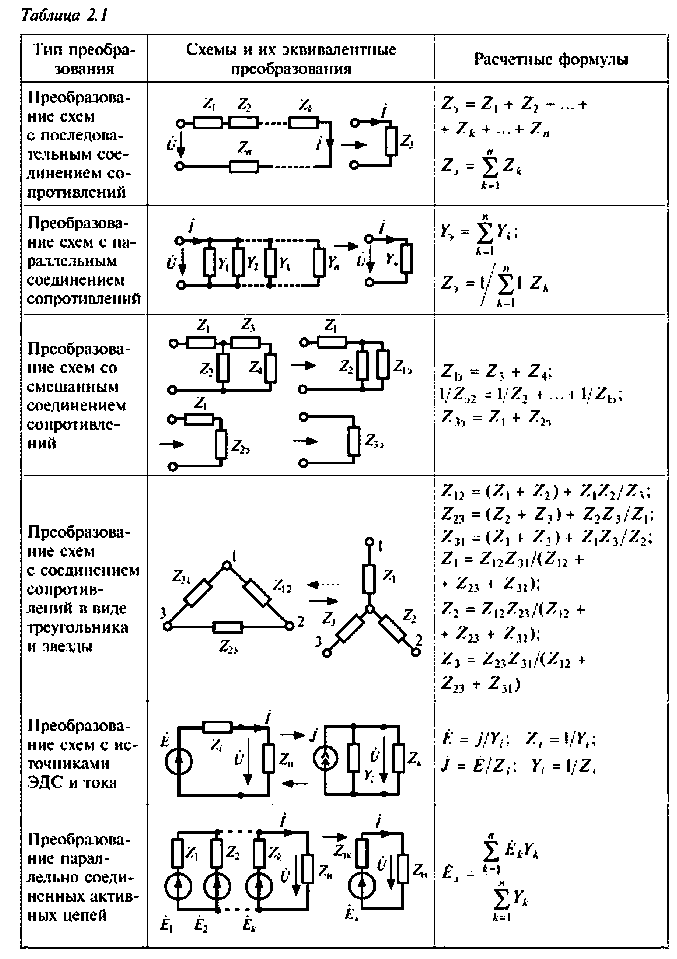
С помощью эквивалентных преобразований расчет простых цепей удается выполнить по закону Ома. Для этого расчет производят путем постепенной замены групп элемента одним эквивалентным («свертывание» схемы), а затем постепенным возвращением к исходной цепи («развертывание» схемы). Применение подобных преобразований к участкам сложных цепей во многих случаях также позволяет упростить решение задач.

Эквивалентные преобразования источников энергии, приведенные в табл. 2.1, справедливы только для реальных источников тока и напряжения, имеющих конечное внутреннее сопротивление.

Расчет цепей в ряде случаев удается упростить, если применить прием эквивалентного переноса идеальных источников без изменения электрического баланса и цепи. При переносе величину и направление источников не изменяют, чтобы не изменить токи в преобразованной схеме.

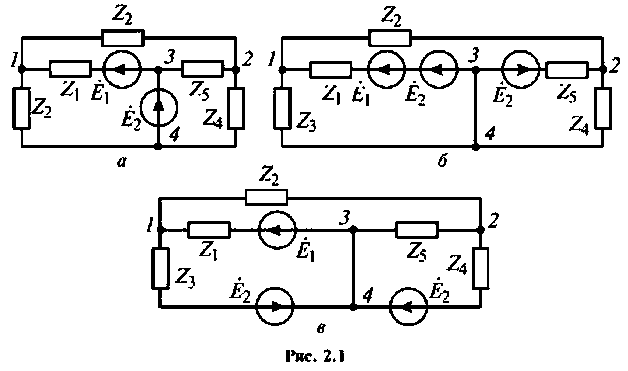
Идеальный источник напряжения, подключенный к некоторому узлу, можно перенести из данной ветви во все другие ветви, подключенные к тому же узлу. Например, в цепи (рис. 2.1, а) источник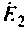 

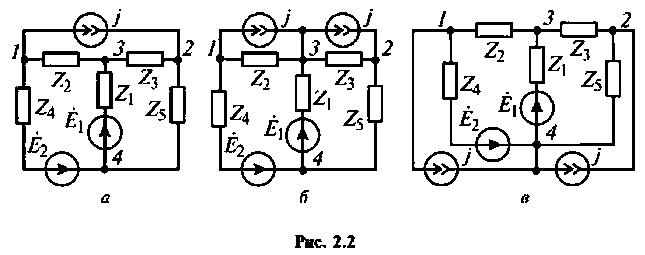
Идеальный источник тока, составляющий один контур с несколькими ветвями, можно заменить несколькими такими же источниками, включенными параллельно каждой ветви этого контура (перенести в каждую ветвь контура). Примеры применения этого правила переноса идеального источника тока приведены на рис. 2.2.

Из рассмотренных правил переноса идеальных источников следует и обратное утверждение: несколько идеальных одинаковых источников в разных ветвях при определенных условиях можно заменить соответственно одним источником без изменения электрического баланса в цепи.

Примеры решения задач:

Пример 2.2.1.

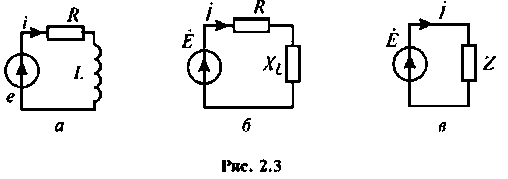
Рассчитать ток в последовательной RL-цепи (рис.2.3,a), напряженке на элементах и комплексную мощность. Построить векторную диаграмму.

Дано: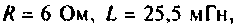 на входе цепи действует ЭДС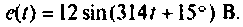

Решение

1.Составим комплексную схему замещения цепи (рис.2.3,б) и произведем эквивалентное преобразование схемы, заменив два элемента одним эквивалентным: 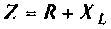(рис. 2.3, в).

Рассчитаем комплексное сопротивление индуктивности

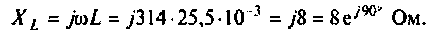
Комплексное сопротивление цепи

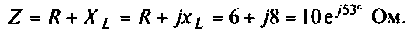
2. Рассчитаем комплексную амплитуду тока в цепи по закону Ома

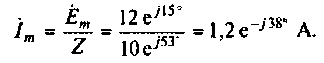
Найдем мгновенное значение тока (оригинал). Для этого умножим комплексное изображение на оператор вращения и, в соответствии с формулой Эйлера, возьмем мнимую часть комплексного числа

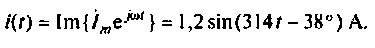
3. Рассчитаем комплексную амплитуду напряжения на элементах цепи:

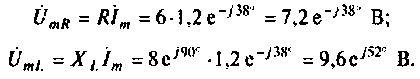
Следовательно, напряжение на элементах определяется выражениями:

4. Рассчитаем комплексную мощность в цепи

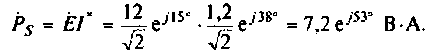
5.Построим векторную диаграмму (рис.2.4). Для последовательной цепи векторную диаграмму удобно строить начиная с вектора тока, общего для всех элементов.

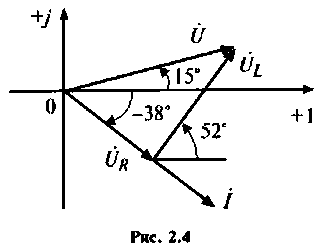
Из решения задачи видно, что ток в цепи с индуктивностью отстает по фазе от входного напряжения.

Пример 2.2.2.

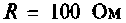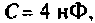Рассчитать токи в цепи (рис.2.5, а), образованной параллельным соединением элементов и определить комплексное, полное, активное и реактивное сопротивления цепи. Построить векторную диаграмму.

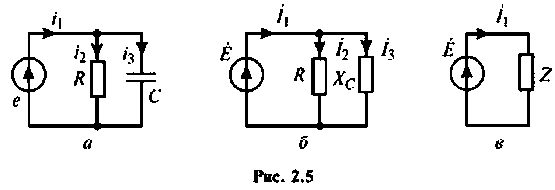
На входе цепи включен источник напряжения с параметрами: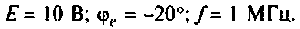  

Решение

1.Составим комплексную схему замещения цепи (рис.2.5,б) и заменим параллельно соединенные элементы одним эквивалентным сопротивлением (рис. 2.5, в)

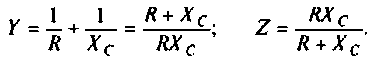
Комплексное сопротивление емкости

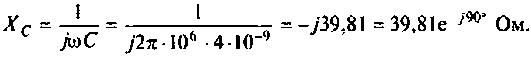
Определим комплексное сопротивление цепи как

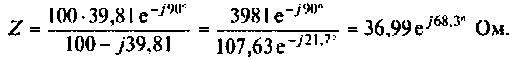
Отсюда получим:

• полное сопротивление цепи
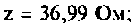
• активное сопротивление
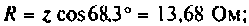
• реактивное сопротивление

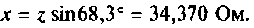
2. Рассчитаем ток в обшей ветви. В соответствии со схемой (рис. 2.5, в) по закону Ома получим

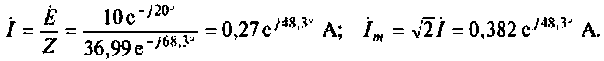
По формуле Эйлера перейдем к оригиналу

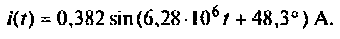
3. Рассчитаем токи в параллельных ветвях. В соответствии с исходной схемой (рис. 2.5, б) . 

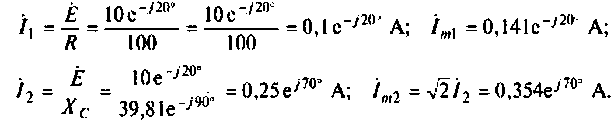
Следовательно,

(

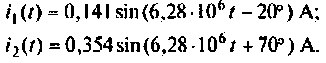
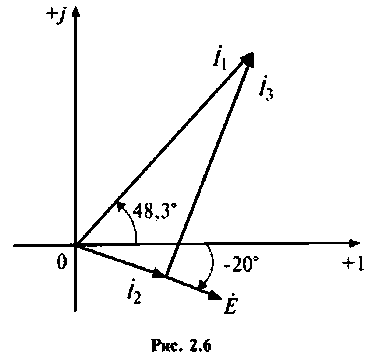
4.Построим векторную диаграмму (рис. 2.6). Для параллельной цепи построение диаграммы удобно начинать с вектора напряжения, в данном случае вектора 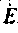,общего для всех элементов,

Полученное решение показывает, что ток в цепи с емкостью опережает но фазе напряжение на входе цепи.

Пример 2.2.3.

Рассчитать токи в ветвях цепи (рис.2.7) и напряжения на элементах, полное, активное и реактивное сопротивления цепи. Построить векторную диаграмму.    

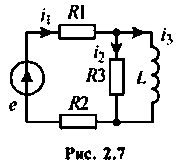
Дано: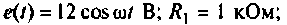

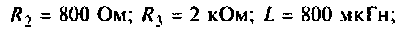
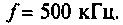
Решение

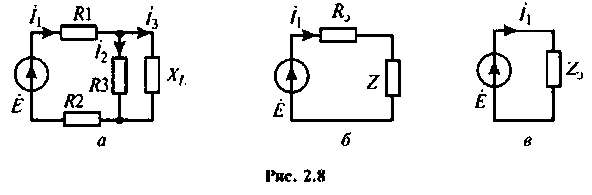
1. Составим комплексную схему замещения цепи (рис. 2.8, а) и произведем эквивалентное преобразование (свертывание) исходной цепи в одноконтурную цепь (рис.2.8, б, в).

Заменим последовательно соединенные сопротивления R1 и R2 эквивалентным сопротивлением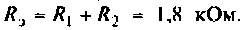

Параллельно соединенные сопротивления 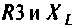заменим эквивалентным комплексным сопротивлением

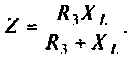
Комплексное сопротивление индуктивности

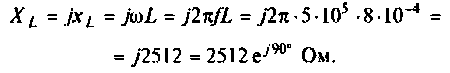
Следовательно,

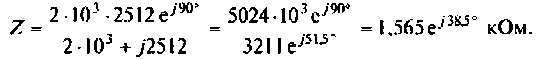
Последовательно соединенные сопротивления 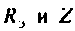заменим одним эквивалентным

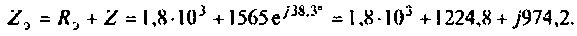
Отсюда

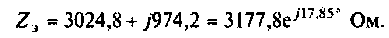
Таким образом, полное сопротивление цепи 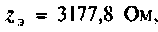активная составляющая  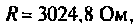а реактивная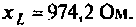

2. Ток 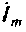в общей ветви найдем по закону Ома. В соответствии со схемой цепи (рис. 2.8, в) получим

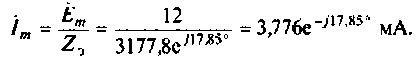
Перейдя к оригиналу по формуле Эйлера, получим

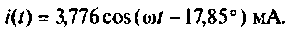
3. Рассчитаем напряжения на элементах 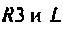цепи по эквивалентной схеме (рис. 2.8, б).

При параллельном соединении элементов напряжения на них одинаковые. Поэтому

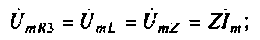
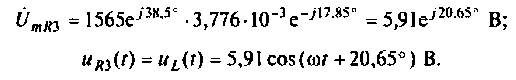
4. Перейдем к исходной схеме замещения и рассчитаем остальные неизвестные токи и напряжения. По формуле для делителя тока рассчитаем:

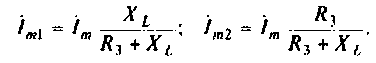
Подставив численные значения, найдем:

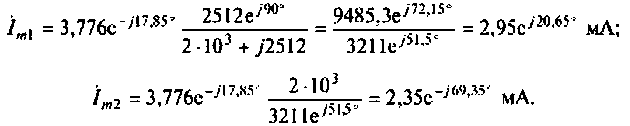
По формуле Эйлера перейдем к мгновенным значениям токов:

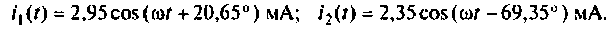
Напряжения на активных сопротивлениях:

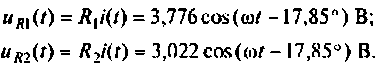
5. Построим векторную диаграмму токов и напряжений (рис. 2.9).

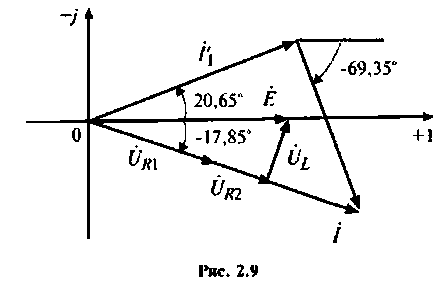
Из диаграммы видно, что ток источника (ток/в обшей ветви) отстает но фазе от ЭДС источника. Это обусловлено наличием в цепи индуктивности.