Методы проецирования в начертательной геометрии с примерами

Содержание:

Правила начертательной геометрии предусматривают построение изображений плоских или объёмных предметов с помощью приёма, называемого проецированием.

В начертательной геометрии для решения геометрических задач используется графический способ, при котором геометрические свойства предметов изучаются непосредственно по чертежу'. Для того, чтобы чертеж соответствовал изображаемому предмету, он должен быть построен по определенным геометрическим законам. Правила построения изображений в начертательной геометрии основаны на методе проекции. Метод проекций предполагает наличие плоскости проекций, объекта проецирования и проецирующих лучей.

Принятые обозначения:

Обозначения геометрических фигур

1.    Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита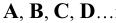

2.   Последовательность точек (и других элементов) - подстрочными индексами: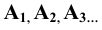

3.    Линии в пространстве - по точкам, определяющим линию или строчными буквами латинского алфавита: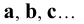

4.    Углы - строчными буквами греческого алфавита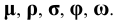

5.    Плоскости - строчными буквами греческого алфавита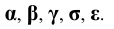

6.    Поверхности - римскими цифрами 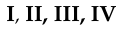а также прописными буквами русского алфавита: цилиндр - 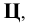конус -  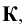     сфера -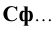

7.    Плоскости проекций - строчной буквой греческого алфавита 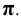 Произвольная плоскость -  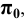 горизонтальная -  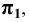     фронтальная - 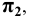профильная -  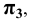любая дополнительная -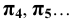 

8.    Оси проекций - строчными буквами 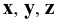или (при введении дополнительных плоскостей)  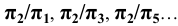Начало координат -        прописной буквой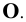

9.    Проекции точек:

• на произвольную плоскость
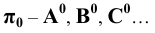
• на горизонтальную плоскость
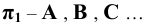
• на фронтальную плоскость
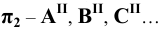
• на профильную плоскость
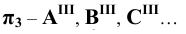
• на дополнительную плоскость

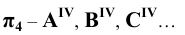
10.    Проекции линий - по проекциям точек, определяющих линию; кроме того:

• горизонтальная линия - буквой
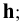
• фронтальная линия - буквой
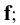
• профильная линия - буквой

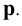
11.    Обозначение плоскостей, заданных следами:

• горизонтальный след плоскости
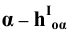
• фронтальный след плоскости
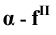
• профильный след плоскости

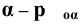
В тех случаях, когда плоскость не требует наименования, обозначение следов упрощенно -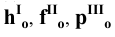

Для проецирующих плоскостей задаётся проекция плоскости:

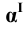• - горизонтально - проецирующая плоскость
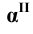• - фронтально - проецирующая плоскость
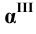• - профильно - проецирующая плоскость

Точки схода следов плоскости - прописными буквами X, Y, Z с индексом соответствующей плоскости: Xtt, Ya, Ztt.

12.    При преобразовании эпюра (чертежа) вращением (или совмещением) в новом положении:

• точки -
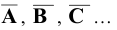
• плоскости -
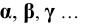
• следы плоскости -

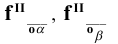
После второго вращения соответственно: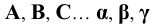  

Новое положение точки схода следов при вращении плоскости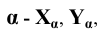  

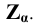
Обозначения отношений между геометрическими элементами

1.    Совпадение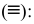

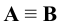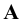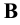- точки и совпадают.

2.    Параллельность ( ):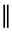

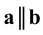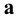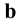- прямые  и параллельны.

3.    Перпендикулярность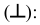

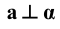- Прямая 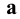перпендикулярна плоскости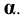

Обозначения теоретико-множественные

1.    Принадлежность ( );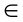

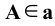- точка 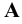принадлежит прямой .

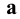2.    Включение ():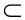

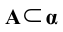- прямая a принадлежит плоскости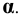

3.    Пересечение ( ):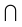

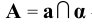- точка 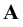есть пересечение прямой 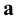с плоскостью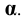

4.    Импликация - логическое следствие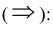

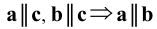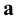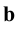- если и параллельны прямой  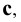то они параллельны между собой.

Методы проецирования

Методы проецирования - это правила построения изображений, рассматриваемых в начертательной геометрии и применяемые в техническом черчении.

Изображение на плоскости предмета, расположенного в пространстве, полученное при помощи прямых линий - лучей, проведенных через каждую характерную точку предмета до пересечения этих лучей с плоскостью, называется проекцией этого предмета на данную плоскость.

Различают два метода проецирования: центральное и параллельное.

Центральное проецирование

Предположим, что в пространстве заданы (Рис. 1.1) кривая 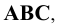плоскость 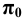и точка 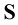. Проведём из точки  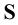через точк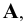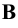и и 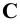кривой 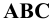прямые линии и отметим точки пересечения последних с плоскостью .  

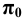Обозначим полученные точки соответственно буквами 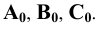 Исходные и построенные элементы получили в начертательной геометрии названия: 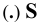- полюс (центр) проецирования; плоскость 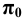- плоскость проекций; прямые 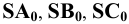- проецирующие лучи; кривая 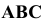- оригинал; точки 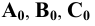- центральные проекции точек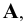 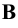 ,  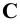на плоскости 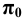(изображение); кривая 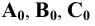- центральная проекция кривой .

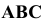Центральное проецирование - это проецирование на заданную плоскость из заданного полюса (центра) проецирования.

Основные свойства центрального проецирования:

• любой геометрический элемент имеет на плоскости проекций единственную проекцию;
• любая точка на плоскости проекций является проекцией бесчисленного множества точек (любой точки, расположенной на                         проецирующем луче);
• проекцией прямой линии является прямая линия.

Достоинством центрального проецирования является наглядность изображения.

Недостаток - сложность определения истинных размеров оригинала по его изображению. Это ограничивает применение центрального проецирования, так как в технике определение истинных размеров проецируемого предмета по его изображению является одним из основных требований.

Данный метод, называемый перспективой, применяется в живописи, архитектуре. Кроме того, фотографии и киноизображения также являются центральными проекциями.

Дополнительное объяснение центрального проецирования:

Аппарат проецирования включает в себя проецирующие лучи, проецируемый объект и плоскость, на которой получается изображение оригинала.

Изображение точки 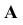на плоскости 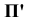(рис. 1) - точка 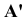получается в пересечении проецирующего луча, проходящего через точку 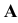, с плоскостью 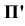. Все лучи проецирующие геометрическую фигуру, исходят из одной точки 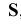, называемой центром проекций. Если эта точка находится на определенном расстоянии от плоскости проекций, то такое проецирование называется центральным.

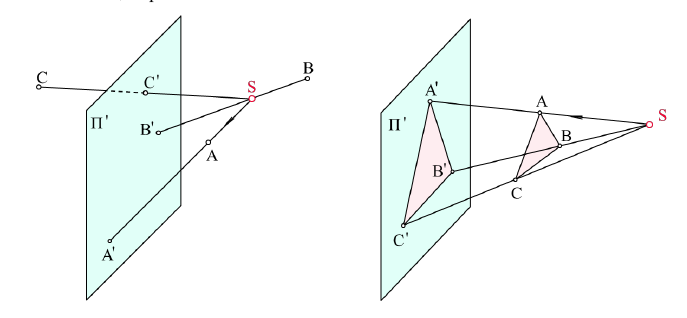
Рисунок 1.1 - Центральное проецирование

Центральное проецирование обладает наглядностью, оно используется при построении изображений архитектурно-строительных объектов, но дает значительное искажение размеров, вследствие чего не применяется для выполнения чертежей.

Подробное объяснение центрального проецирования:

Задается плоскость проекций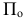и центр проецирования S, точка А, не лежащая в плоскости.

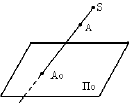
Проведем из S через А прямую до пересечения с плоскостью 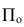. Получим центральную проекцию 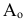точки A. 

• S - центр или полюс проецирования    /а
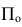• - плоскость проекций
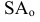• - проецирующий луч (проецирующая прямая) 
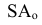•  - центральная проекция точки А на плоскость

1    свойство: при заданных плоскости проекций и центре проёцирования одна точка в пространстве имеет одну центральную проекцию.

Но если есть проекция точки, S и П, то точку в пространстве найти нельзя.

2    свойство: каждая точка на плоскости проекций может быть проекцией бесконечного множества точек.

Центральным проецированием может быть построена проекция любой линии или поверхности как множество проекций всех её точек.

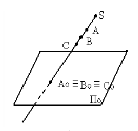
Центральные проекции линии не определяют проецируемую линию.

Для построения проекций линий, поверхностей или тел часто достаточно построить проекции лишь некоторых характерных точек.
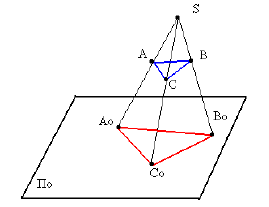
ПРИМЕР: При построении на 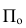проекции АВС достаточно построить проекции 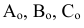трех его точек - вершин А, В и С.

Центральное проецирование применяют для изображения предметов в перспективе, но для технического черчения этот метод неудобен.

Параллельное проецирование

Параллельное проецирование - проецирование с помощью параллельных проецирующих лучей, что наблюдается при бесконечном удалении полюса от плоскости проекций.

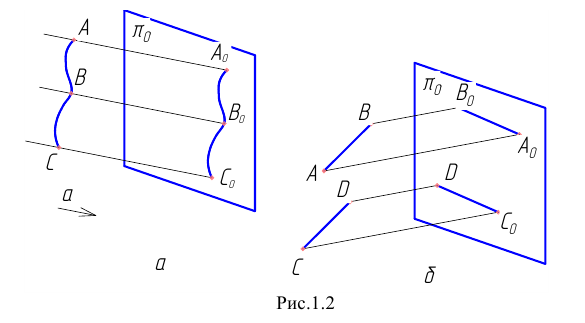
Пусть (Рис. 1.2, а) требуется построить изображение кривой 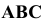на плоскости 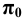. Проведём через точки кривой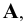 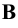 ,  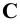проецирующие лучи, параллельные произвольному направлению 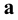и продолжим эти лучи до пересечения с плоскостью 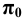. Полученная проекция 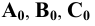- параллельная проекция кривой 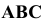на плоскость .

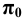Параллельное проецирование обладает теми же свойствами, что и центральное. Кроме того, параллельные прямые проецируются в виде параллельных прямых (см. Рис. 1.2, б); отношение отрезков двух параллельных прямых 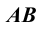и 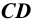(см. Рис. 1.2, б) равно отношению проекций этих отрезков.

Параллельное проецирование разделяется на косоугольное и прямоугольное.

Косоугольное проецирование - это проецирование с помощью лучей, наклонённых к плоскости проекций под некоторым отличным от прямого углом.

Прямоугольное (ортогональное) проецирование - это проецирование с помощью лучей, перпендикулярных к плоскости проекций.

Плоскость проекций обычно относят к декартовой системе координат. Так, прямоугольное проецирование на горизонтальную и вертикальную плоскости проекций получило наименование «Метод прямоугольного проецирования на плоскости координат» (метод Г. Монжа).

Метод прямоугольного проецирования положен в основу выполнения технических чертежей.

Дополнительное объяснение параллельного проецирования:

При параллельном проецировании проецирующие лучи параллельны заданному направлению 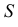(рис. 2). Точки пересечения проецирующих лучей, проходящих через точки 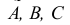с плоскостью проекций 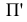- параллельные проекции 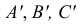плоскости .

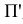Параллельное проецирование можно рассматривать как частный случай центральною при бесконечно удаленном центре проекций В зависимости от направления проецирующих лучей относительно плоскости проекций параллельное проецирование может быть прямоугольным (проецирующие лучи перпендикулярны плоскости проекций) и косоугольным (проецирующие лучи составляют с плоскостью проекций угол, не равный 90°).

Если центр проекций удален в бесконечность, то все проецирующие лучи становятся параллельными и проецирование называется параллельным. В этом случае задается направление проецирования .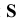

Ортогональное (прямоугольное) проецирование есть частный случай параллельного проецирования, когда все проецирующие лучи перпендикулярны к плоскости проекций .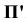

Ортогональная проекция получила наибольшее распространение в технических чертежах. Чертежи, полученные рассмотренными методами проецирования, не обладают свойством обратимости, т.е. по данному чертежу воспроизвести оригинал не решается однозначно.

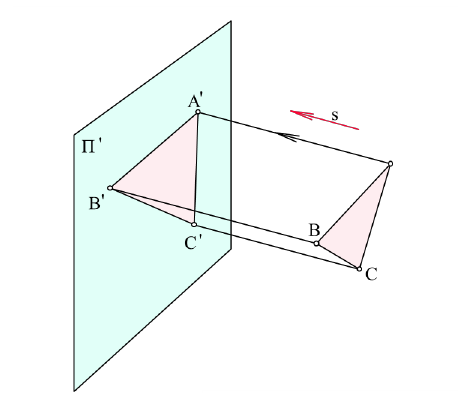
Рисунок 1.2 - Параллельное проецирование

Подробное объяснение параллельного проецирования:

Его можно рассматривать как частный случай центрального, при котором центр проецирования удален в бесконечность.

Применяют параллельные проецирующие прямые, проведенные в заданном направлении.

Если направление проецирования перпендикулярно плоскости проекций, то проецирование называют прямоугольным или ортогональным.

При параллельном проецировании сохраняются все свойства центрального, а так же возникают следующие свойства:

• а) Проекции взаимно // прямых //, а отношение длин отрезков таких прямых равно отношению длин их проекций
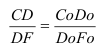
• б) Плоская фигура, // плоскости проекций проецируется на эту плоскость в натуральную величину
• в) Если прямая перпендикулярна направлению проецирования, то её проекци ей является точка

Если есть центр параллельной проекции, мы не сможем определить положение точки в пространстве.

Гаспар Монж предложил взять две взаимно перпендикулярные плоскости проекций (горизонтальную 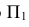и фронтальную 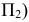и используя метод прямоугольного проецирования направить проецирующие лучи перпендикулярно плоскостям.

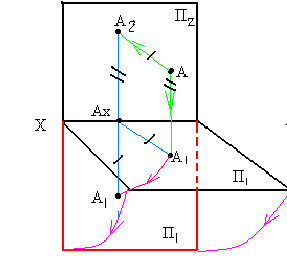
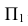- горизонтальная плоскость проекций 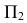-фронтальная плоскость проекций X- ось проекций- линия пересечения плоскостей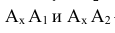

Ах А] и АхА2- перпендикулярны оси X -линии связи

Если есть в пространстве точка А, то опускаем из неё перпендикуляр на 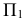(горизонтальная проекция точки А - 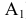) и на плоскость 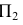(фронтальная проекция точки А -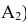

Но данное наглядное изображение точки в системе 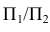    для целей черчения неудобно.

Преобразуем его так, чтобы горизонтальная плоскость проекций совпала с фронтальной, образуя одну плоскость чертежа.

Это преобразование осуществляется путем поворота вокруг оси X плоскости П| на угол 90° вниз. При этом 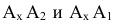образуют один отрезок, расположенный на перпендикуляре к оси проекций X, называемом линией связи.

Получили чертеж под названием эпюр Монжа.

Горизонтальная и фронтальная проекции всегда лежат на одной линии связи у перпендикулярной оси.

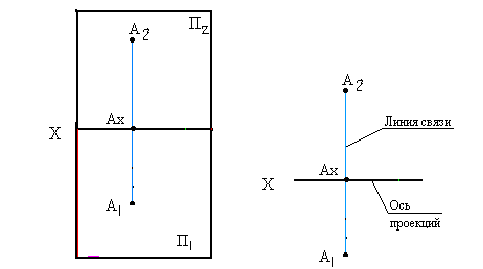
В зависимости от сложности для полного выявления форм деталей бывает необходимо три и более изображений. Поэтому вводят три и более плоскостей проекций.

Проецирование точки на три плоскости проекций. Комплексный чертеж точки.

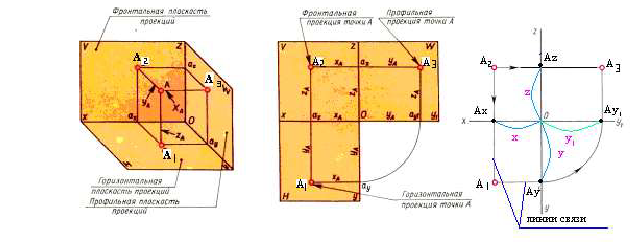
Получили эпюр Монжа для трех плоскостей или комплексный чертеж точки А

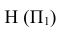- горизонтальная плоскость проекций  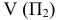- фронтальная плоскость проекций 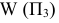- профильная плоскость проекций 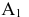- горизонтальная проекция точки А 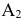- фронтальная проекция точки А 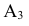- профильная проекция точки А 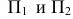-образуют ось X 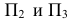-образуют ось Z 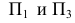-образуют ось Y

Две проекции точки лежат на одной линии связи, перпендикулярной оси.

Отрезки проецирующих линий от точки А до плоскостей проекций - координаты точки 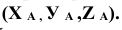. Задаются числами.

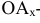- абсцисса точки А-координата 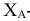- расстояние от А до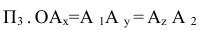 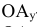- ордината точки А-координата 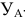- расстояние от А до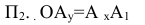 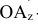          аппликата точки А-координата 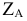- расстояние от А до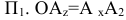

Проецирование на плоскости координат

Плоскости координат могут в пространстве располагаться произвольно. Принято одну из плоскостей располагать горизонтально, а две другие - вертикально. Одну из вертикальных плоскостей координат располагают перед наблюдателем (фронтально).

Зададим (Рис. 1.3) прямоугольную систему координат 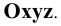 Обозначим плоскости 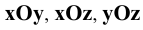соответственно буквами 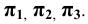Эти плоскости называют горизонтальной 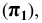фронтальной 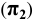и профильной 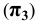плоскостями проекций.

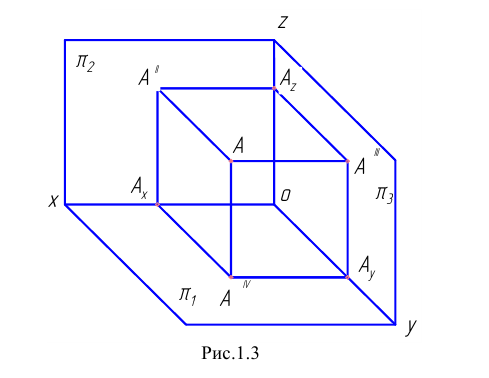
Возьмём произвольную точку 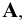расположенную над плоскостью 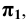перед плоскостью 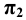и слева от плоскости  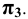Спроецируем эту точку прямоугольно на плоскости 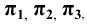для чего опустим из точки 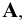перпендикуляры на данные плоскости. В точках пересечения перпендикуляров с упомянутыми плоскостями получим точки  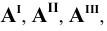которые соответственно называются горизонтальной, фронтальной и профильной проекциями точки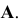

Каждая пара проецирующих лучей определяет плоскость, параллельную плоскости координат и, следовательно, перпендикулярную к соответствующей оси координат. Так плоскость 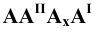перпендикулярна к оси 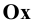и пересекается с ней в точке 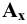, аналогичные рассуждения справедливы для плоскостей  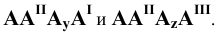В результате проделанных построений получим параллелепипед, называемый параллелепипедом координат точки 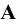. Отрезки 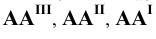определяют расстояния от точки 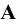до плоскостей координат и называются координатами точки 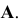Обозначают: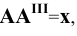 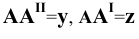. Нетрудно заметить, что отрезк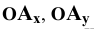и и 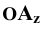  численно равны координатам точки 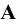, т.е.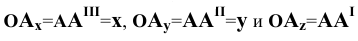

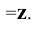
Таким образом, положение точки 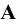определяется тремя её координатами, а положение каждой из ее проекции 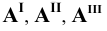- двумя координатами.

В общем случае плоскости 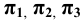(Рис. 1.4, а) делят пространство на восемь частей (трёхгранных углов) называемых октантами или координатными углами.

Причём для правой системы координат, изображённой на Рис. 1.4, а принята следующая нумерация углов:

• I угол - левый, передний, верхний (х, у, z);
• II угол - левый, задний, верхний (х, -у, z);
• III угол - левый, задний, нижний (х, -у, -z);
• IV угол - левый, передний, нижний (х, y,-z);
• V угол - правый, передний, верхний (-х, у, z);
• VI угол - правый, задний, верхний (-х,-у, z);
• VII угол - правый, задний, нижний (-х, -у, -z);
• VIII угол - правый, передний, нижний (-x, y, -z);

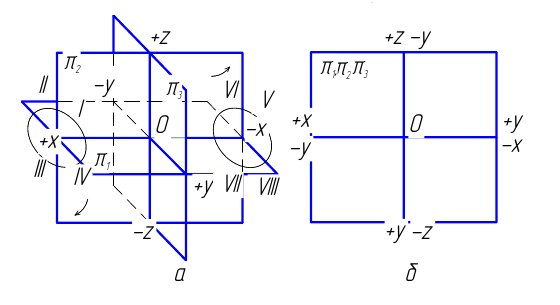
Практически изображение выполняется на одной плоскости (листе бумаги, доске и т. п.), называемой плоскостью чертежа. С этой целью плоскость 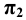мысленно совмещают с плоскостью чертежа, а плоскост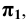и и 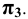совмещают с плоскостью 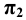вращением вокруг осе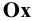й и 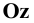в направлениях, указанных на Рис. 1.4, а стрелками. Изображение плоскостей и осей координат, совмещённых с плоскостью чертежа, показано на Рис. 1.4, б. Следует обратить внимание, что ось 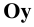изображается дважды, совмещаясь соответственно с осями 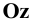и .

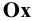Проецируемая точка может располагаться в любом из координатных углов (октантов). Поэтому для построения её проекций кроме численных значений координат необходимо учитывать их знаки.

Рассмотрим случай общего положения точки, т.е. случай, когда требуется построить проекции точки 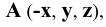 причём 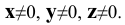Сначала построим косоугольные проекции заданной точки. Для этого нанесём на чертеже оси координат и отложим на них заданные значения координат с учётом их знаков (Рис. 1.5, а). Получим точки 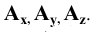. Далее строим горизонтальную 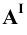, фронтальную 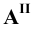и профильную 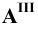проекции в точках пересечения прямых, проведённых из 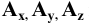параллельно соответствующим осям координат. Изображение точки А получим в точке пересечения перпендикуляров, восстановленных к плоскостям проекций из точек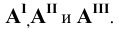 

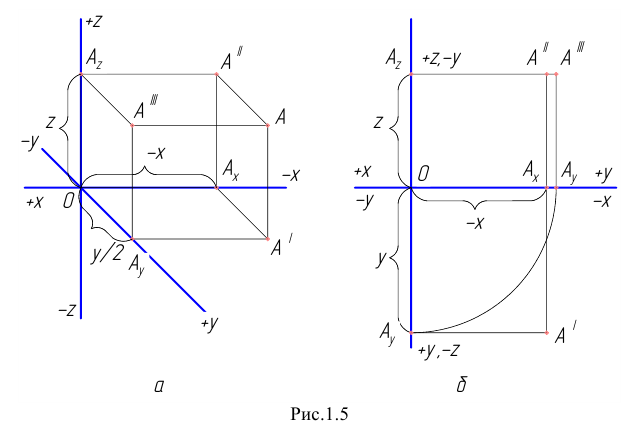
По полученному чертежу легко установить, что данная точка 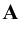расположена в пятом октанте.

Построим прямоугольные проекции точки 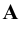. Для этого на чертеже (см. Рис. 1.5, б) проводим оси координат  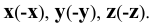Затем откладываем на осях заданные значения координат с учётом знака и получаем точки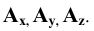 

При этом координата 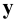всегда откладывается дважды: на оси  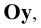совмещённой с осью 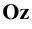(вертикальная ось 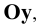), и на оси 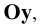совмещённой с осью 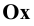(горизонтальная ось ). Находим прямоугольные проекции точки 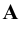в пересечении перпендикуляров, восстановленных из 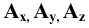к соответствующим осям координат. Эти перпендикуляры показывают на чертеже тонкими сплошными линиями проекционной связи.

Отметим, что в прямоугольных проекциях горизонтальная 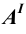и фронтальная 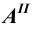проекции точки  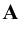всегда расположены на одной вертикальной прямой, а фронтальная 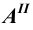и профильная 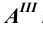проекции - на одной горизонтальной прямой.

Изображения, полученные при совмещении плоскостей проекций с плоскостью чертежа, называются эпюрами. Эпюр (эпюра) - чертёж, на котором пространственная фигура изображена методом ортогональных проекций на три плоскости; эпюр позволяет определить форму и размеры проецируемого предмета, так как координаты 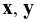и 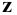любой его точки могут быть установлены непосредственно по чертежу.

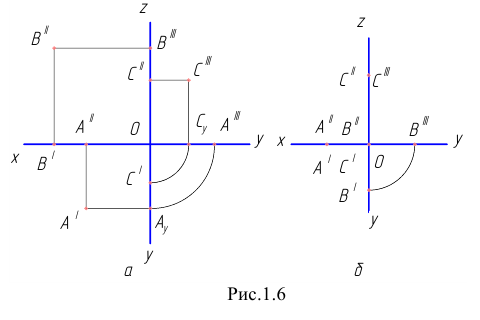
В частных случаях точка может быть расположена в одной из плоскостей координат или лежать на одной из осей (Рис. 1.6, а, б). При этом, если точка лежит в плоскости координат, то её проекция на данную плоскость совпадает с самой точкой, а две другие её проекции расположены на осях координат (см. Рис. 1.6, а). Если же точка лежит на оси координат, то две её проекции совпадают с самой точкой, а третья совпадает с началом координат (см. Рис. 1.6, б).

• Чертежи на заказ

Аксонометрические проекции

Если оси прямоугольной системы координат и отнесённый к ним предмет спроецировать центрально или параллельно на некоторую плоскость, то полученное изображение называется аксонометрией. Рассмотрим наиболее часто употребляемые на практике виды аксонометрических проекций.

Косоугольным аксонометрическим проецированием на фронтальную плоскость называют косоугольное проецирование на плоскость, совмещённую с плоскостью 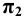прямоугольной координатной системы, к которой отнесён проецируемый предмет.

Возьмём прямоугольную координатную систему (Рис. 1.7, а) и спроецируем её косоугольно на плоскость 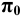, совмещённую с плоскостью  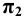данной системы. Проекции осе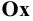й и 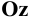на плоскость 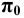совпадают с этими осями. Начало координат тоже будет собственной проекцией. Остаётся спроецировать на плоскость ось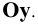

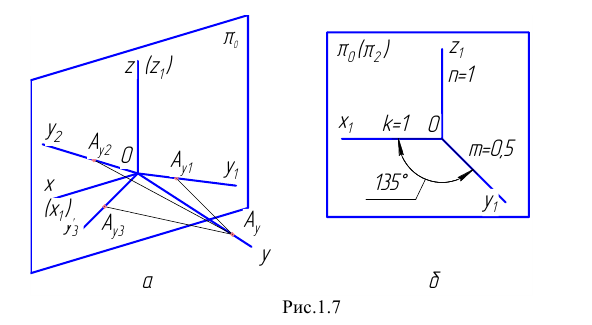
Для этого выберем на оси 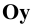произвольную точку 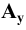и спроецируем её на плоскость 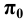с помощью произвольного проецирующего луча, пересекающего плоскость 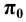например в точке 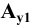. Прямая 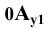будет косоугольной проекцией оси 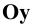на плоскост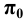ь (ось ).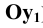

Если изменять направление проецирования, то на плоскости 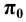можно получить бесконечное множество изображений точки  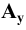и соответственно осей  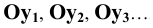Решение будет однозначным, если задать направление проецирования. Оно задаётся углами между проекциями осей координат и так называемыми коэффициентами искажения. Коэффициентом искажения для данной оси координат называется отношение длины проекции отрезка упомянутой оси к истинной длине самого отрезка.

Обозначим:  k  - коэффициент искажения для оси 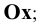m - для оси 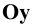; n - для оси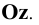

При косоугольном проецировании на фронтальную плоскость (см. Рис. 1.7, а, б) имеем 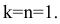 Для оси 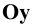значение m может изменяться в пределах 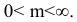. Из соображений большей наглядности принимают m=0,5, а угол между проекциями осе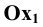й и 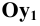составляет 135° при  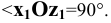Косоугольные проекции осей координат на фронтальную плоскость в совмещении с плоскостью чертежа показаны на Рис. 1.7, б.

Иногда данную проекцию называют косоугольной диметрией в связи с тем, что два измерения по 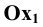оси и оси 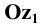равны между собой (k = n = 1).

Прямоугольной изометрией называют случай прямоугольного проецирования на плоскость, одинаково наклонённую к трём плоскостям проекций. Такая плоскость проекций пересекает оси координат на равных расстояниях от начала координат.

Изобразим (Рис. 1.8, а) прямоугольную координатную систему 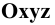и отложим на осях координат равные в натуре отрезки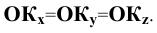

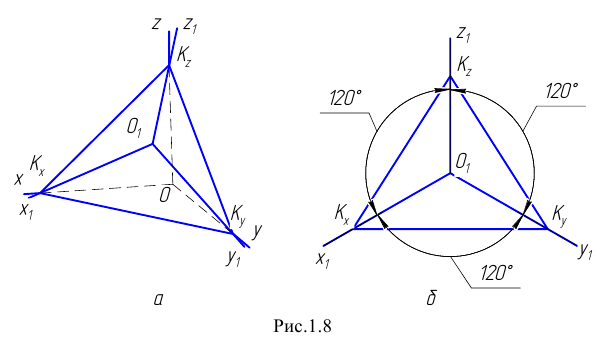
Соединим попарно прямыми линиями точки 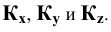 Треугольник 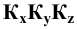будет изображением части плоскости, равно наклонённой к плоскостям координат. Примем эту плоскость за плоскость проекций и спроецируем на неё прямоугольно оси координат. Точки  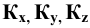 являются собственными проекциями. 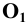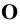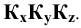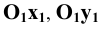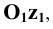Проекцию начала координат получим в точке пересечения перпендикуляра, опущенного из точки на плоскость  Тогда искомые проекции осей координат изображаются в виде прямых и проведённых из точки 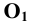через точки  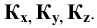Можно показать, что оси координат 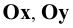и 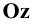проецируются с одинаковыми искажениями, причём натуральные коэффициенты искажения k=m=n=0,82. Углы между проекциями осей координат:  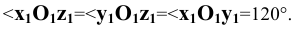Изометрические проекции осей координат в совмещении с плоскостью чертежа показаны на Рис. 1.8, б.

Если изометрическая проекция имеет целью выявление формы предмета (без наглядного отражения его размеров), то при построении точек допускается откладывать на осях значения координат точек с приведенными коэффициентами искажения, равными единице (k=m=n=l). При этом изображение предмета получается увеличенным в отношении 1,0/0,82=1,22.

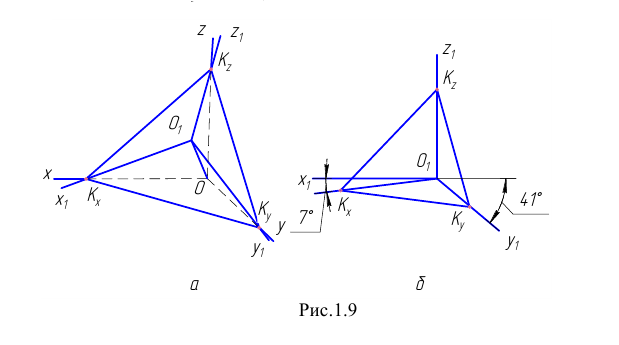
Прямоугольной диметрией называют случай прямоугольного проецирования на плоскость, равно наклонённую к двум осям координат. Обычно проецируют на плоскость, равно наклонённую к плоскостям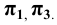

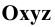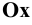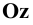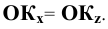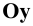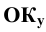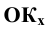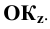Изобразим (Рис. 1.9, а) прямоугольную координатную систему и отложим на осях и равные в натуре отрезки По оси отложим произвольный отрезок не равный и Плоскость, определяемая треугольником 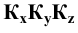одинаково наклонена к плоскостям 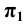и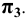

Спроецируем на неё прямоугольно начало координат (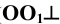 плоскости 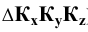) и оси координат ( 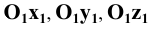— прямые, проведённые из точки 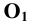через точки 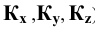). Поскольку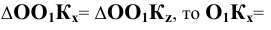 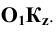. Следовательно,  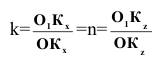Значение коэффициента искажения m, исходя из условий получения наиболее наглядного изображения, принимают равным k/2=n/2. При этом k=n=0,94; m=0,47; 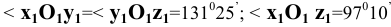На практике обычно принимают k=n=l, m=0,5. В этом случае линейные размеры изображения увеличиваются в отношении 1,0/0,94=1,06.

Диметрические проекции осей координат в совмещении с плоскостью чертежа показаны на Рис. 1.9, б.

Инженерная и машинная графика - одна из дисциплин, составляющих основу всего общеинженерной подготовки специалистов.

Теоретической базой инженерной и машинной графики является начертательная геометрия, позволяющая создать одно из гениальнейших изобретений человеческой мысли - чертеж. Чертеж - это своеобразный графический язык, с помощью которого, используя лишь точки, линии, геометрические знаки, буквы и цифры, изображаются самые разнообразные поверхности, машины, приборы, инженерные сооружения и т. д.

Начертательная геометрия возникла из потребностей практической деятельности человека. Задачи строительства различных сооружений, крепостных укреплений, жилья, храмов требовали предварительного их изображения. От примитивных рисунков, передававших приближенные геометрические формы сооружений, постепенно совершался переход к составлению проекционных чертежей, отражавших геометрические свойства изображаемых на них объектов.

Выдающуюся роль в развитии начертательной геометрии как науки сыграл французский геометр и инженер Гаспар Монж, который систематизировал и обобщил накопленный к тому времени опыт и теоретические познания в области изображения пространственных фигур на плоскости. В своем труде «Начертательная геометрия», изданном в 1798 году, Г. Монж дал первое научное изложение общего метода изображения пространственных фигур на плоскости.

Начертательная геометрия способствует развитию пространственного воображения и логического мышления.

Впервые отдельные правила и приемы построения изображений были систематизированы и развиты французским ученым Гаспаром Монжем (1746-1818). Изложенный Гаспаром Монжем метод параллельного проецирования является основным методом, используемым при выполнении технических чертежей в настоящее время.

Материал в учебном пособии изложен кратко в объеме, соответствующем количеству учебного времени, отведенного на изучение предмета. Теоретический материал сопровождается примерами решения задач. В конце каждой главы имеются вопросы для закрепления проработанного материала.

Может быть использовано в качестве учебного пособия при обучении студентов технического профиля очной и заочной форм обучения.

Свойства прямоугольного проецирования

1. Каждая точка и прямая в пространстве имеет единственную проекцию на плоскости, так как через любую точку в пространстве можно провести только один проецирующий луч.
2. Каждая точка на плоскости проекций может быть проекцией множества точек, если через них проходит общий проецирующий луч.
3. Если точка принадлежит прямой, то проекция точки принадлежит проекции этой прямой.
4. Отношение отрезков прямой равно отношению их проекций.
5. Отношение отрезков параллельных прямых равно отношению их проекций.
6. Если прямая перпендикулярна плоскости проекций, то проекцией этой прямой является точка.
7. Если отрезок прямой параллелен плоскости проекций, то на эту плоскость отрезок спроецируется в натуральную величину.

Комплексный чертёж точки (эпюр точки)

Комплексный чертеж (эпюр) точки состоит из двух или трех ортогональных проекций. Эти проекции получают на взаимно перпендикулярных плоскостях проекций. Одна из плоскостей проекций Н называется горизонтальной плоскостью проекций, вторая V - фронтальной, а третья W - профильной.

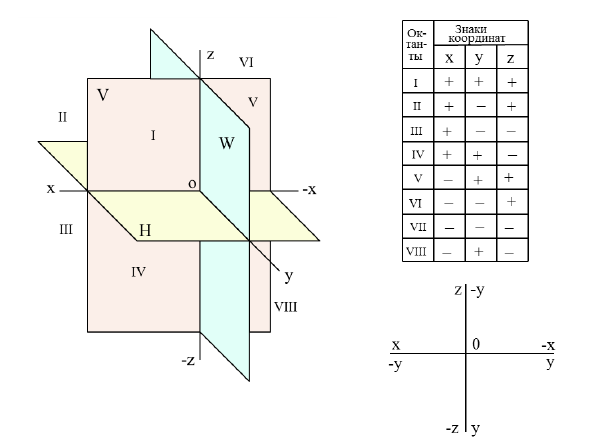
Рисунок 1.3 - плоскости проекций, знаки координат

Спроецируем точку А на плоскости проекций Y, V и W. Точка А' называется горизонтальной проекцией точки А, точка А" - ее фронтальная проекция, точка А''' - ее профильная проекция. Расстояние 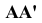точки 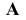от плоскости 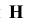называется высотой точки A (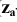-аппликата), ее расстояние 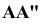от плоскости V - глубиной точки А ( 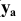- ордината), а расстояние 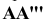от плоскости 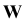- широтой точки А ( 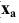-абсцисса).

Таким образом, какая-либо точка пространства А будет определяться тремя ее координатами: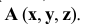

Чтобы получить плоский чертеж точки А, плоскости Н и W вращают до совмещения с плоскостью V. Прямые , соединяющие проекции точки А, называются линиями связи и соответственно перпендикулярны к осям х и z. Проекции точки А определяются координатами: А' (х,у), A" (x,z), А"' (у,z). Полученный эпюр точки будет обратимым чертежом.

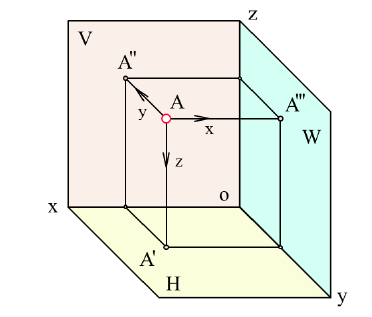
Рисунок 1.4 - Точка в системе плоскостей проекций

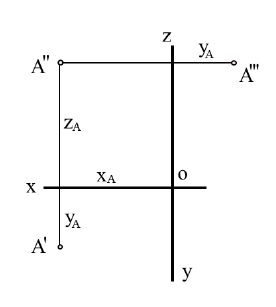
Рисунок 1.5 - Эпюр точки

Центральный метод проецирования

В пространстве выбирают произвольную точку S - центр проецирования и плоскость П' - плоскость проекций или картинную плоскость (рис. 2.1). Для получения центральной проекции предмета, например отрезка [AB], необходимо через центр проекций и каждую точку предмета (точки A и B) провести прямые до пересечения с картинной плоскостью. Эти прямые называются проецирующими лучами. Точка пересечения проецирующего луча с картинной плоскостью называется проекцией точки на эту плоскость.

Проекция предмета на плоскость - это множество проекций всех его точек на заданную плоскость.

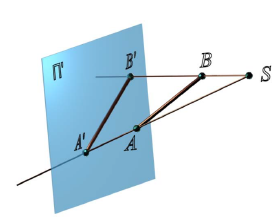
Рис. 2.1. Центральный метод проецирования:
[ SA) и [ SB) - проецирующие лучи;
A[ ' = 'SA ) П' и B [='SB) П' - центральные проекции точек A и B на плоскость П'

Чертежи, полученные методом центрального проецирования, отличаются большой наглядностью, поскольку построены на том же принципе, что и аппарат человеческого зрения. Однако такие чертежи сложно выполнять и измерять, поскольку размеры предмета искажаются.

Параллельный метод проецирования

Если центр проекций удалить в бесконечность, то угол между проецирующими лучами будет стремиться к нулю, и проецирующие лучи окажутся параллельными (рис. 2.2).

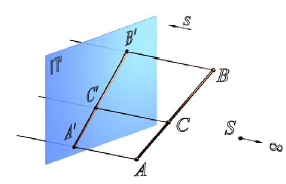
Рис. 2.2. Параллельный метод проецирования: s - направление проецирования;
[SA), [SB) и [SC) - проецирующие лучи;
A', B' и C' - параллельные проекции точек A, B и C на плоскость П' в направлении s

 Свойства параллельных проекций

1. Проекцией точки является точка (см. рис. 2.2).
2. Проекцией прямой линии является прямая линия (см. рис. 2.2), за исключением случая, когда прямая параллельна направлению проецирования.
3. При параллельном проецировании сохраняются пропорции.
4. Если точка принадлежит какой-либо линии, то проекция этой точки принадлежит проекции этой линии C ∈ AB C'∈ A'B' (см. рис. 2.2).
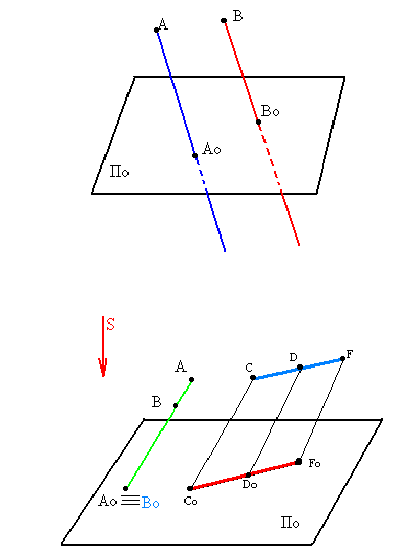
5. Если прямые параллельны между собой, то их проекции также параллельны (рис. 1.3).

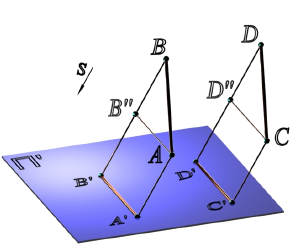
Рис. 2.3. Проекции параллельных прямых:
[AB ]//[DC] [A' B']//[D' C']

Ортогональные проекции

Если направление проецирования s перпендикулярно плоскости проекций, то метод проецирования называется ортогональным (рис. 2.4), а полученные проекции - ортогональными.

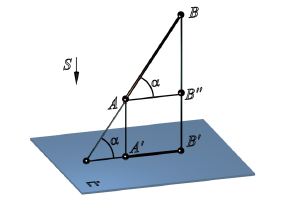
Рис. 2.4. Ортогональное проецирование:
s 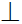П', ∣A'B '∣ = ∣AB''∣=∣AB∣ x cos α
 

Ортогональное проецирование является частным случаем параллельного проецирования и имеет те же свойства.

Изображения, полученные при проецировании на одну плоскость проекций, не являются обратимыми, то есть задача о восстановлении оригинала по заданной проекции a´ не решается однозначно. Проекции всех точек, расположенных на проецирующем луче AA ´ на плоскость П', совпадают.

Для получения обратимых чертежей нужны некоторые дополнительные условия. Например, изображаемый предмет жестко связывают с координатными осями и проецируют на плоскость вместе с ними. Такие чертежи называются аксонометрическими. Другой метод состоит в том, что предмет проецируют на несколько взаимно перпендикулярных плоскостей проекций. Такие чертежи называются ортогональными и именно они получили наибольшее распространение в технике.