Метод узловых потенциалов

Метод узловых потенциалов:

Метод базируется на первом законе Кирхгофа и законе Ома для участка цепи с ЭДС. Неизвестными величинами считают потенциалы узлов, при этом потенциал одного из узлов принимают равным нулю. Это вполне допустимо, так как ток каждой ветви зависит не от абсолютных значений потенциалов ее узлов, а от их разности.

Пусть потенциал узла 4 равен нулю (рис. 3.1). Тогда уравнения для узлов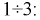

• 1 узел: 
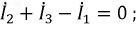
• 2 узел: 
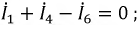
• 3 узел: 

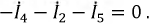
Токи в ветвях на основании закона Ома выражаются:

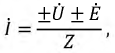
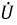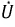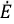где - напряжение на зажимах соответствующих ветвей; знаки перед и  выбираются в зависимости от того, совпадает или не совпадает направление тока 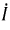с положительными направлениям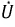и  и 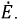Тогда токи ветвей:

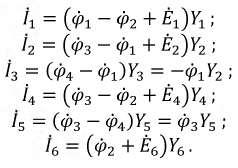
Найденные уравнения подставляются в исходную систему уравнений, составленную по первому закону Кирхгофа. После несложных алгебраических преобразований получаем новую систему уравнений относительно неизвестных потенциалов узлов 

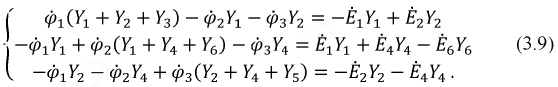
Разберем структуру любого уравнения, например, первого. Потенциал первого узла 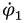умножается на сумму проводимостей всех ветвей, образующих данный узел: 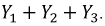Со знаком "-" записываются слагаемые вида  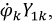где 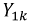- проводимость 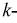ой ветви, входящей в узел 1,  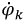- потенциал соседнего (смежного) узла.

В правой части уравнения слагаемые вида 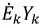записываются со знаком “+” в том случае, если источник ЭДС направлен к рассматриваемому узлу, в противном случае - со знаком "-".

Найденные потенциалы могут иметь различные знаки. С этими знаками значения потенциалов подставляются в уравнения для нахождения токов.

Систему уравнений (3.9) можно переписать в обобщенной форме, как это ранее было сделано в методе контурных токов.

Метод двух узлов

Этот метод является частным случаем метода узловых потенциалов.

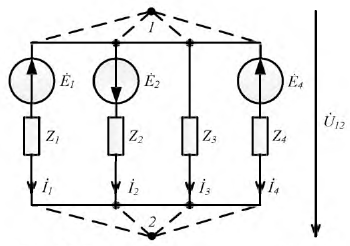
Рис. 3.2. Разветвленная цепь с двумя узлами

Для схемы по рис. 3.2 выполним следующие рассуждения. Пусть, к примеру, 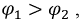тогда потенциал 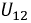убывает от узла 1 к узлу 2. По методу узловых потенциалов, полагая, что 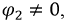получим следующие уравнения:

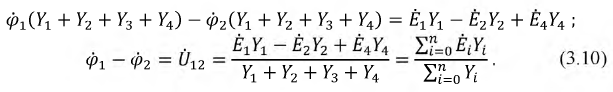
Для произвольно выбранных направлений токов имеем

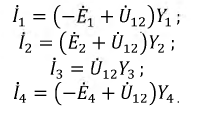
Проверка правильности полученных результатов осуществляется по первому закону Кирхгофа.