Метод узловых и контурных уравнений

Метод узловых и контурных уравнений:

Метод узловых и контурных уравнений для расчета сложных электрических цепей подразумевает составление системы уравнений по законам Кирхгофа. При составлении системы уравнение должно учитываться следующее.

1. Число уравнений равно числу токов в цепи (число токов par но числу ветвей в рассчитываемой цепи). Направление токов ветвях выбирается произвольно.
2. По первому закону Кирхгофа составляется (
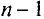
3. Остальные уравнения составляются по второму закону Кирхгофа.

В результате решения системы уравнений определяются искомые величины для сложной электрической цепи (например, все-таки при заданных значениях ЭДС источников Е и сопротивлений резисторов). Если в результате расчета какие-либо токи полу чаются отрицательными, это указывает на то, что их направление противоположно выбранному.

Пример 4.9

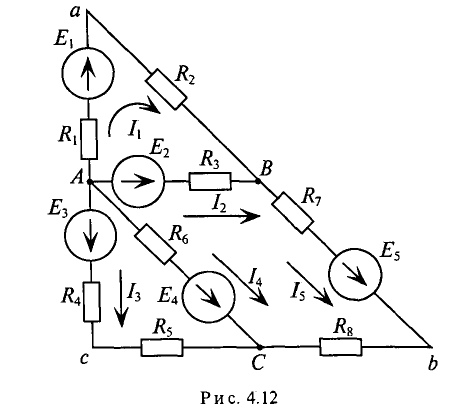
Составить необходимое и достаточное количество уравнений по законам Кирхгофа для определения всех токов в цеп (рис. 4.12) методом узловых и контурный уравнений.

Решение

В рассматриваемой сложной цепи имеется 5 ветвей, следовательно, 5 различных токов, поэтому для расчета необходимо составить 5 уравнений, причем 2 уравнения — по первому закон Кирхгофа (в цепи n = 3 узловых точки А, В и Q и 3 уравнения -по второму закону Кирхгофа (внутренним сопротивлением источников пренебрегаем, т.е.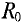

Составляем уравнения:

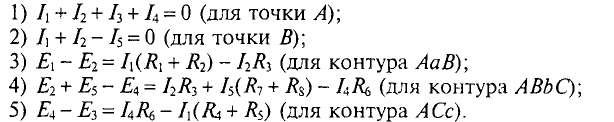
Обход по часовой стрелке.

Пример 4.10

Определить токи в примере 4.7 методом узловых и контурных нений (схема рис. 4.10) при тех же заданных условиях.

Решение

При выбранном в схеме рис. 4.10 направлении токов составим необходимое и достаточное количество уравнений по законам Кирхгофа:

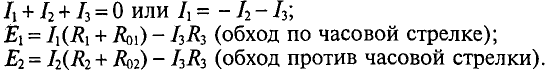
В уравнение (2) подставляются значения тока 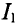из уравнения и числовые значения заданных величин. Тогда уравнения (2) и будут выглядеть так:

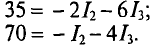
Для сокращения тока 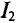при суммировании уравнений (2) и (3) числовые значения уравнения (3) умножаются на 2 (два).

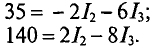
Результаты суммирования:

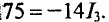
Откуда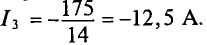

Из уравнения (3):

И из уравнения (1):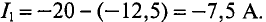

Очевидно, что полученный результат совпадает с результатом, полученным методом узлового напряжения.