Метод пространства состояний электрических цепей

Содержание:

Анализ электрических цепей методом пространства состояний:

Все переменные величины, характеризующие динамическую систему G (рис. 9.1) или имеющие определенное к ней отношение, целесообразно разделить на три группы: 1) входные переменные или входные воздействия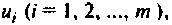

Величины 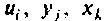   предполагаются функциями времени 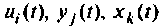и обозначают соответственно значения величин  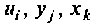в момент времени t. Как известно, электрические процессы в любой схеме определяются параметрами 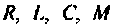и функциями источников 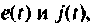а также независимыми начальными условиями переменных при 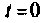— токами в индуктивных элементах 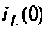и напряжениями на емкостных элементах  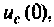которые должны быть известны или рассчитаны. Через  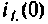и

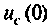выражаются искомые переменные состояния цепи или системы. Они же определяют энергетическое состояние схемы. Поэтому в качестве переменных состояния 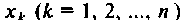целесообразно выбирать токи  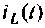и напряжения  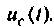Источники, включенные в схему, можно назвать входными переменными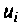 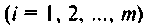или вектором входа 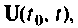искомые величины — выходными переменными 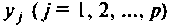или вектором выхода  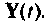Для цепи с 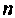независимыми токами 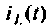и напряжениями 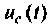должны быть заданы 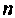независимых начальных условий.

Множество всех значений, которые может принять вектор входа 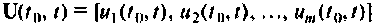 в момент времени t образует пространство входа системы. Аналогично множество всех значений, которые может принять вектор выхода 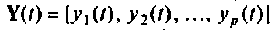в момент времени образует пространство выхода системы, и множество всех значений, которые может принять вектор состояния 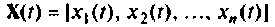в момент времени t образует пространство состояний системы. В любой момент времени t состояние системы определяется вектором  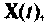являющимся функцией вектора начального состояния 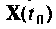и вектора входа  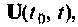т. е.

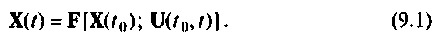
Вектор выхода 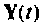также является функцией 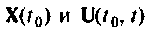и может быть записан как

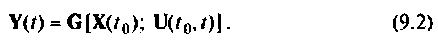
Уравнения (9.1) и (9.2) часто называют уравнениями состояния системы. Для систем, описываемых линейными дифференциальными уравнениями, уравнения состояния (9.1) и (9.2) сводятся к следующим:

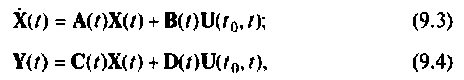
где 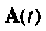— матрица коэффициентов размерности 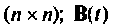— матрица управления (выхода) размерности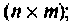 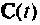— матрица выхода размерности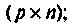 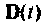— матрица обхода системы раз-мерности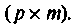

На рис. 9.2 изображена обобщенная схема, динамика которой описывается уравнениями (9.3) и (9.4) [4, 8].

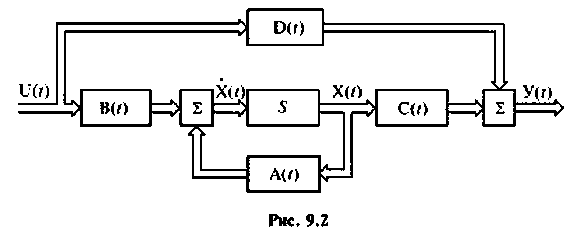
Если система стационарная, то ее динамика описывается уравнениями состояния, матрицы которых имеют элементы, не изменяющиеся во времени,  т. е.

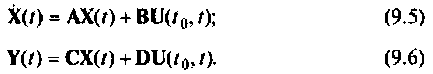
Матрица коэффициентов А определяет структуру системы, параметры элементов и их взаимные связи. Динамические свойства системы в основном определяются этой матрицей. Матрица управления В показывает связь управляющих (возмущающих) воздействий 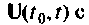переменными состояния. 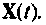При отсутствии входных воздействий, когда требуется исследовать свободное движение системы, матрица управление В равна нулю. Матрица С формирует выходные переменные 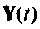из переменных состояний 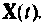И наконец, матрица обхода системы D показывает непосредственное влияние входных воздействий 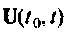на выходные координаты без преобразования вектора 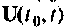динамической системой.

Следует отметить, что уравнения состояния (9.5) и (9.6) — это матричная запись системы линейных дифференциальных уравнений 1-го порядка с постоянными коэффициентами, описывающими динамику соответствующей линейной системы а взаимные связи между переменными состояния, входными и выходными величинами.

Уравнения (9.5) и (9.6) принято называть стандартной формой записи уравнений динамики линейных управляемых систем с постоянными параметрами, имеющих произвольную структуру и произвольное число входов и выходов. Стандартная форма отличается компактностью и удобством преобразования. Процедура решения уравнений состояния в конечном итоге сводится к матричным преобразованиям над А, В, С и D, что весьма удобно для программирования на цифровых ЭВМ. Уравнения (9.5) и (9.6) являются исходной информацией при исследовании и проектировании систем управления методом пространства состояний. К такому виду можно привести формы записи уравнений динамики (передаточные функции, дифференциальные уравнения высокого порядка, матричные передаточные функции многомерных систем и т. д.), применяемые в классических методах исследования систем.

Получение уравнений состояния является начальным этапом исследования систем и цепей в современной теории управления.

Методы составления уравнений состояния электрических цепей и динамических систем

Чтобы найти уравнения состояния (9.5) и (9.6), необходимо динамику электрических цепей представить системой дифференциальных уравнений 1-го порядка. В качестве иллюстрации рассмотрим систему третьего порядка, описываемую уравнением

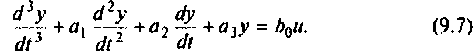
Для записи этого уравнения в векторно-математической форме положим

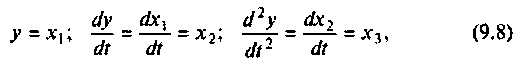
и тогда вместо уравнения (9.7) с учетом (9.8) получим: 

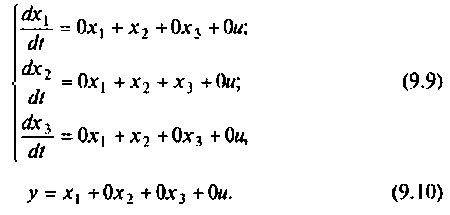
Система уравнений (9.9) совместно с уравнением (9.10) в матричной форме запишется:

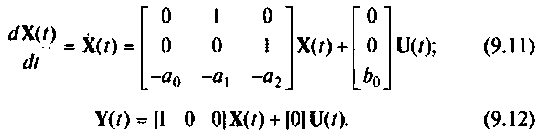
Уравнения (9.11) и (9.12) дают конкретный вид матриц А, В, С и D уравнений (9.5) и (9,6).

Приведенный выше метод может с успехом применяться для систем с одним входом и выходом. В многоконтурных системах с несколькими входами и выходами указанная процедура реализуется не так просто поэтому существуют другие способы получения уравнений состояния (9.5) и (9.6).

Наиболее распространенным способом получения уравнений состояния исследуемой системы является представление ее в виде схемы системы в переменных состояния. Эта схема составляется из интеграторов, усилителей и суммирующих устройств. Обычно выходы интеграторов выбираются в качестве координат (переменных) состояния системы. Схема в переменных состояния даст наглядную физическую интерпретацию координат системы и описывает их взаимную связь. Схемы непрерывных систем в переменных состояния совпадают со схемами моделирования этих систем на аналоговых вычислительных машинах. Существует много разновидностей схем моделирования для одной и той же системы [8], отсюда и неоднозначность описания системы управления уравнениями состояния.

Сначала рассмотрим методы построения схем в переменных состояния для систем с одним входом и выходом, динамика которых описывается дифференциальным уравнением вида

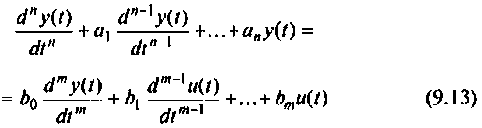
при начальных условиях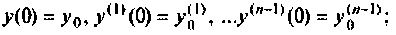  

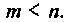
Затем будут показаны некоторые примеры, применяемые при построении схем в переменных состояния для систем более сложной структуры, динамика которых не может быть описана одним уравнением вида (9.13). Конечным результатом построения схем в переменных состояния будет получение уравнений состояния (9.5) и (9.6).

Метод комбинирования производных

Рассмотрим сначала более простой случай, когда начальные условия уравнения (9.13) нулевые. При этом уравнение (9.13) в операторной форме запишется как

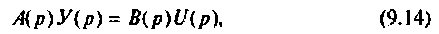
где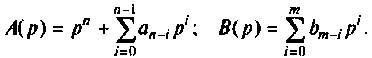  

Представим уравнение (9.14) в виде отношения 

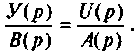
Это уравнение заменим следующими двумя:

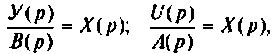
где 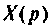— изображение вспомогательной переменной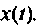

В дифференциальной форме последние два уравнения примут вид

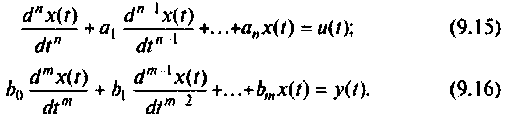
Таким образом, вместо решения уравнения (9.13) можно решить уравнения (9.15) и (9.16). Составим схему решения уравнения (9.15), для этого разрешим его относительно старшей производной:

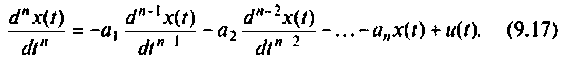
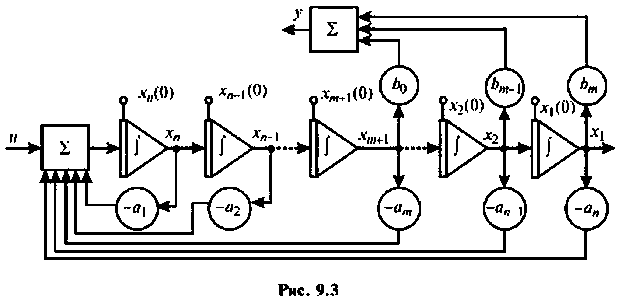
Предположим, что 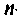-я производная функции 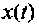известна, тогда, подавая ее на цепочку последовательно соединенных интеграторов, на выходе каждого последующего шифратора будем иметь производные от функции 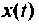более низких порядков. Если каждую из этих производных умножить на соответствующий коэффициент а, и образовать их отрицательную сумму вместе с функцией  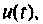то получим правую часть уравнения (9.17), т. е. 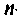-ю производную функции 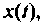которая ранее предполагалась известной. Функция  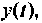которая является решением уравнения (9.13), получается линейной комбинацией производных от 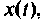взятых с коэффициентами 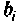в соответствии с уравнением (9.16). Схема решения уравнений (9.15) и (9.16) приведена на рис. 9.3.

При ненулевых начальных условиях уравнения (9.13) необходимо их перевести в начальные условия (9.15). Предполагая, что уравнения (9.15) и (9.16) эквивалентны (9.13) и при ненулевых начальных условиях, запишем эти уравнения в операторной форме:

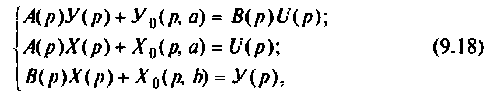
где 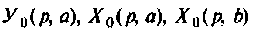 — полиномы начальных условий.

Подставляя 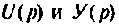из последних двух уравнений (9.18) в первое, получаем

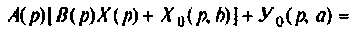
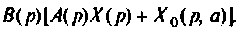
Из этого уравнения находится тождественное равенство, по которому определяются начальные условия уравнения (9.15) по известным начальным условиям (9.13)

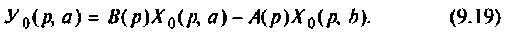
Приравнивая коэффициенты при одинаковых степенях р этого равенства, находим начальные условия 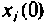интеграторов схемы на рис. 9.3.

Если в качестве переменных состояния 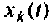выбрать выходные величины интеграторов схемы (см. рис. 9.3), то получим следующую систему уравнений:

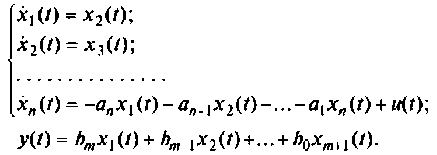
Записывая эту систему уравнений в матричной форме вида (9.5) и (9.6)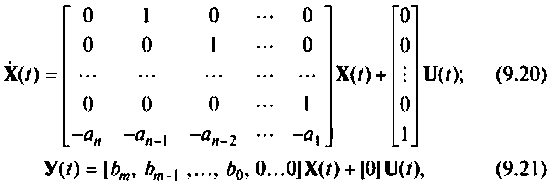

получаем конкретный вид матриц А, В, С и D.

Применение этого метода для составления уравнений состояния не требует преобразования уравнения (9.13). Можно непосредственно по виду уравнения (9.13) составлять схему в переменных состояния, так как его коэффициенты являются и коэффициентами схемы в переменных состояния. Пересчет начальных условий происходит по уравнению (9.19).

Пример 9.1.

Составить уравнения состояния для системы, динамика которой описывается дифференциальным уравнением

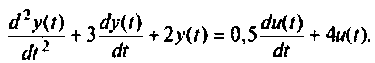
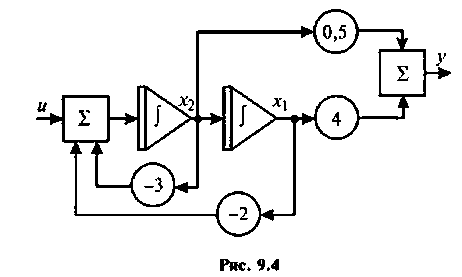
Схема в переменных состояния приведена на рис. 9.4. Из схемы в переменных состояния получаем уравнения:

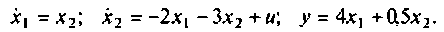
Эта система уравнений в матричной форме имеет вид:

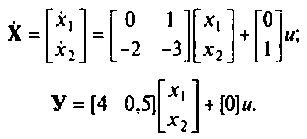
Следовательно, 

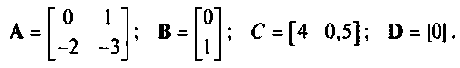
Метод последовательного интегрирования

Запишем уравнение (9.13) и операторной форме при нулевых начальных условиях в виде

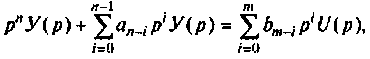
откуда

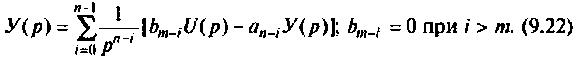
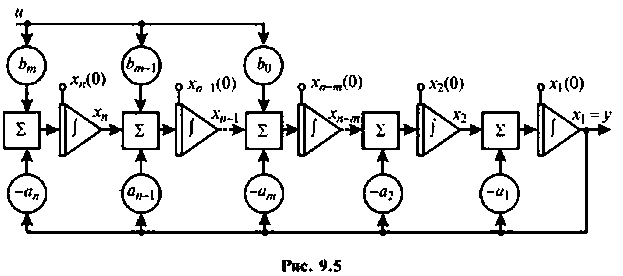
Составим цепочку из 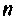последовательно соединенных интеграторов. Сигнал на выходе крайнего правого интегратора примем за 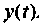. Выполнение равенства (9.22) обеспечится в том случае, соли на вход крайнего левого и интегратора подать разность 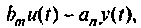на вход следующего — разность  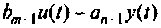и выход предыдущего интегратора и т. д. Схема решения уравнения (9.22) тогда примет вид, показанный на рис. 9.5.

Если снова выбрать в качестве переменных состояния 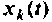выходы интеграторов схемы рис. 9.5, то получим систему уравнений:

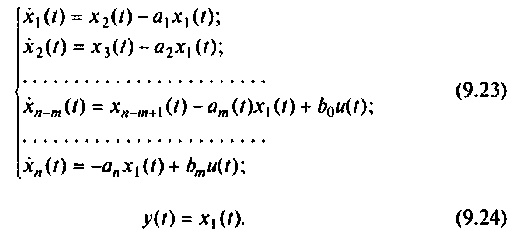
При ненулевых начальных условиях уравнения (9.13) начальные условия интеграторов схемы определяются соотношением [8]

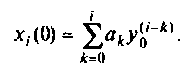
Записывая эту систему уравнений в форме уравнений (9.5) и (9.6), находим матрицы А, В, С и D:

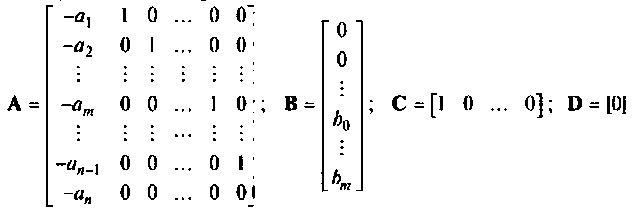
Как и для метода комбинирования производных, коэффициенты уравнения (9.13) являются одновременно и коэффициентами схемы и переменных состояния. Поэтому, зная общую структуру схемы в переменных состояния, можно непосредственно по виду уравнения (9.13) построить соответствующую схему в переменных состояния и найти уравнения состояния в виде (9.5) и (9.6).

Пример 9.2. 

Составить уравнения состояния для системы, описываемой уравнением

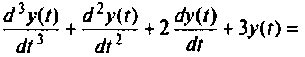
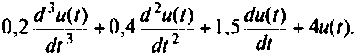
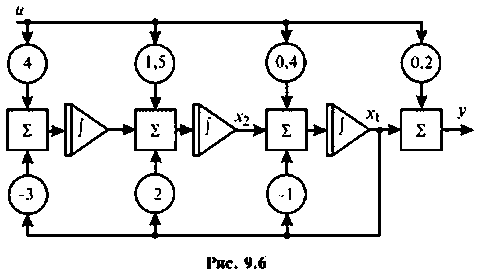
Схема а переменных состояния, построенная методом непосредственно интегрирования, показана на рис. 9.6. Из схемы получаем систему уравнений 1-го порядка:

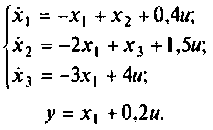
В матричной форме эта система уравнений имеет вид:

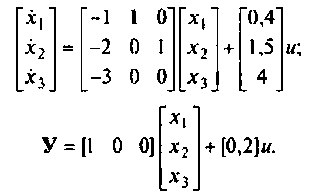
Из последних уравнений ясно видны матрицы А, В, С. D.

В примере 9.2 матрица D отлична от нуля. Это имеет место в тех случаях, когда 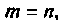 т.е. максимальная степень производной правой части дифференциального уравнения равна максимальной степени производной левой части уравнения. Если 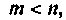то матрица D всегда будет нулевой матрицей. Случай 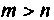соответствует физически нереализуемой системе, поэтому представляет только чисто теоретический интерес и здесь не рассматривается.

Метод разложения передаточной функции на элементарные дроби

Весьма перспективным для анализа цепей и систем методом пространства состояний является построение схемы в переменных состояния путем разложения передаточной функции на элементарные дроби. Суть его заключается в следующем. Уравнение (9.13) представляется в виде передаточной функции

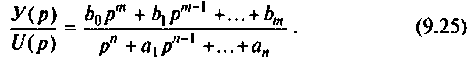
Разложим эту передаточную функцию на элементарные дроби

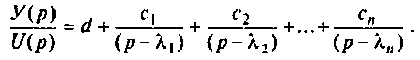
Отсюда

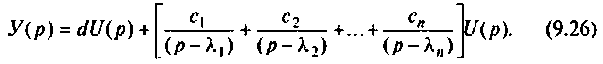
Коэффициент d будет отличен от нуля при 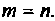Схема в переменных состояния уравнения (9.26) показана на рис. 9.7. Уравнения состояния имеют вид:

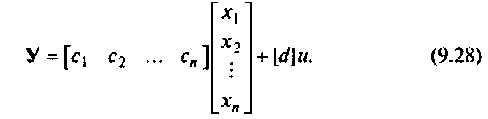
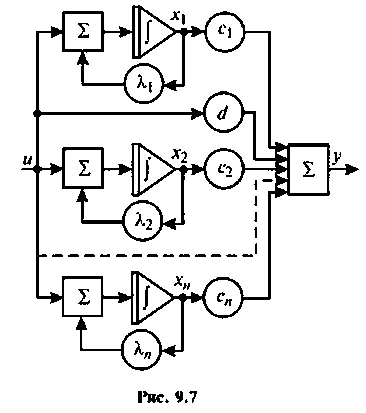
Как видно из выражения (9.27), матрица А является диагональной.

Пример 9.3.

Составим уравнения состояния для электрической цепи второго порядка, передаточная функция которой имеет вид

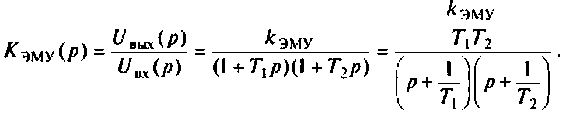
Полюса этой передаточной функции равны:

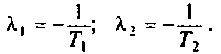
Представим передаточную функцию 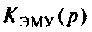в виде суммы элементарных дробей

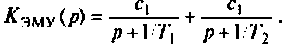
Коэффициенты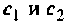

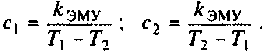
Таким образом, необходимо составить схему в переменных состояния для уравнения

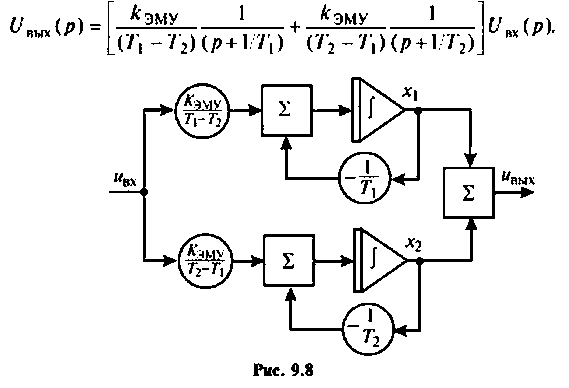
Схема в переменных состояния показана на рис. 9.8. Уравнения, связывающие переменные состояния 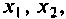 входную и выходную величины 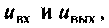имеют вид

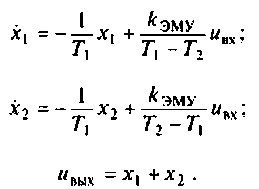
В матричном виде эти уравнения запишем таким образом:

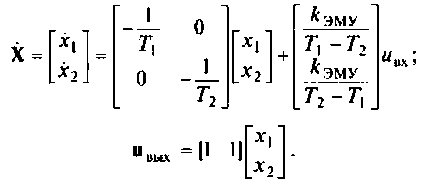
При наличии кратных полюсов передаточной функции (9.25) матрица А будет представлена в канонической форме Жордана [8]. Ниже будет показано, что вычислительная процедура значительно упрощается, если матрица А диагональная или имеет каноническую форму Жордана. Основная трудность получения уравнений состояния вида (9,27) и (9,28) состоит в нахождении полюсов передаточной функции (9.25).

Преобразование неоднородных уравнений состояния в однородные

В результате построения схемы и переменных состояния можно получить уравнения состояния в виде (9.5). Это система неоднородных дифференциальных уравнений первого порядка. Их решение будет содержать две составляющие — свободную и вынужденную. Первая зависит от динамики системы и начального значения вектора переменных состояния 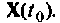 Вторая зависит также от матрицы А и вектора входных воздействий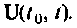

Свободная составляющая определяется решением однородного уравнения

когда вектор входного воздействия 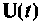 в выражении (9.5) предполагается нулевым.

Имеет смысл попытаться преобразовать систему неоднородных уравнений (9.5) в однородную вида (9.29). Цель этого преобразования заключается в том, чтобы получить уравнения состояния системы при наличии внешних воздействий 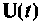, содержащие только переменные состояния. При этом значительно упрощается решение уравнений состояния.

Преобразование системы неоднородных уравнений в однородную можно осуществить в том случае, если вектор внешних воздействий 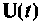представляется в виде решения определенного линейного однородного дифференциального уравнения (системы уравнений) с постоянными параметрами. Схема в переменных состояния для формирования вектора 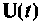будет иметь свои переменные состояния 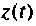с начальным значением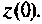

Рассмотрим методику построения схем в переменных состояния для формирования некоторых часто встречающихся входных воздействий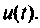

Построение схем в переменных состояния для типовых входных воздействий

Входное воздействие в виде полиномиальной функции:

Полиномиальное входное воздействие описывается функцией

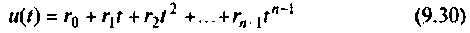
при 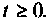Обозначим

и продифференцируем уравнение (9.31) по t. Тогда

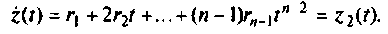
Аналогично

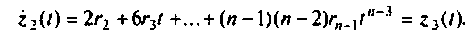
Продолжая этот процесс до тех пор, когда очередная производная будет равно нулю, получим следующую систему уравнений:

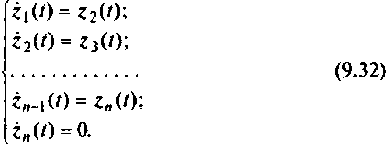
Величины 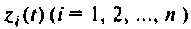называются переменными (координатами) состояния входа. Система дифференциальных уравнений (9.32) показывает, что полиномиальное воздействие можно получить с помощью цепочки последовательно соединенных интеграторов, как изображено на рис. 9.9.

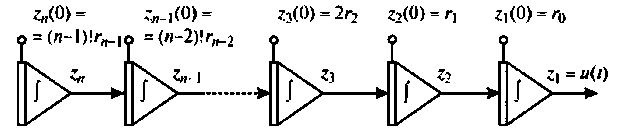
Начальные условия на интеграторах:

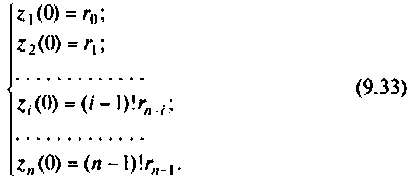
Выходом этой системы является заданное входное воздействие, определяемое переменной состояния 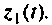Матрицы 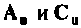уравнений состояния (9.32) находятся из выражений (9.32) и (9.31)

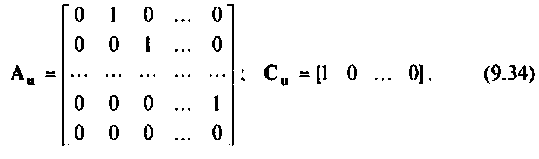
Пример 9.4. 

Составить схему в переменных состояния для формирования линейного воздействия 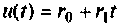и найти соответствующие уравнения состояния.

Систему уравнений, решением которой будет линейная функция, получим из выражения (9.32)

         

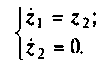
При начальных условиях 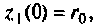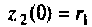выходной сигнал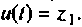

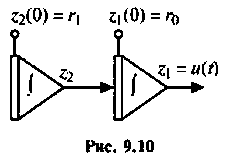
Схема о переменных состояния показана на рис. 9.10,

В матричном виде уравнения состояния схемы (рис. 9.10) будут иметь вид
      

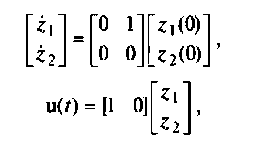
отсюда матрицы 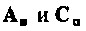равны:

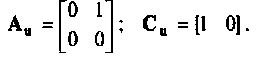
Входное воздействие в виде гармонической функции

В общем случае гармоническое воздействие представляется в виде

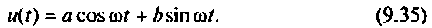
Решение дифференциального уравнения

даст гармонический сигнал. Это уравнение может быть записано в виде двух уравнений первого порядка

с начальными условиями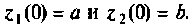

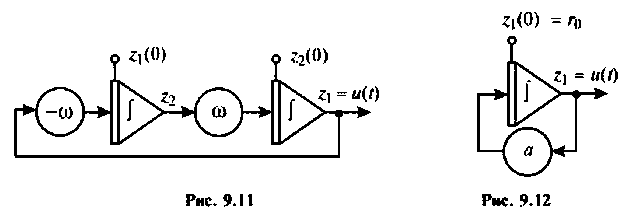
Схема в переменных состояния, которая следует из формул (9.37), показана на рис. 9.11. Сигнал 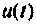определяется выражением

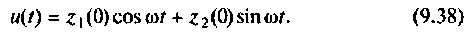
Изменяя начальные условия 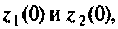можно получать гармонические сигналы различной фазы и амплитуды.

Входное воздействие в виде экспоненциальной функции

Экспоненциальное входное воздействие описывают функцией

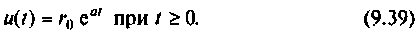
Пусть 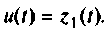Тогда

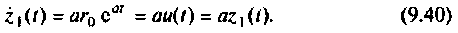
Начальное значение 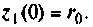Схема в переменных состояния системы, использующая это последнее уравнение, показана на рис. 9.12. Переменная 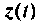является воздействием экспоненциального вида.

Методика преобразования неоднородных уравнений состояния в однородные

Для преобразования системы неоднородных уравнений (9.5) в однородную (9.29) необходимо вектор 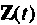 рассматривать совместно с переменными состояния системы 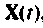, т. е. включить вектор 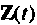в число координат системы (рис. 9.13).

Допустим, что входной вектор 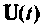есть решение уравнений состояния

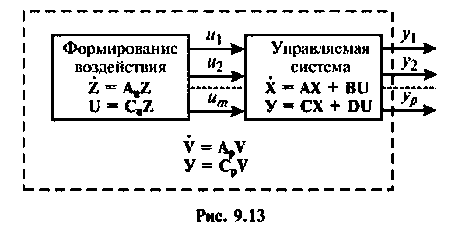
полученных путем построения схемы и переменных состояния дифференциального уравнения, решением которого и является вектор 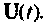Вектор 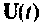будет входным для исследуемой системы с уравнениями состояния вида (9.5) и (9.6). Подставим уравнение (9.42) в (9.5) и (9.6)

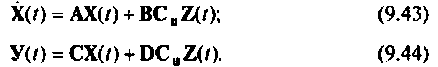
Объединим в одну систему уравнения (9.43) и (9.41)

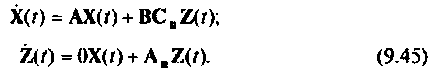
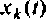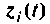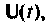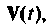Обозначим расширенный вектор, включающий как переменные состояния управляемой системы, так и переменные состояния схемы в переменных состояния входного воздействии через т. е.

Уравнения (9.43), (9.44) и (9.45) объединим и запишем в виде:

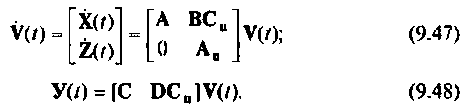
Обозначая

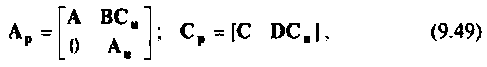
получаем

Матрица 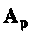побила название расширенной матрицы коэффициентов, 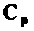— расширенной матрицы выхода, a 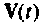— расширенного вектора состояния.

Применение методики преобразования неоднородной системы уравнений состояния в однородную проиллюстрируем на примере.

Пример 9.5.

Найти матрицы 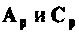для системы примера 9.1 при линейном входном воздействии. Из примера 9.1

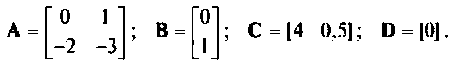
Для линейного воздействия

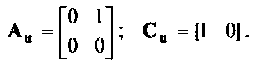
Подставляя 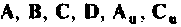в (9.49), получаем

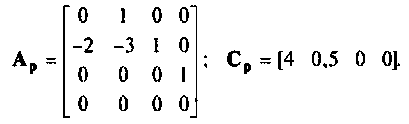
На практике часто пользуются следующим приемом при преобразовании неоднородных уравнений (9,5) и (9.6) в однородные. Составляется расширенная схема в переменных состояния, включающая схемы в переменных состояния входного воздействия и собственно динамической системы. Из этой схемы непосредственно получают расширенные матрицы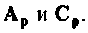

Пример 9.6.

Для условий примера 9.5 найти матрицы 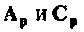(рис. 9.14).

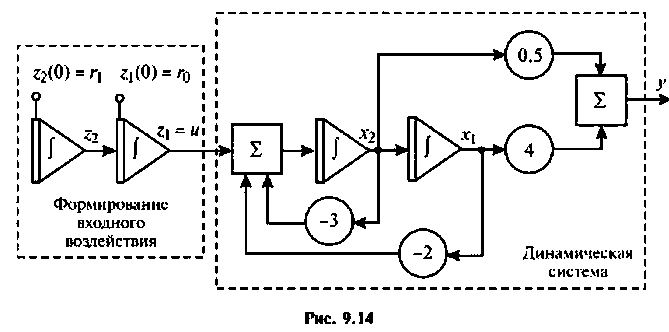
Расширенная схема о переменных состояния показана на рис. 9.14. Из нее получаем:

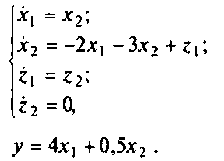
В матричной форме эту систему уравнений можно записать, если обозначить 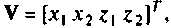 так

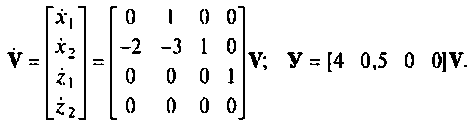
Результаты примеров 9.5 и 9.6 совпадают.

Формы решения уравнений состояния

Рассмотренные методы построения схем в переменных состояния позволяют получить математическое описание динамики линейной стационарной системы и электрической цепи в виде векторно-матричной системы дифференциальных уравнений первого порядка. Рассмотрим решение этих уравнений.

Форма решения однородных уравнений состояния

Если на систему не подаются внешние воздействия, то 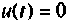и уравнение (9.5) становится однородным

Решение этого уравнения описывает динамику системы за счет ненулевых начальных условий (свободное движение), когда внешние силы равны нулю. Предположим, что движение начинается в момент 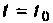 из начального состояния 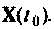Решение уравнения (9.52) можно получить по аналогии с решением скалярного уравнения в виде

Действительно, если подставить решение (9,53) в (9.52), предварительно взяв производную от (9.53), то получим тождество. Следовательно, (9.53) является решением однородного матричного уравнения (9.52).

Если обозначить

то уравнение (9.53) можно записать как

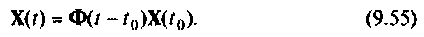
Выходной вектор системы будет иметь вид

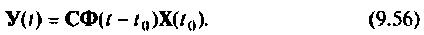
Матрица 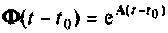называется матрицей перехода (переходной матрицей) состояния системы. Матрица перехода 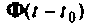описывает движение конца вектора состояния 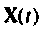в пространстве состояния из начальною положения 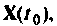а следовательно, и изменение (переход) состояния системы. Вектор 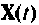дает возможность контролировать все координаты (переменные) состояния системы, поэтому решение (9.55) несет в себе полную информацию о динамике системы. Необходимо отметить, что объем вычислений при определении матрицы перехода 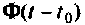состояния системы обычно больше, чем при решении линейного дифференциального уравнения относительно зависимой переменной. Однако имеющаяся дополнительная информация в результате вычисления матрицы перехода позволяет провести более глубокий и всесторонний анализ динамики исследуемой системы и электрических цепей.

Форма решения неоднородных уравнений состояния

Решение уравнения (9.5) будем искать в форме, аналогичной выражению (9.55). Положим

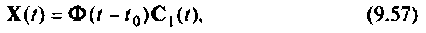
где 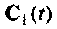— вектор, зависящий от времени и заменяющий вектор начального состояния 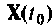в уравнении (9.55) при отсутствии внешних воздействий.

Дифференцируя выражение (9.57) по t, получаем

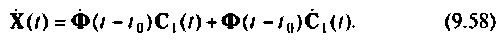
Учитывая, что 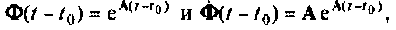уравнение (9.58) запишем в виде

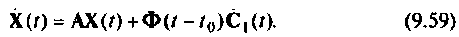
Если выражение (9.57) является решением уравнения (9.5), то величины в правых частях уравнений (9.5) и (9.59) должны быть одинаковыми.

Отсюда

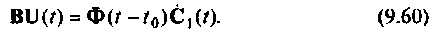
Решая это уравнение относительно 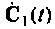получаем

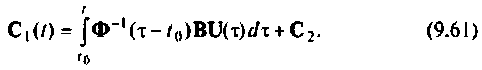
Подставив выражения (9.61) в (9.57), имеем

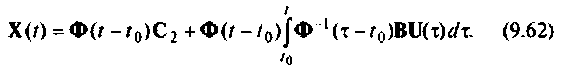
Учитывая, что

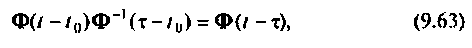
выражение (9.62) примет вид

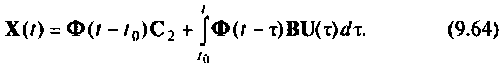
Постоянную интегрирования 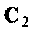 можно определить, если в уравнении (9.64) принять 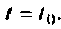Тогда

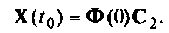
Так как 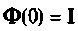то

Таким образом,

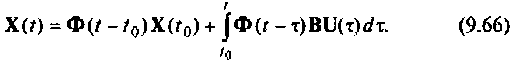
Вектор выхода 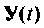будет иметь вид

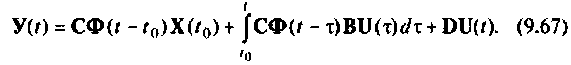
Первое слагаемое выражения (9.67) — составляющая выходного вектора за счет ненулевых начальных условий 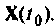 Она совпадает с решением однородного уравнения (9.52). Второе слагаемое характеризует реакцию системы на внешнее воздействие  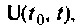третье — представляет собой непосредственное влияние вектора входа 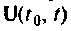на выход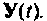

Аналитический подход к вычислению матрицы перехода

Формы решения однородной (9.56) и неоднородной (9.67) систем уравнений состояния содержат матрицу перехода 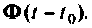Поэтому одной из центральных задач исследования систем является нахождение матрицы перехода. Существует много методов определения 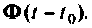Основные подходы базируются на теореме Сильвестра [8, 33], а также к ним относится метод разложения  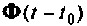в бесконечный ряд и метод комплексной плоскости, которые мы и рассмотрим ниже.

Далее рассматриваются и обосновываются аналитические методы вычисления матрицы перехода 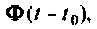применяемые в практике анализа и синтеза электрических цепей и динамических систем. Они иллюстрируются примерами.

Метод разложения матрицы перехода в бесконечный ряд

Переходная матрица 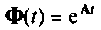раскладывается в бесконечный ряд

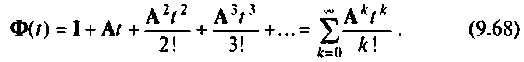
Этот метод наиболее трудоемок, если элементы матрицы 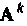«не исчезают» при небольших 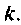После выполнения суммирования следует найти в замкнутом виде каждый элемент матрицы  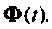Это непростая задача, и если порядок 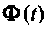недостаточно низкий, то задача может оказаться и непреодолимой. Однако метод разложения и бесконечный ряд весьма удобен при вычислении 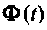на цифровых вычислительных машинах, что и будет показано несколько ниже.

Пример 9.7.

Найти матрицу перехода 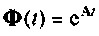для матрицы

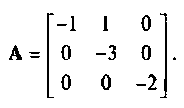
Степени 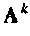находят последовательным умножением

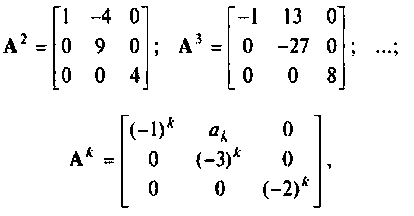
где 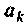 определяют по рекуррентной формуле

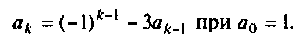
Переходная матрица

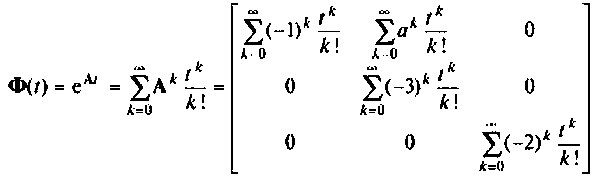
Если свернуть бесконечные ряды внутри матрицы 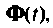получим

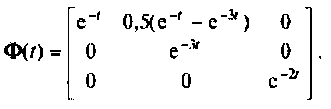
Метод комплексной плоскости

Возьмем преобразование Лапласа от обеих частей уравнения (9.52)

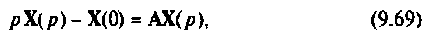
отсюда

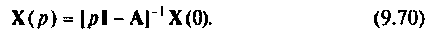
Применив к уравнению (9.70) обратное преобразование Лапласа,  получим

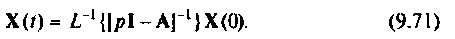
Сравнивая выражения (9.53) и (9.71), приходим к выводу, что

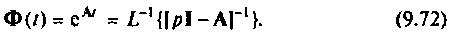
Основная трудность этого метода состоит в нахождении матрицы, обратной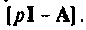

Пример 9.8.

Найти матрицу перехода 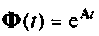, если

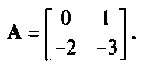
Найдем матрицу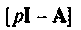

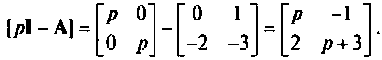
Матрица, обратная 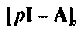имеет вид

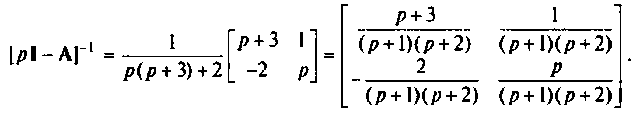
Пользуясь таблицей преобразования Лапласа [26, 28], находим

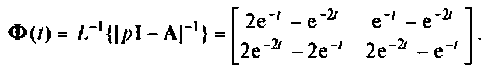
Рассмотренный метод комплексной плоскости дает возможность проследить физическим смысл матрицы перехода 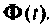Произвольный 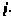-й член 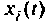уравнения (9.55) при 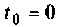можно записать в виде суммы

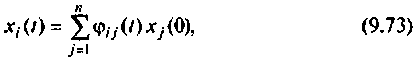
где — элемент матрицы 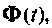стоящий на пересечении 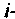-й строки и 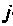-го столбца. Элемент  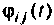можно определить, положив равным единице 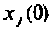и считая начальные условия для остальных переменных состояния равными нулю, тогда 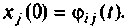Применительно к схемам в переменных состояния это эквивалентно подаче единичного начального условия на выход интегратора 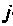и наблюдению за выходом интегратора  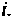Однако единичное начальное условие на выходе интегратора равносильно подаче единичного мгновенного импульса на вход этого интегратора. Следовательно  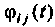представляет собой реакцию на выходе интегратора 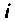при подаче единичного мгновенного импульса на вход интегратора в то время как начальные условия остальных интеграторов равны нулю. Поэтому 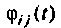можно интерпретировать как импульсную переходную функцию от входа сумматора на входе интегратора 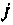к выходу интегратора 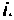Эти импульсные переходные функции образуют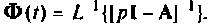

При рассмотрении физического смысла матрицы перехода 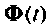было указано, что каждый элемент 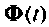можно интерпретировать как импульсную переходную функцию определенной части схемы в переменных состояния. Выражение (9.73) показывает, что реакция системы на единичный мгновенный импульс будет содержать конечное число составляющих 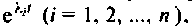которые получили название «частот» системы [8, 33]. Они позволяют проводить оценку характера решения уравнений состояния и дают возможность творчески решать задачи расчета и проектирования электрических цепей и систем. Например, путем выбора начальных условий или специальным формированием выходной координаты можно добиться отсутствия на выходе нежелательной «частоты» системы.

Построение алгоритмов вычисления матрицы перехода

Основой для разработки алгоритмов вычисления матрицы перехода 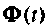  служат рассмотренные выше методы, применяемые для аналитического подхода к ее определению. Рассмотрим алгоритм по методу разложения в бесконечный ряд.

При использовании этого метода для машинного определения матрицы 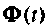возникают две самостоятельные задачи. Во-первых, вычисление каждого последующего члена бесконечного ряда

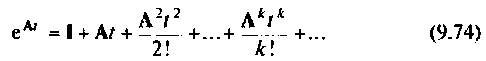
с одновременным их суммированием и, во-вторых, оценка точности вычисления, поскольку ряд (9.74) необходимо ограничивать конечным числом членов.

Алгоритм вычисления бесконечного ряда

При решении этой задачи воспользуемся рекуррентными соотношениями, позволяющими наиболее просто и экономно составить алгоритм вычисления бесконечною ряда (9.74). Обозначим

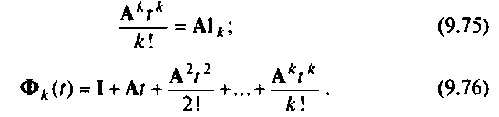
Тогда

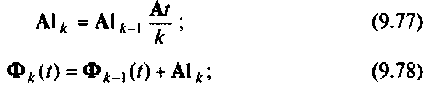
при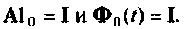

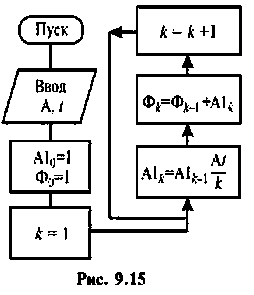
Таким образом, вычисление ряда (9.74) состоит из последовательных циклов, в каждом из которых будут использоваться результаты предыдущих вычислений. На рис. 9.15 показана схема алгоритма вычисления 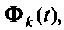использующего рекуррентные соотношения (9.77) и (9.78). Алгоритм не имеет условия, по которому будет закончен счет ( 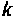ограничено), и поэтому число членов ряда (9.74) не определено.

 

Критерий ограничения бесконечного ряда

Вычисление матрицы перехода с точностью, не хуже заданной, требует способа оценки остаточного члена бесконечного ряда (9.74). Если ряд (9.74) ограничить первыми 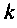членами, то остаточный член 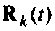примет вид

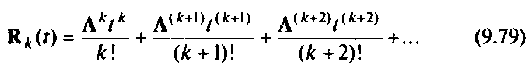
Представим остаточный член (9.79) в следующем виде:

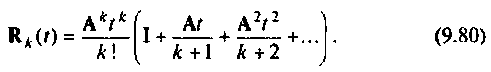
Заменим правую часть ряда (9.80) мажорирующим матричным рядом, где каждый член будет не меньше соответствующего члена ряда (9.80). Тогда вместо (9.80) можно записать

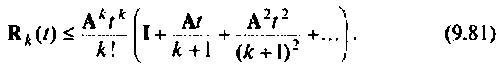
Правая часть этого выражения является матричной геометрической прогрессией с начальным членом 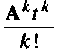и знаменателем  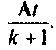Если норма знаменателя геометрической прогрессии меньше единицы, т. е.
(9.82)

то выражение (9.81) запишется так [8]:

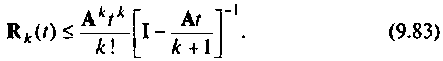
Таким образом, остаточный член матричного ряда (9.74) можно оценивать по матрице в правой части выражения (9.83) при выполнении условия (9.К2). С увеличением 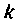каждый член матрицы (9.83) будет уменьшаться. Значение 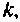при котором наибольший член матрицы (9.83) будет меньше заданной точности 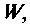и определяет число членов ряда (9.74).

Использование критерия (9.83) для ограничения числа членов бесконечного ряда требует вычисления нормы матрицы, так как

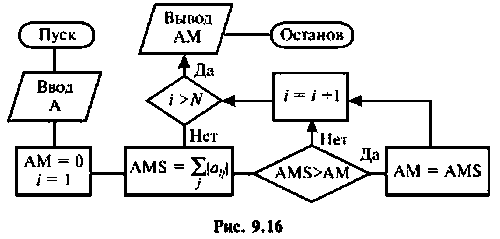
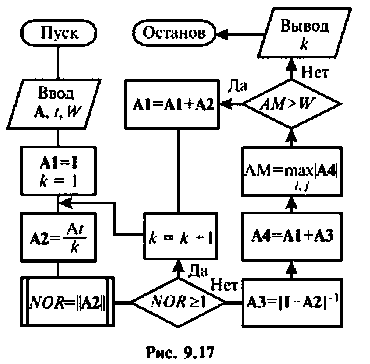
выражение (9.83) справедливо только при выполнении условия (9.82). На рис. 9.16 показана схема алгоритма вычисления нормы произвольной матрицы А. В качестве ее нормы выбрана максимальная сумма абсолютных значений элементов строки матрицы А. Этот алгоритм должен быть составной частью оценки числа членов ряда (9.74).

На рис. 9.17 приведена схема алгоритма, но которому можно определить число членов ряда (9.74), обеспечивающих точность вычисления матрицы перехода не хуже заданной. Алгоритм использует правую часть выражения (9.83) и имеет итерационный характер.

Алгоритм (рис. 9.17) требует достаточно сложной операции обращения матрицы. Целесообразно матричную оценку точности вычисления 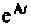(9.83) заменить скалярной. В качестве такой оценки возьмем норму остаточного числа

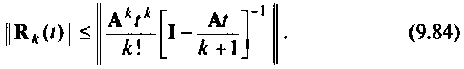
Проведем преобразования правой части критерия (9.84)

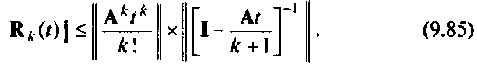
Известно [30], что если

  и

  то

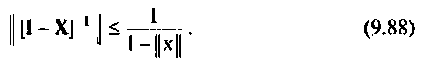
Заменяя норму обратной матрицы в выражении (9.85) и учитывая, что

получаем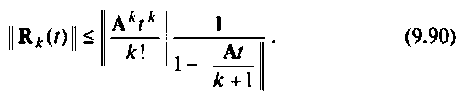      

Рассмотрим построение алгоритма вычисления матрицы перехода 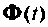с использованием скалярной оценки (9.90) остаточного члена ряда (9.74).

Алгоритм должен содержать цикл по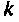и при каждом новом значении 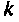вычислять очередной член ряда (9.74) и норму матрицы 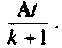Если

то можно использовать скалярную оценку остаточного члена матричного ряда (9.74). Для этого необходимо определять норму последующего слагаемого ряда (9.74) и при выполнении условия

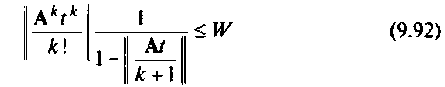
ограничивать число членов ряда (9.74). Поскольку

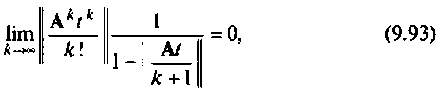
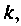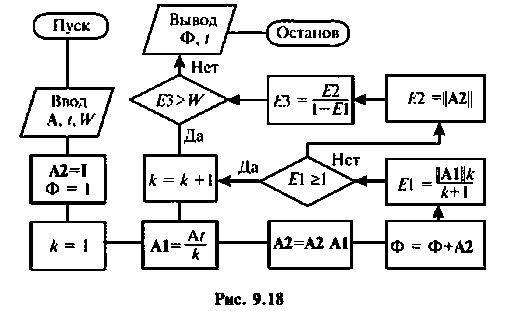
всегда найдется такое значение которое обеспечит требуемую точность 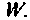На рис. 9.18 приведена схема алгоритма вычисления матрицы перехода 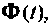включающая скалярную оценку остаточного члена.

Ниже представлен вариант программы вычисления переходной матрицы  в соответствии с алгоритмом (рис. 9.18), составленный в среде Mathcad [43].

Исходные параметры системы (из примера 9.9.5):

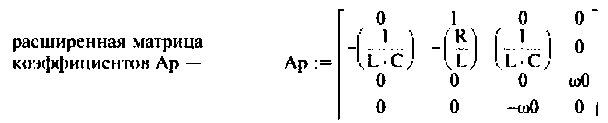
Программа вычисления матрицы перехода

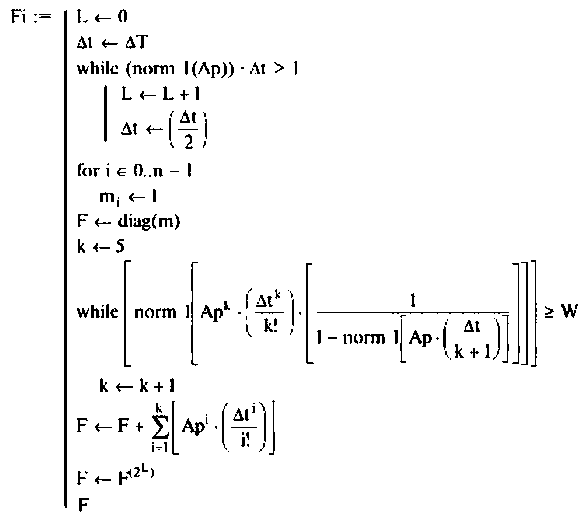
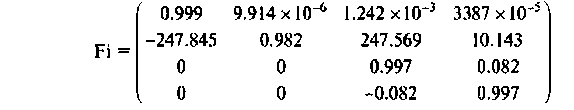
Метод разложения 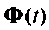  в бесконечный ряд позволяет определить матрицу перехода для одного момента времени t. Если требуется иметь зависимость матрицы перехода  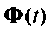 от времени, то необходимо вычислять 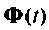для дискретных моментов времени, в результате этого получим функцию перехода в табличном виде. Такая информация может быть использована при анализе характера поведения 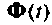во времени, а также при использовании решений уравнений состояния, представленных выражениями (9.53) и (9.62).

Иногда, особенно при решении задач проектирования, требуется иметь функцию перехода в аналитическом виде, т. е. в виде матрицы, элементами которой являются функции времени. Такой вид 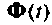дает возможность более глубоко и с меньшими затратами времени оценить характер поведения 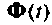и тем самым наметить пути совершенствования системы и повышения ее качественных показателей. Рассматриваемые ниже методы вычисления матрицы перехода 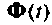позволяют решать эти задачи.

Аналитический подход к решению уравнений состояния

Формы решения уравнений состояния получены в разд. 9.4. Форма решения (9.53) применяется при исследовании как свободного движения системы, так и вынужденного, если входной вектор 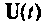можно представить как решение некоторой линейной системы дифференциальных уравнений первого порядка, т.е. применить процедуру расширения матрицы коэффициентов и матрицы выхода. Форма решения (9.62) является более общей и, естественно, ее практическое использование требует больших усилий и навыков исследования. Приведенные ниже примеры показывают процедуру аналитического решения уравнений состояния: при исследовании свободного движения системы (пример 9.9), свободного и вынужденного движения при построении расширенной схемы в переменных состояния (пример 9.10).

Пример 9.9.

Найти свободное движение системы, схема которой в переменных состояния приведена на рис. 9.4, при начальных условиях 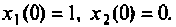Матрицы А, В, С и D для этой системы получены в примере 9.1

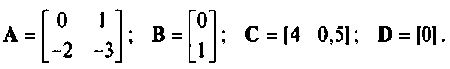
Поскольку требуется исследовать свободное движение, то 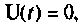а уравнения состояния становятся однородными, и их решение имеет вид (9.53)

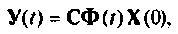
где 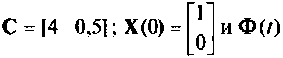 из примера 9.7

Таким образом

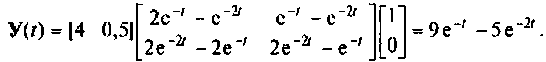
Пример 9.10. Найти реакцию 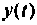 системы 

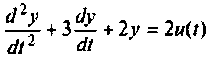
и ошибку 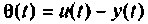при линейном воздействии 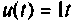и начальных условиях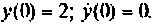

Расширенная схема в переменных состояния показана на рис. 9.19. Уравнения состояния расширенной системы имеют вид

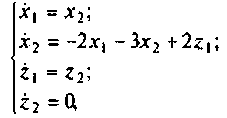
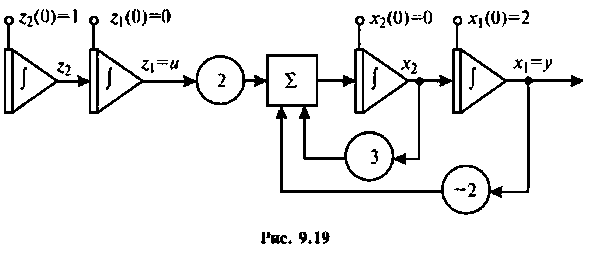
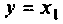
при начальных условиях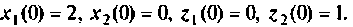

Обозначая 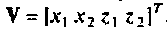получаем

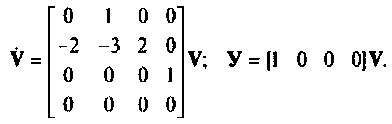
Решение этой системы уравнений можно записать в виде

.

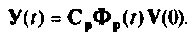Матрицу перехода представим бесконечным рядом

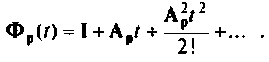
Степени 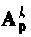найдем последовательным умножением:

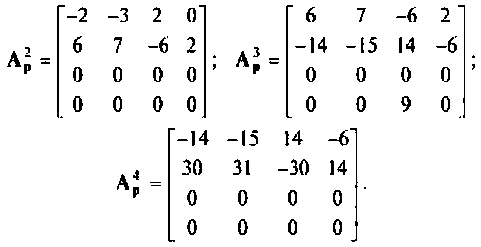
Для нахождения 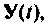вообще говоря, нет необходимости определять все элементы матрицы 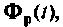поскольку 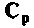и вектор 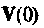имеют нулевые элементы. Поэтому определим, какие из элементов матрицы 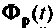необходимы при решении поставленной задачи. Представим 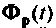в общем виде и найдем произведение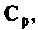

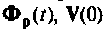
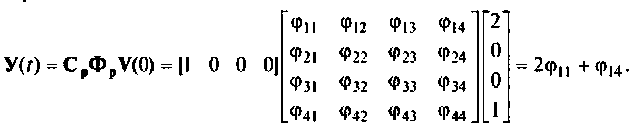
Для определения 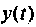 достаточно знать два элемента матрицы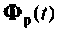 

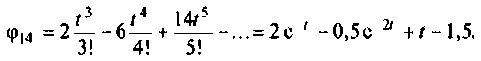
Таким образом,

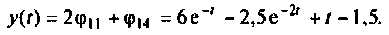
Входное воздействие 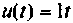связано с переменной состояния 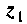соотношением (см. рис. 9.19)

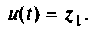
Переменная состояния

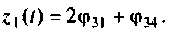
Учитывая, что 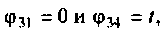получаем

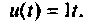
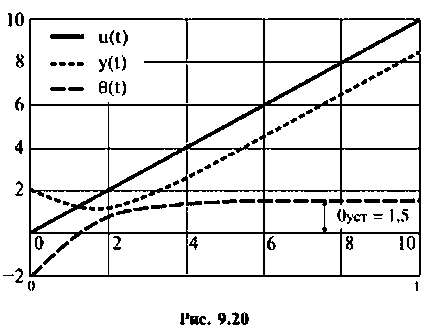
Этот результат очевиден из условия задачи. Ошибк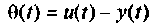а равна

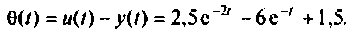
На рис. 9.20 показаны 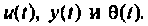При 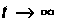установившаяся ошибка равна 1,5.

Построение алгоритмов решения уравнений состояния

Рассмотренные примеры показывают основные вычислительные трудности, возникающие при решении задач исследования линейных динамических систем. Более общая форма решения (9.62) требует аналитического интегрирования достаточно сложных функций, особенно если вектор входных воздействий 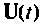не может быть представлен комбинацией стандартных функций. Может возникнуть такая практическая ситуация, при которой вообще невозможно будет провести интегрирование. Кроме того, аналитический метод решения может применяться только при аналитически заданном векторе входных воздействий. Следовательно, решать задачи при табличном или графическом представлении 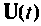невозможно. Все вышесказанное требует разработки алгоритмов решения уравнений состояния и использования вычислительных машин для исследования динамических систем. Сначала рассмотрим построение алгоритма для исследования свободного движения системы, который может без изменений применяться и для исследования вынужденного движения при наличии расширенных уравнений состояния. Затем будет описан общий случай, соответствующий алгоритмизации формы решения (9.62).

Построение алгоритмов решения однородных уравнений состояния

Простой алгоритм. Выходной вектор при отсутствии входных воздействий определяется по формуле (9.53)

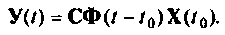
Построение алгоритма для вычисления 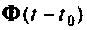достаточно подробно было рассмотрено в разд. 9.6, поэтому в дальнейшем будем считать, что алгоритм определения 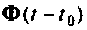известен, и на схеме он будет обозначаться одним символом.

Схема алгоритма решения системы однородных уравнений состояния показана на рис. 9.21. Исходными данными для алгоритма являются матрицы А, С и вектор начальных условий 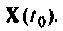 Интегрирование уравнений состояния ведется с шагом .

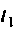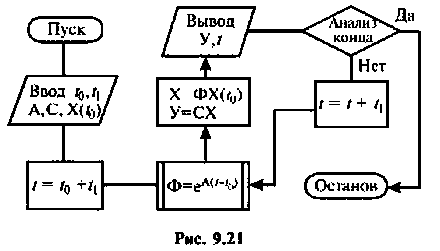
Условный оператор конца счета должен формироваться исходя из решения конкретной задачи.

Итерационный алгоритм. Алгоритм (см. рис. 9.21) имеет один существенный недостаток — обычно шаг 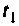намного меньше, чем максимальное время исследования динамики Поэтому возникает необходимость многократного вычисления 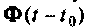при достаточно больших  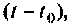что требует значительного машинного времени. Имеется возможность сократить затраты машинного времени путем применения итерационного процесса вычисления 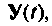когда для определения каждого последующего значения  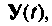используются результаты предыдущих вычислений. При этом достаточно вычислить матрицу перехода 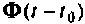только для одного момента времени 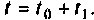Сущность итерационного процесса заключается в следующем. Вектор переменных состояния 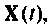рассчитанный для момента времени 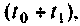принимается за начальный вектор вместо 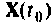и используется для расчета 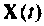в момент времени 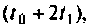т. е.

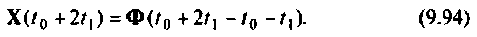
Повторяя этот процесс многократно, получаем последовательность значений вектора переменных состояния 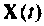в моменты времени 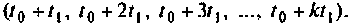Эта последовательность в каждом цикле используется для вычисления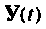

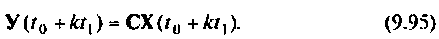
Схема итерационного алгоритма вычисления 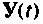показана на рис. 9.22. Алгоритм вычисления 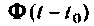находится вне цикла по и поэтому определение 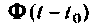осуществляется один раз только для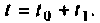 

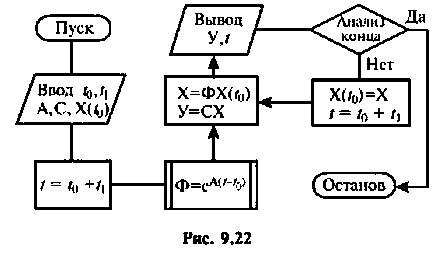
Такое построение алгоритма обусловливает накопление ошибок за счет неточного вычисления 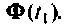 Действительно, при использовании итерационной процедуры счета вектор переменных состояния при 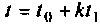равен

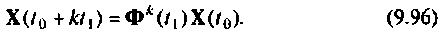
Допустим, что матрица 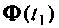определена с матричной погрешностью  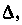т. е.

где 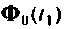— точное значение матрицы 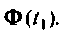Тогда

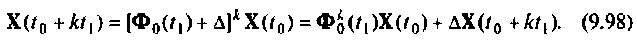
Ошибка 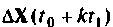 определяется выражением

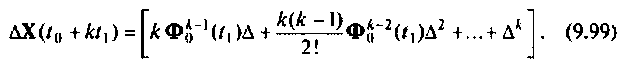
Ошибка 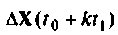будет расти с увеличением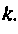

Итерационный алгоритм с компенсацией ошибок. Для компенсации накапливаемых ошибок в итерационном процессе можно применить метод уточнения вектора 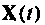в момент 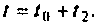С этой целью определяется не одна матрица перехода 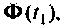а две: 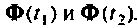При этом целесообразно применить соотношение

где 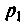— целое число.

Сначала итерационный процесс использует матрицу 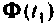 для вычисления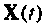

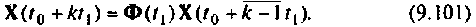
При 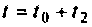вектор переменных состояния 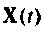вычисляется с использованием матрицы 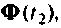т. е.

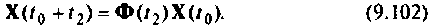
При необходимости можно использовать не одну матрицу 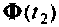для уточнения вектора 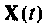в моменты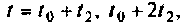 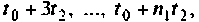а несколько, значения которых рассчитаны для моментов времени 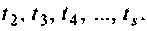Матрица 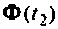компенсирует ошибки в моменты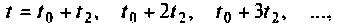 

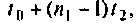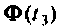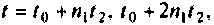
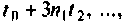
 матрица — в моменты 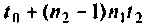. Точность вектора  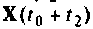определяется точностью матрицы 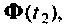и поэтому накопленные ошибки 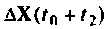в соответствии с выражением (9.99) ликвидируются. В этот же момент времени

заменяется вектор начальных условий 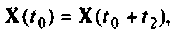новое значение становится равным 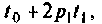увеличивается на величину. Далее вычисление  снова происходит с матрицей 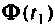до нового значения 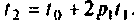Когда текущее время t достигает значения  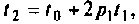снова происходит компенсация ошибок.

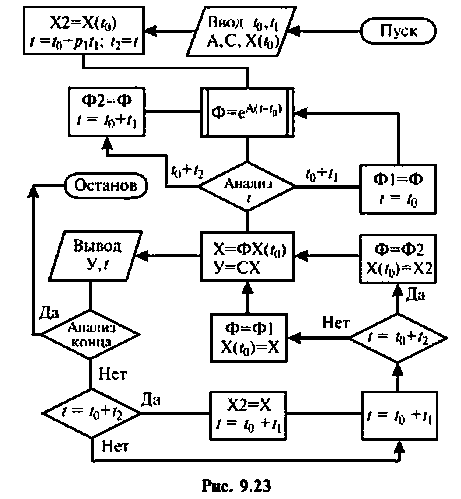
Выбором соотношений между 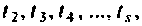а также их количества можно обеспечить требуемую точность и малый шаг вычисления для достаточно длительных процессов при минимальной затрате машинного времени. На рис. 9.23 показана схема алгоритма, где применен однотактный способ компенсации накапливаемых ошибок. Сначала определяются матрицы 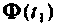и 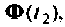которые хранятся в памяти и используются для вычисления 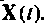Два условных оператора  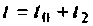дают разветвление алгоритма, позволяющее использовать матрицу 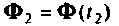для уточнения вектора 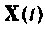при 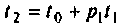последующим изменением момента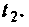

Построение алгоритмов решения неоднородных уравнений состояния

Алгоритмизации подлежит уравнение 

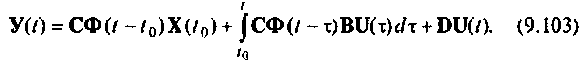
Первое его слагаемое отражает свободное движение системы за счет ненулевых начальных условий, второе и третье — определяют вынужденную составляющую решения.

Уравнение (9.103) удобно представить в виде следующих двух уравнений:

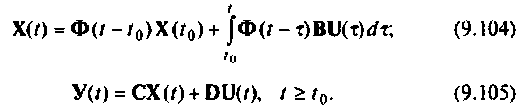
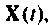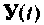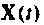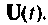Уравнение (9.104) определяет вектор переменных состояния а (9.105) — выходной вектор по известным векторам и  Подставив  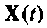в (9.105), получим уравнение (9.103).

Итерационный алгоритм. Если принять 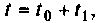то выражение (9.104) можно записать

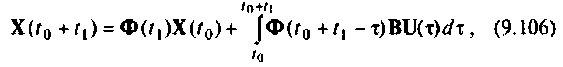
где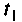 — шаг дискретности вычисления вектора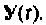

Для вычисления интеграла правой части уравнения (9.106) можно применять различные формулы приближенного вычислении определенных интегралов [4, 29]. Простой и удобной для применения является формула трапеции. Выбором шага дискретности можно обеспечить необходимую точность приближенного вычисления интеграла. Применение более сложных формул (Симпсона, Ньютона-Котеса, Гаусса, Маркова, Чебышева и др.) хотя и дает высокую точность интегрирования, однако затрудняет программирование и понимание построения алгоритма вычисления вектора состояния (9.106). Применение формулы трапеций позволяет выражения (9.106) и (9.105) привести к следующему виду:

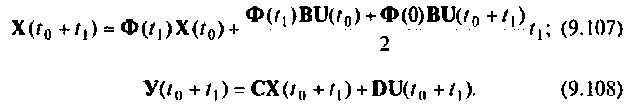
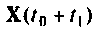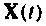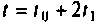Если принять за начальный вектор переменных состояния, то при равен

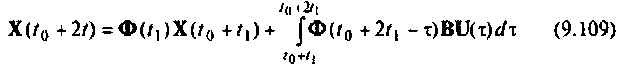
или после применения формулы трапеций

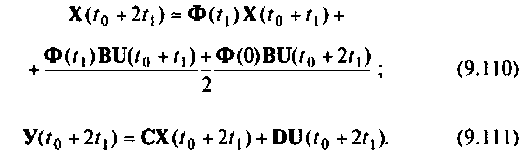
Сравнивая выражения (9.107) и (9.108) с (9.109) и (9.111), видим, что они идентичны по своему виду, за исключением аргументов вектора начальных условий и вектора выходных воздействий. Это дает возможность построить итерационный алгоритм вычисления переход к следующей итерации осуществляется изменением текущего времени на значение шага дискретности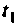 и вектора начальных условий. В каждой итерации используются только матрицы перехода при 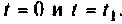Поэтому достаточно вычислить эти матрицы раз.

Схема алгоритма показана на рис. 9.24.

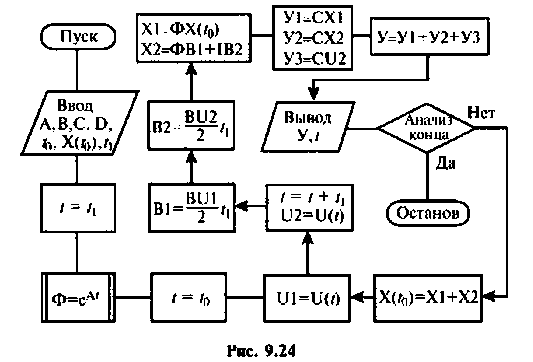
Исходными данными для него являются матрицы А, В, С и D. вектор начальных условий 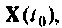начальное время  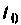и шаг дискретности 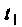. Сначала рассчитывается матрица 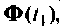затем находятся 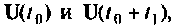которые используются для вычисления 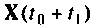и в конечном итоге 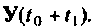Логический оператор «анализ конца» проверяет условия выполнения конца расчета, заданного для конкретной задачи. При невыполнении этого условия присваивается новое значение вектору начальных условий и начинается следующая итерация счета. На входе можно иметь как отдельные составляющие выходного вектора, соответствующие слагаемым уравнения (9.106), так и суммарное значение вектора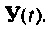

Порядок исследования электрических цепей в среде Mathcad методом пространства состояния

(на примере схемы на рис. 925)

1. Составить согласно принципиальной схеме уравнение электрической цепи в дифференциальной форме.
2. Составить расширенную схему электрической цепи в переменных состояния.
3. Составить в стандартной форме уравнения состояния электрической цепи.
4. Экспериментально построить вектор выхода электрической цепи.

Исходные параметры системы уравнений состояния:

Параметры вектора входа:

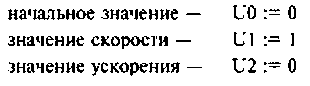
Исходные параметры электрической цепи:

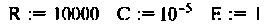
расширенной матрицы коэффициентов Ар —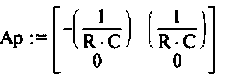 
расширенной матрицы выхода Ср  —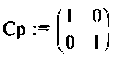                 

вектора начальных условий —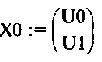                              

Программа вычисления матрицы перехода

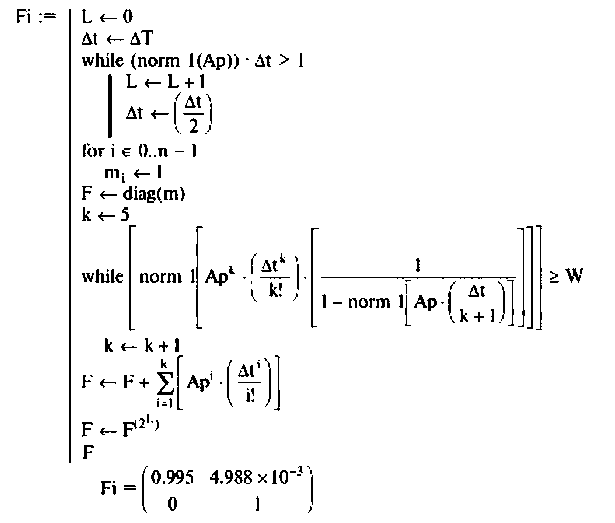
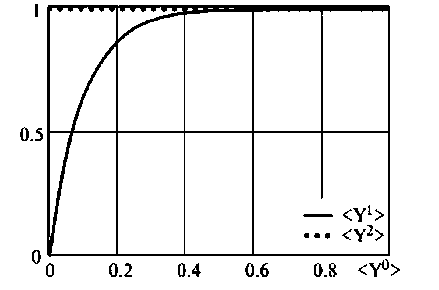
Примеры решения задач

Пример 9.9.1.

Построить методом пространства состояний переходные функции тока 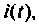 напряжения на емкости 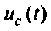и сопротивлении 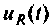для электрической цепи, приведенной на рис. 9.25.

Дано: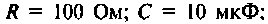

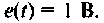
Решение

1. Составляем уравнение электрической цепи

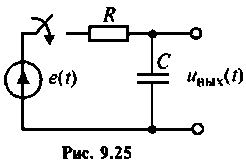
2. Составляем расширенную схему в переменных состояния для составления расширенных уравнений состояния. Уравнение (9.112) представим в виде

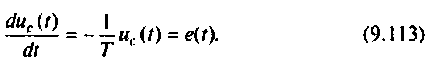
Расширенная схема в переменных состояния для решения уравнения (9.113), составленная по методу комбинирования производных, приведена на рис. 9.26.

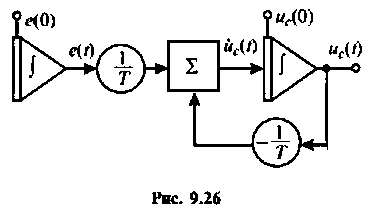
По схеме в переменных состояния записываем уравнения состояния в виде

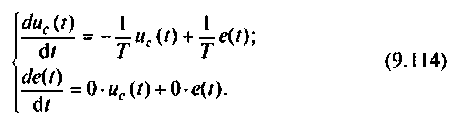
В качестве переменных вектора выхода принимаем напряжения 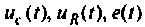и ток 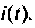 Для этих переменных уравнения вектора выхода запишем в виде

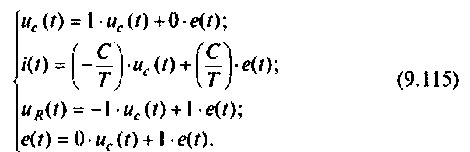
В матричной форме уравнения состояния принимают вид

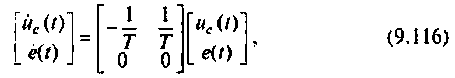
или 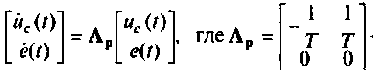— расширенная матрица коэффициентов электрической цепи.

В матричной форме уравнения вектора выхода принимают вид
      
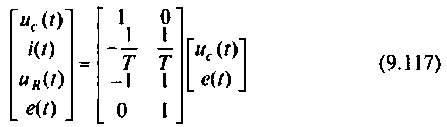
или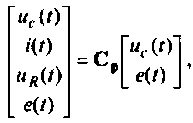 где 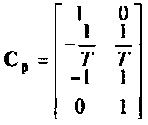— расширенная матрица выхода электрической цепи.

Вектор начальных условий по условию задачи принимает вид

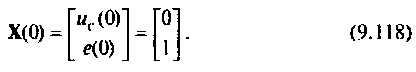
Решение уравнений состояния и формирование вектора выхода проведем в среде Mathcad.

Исходные параметры системы

Параметры электрической цепи

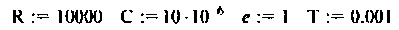
Вводим символьное обозначение матриц:

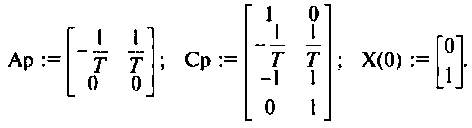
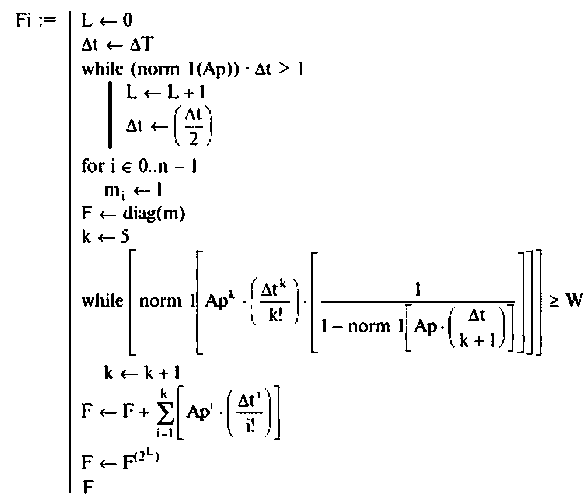
Программа вычисления матрицы перехода

Матрица перехода при 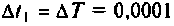с принимает вид

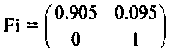
Программа вычисления и построения вектора выхода

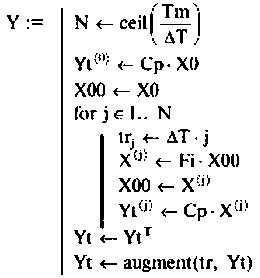
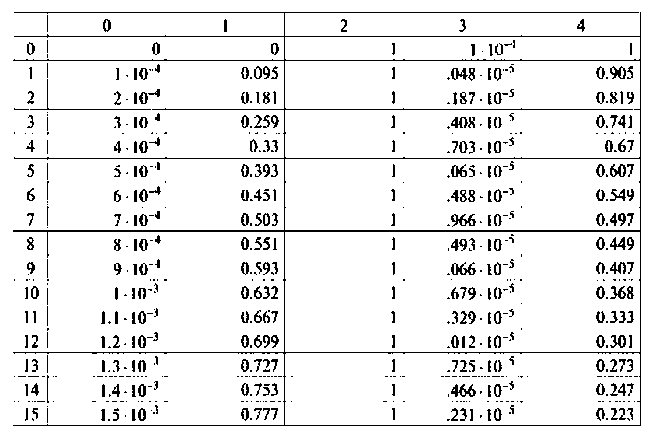
Переменные вектора выхода показаны па рис. 9.27.

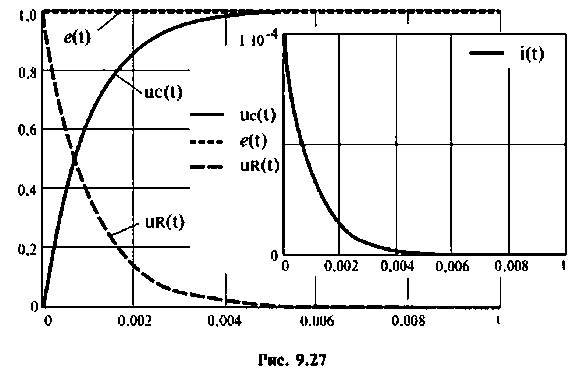
Пример 9.9.2. 

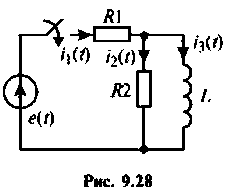
Для электрический цепи (рис. 9.28) после замыкания ключа составить уравнение равновесия, расширенную схему в переменных состояния, уравнения состояния. Решить уравнения состояния в среде Mathcad методом пространства состояний. Вектор выхода сформировать из переменных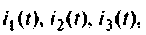 

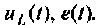
Дано: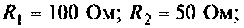

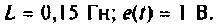
Решение

1. Составляем уравнение электрического равновесия для цепи в виде

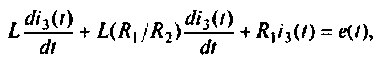
или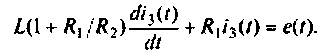  

2.Составляем расширенную схему в переменных состояния. Уравнение равновесия преобразуем к виду

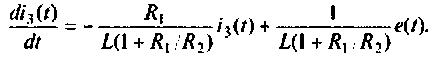
Схема в переменных состояния, составленная по методу комбинирования производных, представлена на рис. 9.29.

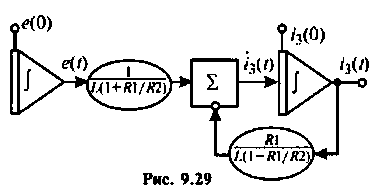
3. По виду схемы в переменных состояния составляем уравнения состояния. Схема в переменных состояния содержит два интегратора, следовательно, порядок уравнения 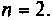На втором интеграторе реализована модель источника ЭДС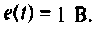 

Уравнения состояния в матричной форме принимают вид 

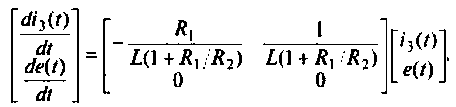
Расширенная матрица коэффициентов представляется в виде

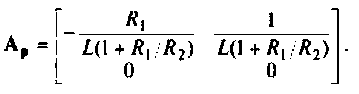
4. Уравнения вектора выхода системы в матричной форме имеют вид

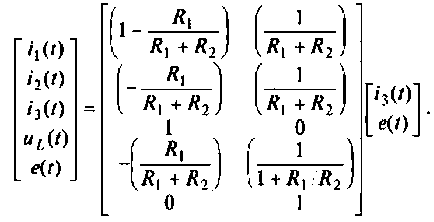
Расширенная матрица выхода и вектор начальных условий по условию задачи представлены соответственно в виде:

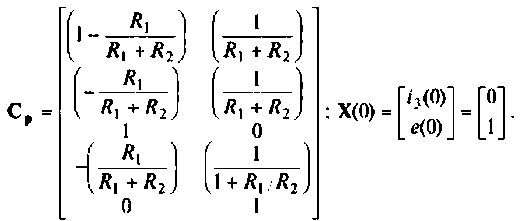
В среде Mathcad решаем систему уравнений состояния и из переменных состояния формируем вектор выхода электрической цепи.

Выходные переменные приведены на рис. 9.30.

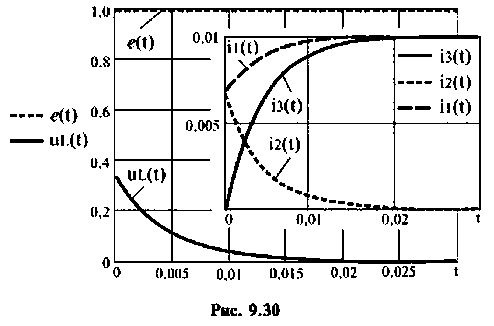
Пример 9.9.3.

Для электрической цепи, приведенной на рис.9.31, после замыкания ключа составить уравнение равновесия, расширенную схему в переменных состояния. Решить уравнения состояния в среде Mathcad. Вектор выхода сформировать из переменных состояния: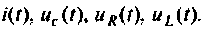

Дано: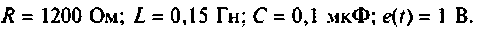

Решение

1.Составляем по второму закону Кирхгофа уравнение электрического равновесия для цепи после ее переключения в виде

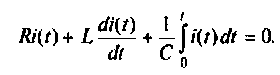
Так как 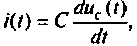 то после подстановки уравнение примет вид

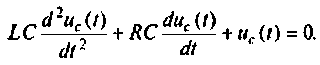
2. Составляем схему электрической цепи в переменных состояния. Так как после переключения внешний источник ЭДС отсутствует, т.е. 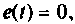то расширения схемы не требуется.

Разрешим уравнение равновесия относительно старшей производной, тогда

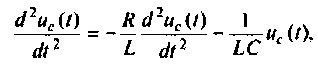
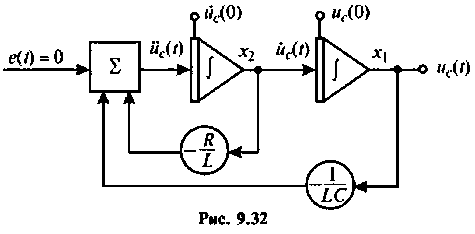
а схема в переменных состояния для решения этого уравнения имеет вид (рис. 9.32).

3. По схеме в переменных состояния (рис. 9.32) составляем уравнения состояния:

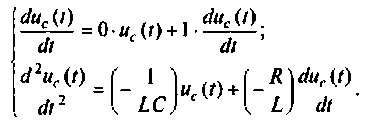
или в матричной форме

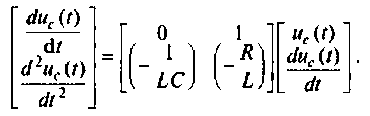
Матриц коэффициентов определяется выражением 

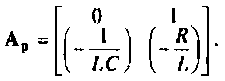
4. Формируем из переменных состояния вектор выхода. Уравнения выхода имеют вид

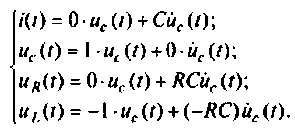
В матричной форме

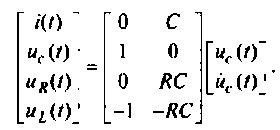
Матрица выхода и вектор начальных условий принимают вид:

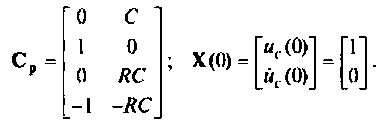
5.Решение уравнений состояния можно выполнить любым численным методом. На рис. 9.33 приведены переменные вектора выхода, вычисленные методом пространства состояний в среде Mathcad по программе, приведенной в задаче 9.9.1.

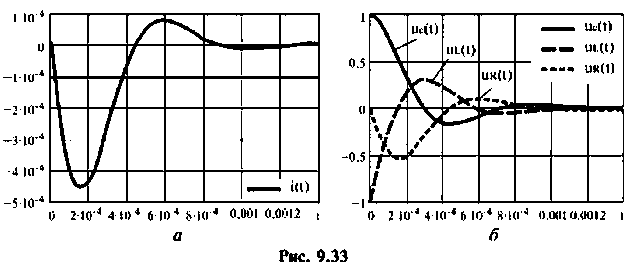
Пример 9.9.4.

Задана электрическая цепь (рис.9.34). Требуется составить уравнение равновесия цепи по второму закону Кирхгофа после замыкания ключа и расширенную схему в переменных состояния. Получить и решить уравнения состояния любым численным методом с применением ПЭВМ, сформировать вектор выхода из переменных состояния:

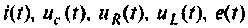 и построить их графики.

 Дано: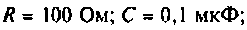 

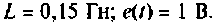
Решение

1. Записываем уравнение электрического баланса цепи в виде 

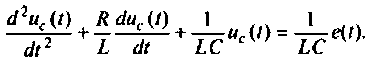
2. Составляем расширенную схему в переменных состояния при 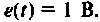Уравнение равновесия запишем в виде

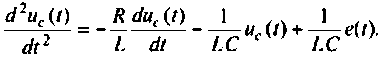
С учетом входного воздействия схема в переменных состояния электрической цепи может быть представлена в виде, приведенном на рис. 9.35.

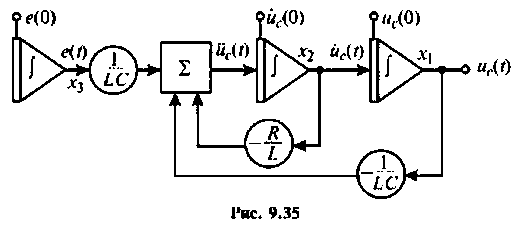
3. В соответствии со схемой в переменных состояния запишем уравнении состояния электрической цепи

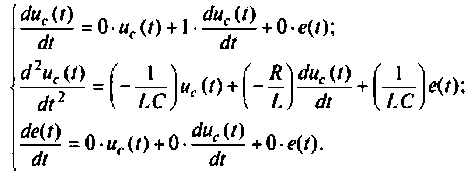
В матричной форме уравнения состояния имеют вид

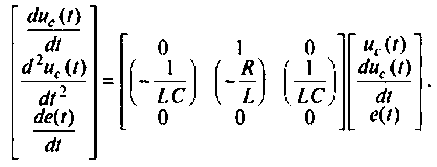
Расширенная матрица коэффициентов представляется в виде

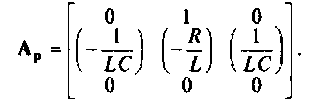
Вектор начального состояния из условия задачи запишем в виде
 

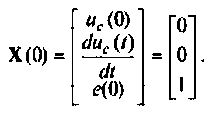
4. Определяем уравнения выхода из заданных переменных состояния электрической цепи.

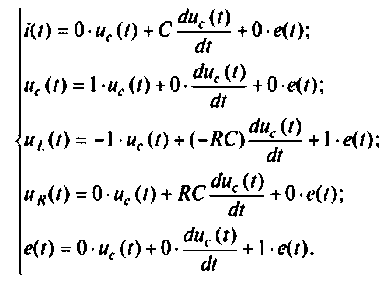
В матричной форме уравнения вектора выхода имеют вид
  
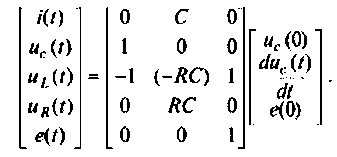
Матрица коэффициентов выхода

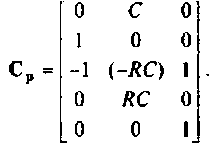
5. Решение уравнений состояния выполняем в среде Mathcad с помощью программы из задачи 9.9.1.

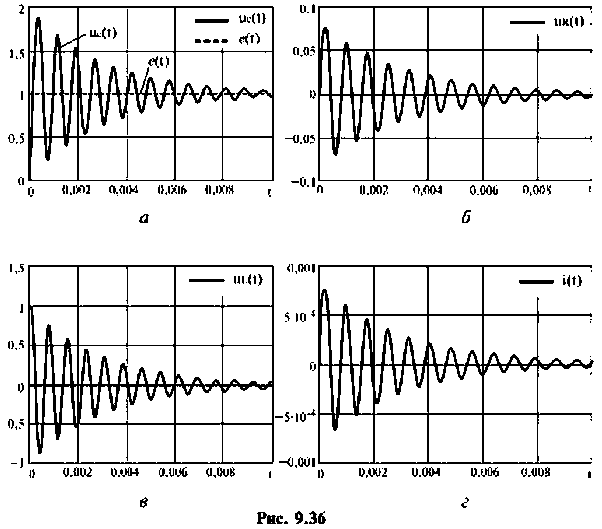
Переменные вектора выхода приведены на рис. 9.36.

Из переменных вектора выхода наглядно видно, что реакция последовательного колебательного контура на единичное воздействие — переходная функция — имеет слабозатухающий колебательный характер.

Пример 9.9.5.

По электрической схеме, представленной на рис.9.37, после замыкания ключа составить уравнение электрического равновесия по второму закону Кирхгофа, расширенную схему в переменных состояния, уравнения состояния и выхода из переменных состояния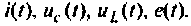

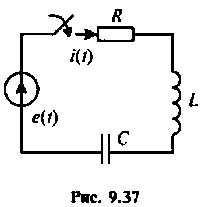
Дано:

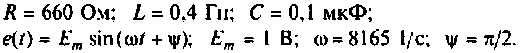
Решить уравнения состояния одним из численных методов в среде Mathcad и построить графики компонентов вектора выхода.

Решение

1. Записываем уравнение электрического равновесия для электрической цепи

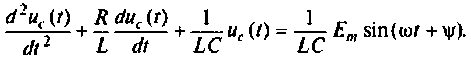
2.Составляем расширению схему в переменных состояния при 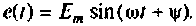 Схема приведена на рис. 9.38.

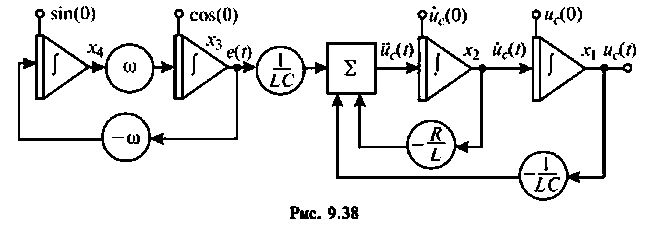
Схема модели гармонического воздействия 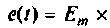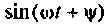выполнена на интеграторах 3 и 4, а модель цепи реализована на интеграторах 1 и 2.

3. Составляем уравнения состояния по схеме в переменных состояния

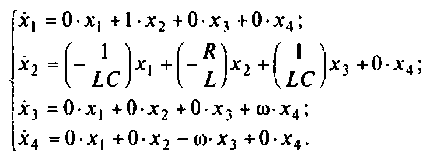
Запишем уравнения и матричной форме в виде 

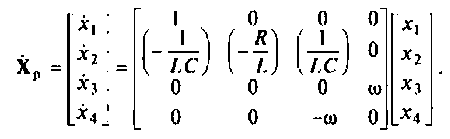
Расширенная матрица коэффициентов системы имеет вид 

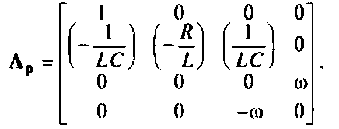
Вектор начального состояния системы для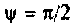

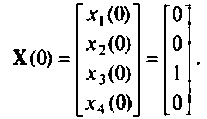
4. Составляем уравнения вектора выхода из переменных состояния

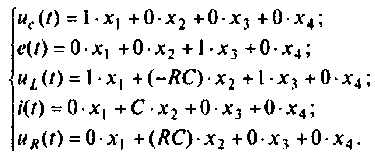
В матричной форме уравнения выхода имеют вид

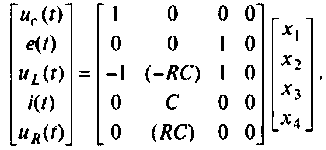
Расширенная матрица выхода запишется и виде

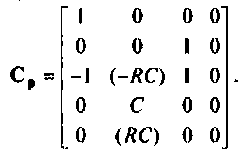
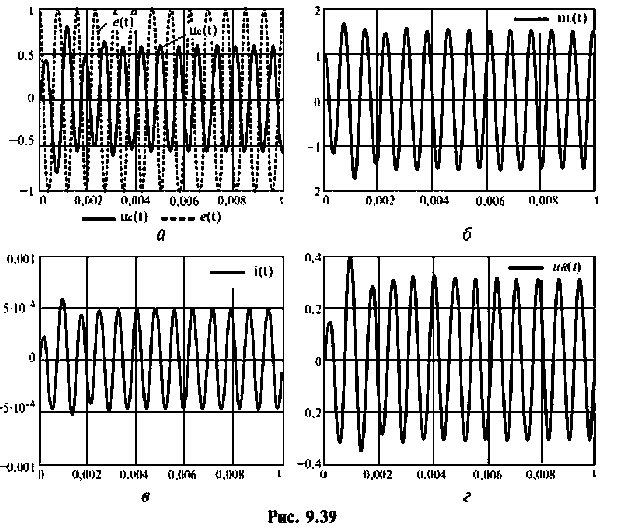
5. Решение уравнений состояния выполним в среде Mathcad по программе, представленной в задаче 9.9.1. Переменные вектора выхода представлены на рис. 9.39.