Метод преобразования схем электрических цепей

Метод преобразования схем:

Метод преобразования электрических схем применяют для расчета сложных цепей путем преобразований треугольника сопротивлений в эквивалентную звезду или звезды сопротивлений в эквивалентный треугольник.

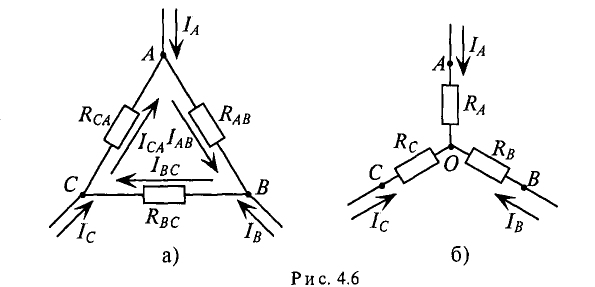
Контур, состоящий из трех сопротивлений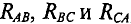

Электрическая цепь, состоящая из трех сопротивлений Ra, Rb и Rc, соединенных в одной узловой точке О, образует звезду сопротивлений (рис. 4.66).

Расчет некоторых сложных цепей значительно упрощается, если соединение звездой в них заменить соединением треугольником или наоборот.

Преобразование схемы должно производиться так, чтобы при неизменном напряжении между точками А, В и С токи 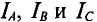звезды и треугольника оставались без изменений.

Треугольник и звезда, удовлетворяющие этому условию, называются эквивалентными.

Для такого преобразования рекомендуется изображать схему цепи без заменяемого треугольника (или звезды), но с обозначенными вершинами А, В, и С и к этим обозначенным вершинам подсоединить эквивалентную звезду (или треугольник).

При замене треугольника эквивалентной звездой сопротивления звезды определяются следующими выражениями:

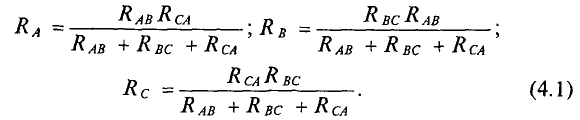
Таким образом, каждое сопротивление эквивалентной звезды равно отношению произведения двух примыкающих к соответствующей узловой точке сопротивлений треугольника к сумме трех его сопротивлений.

При замене звезды эквивалентным треугольником каждое составление треугольника определяется следующими выражениями:

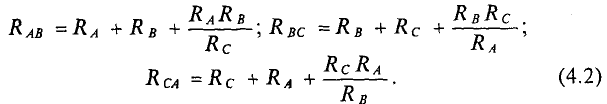
Каждое сопротивление эквивалентного треугольника равно сумме трех слагаемых: двух примыкающих к соответствующим точкам сопротивлений звезды и отношению произведения этих сопротивлений к третьему сопротивлению звезды.

Пример 4.4

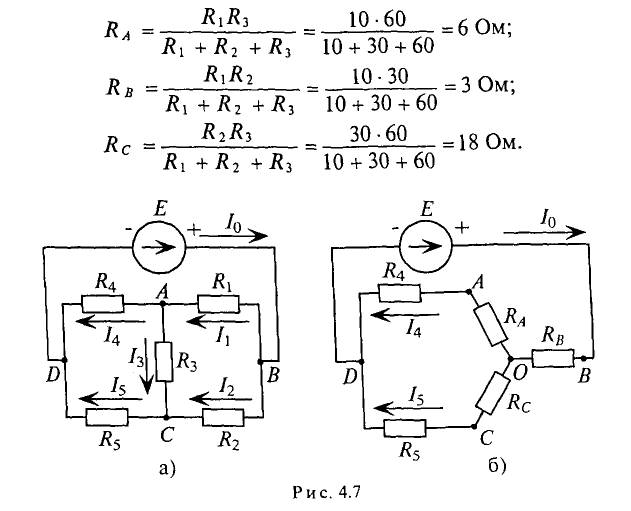
Определить токи во всех ветвях цепи (рис. 4.7а) при следующих сходных данных: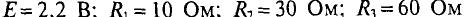

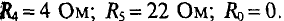
Решение

Для расчета этой цепи заменим треугольник сопротивлений, подключенных к точкам А, В и С, эквивалентной звездой, подученной к тем же точкам (рис. 4.76). Определим величины сопротивлений эквивалентной звезды:

Пример 4.6

Определить токи во всех ветвях цепи, схема которой приведена на рис. 4.8а, если задано:

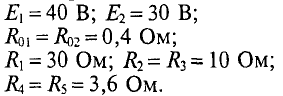
Решение

Количество ветвей и соответственно различных токов в  цепи (рис. 4.8а) равно пяти. Произвольно выбирается направление этих токов.

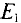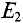Расчетных схем две, так как в цепи два источника с ЭДС и . Вычисляются частичные токи, созданные в ветвях первым источником 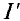. Для этого изображается та же цепь, только вместо 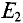— его внутреннее сопротивление 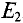Направление частичных токов в ветвях указаны в схеме рис. 4.86.

Вычисление сопротивлений и токов производится методом свертывания.

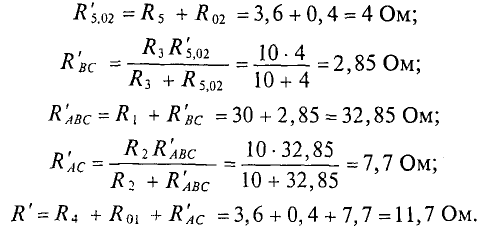
Первые частичные токи в цепи (рис. 4.86), созданные источником Еи имеют следующие значения:

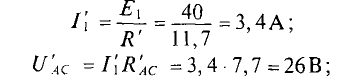
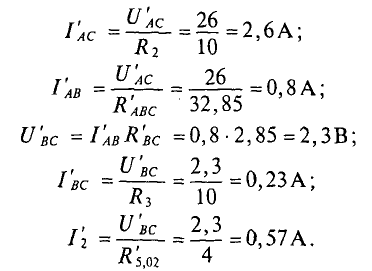
Вычисляются частичные токи, созданные вторым источником. Для этого изображается исходная цепь, в которой источник 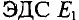заменен его внутренним сопротивлением 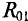. Направления частичных токов в ветвях указаны на схеме рис. 4.8в. Сопротивления и токи определяются методом свертывания.

Вторые частичные токи в цепи (рис. 4.8в) имеют следующие значения:

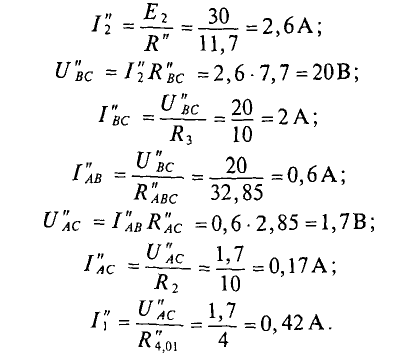
Искомые токи в рассматриваемой цепи (рис. 4.8а) определяют алгебраической суммой частичных токов (см. рис. 4.8):

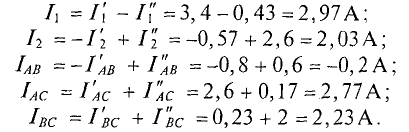
Ток 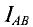имеет знак «минус», следовательно, его направлен противоположно произвольно выбранному, он направлен из точки А в точку В.