
Метод математической индукции с примерами решения
Содержание:
Метод математической индукции
При решении математических задач иногда возникает потребность обосновать, что определенное свойство выполняется для произвольного натурального числа 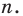
Проверить данное свойство для каждого натурального числа мы не можем — их количество бесконечно. Приходится рассуждать так: 1) я могу проверить, что это свойство выполняется при 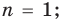
Такой способ рассуждений при доказательстве математических утверждений называется методом математической индукции. Он является одним из универсальных методов доказательства математических утверждений, в которых содержатся слова «для любого натурального п» (возможно, не сформулированные явно). Доказательство с помощью этого метода всегда состоит из двух этапов:
1) начало индукции: проверяется, выполняется ли рассматриваемое утверждение при 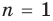 ;
;
2) индуктивный переход: доказывается, что если данное утверждение выполняется для 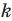 , то оно выполняется и для
, то оно выполняется и для 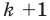 .
.
Таким образом, начав с 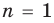 , мы на основании доказанного индуктивного перехода получаем, что сформулированное утверждение справедливо и для
, мы на основании доказанного индуктивного перехода получаем, что сформулированное утверждение справедливо и для 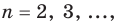 то есть для любого натурального п.
то есть для любого натурального п.
На практике этот метод удобно применять по схеме, приведенной в таблице 14.
Схема доказательства утверждений с помощью метода математической индукции
1. Проверяем, выполняется ли данное утверждение при  (иногда начинают с
(иногда начинают с  ).
).
2. Предполагаем, что заданное утверждение справедливо при  где
где  (другой вариант — при
(другой вариант — при  ).
).
3. Доказываем (опираясь на предположение) справедливость нашего утверждения и при 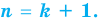
4. Делаем вывод, что данное утверждение справедливо для любого натурального числа 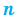 (для любого
(для любого  ).
).
Пример:
Докажите, что для любого натурального 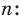
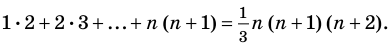
Решение:
► Для удобства записи обозначим
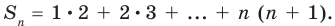
1. При 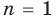 равенство выполняется:
равенство выполняется: 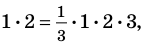 то есть
то есть 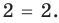
2. Предполагаем, что заданное равенство верно при 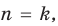 где
где 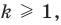 то есть
то есть 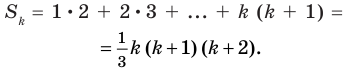 (1)
(1)
3. Докажем, что равенство выполняется и при 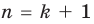 , то есть докажем, что
, то есть докажем, что 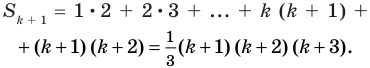 .
.
Учитывая, что 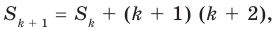 и подставляя
и подставляя 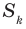 из равенства (1), получаем
из равенства (1), получаем 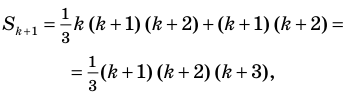
что и требовалось доказать.
4. Итак, заданное равенство верно для любого натурального 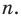
Примеры решения задач:
Пример №429
Докажите, что 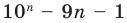 делится на 81 при любом натуральном
делится на 81 при любом натуральном 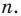
Комментарий:
Поскольку утверждение необходимо доказать для любого натурального 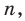 то используем метод математической индукции по схеме, приведенной в таблице 14. При выполнении индуктивного перехода (от
то используем метод математической индукции по схеме, приведенной в таблице 14. При выполнении индуктивного перехода (от 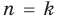 к
к 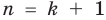 ), представим выражение, полученное при
), представим выражение, полученное при 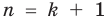 , как сумму двух выражений: того, что получили при
, как сумму двух выражений: того, что получили при 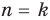 , и еще одного выражения, которое делится на 81.
, и еще одного выражения, которое делится на 81.
Доказательство:
1. ►Проверяем, выполняется ли данное утверждение при 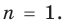 Если
Если 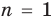 , данное выражение равно 0, то есть делится на 81. Таким образом, данное свойство выполняется при
, данное выражение равно 0, то есть делится на 81. Таким образом, данное свойство выполняется при 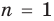 .
.
2. Предполагаем, что данное утверждение выполняется при 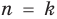 , то есть что
, то есть что 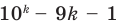 делится на 81.
делится на 81.
3. Докажем, что данное утверждение выполняется и при 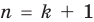 , то есть что
, то есть что 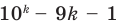 делится на 81.
делится на 81.
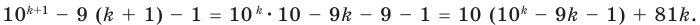
Выражение в скобках — это значение заданного выражения при 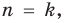 которое по предположению индукции делится на 81. Следовательно, каждое слагаемое последней суммы делится на 81, тогда и вся сумма, то есть
которое по предположению индукции делится на 81. Следовательно, каждое слагаемое последней суммы делится на 81, тогда и вся сумма, то есть 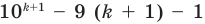 , делится на 81. Таким образом, данное утверждение выполняется и при
, делится на 81. Таким образом, данное утверждение выполняется и при 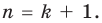
4. Следовательно, 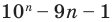 делится на 81 при любом натуральном
делится на 81 при любом натуральном 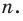
Пример №430
Докажите, что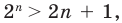 если
если 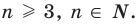
Комментарий:
Поскольку утверждение должно выполняться, начиная с 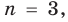 то проверку проводим именно для этого числа. Записывая предположение индукции, удобно воспользоваться тем, что по определению понятия «больше»
то проверку проводим именно для этого числа. Записывая предположение индукции, удобно воспользоваться тем, что по определению понятия «больше» 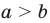 тогда и только тогда, когда
тогда и только тогда, когда 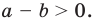 Доказывая неравенство при
Доказывая неравенство при 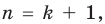 снова используем то же определение и доказываем, что разность между его левой и правой частями положительна.
снова используем то же определение и доказываем, что разность между его левой и правой частями положительна.
Доказательство:
1. При 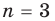 получаем
получаем 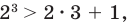 то есть
то есть 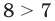 — верное неравенство. Таким образом, при
— верное неравенство. Таким образом, при 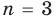 данное неравенство выполняется.
данное неравенство выполняется.
2. Предполагаем, что данное неравенство выполняется при 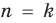 (где
(где  ):
):
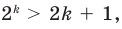 то есть
то есть 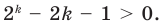 (1)
(1)
3. Докажем, что данное неравенство выполняется и при 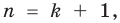 то есть докажем, что
то есть докажем, что 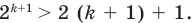
Рассмотрим разность:
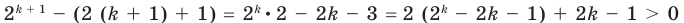
(поскольку выражение в скобках по неравенству (1) положительно и при 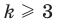 выражение
выражение 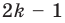 также положительно). Следовательно,
также положительно). Следовательно, 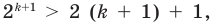 то есть данное неравенство выполняется и при
то есть данное неравенство выполняется и при 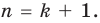
4. Итак, данное неравенство выполняется при всех натуральных 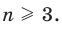
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |