Метод контурных токов

Содержание:

Метод контурных токов:

Контурным током называют условный ток, протекающий внутри независимого контура.

Напомним, что контуры называются независимыми (подробнее см. разд. 2.1), если они отличаются друг от друга хотя бы одним элементом (ветвью). Направление отсчёта контурного тока выбирается произвольно и независимо от выбора направлений отсчётов контурных токов в других контурах. В отличие от метода токов ветвей, рассмотренного в лекции 4, данный метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной числу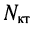

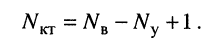
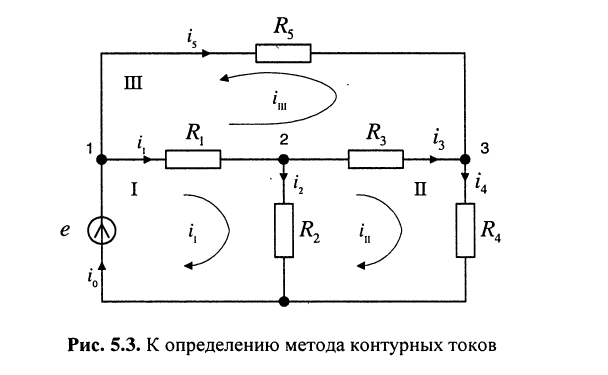
Предварительно покажем, что при известных контурных токах можно найти токи всех ветвей, а потому и напряжения на всех элементах цепи. Действительно, ток в любом элементе (ветви) определяется по первому закону Кирхгофа (ЗТК) как алгебраическая сумма контурных токов, протекающих в этом элементе. Например, при выбранных в удлинителе (рис. 5.3) направлениях отсчётов токов элементов и контурных токов имеем:

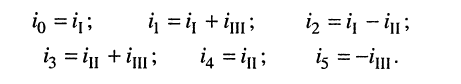
Зная токи, протекающие в элементах, можно по закону Ома определить напряжения на каждом из них.

Определение:

Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются контурные токи, называется методом контурных токов.

Составление контурных уравнений

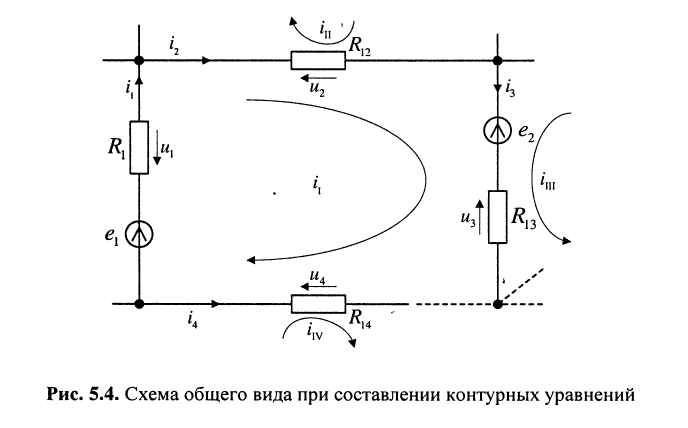
При составлении системы контурных уравнений воспользуемся вторым законом Кирхгофа и будем полагать, что (рис. 5.4):

• цепь согласно (5.4) содержит 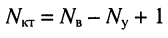независимых контуров;
• в цепи имеются источники напряжения с ЭДС
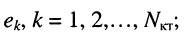
• все 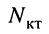независимых контуров непосредственно связаны друг с другом, т. е. для к-го и 1-го контуров имеется хотя бы один                  элемент 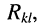который входит в оба эти контура, причём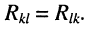

При этих условиях, выбранных независимых контурах и заданных направлениях отсчётов контурных токов запишем уравнение для первого контура (см. рис. 5.4) согласно второму закону Кирхгофа:

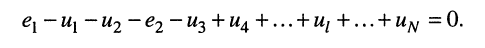    (5.5)

Выразим напряжения на элементах 1-го контура через токи ветвей по закону Ома:

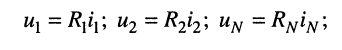
или в общем виде:

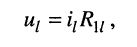   (5.6)

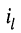• — ток в 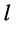-ой ветви; 
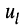•  — напряжение в 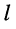-ой ветви;
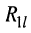•   — сопротивление элемента, общего для 1-го и 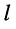-го контуров.

Подставим (5.6) в (5.5)

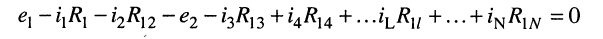        (5.7)

и выразим токи ветвей через контурные токи, нумерация которых осуществляется римскими цифрами и прямыми латинскими буквами. Из рис. 5.4 видно, что:

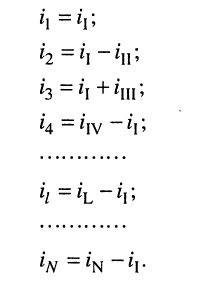
Произведём замену токов ветвей в выражении (5.7) через соотношения (5.8):

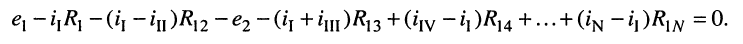
Умножим полученное уравнение на-1, раскроем скобки, приведём подобные члены и перенесём в правую часть известные значения напряжений источников; после выполнения этих действий контурное уравнение принимает вид

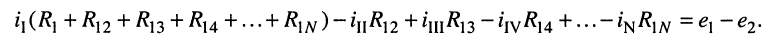
Подобное уравнение можно было бы составить и для любого другого контура, поэтому полученный результат позволяет сделать обобщающие выводы:

• в левую часть каждого из уравнений входит N слагаемых, пропорциональных искомым контурным токам
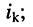
• коэффициент при контурном токе 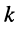-го контура, для которого составляется уравнение, представляет собой арифметическую  сумму сопротивлений этого контура;
• остальные слагаемые представляют собой произведение сопротивления элемента 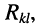общего для 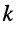-го и 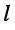-го контуров, на контурный ток 1-го контура; эти слагаемые входят в уравнение со знаком "+", если направления токов 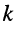-го и -го 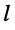контуров в элементе 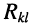совпадают; в противном случае они входят в уравнение с отрицательным знаком.

Аналогично записываются узловые уравнения для всех других контуров цепи, в результате чего образуется система контурных уравнений вида:

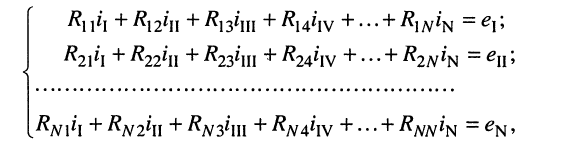          (5.9)

где:

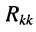• — собственное сопротивление k-го контура, оно определяется как арифметическая сумма сопротивлений всех элементов 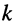-го          контура;
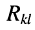• — взаимное сопротивление 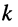-го и -го 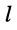контуров цепи 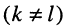, оно является сопротивлением элемента, общего для 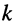-го и 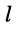-го        контуров; слагаемые вида 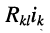входят со знаком "+" при совпадении направлений токов в этих контурах; если связь между 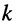-ым        и 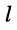-ым контурами осуществляется через несколько элементов активного сопротивления, то 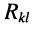представляет собой   арифметическую сумму соответствующих взаимных сопротивлений, причём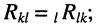
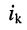• — контурный ток 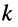-го контура цепи;
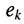• — контурная ЭДС -го контура цепи, представляющая собой алгебраическую сумму ЭДС независимых источников, имеющихся         в контуре; слагаемые этой суммы имеют знак "+", если заданное направление отсчёта ЭДС источника совпадает с выбранным                 направлением отсчёта контурного тока.

Система контурных уравнений (5.9) составлена относительно неизвестных контурных токов и записана в канонической форме, а именно:

• контурные ЭДС, как свободные члены, записываются в правых частях уравнений;
• неизвестные контурные токи записываются в левых частях уравнений с последовательно возрастающими индексами;
• уравнения располагаются в соответствии с порядковыми номерами контуров.

Пример 5.2.

Записать систему контурных уравнений для удлинителя (рис. 5.3).

Решение. Предварительно найдём собственные и взаимные сопротивления трёх контуров:

 I контура:

•    собственное сопротивление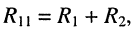
•    взаимные сопротивления: со вторым контуром 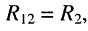с третьим контуром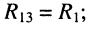

II контура:

•    собственное сопротивление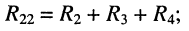
•    взаимные сопротивления: с первым контуром 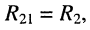с третьим контуром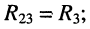

III контура:

•    собственное сопротивление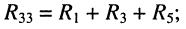
•    взаимные сопротивления: с первым контуром 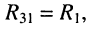с третьим контуром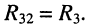 

Заметим, что:

• направление контурного тока 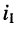совпадает с направлением контурного тока 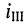и противоположно направлению контурного
•        тока
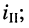
• направления контурных токов 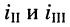совпадают;
• в контуре I имеется контурный независимый источник с ЭДС, равной 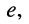а два других контура источников не имеют.

Теперь можно записать систему контурных уравнений, руководствуясь указанными ранее правилами:

 

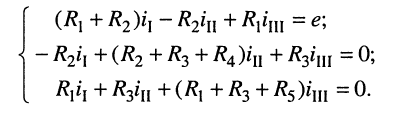
Особенности составления контурных уравнений

Рассмотренные ранее цепи не содержали независимых источников тока, поэтому количество контурных уравнений согласно (5.4) равно количеству независимых контуров. Однако цепь может иметь несколько источников токов. В этом случае следует выбрать такое дерево цепи, при котором источники токов входили бы в число соединительных элементов. Тогда через каждый источник тока будет проходить ток только одного контура, который равен задающему току источника. Поэтому уменьшается как число неизвестных контурных токов, так и число контурных уравнений. Следовательно, если цепь содержит 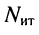источников тока, то известно 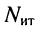контурных токов, а число контурных уравнений оказывается равным

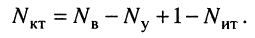       (5.10)

Пример 5.3.

Записать систему контурных уравнений для цепи, схема которой изображена на рис. 5.5.

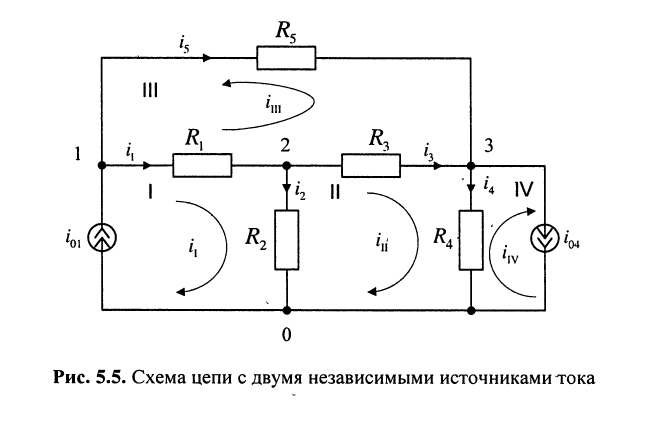
Решение. Цепь содержит два источника тока: в первом и четвёртом контурах, где контурные токи совпадают с токами источников:

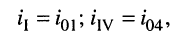
поэтому достаточно записать только два контурных уравнения — для второго и третьего контуров.

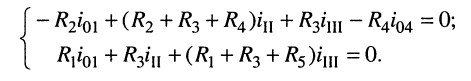
В уравнении для третьего контура отсутствует слагаемое, содержащее ток 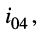поскольку взаимное сопротивление этого контура с четвёртым равно нулю, т. е. между этими контурами нет никакой связи.

Важно:
метод контурных токов применяют в тех случаях, когда число контурных уравнений меньше числа узловых уравнений, а также при анализе колебаний в линейных электрических цепях произвольной конфигурации, содержащих все виды элементов.

Решение системы контурных (узловых) уравнений

Решение системы контурных (узловых) уравнений состоит в нахождении неизвестных контурных токов (узловых напряжений) для последующего вычислением токов и напряжений на элементах цепи. Если параметры цепи (сопротивления, проводимости, токи источников токов, ЭДС источников напряжений) заданы численно, то решение систем осуществляется с помощью специальных пакетов программ математического моделирования, например, Matlab или Matcad.

Основные понятия теории определителей

При теоретическом анализе удобнее использовать методы теории определителей, позволяющие записать решения в компактной форме. Прежде чем обращаться к этим методам, дадим основные понятия теории определителей.

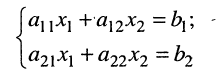        (5.11)

с неизвестными 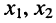 и свободными членами 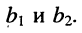Решая эту систему, получаем:

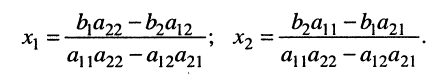                                                                                        (5.12)

Стоящее в знаменателях полученных дробей выражение 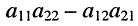 называется определителем (детерминантом) второго порядка и записывается в виде

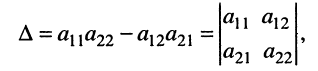           (5.13)

где вертикальные чёрточки являются знаком определителя. С помощью этого обозначения формулы (5.13) можно записать в виде

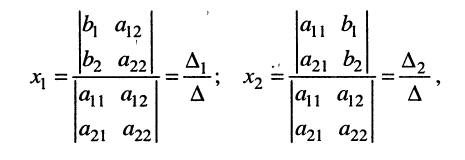         (5.14)

где 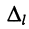— определитель, полученный из определителя системы заменой столбца коэффициентов при 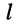-ой неизвестной столбцом свободных членов.

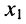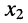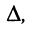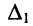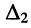Из соотношений (5.14) следует: каждая из неизвестных и   равна дроби, у которой в знаменателе стоит определитель системы а в числителе — определитель  и  соответственно, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при данной неизвестной.

Подобным образом решается система уравнений любого порядка. Остаётся выяснить, как вычислять определители, если их порядок больше двух.

Рассмотрим вычисление определителя на примере системы третьего порядка:

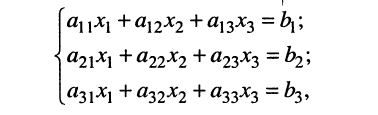
решение которой приводит к дробям вида (5.12), где в знаменателе оказывается выражение

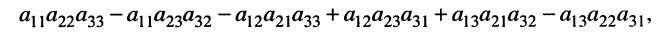          (5.15)

называемое определителем третьего порядка и обозначаемое

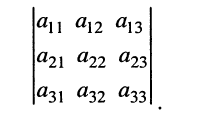           (5.16)

Применяя к (5.16) выражение (5.15), запишем определитель (5.16) в более удобной и наглядной форме:

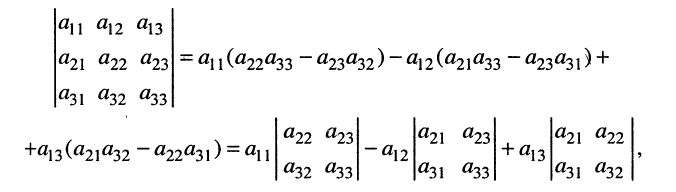                                                           (5.17)

по которой можно вычислять значение определителя третьего порядка. Нетрудно видеть, что правая часть равенства состоит из суммы произведений коэффициентов (элементов) первой строки и определителей второго порядка с нужными знаками. Эти определители называются минорами и получаются из исходного определителя вычёркиванием первой строки и соответствующего данному элементу столбца. Например, минор относительно элемента 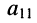получается вычёркиванием первой строки и первого столбца (рис. 5.6, а), минор относительно элемента 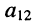получается вычёркиванием первой строки и первого столбца (рис. 5.6, б). Таким образом, получено разложение определителя третьего порядка по элементам первой строки.

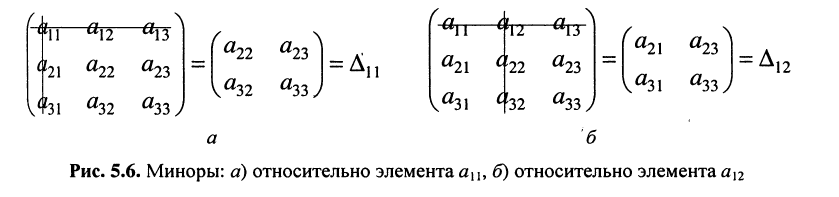
Подобные разложения можно произвести относительно элементов любой строки, предварительно записав соответствующие миноры.

Определение:

Минором 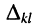 относительно 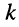-ой строки и 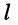-ro столбца (относительно элемента аи) называется определитель, получаемый из исходного определителя, если в последнем вычеркнуть 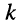-ю строку и 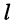-ый столбец.

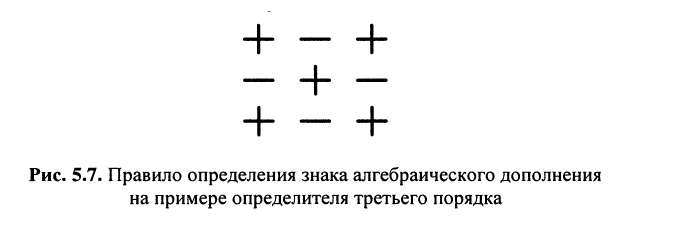
Знак минора определяется по формуле 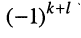или же по мнемоническому правилу: для левого верхнего элемента всегда берётся "+", а для других элементов — в шахматном порядке по схеме, представленной на рис. 5.7.

Определение:

Алгебраическим дополнением 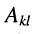относительно к-ой строки и 1-го столбца (относительно элемента 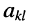) называется минор, взятый с нужным знаком по правилу  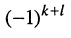,  т. е.

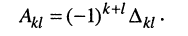    (5.18)

Из сказанного следует: определитель равен сумме произведений элементов какого-нибудь из рядов (строки или столбца) на алгебраические дополнения этих элементов.

При вычислении определителей больших порядков их предварительно разлагают на алгебраические дополнения. Отметим также, что подобно (5.14) для любой системы, у которой 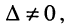имеет место формула для вычисления 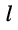-ой неизвестной (формула, или правило Крамера)

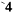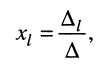       (5.19)

т. е. каждая 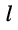-ая неизвестная равна дроби, у которой в знаменателе стоит определитель системы, а в числителе — определитель, полученный из определителя системы подстановкой столбца свободных членов вместо столбца коэффициентов при 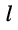-ой неизвестной.

Габриэль Крамер (1704—1752) — швейцарский математик, заложивший в 1750 г. основы теории определителей.
 

Применение теории определителей для решения контурных (узловых) уравнений

Применяя методы теории определителей к системе контурных уравнений (5.9), по формуле Крамера находим решение для первого контурного тока

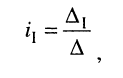
где

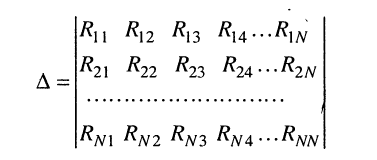        (5.20)

представляет собой определитель системы контурных уравнений (5.9), а

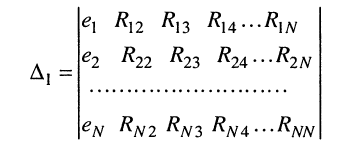
находится из определителя (5.20) при замене в нём первого столбца свободными членами. Заметим, что определитель (5.20) является симметричным относительно главной диагонали, поскольку 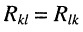при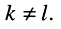

Разлагая определитель 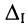на алгебраические дополнения по элементам первого столбца, получаем выражение для первого контурного тока

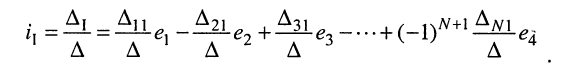    (5.21)

Аналогичное решение можно найти и для L-го контурного тока, разлагая определитель 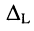на алгебраические дополнения по элементам 1-го столбца:

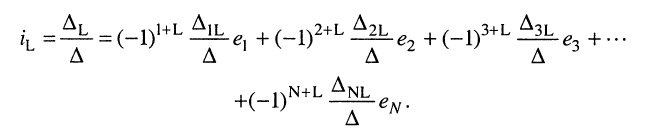        (5.22)

Полученное общее решение (5.22) системы контурных уравнений (5.9) показывает, что реакция в виде токов в электрической цепи представляет собой сумму реакций, вызываемых каждым из воздействий 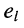в отдельности в предположении, что все другие источники отсутствуют. Этот факт является следствием линейности электрической цепи, описываемой системой линейных уравнений, и составляет содержание принципа наложения.

Аналогичным образом рассчитывается система узловых уравнений (5.2).
 

Примеры использования теории определителей

Задача 5.1.

Цепь имеет единственный источник напряжения 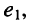по отношению к которому сама цепь представляет собой пассивный резистивный двухполюсник (рис. 5.8). Требуется найти входное сопротивление двухполюсника.

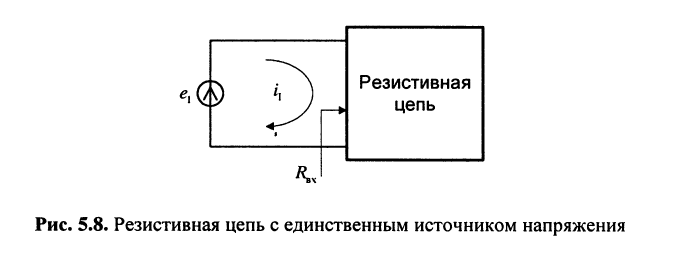
Решение. Для удобства назовём контур, замыкающийся через источник, первым. Тогда из (5.21) следует

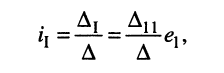       (5.23)

и согласно закону Ома имеем

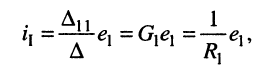
откуда получаем соотношение

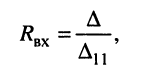     (5.24)

называемое входным сопротивлением двухполюсника. Оно представляет собой эквивалентное сопротивление пассивного резистивного двухполюсника.

Заметим, что в резистивном двухполюснике электрическая энергия может только рассеиваться, поэтому при выбранных на рис. 5.8 направлениях отсчёта тока и напряжения коэффициент 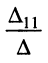в (5.23) представляет собой вещественное положительное число, что справедливо и для (5.24). Следовательно, любой резистивный двухполюсник ведёт себя подобно резистивному элементу, сопротивление которого равно входному сопротивлению двухполюсника.

Задача 5.2.

Найти ток в заданной ветви резистивной цепи (рис. 5.9), имеющей единственный источник напряжения в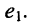 

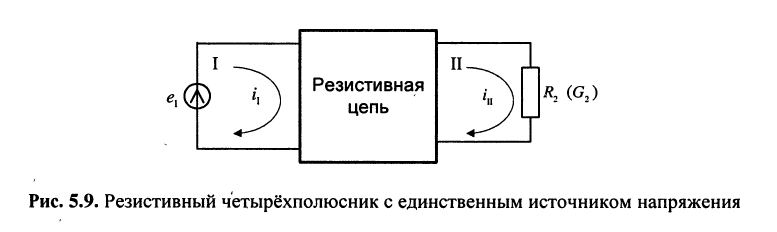
Решение. Такую цепь можно рассматривать как резистивный четырёхполюсник, в котором вновь для удобства обозначим контур, содержащий источник напряжения, первым (I), а контур, содержащий интересующую нас ветвь, вторым (II).

При выбранных направлениях отсчёта ЭДС источника 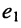и тока второго контура 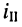согласно (5.22) при 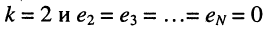получаем:

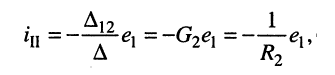     (5.25)

где

 

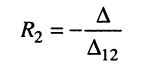
представляет собой собственное сопротивление второго контура и потому эквивалентное сопротивление четырёхполюсника.

Метод контурных токов

При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вычисления.

Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений

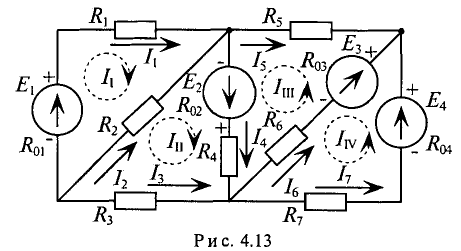
Ту же задачу можно решить, записав только 4 уравнения по второму закону Кирхгофа, если воспользоваться методом контурных токов.

Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи 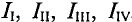. Контурный ток — это расчетная величина, измерить которую невозможно.

Как видно из рис. 4.13, отдельные ветви схемы входят в два смежных контура. Действительный ток в такой ветви определяется алгебраической суммой контурных токов смежных контуров.

Таким образом

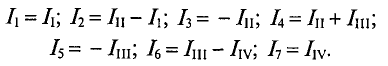
Для определения контурных токов составляют т уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторону от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контурными токами смежных контуров (по другую сторону знака равенства).

Для данной схемы (рис. 4.13) необходимо составить 4 уравнений. Со знаком «плюс» записываются ЭДС и падения напряжено разные стороны знака равенства), действующие в направлении контурного тока, со знаком «минус» — направленные проконтурного тока.

Система уравнений для схемы (рис. 4.13):

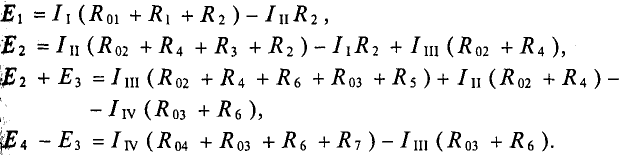
Решением системы уравнений вычисляются значения контур-токов, которые и определяют действительные токи в каждой и схемы (рис. 4.13).

Пример 4.11

Определить токи во всех участках сложной цепи (рис. 4.14), если: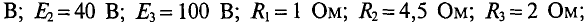

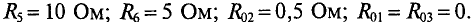
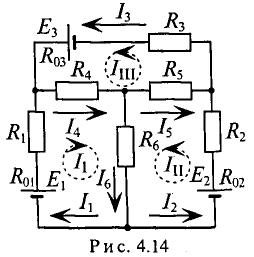
Решение

Необходимо составить 3 уравнения по второму закону для определения контурных токов 1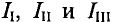 (направление урных токов выбрано произвольно указано пунктирными линиями).

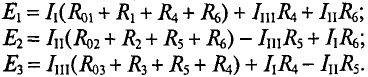
Подставляются числовые значения величин

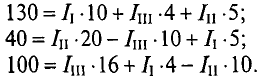
Из уравнения (2) определяется ток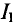

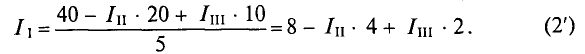
Значение тока 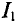(выражение (2')) подставляется в уравнение (1):

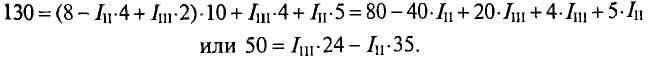
То же значение тока 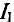подставляется в уравнение (3):

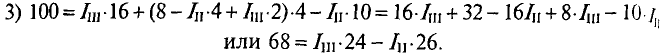
Из полученного уравнения (3) вычитается полученное уравнение (1). В результате получим

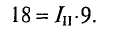
Откуда контурный ток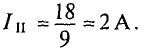

Из уравнения (3) определяется контурный ток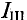

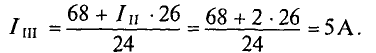
Из уравнения (2') определяется ток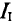

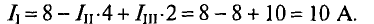
Вычисляются реальные токи в заданной цепи:

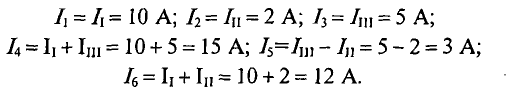
Проверяется правильность решения для 1 -го контура (рис. 4.14).

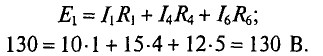
Решение правильное.

Такую же проверку можно произвести и для других контуров (2-го и 3-го):

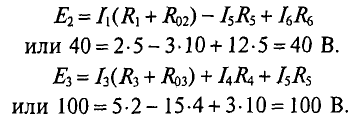
Проверка показала правильность решения.

Определение метода контурных токов

Данный метод является фундаментальным и применим для расчета любых электрических цепей. Он базируется на уравнениях, составленных по второму закону Кирхгофа. В схеме выделяются независимые контуры, в каждом из них произвольно выбираются направления контурных токов и составляются уравнения по второму закону Кирхгофа. Для цепи по рис. 3.1 имеем:

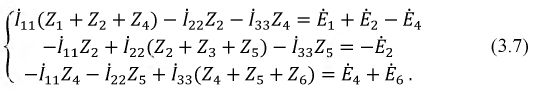
Введем в полученную систему уравнений обобщенные параметры:

собственное сопротивление контура - сумма сопротивлений, входящих в состав контура, например, для первого контура:

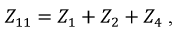
смежные сопротивления - сопротивления на границах контуров, например, 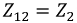 сопротивление на границе первого и второго контуров, суммарная ЭДС, например, для первого контура:

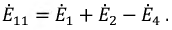
Тогда система уравнений примет вид:

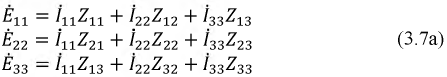
Используя матричный метод расчета, можем записать:

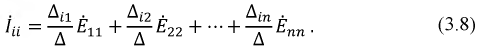
В уравнении (3.8) - главный определитель системы (3.7a), a 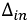 - алгебраическое дополнение для соответствующей контурной ЭДС. В ветвях, которые не граничат с другими контурами, реальные токи будут:

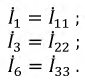
Токи ветвей, находящихся на границах контуров:

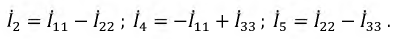
Справочный материал по методу контурных токов

Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурное токи, замыкающиеся в контурах.

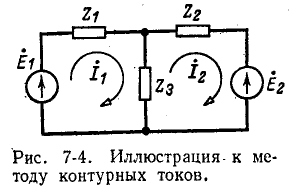
На рис. 7-4 в виде примера показана двухконтурная электрическая цепь, в которой 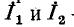— контурные токи. Токи в сопротивлениях 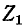и 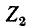равны соответствующим контурным токам; ток в сопротивлении 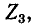являющемся общим для обоих контуров, равен разности контурных токов 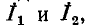так как эти токи направлены в ветви 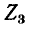встречно*. При этом если положительное направление искомого тока в ветви 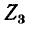принять совпадающим с направлением контурного тока 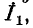то ток в ветви будет равен 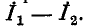В противном случае он будет равен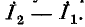

Число уравнений, записываемых для контурных токов по второму закону Кирхгофа, равно числу независимых контуров, т. е. для электрической схемы с числом узлов q и числом ветвей р задача нахождения контурных токов сведется к решению системы р — q + I уравнений. Так, в схеме рис. 7-4 q = 2, р = 3; следовательно, число уравнений равно 3 — 2+1=2 (число независимых контуров). 

Следует отметить, что если положительное направление одного из контурных токов 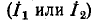изменить на обратное, то ток в ветви 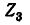будет равен сумме этих токов.

Условимся сумму комплексных сопротивлений, входящих в контур, называть собственным сопротивлением контура, а комплексное сопротивление, принадлежащее одновременно двум или нескольким контурам, — общим сопротивлением этих контуров.

Положительные направления контурных токов задаются произвольно. Направление обхода каждого контура принимается обычно совпадающим с выбранным положительным направлением контурного тока; поэтому при составлении уравнения по второму закону Кирхгофа падение напряжения от данного контурного тока в собственном сопротивлении контура берется со знаком плюс. Падение напряжения от тока смежного контура в общем сопротивлении берется со знаком минус, если контурные токи в этом сопротивлении направлены встречно, как это, например, имеет место в схеме рис. 7-4, где направление обоих контурных токов выбрано по ходу часовой стрелки.

Для заданной электрической схемы с двумя независимыми контурами (рис. 7-4) могут быть записаны два уравнения по второму закону Кирхгофа, а именно:,

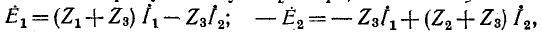
где 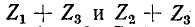— собственные сопротивления контуров 1 и 2; 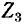— общее сопротивление контуров 1 и 2 (знак минус в уравнениях обусловлен выбором положительных направлений контурных токов).

Если заданная электрическая схема содержит п независимых контуров, то на основании второго закона Кирхгофа получается система из п уравнений:

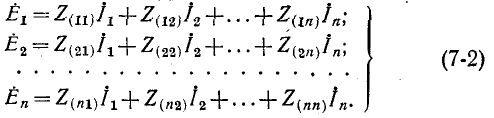
Здесь 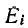— контурная э. д. с. в контуре 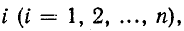т. е. алгебраическая сумма э. д. с., действующих в данном контуре; э. д. с., совпадающие по направлению с направлением обхода, берутся со знаком плюс, а направленные встречно — со знаком минус;

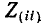— собственное сопротивление контура i;

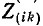— общее сопротивление контуров 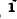i и k. 

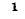Индексы собственных и общих сопротивлений контуров заключены в скобки для отличия их от входных и передаточных сопротивлений, приводимых в последующих разделах книги.

В соответствии со сказанным ранее собственные сопротивления 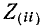войдут со знаком плюс, поскольку обход, контура принимается совпадающим с положительным направлением контурного тока 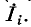Общие сопротивления 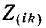войдут со знаком минус, когда токи 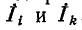направлены в них встречно.

Решение уравнений (7-2) относительно искомых контурных токов может быть найдено с помощью определителей:

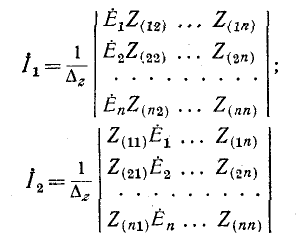
ит. д., где определитель системы

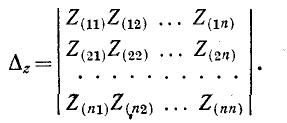
Согласно правилу разложения определителя по элементам столбца определитель равен сумме произведений элементов столбца на их алгебраические дополнения. Поэтому решение уравнений запишется в виде

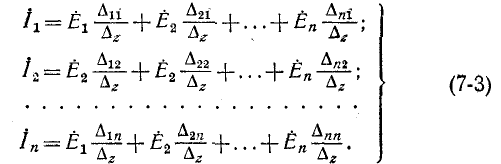
 Определитель снабжен индексом z, так как его элементами являются комплексные сопротивления.

На практике во многих случаях решение системы уравнений (7-2) может быть выполнено более просто последовательным исключением неизвестных,

Здесь Дitl — алгебраическое дополнение элемента Z{lk) определителя системы, т. е. умноженный на (—1)‘+* минор элемента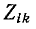 (минор образуется из определителя системы исключением из него i-й строки и 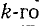столбца).

Сокращенно система уравнений (7-3) записывается в виде:

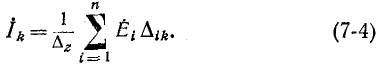
Первый индекс алгебраического дополнения i, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру контура, контурная э. д. с. которого умножается на данное алгебраическое дополнение. Второй индекс 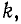обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру контура, для которого вычисляется контурный ток.

Уравнения (7-2), выражающие второй закон Кирхгофа, записаны в предположении, что источниками электрической энергии служат источники э. д. с. При наличии в электрической схеме источников тока они могут быть заменены эквивалентными источниками э. д. с.

Если проводимости источников тока равны нулю, то целесообразно выбрать заданные токи в качестве контурных; тогда число неизвестных контурных токов и соответственно число уравнений сократятся на число заданных токов.

Если в заданной электрической схеме имеются параллельные ветви, то замена их эквивалентным комплексным сопротивлением сокращает число контуров (за счет тех, которые образованы параллельными ветвями).

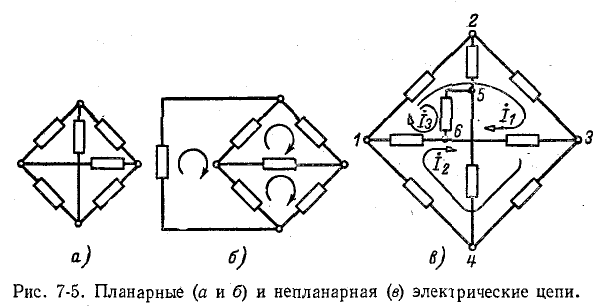
Электрические цепи могут быть планарными или непланарными.

Планарная, или плоская, электрическая цепь может быть вычерчена на плоскости в виде схемы с непере-крещивающимися ветвями. В некоторых случаях пересечение ветвей в электрической схеме, являющееся результатом Принятого способа начертания схемы, устраняется при другом способе изображения данной планарной электрической цепи, как это, например, представлено на рис. 7-5.

Электрическая цепь, приведенная на рис. 7-5, а, планарна, так как имеющееся пересечение ветвей устранимо в соответствии с рис. 7-5, б.

Не планарная электрическая цепь не может быть вычерчена на плоскости в виде схемы с неперекрещиваю-щимися ветвями. Примером такой электрической цепи служит приведенная на рис. 7-5, в непланарная цепь, пересечение ветвей в которой не может быть устранено.

Если направление контурных токов во всех контурах планарной электрической цепи одинаково, например совпадает с ходом часовой стрелки, то общие сопротивления смежных контуров входят в систему уравнений (7-2) со знаком минус, так как контурные токи смежных контуров

направлены в общих ветвях встречно. Направление контурных токов по ходу часовой стрелки принимается во всех контурах, кроме внешнего, охватывающего всю схему. В последнем контурный ток направляется против часовой стрелки'(см. пример 7-2). Это правило, однако, не является обязательным.

В случае непланарной электрической цепи не представляется возможным иметь в общих ветвях только разности контурных токов, как это, например, видно из схемы рис. 7-5, в.

Пример 7-2. 

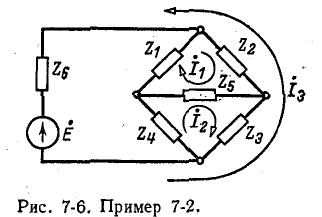
Пользуясь методом контурных токов, определить ток в диагонали бюстовой схемы рис. 7-6.

Выбранные положительные направления контурных токов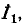 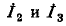указаны на схеме стрелками. Число уравнений, записываемых по второму закону Кирхгофа, равно трем (по числу независимых контуров):

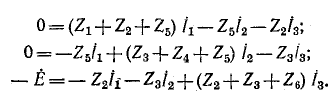
Решение полученной системы уравнений относительно контурных токов 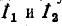дает:

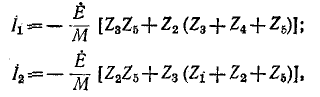
где М имеет то же значение, что и в примере 7-1.

Искомый ток в диагонали мостовой схемы равен разности контурных токов:

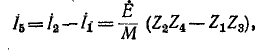
что совпадает с полученным в примере 7-1 ответом.

Следует заметить, что если в заданной схеме контуры выбрать так, чтобы через ветвь 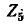проходил только один контурный ток, то искомый ток в ветви 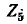будет равен именно Рис. 7-6. Пример 7-2. этому контурному току, т, е.

задача сведется к нахождению только одного контурного тока (вместо двух).