Математика - язык физики с примерами

Математика - язык физики:

Физика всегда была тесно связана с математикой.

Многие теории современной математики возникли благодаря тому, что необходимо было решить проблемы, возникающие в процессе познания физического мира. Например, чтобы создать теоретическую основу классической механики, И. Ньютон применил математические модели, давшие толчок к формированию дифференциального исчисления. В свою очередь физики для доказательства теоретических положений и подтверждения гипотез широко используют математику, ее понятийный аппарат. Поэтому не случайно математику считают языком физики.

Физические величины по своим математическим свойствам бывают скалярными или векторными. В зависимости от этого математические действия над ними выполняются согласно разным правилам. В частности, со скалярными величинами (путь, масса, работа, мощность и т. д.) поступают как с действительными числами. Например, сумма скалярных физических величин вычисляется как алгебраическая сумма их числовых значений.

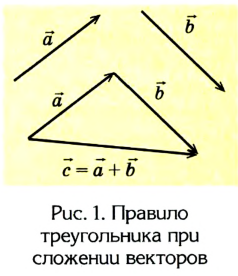
Векторные величины (перемещение, скорость, сила и т. д.) подчинены иным правилам, которые учитывают их направление. В частности, сумма векторных величин вычисляется как геометрическая сумма векторов, результирующая которых также является вектором. Чтобы сложить векторы, применяют правило треугольника или правило параллелограмма.

1.    Правило треугольника (рис. 1): чтобы сложить два вектора

2.    Правило параллелограмма (рис. 2): чтобы сложить два вектора следует совместить начала этих векторов и построить на их основе параллелограмм, диагональ которого будет результирующим вектором суммы векторов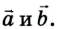

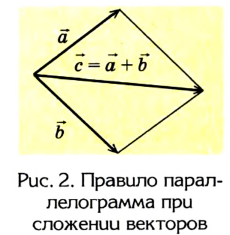
Любой вектор можно разложить на

составляющие, в частности по осям прямоугольной (декартовой) системы координат (рис. 3). Данное свойство векторов часто используют при решении задач динамики.

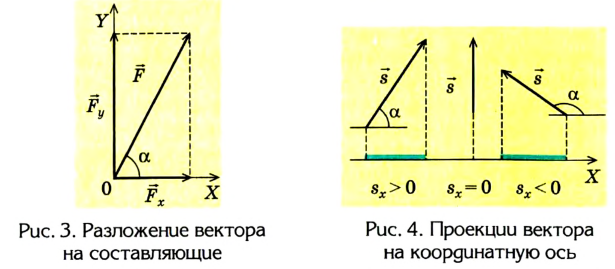
В кинематике часто ищут проекции вектора на соответствующую координатную ось. Они могут быть положительными, отрицательными или равными нулю, поскольку учитывают числовое значение косинуса угла а между вектором и координатной осью (рис. 4):

• Заказать решение задач по физике

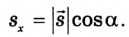
Приближенные вычисления:

Сейчас, когда человек владеет мощным арсеналом вычислительной техники (разнообразные калькуляторы, компьютеры и т. д.), соблюдение правил приближенных вычислений особенно важно, поскольку можно исказить достоверность результата. В физике, выполняя какие-либо вычисления, следует помнить о точности результата, которой можно или необходимо (если ее задают) достичь. Недопустимо производить вычисления с большей точностью, нежели это задано данными физической задачи или требуется условиями проведения эксперимента (В школьном лабораторном эксперименте вычисления проводят, как правило, не более чем с двумя значащими цифрами.
).

Например, выполняя математические действия над числовыми значениями физических величин, которые обладают двумя достоверными (значащими) цифрами, нельзя записывать результат вычислений с точностью, выходящей за пределы двух достоверных цифр, даже если в конечном счете имеем их больше.

Пример: 2,7 • 3,4 = 9,2 (но не 9,18); 72 : 53 = 1,4 (но не 1,358...).

Значения физических величин необходимо записывать, указывая лишь знаки достоверного результата. Например, если числовое значение величины 39 600 имеет три достоверных знака (абсолютная погрешность результата равна 100), то результат следует записать в виде .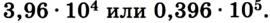
При подсчете достоверных цифр не учитываются нули слева от числа.

Для того чтобы результат вычислений был корректным, его необходимо округлить, оставив лишь действительное значение величины. Если числовое значение величины содержит лишние (недостоверные) цифры, превышая заданную точность, то последняя сохраняемая цифра увеличивается на 1 при условии, когда излишек (лишние цифры) равен или больше половины значения следующего разряда числа.

Пример: Округление до трех достоверных цифр: а) 0,46281 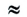0,463; 6)1835 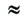1840; в) 1,4817 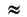1,48; г) 7,6394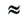7,60.

В различных числовых значениях величины ноль может быть как достоверной, так и недостоверной цифрой. В приведенном выше примере в случае б) он является недостоверной цифрой, а в г) - достоверной, значащей. В физике, когда желают подчеркнуть достоверность разряда числового значения физической величины, в записи значения величины в стандартном виде указывают «0». Например, значение массы 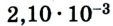кг указывает на то, что в данном результате имеется три достоверные цифры и измерение проведено с соответствующей точностью, а значение 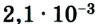кг имеет лишь две достоверные цифры.

Следует помнить, что результат действий над числовыми значениями физических величин является приближенным результатом, который учитывает точность вычислений или погрешность измерений. Поэтому при приближенных вычислениях следует руководствоваться такими правилами подсчета достоверных цифр:

1. При выполнении математических действий с числовыми значениями физических величин в их результате следует указывать столько достоверных знаков, сколько их имеет числовое значение с наименьшим количеством достоверных знаков.
2. Во всех промежуточных расчетах целесообразно сохранять на одну цифру больше, чем их имеет числовое значение с наименьшим количеством достоверных знаков. В окончательном результате эта «дополнительная» цифра отбрасывается путем округления.
3. Если отдельные данные имеют больше достоверных знаков, нежели другие, их значения целесообразно предварительно округлить (можно сохранить одну «избыточную» цифру) и после этого производить вычисления.