Математическое моделирование в экономике - этапы, виды и использование

Содержание:

Моделирование в научных исследованиях использовалось с древних времен и постепенно охватило все новые отрасли науки: техническое проектирование, строительство и архитектура, астрономия, физика, химия, биология и, в конечном счете, общественные науки. Большие успехи и признание практически во всех отраслях современной науки принесли метод моделирования в ХХ веке. Однако долгое время методология моделирования разрабатывалась самостоятельно отдельными науками. Не было единой системы понятий, единой терминологии. Лишь постепенно была признана роль моделирования как универсального метода научного познания.

Термин "модель" широко используется в различных сферах человеческой деятельности и имеет множество смысловых значений. Рассмотрим только такие "модели", которые являются инструментами получения знаний.

Модель - это материальный или мысленно представленный объект, который заменяет собой первоначальный объект в процессе исследования, так что его непосредственное изучение дает новые знания о первоначальном объекте

Моделирование относится к процессу построения, исследования и применения моделей. Она тесно связана с такими категориями, как абстракция, аналогия, гипотеза и т.д. Процесс моделирования обязательно предполагает как построение абстракций и аналогий, так и построение научных гипотез.

Моделирование как метод научного познания

Главной особенностью моделирования является то, что оно является методом опосредованного познания с помощью суррогатных объектов. Модель функционирует как специальное средство познания, которое исследователь размещает между собой и объектом и с помощью которого исследует интересующий его объект. Именно эта особенность метода моделирования определяет конкретные формы использования абстракций, аналогий, гипотез, других категорий и методов познания.

Необходимость использования метода моделирования определяется тем, что многие объекты (или проблемы, связанные с ними) вообще нельзя изучать напрямую, или это исследование требует много времени и денег.

Процесс моделирования включает три элемента: 1) субъект (исследователь), 2) объект исследования, 3) модель, которая передает отношения между узнаваемым субъектом и узнаваемым объектом.

Объект A считается существующим или созданным. Мы строим (материально или ментально) или находим в реальном мире другой объект B - модель объекта A. Фаза создания модели предполагает наличие определенных знаний об исходном объекте. Познавательные возможности модели определяются тем, что модель воспроизводит все существенные особенности исходного объекта. Вопрос о необходимости и достаточной степени сходства оригинала и модели требует специального анализа. Очевидно, что модель теряет свой смысл как в случае идентичности с оригиналом (тогда она перестает быть оригиналом), так и в случае чрезмерного отклонения от оригинала во всех существенных отношениях.

Таким образом, изучение одних аспектов моделируемого объекта происходит за счет отказа от рассмотрения других аспектов. Поэтому любая модель заменяет оригинал только в строго ограниченном смысле. Из этого следует, что для объекта можно создать несколько "специализированных" моделей, ориентированных на конкретные стороны исследуемого объекта или характеризующих объект с различной степенью детализации.

На втором этапе процесса моделирования модель выступает в качестве самостоятельного объекта исследования. Одной из форм такого исследования является проведение "модельных" экспериментов, в ходе которых намеренно изменяются условия работы модели и систематизируются данные о ее "поведении". Конечным результатом этого этапа является совокупность знаний о модели R.

Третья стадия предполагает перенос знаний из модели в оригинал, т.е. формирование совокупности знаний S об объекте. Этот процесс передачи знаний протекает по определенным правилам. Знания о модели должны быть скорректированы с учетом тех свойств исходного объекта, которые не учитывались или не изменялись при построении модели. Мы можем обоснованно перенести любой результат от модели к оригиналу, если этот результат обязательно связан с особенностями сходства оригинала и модели. Однако, если определенный результат исследования модели связан с разницей между моделью и оригиналом, то этот результат непригоден для передачи.

Четвертый этап - практическая проверка знаний, полученных с помощью моделей, и их использование при построении обобщенной теории объекта, его трансформации или управления.

Чтобы понять суть моделирования, важно не упускать из виду тот факт, что моделирование - не единственный источник знаний об объекте. Процесс моделирования "встроен" в более общий процесс познания. Этот факт учитывается не только на этапе построения модели, но и на заключительном этапе, когда результаты исследований, полученные на основе различных когнитивных инструментов, объединяются и обобщаются.

Моделирование - это циклический процесс. Это означает, что за первым четырехступенчатым циклом могут последовать второй, третий и так далее. В то же время знания об изучаемом объекте становятся все более точными, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, вызванные плохим знанием объекта и ошибками при построении модели, могут быть исправлены в последующих циклах. Таким образом, методология моделирования предоставляет большие возможности для саморазвития.

Математическое моделирование - это изучение явлений и объектов в экономике с использованием математических моделей.

Этапы математического моделирования

Построение математических моделей состоит из нескольких этапов.

На первом этапе определяются задачи и разрабатывается концептуальная модель. Объект моделирования, его функциональное назначение, окружающая среда описываются устно, определяются отдельные элементы, свойства объекта, возможные состояния, идентифицируются связи между элементами. Такое предварительное представление объекта является концептуальной моделью.

На втором этапе происходит построение модели. На основе осмысленного описания объекта проводится анализ исходного набора характеристик объекта, идентифицируются важнейшие характеристики, определяются контролируемые и неконтролируемые параметры, вводятся их метки, создается система ограничений и строится объектная функция. Таким образом, результатом этого этапа является математическая модель объекта.

Следует учитывать, что простота модели зависит от выбора переменных. При составлении ограничений необходимо убедиться, что все условия ограничений присутствуют в модели.

На третьем этапе определяются метод и алгоритм решения. Тот или иной метод теории оптимального решения зависит от характера и структуры объективной функции и ее ограничений.

На четвертом этапе проверяется адекватность модели и, при необходимости, вносятся коррективы в модель. Верификация выражается в определении степени соответствия модели критериям практики, т.е. соответствия результатов наблюдений и теоретических последствий модели. На этапе монтажа могут потребоваться дополнительные исследования на месте. Подгонка математической модели может быть выполнена одним из трех способов:

• Расширение внешних факторов;
• Переход к более высокой степени нелинейности;
• Расширение списка ограничений.

На пятом этапе ведется поиск решений. После достижения удовлетворительного уровня адекватности модели используется соответствующий алгоритм для определения оптимального решения на модели.

На шестом этапе найденное решение реализуется на практике.

Математическая модель редко может быть выбрана из имеющихся моделей. Параметризация производится таким образом, чтобы модель соответствовала исследуемому объекту.

Виды математических моделей

Построение математических моделей в экономике осуществляется для достижения одной из перечисленных целей:

Теоретические модели используются для изучения общих закономерностей экономических систем, а также их свойств;
Прикладные модели создаются для разработки конкретных рекомендаций по практическим решениям и носят оптимизационный характер.
Все математические модели разделены:

• Макроэкономические, которые описывают экономику всего государства и связывают воедино агрегированные показатели: ВНП, НДП, инфляцию, занятость и др. Такие модели обычно носят теоретический характер.
• Микроэкономические модели, в которых моделируемая система является единой фирмой. Эти модели называются полуэмпирическими (смешанные модели).

На рисунке 1 показана общая картина экономического развития и роль математического моделирования в нем.

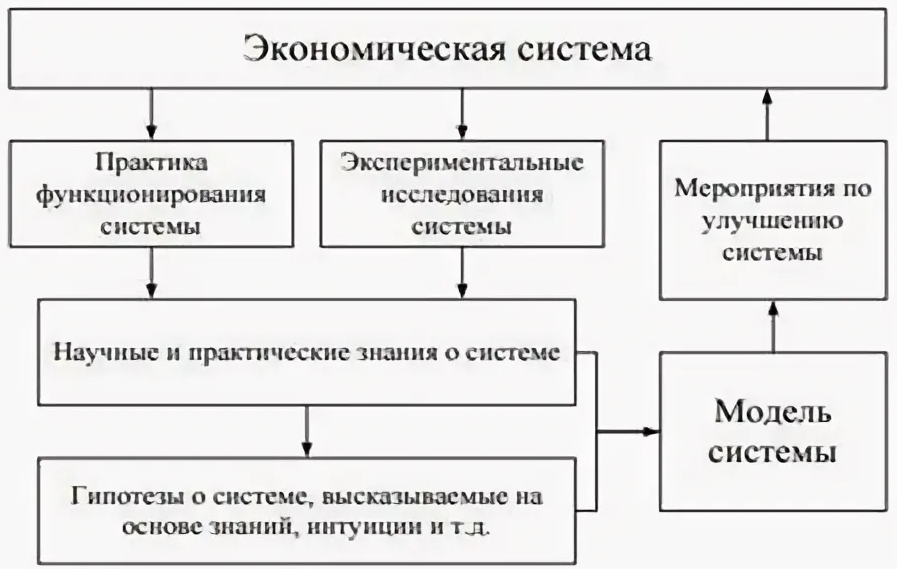
Рисунок 1: Роль моделирования в экономической системе. 

При создании математических моделей в экономике необходимо учитывать, что многие свойства таких моделей нельзя точно определить, так как на их ценность сильно влияет "человеческий фактор". Поэтому свойства экономических моделей являются случайными переменными.

Экономические и математические модели являются в некоторой степени неопределенными. При теоретическом моделировании эта неопределенность остается за рамками исследований, в то время как при прикладном моделировании неопределенность должна приниматься во внимание. Всегда будет вероятность иного развития реальной ситуации, поэтому в модель необходимо встроить контрмеры или страховые меры для таких случаев.

Использование математического моделирования в бизнесе

Внедрение математических методов в экономику сопровождалось преодолением некоторых трудностей, связанных с развитием математики за счет потребностей физических и инженерных наук. Здесь главная причина скрыта в природе экономических процессов и самой экономической науке.

Многие объекты, изучаемые экономической наукой, могут быть охарактеризованы термином "сложная система".

Система - это набор элементов, которые взаимодействуют и формируют определенную целостность.

Важным свойством любой системы является возникновение, то есть наличие свойств, не присущих какому-либо элементу системы. Поэтому при изучении систем недостаточно разбивать их на элементы, а затем изучать. Так же и в экономических исследованиях - нет таких экономических объектов, которые можно было бы рассматривать как отдельные элементы.

Сложность системы зависит от количества ее элементов, их соединений, взаимоотношений системы и внешней среды. Например, экономика страны имеет все характеристики сложной системы, так как она сочетает в себе многие элементы, ее внутренние отношения разнообразны.

Сложность экономики в некоторых случаях являлась оправданием невозможности ее моделирования, исследований с использованием математики. Однако эта точка зрения оказалась ошибочной. Любой объект может быть смоделирован. И именно сложные объекты представляют наибольший интерес, потому что в этих условиях моделирование дает свои результаты.

Потенциальная вероятность математического моделирования в экономике не означает его успешного применения в той или иной ситуации. В экономической системе всегда существуют неформализованные проблемы и ситуации, когда математическое моделирование недостаточно эффективно.