Математическая логика - основы с примерами решения
Легкость математики основана на возможности чисто логического ее построения, трудность, отпугивающая многих, - на невозможности иного изложения.
(Хуго Штейнгаус)
Знания за пределами математики и доказательной логики состоят из предположений. Предположения, составляющие математические знания, закрепляются доказательными рассуждениями и подкрепляются правдоподобными рассуждениями. Математическое доказательство является доказательным рассуждением, косвенные улики юриста, индуктивные доводы физика, статистические доводы экономиста относятся к правдоподобным рассуждениям. Доказательное рассуждение надежно, неоспоримо, окончательно. Правдоподобное рассуждение рискованно, спорно, условно.
Доказательное рассуждение имеет жесткие стандарты, кодифицированные и выясненные логикой, являющейся теорией доказательных рассуждений. Стандарты правдоподобных рассуждений текучи и нет никакой теории таких рассуждений, которая могла бы сравниться с доказательной логикой или обладала бы сравнимой с ней согласованностью.
Доказательные рассуждения. Все новые знания о мире связаны с правдоподобными рассуждениями.
Доказательное рассуждение и правдоподобное рассуждение не противоречат друг другу; они, напротив, друг друга дополняют. В строгом рассуждении главное - отличать доказательство от догадки, обоснованное доказательство от необоснованной попытки. В правдоподобном рассуждении главное - отличать одну догадку от другой, более разумную догадку от менее разумной.
Часто математические утверждения касаются бесконечного множества объектов, и перебрать эти объекты невозможно. Такой перебор можно заменить следующим методом рассуждения: если данное утверждение истинно в одном случае, то оно окажется истинным и в следующем за ним случае, а значит и во всех случаях. Такой метод рассуждения называется методом математической индукции.
Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Обобщение часто делается при переходе от одного предмета к целому классу, содержащему этот предмет.
Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном. Специализация часто производится при переходе от целого класса предметов к одному предмету, содержащемуся в этом классе.
Аналогия. Две системы аналогичны, если они согласуются в ясно определенных отношениях соответствующих частей. Это отношение имеет ясный смысл, если отношения управляются одними и теми же законами.
Далее приводятся некоторые основные факты математической логики, которую еще называют формальной логикой. Формальной потому, что она позволяет проверить правильность рассуждений независимо от их содержания. Цепочки рассуждений в совершенно разных областях математики и других наук можно одинаково описать на языке логики и убедиться в их справедливости или ошибочности.
Высказывания и логические связки
Многие математические понятия удобно записывать в виде выражений, содержащих некоторые логические символы. Так, символ V, называемый квантором общности, используется вместо слов: «для любого», «для всех», «каково бы ни было...» и т.д., а символ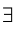 
Основной объект математической логики - высказывание. Высказыванием называется повествовательное предложение, которое может быть классифицировано либо как истинное, либо как ложное, но не как и то, и другое вместе.
Содержание высказывания несущественно: лишь бы это предложение могло быть либо истинным, либо ложным. При этом вовсе не обязательно указывать способ проверки истинности. Главное, что высказывание не может быть истинным и ложным одновременно. Если высказывание истинно, будем говорить, что его значение истинности - истина (или t (от английского true); если - ложно, то значение истинности - ложь (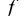 
Высказывания в математической логике обычно обозначаются прописными латинскими буквами: А, В, С и т.д. Для того чтобы из высказываний получать новые высказывания, применяются специальные операции - логические связки. Рассмотрим пять основных логических связок. Сначала дадим неформальное объяснение. Однако оно чревато неточностями, поэтому дадим логическим операциям также строгое определение. Определить высказывание — значит, указать, в каких случаях оно истинно, а в каких ложно.
Отрицание — это высказывание, которое получается из данного высказывания А с помощью слова «не». Отрицание можно обозначать по-разному: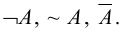 
.
Простое добавление слова «не» к высказыванию чаще всего будет противоречить языковым нормам. Поэтому в конкретных случаях
требуется «перевод» полученного высказывания на русский язык. Пусть, например, А = «Завтра пойдет дождь». Что значит «Не (Завтра пойдет дождь)»: «Дождь пойдет не завтра», «Завтра пойдет не дождь» или «Завтра не пойдет дождь»? Здравый смысл подсказывает, что отрицанием высказывания А является третье предложение. Чтобы определить точно, дадим формальное определение отрицания.
Отрицанием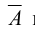 
высказывания А называется такое высказывание, которое принимает значение / (ложно), если высказывание А истинно, и значение t (истинно), если высказывание А ложно. В нашем примере этому условию удовлетворяет только третье предложение. Итак, 
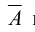= «Завтра не пойдет дождь».
Дизъюнкция - это высказывание, которое получается из двух данных высказываний А и В с помощью союза «или». Дизъюнкция обозначается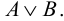 
.
Дизъюнкция строится с помощью неисключающего «или». Таким образом, дизъюнкция A v В истинна, когда истинно, по крайней мере, одно из высказываний А и В или оба вместе. Другими словами, дизъюнкция ложна в том и только в том случае, когда оба высказывания ложны.
Конъюнкция - это высказывание, которое получается из двух данных высказываний А и В с помощью союза «и». Конъюнкция обозначается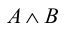 
. Конъюнкция 
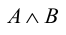справедлива в том и только в том случае, когда оба высказывания истинны.
Импликация образуется из высказываний А и В с помощью слов «если... то...». Получается высказывание вида «если А то В». Напомним, что математическая логика носит формальный характер, содержанием высказываний она не, занимается.
На примере импликации хорошо видна разница между обычным языком и языком логики. В обычном языке сложное предложение «если А, то В» предполагает между А и В отношение посылки и следствия, или же причины и обусловленного ею действия.
Импликация обозначается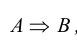 
, при этом говорят: «А влечет В» или «В при условии, что А», «В, если А», «А есть достаточное условие для В», «В есть необходимое условие для А».
Договорились, что импликация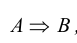 
ложна в том и только в том случае, когда высказывание А истинно, а высказывание В ложно. Такое определение подсказано здравым смыслом: разумно считать импликацию истинной, если В истинно, независимо от значения А; если оба участника импликации ложны, импликация, естественно, также истинна. В единственном случае, когда «предпосылка» импликации истинна, а «вывод» ложен, импликация считается ложной.
Эквиваленция образуется из высказываний А и В с помощью слов «...тогда и только тогда, когда...»:
Утверждение «А тогда и только тогда, когда В» не означает в логике, что составляющие высказывания А и В имеют одно и то же значение или один и тот же смысл.
Эквиваленция обозначается 
, Синонимы для эквиваленции: «если А, то В, и если В, то А», «А в том и только в том случае, когда «И есть необходимое и достаточное условие для В», «В есть необходимое и достаточное условие для А». Разумное определение эквиваленции: эквиваленция истинна в том и только в том случае, когда высказывания А и В имеют одинаковое значение истинности (либо оба истинны, либо оба ложны).
Новые высказывания (отрицание, дизъюнкция, конъюнкция, импликация и эквиваленция) образуются из существующих высказываний с помощью операций, или логических связок, имеющих те же названия.
В логике, как и в арифметике, операции делятся по старшинству. Это позволяет при записи сложных высказываний избегать большого количества скобок. Порядок выполнения операций таков: приоритет имеет отрицание, затем на одном уровне — дизъюнкция и конъюнкция, следующая связка — импликация и, наконец, самая последняя — эквиваленция.
Лекции по предметам: