Логарифмические выражения с примерами решения

Мы уже умеем по значению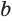

Пример:

Решим уравнение .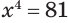

По определению арифметического корня находим, что 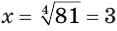. Учитывая, что показатель степени четный, находим другой корень этого уравнения — число 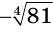, т. е. число -3.

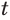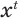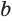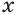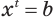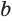Теперь поставим задачу нахождения показателя степени по ее значению и основанию , иными словами, задачу решения уравнения вида , где и 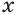— некоторые числа.

Пример:

Решим уравнение .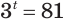

Это уравнение можно записать как 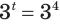. Учитывая следствие 1 из параграфа 11, можем утверждать, что уравнение имеет единственный корень 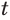= 4.

Обратим внимание на то, что при решении уравнения 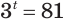мы его левую и правую части представили степенями с одним основанием 3. Но, например, уравнение 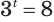таким приемом решить не получится, так как число 8 не представляется рациональной степенью числа 3. Вместе с этим уравнение 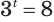имеет действительный корень, что показывает рисунок 163.

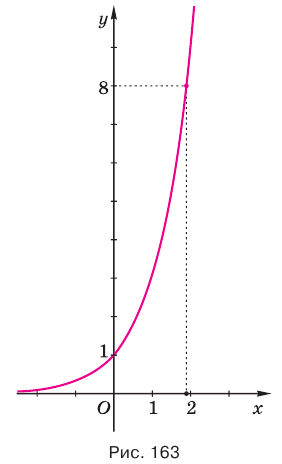
Этот корень называют логарифмом числа 8 по основанию 3 и обозначают 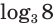. Таким образом, корнем уравнения 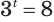является число 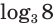, приближенно равное 1,89.

Логарифмом числа 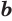при основании 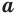, , 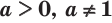называется показатель степени, в которую нужно возвести основание 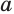, чтобы получить число .

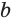Логарифм числа 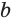при основании 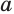обозначают .

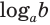Пример:

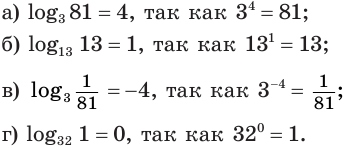
Таким образом, учитывая определение логарифма числа, корень уравнения 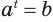можно записать как 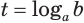. Иными словами, равенства 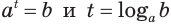выражают одну и ту же связь между числам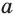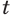и , и 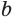, т. е. равносильны:

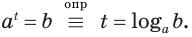
Пример:

Решим уравнение .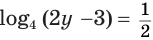

Определение логарифма позволяет данное уравнение заменить равносильным уравнением 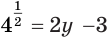, корнем которого является число 2,5.

Определение логарифма коротко можно представить равенством

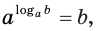
которое называют основным логарифмическим тождеством.

Пример:

Вычислим значение выражения .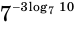

Используем свойство возведения степени в степень и основное логарифмическое тождество:

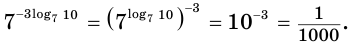
Из свойств показательной функции следует, что выражение 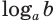имеет значение только при .

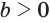Пример:

Найдем область определения выражения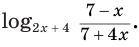

Данное выражение имеет значение, если основание логарифма 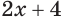положительно и не равно единице, а подлогарифмическое выражение 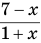положительно, т. е. если истинна система условий 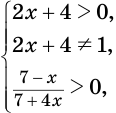, которая равносильна системе 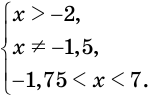. Эта система дает (рис. 164) такую равносильную совокупность условий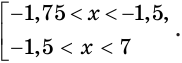

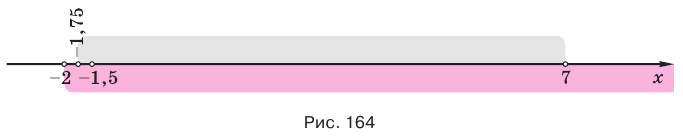
Из определения логарифма следует, что

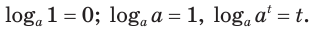
Действие нахождения логарифма числа называется логарифмированием.

Введение действия логарифмирования порождает новый класс логарифмических выражений, т. е. выражений, которые содержат по крайней мере одно действие нахождения логарифма из выражения с переменной. При преобразованиях логарифмических выражений используются свойства действия логарифмирования. Установим эти свойства.

Теорема 5.

При любом положительном и не равном единице основании:

логарифм произведения положительных множителей равен сумме их логарифмов:

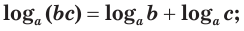
логарифм частного с положительными делимым и делителем равен разности логарифмов делимого и делителя:

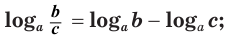
логарифм любой действительной степени положительного числа равен произведению показателя степени и логарифма основания:

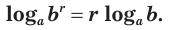
Доказательство:

Пусть 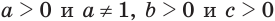, 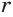— любое действительное число.

Основное логарифмическое тождество позволяет записать равенства:

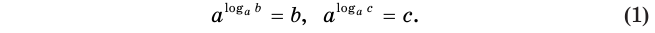
Перемножив их, получим:

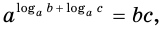
откуда, по определению логарифма:

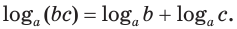
Если разделить первое равенство из (1) на второе, то получим, что

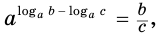
откуда, по определению логарифма:

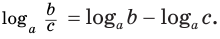
Возведя первое равенство из (1) в степень с показателем 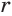, придем к равенству

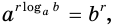
откуда, по определению логарифма:

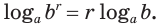
Обращаем внимание на то, что при применениях тождеств, установленных теоремой 5, нужно следить за тем, чтобы все подлогарифмические выражения были положительными.

Пример:

Прологарифмируем выражение:

а) 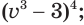б)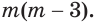

а) Получим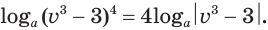

б) Выражение 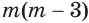можно логарифмировать, если истинно условие 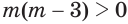, т. е. если множител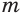и и 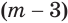или оба положительны, или оба отрицательны.

Если оба множителя 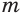и 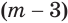положительны, т. е. если 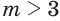, то 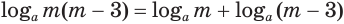. А если оба множителя 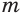и 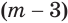отрицательны, т. е. если 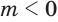, то .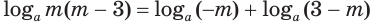

Действие, обратное логарифмированию, называют потенцированием.

• Заказать решение задач по высшей математике

Пример:

Пропотенцируем выражение .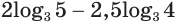

Будем последовательно получать:

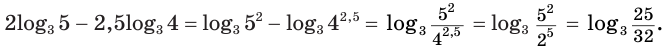
Логарифмы чисел находят с помощью специальных таблиц или калькулятора. И в том, и в другом случае находят десятичные или натуральные логарифмы.

Десятичным логарифмом числа называют логарифм этого числа по основанию 10.

Для десятичного логарифма вместо 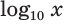пишут .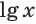

Натуральным логарифмом числа называют логарифм этого числа по основанию 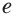, где 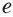— иррациональное число, приближенно равное 2,718281828... . Число 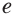, как и число 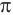играет важную роль во многих разделах математики и в ее применениях.

Для натурального логарифма вместо 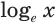пишут .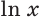

Для вычислений достаточно иметь возможность находить логарифмы по одному основанию, так как тогда можно найти логарифм числа по другому основанию. Это позволяет делать формула перехода к другому основанию.

Теорема 6.

Логарифм числа по данному основанию равен логарифму числа по новому основанию, деленному на логарифм данного основания по новому основанию:

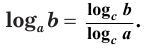
Доказательство:

Пусть 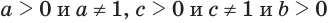. Тогда, в соответствии с основным логарифмическим тождеством, можем записать 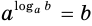. Прологарифмировав это равенство по основанию 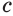, получим 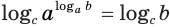, или, используя свойство логарифма степени, 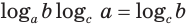. Отсюда

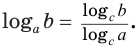
Пример:

Найдем, через сколько лет удвоится пятипроцентный вклад в банк.

Пусть имеется вклад в 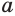р. Тогда через 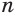лет пятипроцентный вклад станет равным 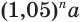. Нас интересует такое значение переменной 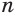, при котором вклад станет больше в два раза, т. е. 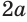. Получили уравнение 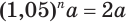. Решим его:

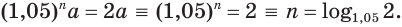
Вычисления проведем с помощью калькулятора, на котором есть клавиша для нахождения десятичных логарифмов:

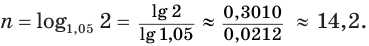
Таким образом, удвоение пятипроцентного вклада произойдет через 14,2 года.

Открытие логарифмов было вызвано в XVI в. быстрым развитием астрономии и усложнением астрономических вычислений, которые имели непосредственное практическое значение при определении местонахождения судов по Солнцу и другим звездам. Логарифмы быстро вошли в практику.

Первые логарифмические таблицы были составлены в одно время и независимо друг от друга шотландским математиком Джоном Непером (1550—1617) и швейцарским математиком и астрономом Йобстом Бюрги (1552—1632). В 1623 г. английский математик Эдмунд Гантер изобрел логарифмическую линейку, с помощью которой действия над числами — умножение, деление — заменяются действиями сложения и вычитания над логарифмами этих чисел. На рисунке 165 показана одна из логарифмических линеек. Сейчас нужные вычисления проводятся с помощью калькуляторов. Леонард Эйлер (1707—1783) установил, что действие логарифмирования является обратным действию возведения в степень. Термин логарифм предложен Джоном Непером. Современное определение логарифма впервые дано в 1742 г. английским математиком Вильямом Гардинером.