Линии второго порядка - определение и вычисление с примерами решения

Содержание:

Линии второго порядка

Окружность

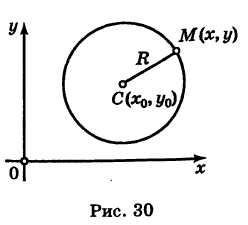
Выведем уравнение окружности (рис. 30) с центром С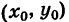

MC=R.

Отсюда, вспоминая формулу расстояния между двумя точками, имеем

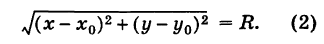
Так как обе части равенства (2) положительны, то, возводя в квадрат, получим равносильное уравнение

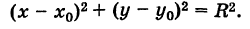
Итак, координаты любой точки М (х, у) данной окружности удовлетворяют уравнению (3). Справедливо также обратное утверждение.

Таким образом, уравнение (3) представляет собой уравнение окружности радиуса R с центром в точке С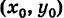. Это уравнение назвают нормальным уравнением окружности.

В частности, полагая х0 = 0 и у0 = 0, получим уравнение окружности с центром в начале координат

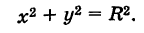
Уравнение окружности (3) после несложных преобразований можно привести к виду

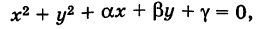
где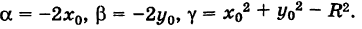

Таким образом, окружность является кривой второго порядка.

Сравнивая уравнение (5) с общим уравнением кривой второго порядка

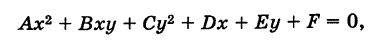(6)

мы видим, что в (5) В = 0 и, кроме того, А — 1, С = 1, т. е. А = С. Обратно, положим в (6) В = 0 и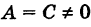

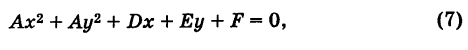
Деля уравнение (7) почленно на 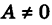и полагая

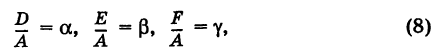
мы приходим к уравнению вида (5).

Уравнение (7) называется общим уравнением окружности. Заметим, однако, что не всякое уравнение (7) является уравнением действительной окружности. Легко показать, что (7) определяет действительную кривую (окружность) лишь при 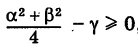где 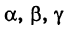выражаются равенствами (8).

Таким образом, действительная кривая второго порядка является окружностью тогда и только тогда, когда: 1) коэффициенты при квадратных текущих координат равны между собой и 2) отсутствует член, содержащий произведение текущих координат.

Центральные кривые второго порядка

Рассмотрим уравнение второго порядка

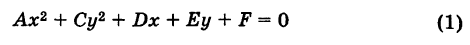
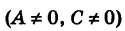без члена с произведением координат х и у (В = О)1. Дополняя члены, содержащие x и у соответственно, до полных квадратов, будем иметь

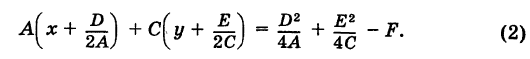
В нашем кратком курсе при рассмотрении общих уравнений кривых второго порядка мы ограничимся лишь этим случаем.

Отсюда, полагая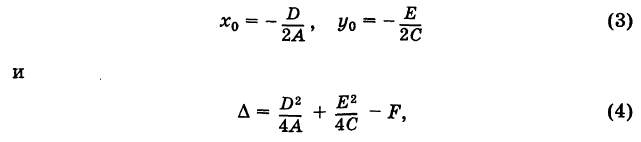

получаем

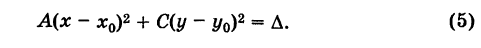
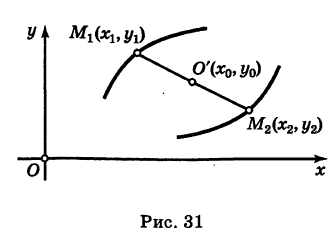
Точка О'(х0, у0) представляет собой центр симметрии кривой (5) (центр кривой). Действительно, если точка Мх(х19 У\) лежит на кривой (5), то симметричная ей относительно О' точка М2(х2, у2) где 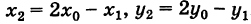- очевидно, также лежит на кривой (5) (рис. 31).

Параллельные осям координат Ох и Оу прямые у = у₀ и х = х₀ являются осями симметрии кривой (5) (оси кривой). Действительно, если точка 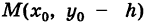лежит на кривой (5), то симметричная ей относительно прямой у = у0 точка 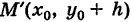также лежит на этой кривой. Аналогичным свойством обладает прямая х = х0.

В дальнейшем, для простоты исследования, будем предполагать, что центр кривой находится в начале координат, т. е. х₀ = О, 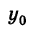= 0. Тогда уравнение кривой примет вид

Определение: Кривая второго порядка (6) называется эллипсом (точнее, принадлежит эллиптическому шипу)у если коэффициенты А и С имеют одинаковые знаки, т. е.

Для определенности будем полагать, что А > 0 и С > 0 (так как в противном случае знаки членов уравнения (6) можно изменить на обратные).

Возможны три случая: 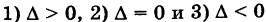. В первом случае, 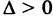, имеем действительный эллипс

где числа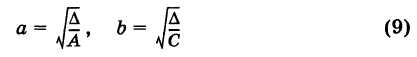

называются полуосями эллипса. Обычно полагают 0 < b < а (этого всегда можно добиться путем надлежащего выбора осей Ох и Оу). Уравнение (8) называется каноническим уравнением эллипса с полуосями аиЬ (рис. 32). Точки А (а, 0), В (О, Ь), А' (-а, 0), В' (0, -Ь) называются вершинами эллипса, а отрезки А'А = 2а и = -26 — его осями. Отметим, что из уравнения (8) имеем .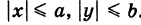

Заметим, что при а = b получаем окружность

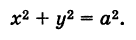
Во втором случае, Д = О, кривая (6) представляет собой точку О (0, 0) (вырожденный эллипс).

Наконец, в третьем случае, Д < 0, кривая (6) не имеет действительных точек; ее условно называют мнимым эллипсом.

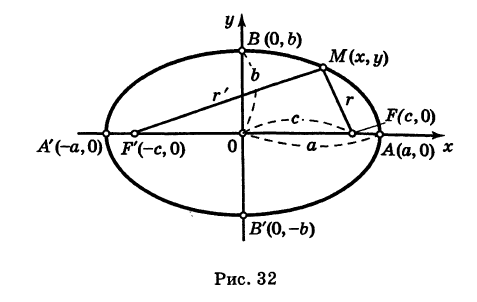
Определение: Кривая второго порядка (6) называется гиперболой (точнее, кривой гиперболического типа), если коэффициенты А и С имеют противоположные знаки, т. е.

Положим, для определенности, А > О, тогда С < 0. Возможны три случая: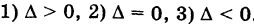

В первом случае, 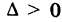, имеем гиперболу с каноническим уравнением

где 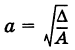(действительная полуось) и 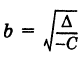(мнимая полуось) (рис. 33). Точки А (а, 0) и А\-а, 0) называются вершинами гиперболы. Отметим, что .

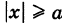Во втором случае, А = 0, получаем пару пересекающихся прямых (вырожденная гипербола)

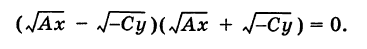
Наконец в третьем случае, 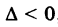, получим гиперболу

с полуосям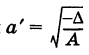и и 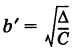. Если а' = а и = то гипербола (12) называется сопряженной к гиперболе (11); ее вершины: В (0, 6) и Б' (0, -6) (рис. 33).

Отрезок А'А = 2а называется действительной осью, а отрезок В'В = 2Ь — мнимой осью гиперболы (11).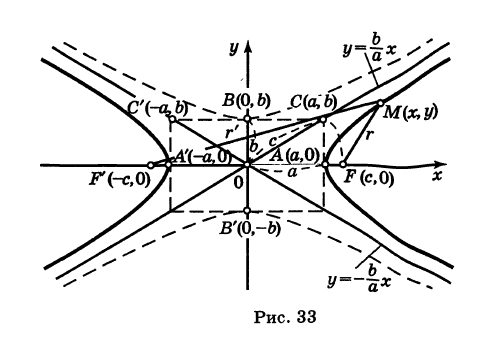

Пример:

Определить вид и расположение кривой

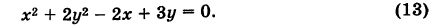
Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, будем иметь

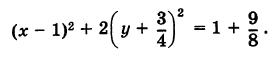
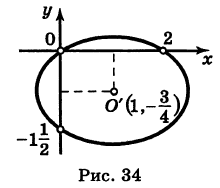
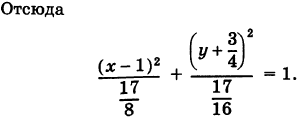
Следовательно, кривая (13) представляет собой эллипс с полуосям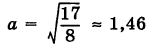и и 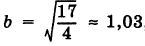, центр которого находится в точке 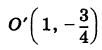(Рис. 34).

Фокальные свойства центральных кривых второго порядка

Точки F (с, 0) и F' (-с, 0), где

называются фокусами, соответственно, эллипса, заданного каноническим уравнением (8), рис. 32 (знак -), и гиперболы, заданной каноническим уравнением (11), рис. 33 (знак +). Отношение

называется эксцентриситетом центральной кривой второго порядка.

Из формулы (1) имеем: для эллипса 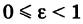, для гиперболы 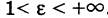. Заметим, что для окружности 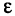= 0.

Пусть г = MF и г' = MF' — расстояния от точки М центральной кривой второго порядка до ее фокусов (так называемые фокальные радиусы точки М). Имеем

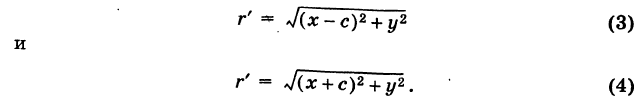
Так как

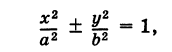
где знак плюс соответствует эллипсу, знак минус — гиперболе, то

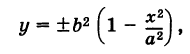
и, следовательно, с учетом (1) получаем

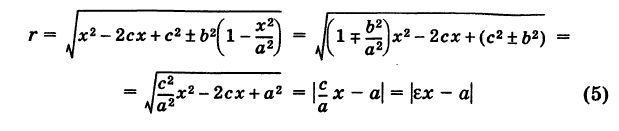
и, аналогично,

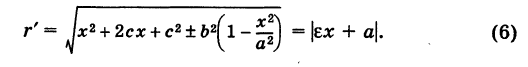
Если кривая — эллипс, то 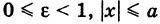, и поэтому

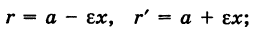
отсюда

причем для любых г и г', удовлетворяющих равенству (7), существует точка данного эллипса.

Таким образом, для любой точки эллипса сумма ее фокальных радиусов есть величина постоянная (характеристическое свойство эллипса). Это свойство часто принимают за определение эллипса.

Для гиперболы имеем 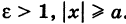. Поэтому

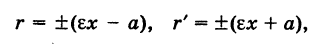
где знак плюс соответствует правой ветви гиперболы (х > 0), а знак минус — левой ветви (х < 0). Отсюда

Итак, для любой точки гиперболы модуль разности ее фокальных радиусов есть величина постоянная (характеристическое свойство гиперболы).

• Заказать решение задач по высшей математике

Эллипс как равномерная деформация окружности

Рассмотрим окружность радиуса а. Выберем некоторую прямоугольную систему координат Оху, начало которой, для простоты, поместим в центре окружности 0(0, 0). Текущие координаты точки окружности М, для удобства дальнейших рассуждений, обозначим через X и У. В таком случае уравнение окружности будет иметь вид

Произведем равномерную деформацию окружности (1) в направлении одного из ее диаметров, который, без нарушения общности рассуждения, можно считать вертикальным, т. е. направленным по оси Оу. Пусть k — коэффициент деформации окружности в выбранном направлении, т. е. k есть отношение длины преобразованного вертикального отрезка к его первоначальной длине. Заметим, что при 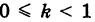мы имеем равномерное сжатие, а при k > 1 — равномерное растяжение окружности.

Предположим, что при нашей деформации точка окружности М(Х, У) переходит в некоторую точку М(х, у) преобразованной кривой (рис. 35). Так как точки М и М' лежат на одной и той же вертикали, то имеем

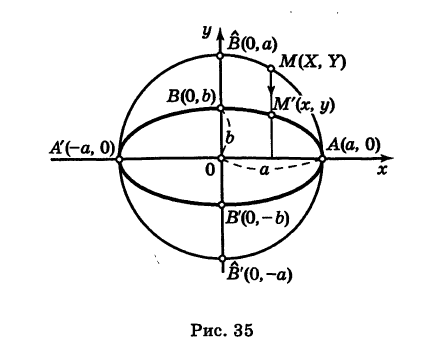
Отсюда при 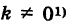получим

Подставляя эти выражения в уравнение (1), находим 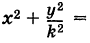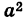, или

где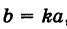 т. е. преобразованная точка М' 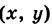расположена на эллипсе с полуосями а и Ь.

Обратно, если точка М'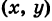 принадлежит эллипсу (4), то соответствующая ей в силу (2) точка М(Х, У) лежит на окружности (1).

Таким образом, результат равномерной деформации окружности вдоль одного из ее диаметров представляет собой эллипс.

Асимптоты гиперболы

Рассмотрим гиперболу (см. рис. 33)

Решая уравнение (1) относительно у, получаем

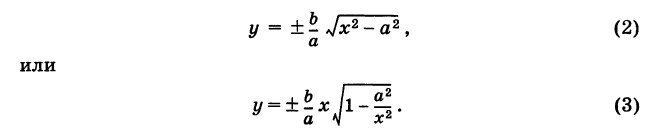
Если \х\ неограниченно возрастает, то 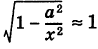и, следовательно, в некотором смысле, имеет место приближенное равенство

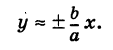
Покажем, что ветви гиперболы (1) сколь угодно близко подходят к прямым (см. рис. 33)

носящим название асимптот гиперболы. Действительно, например, при х > О возьмем в формулах (2) и (4) знаки плюс. Рассмотрим соответствующие точки М (х, у) гиперболы (2) и N (х, У) прямой (4), имеющие одну и ту же абсциссу х. Тогда

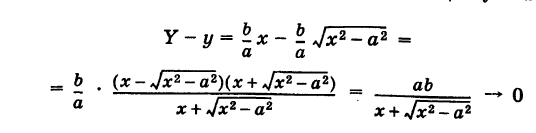
при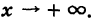

Аналогично рассматриваются еще три случая: знаки минус в (2) и в (4) при 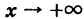; в (2) знак плюс, в (4) минус при 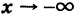и, наконец, в (2) минус, в (4) плюс при 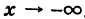. Заметим, что сопряженная гипербола

как нетрудно проверить, имеет общие асимптоты с гиперболой (1).

Для равнобочной гиперболы (а = Ь)

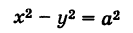
ее асимптоты у = ±х взаимно перпендикулярны.

График обратной пропорциональности

Рассмотрим кривую (рис. 36)

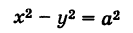
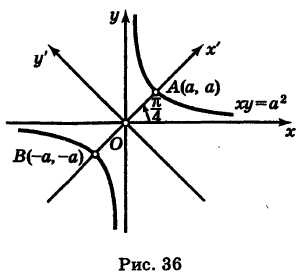Выбирая за новые оси координат Ох' и Оу' биссектрисы координатных углов и учитывая, что угол поворота 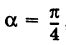будем иметь

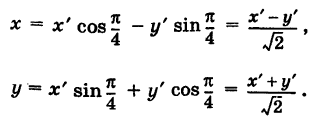
Отсюда на основании (1) получаем

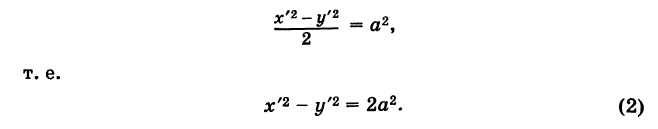
Таким образом, графиком обратной пропорциональности (1) является равнобочная гипербола.

Нецентральные кривые второго порядка

Кривая второго порядка называется нецентральной, если она или не имеет центра симметрии, или же имеет бесконечно много центров симметрии (т. е. не имеет единственного центра). Рассмотрим кривую второго порядка

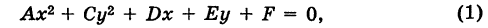
где 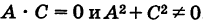. Для определенности будем считать, что

Кроме того, предположим, что 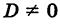, в противном случае мы бы имели пару параллельных прямых.

Дополняя в уравнении (1) члены с у до полного квадрата, будем иметь 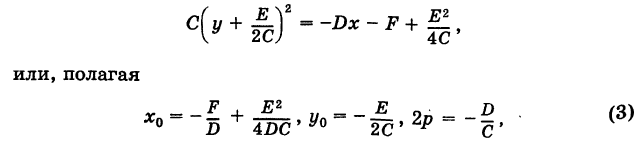получим

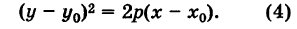
Кривая (4) называется параболой (рис. 37); точка О' (х0, у0) носит название вершины параболы у а число р называется параметром параболы. Легко убедиться, что прямая у = Уо является осью симметрии параболы (ось параболы); центра симметрии парабола (4) не имеет.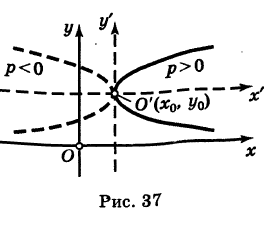

Если вершина параболы находится в начале координат, а ее осью является ось Ох, то мы получаем так называемое каноническое уравнение параболы причем параметр р здесь обычно считается положительным (этого можно добиться, выбирая надлежащее направление оси Ох; рис. 38, а).

Заметим, что если поменять ролями оси Ох и Оу, то каноническое уравнение параболы примет вид

Это уравнение параболы с вертикальной осью (рис. 38, б).

Фокальное свойство параболы

Рассмотрим параболу (рис. 38, а)

Точка 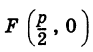называется ее фокусом, а прямая 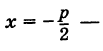директрисой.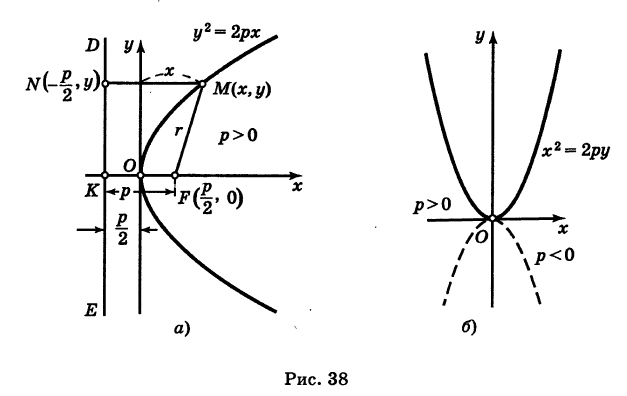

Для точки М(х, у) ее фокальный радиус г = MF равен

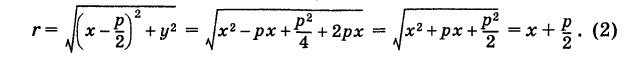
Далее, расстояние от этой точки до директрисы равно

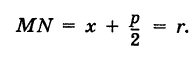
Таким образом, парабола представляет собой множество всех точек плоскости, равноотстоящих от данной точки (фокуса) и от данной прямой (директрисы). Это характеристическое свойство параболы.

Пример:

Определить координаты фокуса и уравнение директрисы параболы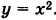

Решение:

Сравнивая это уравнение с уравнением (6), получим 2р = 1; отсюда р = 1/2. Следовательно, фокус параболы имеет координаты (0, 1/4), а уравнение директрисы есть у = -1/4.

График квадратного трехчлена

Рассмотрим квадратный трехчлен

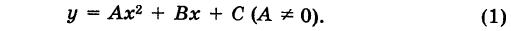
Отсюда

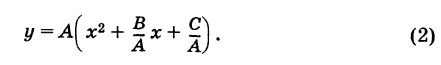
Дополняя выражение, стоящее в скобках, до полного квадрата, получим

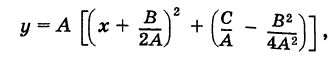
или

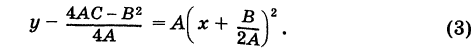
Если положить

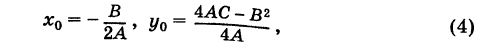
то из формулы (3) получим

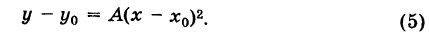
Делая параллельный перенос системы координат

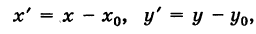
окончательно будем иметь

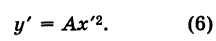
Уравнение (6) , формула (6) представляет собой каноническое уравнение параболы с вертикальной осью, вершина которой находится в точке 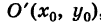и параметр 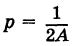. Таким образом, график квадратного трехчлена является параболой с вершиной в точке 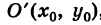, ось которой параллельна оси Оу (парабола со смещенной вертикальной осью; рис. 39).

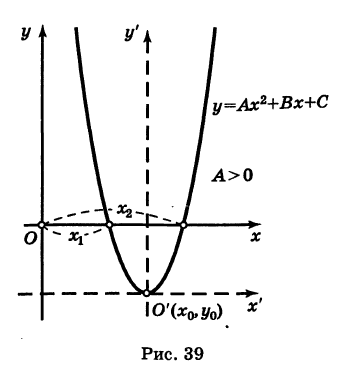
Заметим, что абсциссы 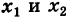точек пересечения параболы (1) с осью Ох являются корнями квадратного уравнения

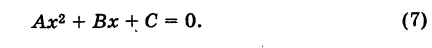
На этом свойстве основан графический способ решения квадратного уравнения (7).

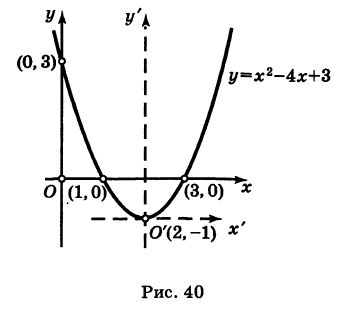
Пример:

Привести уравнение 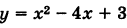к каноническому виду и построить соответствующую параболу.

Решение:

Перенося свободный член в левую часть уравнения и дополняя правую часть до полного квадрата, будем иметь у - 3 + 4 = = х2- 4х + 4, или

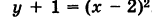
Полагая х-2=х',у + 1 = у', получим

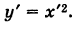
Таким образом, заданное уравнение есть уравнение параболы с вершиной в точке 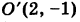и осью симметрии параллельной оси Оу (рис. 40).