Линии с распределенными параметрами

Содержание:

Линии с распределенными параметрами:

До сих пор мы исследовали электрические цепи, содержащие сосредоточенные параметры

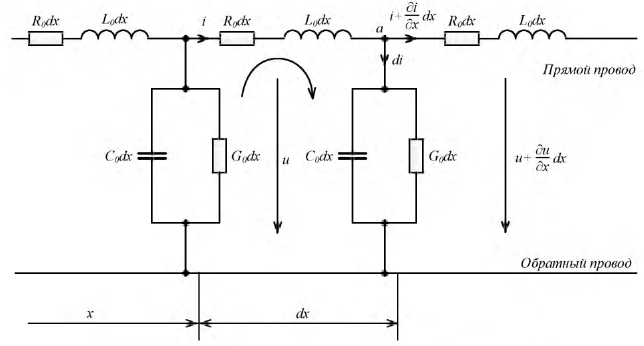
Рис. 11.1. Участок линии с распределенными параметрами

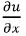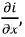Поскольку мгновенные токи и напряжения являются функциями двух переменных, используем в последующих рассуждениях частные производные  и  считая, что это скорости изменения тока и напряжения в направлении координаты 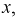тогда (см. рис. 11.1.) 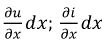— это приращение тока и напряжения на участке длиной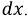 

Составим уравнения по законам Кирхгофа для данного участка цепи.

По первому закону для узла 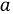запишем:

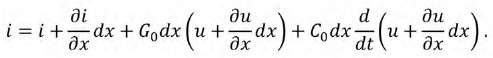
По второму закону для контура составим уравнение:

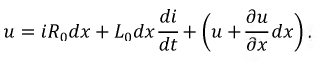
Сделаем соответствующие преобразования полученных выражений. Для этого раскроем скобки и исключим из рассмотрения производные второго порядка малости, а после деления всех слагаемых на 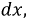получим базовую систему дифференциальных уравнений линии с распределенными параметрами (11.1.):

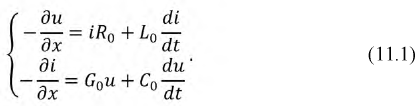
Эти уравнения называют также телеграфными. При известных граничных и начальных условиях из этих уравнений можно определить мгновенные значения напряжения 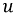и тока  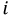в любой момент времени и в любом сечении линии.

Работа линии в установившемся режиме

Если линия питается от источника синусоидального тока или напряжения, то в установившемся режиме напряжения и токи также синусоидальны. Переходя от мгновенных значений токов и напряжений к их комплексным изображениям, перепишем систему уравнений (11.1) в следующем виде:

Система уравнений (11.2) содержит простые производные вследствие того, что комплексные величины не являются функциями времени, и поэтому количество переменных сократилось до одной - это координата линии 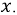Можно представить систему в еще более компактном виде:

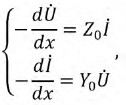
где 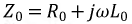- продольное сопротивление линии,

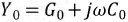- поперечная проводимость, причем:

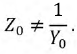
Решая систему уравнений (11.2) относительно напряжения, получим дифференциальное уравнение второго порядка (11.3):

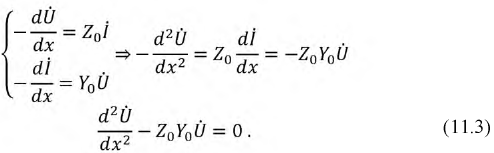
Его решение:

где 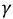 — комплексная постоянная распространения линии, 1/км:

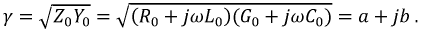
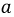- коэффициент затухания, характеризующий затухание в линии на единицу ее длины;  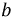- коэффициент фазы, характеризующий изменение фазы в линии на единицу ее длины; 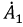и 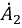 - неизвестные комплексные постоянные интегрирования, которые могут быть определены из граничных условий на концах линии.

Аналогичного рода рассуждения позволят записать уравнение для тока:

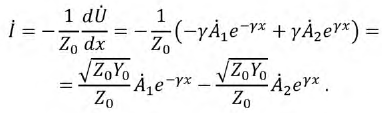
Введем понятие волнового сопротивления линии:

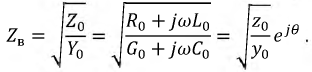
Тогда окончательно запишем:

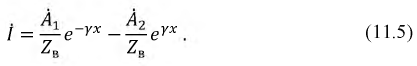
Для дальнейшего анализа процессов, происходящих в длинных линиях, перейдем от комплексов напряжения и тока к их мгновенным значениям, приняв, что:

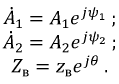
Мгновенное значение напряжения в линии:

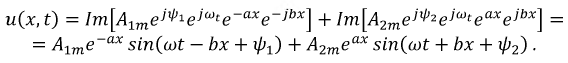
Аналогичные рассуждения позволят записать и функцию тока:

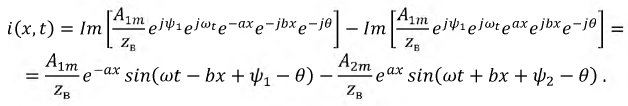
Представленные выражения для тока и напряжения показывают, что они являются одновременно функциями времени и координаты. Их можно рассматривать как сумму двух волн: первое слагаемое - падающая волна, движущаяся от начала линии к концу. Второе слагаемое - отраженная волна, перемещающаяся от конца линии к началу, а сумма этих волн представляет собой бегущую волну.

Оценим скорость перемещения электромагнитных волн в линии. Фазовой скоростью волны 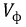называется скорость перемещения фазы колебания, которая в течение времени 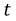и по мере увеличения расстояния  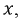пройденного волной, остается постоянной:

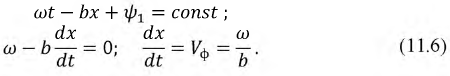
Наибольшая фазовая скорость достигается в воздушных линиях связи, эта скорость близка к скорости света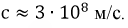

В кабельных линиях:

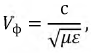
где 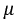 - относительная магнитная проницаемость изоляции, 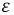- относительная диэлектрическая проницаемость среды, окружающей провода. Если известна фазовая скорость, можно определить длину волны:

Понятие «длинной» и «короткой» линии весьма условно и определяется частотой питающего эту линию генератора, поэтому одна и та же линия может считаться как длинной, так и короткой. Так, например, длина электромагнитной волны тока и напряжения у воздушной линии передачи при частоте генератора 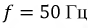будет:

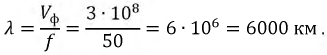
Исследуем бегущую волну. Пусть в момент времени 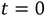падающая волна проходит через ноль в начале линии, тогда закон распределения этой волны напряжения вдоль координаты  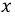будет иметь вид, представленный на рис. 11.2

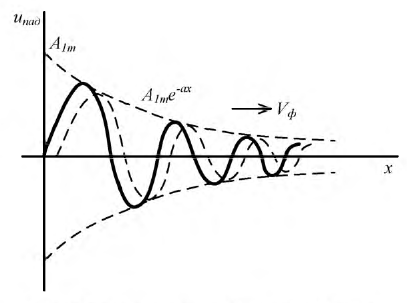
Рис. 11.2. Падающая вона напряжения в линии

Для какого-то момента времени функция сместится и займёт новое (пунктирное) положение.

На рис. 11.3 изображена отраженная волна также для двух разных моментов времени. Однако в реальности нет ни падающих, ни отраженных волн, а есть единый закон распределения токов и напряжений вдоль длины линии. Тем не менее, введение понятия падающих и отраженных волн облегчает расчет таких цепей. То же самое касается функции которая также представляется суммой падающих и отраженных волн.

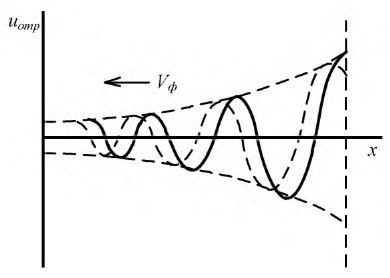
Рис. 11.3. Отраженная волна напряжения в линии

Уравнения линии в гиперболических функциях

Рассмотрим ранее полученные уравнения комплексных напряжений и тока:

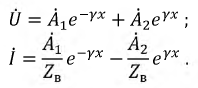
Комплексные коэффициенты 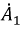и 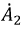могут быть определены, если известны граничные условия на концах линии. Определим коэффициенты 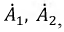приняв 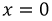(начало линии):

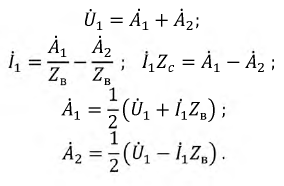
Найденные коэффициенты подставим в исходную систему уравнений:

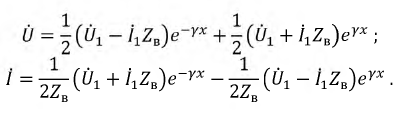
Полученные соотношения можно упростить, если воспользоваться гиперболическими функциями:

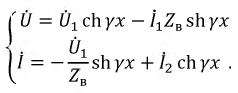
Данная система позволяет определить напряжение и ток в любом сечении линии при отсчете координаты 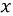от начала к концу. В том случае, если задан режим работы нагрузки  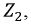то можно получить аналогичную систему при отсчете от конца линии к началу.

Изменив знак координаты 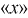 на 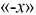 в предыдущей системе, получим новую систему уравнений (11.8), учитывая, что гиперболический синус - функция нечетная, а гиперболический косинус - четная.

Тогда окончательно получим:

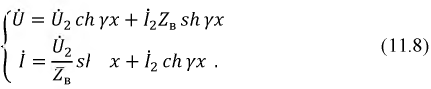
Данная система имеет важное практическое значение, так как позволяет установить связь между входными и выходными токами и напряжениями в линии при известной нагрузке.

Полученные уравнения позволяют определить ее входное сопротивление. По определению это такое сосредоточенное сопротивление, которым можно заменить всю линию с нагрузкой на ее конце, и при этом режим работы генератора не изменится. Положив в системе (11.8) 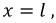определим параметр 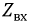по выражению:

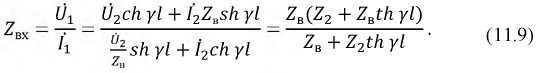
Из (11.9) следует, что входное сопротивление линии определяется ее вторичными параметрам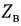и и 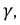 общей длиной  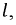а также значением нагрузки 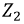в ее конце.

Нагрузочный режим работы линии

В нагруженной линии существуют падающие и отраженные волны. Взяв отношение отраженной волны напряжения или тока к напряжению или току падающей волны в любой точке линии, получим комплексный коэффициент отражения по напряжению 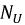 или по току 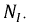Определим коэффициент 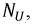используя выражения для падающих и отраженных волн. Из первого уравнения системы (11.8) для 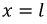получим:

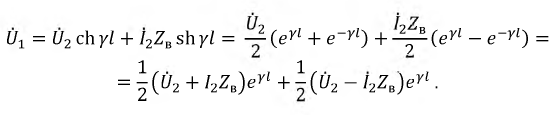
Тогда коэффициент отражения по напряжению равен:

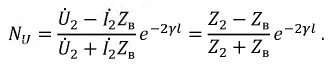
С помощью известного коэффициента отражения нетрудно найти любую составляющую  и при одной известной.

Отражение может произойти не только от конца или начала линии, но и от любой неоднородности в ней. Полученный результат позволяет сделать важный практический вывод: отсутствие отраженной волны 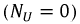говорит о том, что в линии существуют только прямые (падающие волны). Это возникает при условии, когда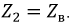 

Оценим входное сопротивление линии при согласованной нагрузке. При этом выражение входного сопротивления будет:

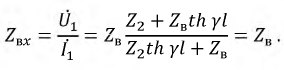
Из этого следует, что линию, согласованную с нагрузкой, можно отсоединить от генератора и заменить некоторым сосредоточенным сопротивлением равным 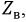при этом режим работы генератора не изменится. Комплексная функция входного сопротивления 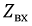является сложной и зависит от целого ряда параметров, поэтому ее можно представить в виде:

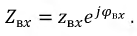
При этом и модуль, и фаза входного сопротивления являются независимыми функциями и имеют волнообразный характер изменения. На рис. 11.4 и 11.5 показаны зависимости модуля и фазы входного сопротивления от длины линии.

Рис. 11.4. Зависимость модуля входного сопротивления от длины линии.

С ростом длины линии модуль входного сопротивления становится все меньше, стремясь при этом к волновому сопротивлению линии. Это объясняется тем, что с ростом длины роль отраженных волн становится меньше, и при бесконечной длине отраженная волна вообще отсутствует. Такой же режим имеет место в линии, согласованной с нагрузкой, с той лишь разницей, что 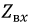будет константой и равной  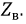Аналогичные рассуждения можно провести и для фазы входного сопротивления. При этом фаза имеет знакопеременный характер.

Рис. 11.5. Зависимость фазы входного сопротивления от длины линии

Существуют точки по длине линии, где фаза обращается в ноль, а отрезки между этими соседними точками носят название резонансных участков линии.

Мощность, передаваемая по линии при согласованной нагрузке, называется естественной или натуральной мощностью. Определим КПД линии в этом режиме.

Мощность, получаемая линией:

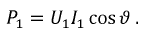
Мощность , отдаваемая в нагрузку:

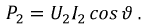
Тогда:

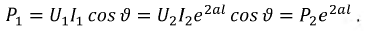
Итоговое выражение для КПД линии будет:

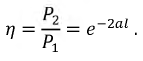
Короткое замыкание и холостой ход линии

По данным опытов холостого хода и короткого замыкания определяют вторичные параметры лини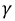и: и 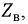 используя выражение (11.9).

Режим короткого замыкания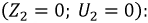

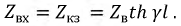
Режим холостого хода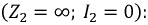

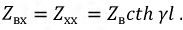
Из полученных соотношений можно получить значение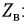 

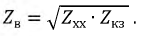
Зная комплексное сопротивление холостого хода и короткого замыкания, найдем:

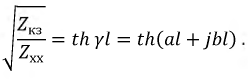
Коэффициенты 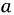и 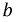 определяются по соответствующим номограммам при известной длине линии. Входное сопротивление линии при произвольной нагрузке также можно выразить через сопротивления холостого хода и короткого замыкания:

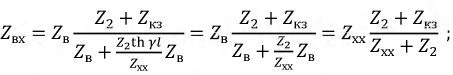
Линия без искажения

Рассматривая линию как канал передачи информации от источника к приемнику, важно иметь оценку искажений, которые накладывается на передаваемые сигналы. Указанные искажения имеют место, когда для различных гармонических составляющих сложного сигнала (музыка, речь) коэффициент затухания и фазы отдельных гармоник различны. Чтобы искажения отсутствовали, необходимо поддерживать коэффициент затухания 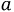и фазовую скорость  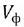постоянными. Отметим, что указанные типы искажений имеют место в обычных воздушных и особенно в кабельных линиях связи. Для выявления условий, когда искажения отсутствуют, выполним преобразования с функцией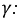 

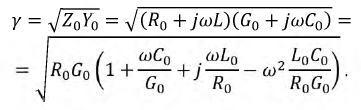
Делая преобразования подкоренного выражения и приняв, что:

получим:

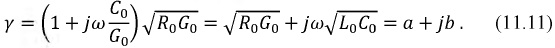
Из полученного уравнения следует, что коэффициент затухания не зависит от частоты, в то время как коэффициент фазы прямо ей пропорционален, а, следовательно, фазовая скорость не зависит от частоты. Все это соответствует понятию линии без искажений. Таким образом, главное условие реализации этой линии - выполнение соотношения по формуле (11.10).

На практике это условие не выполняется, т.к. 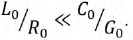 Для устранения данного неравенства стараются изменить первичные параметры линии. Это можно сделать за счет:

1) уменьшения 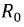(использования проводов большего диаметра и с большой проводимостью);

2) включения сосредоточенных индуктивностей в линию.

Отметим особенности такой линии: она обладает минимальным затуханием при заданных параметрах 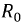и 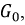постоянной фазовой скоростью, кроме того, волновое сопротивление такой линии - вещественное число, также не зависящее от частоты:

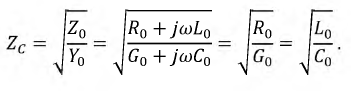
Для мгновенных токов и напряжений в любом сечении их связь определяется постоянным сопротивлением:

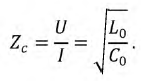
Мгновенные значения энергии электрического и магнитного полей при согласованной нагрузке равны между собой:

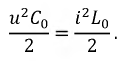
При произвольной нагрузке это условие выполняется отдельно для падающей и отраженной волны.

Линия без потерь

Эффективность работы любой линии, а особенно кабельной линии связи, будет тем выше, чем меньше 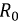и проводимость изоляции  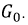Потери энергии в таких линиях снижаются и их КПД возрастает. В том случае, когда все тепловые потери невелики по сравнению с мощностью нагрузки, то параметрам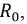и и 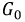можно пренебречь, а с ростом частоты неравенства 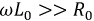и 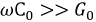еще более углубляются.

Рассмотрим идеальную линию, у которо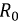й и 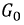 равны нулю. Линия, для которой это условие выполняется, носит название линии без потерь. Вторичные параметры принимают вид:

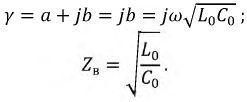
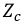- вещественное число.

Линия без потерь близка к линии без искажений, но отличается полным отсутствием затухания. Полученный результат позволяет подкорректировать систему уравнений (11.8), которые были получены для линии с потерями.

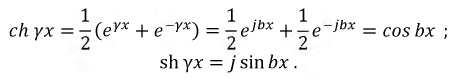
С учетом сказанного представим систему уравнений для комплексов токов и напряжений в любом сечении линии в виде:

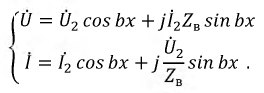
Как и прежде для линии без потерь можно считать, что ток и напряжение есть сумма падающих и отраженных волн. Однако в этом случае их амплитуда остается неизменной. Волновое сопротивление такой линии рассчитывается по формуле:

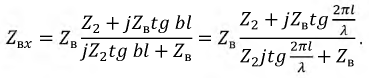
Можно записать выражения для мгновенных значений токов и напряжений. Приняв 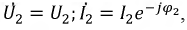 получим:

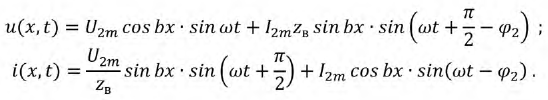
Стоячие волны в линии

Рассмотрим особенности режима работы линии без потерь в двух предельных ее режимах: холостого хода и короткого замыкания.

Режим холостого хода: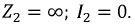

Уравнения для тока и напряжения примут вид:

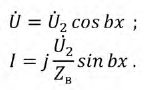
Переходя от комплексов токов и напряжений к их временным зависимостям, получим:

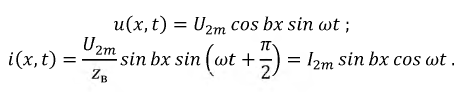
Представленные уравнения являются произведением двух функций различных аргументов, одна из них есть функция координаты, другая - времени. Отсутствие затухания в линии позволяет считать, что результирующий процесс также представлен суммой падающих и отраженных волн, амплитуды которых неизменны. Это и есть стоячие волны. Воспользовавшись известными тригонометрическими преобразованиями, запишем выражения для мгновенных токов и напряжений в виде суммы двух волн:

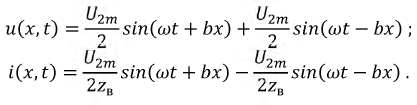
Иначе говоря, стоячей волной называется процесс наложения двух волн - падающей и отраженной - с одинаковыми амплитудами.

Анализ полученных уравнений показывает, что амплитуды тока и напряжения зависят от координаты 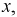и, следовательно, существуют такие ее значения, при которых мгновенный ток или напряжение обращается в ноль (при 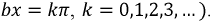В частности, напряжение будет иметь максимальное значение в то время, когда ток обращается в ноль и наоборот. Координаты линии, где напряжения или токи принимают максимальные значения, называются пучностями, соответственно узлы - это места, где функции обращаются в ноль. Таким образом, пучностям напряжения соответствуют узлы тока и наоборот.

При холостом ходе линии в точках, отстоящих от её конца на расстоянии 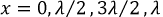любой момент времени наблюдаются пучности напряжения и узлы тока, а при  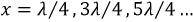— узлы напряжения и пучности тока.

Полученные выражения позволяют построить графики распределения напряжения и тока вдоль линии для различных моментов времени (рис. 11.6,a,b): 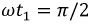 (сплошная линия),  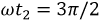(пунктирная линия).

Из представленных функций тока и напряжения очевидно, что, начиная от конца линии через происходит чередование узлов и пучностей соответствующей функции.

Режим короткого замыкания: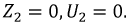 

Уравнения для тока и напряжения примут вид:

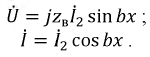
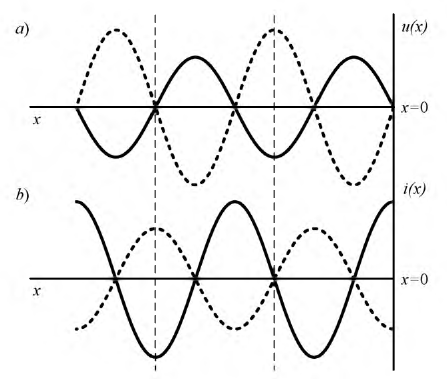
Рис. 11.6. Стоячие волны напряжения a) и тока b) для разных моментов времени

Мгновенные значения тока и напряжения в линии изменяются по законам:

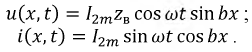
Аналогично режиму XX можно представить мгновенные значения тока и напряжения в виде суммы двух волн - падающих и отражённых:

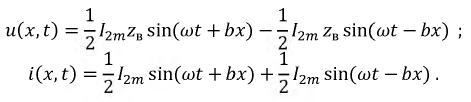
При коротком замыкании линии в точках, отстоящих от конца линии на расстоянии 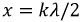имеем пучности тока и узлы напряжения, на расстояниях 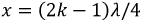- узлы тока и пучности напряжения.

Такие же графики мгновенных токов и напряжений для разных моментов времени можно построить и для режима короткого замыкания. Единственное отличие будет состоять в том, что токи и напряжения поменяются местами. Помимо холостого хода и короткого замыкания стоячие волны могут возникнуть в линии и при чисто реактивной нагрузке на ее конце.

В стоячих волнах обмен энергией возможен лишь между двумя соседними узлами тока и напряжения. Таким образом, энергия может передаваться от источника к приемнику только с помощью бегущих волн.

Входные сопротивления линии в режимах холостого хода и короткого замыкания соответственно равны:

На рис. 11.7 в качестве примера представлена функция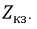 

Рис. 11.7. Распределение модуля входного сопротивления по длине линии в режиме короткого замыкания

В режиме стоячей волны линия представляет собой чисто реактивное сопротивление, причем его характер в зависимости от длины может быть как индуктивным, так и емкостным.

Четвертьволновый трансформатор

Рассмотрим линию без потерь длиной, равной четверти длины волны и замкнутой на активное сопротивление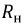

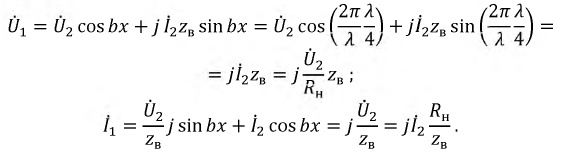
Входное сопротивление линии:

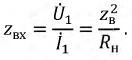
Предположим, что необходимо согласовать генератор с внутренним сопротивлением 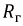и приемник с сопротивлением 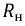или две линии с такими же сопротивлениями. Тогда достаточно включить между ними отрезок линии без потерь длиной в четверть волны с волновым сопротивлением  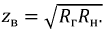Такую линию называют четвертьволновым трансформатором с коэффициентом, равным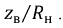

Линия как четырехполюсник

Уравнения четырехполюсника в 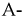форме имеют вид:

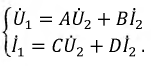
Для линии получены соотношения:

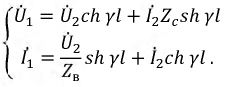
Сопоставление уравнений показывает, что они идентичны и это позволяет записать:

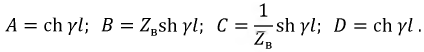
Таким образом, линия может быть заменена эквивалентным четырехполюсником. Основное уравнение четырехполюсника 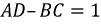 реализуется и для линии в форме уравнения:

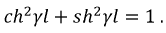
Рассмотренная выше теория четырехполюсников может быть применена и для расчета режимов работы линии. Она может быть представлена  и образными схемами замещения, каскадными схемами, с помощью которых проще рассчитывать искажения, вносимые линиями в передаваемые по ним сигналы.