
Линейный регрессионный анализ - определение и вычисление с примерами решения
Содержание:
Уравнение линейной регрессии:
Регрессия - это оценка зависимости одной случайной величины от другой случайной величины.
Уравнением регрессии 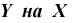
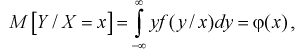
Функцию 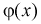 называют модельной функцией регрессии Y на X, а ее график - модельной линией регрессии Y на X. Уравнение (12.1) называется уравнением регрессии 1-го рода. Функцией
называют модельной функцией регрессии Y на X, а ее график - модельной линией регрессии Y на X. Уравнение (12.1) называется уравнением регрессии 1-го рода. Функцией 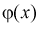 может представляться полином
может представляться полином 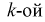 степени
степени 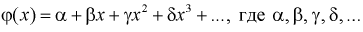 - коэффициенты уравнения регрессии.
- коэффициенты уравнения регрессии.
Пусть заданы две генеральные случайные величины Х и Y и выборочные пары их значений: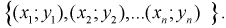 Если эти выборочные значения нанести на плоскость в декартовой системе координат X, У, то получим диаграмму в виде точек (диаграмму рассеивания), которая называется корреляционным полем.
Если эти выборочные значения нанести на плоскость в декартовой системе координат X, У, то получим диаграмму в виде точек (диаграмму рассеивания), которая называется корреляционным полем.
Пример:
Пусть изучаем зависимость веса человека от его роста для определенной группы людей. Для этого, например, в группе студентов проводим измерения веса, пусть это будет случайная величина 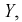 и роста - случайная величина X для каждого студента. Результаты занесли в таблицу в виде выборочных пар их значений:
и роста - случайная величина X для каждого студента. Результаты занесли в таблицу в виде выборочных пар их значений: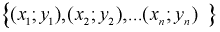 и нанесли на плоскость в системе координат X,Y. В результате получим корреляционное поле (рис. 12.1). Изобразим на рисунке предполагаемую теоретическую зависимость между У и Х в виде жирной линии - это и есть модельная линия регрессии У на X. Она, допустим, описывается определенной аналитической зависимостью
и нанесли на плоскость в системе координат X,Y. В результате получим корреляционное поле (рис. 12.1). Изобразим на рисунке предполагаемую теоретическую зависимость между У и Х в виде жирной линии - это и есть модельная линия регрессии У на X. Она, допустим, описывается определенной аналитической зависимостью 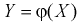 , т. е. модельной функцией регрессии У на X.
, т. е. модельной функцией регрессии У на X.
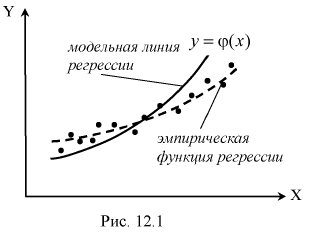
Аппроксимируем корреляционное поле (см. на рис. 12.1) пунктирной линией - это будет эмпирическая линия регрессии, которая может описываться несколько другой аналитической зависимостью. Понятно, что вид эмпирической линии регрессии (зависимость веса человека от его роста) зависит от многих факторов: возраста, национальности, пола и т. д. Сравнение модельной и эмпирической линий регрессии позволяет выявить справедливость наших теоретических предположений.
Рассмотрим линейную регрессию. Предположим, что между Х и Y существует линейная зависимость: 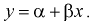 Допустим, что при любом значении X мы можем измерить значение Y с некоторой ошибкой
Допустим, что при любом значении X мы можем измерить значение Y с некоторой ошибкой 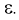 Тогда выборочное значение
Тогда выборочное значение 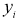 можно представить в следующем виде:
можно представить в следующем виде:
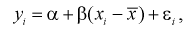 (12.2)
(12.2)
где 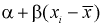 - точная линейная зависимость,
- точная линейная зависимость,
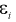 - ошибка.
- ошибка.
Будем предполагать, что 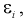 величина ошибки, - это случайная величина с нормальным законом распределения с
величина ошибки, - это случайная величина с нормальным законом распределения с 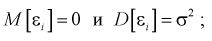 обозначим
обозначим 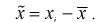
Исходя из выборочных значений можно каким-либо методом найти точечные оценки коэффициентов 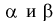 уравнения регрессии (12.2).
уравнения регрессии (12.2).
Уравнение, в которое входят оценки 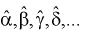 коэффициентов уравнения регрессии
коэффициентов уравнения регрессии 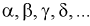 и которое является приближенным выражением модельной функции регрессии Y на X, называется эмпирической функцией регрессии или уравнением регрессии 2-го рода:
и которое является приближенным выражением модельной функции регрессии Y на X, называется эмпирической функцией регрессии или уравнением регрессии 2-го рода: 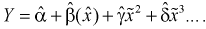
Сформулируем суть регрессионного анализа.
Регрессионный анализ - это анализ функций регрессий первого и второго рода, состоящий в следующем:
- Нахождение точечных и интервальных оценок параметров функции регрессии 1-го рода.
- Осуществление точечного и интервального оценивания условных математических ожиданий, необходимого для предсказания средних значений одной случайной величины, соответствующих определенным фиксированным значениям другой случайной величины.
- Проверка согласованности найденной эмпирической функции регрессии с экспериментальными данными.
Для определения точечных оценок параметров функции регрессии чаще используется метод наименьших квадратов.
Метод наименьших квадратов
Метод наименьших квадратов (МНК) позволяет так выбрать параметры 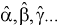 эмпирической функции регрессии, что она будет наилучшей оценкой модельной функции регрессии в том смысле, что сумма квадратов отклонений наблюдаемых значений переменной Y от соответствующих ординат эмпирической функции регрессии будет наименьшей.
эмпирической функции регрессии, что она будет наилучшей оценкой модельной функции регрессии в том смысле, что сумма квадратов отклонений наблюдаемых значений переменной Y от соответствующих ординат эмпирической функции регрессии будет наименьшей.
Параметры 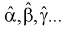 эмпирической функции регрессии
эмпирической функции регрессии 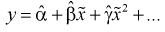 находятся методом наименьших квадратов из условия
находятся методом наименьших квадратов из условия
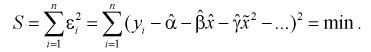 (12.3)
(12.3)
МНК обеспечивает наилучшее согласование теоретической зависимости 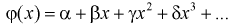 и экспериментальных данных.
и экспериментальных данных.
Подробнее рассмотрим применение МНК для определения точечных оценок параметров функции регрессии. В результате проведения п опытов получаем двумерную выборку 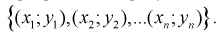 Пусть эмпирическая функция регрессии линейна, т. е.
Пусть эмпирическая функция регрессии линейна, т. е. 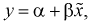 (значок
(значок  над коэффициентами
над коэффициентами 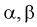 опускаем для упрощения записи), тогда (12.3) принимает вид
опускаем для упрощения записи), тогда (12.3) принимает вид
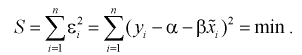 (12.4)
(12.4)
Для определения минимума функции 5 необходимо найти производные по интересующим нас параметрам, приравнять их к нулю и решить полученные уравнения. Вычисляем частные производные и приравниваем их к нулю:
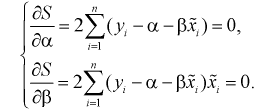 (12.5)
(12.5)
Раскрываем знак суммы:
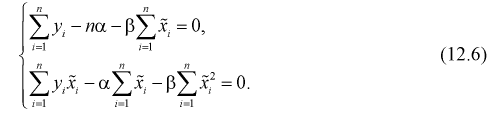
Учтем, что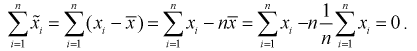
Тогда из (12.6) получаем точечную оценку коэффициента 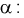

Из второго уравнения (12.6) имеем
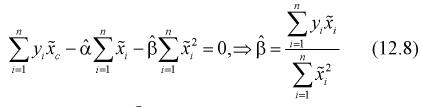
После определения точечных оценок обычно проверяют предположение о виде эмпирической функции регрессии: линейная она или нелинейная. На практике условное математическое ожидание 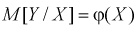 (или уравнение регрессии 1-го рода) часто считают линейной функцией, т. е.
(или уравнение регрессии 1-го рода) часто считают линейной функцией, т. е. 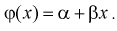 Это предположение является гипотезой, которая проверяется путем оценки коэффициента корреляции.
Это предположение является гипотезой, которая проверяется путем оценки коэффициента корреляции.
Корреляционный анализ - это анализ оценок коэффициента корреляции 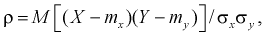 который позволяет ответить на вопрос, существует ли линейная функциональная зависимость между математическим ожиданием случайной величины X и случайной величины У. Если ответ положительный, то метод корреляционного анализа позволяет измерить степень близости статистической зависимости (т. е. экспериментальных данных) к функциональной.
который позволяет ответить на вопрос, существует ли линейная функциональная зависимость между математическим ожиданием случайной величины X и случайной величины У. Если ответ положительный, то метод корреляционного анализа позволяет измерить степень близости статистической зависимости (т. е. экспериментальных данных) к функциональной.
Коэффициент корреляции (оценки)
При изучении курса теории вероятностей в разделе 4.2 мы определили ковариацию или корреляционный момент
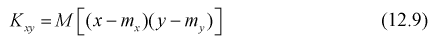
и коэффициент корреляции
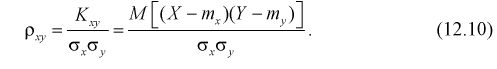
Для оценки связи между случайными величинами X и Y применяют точечные оценки 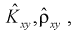 которые называются эмпирическим корреляционным моментом и эмпирическим коэффициентом корреляции'.
которые называются эмпирическим корреляционным моментом и эмпирическим коэффициентом корреляции'.
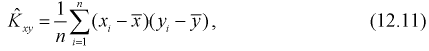
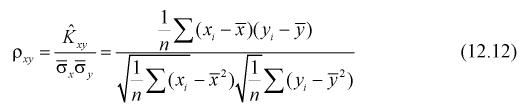
Найдем связь между точечной оценкой коэффициента 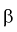 линейного уравнения регрессии (12.2) и оценкой коэффициента корреляции
линейного уравнения регрессии (12.2) и оценкой коэффициента корреляции 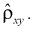
Преобразуем 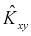 (12.11):
(12.11):
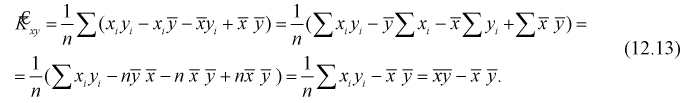
Рассмотрим оценку 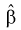 (12.8). Преобразуем выражение:
(12.8). Преобразуем выражение:
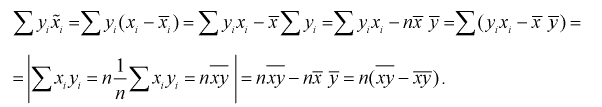
Данное выражение определяется через выборочную дисперсию 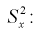
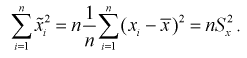
Тогда оценка 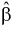 (12.8) определится через
(12.8) определится через 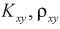 так:
так:
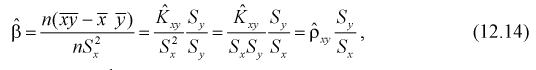
где 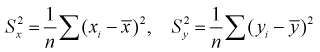 - выборочные дисперсии
- выборочные дисперсии
Уравнение линейной регрессии (12.2) будет иметь вид

Влияние значений коэффициента корреляции 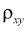 на функциональную зависимость между
на функциональную зависимость между 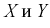 иллюстрирует рис. 12.2.
иллюстрирует рис. 12.2.
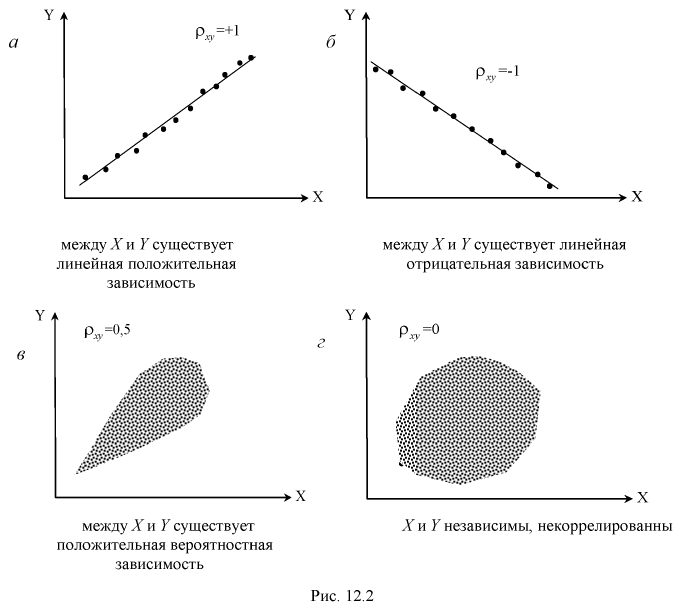
Чем ближе по модулю коэффициент корреляции к единице, тем точнее линейная зависимость между случайными величинами X и У, (тем ближе к линии регрессии располагаются точки на диаграмме рассеивания). Чем ближе 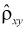 к нулю, тем слабее эта зависимость. Говорят, что при
к нулю, тем слабее эта зависимость. Говорят, что при 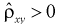 (см. рис. 12.2, а, в) между Х и Y существует положительная корреляция. При
(см. рис. 12.2, а, в) между Х и Y существует положительная корреляция. При 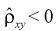 (см. рис. 12.2, б) между У и Y существует отрицательная корреляция. При
(см. рис. 12.2, б) между У и Y существует отрицательная корреляция. При 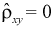 (см. рис. 12.2, г) Х и Y некоррелированны.
(см. рис. 12.2, г) Х и Y некоррелированны.
Поскольку коэффициент корреляции 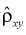 характеризует степень линейной зависимости, то при
характеризует степень линейной зависимости, то при 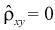 может оказаться, что между X и Y существует нелинейная связь.
может оказаться, что между X и Y существует нелинейная связь.
Построение доверительных интервалов для коэффициентов уравнения регрессии
Доверительные интервалы для коэффициентов уравнения регрессии позволяют для заданной доверительной вероятности 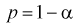 выяснить, насколько сильно могут отклоняться коэффициенты эмпирической функции регрессии от соответствующих коэффициентов модельной функции регрессии. Это позволит оценить точность определения коэффициентов уравнения регрессии, корректировать объемы выборки для проведения теоретических исследований.
выяснить, насколько сильно могут отклоняться коэффициенты эмпирической функции регрессии от соответствующих коэффициентов модельной функции регрессии. Это позволит оценить точность определения коэффициентов уравнения регрессии, корректировать объемы выборки для проведения теоретических исследований.
В разделе 12.2 были определены точечные оценки коэффициентов уравнения регрессии по выборочным данным:
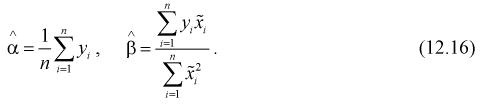
Вычислим дисперсии точечных оценок 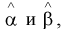 т. е. определим рассеивание случайной величины Y относительно линии регрессии
т. е. определим рассеивание случайной величины Y относительно линии регрессии 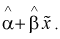 Ранее мы положили (см. раздел 12.1), что
Ранее мы положили (см. раздел 12.1), что 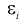 - величина ошибки, которая распределена по нормальному закону
- величина ошибки, которая распределена по нормальному закону 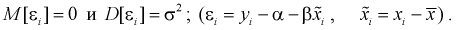 Полагая, что дисперсия Y постоянная и не зависит от X, можно
Полагая, что дисперсия Y постоянная и не зависит от X, можно  рассматривать в последующих преобразованиях как постоянную величину. Тогда
рассматривать в последующих преобразованиях как постоянную величину. Тогда
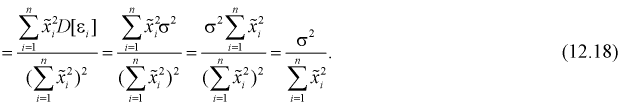
Заменяя дисперсию 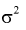 на оценку
на оценку 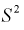 , определяемую как
, определяемую как 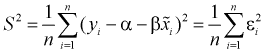 , можно показать, что величина
, можно показать, что величина 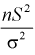 имеет закон распределения
имеет закон распределения 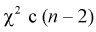 степенями свободы.
степенями свободы.
Для получения доверительного интервала для коэффициента 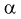 возьмем разность между точечной оценкой
возьмем разность между точечной оценкой 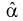 и коэффициентом
и коэффициентом 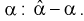 Нормируем ее, разделим на
Нормируем ее, разделим на 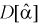 и обозначим как
и обозначим как 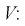

Аналогично для коэффициента 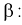

Подставляя в (12.19), (12.20) выражения (12.17), (12.18) и разделив (12.19), (12.20) на 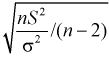 , получим
, получим
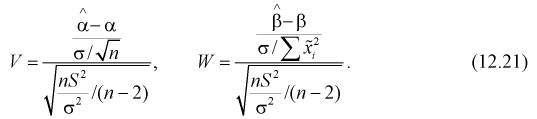
Эти случайные величины имеют закон распределения Стьюдента с 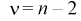 степенями свободы.
степенями свободы.
Зная закон распределения случайной величины V (плотность распределения 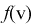 закона распределения Стьюдента), можно найти вероятность ее попадания в интервал
закона распределения Стьюдента), можно найти вероятность ее попадания в интервал 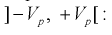
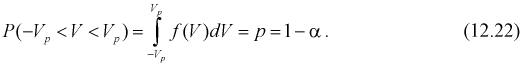
Из условия (12.22) для заданной доверительной вероятности 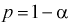 и числа степеней свободы
и числа степеней свободы 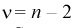 по таблицам распределения Стьюдента находим квантили
по таблицам распределения Стьюдента находим квантили 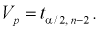 . Считая
. Считая 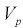 известными и подставляя вместо
известными и подставляя вместо 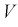 выражения (12.21) в правую часть выражения (12.22), получим неравенство
выражения (12.21) в правую часть выражения (12.22), получим неравенство
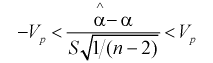
Решая неравенство относительно 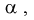 находим доверительный интервал для коэффициента
находим доверительный интервал для коэффициента 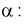 :
:
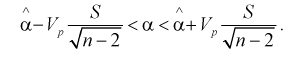 (12.23)
(12.23)
Аналогично поступим для случайной величины W , записывая условие
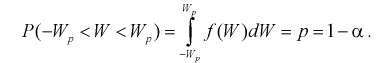 (12.24)
(12.24)
Определяя квантили 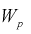 по таблицам распределения Стьюдента, решаем неравенство в правой части (12.24):
по таблицам распределения Стьюдента, решаем неравенство в правой части (12.24):
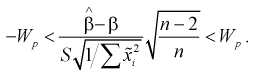 (12.25)
(12.25)
Из (12.25) получаем доверительный интервал для коэффициента 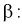
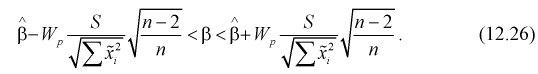
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |