Линейный оператор - свойства и определение с примерами решения

Содержание:

Пусть в пространстве R имеются два базиса: старый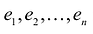

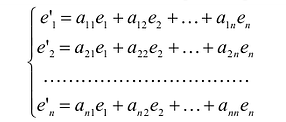
Полученная система означает, что переход от старого базиса 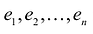к новому 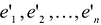задается матрицей перехода:

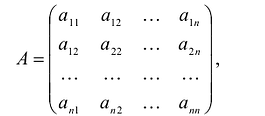
разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.

Матрица А — неособенная, так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса 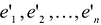к старому базису 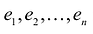осуществляется с помощью обратной матрицы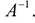

Найдем зависимость между координатами вектора в разных базисах. Пусть рассматриваемый вектор X имеет координаты 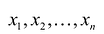относительно старого базиса и координаты 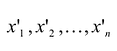относительно нового базиса, т.е.:

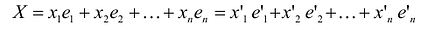
Подставив значения 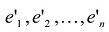из системы в левую часть этого равенства, получим после преобразований:

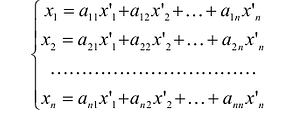
т.е. в матричной форме: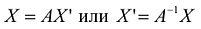

Линейное преобразование переменных

Линейным преобразованием переменных называется выражение системы переменных 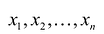через новую систему переменных 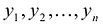с помощью линейных однородных функций:

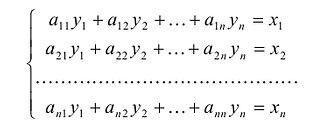
Линейное преобразование вполне определяется матрицей 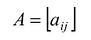размером nхn, составленной из коэффициентов при 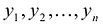. Эту матрицу называют матрицей линейного преобразования или матрицей линейного оператора.

Пусть U и V - два линейных пространства размерности n и m соответственно. Отображение 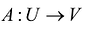называется линейным оператором, если:

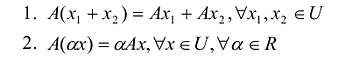
Линейное преобразование переменных с квадратной матрицей А называется невырожденным, если матрица А невырожденная и вырожденным, если матрица А вырожденная.

Теорема. Для всякого невырожденного линейного преобразования переменных с квадратной матрицей А существует обратное преобразование, которое является также линейным, и его матрица равна .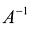

Собственные значения и собственные вектора матриц

Число 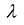называется собственным значением (или характеристическим числом) квадратной матрицы А порядка n, если можно подобрать такой n-мерный ненулевой вектор 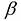что .

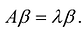Для того, чтобы найти собственные значения матрицы А, рассмотрим матрицу:

Если раскрыть определитель матрицы А- хЕ, то получится многочлен n-й степени:

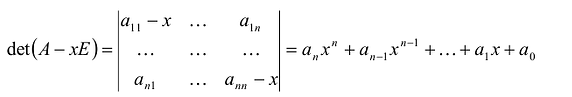
Этот многочлен называется характеристическим многочленом матрицы А. Его коэффициенты 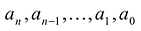зависят от элементов матрицы А. Понятие многочлена будет подробно разобрано в следующем разделе.

Следует отметить, что 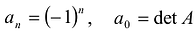. Уравнение 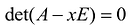называется характеристическим уравнением матрицы А.

Теорема. Множество S(A) всех собственных значений матрицы А совпадает с множеством всех решений характеристического уравнения 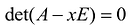матрицы А.

Доказательство:

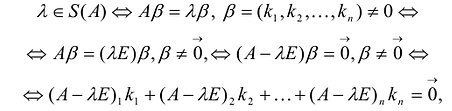
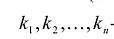- ненулевой набор чисел, 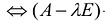- вырожденная матрица 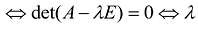- решение уравнения:

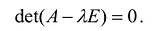
Собственным вектором квадратной матрицы А порядка n принадлежащим ее собственному значению 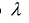называется n -мерный вектор 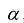, для которого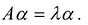

Множество всех собственных векторов матрицы А, принадлежащих ее собственному значению 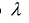, обозначим через 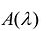. Отыскание собственных векторов сводится к решению однородной системы линейных уравнений.

• Заказать решение задач по высшей математике

Теорема. Множество 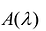всех собственных векторов матрицы А порядка n принадлежащих ее собственному значению 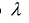, совпадает с множеством всех решений однородной системы линейных уравнений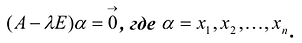

Доказательство:

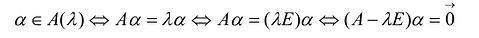
В развернутом виде равенство 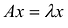записывается как система уравнений:

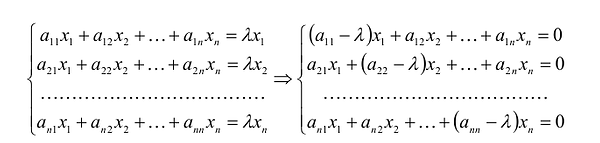
Если зафиксировано число 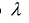, то задача нахождения собственного вектора матрицы А сводится к поиску ненулевого решения системы n линейных однородных уравнений с n неизвестными 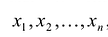, которые являются координатами вектора х. Эта система имеет ненулевое решение только тогда, когда выполняется условие:

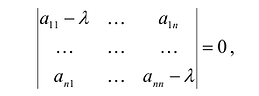
т.е. число 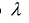является собственным числом матрицы А.

Знание всех собственных векторов матрицы А позволяет решить задачу диагонализации этой матрицы, то есть нахождения треугольной или диагональной матрицы, имеющий такие же собственные значения.

Теорема: Предположим, что квадратная матрица А n-го порядка имеет п линейно независимых собственных векторов. Тогда если взять эти векторы в качестве столбцов матрицы S, то матрица 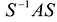будет диагональной матрицей, у которой на диагонали стоят собственные значения матрицы А, т.е.: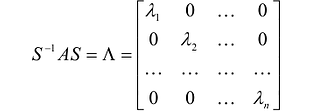

Теорема: Если 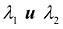- два различных собственных значения симметрической матрицы Ау то соответствующие им собственные векторы 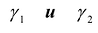удовлетворяют соотношению 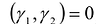т. е. они ортогональны.

Таким образом, собственные значения симметрической матрицы различны, а, значит, если пронормировать соответствующие им собственные векторы, то система собственных векторов матрицы А станет ортонормированной, а матрица S, столбцами которой будут эти векторы, станет ортогональной.

Ортогональной называется вещественная квадратная матрица, у которой соответствующая ей система векторов-столбцов является ортонормированной системой евклидова пространства.

Теорема, Матрица А является ортогональной тогда и только тогда у когда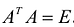

В соответствии с этой теоремой 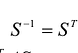, и преобразование 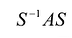эквивалентно преобразованию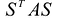

При определении характеристических чисел матрицы было введено новое понятие характеристического многочлена. Подробный анализ понятия многочлена приводится в следующем разделе.