Линейные цепи при гармоническом воздействии

Содержание:

Простейшие линейные цепи при гармоническом воздействии:

Знакомство со свойствами электрических цепей и методами их анализа начнем с рассмотрения простейших линейных цепей при гармоническом воздействии. Если значения функции времени a(t) изменяются по синусоидальному или косинусоидальному закону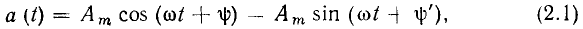

где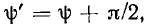

Традиционно в электротехнической литература используют синусную форму записи гармонической функции, а в радиотехнической — косинусную, которой и будем пользоваться в дальнейшем. Обе формы записи являются равноценными, отличаются только началом отсчета - значений функции и их можно проиллюстрировать одной и той же кривой (рис. 2.1, а).

Наибольшее значение гармонической функции 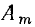называется амплитудой. Ее размерность совпадает с размерностью гармонической функции. Наименьшее значение гармонической функции равно —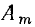. Аргумент 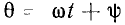функции, записанной в косинусной форме, называется мгновенной фазой (фазой). Если гармоническая функция задана в синусной форме a(t)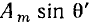 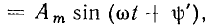то ее фаза находится по формуле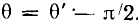

Величина 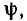равная значению мгновенной фазы 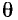при t= 0, называется начальной фазой. Фаза и начальная фаза гармонической функции выражаются в радианах (рад) или градусах.

Фаза гармонической функции линейно увеличивается во времени. Скорость ее изменения 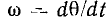называется угловой частотой. Она выражается в радианах в секунду (рад/с).

Гармонические функции времени представляют собой простейший вид периодических функций. В общем случае функция времени называется периодической, если ее значения повторяются через определенные промежутки времени. Наименьший промежуток времени Т, через который наблюдается повторение значений функции, называется периодом. Таким образом, если a (t) — периодическая функция времени с периодом Т, то для нее должно выполняться равенство

где n — произвольное целое число.

Величина, обратная периоду Т, называется частотой:

 

Частота выражается в герцах (Гц).

Режим работы электрической цепи, при котором напряжения и токи всех ветвей являются периодическими функциями времени или сохраняют неизменные значения, называется установившимся. Строго говоря, электромагнитный процесс является периодическим только в том случае, если условие периодичности (2.2) выполняется на неограниченно большом промежутке времени 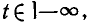т. е. если рассматриваемый процесс существует в цепи неограниченно длительное время. Если процесс возник или прекратился при каком-то конечном значении t, то в этот момент его периодичность нарушается. Постоянные токи и напряжения в ряде случаев также удобно рассматривать как периодические с периодом  и частотой, равной нулю.

Очевидно, что процессы, имеющие место в реальных цепях, не могут быть бесконечно длительными, поэтому они могут считаться периодическими лишь приближенно. Вследствие этого на практике принимают что установившимся является такой процесс, при котором условие периодичности (2.2) выполняется на достаточно большом интервале времени.

Если токи и напряжения цепи изменяются не по периодическому закону, то режим работы цепи называется неустановившимся. Частным случаем процессов, протекающих в таком режиме, являются переходные процессы, которые имеют место при переходе от одного установившегося режима к другому. Теоретически, переходные процессы в цепи затухают бесконечно долго, и новый установившийся режим наступает только при  Как будет показано далее (см. гл. 6), переходные процессы практически прекращаются (или, точнее, затухают до пренебрежимо малого уровня) через конечный промежуток времени, по истечении которого процесс в цепи можно считать установившимся. Таким образом, представление токов и напряжений в виде гармонических или других периодических функций времени (в том числе и в виде постоянных величин) следует рассматривать как приближенное математическое описание (математическую модель) реальных процессов, имеющих место в электрической цепи.

Определим период и частоту гармонической функции времени. Как известно, cos является периодической функцией 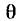с периодом, равным 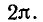Следовательно, изменение времени на период Т соответствует изменению фазы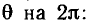

Используя (2.3) и (2.4), находим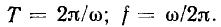

Выражения (2.3), (2.4) позволяют определить также угловую частоту гармонической функции по заданной частоте f или периоду Т

Интервал времени, в котором значения гармонической функции положительны, например называется положительным полупериодом, интервал времени, в котором значения функции отрицательны, например  - отрицательным. Совокупность значений функции на положительном полупериоде называется положительной, а совокупность значений функции на отрицательном полупериоде - отрицательной полуволной.

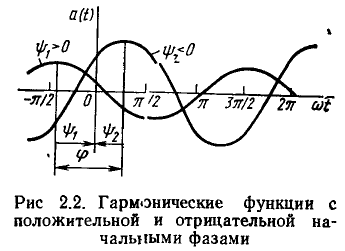
При построении временных диаграмм (графиков) гармонических функций обычно бывает удобным откладывать по оси абсцисс не время t,  а пропорциональную ему величину 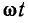 (рис. 2.2). В этом случае смещение точки  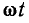= 0 относительно ближайшего максимума функции равно начальной фазе 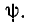Если начало координат (точка 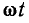= 0) смещено вправо относительно ближайшего максимума гармонической функции, то начальная фаза 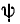является положительной, если влево — отрицательной. Если фазы 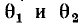двух гармонических функций 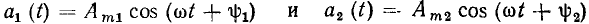отличаются на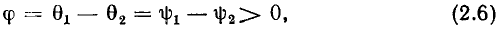

то говорят, что эти функции сдвинуты по фазе, причем функция 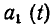опережает по фазе функцию 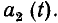Как видно из (2.6), разность фаз этих функций равна разности их начальных фаз и не зависит от времени Две гармонических функции одинаковой частоты совпадают по фазе, если разность их начальных фаз равна нулю; находятся в противофазе, если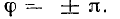

Среднее, средневыпрямленное и действующее значения гармонических токов и напряжений

Токи и напряжения цепи, изменяющиеся по гармоническому или другому периодическому закону, наряду с другими параметрами характеризуются средними за период, средневыпрямленными и действующими значениями.

Среднее значение периодической функции a (t) з а период Т определяется выражением

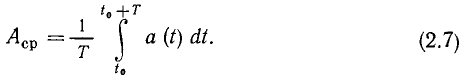
Интеграл, входящий в выражение (2.7), численно равен площади, заключенной между кривой а (t), осью времени и ординатам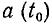и и 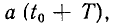причем площади, лежащие выше оси времени, берут со знаком плюс, а площади, лежащие под осью времени, — со знаком минус. Значение не зависит от выбора момента времени 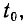поэтому при его определении можно полагать

Среднее значение гармонической функции за период равно нулю, так как площадь, ограниченная положительной полуволной и осью времени, равна площади, ограниченной отрицательной полуволной и осью абсцисс (см. рис. 2.1, а). Таким образом, среднее значение гармонического тока или напряжения за период равно нулю.

Средневыпрямленным значением периодического тока или напряжения называется среднее значение модуля соответствующей периодической функции a (t) за период:

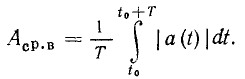
Значение 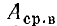пропорционально площади, ограниченной частью кривой 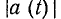и осью времени за период Т, и не зависит от выбора начального момента времени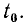

Средневыпрямленное значение гармонического тока или напряжения равно среднему значению соответствующей гармонической функции a (t) на положительном полупериоде (см. рис. 2.1, б)

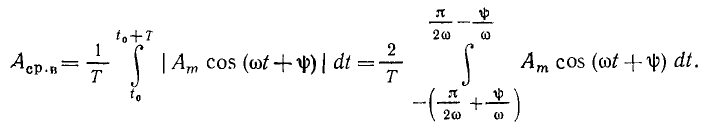
Выполняя интегрирование и полагая 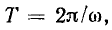находим, что средневыпрямленное значение гармонического тока или напряжения в 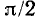раз меньше его амплитуды

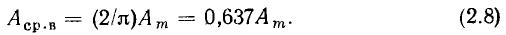
Действующим значением периодической функции a (t) называется среднеквадратическое значение этой функции за период Т:

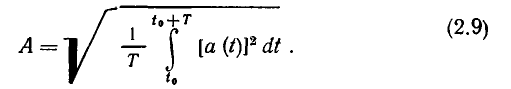
В соответствии с ГОСТ 1494—77 мгновенные значения токов и напряжений ветвей, токов источников тока и э. д. с. источников напряжения, являющихся гармоническими функциями времени, изображают строчными буквами: i = i (t), u = u (t), j= j (t), е=е (t), действующие значения этих величин — соответствующими прописными буквами I, U, J, Е и амплитудные значения — теми же прописными буквами с индексом m: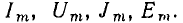 Размерность средних, средневыпрямленных и действующих значений гармонических токов и напряжений совпадает с размерностью соответствующих функций и, следовательно, с размерностью их амплитуд.

При протекании периодического тока i (t) через линейное сопротивление R в нем в соответствии с выражениями (1.12) и (2.9) за период Т выделяется энергия

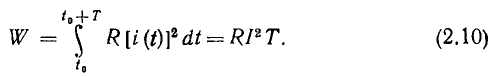
Выражение (2.10) совпадает с выражением для энергии, выделяющейся в сопротивлении при протекании через него постоянного тока I_ = I в течение времени Т (закон Джоуля— Ленца). Таким образом, действующее значение I периодического тока i (t) численно равно значению постоянного тока при протекании которого за время Т выделится такое же количество энергии, как и при протекании тока i (t). Аналогично можно определить и действующее значение U периодического напряжения u (t).

Действующее значение А гармонической функции a(t) в 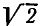раз меньше ее амплитуды:

 

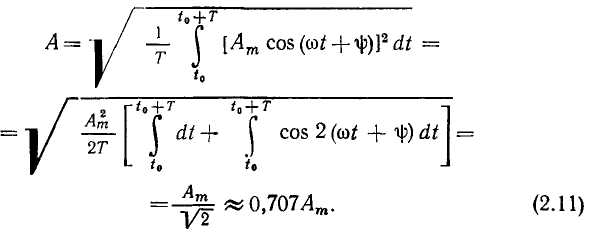
Учитывая, что большинство потребителей реагируют на действующие, а не на максимальные (пиковые) значения токов и напряжений, при описании гармонических токов и напряжений принято указывать их действующие, а не амплитудные значения. Выражая в (2.1) амплитуду 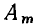через действующее значение А, получаем еще одну форму записи гармонической функции

Линейные операции над гармоническими функциями

Важнейшим свойством гармонических функций времени является то, что в результате линейных операций, производимых над ними (умножением на постоянное число, дифференцированием, интегрированием, алгебраическим сложением нескольких гармонических функций одинаковой частоты), получают гармонические функции той же частоты. Действительно, при умножении гармонической функции 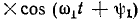на постоянный множитель 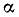получаем новую гармоническую функцию

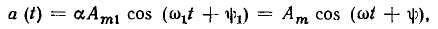
угловая частота 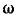и начальная фаза 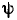которой совпадают с угловой частотой 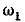и начальной фазой 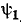исходной функции, а амплитуда 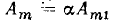отличается от амплитуды исходной функции в 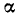раз.

При дифференцировании гармонической функции 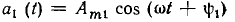 получаем

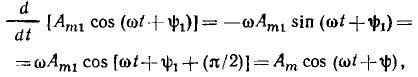
т. е. гармоническую функцию той же частоты; ее амплитуда и начальная фаза равны соответственно

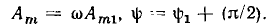
Интеграл от гармонической функции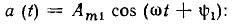

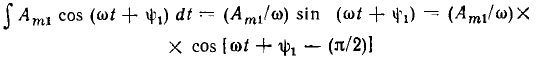
представляет собой гармоническую функцию той же частоты, ее амплитуда и начальная фаза определяются выражениями (постоянная интегрирования принята равной нулю):

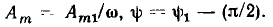
При сложении двух гармонических функций 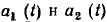одинаковой частоты получают новую гармоническую функцию a(t) той же частоты [2]:

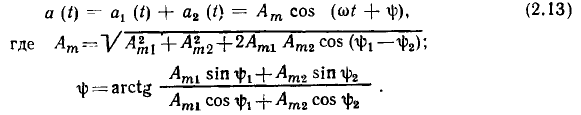
Многократно применяя формулу (2.13), можно убедиться, что результат алгебраического суммирования любого числа гармонических функций одинаковой частоты представляет собой гармоническую функцию этой же частоты. Аналогичным образом можно убедиться, что линейная комбинация любого количества гармонических функций времени одной частоты

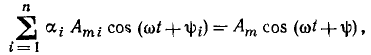
где 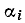= const, является гармонической функцией этой частоты.

Таким образом, линейные операции, выполняемые над гармонической функцией, приводят лишь к изменению ее амплитуды и начальной фазы; в результате линейных операций, выполняемых над совокупностью гармонических функций одной частоты, получается гармоническая функция той же частоты.

Дифференциальное уравнение цепи при гармоническом воздействии

Рассмотрим линейную электрическую цепь с сосредоточенными параметрами, находящуюся под монохроматическим (одночастотным) гармоническим воздействием. Токи всех неуправляемых источников тока и э. д. с. всех неуправляемых источников напряжения такой цепи есть гармонические функции времени частоты оз. Дифференциальное уравнение этой цепи, составленное для любого из неизвестных токов и напряжений у= у (t), имеет вид (1.61), причем правая часть этого уравнения представляет собой линейную комбинацию гармонических функций и их производных, т. е. является гармонической функцией времени той же частоты, что и внешнее воздействие:

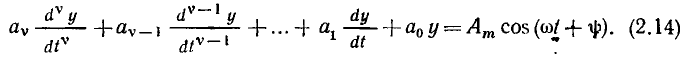
Следовательно, задача анализа линейной цепи с сосредоточенными параметрами при гармоническом воздействии сводится к решению линейного дифференциального уравнения с постоянными коэффициентами, правая часть которого является гармонической функцией времени.

Ограничимся пока рассмотрением установившегося режима, т. е. будем считать, что действующие в цепи источники были подключены при 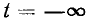 и к настоящему моменту переходные процессы в цепи полностью прекратились. Из теории дифференциальных уравнений известно, что в таком режиме уравнение (2.14) имеет единственное периодическое решение

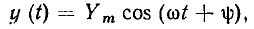
которое является гармонической функцией времени.

Итак, в установившемся режиме токи и напряжения всех ветвей линейной цепи, находящейся под гармоническим воздействием, являются гармоническими Функциями времени одной частоты и, следовательно, задача анализа цепи сводится к определению начальных фаз и амплитуд (или действующих значений) интересующих токов или напряжений.

Метод комплексных амплитуд

Понятие о символических методах:

Установившиеся значения токов и напряжений линейной цепи, находящейся под гармоническим воздействием, могут быть найдены путем непосредственного решения дифференциального уравнения цепи (2.14) при 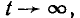однако даже для относительно простых цепей эта задача оказывается весьма трудоемкой. На практике анализ таких цепей обычно выполняют с помощью метода комплексных амплитуд, разработанного в конце прошлого века американскими инженерами Ч. П. Штейнметцем и А. Е. Кеннели. Большой вклад в развитие и теоретическое обоснование метода комплексных амплитуд внесли профессор Петербургского политехнического института В. Ф. Миткевич и советский ученый академик АН УССР Г. Е. Пухов.

Метод комплексных амплитуд, подобно известному логарифмическому методу, основан на идее функционального преобразования, при котором операции над исходными функциями (оригиналами) заменяются более простыми операциями над некоторыми новыми функциями, так называемыми изображениями или символами исходных функций. Методы такого типа будем называть символическими. Независимо от типа используемых функциональных преобразований решение любой задачи символическими методами содержит, как правило, следующие основные этапы:

1. прямое преобразование, в результате которого осуществляется переход от исходных величин (оригиналов) к их символам (изображениям);
2. определение изображений искомых величин путем выполнения по специально установленным правилам операций над изображениями;
3. обратное преобразование, с помощью которого переходят от изображений к оригиналам. В частности, при использовании логарифмического метода исходные величины на первом этапе заменяют их логарифмами. На втором этапе, выполняя необходимые действия над логарифмами исходных величин, находят логарифмы искомых величин; операции над логарифмами оказываются проще, чем соответствующие им операции над исходными величинами (например, умножению исходных величин соответствует сложение их логарифмов, возведению исходной величины в степень m— умножение логарифма этой величины на m и т. д.). На третьем этапе осуществляют обратный переход от логарифмов непосредственно к искомым величинам.

Очевидно, что эффективность каждого из символических методов определяется трудоемкостью прямого и обратного функциональных преобразований и тем, насколько операции над изображениями проще соответствующих им операций над оригиналами.

Комплексные числа и основные операции над ними

Символический метод комплексных амплитуд (комплексный метод, иногда, просто — символический метод) основан на представлении гармонических функций времени с помощью комплексных чисел или, точнее, на преобразовании исходных функций из временной области (области вещественного переменного t) в частотную область (область мнимого аргумента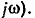

Напомним, что комплексным числом 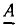 называется выражение вида

где 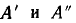— действительные числа, называемые соответственно вещественной и мнимой частями комплексного числа; 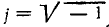— мнимая единица. Вещественную и мнимую части комплексного числа иногда обозначают: 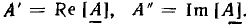. Выражение (2.15) — это алгебраическая форма записи комплексного числа.

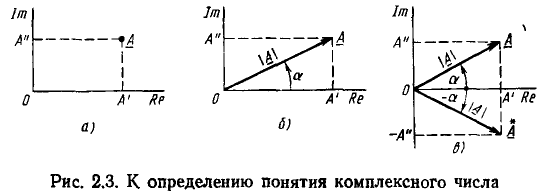
Комплексное число 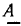изображается на комплексной плоскости в виде точки А, абсцисса которой равна А', а ордината — А" (рис. 2.3, а). Ось абсцисс, на которой откладывается вещественная часть комплексного числа, называется действительной (Re); ось ординат, на которой откладывается мнимая часть, — мнимой (Im).

Каждой точке А комплексной плоскости и, следовательно, каждому комплексному числу А можно поставить в соответствие вектор А, проведенный из начала координат в точку А (рис. 2.3, б). Длину вектора, изображающего комплексное число, называют модулем этого числа

Угол 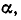образуемый вектором 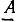с положительным направлением вещественной оси, называют аргументом комплексного числа:

Положительное направление отсчета 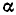— против часовой стрелки. Аргумент комплексного числа может иметь бесконечное множество значений, отличающихся Друг от друга на 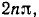где n — целое число. Главное значение аргумента заключено в промежутке —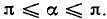

Как видно из рис. 2.3, б, вещественная А' и мнимая A" части комплексного числа 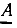 есть проекции вектора  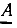на действительную и мнимую оси соответственно: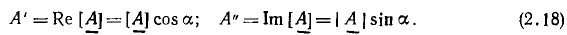

Подставляя соотношения (2.18) в выражение (2.15), можно перейти от алгебраической формы записи комплексного числа к тригонометрической:

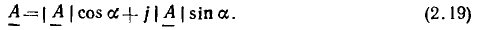
Далее, используя формулу Эйлера:

где е — основание натурального логарифма, получаем показательную форму записи комплексного числа

Комплексные числа 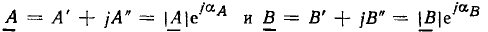считаются равными, если попарно равны их действительные н мнимые части: A' = В’, А" = В" (или, что то же самое, равны их модули  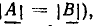а аргументы отличаются на 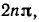где n — целое число;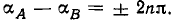

Два комплексных числа 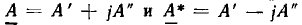называются сопряженными, если их действительные части равны, а мнимые отличаются только знаком. Точки на комплексной плоскости, изображающие сопряженные комплексные числа, симметричны относительно действительной оси (рис. 2.3,в). Модули сопряженных чисел равны, а главные значения их аргументов отличаются только знаком:

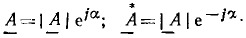
 Понятий «больше» и «меньше» для комплексных чисел не существует. Арифметические операции над комплексными числами выполняются так же, как над обыкновенными двучленами, имея в виду, что 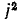= — 1. Операции сложении и вычитания удобнее выполнять, используя алгебраическую форму записи:

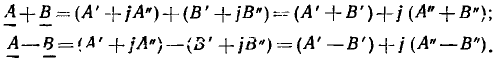
Очевидно, что сумма двух сопряженных комплексных чисел  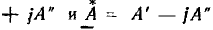                            представляет собой действительное число

Умножение, деление и возведение в степень комплексных чисел удобнее проводить в показательной форме:

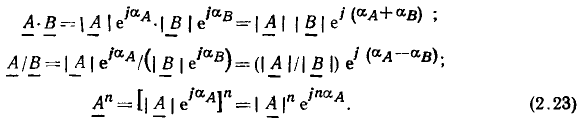
Из выражений (2.23) следует, что при умножении вектора 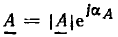на действительное число m получается новый вектор, модуль которого в m раз больше модуля вектора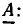

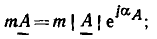
при умножении вектора 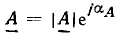на вектор 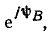модуль которого равен единице, получается новый вектор, повернутый относительно вектора 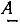на угол 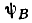против часовой стрелки:

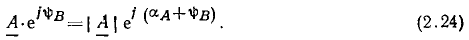
Из (2.24) и формулы Эйлера следует также, что умножение вектора 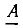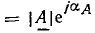на вектор

равносильно повороту вектора 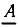на угол 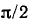против часовой стрелки:

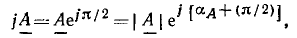
а умножение вектора 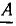на вектор

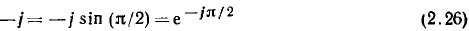
приводит к повороту вектора 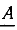на угол 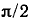по часовой стрелке:

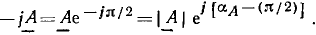
Наконец, умножение вектор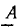а на 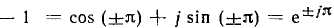равносильно изменению аргумента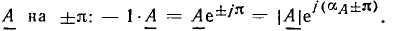

Умножение и деление комплексных чисел можно производить также и в алгебраической форме:

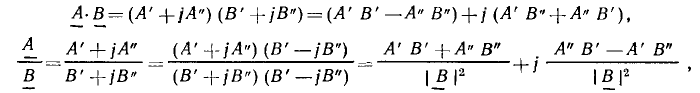
причем при выполнении деления учитывается, что произведение двух комплексно сопряженных чисел есть действительное число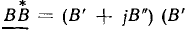      

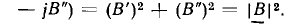
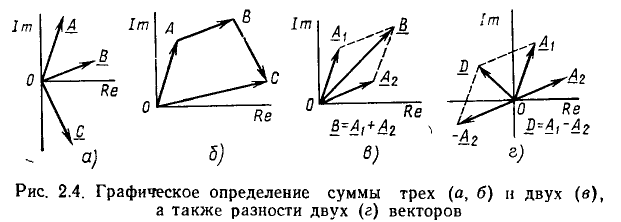
Суммирование комплексных чисел во многих случаях бывает удобно производить графически, используя правила действий над векторами. Вектор 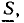равный сумме векторов 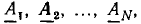может быть построен следующим образом: из начала координат строят вектор 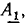из его конца, как из начала координат, строят вектор 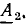из конца вектора 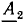строят вектор 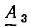и т. д. Вектор, замыкающий ломаную линию, образованную из слагаемых векторов, представляет их сумму 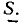Так, вектор 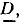равный сумме векторов 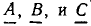(рис. 2.4, а, б), равен замыкающей ОС = D ломаной линии ОАВС, построенной из векторов А = ОА, В = АВ, С — ВС. Вектор В, равный сумме двух векторов 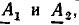— диагональ параллелограмма, построенного на сторонах (рис. 2.4, в). 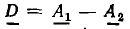Разность может быть найдена как сумма векторов 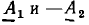(рис. 2.4, г).

Комплексные изображения гармонических функций времени

Каждой гармонической функции времени а (t) можно поставить в соответствие комплексное число а, называемое мгновенным или текущим комплексом гармонической функции:

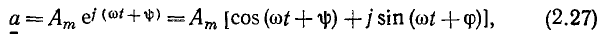
модуль которого равен амплитуде гармонической функции 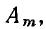а аргумент — ее фазе 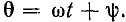Как видно из выражения (2.27), вещественная часть мгновенного комплекса а равна исходной гармони, ческой функции

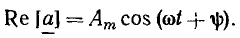
Пример 2.1. Мгновенные комплексы гармонического тока 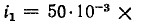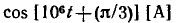и гармонического напряжения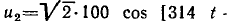 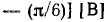                   равны соответственно  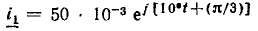и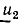

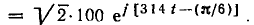
Вещественные части этих комплексов есть исходные гармонические функции:

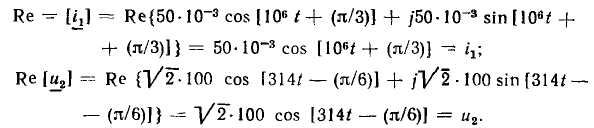
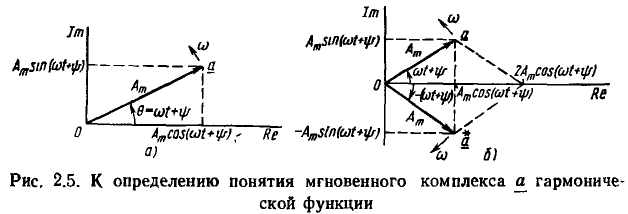
Геометрически мгновенный комплекс а может быть представлен в виде вектора 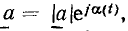длина которого |а| в определенном масштабе равна амплитуде 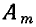соответствующей гармонической функции, а аргумент а (t) изменяется во времени по такому же закону, как и фаза гармонической функции 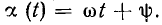Для того чтобы обеспечить этот закон изменения аргумента, вектор а должен вращаться в комплексной плоскости против часовой стрелки с угловой скоростью 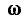(рис. 2.5, а). В момент времени t = 0 вектор а должен образовывать с положительным направлением вещественной оси угол 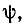равный начальной фазе рассматриваемой гармонической функции. Как видно из рис. 2.5,а, проекция вектора а на вещественную ось в выбранном масштабе времени равна мгновенному значению исходной гармонической функции времени а (t) = Re [a].

Используя понятие комплексных сопряженных чисел и выражение (2.22), мгновенное значение гармонической функции а (t) можно оп

ределить так же, как полусумму мгновенного комплекса 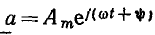 и сопряженного ему комплексного числа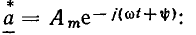

 

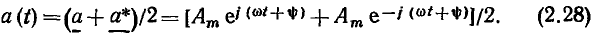
Векторы имеют одинаковую длину, противоположные по знаку начальные фазы и вращаются в комплексной плоскости в противоположных направлениях с одинаковой угловой скоростью 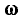(рис. 2.5, б). Проекции этих векторов на действительную ось равны

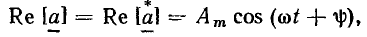
а проекции на мнимую ось имеют различные знаки:

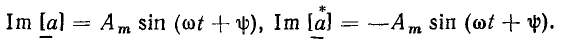
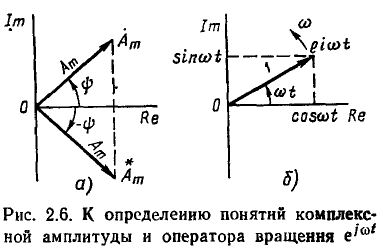
Значение мгновенного комплекса а в момент времени t — 0 называется комплексной амплитудой 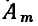гармонической функции времени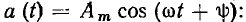

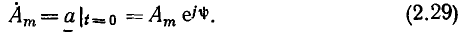
Из выражения (2.29) следует, что комплексная амплитуда гармонической функции времени 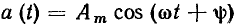представляет собой комплексное число, модуль которого равен амплитуде 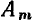рассматриваемой функции, а аргумент — ее начальной фазе 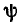. Геометрически комплексная амплитуда может быть представлена в виде неподвижного вектора, расположенного под углом  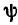к вещественной оси (рис. 2.6, а), длина которого в определенном масштабе равна .

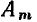Используя понятие комплексной амплитуды, выражение (2.27) для мгновенного комплекса а может быть преобразовано к следующему виду:

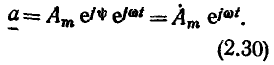
Вектор 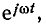называемый оператором вращения, имеет единичную длину и вращается в комплексной плоскости против часовой стрелки с угловой скоростью 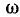(рис. 2.6, б). Всякий неподвижный вектор, будучи умноженным на оператор вращения 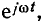начинает вращаться в комплексной плоскости против часовой стрелки с угловой скоростью .

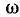В установившемся режиме токи и напряжения всех ветвей электрической цепи, находящейся под гармоническим воздействием, есть гармонические функции времени одной частоты. Каждому из токов и напряжений ветвей электрической цепи a (t) может быть поставлен в соответствие текущий комплекс а. Текущие комплексы, соответствующие токам и напряжениям различных ветвей, изображаются векторами, вращающимися с одинаковой угловой скоростью (неподвижными один относительно другого). Каждый из текущих комплексов токов и напряжений ветвей электрической цепи можно представить в виде произведения соответствующей комплексной амплитуды 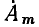на оператор вращения  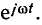Очевидно, что оператор вращения является общим для мгновенных комплексов токов и напряжений всех ветвей и не несет информации о токах или напряжениях конкретных ветвей.

Токи и напряжения отдельных ветвей отличаются только амплитудами и начальными фазами, поэтому информация о них при известной частоте 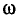содержится в соответствующих комплексных амплитудах. Зная амплитуды и начальные фазы токов или напряжений любой ветви, всегда можно однозначно найти их комплексные амплитуды и, обратно, по известной комплексной амплитуде можно однозначно установить амплитуду и начальную фазу исходного гармонического колебания.

Пример 2.2.

Комплексная амплитуда гармонического тока 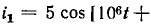 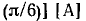                 есть 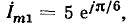а комплексная амплитуда гармонического напряжения 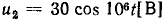равна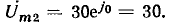

При 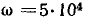рад/с комплексным амплитудам тока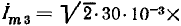 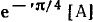 и э.д.с. 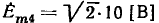соответствуют мгновенные значения тока и э. д. с.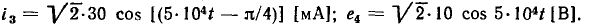

Итак, установлено, что каждой гармонической функции времени a (t) можно единственным образом поставить в соответствие комплексное число 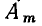(комплексную амплитуду), которое можно рассматривать как изображение этой гармонической функции в комплексной плоскости (по Г. Е. Пухову — комплексное изображение или К-изображение):

Символом К будем обозначать операцию перехода от оригинала (исходной функции времени) к ее изображению в комплексной плоскости. Переход от гармонической функции времени а (t) к ее комплексной амплитуде 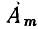может быть выполнен с помощью преобразования [3]

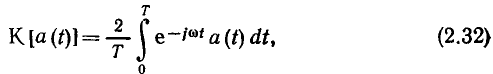
которое в дальнейшем будем называть прямым К-преобразованием или просто К-преобразованием гармонической функции. В справедливости выражения (2.32) можно убедиться путем непосредственной подстановки в него                                  a(t)= 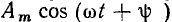 и Т =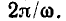

Используя выражения (2.28), (2.29) и (2.30), найдем формулу для обратного перехода от комплексной амплитуды к исходной гармонической функции времени:

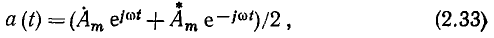
где 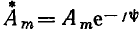— комплексное число, сопряженное с комплексной амплитудой (рис. 2.6, а). Операцию перехода от К-изображения гармонической функции к оригиналу (обратное К-преобразование) будем обозначать

Выражения (2.31) и (2.34), устанавливающие связь между оригиналом и его изображением, могут быть заменены соотношением

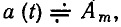в котором использован знак соответствия 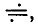означающий взаимное соответствие между функциями, определенными в различных областях.

Как видно из приведенных примеров, прямое и обратное К-преобразования при практических расчетах электрических цепей можно производить непосредственно с использованием определения комплексной амплитуды (2.29) без применения выражений (2.32) и (2.33).

Операции над комплексными изображениями гармонических функций

Найдем операции над комплексными амплитудами, соответствующие линейным операциям (см. § 2.1) над гармоническими функциями времени.

Пусть необходимо умножить гармоническую функцию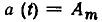 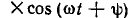на постоянное число а.

Найдем комплексную амплитуду функции 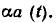В соответствии с определением К-преобразования (2.32) К-изображение функции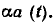

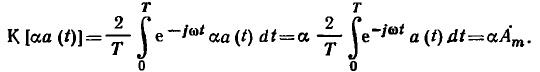
Таким образом, умножение оригинала на произвольное число а соответствует умножению изображения на это же число:

Найдем комплексное изображение суммы гармонических функций времени с комплексными амплитудами 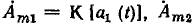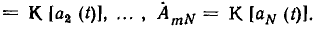В соответствии с (2.32) получаем

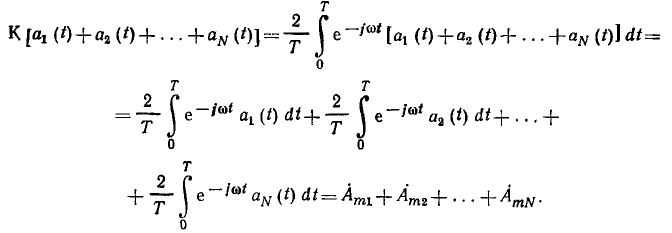
Итак, суммированию гармонических функций времени соответствует, суммирование их комплексных амплитуд:

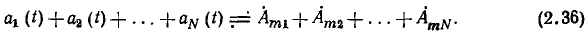
Из выражений (2.35) и (2.36) следует, что линейной комбинации гармонических функций времени соответствует линейная комбинация их комплексных амплитуд:

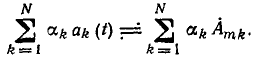
Здесь 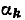— постоянные коэффициенты; N — произвольное целое число.

Найдем комплексное изображение производной гармонической функции времени a (t):

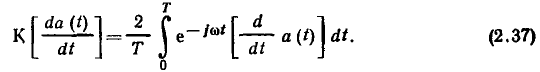
Интегрируя (2.37) по частям, получаем

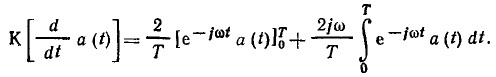
Учитывая, что каждый из сомножителей произведения 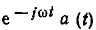является периодической функцией времени с периодом 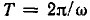и, следовательно,разность значений этого произведения, взятых через период, равна нулю

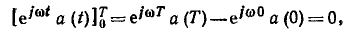
а также, что величина 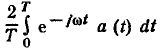представляет собой комплексную амплитуду 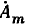гармонической функции а (t), получаем окончательно

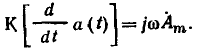
Таким образом, дифференцированию гармонических функций времени соответствует умножение их комплексных амплитуд на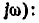

Определим комплексное изображение интеграла от гармонической функции времени a (t)

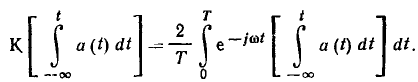
Интегрируя по частям, получаем

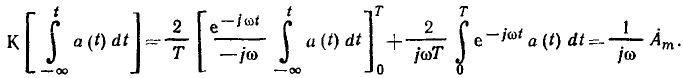
Следовательно, интегрированию гармонических функций времени соответствует деление комплексных амплитуд на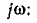

 

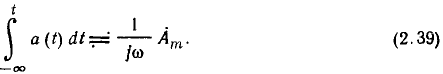
Итак, линейным операциям над гармоническими функциями времени соответствуют линейные операции над их комплексными амплитудами, причем операции дифференцирования и интегрирования заменяются операциями умножения и деления. Эти свойства комплексных изображений гармонических функций позволяют существенно упростить анализ линейных цепей, находящихся под гармоническим воздействием, так как позволяют заменять систему интегро-дифференциальных уравнений электрического равновесия цепи, составленную для мгновенных значений токов и напряжений ветвей, системой алгебраических уравнений для комплексных изображений соответствующих токов и напряжений.

Наряду с комплексной амплитудой 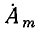в качестве изображения гармонической функции a(t) в комплексной плоскости широко используют другую комплексную величину — комплексное действующее значение  А. По определению, комплексное действующее значение гармонической функции 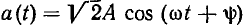представляет собой комплексное число, модуль которого равен действующему значению А гармонической функции, а аргумент — ее начальной фазе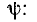

Используя выражения (2.11) и (2.29), можно установить связь между комплексной амплитудой 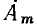гармонической функции a(t) и ее комплексным действующим значением А:

На комплексной плоскости 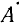изображается в виде вектора, совпадающего по направлению с вектором 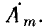Длина вектора 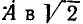раз меньше длины вектора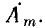

Все правила, устанавливающие соответствие между операциями над гармоническими функциями времени и операциями над их комплексными амплитудами, справедливы и для операций над комплексными действующими значениями гармонических функций.

Величины 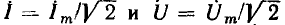обычно называют комплексными током и напряжением цепи.

Комплексные сопротивление и проводимость участка цепи

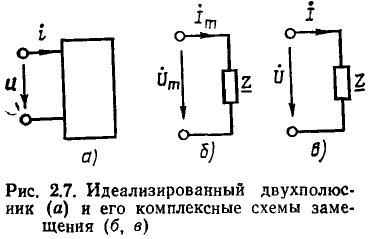
Рассмотрим произвольную линейную цепь с сосредоточенными параметрами, находящуюся под гармоническим воздействием. Выделим участок этой цепи, имеющий два внешних зажима, и не содержащий источников энергии (рис. 2.7, а). Ток i и напряжение u на зажимах этого участка являются гармоническими функциями времени:

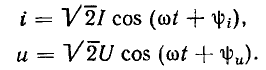
По определению, комплексным входным сопротивлением (комплексным сопротивлением)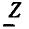 пассивного участка цепи называется отношение комплексной амплитуды напряжения на зажимах участка цепи к комплексной амплитуде тока:

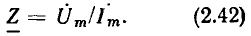
Выражая комплексные амплитуды напряжения и тока через соответствующие комплексные действующие значения 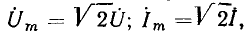устанавливаем, что комплексное сопротивление пассивного участка цепи может быть также найдено как отношение комплексных действующих значений напряжения и тока:

Комплексное входное сопротивление пассивного участка цепи представляет собой в общем случае комплексное число, поэтому оно может быть представлено в показательной

или алгебраической

формах. Величины 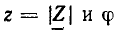называются соответственно модулем и аргументом комплексного сопротивления, величины r и х — его вещественной (резистивной) и мнимой (реактивной) составляющими (модуль комплексного входного сопротивления цепи z называется также полным входным сопротивлением). Представляя комплексные амплитуды и комплексные действующие значения напряжений и токов в показательной форме, находим из (2.42) и (2.43)

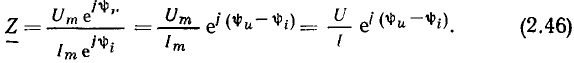
Сравнивая (2.44) и (2.46), устанавливаем, что модуль комплексного сопротивления z равен отношению амплитуд или действующих значений напряжения и тока на зажимах рассматриваемого участка цепи:

а аргумент равен разности начальных фаз напряжения и тока:

В зависимости от фазовых соотношений между напряжением и током величина 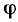может быть больше нуля (напряжение опережает ток по фазе), меньше нуля (напряжение отстает по фазе от тока) или равна нулю (ток и напряжение совпадают по фазе).

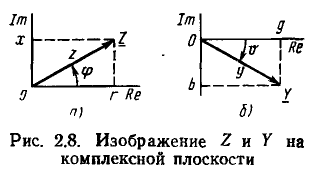
Комплексное входное сопротивление может быть представлено в виде вектора, расположенного в комплексной плоскости, длина которого в определенном масштабе равна z, а угол наклона к положительной вещественной полуоси равен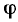 (рис. 2.8, а).

Вещественная r и мнимая х составляющие 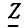представляют собой проекции вектора 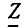на вещественную и мнимую оси соответственно:

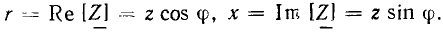
Величина, обратная комплексному входному сопротивлению, называется комплексной входной проводимостью участка цепи

Комплексная входная проводимость (комплексная проводимость) может быть определена как отношение комплексных амплитуд или комплексных действующих значений тока и напряжения на зажимах рассматриваемого участка цепи:

Представляя комплексную проводимость 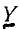 в показательной форме

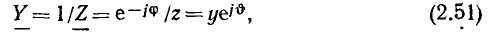
находим, что модуль комплексной входной проводимости 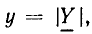называемый полной входной проводимостью цепи, является величиной, обратной модулю комплексного входного сопротивления:

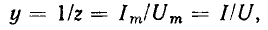
а аргумент входной проводимости 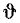равен по абсолютному значению и противоположен по знаку аргументу комплексного входного сопротивления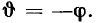

Комплексная входная проводимость участка цепи может быть также представлена в алгебраической форме 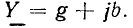Здесь g и b — вещественная (резистивная) и мнимая (реактивная) составляющие входной проводимости, которые можно рассматривать как проекции вектора Y на вещественную и мнимую оси комплексной плоскости (рис. 2.8, б):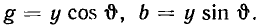

Подставляя в (2.49) 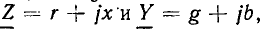находим связь между вещественными и мнимыми составляющими комплексного сопротивления и комплексной проводимости участка цепи:

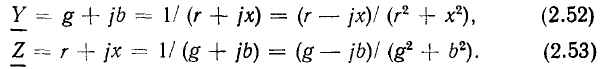
Из выражений (2.52), (2.53) видно, что резистивные составляющие комплексного входного сопротивления и комплексной входной проводимости имеют одинаковые знаки:

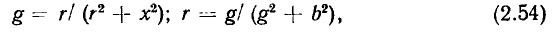
а реактивные составляющие — противоположные:

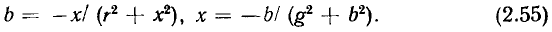
Отметим, что каждая из составляющих комплексного сопротивления (r и х) зависит как от резистивной g, так и реактивной b составляющей комплексной проводимости, а каждая из составляющих комплексной проводимости (g и b) в свою очередь зависит от r и х.

Комплексная схема замещения цепи. Законы Ома и Кирхгофа в комплексной форме

Комплексные сопротивление и проводимость пассивного участка линейной цепи были введены как отношения комплексных действующих значений или комплексных амплитуд напряжения и тока, приложенных к зажимам этого участка цепи. В то же время комплексные сопротивление и проводимость любого участка линейной цепи, составленного из идеализированных пассивных элементов, не зависят от амплитуд (действующих значений) и начальных фаз токов и напряжений и определяются только параметрами элементов, входящих в рассматриваемый участок цепи, способом их соединения между собой и частотой внешнего гармонического воздействия.

Зная комплексное сопротивление (комплексную проводимость) участка цепи и одну из приложенных к данному участку цепи величин: ток 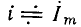или напряжение  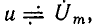можно, используя (2.42), (2.50), найти неизвестное напряжение или неизвестный ток исследуемого участка

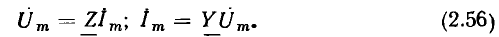
Аналогично комплексные действующие значения напряжения и тока на зажимах участка цепи

Выражения (2.56), (2.57) по структуре напоминают соотношения между мгновенными значениями напряжения и тока на зажимах линейного сопротивления (1.9), (1.10) и являются математической записью закона Ома в комплексной форме. В отличие от выражений (1.13), (1.16), (1.22), (1.23) уравнения (2.56), (2.57) являются алгебраическими.

Используя закон Ома в комплексной форме, каждому участку линейной электрической цепи, составленному из идеализированных пассивных элементов и имеющему два внешних вывода (см. рис. 2.7, а), в том числе любому идеализированному пассивному двухполюсному элементу, можно поставить в соответствие комплексную схему замещения, на которой рассматриваемый участок цепи представлен комплексным сопротивлением или проводимостью, а токи и напряжения на его зажимах — комплексными амплитудами (см. рис. 2.7, б) или комплексными действующими значениями (см. рис. 2.7, в).

Представляя все входящие в моделирующую цепь идеализированные пассивные элементы их комплексными схемами замещения, а токи и э. д. с. всех идеализированных источников — их комплексными амплитудами или комплексными действующими значениями, получаем комплексную схему замещения цепи (эквивалентную схему для комплексных амплитуд или эквивалентную схему для комплексных действующих значений). В отличие от этих схем замещения рассмотренные ранее эквивалентные схемы, на которых были изображены идеализированные двухполюсные элементы и указаны мгновенные значения токов i и напряжений u ветвей и идеализированных источников, будем называть эквивалентными схемами для мгновенных значений.

Таким образом, комплексная схема замещения цепи может быть получена из эквивалентной схемы для мгновенных значений заменой всех идеализированных пассивных двухполюсников их комплексными сопротивлениями (проводимостями) и всех токов и напряжений — их комплексными изображениями.

Мгновенные значения токов и напряжений различных ветвей электрической цепи связаны между собой линейными алгебраическими уравнениями баланса токов и напряжений, составляемыми на основании законов Кирхгофа. Учитывая, что суммированию гармонических функций времени соответствует суммирование их комплексных изображений, перейдем от законов Кирхгофа для мгновенных значений токов и напряжений к законам Кирхгофа для комплексных изображений токов и напряжений, называемых обычно законами Кирхгофа в комплексной форме.

Первый закон Кирхгофа в комплексной форме устанавливает связь между комплексными изображениями токов в каждом из узлов моделирующей цепи: сумма комплексных амплитуд (комплексных действующих значений) токов всех ветвей, подключенных к каждому из узлов электрической цепи, равна нулю:

 

 Здесь k — номер ветви, подключенной к рассматриваемому узлу.

Второй закон Кирхгофа в комплексной форме определяет связь между комплексными изображениями напряжений ветвей, входящих в произвольный контур электрической, цепи: сумма комплексных амплитуд {комплексных действующих значений) напряжений всех ветвей, входящих в любой контур моделирующей цепи, равна нулю:

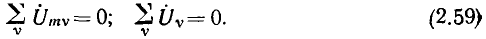
Здесь v — номер ветви, входящей в рассматриваемый контур.

В ряде случаев удобно использовать другую формулировку второго закона Кирхгофа в комплексной форме: сумма комплексных изображений напряжений на всех элементах любого контура моделирующей цепи равна сумме комплексных изображений э. д. с., всех входящих в контур источников напряжения:

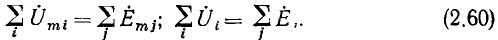
Здесь 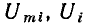— комплексные изображения напряжений всех элементов контура, за исключением источников напряжения;  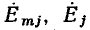— комплексные изображения э. д. с. источников напряжения, действующих в рассматриваемом контуре.

В связи с тем что выражения (2.58)—(2.60) непосредственно вытекают из соотношений (1.37), (1.40) и (1.42), при суммировании комплексных изображений токов и напряжений ветвей электрической цепи в выражениях (2.58)—(2.60) сохраняются те же правила знаков, что и при суммировании мгновенных значений токов и напряжений.

Используя выражения для законов Ома и Кирхгофа в комплексной форме, можно составить систему уравнений электрического равновесия цепи для комплексных изображений токов и напряжений. В отличие от системы уравнений электрического равновесия, составленных для мгновенных значений токов и напряжений, уравнения электрического равновесия для комплексных изображений токов и напряжений являются алгебраическими. Решение таких уравнений намного проще, чем решение дифференциальных уравнений электрического равновесия, составленных для мгновенных значений токов и напряжений. Таким образом, с использованием комплексных схем замещения и составленных на их основании уравнений электрического равновесия цепи в комплексной форме анализ цепи переменного тока становится не сложнее анализа цепи постоянного тока и может производиться с использованием тех же приемов.

Общая схема применения метода комплексных амплитуд

Анализ цепей методом комплексных амплитуд содержит следующие этапы:

1. замена гармонических токов и напряжений всех ветвей их комплексными изображениями, а эквивалентной схемы цепи для мгновенных значений — комплексной схемой замещения;
2. составление уравнений электрического равновесия цепи для комплексных изображений токов и напряжений на основе законов Ома и Кирхгофа в комплексной форме;
3. решение системы уравнений электрического равновесия относительно комплексных изображений интересующих токов и напряжений;
4. переход от комплексных изображений токов и напряжений к их оригиналам.

Идеализированные пассивные элементы при гармоническом воздействии

Сопротивление

Пусть к идеализированному резистивному элементу сопротивлению (см. рис. 1.2) приложено напряжение, изменяющееся по гармоническому закону (рис. 2.9, а):

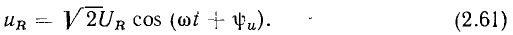
Определим ток сопротивления 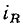и его комплексное входное сопротивление 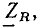а также построим диаграммы, характеризующие зависимость тока, напряжения и мгновенной мощности сопротивления от времени.

Связь между мгновенными значениями тока и напряжение линейного сопротивления определяется законом Ома (1.9). Подставляя (2.61) в (1.9), находим

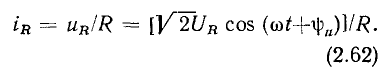Из выражения (2.62) видно, что при гармоническом внешнем воздействии ток сопротивления является гармонической функцией времени той же частоты, что и напряжение (рис. 2.9, б). В общем случае гармонический ток через сопротивление

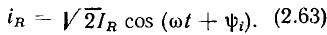
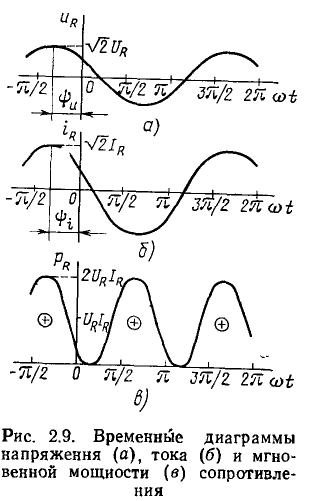
 Сравнивая выражения (2.62) и (2.63), устанавливаем, что ток и напряжение линейного сопротивления совпадают по фазе

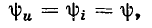
а действующие значения напряжения и тока связаны между собой соотношением 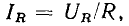 подобным закону Ома для мгновенных значений. Мгновенная мощность сопротивления определяется произведением мгновенных значений напряжения 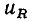и тока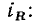

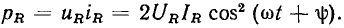
Выражая 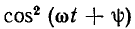 через косинус двойного угла, получаем выражение для мгновенной мощности сопротивления

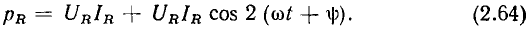
Из выражения (2.64) следует, что мгновенная мощность сопротивления содержит две составляющие: постоянную, равную произведению действующих значений напряжения и тока, и переменную, изменяющуюся во времени по гармоническому закону с частотой, удвоенной по сравнению с частотой воздействующего напряжения (рис. 2.9, в). Максимальное значение мгновенной мощности сопротивления равно 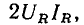а минимальное — нулю.

В связи с тем что ток и напряжение сопротивления имеют одинаковые начальные фазы, они одновременно достигают максимальных значений и одновременно проходят через нуль (рис. 2.9, а, б). Мгновенная мощность сопротивления всегда положительна, причем она обращается в нуль в точках, где ток и напряжение равны нулю, и достигает максимума в моменты времени, когда токи напряжение максимальны по абсолютному значению.

Среднее значение мощности сопротивления за период называется активной мощностью и равно произведению действующих значений напряжения и тока:

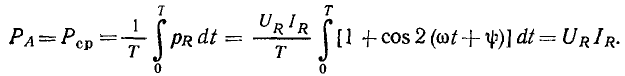
Активная мощность численно равна постоянной составляющей мгновенной мощности и характеризует среднюю за период скорость потребления сопротивлением энергии от источника.

Комплексные ток и напряжение сопротивления I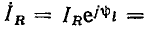 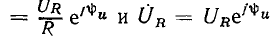имеют одинаковые аргументы и отличаются по модулю в R раз. На комплексной плоскости 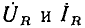изображаются векторами, которые совпадают по направлению и отличаются только масштабом (рис. 2.10, а).

Комплексное сопротивление 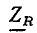идеализированного резистивного элемента — сопротивления равно отношению комплексных действующих значений напряжения и тока:

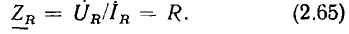
Представляя комплексное сопротивление 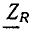в показательной и алгебраической формах

и сравнивая (2.65) с (2.66), устанавливаем, что модуль комплексного сопротивления равен 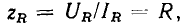 его аргумент 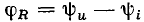=0 и что комплексное входное сопротивление  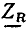идеализированного резистивного элемента сопротивления содержит только вещественную составляющую: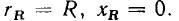

На комплексной плоскости 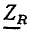изображается вектором, направленным вдоль вещественной оси (рис. 2.10, б). Комплексная проводимость сопротивления 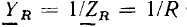также изображается вектором, направление которого совпадает с направлением положительной вещественной полуоси (рис. 2.10, в).

Комплексная схема замещения сопротивления (рис. 2.11) имеет такой же вид, как и эквивалентная схема для мгновенных значений (см. рис. 1.2), и отличается от нее только тем, что мгновенные значения тока 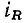и напряжения 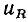заменены их комплексными изображениями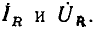

Емкость

Рассмотрим емкость (см. рис. 1.5), к которой приложено напряжение, изменяющееся по гармоническому закону:

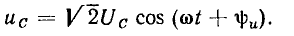
Используя выражение (1.13), найдем

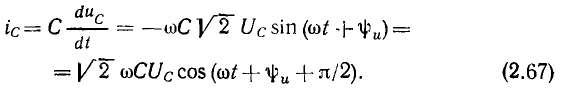
Как видно из (2.67), ток емкости изменяется по гармоническому закону

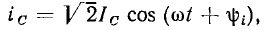
причем начальная фаза тока на 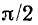больше начальной фазы напряжения: 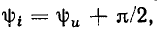т. е. ток емкости опережает по фазе напряжение на 90° (рис. 2.12, а).

Действующее значение тока емкости пропорционально действующему значению напряжения: .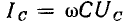

Мгновенная мощность емкости 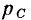при гармоническом воздействии изменяется по гармоническому закону с частотой в два раза большей частоты воздействующего напряжения (рис. 2.12, б):

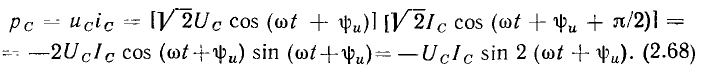
Как видно из временных диаграмм, в течение половины периода изменения мощности ток и напряжение емкости имеют одинаковый знак (емкость заряжается), при этом мгновенная мощность емкости положительна. В течение второй половины периода емкость отдает запасенную энергию (разряжается), при этом ток и напряжение емкости имеют различные знаки, а мгновенная мощность емкости отрицательна. Среднее значение мощности емкости за период (активная мощность) равно нулю:

Энергия запасенная в емкости, определяется в соответствии с выражением (1.18), приложенным к ней напряжением:

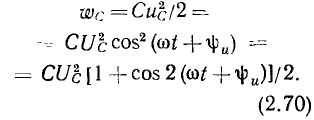
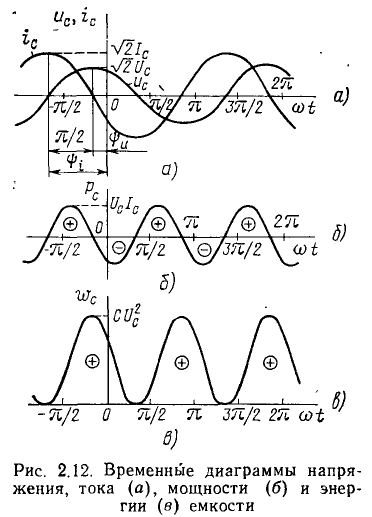
Из выражения (2.70) видно, что энергия емкости содержит две составляющие: переменную и постоянную, причем переменная составляющая энергии изменяется во времени по гармоническому закону с частотой, равной 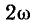(рис. 2.12, в). Энергия емкости достигает максимального значения в те моменты времени, когда напряжение на емкости максимально по абсолютному значению; при уменьшении (по абсолютному значению) напряжения на емкости запасенная в ней энергия уменьшается и становится равной нулю в моменты времени, когда напряжение на емкости равно нулю. Таким образом, емкость периодически обменивается энергией с остальной частью цепи, причем энергия, запасенная в емкости, является неотрицательной величиной. Емкость не содержит внутренних источников энергии и поэтому в процессе разрядки не может отдать больше энергии, чем она получила от остальной части цепи в процессе зарядки.

В связи с тем что ток емкости 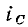 опережает напряжение емкости 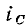по фазе на угол 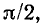комплексные ток и напряжение емкости

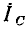
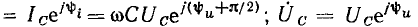
изображаются на комплексной плоскости в виде двух векторов, расположенных таким образом, что вектор 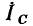повернут относительно вектора на угол 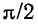против часовой стрелки (рис. 2.13, а). Комплексные сопротивление и проводимость емкости

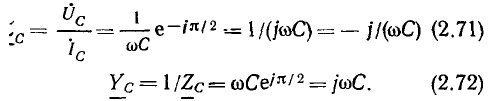
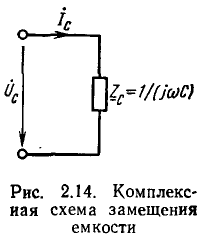
Сравнивая (2.71) и (2.72) с показательной и алгебраической формами записи комплексных сопротивления и проводимости

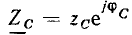
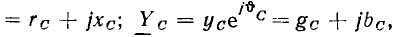
находим модули, аргументы, вещественные и мнимые составляющие входных сопротивления и проводимости емкости: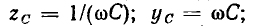

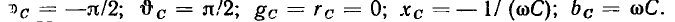
На комплексной плоскости 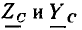изображают векторами, направленными соответственно вдоль отрицательной и положительной мнимых полуосей (рис. 2.13, б, в). Комплексная схема замещения емкости приведена на рис. 2.14.

Индуктивность

Найдем напряжение 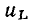на индуктивности (см. рис. 1.7), ток 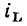которой изменяется по гармоническому закону:

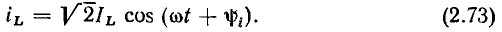
Связь между мгновенными значениями тока и напряжения индуктивности определяется выражением (1.22). Подставляя (2.73) в (1.22), получаем

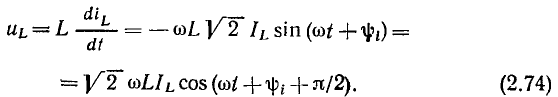
Как видно из (2.74), напряжение индуктивности, находящейся под гармоническим воздействием, является гармонической функцией времени, имеющей ту же частоту, что и воздействующий ток (рис. 2.15, а):

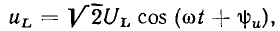
причем начальная фаза напряжения на 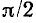больше начальной фазы тока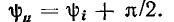

Действующее значение напряжения на индуктивности пропорционально действующему значению тока

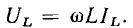
Также, как и мгновенная мощность емкости, мгновенная мощность индуктивности 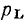при гармоническом воздействии изменяется по гармоническому закону с частотой, равной (рис. 2.15, б):

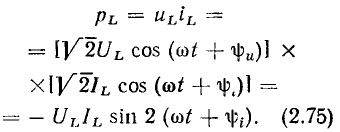
В связи с тем что в индуктивности отсутствует преобразование электрической энергии в другие виды энергии, активная мощность индуктивности равна нулю:

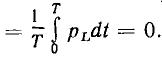
Энергия 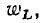запасенная в магнитном поле индуктивности, определяется мгновенным значением тока индуктивности:

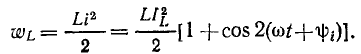
Так же, как и мгновенная энергия емкости, мгновенная энергия индуктивности содержит постоянную и переменную составляющие, причем переменная составляющая изменяется во времени по гармоническому закону с частотой 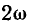(рис. 2.15, в).

Вследствие того что емкость и индуктивность являются дуальными элементами, процессы, имеющие место в этих элементах при гармоническом воздействии, описываются подобными по структуре аналитическими выражениями, а временное диаграммы для индуктивности подобны временным диаграммам для емкости и могут быть получены из последних путем замены напряжения на ток, а емкости на индуктивность.

Комплексный ток 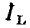 и комплексное напряжение 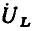индуктивности определяются выражениями

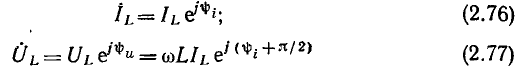
и изображаются на комплексной плоскости в виде пары векторов, длины которых в определенном масштабе равны действующим значениям напряжения и тока индуктивности, причем вектор 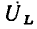повернут относительно вектора  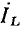на угол 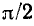против часовой стрелки (рис. 2.16, а).

Используя выражения (2.76), (2.77), находим комплексное сопротивление 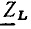 и комплексную проводимость 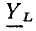индуктивности:

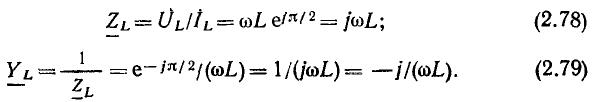
Сравнивая (2.78) и (2.79) с показательной и алгебраической формами записи комплексных сопротивления и проводимости:

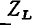
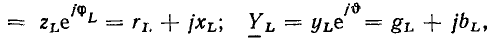
получаем вещественную и мнимую части, модули и аргументы комплексного сопротивления и комплексной проводимости индуктивности: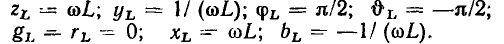

На комплексной плоскости 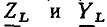изображаются векторами, ориентированными соответственно вдоль положительного или отрицательного направления мнимой оси (рис. 2.16, б, в). Комплексная схема замещения ведена на рис. 2.17.

Таким образом, комплексные сопротивления и проводимости идеализированных пассивных элементов линейных цепей не зависят от амплитуды (действующего значения) и начальной фазы внешнего воздействия и определяются только параметрами соответствующих элементов и частотой внешнего воздействия.

Анализ простейших линейных цепей при гармоническом воздействии

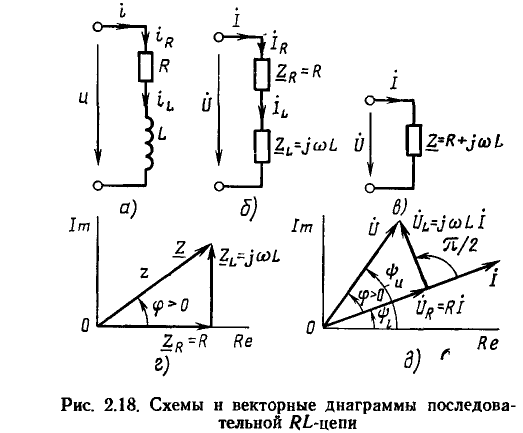
Последовательная RL-цепь:

Рассмотрим идеализированную электрическую цепь, состоящую из последовательно включенных сопротивления R и индуктивности L (рис. 2.18, а). Пусть напряжение u, приложенное к внешним зажимам цепи, изменяется по гармоническому закону

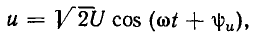
где

— заданные величины. Используя метод комплексных амплитуд, найдем установившееся значение тока i в цепи.

Искомый ток i является гармонической функцией времени той же частоты, что и приложенное напряжение:

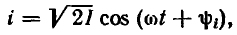
где 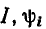— неизвестные действующее значение и начальная фаза тока i.

Представляя сопротивление и емкость комплексными схемами замещения и переходя от тока i и напряжения u к их комплексным изображениям

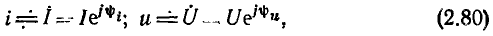
получаем комплексную схему замещения цепи (рис. 2.18, б). Далее, используя законы Ома и Кирхгофа в комплексной форме, составляем систему уравнений электрического равновесия цепи

Здесь 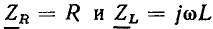— комплексные сопротивления входящих в рассматриваемую цепь идеализированных элементов. Величины R, L и 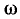заданы.

Подставляя (2.82)—(2.84) в уравнение (2.81), находим соотношение, связывающее комплексные изображения искомого тока и заданного напряжения:

Выражение (2.85) представляет собой математическую запись закона Ома в комплексной форме для рассматриваемого участка цепи, причем 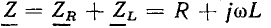есть комплексное входное сопротивление этого участка цепи. Выражению (2.85) можно поставить в соответствие комплексную схему замещения цепи (рис. 2.18, в). Таким образом, комплексное входное сопротивление цепи, состоящей из последовательно включенных сопротивления R и индуктивности L, равно сумме комплексных сопротивлений этих элементов. В дальнейшем убедимся, что аналогично можно найти комплексное сопротивление любого участка цепи, представляющего собой последовательное соединение произвольного количества идеализированных двухполюсных элементов.

Комплексное входное сопротивление рассматриваемой цепи может быть изображено на комплексной плоскости в виде вектора Z, равного геометрической сумме векторов 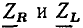(рис. 2.18, г). Длина этого вектора равна, в выбранном масштабе, модулю комплексного входного сопротивления рассматриваемой цепи

а угол наклона к положительной вещественной полуоси — его аргументу

Отметим, что при конечных значениях 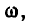L и R угол 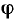лежит в пределах

 Когда аргумент комплексного входного сопротивления 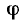какого-либо двухполюсника равен нулю, то говорят, что его входные сопротивление и проводимость имеют чисто резистивный (вещест­венный) характер, когда 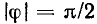— чисто реактивный (мнимый) характер. Если аргумент комплексного входного сопротивления двухполюсника равен 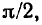то его входные сопротивление и проводимость имеют индуктивный характер, если — емкостной. В рассматриваемом случае значение аргумента ф определяется соотношением (2.88), поэтому входное сопротивление цепи имеет резистивно-индуктивный характер.

Используя (2.85), найдем комплексное действующее значение искомого тока

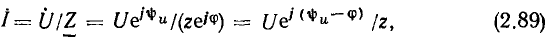
где z и 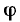определяются соотношениями (2.86) и (2.87). Из выражений (2.89) и (2.80) можно определить действующее значение и начальную фазу тока:

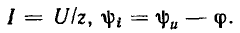
Переходя от комплексного изображения тока к оригиналу, окончательно получаем

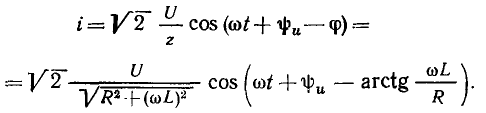
В связи с тем что при заданной частоте внешнего воздействия <в установившиеся значения токов и напряжений цепи полностью определяются их действующими значениями и начальными фазами, на практике обычно не возникает необходимости находить оригиналы токов и напряжений. Задача анализа цепи считается решенной, если найдены комплексные действующие значения соответствующих функций.

Векторные диаграммы для тока и напряжений RL-цепи приведены на рис. 2.18, д. Так как напряжение на сопротивлении совпадает по фазе с током, вектор 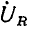совпадает по направлению с вектором 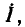вектор 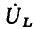повернут относительно вектора  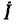на угол 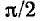против часовой стрелки (напряжение на индуктивности по фазе опережает ток). Независимо от начальной фазы напряжения  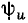вектор 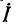повернут относительно вектора 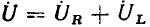по часовой стрелке на угол  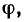 т. е. ток отстает по фазе от напряжения на угол 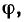равный аргументу комплексного входного сопротивления цепи. Отметим также, что так называемый треугольник напряжений, образованный векторами 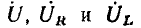(рис. 2.18. д), подобен треугольнику сопротивлений (рис. 2.18, г), образованному векторам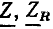и и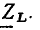

Из векторной диаграммы видно, что действующие значения напряжения на входе цепи U, напряжения на сопротивлении 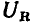и напряжения на индуктивности 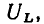которые определяют длину сторон треугольника напряжений, связаны соотношением

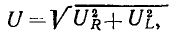
т. е. действующее значение напряжения на входе цепи не равно алгебраической сумме действующих значений напряжений на элементах цепи.

Пример 2.3.

Найдем комплексное входное сопротивление и ток последовательной RL-цепи (рис. 2.18, а), к зажимам которой приложено напряжение u = 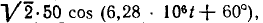В и определим напряжения на элементах цепи R = 5 кОм, L = 1 мГн).

Комплексное входное сопротивление цепи 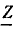равно сумме комплексных сопротивлений входящих в нее элементов:

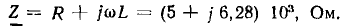
Переходя от алгебраической формы записи к показательной

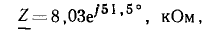
определяем модуль комплексного входного сопротивления z = 8,03 кОм и его аргумент 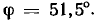 Находим комплексный ток цепи

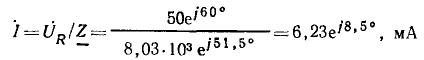
 и комплексные напряжения на сопротивлении и индуктивности

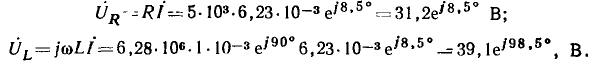
Мгновенные значения соответствующих величин

Последовательная RС-цепь

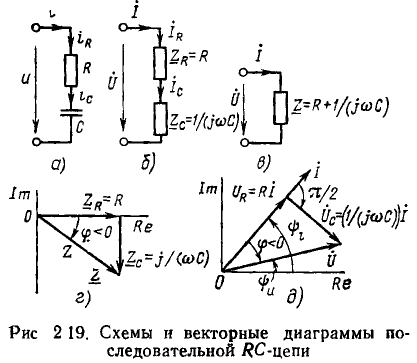
Рассмотрим последовательную RС-цепь (рис. 2.19, а), к зажимам которой приложено напряжение u, изменяющееся по гармоническому закону. Найдем комплексный ток цепи и ее комплексное входное сопротивление.

Переходя к комплексной схеме замещения цепи (рис. 2.19, б) и используя законы Ома и Кирхгофа в комплексной форме, составляем систему уравнений электрического равновесия цепи: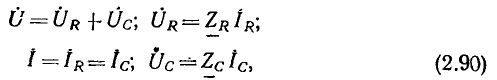

где 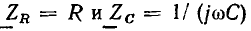— комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему уравнений (2.90) относительно комплексного действующего значения искомого тока, получаем

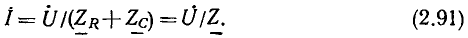
Здесь 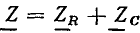— комплексное входное сопротивление рассматриваемой которое равно сумме комплексных сопротивлений последовательно включенных идеализированных элементов. Комплексная схема замещения цепи, соответствующая уравнению (2.91), приведена на рис. 2.19, в. Выразим комплексное сопротивление цепи 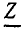через параметры входящих в цепь элементов:

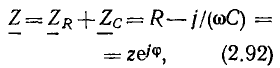
где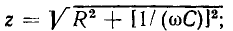 

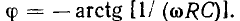
Как видно из выражения (2.92), при конечных значениях 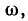R и С угол 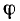лежит в пределах 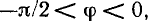т. е. входное сопротивление цепи имеет резистивно-емкостной характер. Векторная диаграмма для комплексного входного сопротивления цепи приведена на рис. 2.19, г.

Подставляя (2.92) в (2.91), окончательно получаем

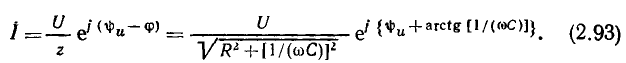
Из выражения (2.93) видно, что ток i опережает приложенное напряжение u по фазе на угол 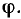Совмещенная векторная диаграмма для тока и напряжений RС-цепи приведена на рис. 2.19, д.

Последовательная RLС-цепь

Рассмотрим последовательную RLС-цепь (рис. 2.20, а), находящуюся под гармоническим воздействием, комплексная схема замещения которой приведена на рис. 2.20, б. Используя законы Ома и Кирхгофа в комплексной форме, составим систему уравнений электрического равновесия цепи

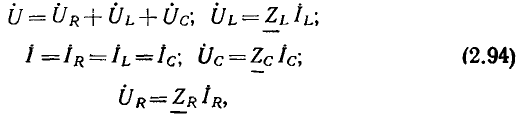
где 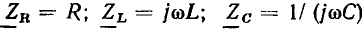— комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (2.94) относительно тока 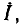получаем

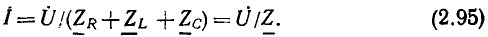
Здесь 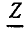— комплексное входное сопротивление последовательной RLC-цепи, равное сумме комплексных сопротивлений входящих в

цепь элементов, которое определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:

Переходя от алгебраической формы записи 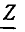к показательной, находим модуль и аргумент комплексного входного сопротивления:

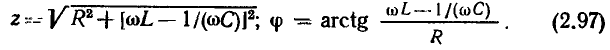
Из выражений (2.97) следует, что характер входного сопротивления цепи зависит от соотношения между мнимыми составляющими комплексного входного сопротивления емкости 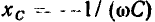 и индуктивности При входное сопротивление цепи имеет резистивно-индуктивный характер Векторная диаграмма, построенная на основании уравнения (2.96) и иллюстрирующая данный случай, представлена на рис. 2.20, г (для большей наглядности векторы изображены немного смещенными один относительно другого). Если то входное сопротивление цепи имеет резистивно-емкостной характер (рис. 2.20, д). При 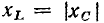мнимые составляющие входного сопротивления емкости хс и индуктивности хъ взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер ( 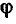= 0) (рис. 2.20, е).

Используя уравнение (2.95), можно по известному напряжению, приложенному к внешним зажимам цепи, найти ток и наоборот. Векторные диаграммы для тока и напряжений цепи, соответствующие различным соотношениям между мнимыми составляющими комплексного сопротивления емкости 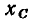и индуктивности 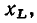приведены на рис. 2.21. 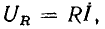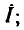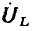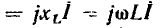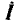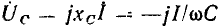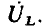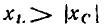Вектор изображающий падение напряжения на сопротивлении, совпадает по направлению с вектором вектор повернут относительно  на 90° против часовой стрелки; вектор направлен противоположно вектору При (рис. 2.21, а) вектор 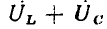совпадает по направлению с вектором 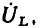ток цепи отстает по фазе от напряжения При (рис. 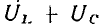2.21, б) вектор совпадает по направлению с вектором 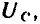ток цепи опережает по фазе напряжение  Если 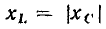 (рис. 2.21,в), то вектор  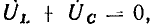напряжение на зажимах цепи 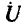равно напряжению на сопротивлении 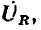ток цепи совпадает по фазе с приложенным напряжением 

Пример 2.4.

Определим комплексное входное сопротивление и комплексный ток последовательной RLC-цепи (см. рис. 2.20, а) с параметрами L=80мкГн, С = 500 пФ, R = 100 Ом, к зажимам которой приложено напряжение 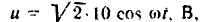для частот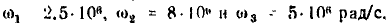

Комплексное входное сопротивление цепи (2 96) ровно сумме комплексных сопротивлений входящих в нее элементов Подставляя в (2.96) параметры элементов цепи, находим комплексное сопротивление цепи при интересующих значениях частоты внешнего воздействия:

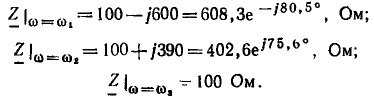
Таким образом, при входное сопротивление цепи имеет резистивноемкостной характер: при 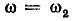— резистивно-индуктивный: при 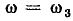— чисто резистивный.

Используя закон Ома в комплексной форме (2.95), находим комплексный ток цепи:

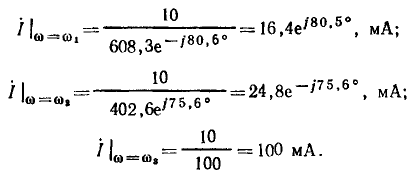
Как и следовало ожидать, согласно характеру комплексного входного сопротивления цепи, при 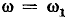— ток опережает напряжение по фазе на угол 80,5°: при 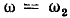— ток отстает по фазе от напряжения на угол 75,6°: при 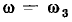напряжение и ток совпадают по фазе.

Параллельная RLC-цепь

Рассмотрим параллельную RLС-цепь (рис. 2.22, а), к зажимам которой приложено напряжение, изменяющееся по гармоническому закону. Комплексная схема замещения цепи, в которой идеализированные двухполюсные элементы представлены их комплексными проводимостями, изображена на рис. 2.22, б.

Используя законы Ома и Кирхгофа в комплексной форме, составим систему уравнений электрического равновесия цепи:

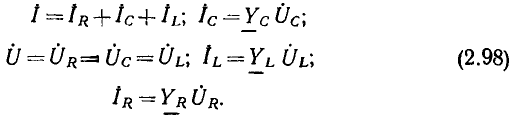
Здесь 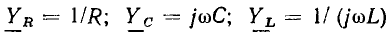— комплексные проводимости входящих в цепь идеализированных пассивных элементов. Решая систему уравнений (2.98) относительно тока 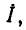получаем

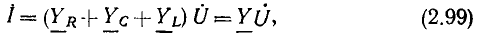
где  — комплексная проводимость параллельной RLС-цепи, равная сумме комплексных проводимостей входящих в Цепь идеализированных элементов. Далее будет показано, что комплексная проводимость любого участка цепи, состоящего из произвольного числа параллельно включенных ветвей, равна сумме комплексных проводимостей этих ветвей. Комплексная проводимость параллельной RLС-цепи, как и комплексная проводимость любой линейной цепи, не зависит от амплитуды (действующего значения) и начальной

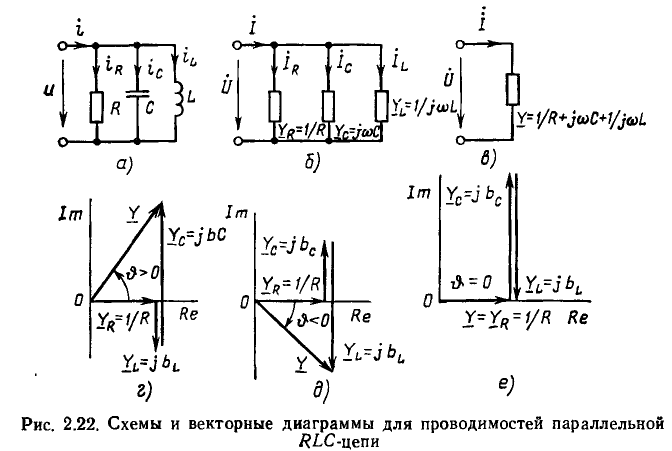
фазы внешнего воздействия, а определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:

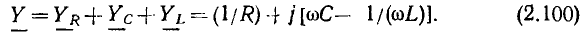
Переходя от алгебраической формы записи к показательной (2.51), найдем модуль у и аргумент 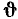 комплексной входной проводимости RLC-цепи:

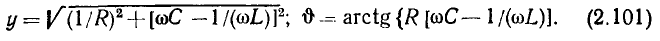
Анализ выражений (2.101) показывает, что характер входной проводимости, а следовательно, и характер входного сопротивления параллельной RLС-цепи зависят от соотношения между реактивными составляющими входной проводимости емкости и индуктивности 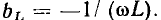 Когда 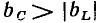 (рис. 2.22, г), входная проводимость цепи имеет резистивно-емкостной характер (аргумент комплексной проводимости 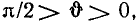поэтому аргумент комплексного входного сопротивления 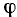лежит в пределах  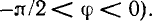При (рис. 2.22, д) входная проводимость цепи имеет резистивно-индуктивный характер, а при 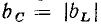(рис. 2.22, е) реактивные составляющие входной проводимости емкости 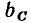и индуктивности 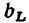взаимно компенсируются и входная проводимость цепи имеет чисто резистивный (вещественный) характер.

Уравнение (2.99) представляет собой математическую запись закона Ома в комплексной форме для параллельной RLС-цепи. Комплексная схема замещения цепи, соответствующая этому выражению, приведена на рис. 2.22, в. Используя уравнение (2.99), можно по заданному напряжению определить ток, текущий через внешние зажимы цепи, и, наоборот, по заданному току определить приложенное к цепи напряжение. Векторные диаграммы для токов и напряжения параллельной RLС-цепи приведены на рис. 2.23.

Уравнения (2.98), описывающие процессы в параллельной RLС-цепи, подобны по структуре уравнениям электрического равновесия ранее рассмотренной последовательной RLC-цепи (2.94) и могут быть получены из одного другое путем замены тока на напряжение, проводимости на сопротивление, емкости на индуктивность. Следовательно, параллельная и последовательная RLС-цепи являются дуальными. Векторные диаграммы дуальных цепей также могут быть получены из одних другие путем упомянутых замен.

Энергетические процессы в простейших цепях при гармоническом воздействии

Мгновенная мощность пассивного двухполюсника:

Рассмотрим произвольный линейный двухполюсник, не содержащий источников энергии. Напряжение и ток на зажимах двухполюсника изменяются по гармоническому закону: 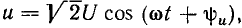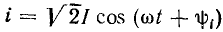(рис. 2.24, а). Найдем мгновенную мощность двухполюсника

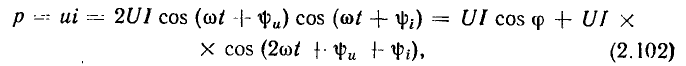
где 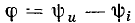— сдвиг фаз между напряжением и током.

Как видно из выражения (2.102), мгновенная мощность пассивного двухполюсника содержит постоянную составляющую 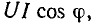значение которой зависит от сдвига фаз между током и напряжением, и переменную составляющую 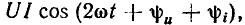амплитуда которой UI не зависит от Среднее значение мгновенной мощности двухполюсника за период (активная мощность) численно равно постоянной составляющей мгновенной мощности

Анализ выражения (2.102) показывает, что особенности энергетических процессов в рассматриваемом двухполюснике полностью определяются характером его входного сопротивления.

Когда входное сопротивление двухполюсника имеет чисто резистивный характер постоянная составляющая мгновенной мощности численно равна амплитуде переменной составляющей; мгновенная мощность изменяется от до 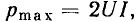принимая только неотрицательные значения. Относительно внешних зажимов двухполюсник ведет себя подобно идеализированному пассивному элементу сопротивлению. В каждый момент времени двухполюсник только потребляет электрическую энергию от источника, необратимо преобразуя ее в другие виды энергии; обмен энергией между двухполюсником и источником энергии отсутствует. Если внутри рассматриваемого двухполюсника имеются энергоемкие элементы (емкости и индуктивности), то они могут обмениваться энергией только между собой, обмена же энергией между этими элементами и источником в установившемся режиме не происходит (более подробно это будет рассмотрено в гл. 3). Нетрудно убедиться, что при 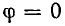уравнение (2.102) вырождается в уравнение (2.64), поэтому временные диаграммы рассматриваемого двухполюсника полностью совпадают с временными диаграммами для сопротивления (см. рис. 2.9).

Если входное сопротивление двухполюсника имеет чисто реактивный характер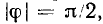 то постоянная составляющая мгновенной мощности равна нулю 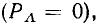мгновенная мощность изменяется по гармоническому закону с частотой, вдвое превышающей частоту внешнего воздействия. В данном случае двухполюсник ведет себя подобно емкости или индуктивности, в течение одной половины периода изменения мощности запасая энергию от источника, в течение второй половины периода полностью отдавая ее источнику. При 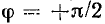уравнение (2.102) может быть преобразовано к виду (2.75), а временное диаграммы совпадут с временными диаграммами для индуктивности (см. рис. 2.15). Если 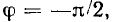уравнение (2.102) совпадает с (2.68), а временное диаграммы цепи имеют такой же вид, как и временное диаграммы для емкости (см. рис. 2.12).

Когда входное сопротивление двухполюсника имеет резистивноемкостной или резистивно-индуктивный характер 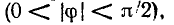постоянная составляющая мгновенной мощности меньше амплитуды переменной составляющей, а мгновенная мощность двухполюсника изменяется от 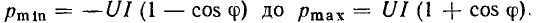В течение большей части периода мгновенная мощность положительна, в остальной части периода — отрицательна (рис. 2.24, б). В двухполюснике имеет место как процесс запасания энергии, так и процесс необратимого преобразования ее в другие виды энергии, так как площадь, ограниченная участком кривой р (t) с положительными ординатами (численно равная энергии, потребляемой двухполюсником от источника), больше площади, ограниченной участком кривой р (t) с отрицательными ординатами (соответствующей энергии, возвращаемой цепью источнику). Характер энергетических процессов в цепи одинаков как при  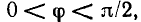так и при (временные диаграммы, приведенные на рис. 2.24, соответствуют

Ни при каких значениях 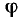 энергия, отдаваемая пассивным двухполюсником во внешнюю по отношению к нему цепь, не может превышать энергию, потребляемую этим двухполюсником от внешней цепи.

Активная, реактивная, полная и комплексная мощности

Активная мощность, которая была определена как среднее значение мгновенной мощности за период, характеризует среднюю за период скорость поступления энергии в двухполюсник и численно равна постоянной составляющей мгновенной мощности (2.103). По знаку активной мощности можно судить о направлении передачи энергии: при 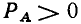двухполюсник потребляет энергию, при 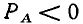— отдает энергию остальной части цепи. Очевидно, что для двухполюсников, не содержащих источников энергии, активная мощность не может быть отрицательной.

Полной мощностью 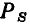называется величина, равная произведению действующих значений тока и напряжения на зажимах цепи:

Полная мощность численно равна амплитуде переменной составляющей мгновенной мощности. Активная мощность двухполюсника может быть выражена через полную мощность:

Из выражения (2.105) видно, что полная мощность есть максимально возможное значение активной мощности цепи, которое имеет место при

Комплексное число 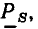модуль которого равен полной мощности цепи 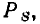а аргумент — углу сдвига фаз между током и напряжением 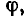называется комплексной мощностью цепи

Переходя от показательной формы записи 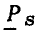к тригонометрической

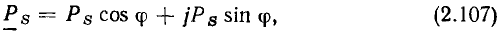
устанавливаем, что вещественная часть комплексной мощности равна активной мощности цепи:

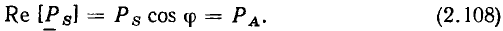
Мнимая часть комплексной мощности представляет собой так называемую реактивную мощность цепи

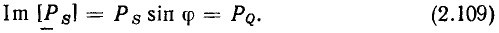
Реактивная мощность характеризует процессы обмена энергией между цепью и источником и численно равна максимальной скорости запасания энергии в цепи. В зависимости от знака угла 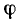реактивная мощность цепи может быть либо положительной, либо отрицательной. По знаку реактивной мощности, таким образом, можно судить о характере запасаемой энергии: при 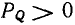энергия запасается в магнитном поле цепи, при — в электрическом. При в цепи отсутствует обмен энергией с источником.

С учетом (2.108) и (2.109) выражение (2.107) можно записать следующим образом: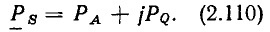

Отсюда следует, что комплексная мощность представляет собой комплексное число, вещественная часть которого равна активной мощности цепи 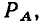а мнимая — реактивной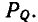

Комплексному числу 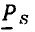можно поставить в соответствие вектор 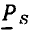, проекции которого на вещественную и мнимую оси равны, соответственно 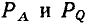(рис. 2.25, а). Прямоугольный треугольник с гипотенузой, равной 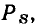и катетами 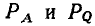называется треугольником мощностей. Из рисунка видно, что полная, активная и реактивная мощности связаны между собой соотношением

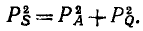
В связи с тем что треугольник мощностей цепи подобен треугольнику сопротивлений этой же цепи (рис. 2.25, б), комплексная мощность 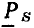и ее компоненты 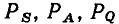могут быть выражены через комплексное сопротивление цепи 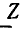и его компоненты z, r, х:

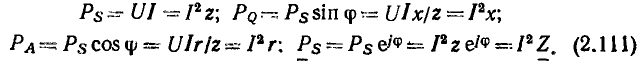
Найдем связь между комплексной мощностью и комплексными действующими значениями тока и напряжения на зажимах цепи. Подставляя в (2.106) выражения (2.104) и (2.48), находим

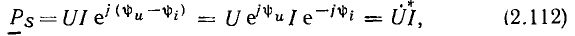
где 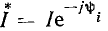— число, комплексно сопряженное с 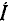(комплексно сопряженный ток).

Таким образом, комплексная мощность цепи равна произведению комплексного напряжения цепи 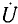на комплексно сопряженный  ток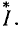

Активная, реактивная, полная и комплексная мощности имеют одинаковую размерность [Дж/с]. Однако для того, чтобы подчеркнуть различный физический смысл, который вкладывается в эти понятия, единицам данных величин присвоены различные названия. Активная мощность, так же как и мгновенная мощность, выражается в ваттах [Вт], полная и комплексная мощности — в вольт-амперах [В • А], реактивная мощность — в вольт-амперах реактивных [вар].

 Пример 2.5.

Напряжение и ток на зажимах произвольного двухполюсника изменяются по гармоническому закону:

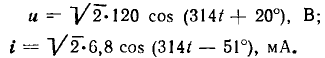
Определим полную, активную, реактивную и комплексную мощности двухполюсника.

Комплексный ток комплексное напряжение и угол сдвига фаз между током и напряжением на зажимах рассматриваемого двухполюсника:

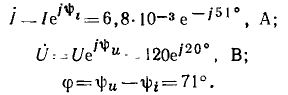
Подставляя эти величины в (2.104), (2.105), (2.109) и (2.112), находим искомые мощности:

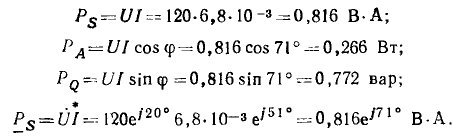
В связи с тем что входное сопротивление цепи имеет резистивно-индуктивный характер реактивная мощность цепи положительна.

Баланс мощностей

Рассмотрим произвольную электрическую цепь, содержащую N идеальных источников напряжения, М идеальных источников тока и H идеализированных пассивных элементов. Пусть 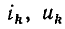— ток и

напряжение k-гo элемента цепи. Из закона сохранения энергии следует, что сумма мгновенных мощностей всех элементов цепи в каждый момент времени равна нулю:

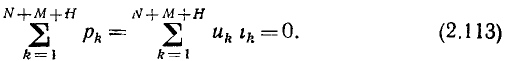
Группируя члены, соответствующие идеализированным активным 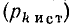и идеализированным пассивным 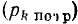элементам, уравнение (2.113) можно преобразовать к виду

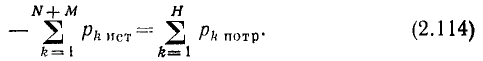
Уравнение (2.114) называют уравнением (условием) баланса мгновенных мощностей. Принимая во внимание, что мгновенная мощность любого элемента характеризует скорость потребления энергии этим элементом (потребляемая мощность), а мгновенная мощность, взятая со знаком минус, характеризует скорость отдачи энергии этим элементом (отдаваемая мощность), условие баланса мгновенных мощностей может быть сформулировано следующим образом: сумма мгновенных мощностей, отдаваемых всеми источниками, равна сумме мгновенных мощностей, потребляемых всеми приемниками энергии (необходимо иметь в виду, что потребляется и отдается не мощность, а электрическая энергия).

Можно показать, что условие, аналогичное (2.114), выполняется и для комплексных мощностей всех элементов:

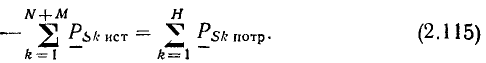
Уравнение (2.115) называется уравнением (условием) баланса комплексных мощностей. Таким образом, сумма комплексных мощностей, отдаваемых всеми идеализированными активными элементами, равна сумме комплексных мощностей всех идеализированных пассивных элементов.

Для практических расчетов электрических цепей условие баланса мощностей удобно представить в следующей форме:

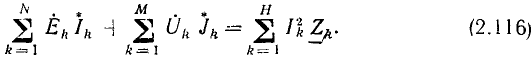
Левая часть выражения (2.116) представляет собой алгебраическую сумму комплексных мощностей, отдаваемых всеми активными элементами. Слагаемое вида 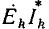есть произведение комплексного действующего значения э.д. с. источника напряжения на комплексно сопряженный ток этого источника; слагаемое вида 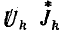равно произведению комплексного напряжения на источнике тока на комлексно сопряженный ток этого источника. Слагаемые, состоящие в левой части выражения выражения (2.116), берут со знаком плюс, если напряжения источников выбраны в соответствии с рис. 2.26. В противном случае соответствующие слагаемые берут со знаком минус. Правая часть уравнения (2.116) есть сумма комплексных мощностей всех идеализированных пассивных элементов, причем каждое слагаемое вида 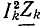равно произведению квадрата действующего значения тока k-го идеализированного пассивного элемента на его комплексное сопротивление.

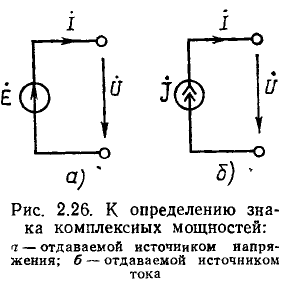
Из условия баланса комплексных мощностей следуют условия баланса активных и реактивных мощностей: активная мощность, отдаваемая всеми источниками, равна активной мощности всех потребителей:

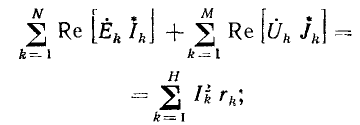
реактивная мощность всех источников равна реактивной мощности всех потребителей:

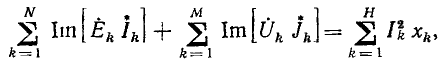
где 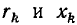— вещественная и мнимая составляющие комплексного сопротивления k-гo элемента.

Пример 2.6.

Определим комплексный ток последовательной RL-цепи (см. рис. 2.18, а) с параметрами элементов R = 8 кОм, L = 4 мГн, к зажимам которой подключен источник э.д.с. 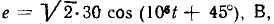 и проверим выполнение условия баланса мощностей.

Находим комплексное входное сопротивление цепи

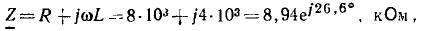
и, используя закон Ома в комплексной форме, находим комплексный ток цепи

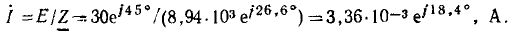
Комплексная мощность, отдаваемая источником напряжения:

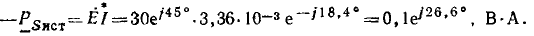
равна комплексной мощности, потребляемой сопротивлением и индуктивностью:

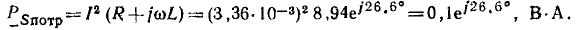
Таким образом, условие баланса комплексных мощностей выполняется.

Коэффициент мощности

При проектировании электроэнергетических систем важное народнохозяйственное значение имеет обеспечение передачи максимальной активной мощности в нагрузку при заданных действующих значениях токов и напряжений. Из выражения (2.103) видно, что повышение 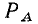при неизменных действующих значениях токов и напряжений может быть достигнуто путем увеличения 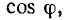т. е. путем уменьшения угла сдвига фаз между током и напряжением. Максимально возможное значение 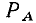равно полной мощности 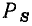и достигается при 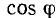= 1. При уменьшении 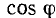для получения заданной активной мощности в нагрузке требуется увеличивать действующие значения токов и напряжений, что ведет к росту потерь энергии в системе и требует увеличения мощности источников энергии.

Величина, характеризующая степень приближения активной мощности нагрузки к максимальному значению 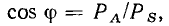называется коэффициентом мощности.

Очевидно, что наивысшее значение коэффициент мощности (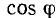= — 1) имеет при чисто резистивном характере нагрузки. Если нагрузка имеет резистивно-емкостной или резистивно-индуктивный характер 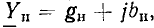то параллельно ей подключают компенсирующий элемент, проводимость которого выбирают равной по абсолютному значению и противоположной по знаку мнимой составляющей проводимости нагрузки:

Комплексное входное сопротивление Z участка цепи, представляющего собой параллельное соединение нагрузки и компенсирующего элемента, будет иметь чисто резистивный характер 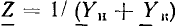= 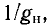что обеспечит максимально возможное значение коэффициента мощности.

Комплексное сопротивление большинства реальных приемников энергии (электродвигателей, электронагревательных элементов, осветительных приборов) имеет резистивно-индуктивный характер: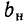

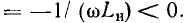
Для компенсации мнимой составляющей проводимости нагрузки параллельно ей должны подключаться компенсирующие конденсаторы, емкость которых рассчитывают в соответствии с условием (2.117):

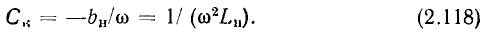
Пример 2.7.

В качестве нагрузки некоторого электротехнического устройства используется двухполюсник, рассмотренный в примере 2.5. Определим тип компенсирующего элемента и рассчитаем его основной параметр (емкость 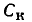или индуктивность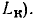

Комплексная проводимость нагрузки

в данном случае имеет резистивно-индуктивный характер следовательно, в качестве компенсирующего элемента необходимо использовать конденсатор. Емкость компенсирующего конденсатора может быть рассчитана по формуле (2.118):

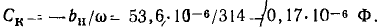
Согласование источника энергии с нагрузкой

Рассмотрим электрическую цепь, состоящую из источника энергии и нагрузки. Пусть источник энергии представлен последовательной схемой замещения (рис. 2.27), причем его внутреннее сопротивление имеет комплексный характер: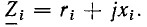

Задача согласования источника энергии с нагрузкой заключается в выборе такого сопротивления нагрузки 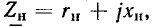при котором в цепи будут выполняться условия, называемые критериями согласования. Рассмотрим согласование источника с нагрузкой по критерию наибольшей активной мощности, передаваемой в нагрузку, и по критерию наибольшего к. п. д.

Активная мощность нагрузки в соответствии с (2.111)

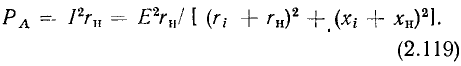
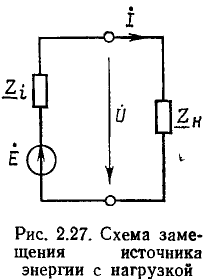
Как видно из (2.119), является функцией двух переменных В связи с тем что вещественная и мнимая 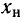составляющие сопротивления нагрузки не зависят одна от другой, выбор значения каждой из этих величин, соответствующего максимуму 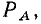можно производить в отдельности.

Величина 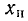входит только в знаменатель выражения (2.119). Очевидно, что максимальное значение активной мощности по этой переменной 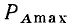будет достигнуто, если

При этом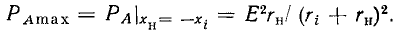

Для определения значения 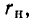соответствующего наибольшему возможному значению (максимум максиморум) активной мощности нагрузки 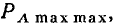продифференцируем 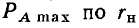и приравняем нулю полученное выражение:

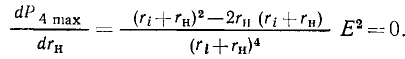
Иначе

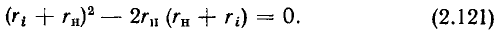
Решая уравнение (2.121), находим значение вещественной составляющей сопротивления нагрузки

при котором активная мощность достигает наибольшего возможного значения (рис. 2.28, а):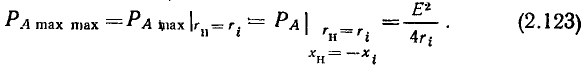

Объединяя условия (2.120) и (2.122), находим, что наибольшее возможное значение активной мощности нагрузки 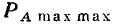соответствует 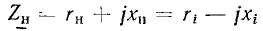или 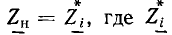— величина, сопряженная с комплексным внутренним сопротивлением источника.

Таким образом, для согласования источника энергии с нагрузкой по критерию наибольшей активной мощности, передаваемой в нагрузку, сопротивление нагрузки должно быть величиной, комплексно сопряженной с внутренним сопротивлением источника. В частном случае, если

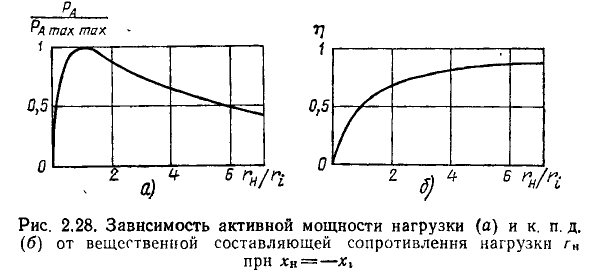
внутреннее сопротивление источника имеет чисто резистивный характер 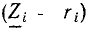, то сопротивление нагрузки должно выбираться равным внутреннему сопротивлению источника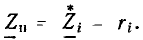

Коэффициент полезного действия цепи (см. рис. 2.27) равен отношению активной мощности, потребляемой нагрузкой к суммарной активной мощности, потребляемой в цепи: )

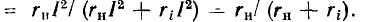
Зависимость к. п. д. от резистивной составляющей сопротивления нагрузки показана на рис. 2.28, б. Из рисунка видно, что к. п. д. цепи монотонно возрастает с ростом 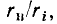приближаясь к  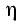=  1 при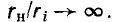

Таким образом, для согласования источника с нагрузкой по критерию максимума к. п. д. необходимо, чтобы резистивная составляющая сопротивления нагрузки была намного больше резистивной составляющей внутреннего сопротивления источника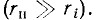

Рассмотренные критерии согласования источника энергии с нагрузкой являются несовместимыми, т. е. не могут выполняться одновременно. В частности, при согласовании источника с нагрузкой по критерию максимальной активной мощности, передаваемой в нагрузку, к. п. д. цепи будет равен 0,5. Очевидно, что мощные электроэнергетические системы не могут работать с к. п. д., при котором половина выработанной энергии теряется на внутреннем сопротивлении источника, поэтому обычно стремятся -к достижению максимально возможного значения к. п. д., выбирая 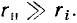Согласование по критерию максимальной активной мощности, передаваемой в нагрузку, широко используется в маломощных радиоэлектронных устройствах, когда независимо от потерь необходимо добиться выделения максимальной мощности сигнала в нагрузке.

Следует отметить, что приведенные рассуждения справедливы только для источников с конечным внутренним сопротивлением. Для источников с = 0 или = 0 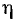 = 1 при любом конечном значении резистивной составляющей сопротивления нагрузки, а выделяемая в нагрузке мощность неограниченно возрастает с уменьшением [при питании от источника напряжения (1.26)] или с увеличением [при питании от источника тока (1.27)]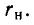 

Преобразования электрических цепей

Понятие об эквивалентных преобразованиях:

Анализ процессов в электрических цепях во многих случаях может быть существенно упрощен за счет использования различных преобразований, в результате которых отдельные участки идеализированных цепей заменяются участками с более простой топологией или участками, более удобными для анализа.

Два участка идеализированной электрической цепи называются эквивалентными, если при замене одного из этих участков другим токи и напряжения остальной части цепи не изменяются. Преобразования электрических цепей, в результате которых некоторые участки электрической цепи заменяются эквивалентными им участками, называются эквивалентными. Из определения эквивалентных участков следует, что они должны иметь одинаковое количество внешних выводов, причем в процессе эквивалентных преобразований токи этих выводов и напряжения между ними должны оста ваться неизменными.

Эквивалентные участки электрических цепей обладают свойствами симметричности (если цепь А эквивалентна цепи Б, то цепь Б эквивалентна цепи А), рефлексивности (цепь А является эквивалентной самой себе) и транзистивности (если цепь А эквивалентна цепи Б, а цепь Б эквивалентна цепи В, то цепи А и В являются эквивалентными). Если эквивалентность двух участков электрической цепи выполняется при любых значениях внешних воздействий, то такие участки являются полностью эквивалентными. Различия между ними не могут быть установлены с помощью каких-либо измерений, проводимых на внешних выводах. Если эквивалентность двух участков выполняется только при определенном значении внешних воздействий, то такие участки являются частично эквивалентными (эквивалентными при заданных условиях). Так, два участка линейной электрической цепи, находящейся под гармоническим воздействием, могут быть либо полностью эквивалентными, либо частично при заданной частоте внешнего воздействия.

Эквивалентные преобразования электрических цепей основаны на эквивалентных (равносильных) преобразованиях соответствующих систем уравнений электрического равновесия. Каждое равносильное преобразование системы уравнений электрического равновесия исходной цепи (приведение подобных членов, исключение неизвестных, замена переменных и т. д.) приводит к эквивалентному преобразованию моделирующей цепи. Соответственно изменяется и условное графическое изображение моделирующей цепи — схема цепи. На практике преобразования электрических цепей проводят без составления систем уравнений электрического равновесия, путем непосредственного преобразования схем по определенным правилам. Систему уравнений электрического равновесия цепи составляют для уже преобразованной цепи, схема которой имеет достаточно простой вид.

Рассмотрим правила преобразования цепей с последовательным и параллельным соединением элементов.

Участки цепей с последовательным соединением элементов

Рассмотрим неразветвленную электрическую цепь (рис. 2.29, а), содержащую N сопротивлений, М емкостей, К индуктивностей и v Неуправляемых источников напряжения (обобщенная одноконтурная цепь).Так как через все элементы цепи протекает один и тот же ток i, то уравнение электрического равновесия, составленное на основе второго закона Кирхгофа и компонентных уравнений, может быть записано в следующей форме:

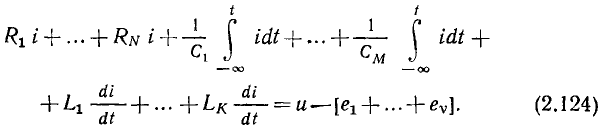
После приведения подобных членов (2.124) принимает вид

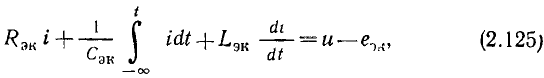
где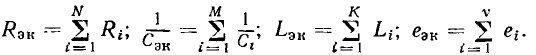

Уравнению (2.125) соответствует преобразованная цепь, схема которой изображена на рис. 2.29, б. Таким образом, ток и напряжение на зажимах обобщенной одноконтурной цепи не изменятся, если каждую из групп последовательно включенных однотипных элементов заменить одним эквивалентным элементом, параметр которого 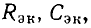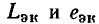рассчитывается в соответствии с (2.125).

Из выражения (2.125) следует, что при последовательном включении сопротивлений, индуктивностей и источников напряжения параметры эквивалентного элемента 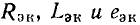равны сумме параметров последовательно включенных элементов соответствующего типа. При этом суммирование э. д. с. источников напряжения производится алгебраически, с учетом их знаков, которые определяются тем, совпадает или не совпадает направление э. д. с. с направлением обхода контура. Очевидно, что 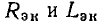будут превышать сопротивление и индуктивность любого из последовательно включенных элементов. При последовательном соединении N одинаковых сопротивлений R или индуктивностей L параметр эквивалентного элемента 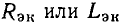будет в N раз больше, чем параметр каждого из последовательно включенных элементов.

При последовательном включении емкостей значение величины, обратной 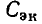, определяется как сумма обратных значений всех последовательно включенных емкостей, причем эквивалентная емкость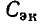

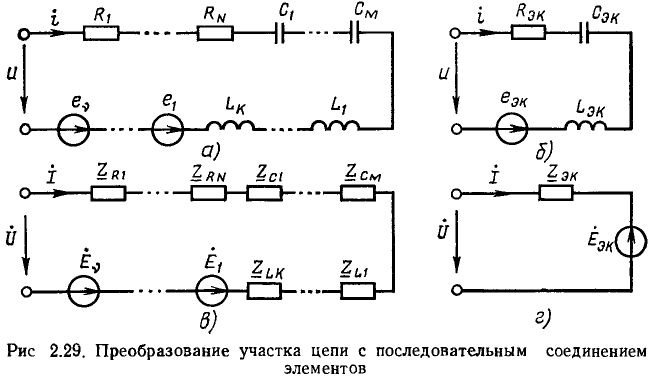
меньше, чем любая из последовательно включенных емкостей. При последовательном включении N одинаковых емкостей эквивалентная емкость 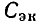в N раз меньше каждой из последовательно включенных емкостей.

Если обобщенная одноконтурная цепь находится под гармоническим воздействием, то от эквивалентной схемы для мгновенных значений (рис. 2.29, а) удобнее перейти к эквивалентной схеме для комплексных действующих значений (рис. 2.29, в). Уравнение электрического равновесия такой цепи, составленное на основании закона Ома и второго закона Кирхгофа в комплексной форме, имеет следующий вид:

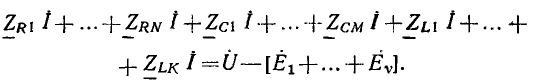
После преобразований получаем

где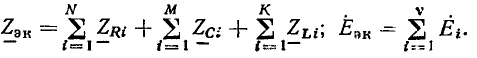  

Комплексная схема замещения цепи, соответствующая уравнению (2.126), приведена на рис. 2.29, г.

Таким образом, любой участок электрической цепи, представляющий собой последовательное соединение произвольного количества идеализированных неуправляемых источников напряжения и идеализированных пассивных двухполюсников, при гармоническом воздействии может быть заменен ветвью, содержащей один источник напряжения, э.д.с. которого равна алгебраической сумме э.д.с. всех последовательно включенных источников, и один пассивный двухполюсник, комплексное сопротивление которого равно сумме комплексных сопротивлений всех последовательно включенных пассивных двухполюсников.

Участки цепей с параллельным соединением элементов

Пусть электрическая цепь (рис. 2.30, а) состоит из параллельно соединенных N сопротивлений, М емкостей, К индуктивностей и v неуправляемых источников тока (обобщенная двухузловая цепь). Все элементы цепи находятся под одним и тем же напряжением u, поэтому уравнение электрического равновесия, составленное на основании первого закона Кирхгофа, может быть записано в форме

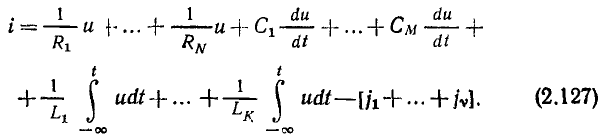
После приведения подобных членов получаем

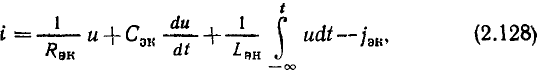
где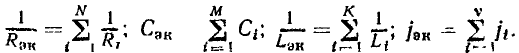

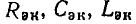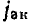Уравнению (2.128) соответствует преобразованная цепь, торой приведена на рис. 2.30, б Видно, что ток и напряжение на зажимах обобщенной двухузловой цепи не изменятся, если каждую из групп параллельно включенных однотипных элементов заменить одним эквивалентным элементом, параметры которою и рассчитываются в соответствии с (2.128).

Из выражения (2.128) следует, что при параллельном включении емкостей и источников тока параметры эквивалентного элемента 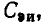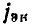равны сумме параметров параллельно включенных элементов соответствующего типа. При этом суммирование токов источников тока производится алгебраически с учетом их знаков, определяемых ориентацией источников относительно узла, для которого составляется уравнение (2.127). Очевидно, что 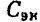превышает по значению любую из параллельно включенных емкостей 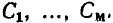При параллельном соединении N одинаковых емкостей  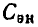= NC.

При параллельном включении сопротивлений или индуктивностей значения величин, обратных 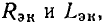будут определяться как сумма обратных значений этих сопротивлений или индуктивностей. Значения 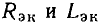будут меньше, чем сопротивление или индуктивность любого из параллельно включенных элементов соответствующего типа. При параллельном включении одинаковых сопротивлений R или индуктивностей L, 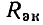= R/N, a 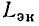= L/N.

Для рассмотрения параметров обобщенной двухузловой цепи при гармоническом воздействии воспользуемся комплексной схемой замещения этой цепи (рис. 2.30,в). Уравнение электрического равновесия цепи в комплексной форме может быть записано следующим образом:

где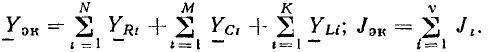

Комплексная схема замещения цепи, соответствующая уравнению (2.129), изображена на рис. 2.30, г.

Таким образом, любой участок электрической цепи, представляющей собой параллельное соединение произвольного количества идеализированных пассивных двухполюсников, может быть заменен одним пассивным двухполюсником, комплексная проводимость которого 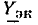 равна сумме комплексных проводимостей всех параллельно включенных двухполюсников. Произвольное количество параллельно включенных идеализированных источников тока может быть заменено одним источником, комплексное действующее значение тока которого 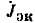равно сумме комплексных действующих значений токов всех параллельно включенных источников.

Переходя в (2.129) от комплексных проводимостей к комплексным сопротивлениям, найдем эквивалентное комплексное входное сопротивление 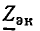группы параллельно включенных идеализированных пассивных двухполюсников:

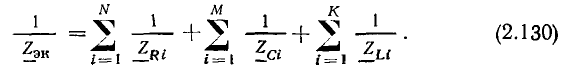
Выражения, подобные (2.129) и (2.130), можно получить для комплексной проводимости и комплексного сопротивления любого участка цепи, являющегося параллельным соединением произвольного количества идеализированных пассивных двухполюсников с заданным комплексным входным сопротивлением или комплексной входной проводимостью

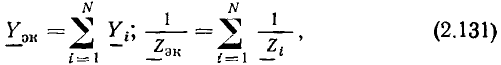
где N — число параллельно включенных двухполюсников.

Используя (2.131), найдем выражение для комплексного входного сопротивления участка цепи, представляющего собой параллельное соединение двух элементов с комплексными сопротивлениями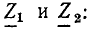

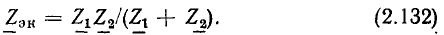
Участки цепей со смешанным соединением элементов

Правила преобразования участков цепей с параллельным или последовательным соединением элементов могут быть применены и для преобразования пассивных участков цепей со смешанным соединением элементов. Преобразование таких участков, представляющих собой сочетание групп параллельно или последовательно включенных элементов, обычно производят в несколько этапов, на каждом из которых группу параллельно включенных элементов заменяют одним двухполюсником, комплексная проводимость которого равна сумме комплексных проводимостей параллельно включенных элементов, а группу последовательно включенных элементов — одним двухполюсником, комплексное сопротивление которого равно сумме комплексных сопротивлений всех последовательно включенных элементов.

Пример 2.8. 

Рассмотрим преобразование участка идеализированной цепи со смешанным соединением элементов (рис. 2.31, а), содержащего группу параллельно включенных элементов и группу последовательно включенных элементов Заменяя параллельно включенные элементы 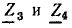одним элементом с комплексным сопротивлением

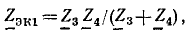
получим преобразованную схему цепи (рис. 2.31, б) с тремя последовательно включенными элементами: 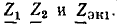Заменяя эти элементы одним с комплексным сопротивлением

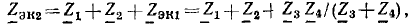
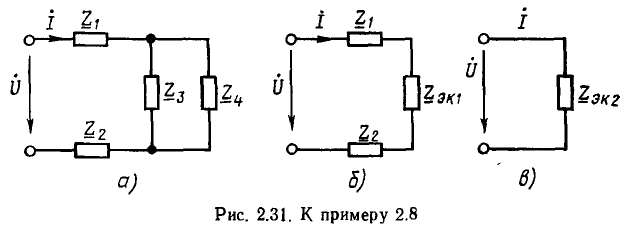
приходим к простейшей преобразованной схеме рассматриваемого участка цепи с одним элементом 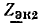(рис. 2.31, в).

 Пример 2.9.

Определим эквивалентную индуктивность цепи с параметрами элементов 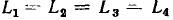= 300 мкГн, схема которой приведена на рис. 2.32.

Участок цепи с тремя параллельно включенными одинаковыми индуктивностями 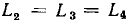обладает эквивалентной индуктивностью, в три раза меньшей, чем каждая из параллельно включенных индуктивностей,  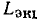        100 мкГн. Этот участок включен последовательно с индуктивностью 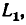поэтому искомая эквивалентная индуктивность

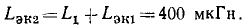
Пример 2.10.

Определим комплексное входное сопротивление участка цепи с параметрами элементов R = 1,5 кОм, 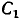= 40 пФ, 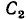= 10 пФ, 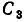= 50 пФ частотой внешнего воздействия f = 1,2 МГц (рис. 2.33).

Параллельно включенные емкости 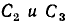могут быть заменены одной эквивалентной емкостью

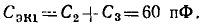
Емкости 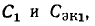включенные последовательно, заменим одной емкостью

Получаем преобразованную цепь (рис. 2.33, б). В результате комплексное входное сопротивление цепи на частоте f — 1,2 МГц

Из рассмотренных примеров следует, что в результате объединения групп последовательно и параллельно включенных элементов происходит постепенное «сворачивание» цепи, причем участок со смешанным соединением пассивных элементов, имеющий два внешних вывода (пассивный двухполюсник), в конечном счете, может быть заменен одним элементом, комплексное сопротивление которого равно входному сопротивлению исходного участка цепи.

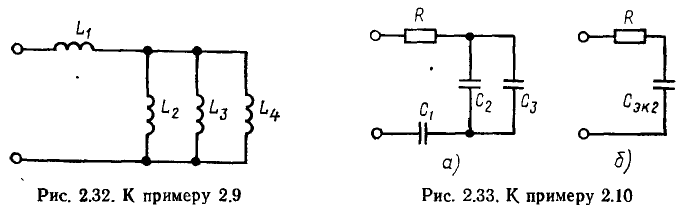
К цепям со смешанным соединением элементов относятся цепные или лестничные цепи, входное сопротивление или входная проводимость которых могут быть представлены в виде цепной (непрерывной) дроби, т. е. с помощью выражения типа

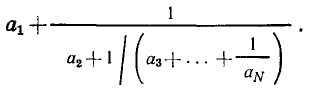
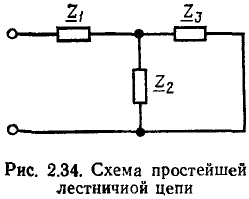
Коэффициенты называются элементами цепной дроби. Число элементов дроби N может быть конечным (конечная цепная дробь) или бесконечным (бесконечная цепная дробь). Рассмотрим простейшую лестничную цепь (рис. 2.34). Нетрудно установить, что входное сопротивление этой цепи

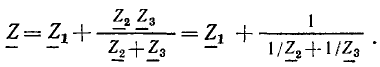
Заменяя в этом выражении сопротивление элемента 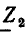его проводимостью 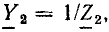получаем окончательно

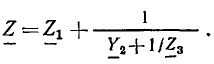
Таким образом, входное сопротивление рассматриваемой цепи может быть представлено в виде конечной цепной дроби, элементы которой равны соответственно 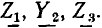Используя аналогичные преобразования, можно представить в виде цепной дроби и входное сопротивление лестничной цепи более общего вида (рис. 2.35, а):

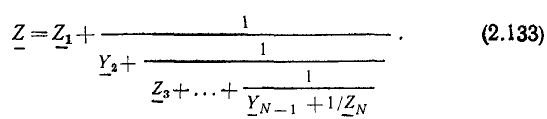
Таким образом, число элементов цепной дроби равно числу идеализированных двухполюсных элементов, образующих лестничную цепь, причем элементами цепной дроби являются комплексные сопротивления двухполюсников, образующих продольные ветви лестничной цепи и комплексные проводимости двухполюсников, входящих в поперечные ветви

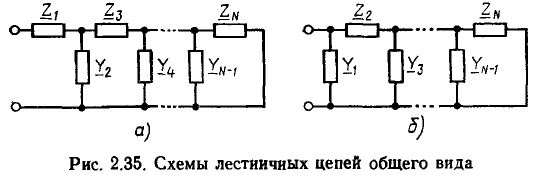
Если лестничная цепь содержит поперечную ветвь, подключенную непосредственно к внешним зажимам цепи (рис. 2.35, б), то в виде цепной дроби может быть представлена входная проводимость

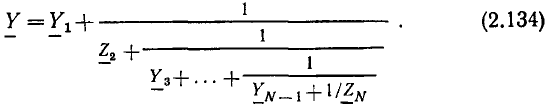
Таким образом, для того чтобы выражения для входных сопротивлений или входных проводимостей лестничных цепей могли быть записаны в виде цепных дробей типа (2.133), (2.134), необходимо элементы, образующие продольные ветви, представить их комплексными сопротивлениями, а элементы, входящие в поперечные ветви, — их комплексными проводимостями.

Эквивалентное преобразование треугольника сопротивлений в звезду и обратное преобразование

Найдем условия эквивалентности двух участков электрической цепи (рис. 2.36, а, б), которые представляют собой соединение пассивных идеализированных двухполюсников треугольником и звездой. По определению, эти участки цепи эквивалентны, если при замене одного участка другим токи выводов 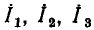и напряжения между выводами 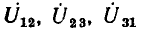останутся неизменными. Учитывая, что из трех напряжений между выводами только два являются независимыми (третье может быть найдено из уравнения баланса напряжений), для эквивалентности треугольника сопротивлений звезде достаточно потребовать, чтобы любая пара из трех напряжений между выводами одной цепи была равна соответствующей паре напряжений другой цепи (при одинаковых значениях токов внешних выводов).

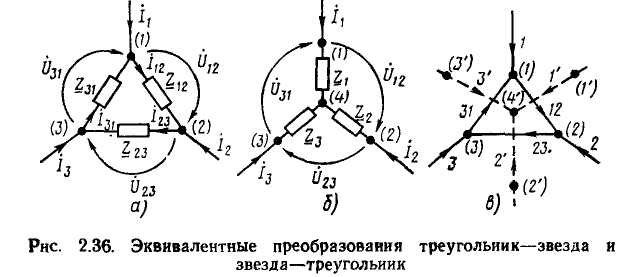
Выразим токи сопротивлений 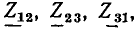образующих стороны треугольника сопротивлений, через токи внешних выводов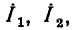 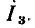Составляя на основании законов Кирхгофа систему уравнений электрического равновесия этого участка цепи

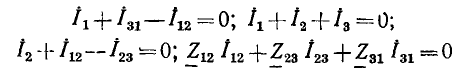
и решая ее относительно токов находим

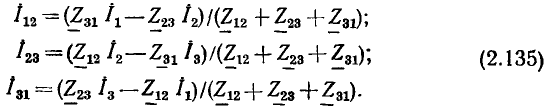
Используя выражения (2.135), определим напряжения между внешними выводами треугольника сопротивлений

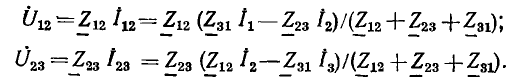
Соответствующие напряжения между внешними выводами звезды (рис. 2.36, б) 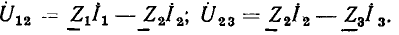Приравнивая напряжения между внешними выводами рассматриваемых участков цепи, находим

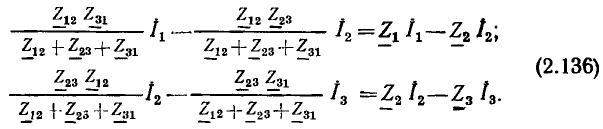
В соответствии со сказанным равенства (2.136) должны выполняться при любых значениях токов внешних выводов. Полагая в (2.136) сначала а затем 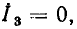определяем соотношения между сопротивлениями, при которых рассматриваемые участки цепей (рис. 2.36, а, б) будут эквивалентными:

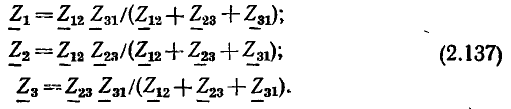
Рассчитав сопротивления по заданным можно осуществить эквивалентную замену треугольника сопротивлений звездой (преобразование треугольник — звезда). Из рис. 2.36 видно, что при этом преобразовании из цепи устраняется контур, образуемый сопротивлениями 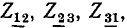и появляется новый узел — место соединения сопротивлений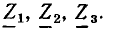

Решая систему уравнений (2.137) относительно 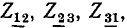получим соотношения, позволяющие производить эквивалентную замену звезды сопротивлений треугольником (преобразование звезда—треугольник):

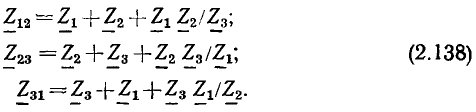
Преобразование звезда-треугольник приводит к уменьшению числа узлов преобразуемой цепи (за счет устранения узла, являющегося местом соединения сопротивлений 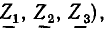однако при этом появляется новый контур, образуемый сопротивлениями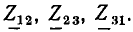

Заменим в выражениях (2.138) комплексные сопротивления элементов их проводимостями. Проведя преобразования, установим, что выражения для комплексных проводимостей элементов, образующих стороны треугольника

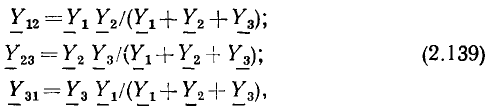
имеют такую же структуру, как и выражения для комплексных сопротивлений, входящих в лучи звезды (2.137). Подобным образом можно получить выражения для комплексных проводимостей лучей звезды 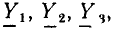которые оказываются аналогичными выражениям для комплексных сопротивлений сторон треугольника (2.138). Учитывая, что рассматриваемые участки обладают дуальными графами (рис. 2.36, в), приходим к заключению, что эти участки цепей являются дуальными.

Выражения (2. 139) могут быть обобщены и для преобразования N-лучевой звезды (см. рис. 1.23, б) в N-угольник (см. рис. 1.23, а):

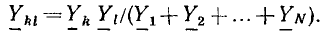
Здесь 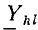— проводимость стороны N-угольника, соединяющей узлы k и l; 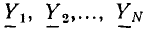—проводимость элементов, образующих лучи звезды.

Обратное преобразование полного N-угольника в N-лучевую звезду в общем случае невозможно.

Применение преобразований треугольник—звезда и звезда—треугольник в ряде случаев позволяет существенно упростить анализ цепей, в частности иногда с помощью этих преобразований удается приводить сложные участки цепей к более простым (параллельное, последовательное или смешанное соединение элементов).

Пример 2.11.

Для цепи с параметрами элементов 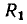 = 20 Ом, 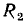= 50 Ом, 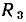= 30 Ом, 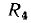= 25 Ом, 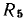=30 Ом; 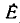= 1,3 В (рис 2.37, а) определим ток ветви, содержащей источник напряжения .

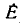Ток 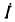 можно найти, решая основную систему уравнений электрического равновесия цепи, однако этот путь весьма трудоемок. Учитывая, что по условию задачи требуется определить только ток независимого источника целесообразно остальную часть цепи, к которой подключен этот источник, заменить комплексным входным сопротивлением. Непосредственное нахождение входного сопротивления пассивного двухполюсника, к которому подключен идеальный источник напряжения, постепенным «сворачиванием» по правилам преобразования участков

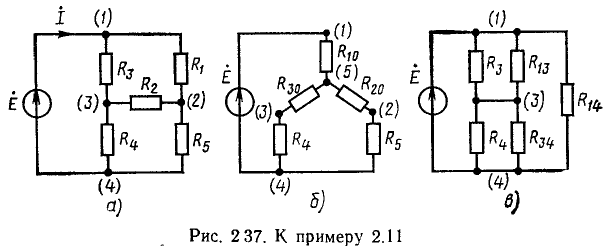
цепей с параллельным и последовательным соединением элементов невозможно, так как в данном двухполюснике отсутствуют последовательно или параллельно включенные элементы.

 Заменим треугольник сопротивлений 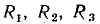звездой сопротивлений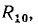 (рис. 2.37, б). Используя формулы (2.137), находим:

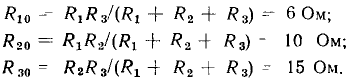
Преобразуя полученную цепь с помощью правил преобразования участков цепей со смешанным соединением элементов, определяем входное сопротивление пассивного двухполюсника R = 26 Ом и искомый ток =150 мА.

Тот же результат может быть получен, если использовать преобразование звезда—треугольник. В частности, заменяя сопротивления (рис. 2.37, а) сопротивлениями

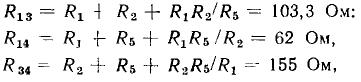
получаем цепь (рис. 2.37, в), которая легко поддается дальнейшим преобразованиям.

Последовательная и параллельная схемы замещения пассивного двухполюсника

Два различных линейных пассивных двухполюсника с одинаковыми комплексными сопротивлениями (комплексными проводимостями) эквивалентны, так как при замене одного из них другим токи и напряжения внешних выводов, соединяющих двухполюсники с остальной частью цепи, не изменяются. Следовательно, условием эквивалентности линейных пассивных двухполюсников является равенство их комплексных сопротивлений (проводимостей).

Комплексное сопротивление любого пассивного двухполюсника 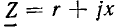можно представить как сумму комплексных сопротивлений двух последовательно включенных двухполюсников, одно из которых имеет чисто резистивный  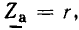a другое 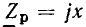— чисто реактивный характер. Комплексную проводимость этого двухполюсника 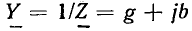можно рассматривать как комплексную проводимость цепи из двух параллельно соединенных элементов с проводимостями 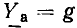и Поэтому, произвольному линейному пассивному двухполюснику, находящемуся под гармоническим воздействием, можно поставить в соответствие две схемы замещения — последовательную (рис. 2.38, а) и параллельную (рис. 2.39, а), причем каждая из них содержит один реактивный элемент и один элемент, входное  сопротивление которого имеет чисто резистивный характер. В общем случае вещественные г, g и мнимые х, b составляющие комплексного входного сопротивления и комплексной входной проводимости двухполюсника являются сложными функциями частоты: 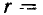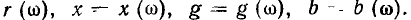При изменении частоты r и g могут изменяться только по значению, а х и b — как по значению, так и по знаку.

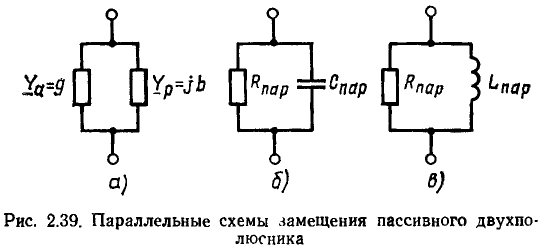
При фиксированном значении угловой частоты 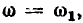вещественные и мнимые составляющие входных сопротивления и проводимости двухполюсника, а следовательно, 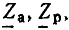а также 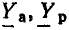элементов последовательной и параллельной схем замещения принимают определенные значения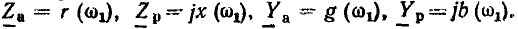

Постоянное вещественное число 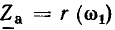можно рассматривать как комплексное сопротивление идеализированного пассивного элемента — сопротивления, входящего в последовательную схему замещения двухполюсника (см. рис. 2.38, б, в):

Мнимое число 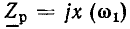в зависимости от знака  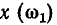можно рассматривать либо как комплексное сопротивление емкости  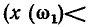0)

либо как комплексное сопротивление индуктивности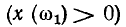

входящих в эту же схему замещения. Параллельная схема замещения двухполюсника (рис. 2.39, б, в) содержит сопротивление

и либо емкость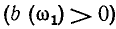

либо индуктивность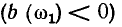

В частном случае, когда входное сопротивление двухполюсника имеет чисто резистивный или чисто реактивный характер, обе схемы замещения вырождаются в одну схему, содержащую единственный идеализированный пассивный элемент (сопротивление, емкость или индуктивность).

Таким образом, при фиксированном значении частоты внешнего воздействия каждому линейному пассивному двухполюснику независимо от числа входящих в него элементов и способа их соединения можно поставить в соответствие эквивалентную схему, содержащую не более двух идеализированных пассивных элементов. Разумеется, такое преобразование будет эквивалентным только при 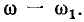Изменение частоты внешнего воздействия может вызывать изменение не только значений параметров элементов последовательной и параллельной схем, замещения двухполюсника, но и характера соответствующих реактивных элементов.

Последовательная и параллельная цепи, схемы которых приведены на рис. 2.38, а и 2.39, а, обладают одинаковыми комплексными сопротивлениями (проводимостями) и поэтому являются эквивалентными. Выбор той или иной цепи и соответственно той или иной схемы замещения двухполюсника при заданной частоте внешнего воздействия производится только исходя из удобства последующего анализа.

При необходимости последовательная и параллельная схемы замещения двухполюсника могут быть преобразованы одна в другую Соотношения между параметрами их элементов однозначно устанавливаются с помощью выражений (2.52) — (2.55) и (2.140)— (2.145). Анализ этих выражений показывает, что при взаимных преобразованиях последовательной и параллельной схем характер реактивного элемента, входящего в схему замещения, не изменяется (табл. 2.1).

Выражения, приведенные в таблице, можно использовать для взаимных преобразований произвольных участков цепей с параллельным и последовательным включением элементов. Например, при заданной частоте внешнего воздействия 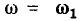участок цепи, представляющий собой последовательное соединение сопротивления  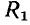и емкости 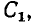может быть заменен эквивалентным участком цепи с параллельно включенными сопротивлением 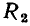и емкость 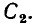Несмотря на то что в данном случае параметры элементов исходной цепи не являются функциями частоты, параметры элементов преобразованной цепи 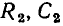зависят от частоты внешнего воздействия. При этом изменение частоты внешнего воздействия приводит только к изменению параметров элементов преобразованной цепи; изменения характера реактивных элементов в данном случае не происходит.

Пример 2.12.

Найдем последовательную и параллельную схемы замещения последовательной RLC-цепи (см. пример 2.4) при частоте внешнего воздействия 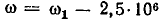рад/с.

Комплексное сопротивление цепи при 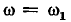имеет резистивно-емкостной характер

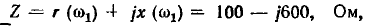
поэтому последовательная и параллельная схемы замещения цепи на данной частоте содержат сопротивление и емкость (см. рис. 2.38, б, 2.39, б). Параметры элементов последовательной схемы замещения в соответствии с выражениями (2.140), (2.141)

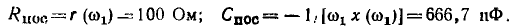
Параметры элементов параллельной схемы замещения найдем, используя формулы, приведенные в табл. 2.1:

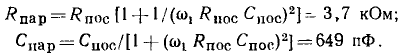
Комплексные схемы замещения источников энергии

Ранее были рассмотрены последовательная и параллельная схемы замещения линеаризованных источников постоянного тока и напряжения (см. рис. 1.16, б, в) и получены соотношения для их взаимного преобразования (1.35), (1.36). Покажем, что аналогичные соотношения выполняются и для линеаризованных источников гармонических токов и напряжений, т. е. для источников, комплексные схемы замещения которых содержат идеальный источник напряжения 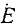и комплексное внутреннее сопротивление 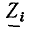(рис. 2.40, а) или идеальный источник тока 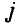и комплексную внутреннюю проводимость 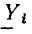(рис. 2.40, б).

В соответствии с последовательной схемой замещения (рис. 2.40, а) комплексное действующее значение напряжения на зажимах линеаризованного источника

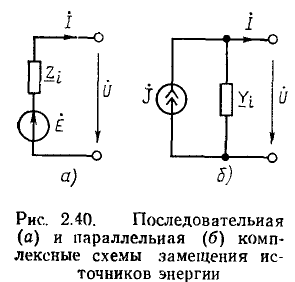
В то же время из параллельной схемы замещения (рис. 2.40, б) получаем

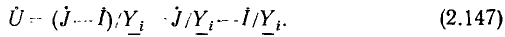
Сравнивая выражения (2.146) и (2.147), находим условия эквивалентности последовательной и параллельной комплексных схем замещения линеаризованного источника гармонических токов и напряжений:

Действительно, выражения (2.148) подобны (1.35), (1.36) и могут быть получены из последних путем замены вещественных внутреннего сопротивления 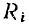 и внутренней проводимости 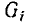- соответственно комплексным сопротивлением 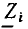и комплексной проводимостью 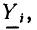а мгновенных значений тока  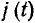и э.д.с. е (t) их комплексными изображениями. Как отмечалось ранее, взаимные преобразования параллельной и последовательной схем замещения возможны только для линеаризованных источников с конечными внутренним сопротивлением и внутренней проводимостью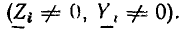

В ряде случаев при анализе цепей возникает необходимость преобразовывать источники, т. е. заменять идеализированный источник одного типа другим. Для линеаризованных источников с конечным внутренним сопротивлением (проводимостью) эта задача решается путем преобразования последовательной схемы замещения источника в параллельную или обратно с помощью выражений (2.148). Если в эквивалентной схеме реального источника содержится только идеальный источник напряжения, однако в цепи, внешней по отношению к нему, имеется произвольный пассивный двухполюсник, включенный последовательно с источником, то его комплексное сопротивление 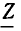можно рассматривать как внутреннее сопротивление линеаризованного источника 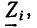что дает возможность воспользоваться для преобразования источника выражениями (2.148). Аналогично, если параллельно идеальному источнику тока включена любая ветвь, составленная из пассивных элементов, то ее комплексную проводимость  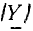можно рассматривать как внутреннюю проводимость линеаризованного источника 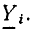Идеальные источники тока и напряжения, которые могут быть преобразованы один в другой таким образом, называются невырожденными.

Формулами (2.148) можно воспользоваться и для взаимного преобразования невырожденных управляемых источников тока и напряжения. Разумеется, при этом характер управляющего воздействия (ток или напряжение) не изменяется.

Если в анализируемую цепь включены идеальный источник напряжения и последовательно с ним нет элементов, сопротивление которых можно рассматривать как внутреннее сопротивление линеаризованного источника, или идеальный источник тока, параллельно которому нет ветвей, проводимость которых можно трактовать как внутреннюю проводимость соответствующего источника, то такие источники называют вырожденными. Вырожденные источники напряжения и тока не могут быть преобразованы один в другой непосредственно с помощью выражений (2.148), однако они могут быть устранены из рассматриваемой цепи с помощью преобразований, получивших название переноса источников.

Перенос источников

Рассмотрим участок идеализированной электрической цепи, содержащий вырожденный источник напряжения (рис. 2.41, а). Покажем, что данный участок цепи может быть заменен одним из эквивалентных ему участков цепей, не содержащим вырожденных источников.

Идеальный источник напряжения 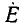из ветви, подключенной между узлами (6) и (7) (рис. 2.41, а), перенесем во все ветви, подключенные к узлу (6) (рис. 2.41, б) или во все ветви, подключенные к узлу (7) (рис. 2.41, в). В обоих случаях перенос источника напряжения произведен без изменения э.д.с. источника и его ориентации относительно направлений обхода контуров 1 и 4. Ветвь, ранее содержавшая источник ,

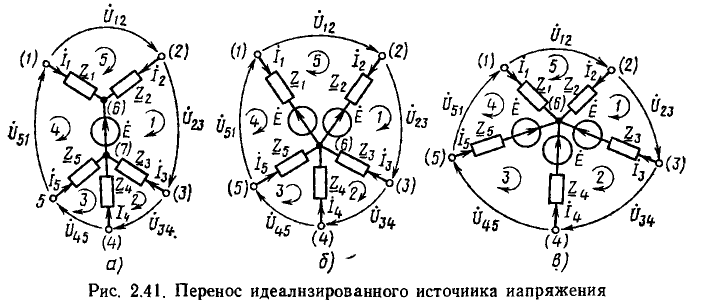
после преобразования исчезает, причем узлы (6) и (7), к которым она была подключена, объединяются в один узел.

Процессы во всех трех идеализированных цепях описываются решениями одной и той же системы уравнений электрического равновесия, составленной на основании законов Кирхгофа:

Следовательно, при замене цепи (рис. 2.41, а) любой из цепей (рис. 2.41, б, в) токи внешних выводов и напряжения между ними не изменяются, т. е. участки этих цепей эквивалентны. В результате переноса источника вырожденный источник напряжения заменен несколькими невырожденными источниками напряжения, которые при необходимости могут быть преобразованы в источники тока с помощью рассмотренных ранее преобразований.

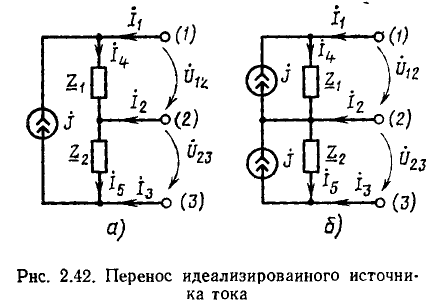
Вырожденный источник тока, включенный между узлами (k) и (l) произвольной электрической цепи, может быть заменен несколькими источниками тока, включенными параллельно любым ветвям электрической цепи, образующим путь между узлами (k) и (l). Например, вырожденный источник тока включенный между узлами (1) и (3) электрической цепи (рис. 2.42, а), может бьт заменен двумя источниками тока, подключенными параллельно ветвям с ком плексными сопротивлениями 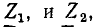образующими путь между этими же узлами (рис. 2.42, б). Источник тока переносится без изменения тока источника и его ориентации относительно узлов (1) и (3). Эквивалентность цепей следует из того, что процессы в них описываются одной и той же системой уравнений электрического равновесия, составленной на основании законов Кирхгофа:

В общем случае в результате переноса источника тока вырожденный источник заменяется несколькими невырожденными источниками, которые при необходимости могут быть преобразованы в источники напряжения с помощью выражений (2.148). Ветвь, ранее содержавшая вырожденный источник тока, после переноса источника исчезает.

Цепи с взаимной индуктивностью

Понятие взаимной индуктивности:

Две или более индуктивных катушек называются связанным и, если изменение тока одной из катушек вызывает появление э. д.с. в остальных. Напомним, что явление наведения э.д.с. в какой-либо индуктивной катушке при изменении тока другой катушки называется взаимоиндукцией, а наведенная э.д.с. — э. д. с. взаимоиндукции.

Рассмотрим две индуктивные катушки, расположенные таким образом, что магнитный поток, вызванный током одной из катушек, пронизывает витки другой катушки (рис. 2.43). Пусть 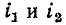— токи первой и второй катушек, а 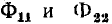— магнитные потоки самоиндукции этих катушек, т. е. магнитные потоки, прони- . зывающие каждую из катушек и вызванные протекающим по ней током. Часть магнитного потока самоиндукции первой катушки 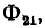которая пронизывает витки второй катушки, назовем потоком взаимоиндукции второй катушки. Часть магнитного потока самоиндукции первой катушки 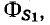которая не пронизывает витки второй катушки, назовем магнитным потоком рассеяния первой катушки, часть магнитного потока самоиндукции второй катушки 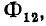которая пронизывает витки первой, называется потоком взаимоиндукции первой катушки, а часть магнитного потока самоиндукции второй катушки 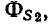которая пронизывает только витки второй катушки, — потоком рассеяния второй катушки (на рис. 2.43 изображено только по одной силовой линии каждого из магнитных потоков). Таким образом, магнитный поток самоиндукции каждой из катушек содержит по две составляющие

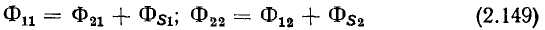
Полный магнитный поток, пронизывающий каждую из катушек, складывается из магнитных потоков самоиндукции и взаимоиндукции:

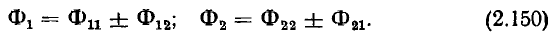
Потокосцепление каждой из катушек так же, как и магнитный поток, имеет две составляющие —потокосцепление самоиндукции 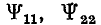и потокосцепление взаимоиндукции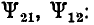

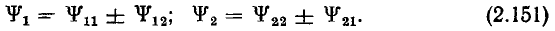
) Когда все витки каждой из катушек пронизываются одинаковыми магнитными потоками, выражения (2.151) могут быть записаны в следующей форме:

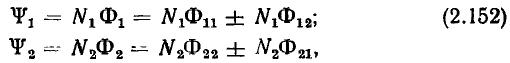
где 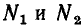— число витков первой и второй катушек.

Знак плюс в выражениях (2.150) — (2.152) соответствует совпадающим по направлению (предполагается, что катушки расположены соосно) магнитным потокам самоиндукции и взаимоиндукции каждой из катушек. Такое включение катушек индуктивности называется согласным (рис. 2.43, а). Знак минус соответствует противоположным направлениям магнитных потоков самоиндукции и взаимоиндукции. Такое включение катушек называют встречным (рис. 2.43, б).

В соответствии с законом электромагнитной индукции (1.19) электродвижущие силы, наводимые в каждой из связанных катушек индуктивности:

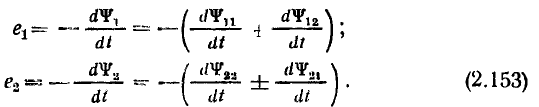
Первое слагаемое в каждом из выражений (2.153) представляет собой э.д.с. самоиндукции, второе — э. д. с. взаимоиндукции. Преобразуем выражения (2.153), формально умножив и разделив каждое из слагаемых на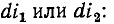

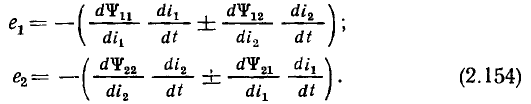
В индуктивных катушках без ферромагнитных сердечников магнитные потоки самоиндукции и взаимоиндукции пропорциональны вызывающим их токам, поэтому производные потокосцеплений потокам могут быть заменены отношением соответствующих величин. Индуктивность каждой катушки 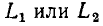есть отношение потокосцепления самоиндукции к вызвавшему его току:

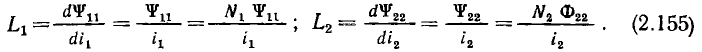
Взаимная индуктивность между катушками 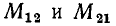— это отношение потокосцепления взаимоиндукции к вызвавшему его току:

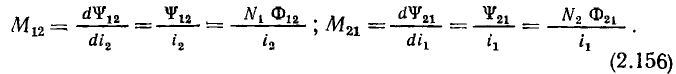
Связанные индуктивные катушки, у которых потоки самоиндукции и взаимоиндукции пропорциональны вызвавшим их токам и, следовательно, величины 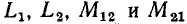не зависят от 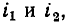называются катушками с линейной индуктивностью. Для них всегда выполняется условие  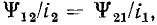поэтому

Взаимную индуктивность выражают в генри (Гн).

С учетом введенных обозначений (2.155), (2.156), (2.157) э.д.с., наводимые в каждой из катушек:

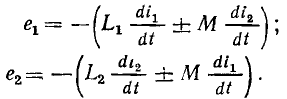
Переходя от э.д. с. к напряжениям на зажимах связанных индуктивных катушек, получаем окончательно

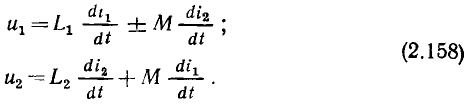
В теории электрических цепей рассмотрение реальных элементов — связанных индуктивных катушек — заменяют рассмотрением их упрощенных моделей — связанных индуктивностей. Связанные индуктивности представляют собой идеализированные элементы, отражающие основные явления, которые присущи связанным индуктивным катушкам: самоиндукцию и взаимоиндукцию, или, в конечном счете, явления запасания энергии в магнитном поле. В связанных индуктивностях не происходит запасания энергии в электрическом поле или преобразования ее в другие виды энергии, что всегда в той или иной мере имеет место в реальных элементах.

Ток и напряжение на зажимах связанных индуктивностей задаются выражениями (2.158). Если рассматриваемая цепь содержит п связанных индуктивностей, то зависимость между токами и напряжениями на их зажимах определяется системой уравнений:

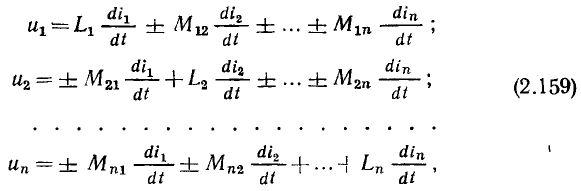
где — взаимная индуктивность между i-й и j-й связанными индуктивностями.

Уравнения (2.158), (2.159) следует рассматривать как компонентные уравнения ветвей, содержащих связанные индуктивности.

Понятие об одноименных зажимах

При анализе цепей с взаимной индуктивностью возникает задача определить, каким образом (согласно или встречно) по отношению к выбранным условным положительным направлениям токов включены рассматриваемые индуктивные катушки и в соответствие с этим какой знак (плюс или минус) необходимо использовать в выражениях (2.158), (2.159). Если конструкции индуктивных катушек, в частности направления их намотки, известны, а направления токов заданы, то для выбора знака в выражениях (2.158), (2.159) или (2.150) — (2.154) достаточно, воспользовавшись правилом буравчика (правоходового винта), определить направления магнитных потоков самоиндукции каждой из катушек. Например, применяя правило буравчика, устанавливаем, что у катушек, изображенных на рис. 2.43, а, направления магнитных потоков самоиндукции и взаимоиндукции у каждой из катушек одинаковы, а у катушек, изображенных на рис. 2.43, б, — противоположны.

При вычерчивании принципиальных электрических схем цепей с взаимной индуктивностью индуктивные катушки изображают с помощью условных графических обозначений, которые не отражают особенностей их конструкции. Для выяснения, является ли данное включение катушек согласным или встречным, вводят понятие одноименных зажимов связанных индуктивных катушек.

Одноименными зажимами двух связанных индуктивных катушек называется пара зажимов, выбранных таким образом, что при одинаковых относительно этих зажимов направлениях токов катушек магнитные потоки самоиндукции и взаимоиндукции в каждой из них суммируются. Одноименные зажимы индуктивных катушек помечают одинаковыми значками (буквами ник, точками, звездочками, треугольниками и т. п.), проставляемыми в непосредственной близости к соответствующим зажимам. Так, на рис. 2.43, а звездочками отмечены одноименные зажимы 1 и 2. Вторую пару одноименных зажимов этих катушек образуют зажимы 1' и 2', специально не обозначенные, так как

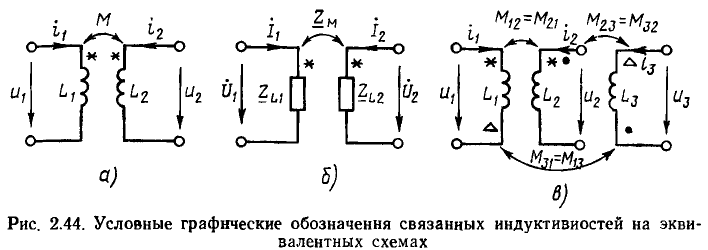
для решения вопроса о том, является ли заданное включение согласным или встречным, достаточно обозначить одну пару одноименных зажимов. На рис. 2.43, б точками обозначены одноименные зажимы 1 и 2'.

Аналогично поступают и при построении эквивалентных схем электрических цепей с взаимными индуктивностями. Условное графическое изображение связанных индуктивностей, используемое при построении таких схем, показано на рис. 2.44, а. Когда общим магнитным потоком связано не две, а большее количество индуктивностей, одноименные зажимы каждой из пар обозначают с помощью различных значков (рис. 2.44, в).

Итак, если токи связанных индуктивностей одинаково ориентированы относительно одноименных зажимов, то такое включение является согласным и в выражениях (2.158) следует использовать знак плюс; в противном случае, включение является встречным и необходимо использовать знак минус (величина М при этом считается положительной). Например, индуктивности на рис. 2.44, а на рис. 2.44, в включены согласно, а индуктивности (рис. 2.44, в) включены встречно.

До сих пор рассматривались только соосно расположенные индуктивные катушки. В общем случае, когда направления осей связанных индуктивных катушек не совпадают, при выборе способа их включения используют несколько иной подход. При этом в выражениях (2.158) берут знак плюс, а взаимную индуктивность рассчитывают по формуле

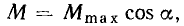
где 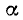— угол между направлением магнитных потоков самоиндукции и взаимоиндукции в центре катушек.

Коэффициент связи между индуктивными катушками

Из качественного рассмотрения процессов в связанных индуктивных катушках следует, что чем сильнее связаны катушки, т. е чем больше магнитного потока, создаваемого током каждой из них, пронизывает другую катушку, тем выше взаимная индуктивность Однако при этом не ясно, как связана взаимная индуктивность с индуктивностями катушек, и чем определяется максимальное значение М. Введем новую величину, количественно характеризующую степень связи между катушками - коэффициент связи. Коэффициент связи 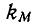представляет собой среднее геометрическое из отношений потока взаимоиндукции к потоку самоиндукции каждой из катушек:

 

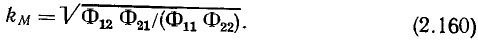
Представляя магнитный поток самоиндукции каждой из катушек в виде суммы потока рассеяния этой катушки и потока взаимоиндукции другой катушки (2.149), получаем

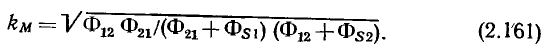
Из выражения (2.161) видно, что значения коэффициента связи лежат в пределах

причем 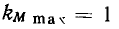только тогда, когда потоки рассеяния обеих катушек равны нулю, или, другими словами, когда магнитный поток, создаваемый током одной катушки, полностью пронизывает другую катушку. Коэффициент связи определяется конструкцией катушки и практически всегда меньше единицы.

Коэффициент связи 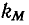 можно выразить через индуктивности связанных катушек и их взаимную индуктивность. Подставляя в (2.160) выражения для потоков самоиндукции  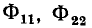и взаимоиндукции  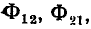полученные из (2.155), (2.156), находим

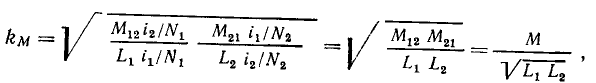
откуда 

Из выражения (2.163) с учетом (2.162) можно определить пределы, в которых изменяются значения взаимной индуктивности:

Таким образом, максимальное значение взаимной индуктивности катушек не может превышать среднего геометрического их индуктивностей.

Цепи с взаимной индуктивностью при гармоническом воздействии

Для анализа цепей с взаимной индуктивностью при гармоническом воздействии можно воспользоваться рассмотренным ранее методом комплексных амплитуд. Переходя в выражениях (2.158) от мгновенных значений токов и напряжений к их комплексным изображениям и принимая во внимание, что дифференцированию гармонических функций времени соответствует умножение их изображений на 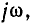получаем компонентные уравнения связанных индуктивностей в комплексной форме

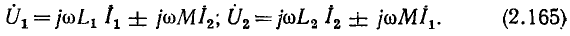
Комплексное действующее значение напряжения на каждой из связанных индуктивностей помимо падения напряжения на комплексном сопротивлении индуктивности 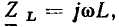вызванного протекающим по ней током, содержит также дополнительный член, который можно рассматривать как падение напряжения на некотором комплексном сопротивлении 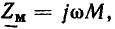называемом сопротивлением связи, вызванное протекающим по нему током другой индуктивности:

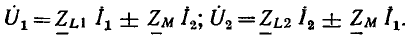
Комплексная схема замещения пары связанных индуктивностей приведена на рис. 2.44, б (другие варианты комплексных схем замещения связанных индуктивностей будут рассмотрены в следующем подпараграфе). Если индуктивной связью охвачено n индуктивностей, то комплексные действующие значения напряжений на их зажимах определяются системой уравнений

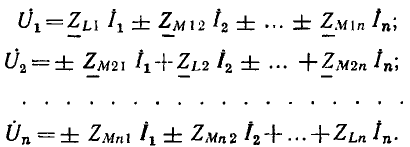
Падения напряжения на сопротивлениях связи 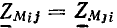берут со знаком плюс при согласном включении индуктивностей и со знаком минус — при встречном.

Система уравнений электрического равновесия цепи с взаимными индуктивностями так же, как и системы основных уравнений ранее рассмотренных цепей, не содержащих взаимных индуктивностей, формируется из компонентных уравнений (уравнений ветвей), а также уравнений баланса токов и напряжений, составленных на основании законов Кирхгофа. При произвольном внешнем воздействии соответствующие уравнения составляются для мгновенных значений токов и напряжений, при гармоническом воздействии — для их комплексных изображений. Напомним, что вид и количество уравнений, составляемых на основании законов Кирхгофа, определяются только топологией цепи и не зависят от входящих в нее элементов. В связи с этим уравнения баланса токов и напряжений цепи, содержащей связанные индуктивности, имеют точно такой же вид, как и уравнения соответствующей ие пи в отсутствие связи между индуктивностями, т. е. при М = 0.

Пример 2.13.

Составим основную систему уравнений электрического равновесия цепи, эквивалентная схема которой для мгновенных значений приведена на рис. 2.45, а.

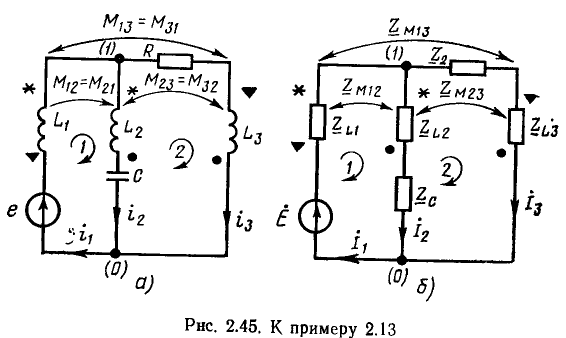
На основании первого и второго законов Кирхгофа для цепи может быть составлено три независимых уравнения

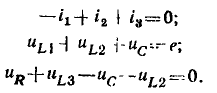
В сочетании с пятью компонентными уравнениями

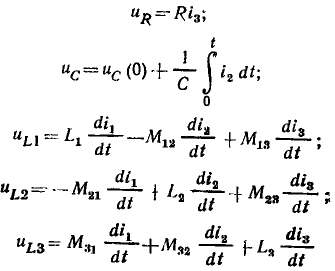
получаем восемь уравнений для определения восьми неизвестных величин: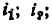 

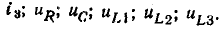
Эквивалентная схема рассматриваемой цепи для комплексных токов и напряжений изображена на рис. 2.45, б, а основная система уравнений электрического равновесия цепи в комплексной форме имеет следующий вид:

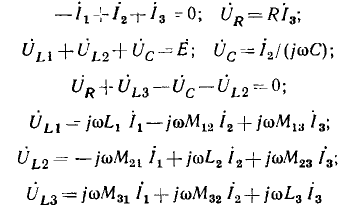
Выражая падения напряжений на всех элементах через соответствующие токи, получаем систему из уравнений

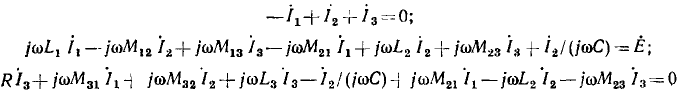
Для определения неизвестных токов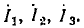 

Эквивалентные преобразования участков цепей со связанными индуктивностями

Рассмотрим эквивалентные преобразования участков цепей, содержащих связанные индуктивности. В частности, покажем возможность замены их участками, не содержащими связанных индуктивностей. Начнем с наиболее простых случаев, когда связанные индуктивности включены последовательно (рис. 2.46, а, б) или параллельно

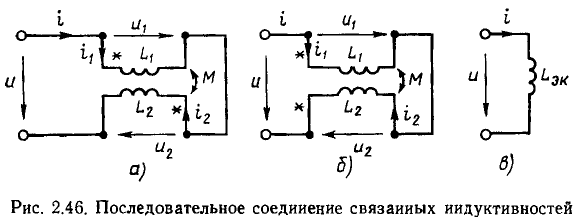
(рис. 2.47, а, б). В этих случаях участок цепи, содержащий связанные индуктивности, имеет два внешних вывода, т. е. представляет собой двухполюсник. Определим его комплексное входное сопротивление и схему замещения.

При последовательном соединении связанных индуктивностей их токи равны, а напряжение на входе рассматриваемого участка цепи есть сумма напряжений на каждой из индуктивностей:

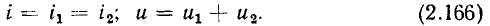
Используя выражения (2.166) и компонентные уравнения связанных индуктивностей (2.158), определяем зависимость между током и напряжением на зажимах рассматриваемого участка цепи:

Как видно из выражения (2.167), участок цепи, содержащий последовательно включенные связанные индуктивности, может быть заменен эквивалентной индуктивностью (см. рис. 2.46, в)

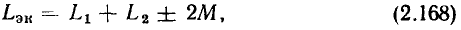
где знак плюс соответствует согласному включению, а минус — встречному. Таким образом, при согласном включении связанных индуктивностей эквивалентная индуктивность получается больше, а при встречном — меньше, чем эквивалентная индуктивность участка цепи, содержащего две последовательно включенные несвязанные индуктивности.

На использовании выражения (2.168) основан простой метод измерения взаимной индуктивности, в соответствии с которым сначала производят измерение эквивалентной индуктивности катушек при согласном 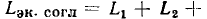 и встречном включении 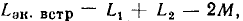а затем по формуле 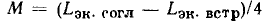рассчитывают М.

При параллельном соединении связанных индуктивностей к их зажимам прикладывается одинаковое напряжение u, а входной ток рассматриваемого участка цепи складывается из токов обеих индуктивностей:

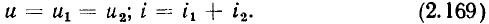
Используя (2.169) и компонентные уравнения связанных индуктивностей (2.158), составляем систему уравнений

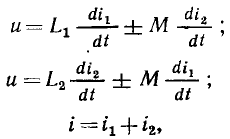
из решения которой находим зависимость между напряжением и током на зажимах рассматриваемого участка цепи:

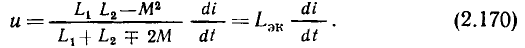
В соответствии с (2.170) участок цепи, представляющий собой две параллельно включенные связанные индуктивности, обладает эквивалентной индуктивностью (рис. 2.47, в)

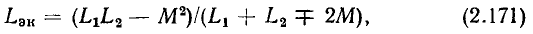
причем знак минус соответствует согласному включению, а знак плюс — встречному.

При 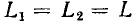выражение (2.171) приводится к виду

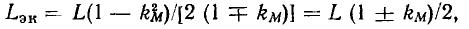
откуда следует, что 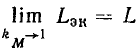при согласном и 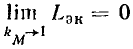при встречном включении индуктивностей.

При коротком замыкании одной из связанных индуктивностей, например индуктивности (см. рис. 2.44, а), участок цепи, содержащий связанные индуктивности, также представляет собой двухполюсник, напряжение и ток на входе которого совпадают с напряжением и током на зажимах индуктивности  (рис. 2.48, а). Решая систему уравнений, описывающую процессы в данном участке цепи

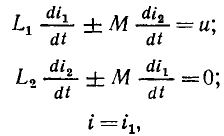
находим

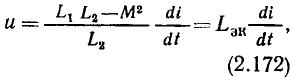
где 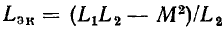 - эквивалентная индуктивность участка цепи.

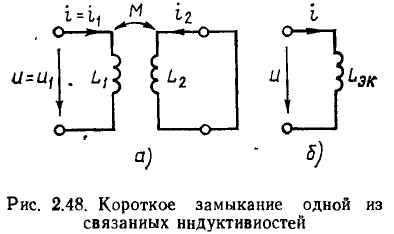
Таким образом, все рассмотренные идеализированные двухполюсники, содержащие связанные индуктивности, при любом воздействии могут быть заменены одной индуктивностью 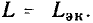Комплексное сопротивление этих двухполюсников имеет чисто реактивный характер: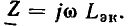

Найдем схему замещения участка цепи, содержащего две связанные индуктивности, включенные таким образом, что они имеют одну общую точку (рис. 2.49, а, б). Используя в качестве исходных компонентные уравнения связанных индуктивностей (2.158), добавим к первому из этих, уравнений и вычтем из него член 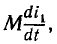 а ко второму уравнению добавим и вычтем член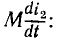

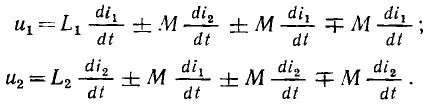
После приведения подобных членов эти уравнения принимают вид

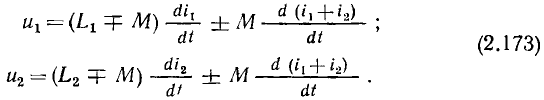
Здесь, как и в полученных ранее выражениях, верхний знак соответствует согласному, а нижний знак — встречному включению связанных индуктивностей.

Системе (2.173) может быть поставлена в соответствие эквивалентная схема участка цепи, не содержащая связанных индуктивностей (рис. 2.49, в). Анализ уравнений (2.173) и эквивалентной схемы показывает, что только при согласном включении и достаточно малом коэффициенте связи  все три индуктивности этой схемы положительны. При встречном включении или при согласном включении при большом коэффициенте связи  одна из 

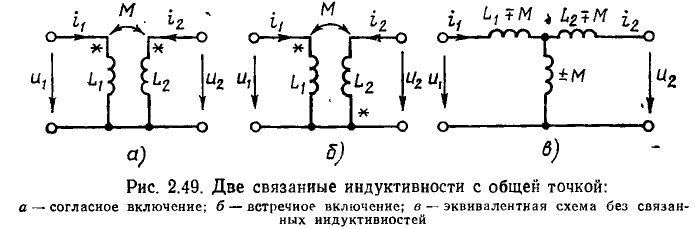
индуктивностей оказывается отрицательной. Очевидно, что такой схеме нельзя поставить в соответствие моделирующую цепь, состоящую из идеализированных элементов — индуктивностей. Эта схема является чисто расчетной: ее применение во многих случаях существенно упрощает анализ цепей со связанными индуктивностями.

В общем случае, если рассматриваемый участок цепи содержит связанные индуктивности, не имеющие общих точек, его можно заменить участком цепи без взаимных индуктивностей, но с управляемыми источниками (рис. 2.50, а и 2.51, а). В первом случае эквивалентная схема содержит источники напряжения, э.д.с. которых равна напряжению на некотором участке цепи; во втором — управляемые источники напряжения, э.д.с. которых пропорциональна производным токов цепи.

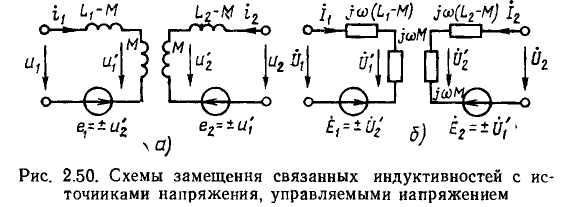
Комплексные схемы замещения преобразованных цепей изображены на рис. 2.50, б и 2.51, б. В справедливости предлагаемых схем можно убедиться, составив по ним систему уравнений электрического равновесия преобразованной цепи и приведя ее к виду (2.158).

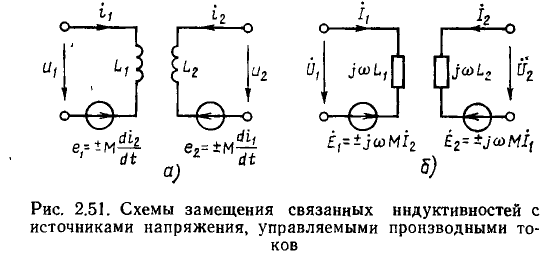
Используя приемы, подобные рассмотренным, можно построить также ряд других схем замещения участков цепей со связанными индуктивностями.

Вариометры с переменной взаимной индуктивностью

В различных радиотехнических устройствах широко используют катушки с переменной индуктивностью, называемые вариометрами. Индуктивность вариометра может изменяться различными способами, например путем изменения числа витков или путем перемещения магнитного нли немагнитного сердечника, однако наибольшее распространение получили вариометры с переменной взаимной индуктивностью.

Вариометр этого типа представляет собой две связанные индуктивные катушки, намотанные на цилиндрические или сферические каркасы и расположенные одна внутри другой так, что внутренняя катушка (ротор) может вращаться относительно неподвижной наружной катушки (статора). Взаимная индуктивность между катушками изменяется при этом по косинусоидальному закону, принимая значения от при = 0 (магнитные потоки ротора и статора совпадают по направлению) до М = 0 при 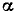= 90° (магнитные потоки в центре ротора и статора перпендикулярны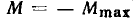) и при 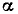= 180° (направления магнитных потоков ротора и статора противоположны).

Обмотки ротора и статора могут быть включены последовательно или параллельно, в ряде случаев применяются вариометры, у которых обмотка ротора закорочена. Максимальные 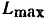и минимальные значения индуктивности

вариометра, соответствующие этим вариантам соединения обмоток ротора и стар , могут быть рассчитаны с помощью выражений (2.168), (2.171), и (2.172). Одним из основных параметров вариометра является коэффициент перекрытия по индуктивности 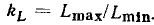  Коэффициент перекрытия определяется максимальным значением взаимной индуктивности  и увеличивается с ростом коэффициента связи между обмотками.

Понятие о линейных трансформаторах

Трансформатором называется устройство для передачи энергии из одной части электрической цепи в другую, основанное на использовании явления взаимоиндукции. Трансформатор состоит из нескольких связанных индуктивных катушек (обмоток), которые для повышения их индуктивности и уменьшения потоков рассеяния размещены на общем ферромагнитном сердечнике. Одну из обмоток трансформатора обычно подключают к источнику энергии, а к остальным обмоткам присоединяют различные нагрузки. Обмотка, подключенная к источнику энергии, называется первичной, остальные обмотки называются вторичными.

В связи с тем, что свойства магнитных материалов существенно зависят от напряженности пронизывающих их магнитных полей и, следовательно, от создающих эти поля токов, трансформатор с ферромагнитным сердечником представляет собой в общем случае устройство с нелинейными характеристиками. Процессы в нем описываются нелинейными дифференциальными уравнениями.

В трансформаторе без ферромагнитного сердечника электрические процессы могут быть описаны линейными дифференциальными уравнениями, поэтому такой трансформатор называется линейным (рис. 2.52). Линейный двухобмоточный трансформатор можно рассматривать как две связанные катушки с линейной индуктивностью. Сопротивления  учитывают потерю энергии в обмотках трансформатора. При необходимости в эквивалентной схеме можно учесть также межвитковые и межобмоточные емкости, которые, как правило, не оказывают существенного влияния на работу трансформатора в в рабочем диапазоне частот. Понятие "линейного трансформатора" оказывается полезным не только при анализе процессов в трансформаторах без ферромагнитного сердечника. В ряде случаев, когда нелинейность магнитных материалов не оказывает существенного влияния на характеристики трансформатора с ферромагнитным сердечником, его приближенно рассматривают как линейный и представляют при анализе цепей с помощью линейной схемы замещения.

Используя компонентные уравнения связанных индуктивностей (2.158), составим уравнения баланса напряжений идеализированной цепи, схема которой изображена на рис. 2.52:

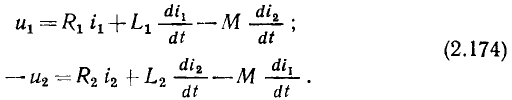
Ограничивая рассмотрение случаем гармонического внешнего воздействия, перейдем в (2.174) от мгновенных значений токов и напряжений к их комплексным изображениям:

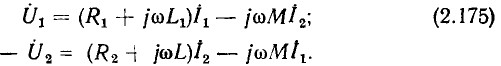
Система уравнений (2.175) при сделанных допущениях описывает соотношения между токами и напряжениями на зажимах трансформаторов различных типов, которые можно приближенно считать линейными, и служит основой для анализа различных цепей с трансформаторами при гармоническом внешнем воздействии.

Пусть в рассматриваемом линейном двухобмоточном трансформаторе ток вторичной обмотки = 0 (режим холостого хода на выходе). Как видно из выражений (2.175), ток первичной обмотки 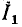в этом случае не равен нулю:

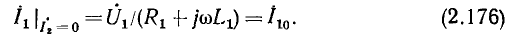
Ток 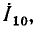потребляемый трансформатором от источника в режиме холостого хода на выходе, называется током намагничивания. При заданной угловой частоте и конечной амплитуде напряжения первичной обмотки ток намагничивания уменьшается с ростом индуктивности первичной обмотки 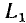и обращается в нуль при

Решим систему уравнений (2.175) относительно напряжения и тока первичной обмотки:

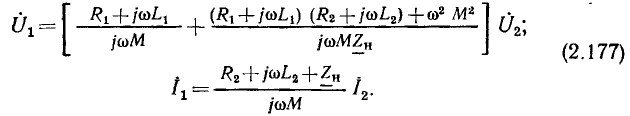
Из выражений (2.177) видно, что напряжение 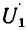и ток 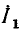 первичной обмотки линейного трансформатора пропорциональны соответственно напряжению 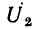и току  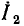вторичной обмотки, причем коэффициенты пропорциональности в обоих случаях зависят от сопротивления нагрузки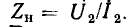

В теории цепей большое значение имеют понятия «совершенного» и «идеального» трансформатора.

Совершенным трансформатором называется идеализированный четырехполюсный элемент, представляющий собой две связанные индуктивности с коэффициентом связи, равным единице. Из определения следует, что в таком трансформаторе (рис. 2.53, а) отсутствуют потоки рассеяния и не происходит запасания энергии в электрическом поле или преобразования электрической энергии и в другие виды энергии. Полагая в выражениях (2.177) 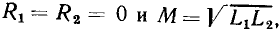 получаем уравнения, определяющие зависимости между токами ^напряжениями обмоток совершенного трансформатора:

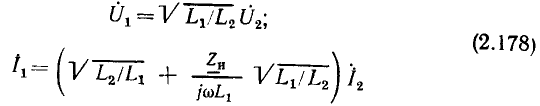
Величина

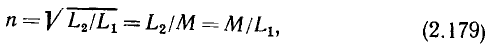
входящая в уравнения (2.178), получила название коэффициента трансформации. Подставляя в (2.179) выражения для индуктивностей катушек (2.155) - рвения для И их взаимных индуктивностей (2.156), находим, что коэффициент трансформации равен отношению числа витков вторичной обмотки к числу витков первичной обмотки

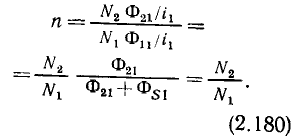
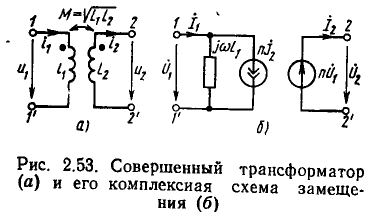
(Напомним, что потоки рассеяния совершенного трансформатора равны нулю, т.е.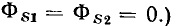 

Используя выражения (2.176) и (2.179), преобразуем уравнения (2.178) к виду

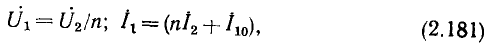
где 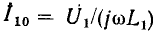 - ток намагничивания совершенного трансформатора.

Согласно выражениям (2.181) отношение напряжения на вторичной совершенного трансформатора к напряжению на первичной обмотке равно коэффициенту трансформации и не зависит от сопротивления нагрузки. Выражениям (2.181) соответствует комплексная комплексная схема замещения совершенного трансформатора, приведенная на рис. 2.53, б.

Совершенный трансформатор, ток намагничивания которого равен нулю, называется идеальным. Из выражений (2.181) видно что ток намагничивания совершенного трансформатора равен нулю только при Подставляя в (2.181) 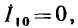получаем компонентные уравнения идеального трансформатора

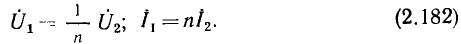
Аналогичный вид будут иметь и соотношения между мгновенными значениями токов и напряжений идеального трансформатора:

Комплексная схема замещения идеального трансформатора изображена па рис. 2.54, а, схема замещения для мгновенных значений на рис. 2.54, б.

Из компонентных уравнений (2.182) и (2.183) следует, что при любом значении сопротивления нагрузки отношение напряжения вторичной обмотки к напряжению первичной обмотки идеального трансформатора равно отношению токов первичной и вторичной обмоток:

В связи с тем что коэффициент трансформации n является действительным числом, напряжение и ток первичной обмотки имеют такие же начальные и мгновенные фазы, как соответственно напряжение и ток вторичной обмотки, и отличаются от них только по амплитуде (действующему значению). Из выражений (2.184) следует, что мгновенная и комплексная мощности, потребляемые первичной обмоткой, равны мгновенной и комплексной мощностям, отдаваемым идеальным трансформатором в нагрузку:

Очевидно, что к.п.д. идеального трансформатора равен единице.

Если к зажимам 2 — 2' идеального трансформатора подключено сопротивление нагрузки 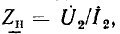то его входное сопротивление со стороны зажимов                 1—1' 

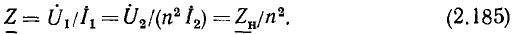
Таким образом, входное сопротивление идеального трансформатора имеет такой же характер, как и сопротивление нагрузки, и отличается от него по модулю в раз. Способность трансформаторов преобразовывать «модуль» сопротивления широко используется в радиоэлектронных устройствах для согласования сопротивления источника энергии с нагрузкой.

В отличие от идеального в реальном трансформаторе происходят потери энергии, он характеризуется в ряде случаев значительными паразитными емкостями, индуктивность его обмоток имеет конечное значение, а потоки рассеяния не равны нулю. Как правило, при разработке конструкции трансформатора предпринимается ряд мер, направленных на приближение его свойств к свойствам идеального трансформатора. С этой целью, в частности, обмотки трансформатора размещают на ферромагнитном сердечнике с высоким значением эффективной магнитной проницаемости. Применение сердечника увеличивает индуктивность обмоток, а также коэффициент связи и приводит к снижению тока намагничивания. Рациональным выбором материалов и конструкции трансформатора добиваются также уменьшения межвитковых и межобмоточных емкостей и снижения всех видов потерь энергии. В зависимости от степени приближения свойств реального трансформатора к свойствам идеального при анализе цепей его можно представлять одной из эквивалентных схем, приведенных на рис. 2.52—2.54, или привлекать более сложные, например нелинейные, схемы замещения.

Пример 2.14.

Рассмотрим применение трансформаторов для согласования источника энергии с нагрузкой. Пусть оптимальное (по какому-либо критерию) сопротивление нагрузки источника энергии равно Сопротивление же нагрузки, например динамического громкоговорителя, равно 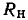и подлежит регулировке. Если эту нагрузку подключить к источнику энергии через согласующий трансформатор с коэффициентом трансформации 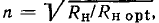свойства которого близки к свойствам идеального трансформатора, то в соответствии с (2.185) входное сопротивление трансформатора 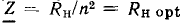и источник энергии окажется нагруженным на сопротивление, равное оптимальному.