Линейные н нелинейные диэлектрики и конденсаторы

Линейные н нелинейные диэлектрики и конденсаторы:

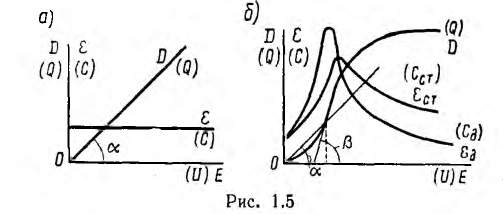
В линейных диэлектриках диэлектрическая проницаемость не зависит от напряженности поля и характеристика D (Е)  для них изображается прямой линией (рис. 1.5, а).

Тогда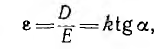

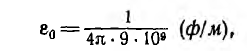
равной диэлектрической проницаемости вакуума.

У большинства нелинейных диэлектриков проницаемость очень велика и зависит от напряженности поля.

Первым из подобных материалов была сегнетова соль, детально исследованная в 1930— 1934 гг. И. В. Курчатовым и П. П. Кобеко и давшая название этой группе диэлектриков — сегнетоэлектрики.

Для образца, впервые подвергающегося воздействию электрического поля, зависимость D(Е) —кривая первоначальной поляризации—представлена на рис. 1.5, б. Для нелинейных материалов возможны два определения диэлектрической проницаемости:

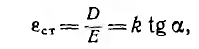
называемая статической проницаемостью и пропорциональная тангенсу угла а наклона секущей в данной точке, и называемая дифференциальной проницаемостью и пропорциональная тангенсу угла 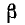наклона касательной в той же точке. Обе величины являются функциями напряженности поля.

Первая используется для расчета статических режимов при неизменном значении напряженности поля, вторая определяет изменение смещения с изменением напряженности поля и используется для расчета динамических процессов при достаточно медленных изменениях напряженности поля.

При быстрых изменениях поля характеристика D (В) называется динамической и отличается от приведенной на рис. 1.5, б статической характеристики. Проницаемость, определяемая значением производной 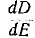из динамической характеристики, называется динамической проницаемостью.

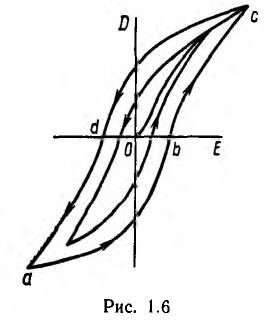
В периодически изменяющихся электрических полях в сегнетоэлектриках имеет место явление диэлектрического гистерезиса (рис. 1.6), заключающееся в несовпадении кривой D (Е) при возрастании напряженности поля (abc) с кривой при убывании поля (cda). Кривая Ос, соединяющая вершины петель гистерезиса, соответствующих разной максимальной напряженности, называется основной кривой поляризации-кривая практически совпадает с кривой первоначальной поляризации. Сегнетоэлектрические свойства зависят от температуры и проявляются лишь в определенном ее интервале.

Основным соотношением для конденсатора является зависимость заряда Q от напряжения U, называемая кулонвольтной характеристикой.

В соответствии с используемым диэлектриком конденсаторы по виду кулонвольтных характеристик делятся на линейные и нелинейные.

Кулонвольтные характеристики Q (U) аналогичны кривым D (Е), так как Q ~ D, a U ~ Е; поэтому кривые рис. 1.5, а и б соответствуют эти емкости совпадают.

Нелинейные конденсаторы находят все большее применение в автоматике, радиотехнике и т. д. Аналогично нелинейным емкостям в нелинейных системах вводятся статическая взаимоемкость и дифференциальная, а также динамическая взаимоемкость

Расчет емкости нелинейного конденсатора может быть произведен,
если задана зависимость D (Е) или е (Е). Так как эти зависимости
теоретически не выводятся, то для приближенного решения подбирают
по кривой D (Е) аппроксимирующую функцию.

Далее приведен пример подобного расчета плоского конденсатора, для которого
также кулонвольтным характеристика с при величинах, указанных в скобках.
Для нелинейных конденсаторов вводятся понятия статической емкости

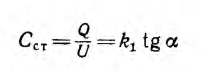
и дифференциальной, а также динамической емкости

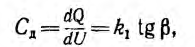
являющихся функциями напряжения (см. рис. 1.5, б). Для линейных конденсаторов эти емкости совпадают. Нелинейные конденсаторы нахожят все большое применение в автоматике.

Аналогично нелинейным емкостям в нелинейных емкостях вводятся статистическая взаимоемкость

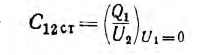
и дифференциальная, а также динамическая взаимоемкость

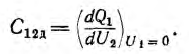
Емкость плоского нелинейного конденсатора

Расчет емкости нелинейного конденсатора может быть произведен, если задана зависимость D(Е) или е(Е). Так как эти зависимости теоретически не выводятся, то для приближенного решения подбирают по кривой D (Е) аппроксимирующую функцию. Далее приведен пример подобного расчета плоского конденсатора,
для которого

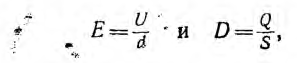
где d — толщина диэлектрика; S — площадь пластин.

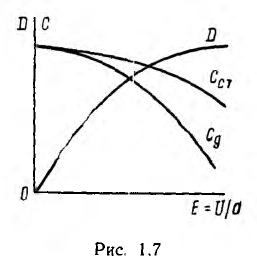
Пусть аппроксимирующая функция для характеристики (рис. 1.7) будет

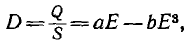
где а и b — постоянные.

Для определения емкости, как функции напряжения, надо подставить в это уравнение :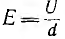

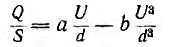
откуда статическая емкость

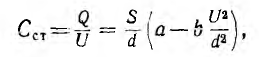
а дифференциальная емкость

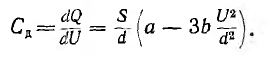
Кривые обеих емкостей в функции напряжения представлены на рис. 1.7.