
Линейные электрические цепи
Содержание:
Линейные электрические цепи:
Простая электрическая цепь состоит из источника и приемника электрической энергии. Если приемник представляет собой резистор, имеющий сопротивление R или проводимость G (рис. 3.1, а), то ток I и напряжение U источника связаны
законом Ома:
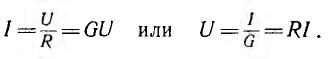
Для расчета электрических цепей и необходимо учитывать направление токов и напряжений. Хотя в общем случае ток является движением электрических зарядов разных знаков в противоположные стороны, условным положительным направлением тока принято считать направление перемещения положительных зарядов, т.е. в приемнике - от положительного зажима источника к отрицательному. Если ток идет в противоположном направлении, он получает отрицательный знак.
В соответствии с равенством U = RI положительное направление напряжения совпадает с положительным направлением тока, для встречного направления тока напряжение также получает отрицательный знак. Если направление тока (напряжения) неизвестно, его приходится выбирать произвольно и определять направление в результате расчета по знаку тока (напряжения).
В дальнейшем в большинстве случаев для краткости условное положительное направление называется просто направлением.
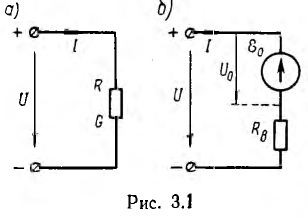
В цепи рис. 3.1, а источник расходует энергию, переходящую в сопротивлении в тепло; при этом мощность определяется законом Джоуля — Ленца:
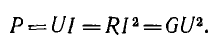
В системе СИ единицей мощности является в•а = вт (ватт).
Примером приемников, преобразующих электрическую энергию в другие виды, может служить индуктивный электрический двигатель. Как показано, в двигателе возникает э. д. с. индукции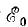 , направленная навстречу приложенному напряжению, а следовательно, и току; кроме того, двигатель имеет, очевидно, внутреннее сопротивление RB. Такого рода приемник может быть представлен в виде схемы, показанной на рис. 3.1, б. Аналогичен случай зарядки аккумулятора, когда ток направлен против э. д. с. аккумулятора, за счет чего и происходит превращение электрической энергии в химическую.
, направленная навстречу приложенному напряжению, а следовательно, и току; кроме того, двигатель имеет, очевидно, внутреннее сопротивление RB. Такого рода приемник может быть представлен в виде схемы, показанной на рис. 3.1, б. Аналогичен случай зарядки аккумулятора, когда ток направлен против э. д. с. аккумулятора, за счет чего и происходит превращение электрической энергии в химическую.
Таким образом, в этих случаях в цепи действует напряжение U источника и встречная э.д.с. 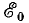 приемника, и выражение для тока по закону Ома получает вид:
приемника, и выражение для тока по закону Ома получает вид:
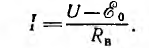
Однако такой приемник можно заменить эквивалентным сопротив
лением. Так как напряжение U0 на участке цепи с э.д.с. 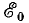 по величине равно
по величине равно 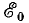 и направлено ей навстречу, т.е. U0 = —
и направлено ей навстречу, т.е. U0 = —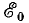 , эквивалентное сопротивление этого участка
, эквивалентное сопротивление этого участка
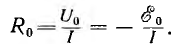
Иногда расчет цепей упрощается, если произвести обратную замену какого-либо сопротивления R0, по которому проходит ток I эквивалентной э. д. с., равной, очевидно,
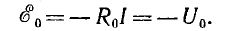
Отрицательный знак указывает на то, что эквивалентная э.д.с. направлена навстречу току.
Сложная электрическая цепь и ее графическое изображение, называемое схемой, состоит из ветвей. Ветвью называется участок, по которому проходит один и тот же ток. Точки, в которых сходятся не менее трех ветвей, называются узлами. В сложной цепи и ее схеме всегда имеются несколько замкнутых контуров, состоящих из разных ветвей.
Для любого узла на основе принципа непрерывности тока может быть написан первый закон Кирхгофа:
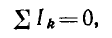
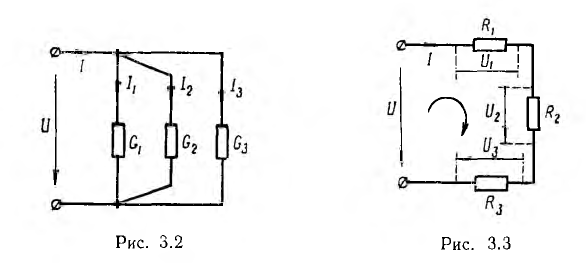
т. е. алгебраическая сумма токов в ветвях, образующих узел, равна нулю. При этом токи, уходящие от узла, считаются положительными, а токи, приходящие к узлу — отрицательными (или наоборот). Например, в параллельной цепи с одним источником (рис. 3.2) токи совпадают по направлению с напряжением и для каждого из двух узлов цепи можно написать:
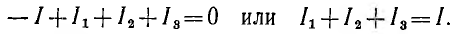
Деление этого равенства на общее для всех ветвей напряжение U дает:
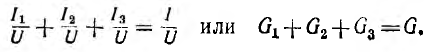
Следовательно, проводимость всей цепи равна сумме проводимостей параллельно соединенных приемников.
Если выразить напряжения на ветвях, образующих любой контур, через потенциалы ϕ узлов, к которым примыкают ветви, то сумма этих напряжений
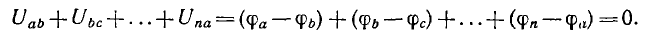
Это и есть второй закон Кирхгофа:
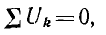
т.е. алгебраическая сумма напряжений на ветвях, образующих контур, равна нулю. При этом напряжения ветвей, у которых потенциал первого по направлению обхода узла выше, чем второго, считаются положительными, остальные — отрицательными. Применяя это правило для последовательной цепи с одним источником и учитывая, что все напряжения совпадают по направлению с током, для указанного на рис. 3.3 направления обхода надо написать:
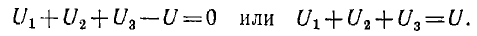
Деление этого равенства на общий для всей цепи ток I дает
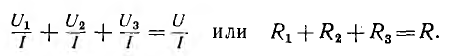
Следовательно, сопротивление всей цепи равно сумме сопротивлений последовательно соединенных приемников.
Основной задачей расчета электрической цепи является ее анализ, который обычно заключается в определении токов, напряжений и мощностей ветвей цепи по заданным их сопротивлениям или проводимостям и по заданным источникам электрической энергии. Эти задачи имеют однозначное решение, которое для линейных цепей может быть получено составлением и решением системы алгебраических уравнений с учетом законов Кирхгофа, Ома и Джоуля— Ленца.
Второй важной задачей расчета цепей является синтез, т. е. создание цепи с заданными свойствами.
Источники напряжения и тока и их эквивалентность
В зависимости от принципа действия источники электрической энергии можно разделить на источники напряжения (э.д.с.) и источники тока. Так, например, химические источники электрической энергии основаны на возникновении разности потенциалов между различными электродами, помещенными в электролит. Эта разность потенциалов, наибольшая при разомкнутой цепи, т. е. при холостом ходе, и называется э. д. с.  . При нагрузке разность потенциалов становится меньше э. д. с.
. При нагрузке разность потенциалов становится меньше э. д. с. 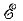 из-за появления встречной э.д.с. поляризации и падения напряжения во внутреннем сопротивлении и называется напряжением U.
из-за появления встречной э.д.с. поляризации и падения напряжения во внутреннем сопротивлении и называется напряжением U.
Индуктивные генераторы основаны на возникновении э.д.с. индукции при изменении магнитного поля . При нагрузке их напряжение U также становится меньше э. д. с.  холостого хода, в частности из-за падения напряжения во внутреннем сопротивлении.
холостого хода, в частности из-за падения напряжения во внутреннем сопротивлении.
Таким образом, эти источники являются источниками напряжения; при расчете цепей источники напряжения обычно заменяются эквивалентной схемой (рис. 3.4), состоящей из последовательного соединения источника постоянной э.д.с.  и внутреннего сопротивления RB, величина которого учитывает все причины изменения напряжения при нагрузке.
и внутреннего сопротивления RB, величина которого учитывает все причины изменения напряжения при нагрузке.
Как было принято, направление напряжения Uсовпадает с направлением тока I во внешней цепи — от плюса к минусу, что может быть учтено индексом ±, т. е. U+. Тогда э. д. с. в источнике, также совпадающая по направлению с током, но текущим в источнике от минуса к плюсу, должна быть обозначена 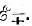 . При холостом ходе
. При холостом ходе 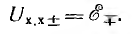
При нагрузке можно применить закон Ома, сложив внешнее R и внутреннее RB сопротивления:
откуда 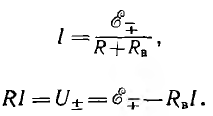
Обычно это соотношение записывают без индексов: 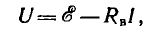 но при этом следует помнить о противоположных положительных направлениях U и
но при этом следует помнить о противоположных положительных направлениях U и 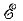 .
.
При внешних сопротивлениях R, много больших, чем внутреннее сопротивление 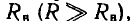 , напряжение U остается практически постоянным
, напряжение U остается практически постоянным 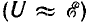 .при изменении R.
.при изменении R.
Емкостные генераторы основаны на возникновении тока при изменении электрического поля. При коротком замыкании они отдают во внешнюю цепь весь генерируемый ими внутренний ток J.
При нагрузке, т. е. включении сопротивления, появляется напряжение, и ток внешней цепи I становится меньше J, в частности, из-за
утечки через несовершенную изоляцию генератора.
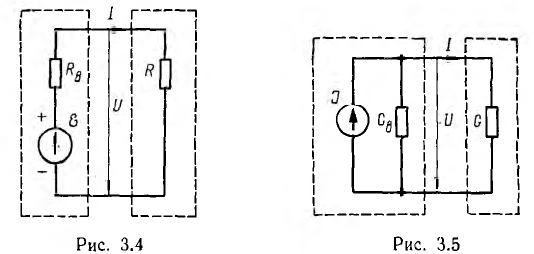
Таким образом, этот источник электрической энергии является источником тока. При расчете цепей он обычно заменяется эквивалентной схемой (рис. 3.5), состоящей из параллельного соединения источника постоянного внутреннего тока J и внутренней проводимости GB, величина которой учитывает все причины изменения внешнего тока при нагрузке. Тогда напряжение U и ток I в проводимости G нагрузки будут:
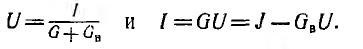
При проводимостях G нагрузки, много больших, чем внутренняя проводимость 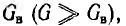 ток I нагрузки остается практически неизменным
ток I нагрузки остается практически неизменным 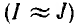 при изменении G.
при изменении G.
При расчете цепей принцип действия реальных источников электрической энергии несуществен и источник напряжения может быть заменен источником тока, ему эквивалентным, т. е. таким, который не вызовет изменения напряжений и токов остальных участков цепи.
Аналогично всякий источник тока может быть заменен эквивалентным ему источником напряжения. Такие замены в ряде случаев упрощают расчеты. Так как каждый из этих источников определяется двумя параметрами (см. рис. 3.4 и 3.5), условиями эквивалентности должны быть два равенства, например, равенство напряжений при холостом ходе 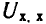 и токов при коротком замыкании
и токов при коротком замыкании 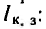
откуда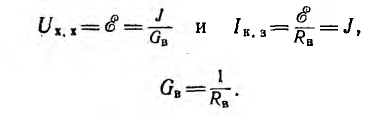
Таким образом, источник тока, эквивалентный источнику напряжения, должен генерировать ток, равный току короткого замыкания источника напряжения, и иметь параллельное внутреннее сопротивление, равное последовательному внутреннему сопротивлению источника напряжения.
Положительное направление тока J выбирается таким, чтобы направление тока во внешней цепи осталось тем же.
При равенстве полезных мощностей Р=UI, отдаваемых эквивалентными источниками во внешнюю цепь, полные мощности (т. е. вместе с потерями в их внутреннем сопротивлении) Рн источника напряжения и Рт источника тока
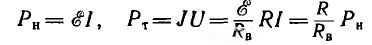
и их к.п.д., равные отношению полезной мощности к полной их мощности,
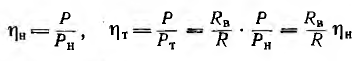
в общем случае не равны между собой. К. п. д. 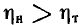 при
при 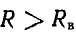 а
а 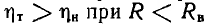 и лишь при R = Rв полные мощности и к.п.д. эквивалентных источников становятся одинаковыми.
и лишь при R = Rв полные мощности и к.п.д. эквивалентных источников становятся одинаковыми.
Линия передачи и работа источника на нагрузку
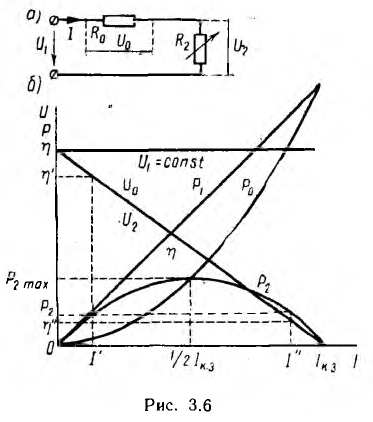
В качестве первой, наиболее простой задачи на расчет цепи практический интерес представляет исследование передачи энергии постоянным током (рис. 3.6, а) от источника с постоянным напряжением U1 через постоянное сопротивление R0 обоих проводов линии к переменному сопротивлению R2 нагрузки.
Если пренебречь током утечки между проводами линии через несовершенную изоляцию, то ток цепи
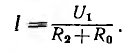
По мере уменьшения R2 ток I будет расти от нуля при холостом ходе (R2 =  ) до максимального значения
) до максимального значения 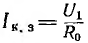 при коротком замыкании (R2= 0).
при коротком замыкании (R2= 0).
В дальнейшем ток I принят за независимую переменную и отложен по оси абсцисс графика рис. 3.6, б.
Напряжение на сопротивлении R0 линии, часто называемое падением напряжения в линии и равное U0 =R0l, растет линейно с током от нуля (холостой ход) до U1 (короткое замыкание).
Напряжение на приемнике
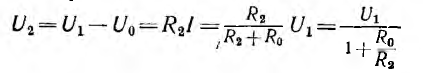
при холостом ходе равно U1; с уменьшением R2 напряжение U2 тоже
уменьшается до нуля при коротком замыкании. График изменения U0 и U2 представляет собой прямую, причем U2 отсчитывается от оси абсцисс, a U0 — от горизонтали U1 = const.
Мощность, отдаваемая источником энергии в цепь,
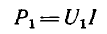
растет пропорционально току.
Мощность, расходуемая в линии (потери),
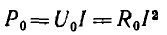
возрастает пропорционально квадрату тока и при коротком замыкании становится равной мощности источника.
Мощность, потребляемая приемником (полезная мощность),
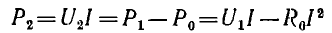
равна нулю при холостом ходе (I = 0) и при коротком замыкании (U2 = 0). Из исследования Р2 (I) на максимум:
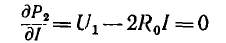
вытекает, что Р2 имеет максимум при 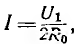 т. е. при R2 = R0.
т. е. при R2 = R0.
Следовательно, при равенстве сопротивлений приемника R2 и линии R0 полезная мощность получает максимальное значение:
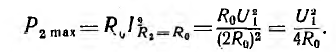
Зависимости 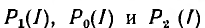 также приведены на рис. 3.6, б.
также приведены на рис. 3.6, б.
К.п. д. η электропередачи равен отношению полезной мощности к мощности источника:
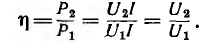
Он равен нулю при коротком замыкании и изменяется, как и U2, по линейному закону, стремясь к единице при холостом ходе. При передаче максимальной мощности к. п. д. равен 0,5; при этом напряжение приемника равно половине напряжения источника.
Из рис. 3.6, б видно, что мощность 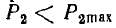 может быть передана при двух режимах, отмеченных одним и двумя штрихами, причем в первом режиме к.п.д. и напряжение на приемнике будут больше, а ток — меньше, чем во втором. Следовательно, из всех физически возможных режимов работы технически целесообразными будут режимы в левой части графика до
может быть передана при двух режимах, отмеченных одним и двумя штрихами, причем в первом режиме к.п.д. и напряжение на приемнике будут больше, а ток — меньше, чем во втором. Следовательно, из всех физически возможных режимов работы технически целесообразными будут режимы в левой части графика до 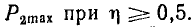 .
.
Режим передачи максимальной мощности применяется в маломощных линиях связи, так как там низкий к. п. д. роли не играет. Передача больших мощностей осуществляется при высоких значениях к. п. д., причем величина оптимального к. п. д., а следовательно, потерь определяется экономическими расчетами. При этом допустимые потери Р0 выражаются в долях полезной мощности P2: 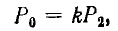 где коэффициент потерь k равен 2÷10%. При передаче мощности P2 на расстояние l (длина проводов 21) при напряжении U2 и, следовательно токе
где коэффициент потерь k равен 2÷10%. При передаче мощности P2 на расстояние l (длина проводов 21) при напряжении U2 и, следовательно токе 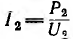 эти потери
эти потери
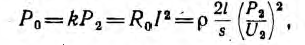
откуда определяется необходимое сечение проводов
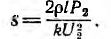
Из этого выражения видно преимущество высокого напряжения: при той же передаваемой мощности сечение провода обратно пропорционально квадрату напряжения. Однако с ростом напряжения увеличивается стоимость изоляции линии. На практике применяют тем большее напряжение, чем больше передаваемая мощность Р2 и дальность передачи I.
Потери в проводах превращаются в тепло и повышают их температуру. В нормах для всех типов и стандартных сечений проводов указан максимально допустимый ток по условиям нагрева. Поэтому полученное по расчету сечение, округленное до ближайшего стандартного, может быть применено лишь в том случае, когда допустимый для него ток равен или больше тока линии; в противном случае приходится выбирать большее сечение.
Первая передача электрической энергии постоянным током была осуществлена Ф. А. Пироцким в Петербурге в 1874 г. от генератора 6 л. с. на расстояние 200 м. В 1880 г. Д. А. Лачинов в статье «Электромеханическая работа» показал, что при больших расстояниях можно сохранить высокий к. п. д. передачи, если увеличить напряжение.
В 1882 г. Депре построил линию передачи от гидроэлектростанции в Мисбахе до Мюнхена длиной 57 км при напряжении около 1000 в, с полезной мощностью 0,25 л.с. и к.п.д. 60%.
В последующие годы линии постоянного тока получили распространение только для передачи небольших мощностей на малые расстояния; для дальних и мощных электропередач стал широко применяться переменный ток, позволяющий весьма просто в начале линии повышать, а в конце понижать напряжение с помощью трансформаторов. В некоторых случаях мощных передач оказалась целесообразной также передача энергии постоянным током, но при сверхвысоком напряжении. В СССР уже ряд лет работает электропередача постоянным током из Волгограда в Донбасс мощностью 720 000 квт при напряжении 800 кв.
Полученные выводы можно перенести на задачу о работе источника напряжения (см. рис. 3.4.) на переменную нагрузку, заменив напряжение их на э.д.с. 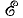 источника, сопротивление R0 линии на внутреннее сопротивление RB источника и обозначив переменную нагрузку R2 через R. Следовательно, источник будет отдавать приемнику максимальную мощность при R = RB но при этом такая же мощность будет расходоваться внутри источника. Обычно источники напряжения работают в более экономичном режиме, когда сопротивление нагрузки в несколько раз превышает внутреннее сопротивление источника.
источника, сопротивление R0 линии на внутреннее сопротивление RB источника и обозначив переменную нагрузку R2 через R. Следовательно, источник будет отдавать приемнику максимальную мощность при R = RB но при этом такая же мощность будет расходоваться внутри источника. Обычно источники напряжения работают в более экономичном режиме, когда сопротивление нагрузки в несколько раз превышает внутреннее сопротивление источника.
Расчет цепей методами преобразования и пропорционального пересчета
Метод преобразования заключается в замене участков цепи более простыми, им эквивалентными, т. е. не вызывающими изменения напряжений и токов в остальной части цепи.
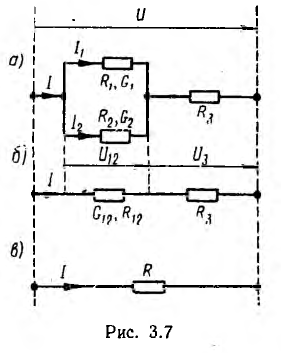
При расчете цепи со смешанным, т. е. параллельно-последовательным соединением приемников, питаемой одним источником (например, рис. 3.7, а) группа приемников, соединенных параллельно, заменяется одним, им эквивалентным (рис. 3.7, б), с проводимостью
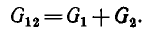
Группа приемников, соединенных последовательно, заменяется одним, им эквивалентным (рис. 3.7, в), с сопротивлением 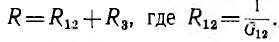
После замены всей цепи одним приемником определяется его ток I при заданном напряжении или напряжение при заданном токе.
Затем схема постепенно разворачивается в первоначальную цепь с попутным определением напряжений и токов отдельных приемников:
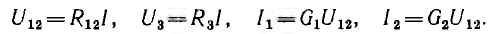
Эту же задачу можно решить методом пропорционального пересчета, задавшись током в одной из параллельных ветвей, что позволит определить напряжения и токи всех ветвей и напряжение всей цепи U', отличное от заданного напряжения U. Так как в линейной цепи токи пропорциональны напряжениям, для получения правильного результата надо полученные значения умножить на U/U'.
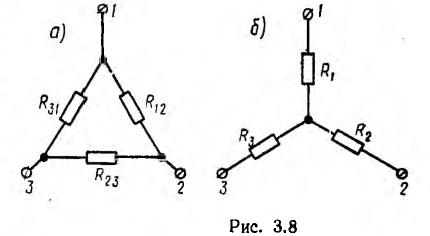
Методы преобразования и пропорционального пересчета применимы для некоторых цепей, не являющихся сочетанием последовательных и параллельных соединений. Их схемы состоят из гак называемых треугольников (рис. 3.8, а) и трехлучевых звезд (рис. 3.8, б). Примером может служить неуравновешенный мост (рис. 3.9, а). Контуры I-2-3-1 и 2-3-4-2 этой цепи, состоящие из трех ветвей, являются треугольниками, узлы 2 и 3 — нулевыми точками звезд. Расчет такой цепи можно свести к задаче на смешанное соединение, если заменить один из треугольников эквивалентной ему звездой или одну из звезд эквивалентным ей треугольником.
Так, треугольник 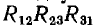 заменен на рис. 3.9, б звездой
заменен на рис. 3.9, б звездой 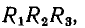 звезда
звезда 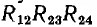 — треугольником
— треугольником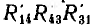 на рис. 3.9, в. Получившиеся цепи являются уже сочетанием последовательно-параллельных соединений и решаются указанными выше путями; затем совершается обратный переход к исходной цепи.
на рис. 3.9, в. Получившиеся цепи являются уже сочетанием последовательно-параллельных соединений и решаются указанными выше путями; затем совершается обратный переход к исходной цепи.
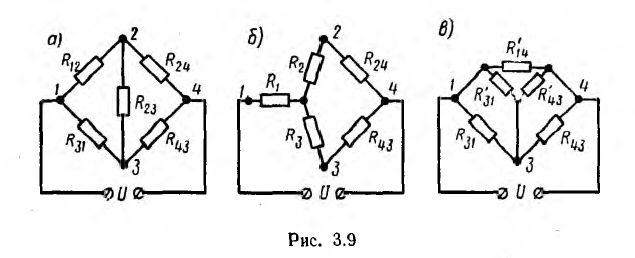
Для эквивалентности треугольника и звезды (см. рис. 3.8) необходимо и достаточно, чтобы результирующе сопротивление между каждой парой точек при отключенной третьей точке у обеих цепей было одинаковым. Так, для точек l, 2 при отключенной точке 3
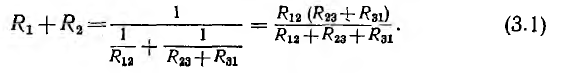
Аналогичные уравнения для точек 2, 3 и 3, 1 можно написать, пользуясь круговой перестановкой индексов 1 , 2 , 3:
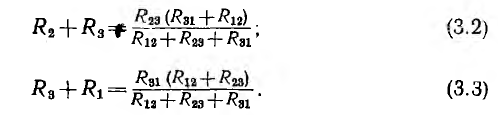
Складывая уравнения (3.1) и (3.3) и вычитая (3.2), можно получить переходные формулы от треугольника к звезде:
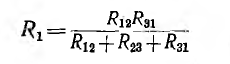
и далее по круговой перестановке
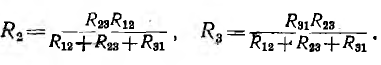
Для вычисления переходных формул от звезды к треугольнику удобно мысленно замкнуть у обеих цепей две одноименные пары точек и приравнять проводимости между этой общей точкой и третьей точкой.
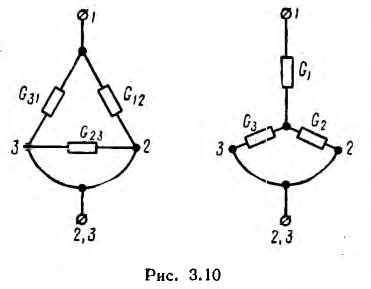
Так, между точкой 2, 3 и тoчкой 1 проводимости (рис. 3.10)
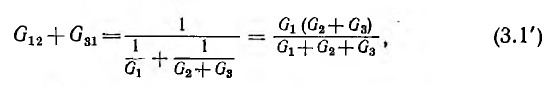
и далее по круговой перестановке индексов
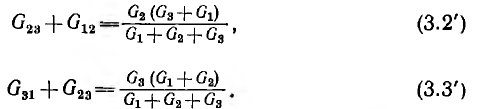
Решая аналогично предыдущему уравнения (З.1'), (3.2'), (3.3'), можно получить переходную формулу
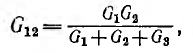
и далее по круговой перестановке
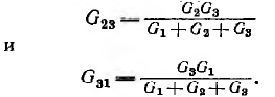
Давая общую оценку методам преобразования и пропорционального пересчета в изложенном виде, можно указать на их простоту, однако их применение ограничено цепями с одним источником энергии.
Расчет цепей по законам Кирхгофа
Две формы записи законов Кирхгофа:
Были даны оба закона Кирхгофа: первый — для узлов и втoрой — для контуров в следующей симметричной форме записи:
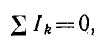
т. е. алгебраическая сумма токов в ветвях, сходящихся в узле, равна нулю.
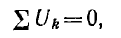
т. е. алгебраическая сумма напряжений на ветвях, входящих в контур, равна нулю.
Если между узлами цепи параллельно включены источник тока и приемник (рис. 3.11, а), можно объединить внутреннюю проводимость
GB с внешней G':
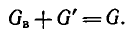
Если в ветви последовательно включены источник напряжения и приемник (рис. 3.11, б), можно объединить внутреннее сопротивление RB с внешним R':
RB + R’ = R.
Тогда для тока I в выходной ветви рис. 3.11, а и напряжения U на ветви рис. 3.11, б можно написать:

Эти равенства следует понимать алгебраически: знак минус сохраняется, когда источники отдают энергию, т. е. когда при выбранных направлениях напряжений и токов и обходе контура J, G (рис. 3.11, а) совпадают действительные направления J и U, а на рис. 3.11, б совпадают направления 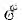 и I.
и I.
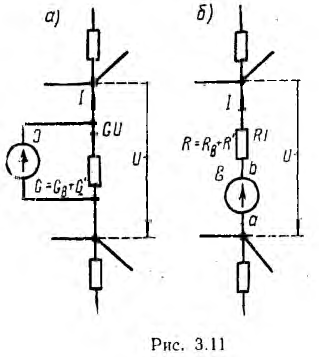
Подставляя эти соотношения в первую форму записи законов Кирхгофа, можно получить вторую симметричную форму их записи:
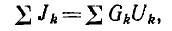
т.е. алгебраическая сумма внутренних токов источников тока в ветвях, сходящихся в узле, равна алгебраической сумме токов в проводимостях остальных ветвей этого узла.
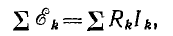
т.е. алгебраическая сумма э.д.с. источников напряжения, входящих в контур, равна алгебраической сумме напряжений на сопротивлениях ветвей этого контура.
Так как обычно источники электрической энергии задаются в виде
источников напряжения, первый закон Кирхгофа записывается в пер
вой форме, а второй — во второй, и система этих уравнений получает
следующий несимметричный вид:
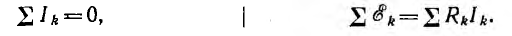
Составление уравнений по законам Кирхгофа
Обычно заданными являются величины и направления всех э. д. с. источников напряжения и внутренних токов источников тока и значения всех внутренних и внешних сопротивлений или проводимостей цепи, а определяют токи и по ним — напряжения ветвей. Поэтому число неизвестных равно числу р ветвей схемы и, следовательно, столько же независимых уравнений нужно составить по первому и второму законам Кирхгофа.
Так как при составлении уравнений необходимо учесть направления всех токов, направлениями токов следует задаться. Применяя первый закон в первой форме записи, токи, приходящие к узлу и уходящие от него, следует брать с разными знаками. Применяя второй закон во второй форме записи, э.д.с. и токи, направления которых совпадают с произвольно выбранным направлением обхода контура, следует считать имеющими положительный знак, остальные — отрицательный, или наоборот.
Уравнения, составленные по первому закону Кирхгофа для цепи с q узлами, будут независимыми лишь для q — 1 узлов, так как уравнение для последнего узла q является следствием предыдущих. Следовательно, по второму закону Кирхгофа надо составить р — (q— 1) = р — q + 1 независимых уравнений.
В большинстве случаев можно изобразить цепь на плоскости так, чтобы она была сочетанием элементарных контуров, не содержащих внутренних ветвей (рис.3.12). Уравнения, составленные для элементарных контуров, будут, очевидно, независимыми, а их число равно необходимому (доказывается в топологии — разделе геометрии).
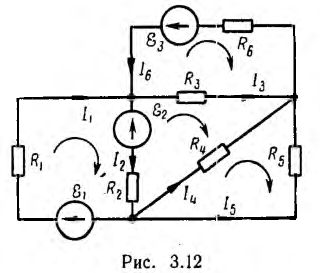
Уравнение для какого-либо другого контура будет, очевидно, следствием уравнений для элементарных контуров, охватываемых этим неэлементарным контуром. Поэтому выбор элементарных контуров для составления уравнений по второму закону Кирхгофа гарантирует от ошибок, возможных при использовании произвольных контуров цепи.
Например, для цепи рис. 3.12, имеющей р = 6 ветвей, q = 3 узла и р—q +1 = 4 элементарных контура, при указанных на схеме направлениях э.д.с., токов и обхода элементарных контуров, независимые уравнения, составленные по первому и второму законам Кирхгофа, имеют вид:
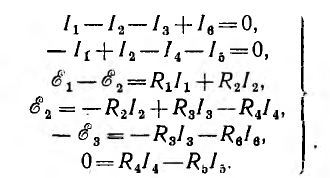
Решая систему уравнений любым известным из алгебры способом, находят все неизвестные токи ветвей. Отрицательный знак указывает на то, что действительное направление тока обратно выбранному.
После определения токов по закону Ома вычисляются напряжения, а по закону Джоуля—Ленца находят мощности. Достоинством рассмотренного метода является его общность, а недостатком — громоздкость решения системы, состоящей из большого числа уравнений. Поэтому кроме непосредственного использования уравнений по законам Кирхгофа применяются основанные на них излагаемые далее методы расчета сложных цепей, упрощающие их схемы (методы наложения и эквивалентного источника энергии) и методы, уменьшающие число неизвестных (методы контурных токов и узловых напряжений).
Метод наложения
Если для узлов и контуров любой электрической цепи, содержащей источники напряжения с э. д. с. 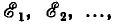 написать уравнения по законам Кирхгофа:
написать уравнения по законам Кирхгофа:
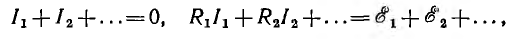
получается система линейных уравнений, из которой ток каждой ветви определяется однозначно.
Если поочередно предположить, что в цепи существует только э. д. с. 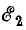 а остальные равны нулю, затем — только э.д.с.
а остальные равны нулю, затем — только э.д.с. 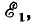 и т. д., можно для каждой э.д.с. вычислить соответствующие ей токи ветвей, составив уравнения по законам Кирхгофа при тех же направлениях э. д. с. и токов:
и т. д., можно для каждой э.д.с. вычислить соответствующие ей токи ветвей, составив уравнения по законам Кирхгофа при тех же направлениях э. д. с. и токов:
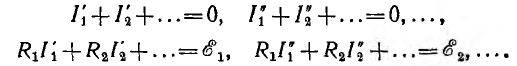
Сложение почленно этих уравнений
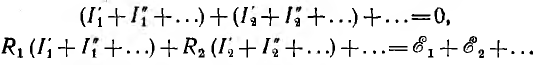
даст систему, которая также имеет единственное решение для всех неизвестных 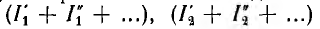 и т. д. Из сравнения исходных и только что полученных уравнений, имеющих одинаковые коэффициенты и правые части, видно, что решения обеих систем должны совпадать и, следовательно,
и т. д. Из сравнения исходных и только что полученных уравнений, имеющих одинаковые коэффициенты и правые части, видно, что решения обеих систем должны совпадать и, следовательно,
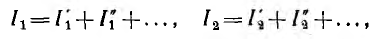
т. е. ток каждой ветви цепи равен алгебраической сумме токов этой ветви, протекающих под действием каждой э. д. с. в отдельности. Это частный случай известного принципа наложения.
На принципе наложения основан метод наложения. Он состоит в определении и последующем суммировании, т. е. наложении, токов ветвей от каждой э.д. с. в отдельности. При этом остальные э. д. с. приравниваются нулю, т. е. нужно мысленно их удалить и представить замкнутыми накоротко каждую пару тех точек цепи, между которыми действуют эти э. д. с. (например, точки а и b на рис. 3.11, 6 ). Тогда от этих источников в цепи остаются только их внутренние сопротивления.
Напряжение на каком-либо участке цепи с сопротивлением R
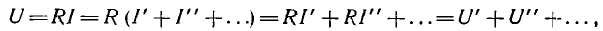
т. е. напряжение на участке цепи равно алгебраической сумме напряжений для каждой составляющей тока. Следовательно, и при определении напряжений может быть применен метод наложения.
Суммируя токи от отдельных групп э. д. с., можно прийти к заключению, что метод наложения справедлив также и для токов и для напряжений от отдельных групп э. д. с., на которые можно произвольно разбить все э. д. с., действующие в цепи.
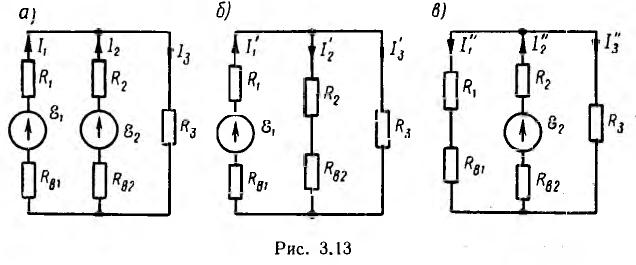
Метод наложения целесообразно применять в том случае, если, приравнивая нулю все э. д. с., кроме одной (или их группы), упрощают цепь. Например, для цепи рис. 3.13, а при 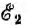 = 0 или
= 0 или 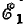 = О получаются, соответственно, параллельно-последовательные цепи рис. 3.13, б и в, легко рассчитываемые методом преобразования. При этом действительное направление составляющих токов определяется направлением э. д. с. и, выбирая произвольно направления результирующих токов, при наложении следует совпадающие с ними по
= О получаются, соответственно, параллельно-последовательные цепи рис. 3.13, б и в, легко рассчитываемые методом преобразования. При этом действительное направление составляющих токов определяется направлением э. д. с. и, выбирая произвольно направления результирующих токов, при наложении следует совпадающие с ними по
знаку составляющие брать положительными, и наоборот. Так, для направлений токов, указанных на рис. 3.13, а — в,
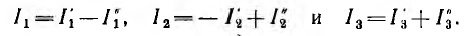
Принцип наложения, как видно из его доказательства, основан на линейном характере уравнений по законам Ома и Кирхгофа при постоянстве коэффициентов уравнений, т. е. сопротивлений цепи.
Очевидно, что принцип наложения справедлив и для случая, когда источниками энергии являются источники тока. Применяя метод наложения в этом случае и считая, например, несуществующим источник в какой-либо ветви, т. е. принимая его внутренний ток J = 0, следует представить себе цепь этого тока разомкнутой; тогда от источника тока в цепи остается только его внутренняя проводимость GB.
Необходимо отметить, что наложение неприменимо для мощностей, так как они являются квадратичными функциями токов и напряжений.
Метод взаимности
Пусть в первую ветвь Т-образной схемы, состоящей из трех разных сопротивлений R1, R2, R3, соединенных звездой (рис. 3.14, а), включена э. д. с. 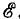 , а выходные зажимы замкнуты (рис. 3.14, б).
, а выходные зажимы замкнуты (рис. 3.14, б).
Направление токов всех ветвей определяется направлением э. д. с. 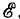
Ток I1 распределится между параллельно соединенными второй и третьей ветвями обратно пропорционально их сопротивлениям.
Тогда ток во второй ветви
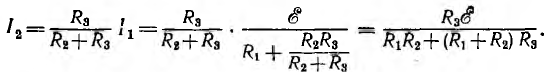
Если поменять местами индексы 1 и 2, очевидно, получится значение тока I1 в первой ветви при таком переносе э. д. с. 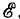 во вторую ветвь, чтобы ее направление совпало с направлением тока I2 (рис. 3.14, в).
во вторую ветвь, чтобы ее направление совпало с направлением тока I2 (рис. 3.14, в).
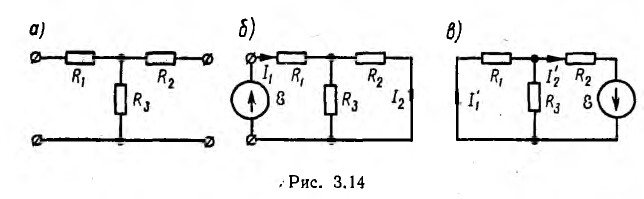
Выражение I2 симметрично относительно этих индексов, поэтому I1 = I2.
Как будет показано , Т-образная схема эквивалентна любой сложной цепи, не содержащей источников энергии и имеющей две пары зажимов. Следовательно, установленный принцип взаимности для Т-образной схемы имеет самый общий характер и может быть сформулирован следующим образом: если э.д.с. 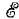 , действуя в любой ветви сколь угодно сложной цепи, не содержащей других э. д. с., вызывает в другой ветви ток I, то перенесенная в нее та же э. д. с. вызовет в первой ветви такой же ток I. Принцип взаимности был установлен Кирхгофом.
, действуя в любой ветви сколь угодно сложной цепи, не содержащей других э. д. с., вызывает в другой ветви ток I, то перенесенная в нее та же э. д. с. вызовет в первой ветви такой же ток I. Принцип взаимности был установлен Кирхгофом.
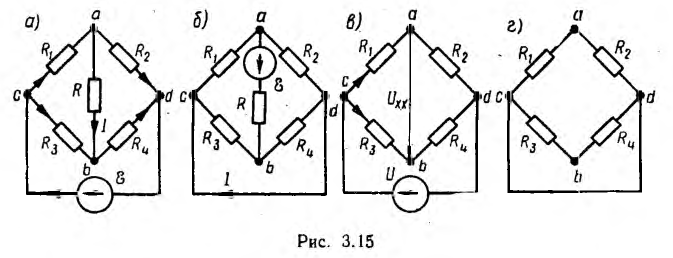
На принципе взаимности основан метод взаимности. Этот метод удобно применять для расчета цепей с одной э. д. с., когда ее перенос упрощает цепь. Пусть, например, в неуравновешенном мосте рис. 3.15, а требуется определить ток в диагонали R, причем источник напряжения не имеет внутреннего сопротивления. Направление токов во всех четырех сторонах моста определяется направлением э. д. с. 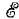 , направление тока I в диагонали выбрано произвольно. Перенос э. д. с.
, направление тока I в диагонали выбрано произвольно. Перенос э. д. с. 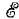 в эту диагональ (рис. 3.15, б) превращает сложную цепь в схему с последовательно-параллельным соединением сопротивлений.
в эту диагональ (рис. 3.15, б) превращает сложную цепь в схему с последовательно-параллельным соединением сопротивлений.
Так как в цепи рис. 3.15, а направление э. д. с. и тока в ветви источника совпадают, направление э. д. с., перенесенной в диагональ, должно также совпадать с выбранным направлением тока I в диагонали (см. рис. 3.15, б). Тогда ток в ветви, где раньше был источник, по величине и знаку равен искомому току I в диагонали.
Метод эквивалентного источника анергии
Этот метод применяется для определения тока (или напряжения) в сопротивлении (проводимости) одной ветви сложной цепи, Если эта ветвь содержит источники энергии, их следует считать принадлежащими к остальной части сложной цепи.
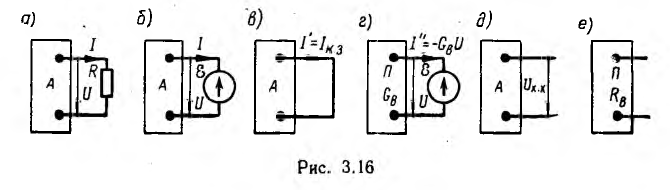
Ветвь, не содержащая источников энергии, называется пассивным двухполюсником, так как она включается в цепь с помощью двух зажимов. Цепь без этой ветви, условно показанная на рис. 3.16, а прямоугольником А, имеет также два зажима и из-за наличия источников носит название активного двухполюсника.
Для обоснования метода сопротивление R исследуемой ветви, заменяется эквивалентной э. д. с. 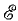 = — RI = —U (рис. 3.16, б), где I и U — искомые ток и напряжение, совпадающие по направлению, после чего применяется метод наложения в два этапа.
= — RI = —U (рис. 3.16, б), где I и U — искомые ток и напряжение, совпадающие по направлению, после чего применяется метод наложения в два этапа.
Сначала принимаются в расчет все источники энергии активного двухполюсника, а э. д. с. 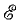 замыкается накоротко (рис. 3.16, в). Тогда ток I' ветви равен, очевидно, току Iк-в короткого замыкания активного двухполюсника, и совпадает , по направлению с током I. Затем учитывается только э. д. с. при этом в источниках напряжения, включенных в активный двухполюсник, замыкаются накоротко э.д. с., а в источниках тока — размыкаются цепи их внутренних токов . Активный двухполюсник превращается в пассивный П
замыкается накоротко (рис. 3.16, в). Тогда ток I' ветви равен, очевидно, току Iк-в короткого замыкания активного двухполюсника, и совпадает , по направлению с током I. Затем учитывается только э. д. с. при этом в источниках напряжения, включенных в активный двухполюсник, замыкаются накоротко э.д. с., а в источниках тока — размыкаются цепи их внутренних токов . Активный двухполюсник превращается в пассивный П
(рис. 3.16, г). Он содержит только внутренние сопротивления источников и все остальные сопротивления своих ветвей. Пусть эквивалентная проводимость этого двухполюсника относительно его зажимов равна GB. Тогда ток ветви для второго этапа, если считать его направление совпадающим с I', равен
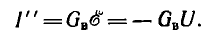
Действительный ток исследуемой ветви с проводимостью 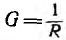 равен алгебраической сумме токов обоих этапов:
равен алгебраической сумме токов обоих этапов:
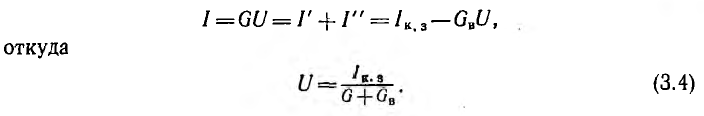
Из аналогии этой формулы с выражением для напряжения источника тока видно, что активный двухполюсник эквивалентен источнику тока (см. рис. 3.5) с внутренним током J, равным току Iкэ короткого замыкания двухполюсника, и с внутренней проводимостью GB, равной проводимости этого же двухполюсника, но без источников энергии.
Из выражения (3.4) следует, что при холостом ходе, т. е. при G = 0, напряжение на выходных зажимах двухполюсника будет:
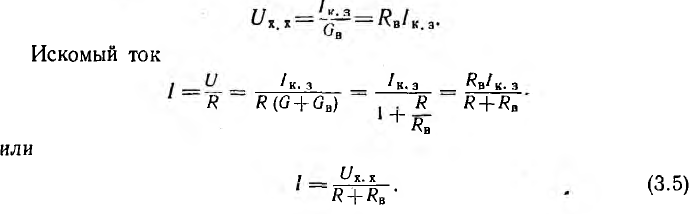
Из аналогии этой формулы с выражением для тока источника напряжения видно, что активный двухполюсник эквивалентен также источнику напряжения (см. рис. 3.4) с э.д.с., равной напряжению Ux.х на зажимах разомкнутого двухполюсника (рис. 3.16, д), и внутренним сопротивлением, равным сопротивлению этого же двухполюсника, но без источников энергии (рис. 3.16, е).
В замене сложной цепи со многими источниками энергии одним источником напряжения или тока и заключается метод эквивалентного источника энергии. Вместо обычногорасчета заданной цепи решаются две более простые задачи — определение Uх.х при разомкнутой или Iкз при короткозамкнутой ветви, что упрощает цепь, и определение RB или G„ при отсутствии источников;
затем найденные величины подставляются в выражения (3.4) или (3.5).
Примером применения метода эквивалентного источника напряжения может служить задача определения тока I в диагонали ab неуравновешенного моста; расчет упрощается при пренебрежении внутренним сопротивлением источника, питающего цепь; направление э. д. с. и выбранные направления токов ветвей указаны на рис. 3.15, а.
Размыкание ветви ab для определения напряжения Uxx (см. рис. 3.15, в) превращает сложную исходную цепь в последовательно параллельную, легко решаемую методом преобразования:
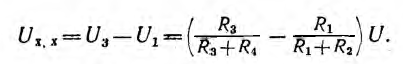
При замыкании накоротко зажимов c u d для определения сопротивления RB цепи между точками а и b (см. рис. 3.15, г) цепь превращается в параллельно-последовательную, откуда
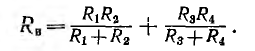
Тогда искомый ток
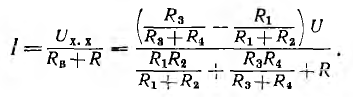
Ток в диагонали будет отсутствовать, если выражение, стоящее в скобках, обратится в нуль. Отсюда вытекает условие равновесия моста:
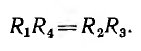
Решая эту же задачу методом эквивалентного источника тока, нужно мысленно осуществить короткое замыкание ветви аb это превращает цепь в параллельно-последовательную, и вычисление тока Iк.з не представляет затруднений.
Методы эквивалентного источника напряжения или тока особенно удобны, если надо определить ток I или напряжение U одной ветви при нескольких значениях ее сопротивления R или проводимости О.
Такая задача часто встречается в практике, так как нагрузка обычно бывает переменной. Тогда в формулах (3.4) и (3.5) изменяют лишь значения G и R, оставляя без изменения остальные вычисленные для этой цепи величины.
Метод контурных токов
Этот метод, предложенный Максвеллом, можно обосновать, предполагая, что в ветвях цепи последовательно с приемниками включены источники напряжения (см. рис. 3.11, б). Примером может служить цепь рис. 3.17, рассчитанная по законам Кирхгофа. Здесь внутренние сопротивления источников объединены с сопротивлениями приемников и произвольно заданы направления токов ветвей. Чтобы обобщить вывод на случай заданных источников тока, их надо заменить эквивалентными источниками напряжения.
Каждому независимому контуру приписывается произвольно направленный контурный ток. Для плоских схем удобно в качестве независимых контуров взять элементарные контуры и придать всем контурным токам одно и то же направление, совпадающее с направлением обхода, например по часовой стрелке. Контурные токи, проходящие также по внешним ветвям, являются для этих ветвей реально существующими, например ток IА = I1 контура А.
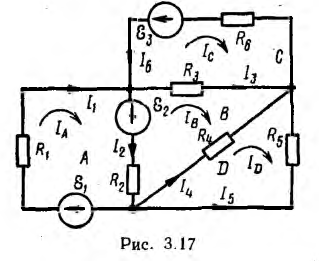
Контурные токи внутренних контуров, например ток Iв контура В, являются
фиктивными величинами, введенными для удобства расчетов. Реальные токи
внутренних ветвей можно найти как разность токов двух контуров, в которые входит эта ветвь; так как для рис. 3.17 выбранное направление тока I2 ветви с R2 совпадает с IА, то
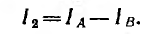 (3.6)
(3.6)
Взятая по направлению обхода алгебраическая сумма всех э. д. с., входящих в контур, называется контурной э. д. с., сумма всех сопротивлений контура называется контурным сопротивлением. Так, для контуров А и В контурные э. д. с. и сопротивления, соответственно, имеют вид:
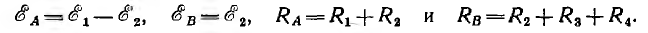
Сопротивление общей ветви двух контуров называется общим сопротивлением, например,
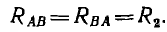
Тогда вместо уравнения по второму закону Кирхгофа для контура А
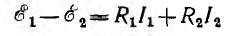
можно написать:
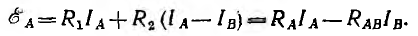
В общем виде система уравнений для всех N= р — q + 1 независимых контуров при их обходе в одном направлении получит вид:
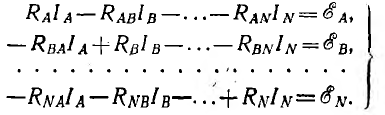
В этой системе уравнений члены с контурным сопротивлением входят с положительным знаком, члены с общим сопротивлением — с отрицательным. Если в каком-либо контуре нет источников э. д. с., в правую часть соответствующего уравнения надо подставить нуль; если два контура не имеют общей ветви, вместо соответствующего общего сопротивления надо также подставить нуль.
Таким образом, вместо системы из р уравнений по первому и второму законам Кирхгофа, по методу контурных токов составляется система из р — q + 1 уравнений только по второму закону Кирхгофа.
Так, для цепи рис. 3.17 вместо шести уравнений (двух по первому и четырех по второму законам Кирхгофа) по методу контурных токов составляется следующая система из четырех уравнений:
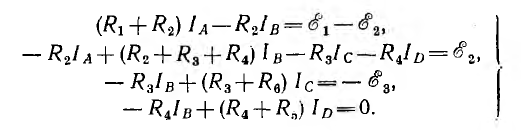
После определения контурных токов находят действительные токи ветвей. Ток внешней ветви совпадает с соответствующим положительным контурным током и противоположен отрицательному. Ток внутренней ветви, определяемый как разность контурных токов (см. формулу 3.6), совпадает с направлением большего контурного тока.
Приведенная выше общая система уравнений для контурных токов стандартна; поэтому без ее составления можно по схеме цепи сразу написать определитель системы уравнений и по нему найти контурные токи.
Метод узловых напряжений
Этот метод, также предложенный Максвеллом, можно обосновать, предполагая, что между узлами цепи включены источники тока параллельно с приемниками (см. рис. 3.11,а). Примером может служить цепь рис.3.18; здесь внутренние проводимости источников объединены с проводимостями приемников.
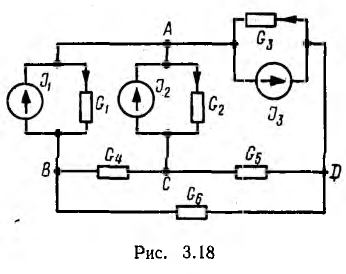
По аналогии с методом контурных токов вводятся новые понятия, что сделано далее на примере цепи рис. 3.18. Узловой ток, равный алгебраической сумме внутренних токов источников тока в ветвях, сходящихся в узле:
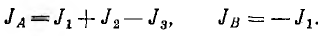
Узловая проводимость, равная сумме проводимостей ветвей, сходящихся в этом узле:
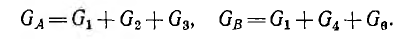
Общая проводимость, равная проводимости ветви, соединяющей два узла:
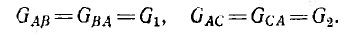
Узловое напряжение, например UA, равное напряжению между узлом А и одним из узлов, принятым за опорный.
Напряжение каждой ветви равно, очевидно, разности узловых напряжений узлов, к которым примыкает данная ветвь. Например, учитывая направления внутренних токов,
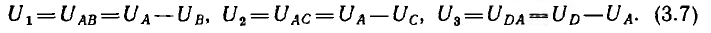
Тогда для узла А вместо уравнения по первому закону Кирхгофа во второй форме, составленного в соответствии с правилом знаков,
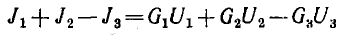
можно написать
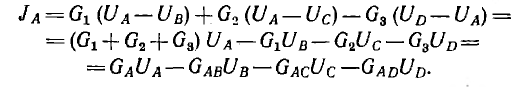
Так как один узел принимается за опорный, его узловое напряжение обращается в нуль.
В общем виде система уравнений для всех М = q —1 независимых узлов, т. е. для всех узлов, кроме опорного, получит вид:
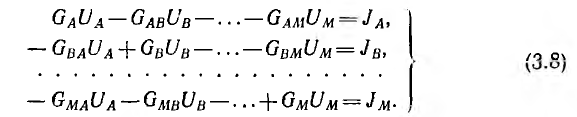 -
-
В эту систему уравнений члены с узловой проводимостью входят с положительным знаком, члены с общей проводимостью — с отрицательным. Если к какому-либо узлу не подключены источники тока, в правую часть соответствующего уравнения надо подставить нуль; если два узла не имеют общей ветви, вместо соответствующей общей проводимости надо также подставить нуль.
Таким образом, вместо системы из р уравнений по первому и второму законам Кирхгофа, по методу узловых напряжений составляется система из q — 1 уравнений только по первому закону Кирхгофа.
Так, для цепи рис. 3.18 вместо шести уравнений для шести неизвестных напряжений всех девяти ветвей по методу узловых напряжений составляется следующая система из трех уравнений (за опорный взят узел D):
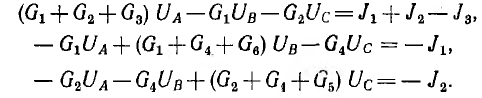
Решая эту систему, находят узловые напряжения, затем из выражений вида уравнений (3.7) — напряжения ветвей и из закона Ома — токи ветвей. Здесь, как и в методе контурных токов, по схеме цепи сразу может быть написан определитель системы уравнений и по нему вычислены узловые напряжения.
Уравнения, составленные методами контурных токов и узловых напряжений, аналогичны, но вместо напряжений в одних участвуют токи в других, и наоборот, а вместо сопротивлений — проводимости.
Целесообразно применять метод, дающий меньшее число уравнений; так, при р— q + 1 < q — 1, т. е. при р < 2 (q — 1), следует применить метод контурных токов, при р > 2 (q — 1) — метод узловых напряжений.
Вывод метода узловых напряжений был дан в предположении, что между узлами цепи включены источники тока параллельно с приемниками (см. рис. 3.11, а). Если же заданы источники напряжения, соединенные с приемниками последовательно (см. рис. 3.11, б), можно рассматривать каждую ветвь как источник напряжения с той же э. д. с. 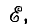 , но с внутренним объединенным сопротивлением R = RB + R'.
, но с внутренним объединенным сопротивлением R = RB + R'.
Этот источник напряжения может быть заменен эквивалентным ему источником тока с внутренним током 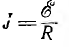 и внутренней проводимостью
и внутренней проводимостью 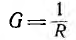 .
.
Тогда уравнения системы для всех М = q— 1 независимых узлов получают вид, аналогичный уравнению для узла А в системе (3.8):
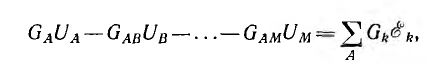
где правая часть является алгебраической суммой произведений 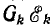 для ветвей с источниками напряжения, сходящихся в узле А.
для ветвей с источниками напряжения, сходящихся в узле А.
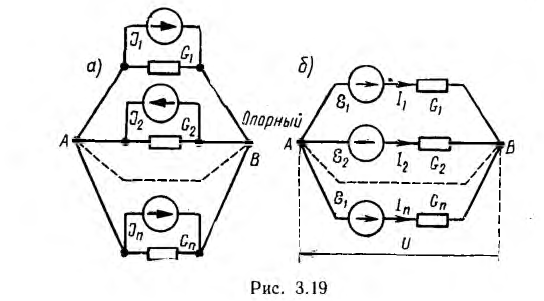
Особенно прост метод узловых напряжений для цепи с двумя узлами (рис. 3.19, а). В этом случае один из двух узлов, например В, будет опорным, члены с общими проводимостями отсутствуют и из системы уравнений останется одно:
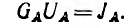
Отсюда определяется узловое напряжение (оно же — напряжение всех ветвей)
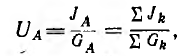
а по нему — токи ветвей.
Если выразить все внутренние токи Jk источников тока через внутренние э.д.с. 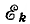 эквивалентных источников напряжения:
эквивалентных источников напряжения:
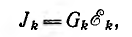
получится узловое напряжение для схемы рис. 3.19, б:
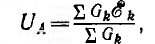
после чего могут быть определены токи ветвей
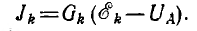
Обобщенные методы расчета линейных электрических цепей
Как было показано, все методы расчета линейных электрических цепей основаны на законах Ома и Кирхгофа и аналогичны для установившихся режимов постоянного и синусоидального тока и для переходных процессов. Они заключаются в составлении и решении системы алгебраических уравнений, связывающих напряжения, токи и сопротивления (проводимости) ветвей цепи, причем при постоянном токе это реальные величины U, I, R или G, при синусоидальном—символические (комплексные) изображения О, I, Z или Y, а при переходных режимах — операторные изображения U (р), I (р), Z (р) или Y (р). После решения системы уравнений для установившихся синусоидальных и для переходных процессов осуществляется переход от символических и операторных изображений искомых величин к их оригиналам — реальным мгновенным значениям напряжений и токов.
В сложных цепях с большим числом ветвей и узлов система уравнений содержит большое число неизвестных и ее приведение к уравнению с одним неизвестным путем исключения остальных неизвестных может оказаться весьма громоздким. Далее вкратце рассматриваются основы расчета цепей с помощью обобщенных аналитических и топологических методов решения систем таких уравнений.
Метод определителей
Этот известный из курса математики метод особенно удобен для решения системы однотипных уравнений, составляемых по методам контурных токов или узловых напряжений. Так, полученная система уравнений для цепи с N-контурными токами, переписанная для синусоидальных токов с заменой буквенных индексов цифровыми:
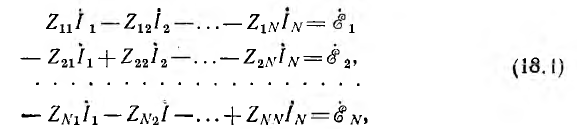
(Z11, Z22, ...— контурные сопротивления, Z12, ..., Z1N— общие с< противления соседних контуров), имеет однотипные решения для всех контурных токов. Например, контурный ток
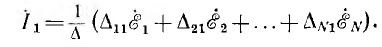
Здесь определитель системы
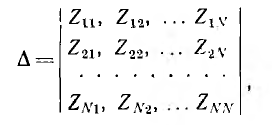
а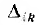 — алгебраические дополнения этого определителя с вычеркнутыми строкой i и столбцом к, умноженные на
— алгебраические дополнения этого определителя с вычеркнутыми строкой i и столбцом к, умноженные на 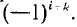 .
.
Далее приводится решение этим методом системы уравнений для контурных токов цепи рис. 7.21, :

Определитель системы:
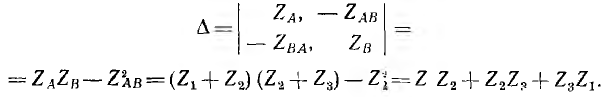
Алгебраические дополнения
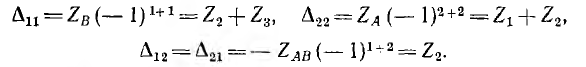
Искомые токи
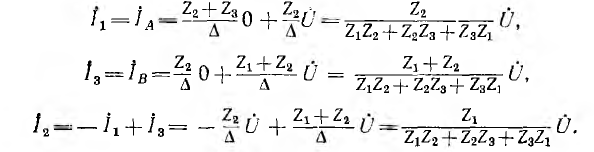
Матричный метод
Матричный метод, использующий матричную алгебру, позволяет получать и записывать системы уравнений электрической цепи в компактной и наглядной форме, удобной та к нее для вычислительных машин.
Далее матричный метод изложен на основе системы уравнений контурных токов (18.1). В такую систему входят три группь величин: искомые величины 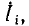 свободные члены
свободные члены 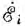 и коэффициент
и коэффициент 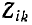 при неизвестных. Индексы i и k принимают все значения от 1 до N, где N — число уравнений, поэтому число коэффициентов
при неизвестных. Индексы i и k принимают все значения от 1 до N, где N — число уравнений, поэтому число коэффициентов 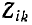 равно 2. Первый индекс соответствует номеру строки, второй — номеру столбца.
равно 2. Первый индекс соответствует номеру строки, второй — номеру столбца.
Каждую из групп искомых и свободных величин можно записать виде таблицы, называемой столбцовой матрицей, от-чаемой двойными чертами с обеих сторон или ее условным символом аиде одной буквы жирным шрифтом:
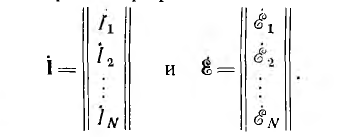
Таблица коэффициентов 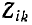 должна иметь столько же строк, сколько и столбцов, т. е. является квадратной матрицей:
должна иметь столько же строк, сколько и столбцов, т. е. является квадратной матрицей:
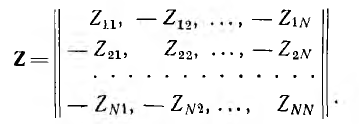
Хотя запись матрицы Z подобна записи определителя 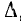 , матрица является набором отдельных элементов, определитель же равен определенному числу при данных значениях его элементов.
, матрица является набором отдельных элементов, определитель же равен определенному числу при данных значениях его элементов.
В матричной алгебре показывается, что при умножении квадратной матрицы Z на столбцовую i с тем же числом строк каждый элемент произведения получается как сумма попарных произведений всех элементов строки i квадратной матрицы Z на соответствующие элементы столбцовой матрицы I. Следовательно,
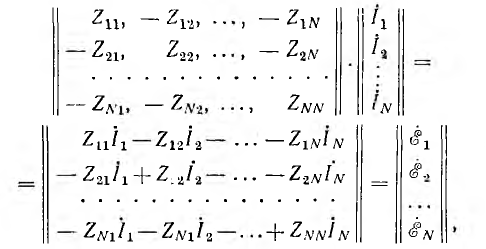
т. е. уравнения по методу контурных токов в краткой матричной форме аписи имеют вид:
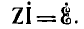
то уравнение решается с помощью обратной матрицы Z-1, которая, будучи умножена справа или слева на Z, дает единичную матрицу:
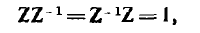
т. е. матрицу, все диагональные элементы которой равны едини и а все остальные — нулю. В матричной алгебре доказывается, что
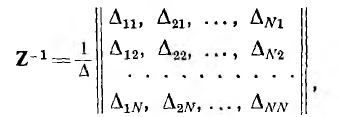
где 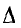 — определитель исходной матрицы, а
— определитель исходной матрицы, а 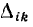 — его алгебраические дополнения. Тогда
— его алгебраические дополнения. Тогда
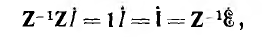
т. е. для получения матрицы тока надо умножить 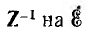 по правила умножения матриц:
по правила умножения матриц:
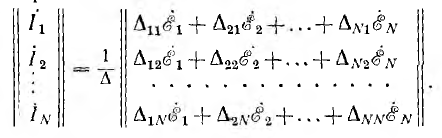
Отсюда получаются все контурные токи путем приравнивания одноименных строк обеих матриц:
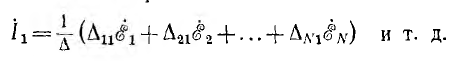
Аналогичным образом решается матричное уравнение YU = J, составленное по методу узловых напряжений.
Матричный метод может быть применен и для составления, и для решения системы уравнений по законам Кирхгофа. Первые строки квадратной матрицы в зависимости от наличия токов и их знака-, входящих в уравнения по первому закону Кирхгофа, состоят из элементов, соответственно равных 0, или +1, или —1. Остальные ее строки, соответствующие уравнениям по второму закону Кирхгофа, состоят из сопротивлений — коэффициентов при токах в этих уравнениях. Умножение квадратной матрицы на столбцовую матрицу токов дает правую столбцовую матрицу свободных членов всех уравнений, т. е. систему всех уравнений по обоим законам Кирхгофа.
Например, система уравнений цепи постоянного тока рис. 3.12, полученная по законам Кирхгофа обычным способом, в матричном методе имеет вид:
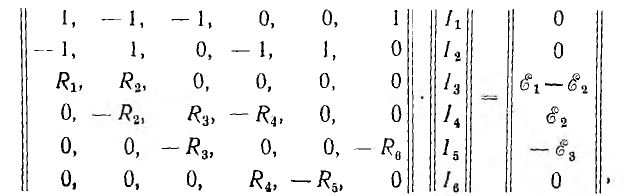
ли, обозначая квадратную матрицу через А,
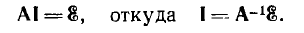
Отсюда видно, что для определения токов ветвей нужно аналогично методу контурных токов составить обратную матрицу А-1 из определителя и алгебраических дополнений, умножить на нее столбцовую матрицу 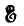 и приравнять одноименные строки этого произведения и столбцовой матрицы токов I.
и приравнять одноименные строки этого произведения и столбцовой матрицы токов I.
Топологический метод
Схема электрической цепи, состоящая из узлов и ветвей, представляет собой геометрическую фигуру, свойства которой не зависят от ее геометрических размеров и вида очертаний. Поэтому топология— раздел геометрии, посвященный свойствам таких фигур, может быть использован для анализа электрических цепей непосредственно по структуре их схем.
Топологический метод расчета цепей изложен далее без вывода основных формул на примере цепи синусоидального тока с источником напряжения U, приключенным к одной паре узлов цепи. Тогда ток I любой ветви цепи может быть определен с помощью передачи
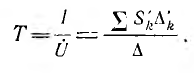
Значение числителя этой дроби будет разъяснено далее. Знаменатель  — определитель системы уравнений, связывающих напряжения и токи исследуемой цепи — в топологическом методе вычисляется без составления этих уравнений по формуле
— определитель системы уравнений, связывающих напряжения и токи исследуемой цепи — в топологическом методе вычисляется без составления этих уравнений по формуле 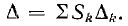 Тогда
Тогда
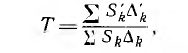
где Sk — величина пути к по ветвям цепи между произвольно выбранной парой ее узлов, вдоль которого узлы данного пути встречаются не более одного раза, равная произведению проводимостей этого пути; S'k — величина пути передачи, содержащего узлы источника и ветвь искомого тока, равная произведению проводимостей ветвей пути передачи; 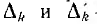 — соответственно алгебраические дополнения пути и пути передачи, равные определителям цепей, остяющихся после короткого замыкания ветвей этих путей. Алгебраические дополнения равны единице, если путь содержит все узлы первоначальной схемы. При вычислении Sк и
— соответственно алгебраические дополнения пути и пути передачи, равные определителям цепей, остяющихся после короткого замыкания ветвей этих путей. Алгебраические дополнения равны единице, если путь содержит все узлы первоначальной схемы. При вычислении Sк и 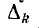 источник напряжения замыкается накоротко.
источник напряжения замыкается накоротко.
Произведения, суммируемые в знаменателе и числителе выражения для Т, вычисляются, соответственно, для всех путей Sk и для всех пу-ей передачи S'k.
Далее для примера определяется передача в мостовой цепи переменно тока (рис. 18.1) от напряжения U источника, подключенного к узлам А и С, к току I4 в ветви с проводимостью Y4. Положительное нг правление этого тока совпадает с заданным направлением напряжени источника.
В этой цепи два пути передачи от узлов А и С источника к вет£» Y4. Величина первого пути передачи по ветви Y3 равна S1 =Y3Y При коротком замыкании этого пути передачи для определения алгебраического дополнения 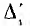 узлы A, D, С соединяются вместе, образу с узлом В одну ветвь, состоящую из параллельно соединенных пров( димостей Y1, Y, Y2. Следовательно,
узлы A, D, С соединяются вместе, образу с узлом В одну ветвь, состоящую из параллельно соединенных пров( димостей Y1, Y, Y2. Следовательно,
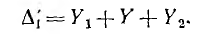
Величина второго пути передачи по ветвям Y1 и Y равна 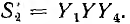 При коротком замыкании этого пути все четыре узл» объединяются, а тогда алгебраическое дополнение этого пути передачи
При коротком замыкании этого пути все четыре узл» объединяются, а тогда алгебраическое дополнение этого пути передачи 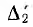 = 1.
= 1.
Пути Sk и их алгебраические дополнения 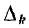 , определяются для пары узлов В и D. При определении S1 узлы А и С источника должны быть закорочены. Тогда соединяются параллельно ветви Y1 и Y2 и ветви Y3 и Y4. Следовательно, первый путь от узла В к узлу D, проходящий последовательно по этим двум параллельным разветвлениям, имеет величину
, определяются для пары узлов В и D. При определении S1 узлы А и С источника должны быть закорочены. Тогда соединяются параллельно ветви Y1 и Y2 и ветви Y3 и Y4. Следовательно, первый путь от узла В к узлу D, проходящий последовательно по этим двум параллельным разветвлениям, имеет величину
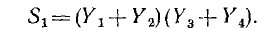
Для определения алгебраического дополнения 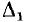 пути S1 его ветви закорачиваются, что приводит к объединению всех четырех узлов. Следовательно,
пути S1 его ветви закорачиваются, что приводит к объединению всех четырех узлов. Следовательно, 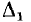 = 1.
= 1.
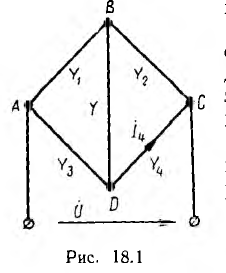
Второй путь от узла В к узлу D проходит но ветви Y, поэтому его величина 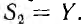 . При закорачивании этого пути и при закороченных узлах источника все остальные ветви оказываются соединенными параллельно. Отсюда
. При закорачивании этого пути и при закороченных узлах источника все остальные ветви оказываются соединенными параллельно. Отсюда
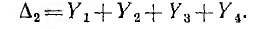
В результате передача
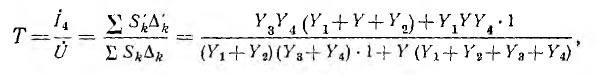
будучи умножена на U, дает искомый ток I4.
В рассмотренном примере цепь проста, из-за чего выгода применения топологического метода по сравнению с классическими методами расчета цепей, например методом эквивалентного источника напряжения, не ощущается. Экономия времени получается при расчете слож' ных цепей, и тем большая, чем сложнее цепь.
Из изложенного видны особенности топологического метода расчета электрических цепей:
- расчет ведется на основе схемы цепи, ветви которой изобрaжаются линиями, характеризуемыми проводимостями;
- расчет проводится по формулам для ряда величин, характеризющих топологические свойства цепи, без составления уравнений по законам Кирхгофа;
- метод применим только для цепей с одним источником энергии при наличии нескольких источников приходится использовать принцип наложения.
Топологический метод называется также методом ненаправленных графов.
Метод направленных графов
Направленным графом или графом сигнала называется совокупность узлов и соединяющих их ветвей, имеющих оправление, указываемое стрелкой. Граф не повторяет электрическую цепь, а представляет собой графическое изображение уравнений, связывающих величины, характеризующие данную цепь. Узел графа, к которому подключена одна уходящая ветвь, характеризуется входным сигналом — свободным членом системы уравнений (заданным напряжением или током), узел с одной входящей ветвью — выходным сигналом, т. е. искомой величиной, остальные узлы — другими неизвестными величинами, которые должны быть исключены в процессе решения задачи.
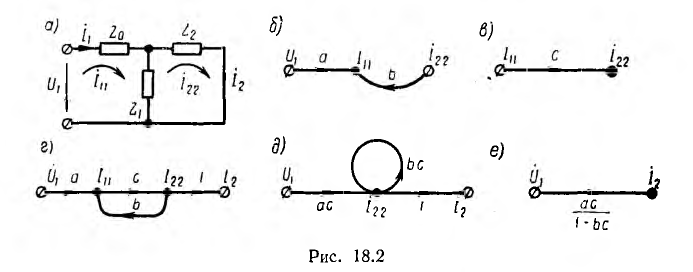
Каждая ветвь характеризуется передачей, являющейся функцией коэффициентов уравнений и равной отношению сигналов выходного (по направлению ветви) узла к входному. К узлам графа может подходить и уходить по нескольку ветвей. Тогда сигнал узла равен сумме сигналов, приходящих к этому узлу, уходящие сигналы не учитываются.
В качестве первого простого примера составлен граф цепи (рис. 18.2, а) на основе символического метода и системы уравнений ю методу контурных токов. Искомым пусть будет ток I2 проходящий по сопротивлению Z2.
Уравнение для первого контура имеет вид:
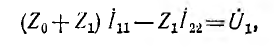
откуда
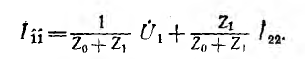
Таким образом, первая составляющая тока 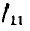 создается сигнале
создается сигнале 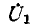 через ветвь с передачей
через ветвь с передачей
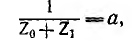
имеющей размерность проводимости, а вторая — сигналом I22 через ветвь с передачей
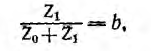
являющейся безразмерной величиной. Тогда уравнение
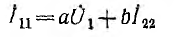
Уравнение для второго контура
где передача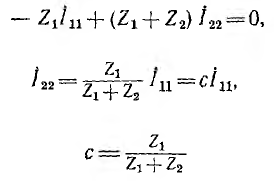
изобразится графом рис. 18.2, е. Граф цепи в целом показан на рис. 18.2, г. Так как искомый ток I2 = I22, передача выходной ветви равна 1.
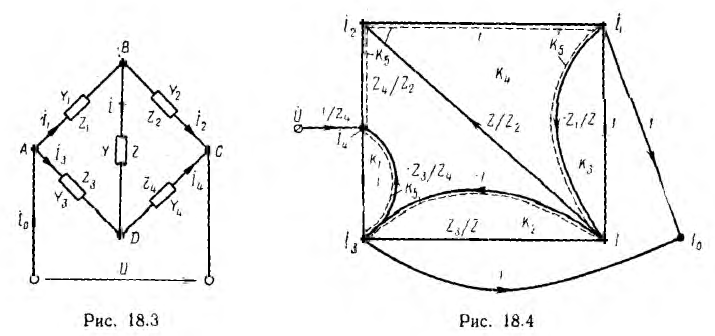
Как пример составления графа для системы уравнений по закона Кирхгофа, рассматривается схема неравновесного моста переменног тока (рис. 18.3), В соответствии с выбранными положительными нanpaвлениями напряжения U и токов всех ветвей этой цепи, независимые равнения по первому закону Кирхгофа имеют вид:
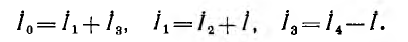
по второму закону Кирхгофа
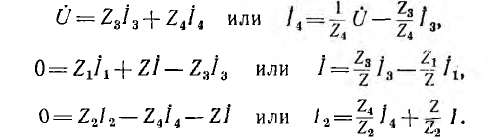
Граф, построенный по этой системе уравнений, показан на рис. 18.4. Его узлами являются сигналы: входной — напряжение U цепи и выходные — все токи. Все узлы связаны между собой ветвями. Ветви имеют направление, показанное стрелкой, к узлу тока, определяемого его уравнением. Например, для тока I — ветви имеют направление от узлов токов I3 и I1, стоящих в правой его части; коэффициенты при них 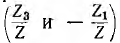 по величине и знаку равны передачам этих ветвей.
по величине и знаку равны передачам этих ветвей.
Граф неравновесного моста значительно упрощается, если его построить для системы уравнений по методу узловых напряжений. В общем случае число уравнений по этому методу меньше числа узлов на единицу . Но в схеме рис. 18.3, где за опорный принят узел С, узловое напряжение UA равно заданному напряжению источника U, поэтому, хотя мост имеет четыре узла, необходимо составить лишь два уравнения для узлов В и D:
Отсюда 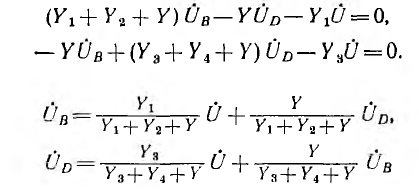
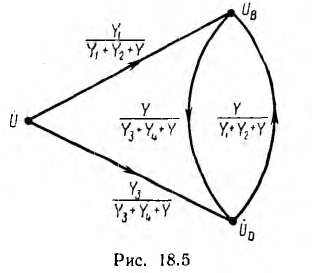
и граф цепи получает вид, изображенный на рис. 18.5, т. е. в отличие от графа рис. 18.4 с семью узлами и двенадцатью ветвями для той же цепи имеет всего три узла и четыре ветви.
Как видно из приведенных примеров, направленный граф цепи начинается от самой цепи как по схеме, так н по числу узлов и ветвей, и зависит от метода составления изображаемых им уравнений. Иногда граф удается построить по схеме цепи без составления и преобразов. ния системы уравнений.
Граф цепи позволяет по заданному входному сигналу — напряжению (току) источника — найти выходной сигнал — ток (напряжение) приемника. Эта задача может быть решена или последовательным упрощением графа, или применением общего выражения для передачи сигнала.
При упрощении исходный граф преобразуется в эквивалентньй граф с одной ветвью, непосредственно связывающей входной и выходной узлы. Например, в графе рис. 18.2, г сначала следует устраши контур сb. Исключение из приведенной выше системы контурных токо тока I11 дает
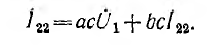
Соответствующий граф показан на рис. 18.2, д. Как видно, он содержит петлю «обратной связи» с передачей bc. Так как передача выходной ветви равна I т. е. I2 = I22, из предыдущего выражения вытекает, что
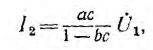
т. е. петля исключается и получается простейший искомый граф (рис. 18.2, е), передача которого равна
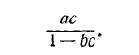
После подстановки значений а, b, с, выраженных через параметры цепи Z0, Z1, Z2, передача получает вид:
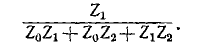
Передача, умноженная на U1, дает искомый ток I2.
В специальной литературе, кроме исключения контура и петли, излагаются способы упрощения графов, имеющих более сложную конфигурацию.
Общее выражение для передачи графа, позволяющее по графу цепи и заданному входному сигналу, например напряжению U источника, непосредственно получить выходной сигнал, например ток I одной из ветвей цепи:
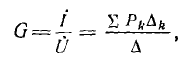
Мэзон вывел на основании теории определителей.
Правая часть этой формулы по структуре аналогична правой части передачи топологического метода, но значение членов числителя другое. Здесь Рк — величина пути по ветвям от узла источник к узлу тока по направлению стрелок, вдоль которого отдельные узлы встречаются не более одного раза, равная произведению передач ветвей этого пути. Например, для графа рис. 18.4 величина единственного пути, соединяющего узел U с узлом 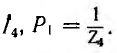 Величины двух путей, соединяющих узел U с узлом I,
Величины двух путей, соединяющих узел U с узлом I,
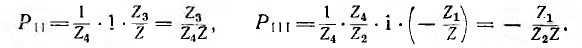
Знаменатель  выражения для G — определитель исходной системы уравнений, который может быть непосредственно по графу вычислен по формуле
выражения для G — определитель исходной системы уравнений, который может быть непосредственно по графу вычислен по формуле
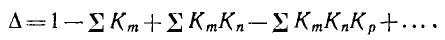
Здесь 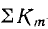 — сумма передач всех контуров графа, равных произведениям передач ветвей, обходимых по направлению стрелок;
— сумма передач всех контуров графа, равных произведениям передач ветвей, обходимых по направлению стрелок; 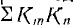 — сумма произведений
— сумма произведений 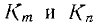 двух не соприкасающихся контуров графа;
двух не соприкасающихся контуров графа; 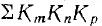 — сумма произведений Кm, Кn и КР трех также не соприкасающихся контуров графа и т. д. Например, передачи контуров графа, показанных на рис. 18.4, равны:
— сумма произведений Кm, Кn и КР трех также не соприкасающихся контуров графа и т. д. Например, передачи контуров графа, показанных на рис. 18.4, равны:
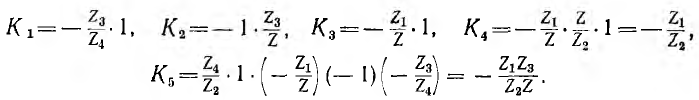
Контур K1 не касается контуров К3 и K4. Следовательно, определитель
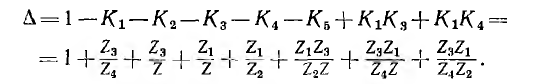
Определитель 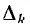 части графа, не касающегося k-го пути, вычисляется по формуле, аналогичной
части графа, не касающегося k-го пути, вычисляется по формуле, аналогичной  , но с учетом только тех контуров, которые не касаются k-vo пути. Например, для графа рис. 18.4 путь P1 касается контуров K1 и К5, поэтому
, но с учетом только тех контуров, которые не касаются k-vo пути. Например, для графа рис. 18.4 путь P1 касается контуров K1 и К5, поэтому
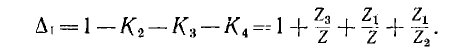
Так как пути 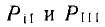 касаются всех контуров,
касаются всех контуров, 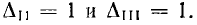 .
.
Произведения 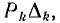 , суммируемые в числителе выражения для передачи графа G, вычисляются для всех путей искомой передачи. Выше в виде примеров были вычислены все величины, входящие в формулу Мэзона для передачи графа
, суммируемые в числителе выражения для передачи графа G, вычисляются для всех путей искомой передачи. Выше в виде примеров были вычислены все величины, входящие в формулу Мэзона для передачи графа 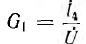 - от узла источника U к узлу I4 и для передачи
- от узла источника U к узлу I4 и для передачи 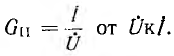 . Следовательно, ток ветви Z4 моста
. Следовательно, ток ветви Z4 моста
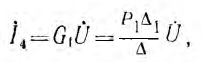
после подстановки значений 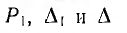
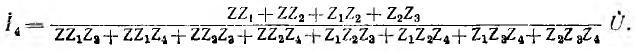
Можно показать, что этот результат совпадает с решением той же задачи топологическим методом. Ток диагонали Z моста
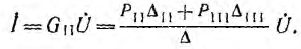
Для получения окончательного результата в это выражение надo также подставить вычисленные значения входящих в него величин. Эта задача может быть решена также применением формулы Мэзона для графа рис. 18.5 системы уравнений, составленной для этой цепи по методу узловых напряжений.
Величины двух путей от узла источника UD к узлу напряжения доопределяющего искомый ток I4 равны
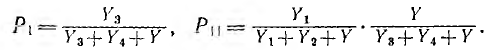
Так как оба пути касаются обоих контуров графа, 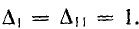
Передача единственного контура, обходимого по направлению стрелок,
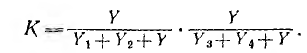
Следовательно, определитель
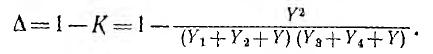
Тогда по формуле Мэзона передача
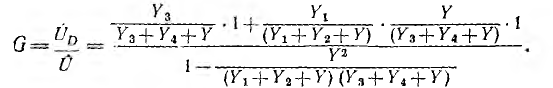
Передача, умноженная на U, дает напряжение UD. которое после очевидного упрощения и умножения на Y4 определяет искомый ток
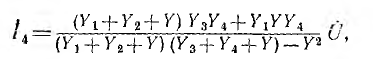
также совпадающий с решением этой задачитопологическим методом. При этом вычисления по формуле Мэзона оказались более простыми, чем для графа рис. 18.4, составленного на основе системы уравнений по законам Кирхгофа.
Из изложенного видны особенности метода графов для расчета электрических цепей:
- Граф строится по системе уравнений, связывающих напряжения и токи цепи или непосредственно по схеме цепи. Он состоит из узлов заданных и искомых напряжений и токов, связи между которыми изображаются ветвями, характеризуемыми соотношениями сопротивлений (проводимостей) ветвей цепи.
- Вид графа для данной цепи отличается для разных методов составления уравнений; граф обычно упрощается при применении метода узловых напряжений.
- Расчет цепи проводится по формулам для ряда величин, характеризующих схему графа.
Рассмотренные примеры расчета простых цепей не смогли показать преимущества применения метода направленных графов по сравнению классическими методами. Экономия времени получается при расчете южных цепей, и тем большая, чем сложнее цепь.
Расчет линейных электрических цепей постоянного тока
Режимы работы источников:
Электрическая цепь, содержащая только линейные элементы, называется линейной. Элемент цепи, сопротивление которого остается постоянным при любых значениях и направлениях тока и нем и напряжении на его выводах, называется линейным.
Рассмотрим неразветвленную линейную электрическую цепь с несколькими источниками энергии (рис. 3.1а).
Величина тока в неразветвленной электрической цепи с несколькими источниками (рис. 3.1) определяется отношением алгебраической суммы ЭДС всех источников к полному сопротивлению цепи

Для определения знаков ЭДС в алгебраической сумме условно задаются направлением обхода контура: по часовой или против часовой стрелки. ЭДС источника, направление которой совпадает с выбранным направлением обхода, учитывают со знаком «плюс».
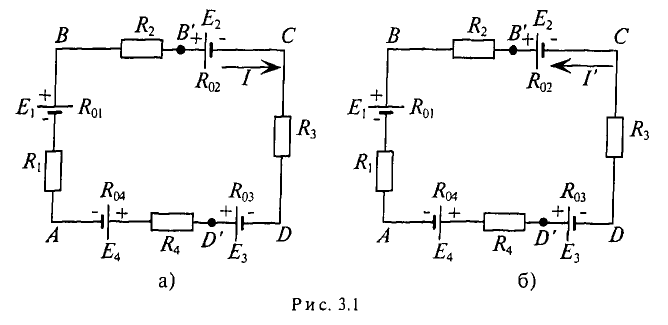
а ЭДС источника, направление которой не совпадает с выбранным направлением обхода, — со знаком «минус». Например (рис. 3.1а) направление обхода выбрано по часовой стрелке, тогда
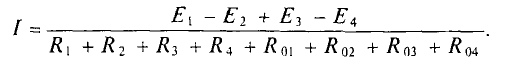
Если в результате расчета величина тока получится со знаком «плюс», то его направление совпадает с выбранным направлением обхода, если же со знаком «минус», то направление тока цепи противоположно выбранному направлению обхода.
Определив, таким образом, величину и направление тока в (Цепи, можно заключить, что направление ЭДС источников не всегда совпадает с направлением тока.
Источники, ЭДС которых совпадают с направлением тока, работают в режиме генератора, а источники, ЭДС которых не совпадает с направлением тока, работают в режиме потребителя.
Если, допустим, в результате расчета цепи (рис. 3.1а) окажется, что ток совпадает с выбранным направлением обхода (по часовой стрелке), то источники с ЭДС 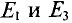 будут работать в режиме генераторов, а
будут работать в режиме генераторов, а 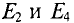 — в режиме потребителей.
— в режиме потребителей.
Напряжение на каждом участке электрической цепи определяется отношением мощности, затраченной на этом участке, деленной на ток, проходящий по этому участку, т. е.
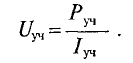
Ток на всех участках неразветвленной цепи имеет одинаковое значение I.
Напряжение на сопротивлении 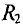 можно определить отношением
можно определить отношением
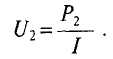
На участке 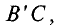 т. е. на клеммах источника
т. е. на клеммах источника 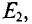 работающего в режиме потребителя, мощность
работающего в режиме потребителя, мощность 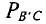 затрачивается на преодоление мощности источника
затрачивается на преодоление мощности источника 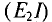 и на потери на внутреннем сопротивлении источника
и на потери на внутреннем сопротивлении источника 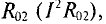 откуда следует
откуда следует
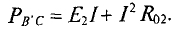
Тогда напряжение 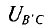 на клеммах источника, работающего в режиме потребителя, равно
на клеммах источника, работающего в режиме потребителя, равно
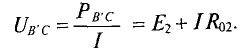
Таким образом, напряжение на зажимах источника, работающего в режиме потребителя, больше, чем ЭДС самого источника на величину падения напряжения на внутреннем сопротивлении этого источника:

А напряжение на клеммах источника, работающего в режиме генератора (2.12), меньше, чем ЭДС источника на величину падения напряжения на внутреннем сопротивлении:

Следовательно, напряжение на любом участке цепи (рис. 3.1а) может быть определено выражением

где U — напряжение на участке между точкой с положительным потенциалом 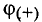 и точкой с отрицательным потенциалом
и точкой с отрицательным потенциалом 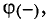 а R — полное сопротивление участка.
а R — полное сопротивление участка.
В формуле (3.4) знак «плюс» ставят для участка, на котором источник работает в режиме потребителя, а знак «минус» для участка, на котором источник работает в режиме генератора.
Пример №1
Определить величину тока 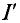 и напряжения на участках
и напряжения на участках 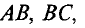
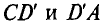 цепи (рис. 3.16), если известно:
цепи (рис. 3.16), если известно:
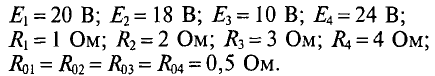
Проверить баланс напряжений.
Решение
Выберем направление обхода по часовой стрелке. Тогда
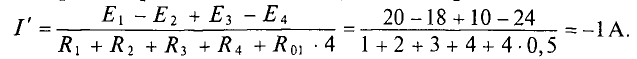
Так как значение тока получили со знаком «минус», то его направление противоположно выбранному направлению обхода, т.е. ток в цепи 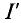 (рис. 3.16) направлен против часовой стрелки. (В дальнейшем знак «минус» не учитывается.) На участке АВ источник работает в режиме потребителя, на участке ВС — в режиме генератора, на участке
(рис. 3.16) направлен против часовой стрелки. (В дальнейшем знак «минус» не учитывается.) На участке АВ источник работает в режиме потребителя, на участке ВС — в режиме генератора, на участке 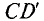 — в режиме потребителя и на участке
— в режиме потребителя и на участке 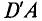 — в режиме генератора. Таким образом
— в режиме генератора. Таким образом
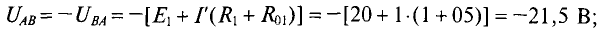
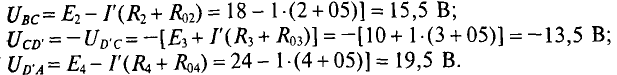
Баланс напряжений в замкнутой неразветвленной цепи соблюдается:
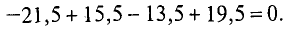
Потенциальная диаграмма
При изучении и расчете некоторых электрических цепей необходимо определить потенциалы отдельных точек цепи и построить потенциальную диаграмму. Для этого можно использовать выражение (3.4) (рис. 3.1а).
На участке АВ точка В имеет положительный потенциал 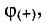 а точка А — отрицательный потенциал
а точка А — отрицательный потенциал 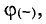 поэтому
поэтому 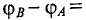
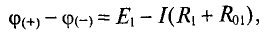 так как источник работает в режиме генератора, т. е.
так как источник работает в режиме генератора, т. е.
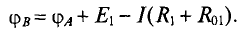
На участке ВС точка В имеет положительный потенциал 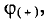 а точка С — отрицательный
а точка С — отрицательный 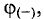 поэтому
поэтому 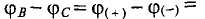
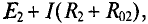 источник с ЭДС
источник с ЭДС 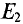 работает в режиме потребителя, т. е.
работает в режиме потребителя, т. е.
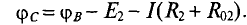
Таким образом, потенциал точки D можно записать
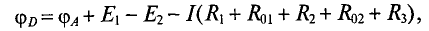
если обходить цепь по направлению тока, или
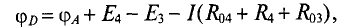
если обходить цепь против направления тока.
Отсюда можно сделать следующий вывод (правило): если обходить цепь или участок цепи по направлению тока, то потенциал в jКаждой точке определяется потенциалом предыдущей точки плюс. ЭДС источника, работающего в режиме генератора, минус ЭДС источника, работающего в режиме потребителя, и минус падение напряжения на участке между точками цепи.
При обходе контура против направления тока знаки ЭДС и падения напряжения изменяются на противоположные.
Это правило особенно удобно применять в тех случаях, когда в цепи имеются участки с несколькими источниками.
Потенциальная диаграмма представляет собой график зависимости потенциалов точек цепи от величины сопротивлений участков между этими точками.
Для построения потенциальной диаграммы одну из точек электрической цепи условно заземляют (потенциал ее принимают равным нулю), а потенциалы остальных точек равны напряжении, между ними и заземленной точкой.
Потенциальная диаграмма представляет собой ломаную линию (рис. 3.3).
Пример №2
Для цепи, изображенной на рис. 3.2, дано:
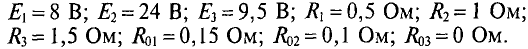
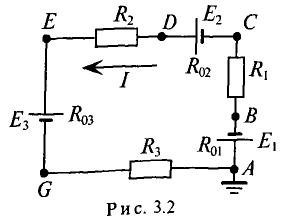
1. Определить величину и направление тока в цепи.
2. Определить потенциал точек В, С, D, Е, G, приняв потенциал точки А равным нулю, 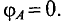
3. Построить потенциальную диаграмму.
4. Составить и проверить баланс мощностей для цепи.
Решение
1. Выбираем направление обхода контура по часовой стрелке, тогда величина тока
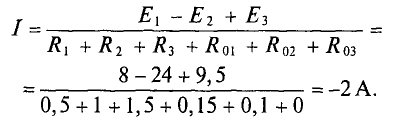
Знак «минус», полученный в результате вычислений, указывает на то что ток направлен против выбранного направления обхода как показано на рис. 3.2. В дальнейших расчетах знак «минус» не учитывается. Таким образом, источник ЭДС 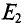 работает в режиме генератора, а
работает в режиме генератора, а 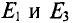 — потребителей.
— потребителей.
2. Для определения потенциалов указанных точек обходим контур по направлению тока. При этом получаем
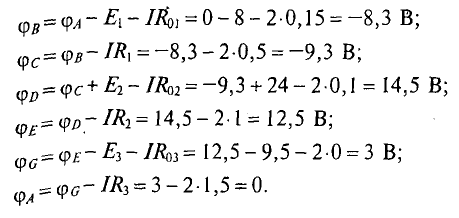
3. Для построения потенциальной диаграммы по оси ординат в масштабе откладываются потенциалы точек, а по оси абсцисс — сопротивления участков. Потенциальная диаграмма изображена на рис. 3.3.
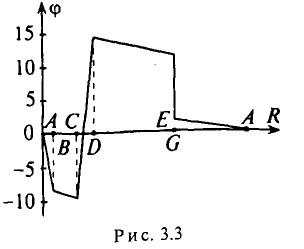
4. Баланс мощностей в электрической цепи с несколькими источниками соблюдается при условиями, что сумма мощностей источников, работающих в режиме генераторов, равна сумме мощностей источников, работающих в режиме потребителей, и потерям мощностей на всех сопротивлениях цепи, включая внутренние сопротивления источников:
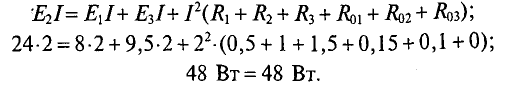
Законы Кирхгофа
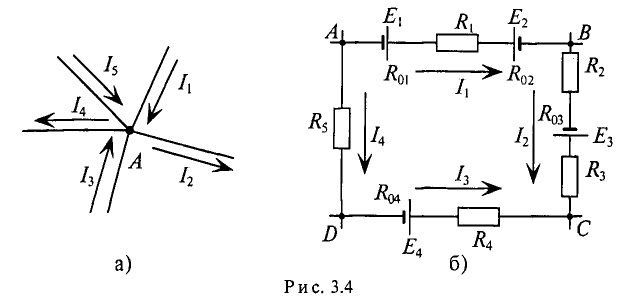
В схемах электрических цепей можно выделить характерные элементы: ветвь, узел, контур.
Ветвью электрической цепи называется ее участок, на всем прошении которого величина тока имеет одинаковое значение. Узлом электрической цепи (узловой точкой) называется место единения электрических ветвей. В узловой точке сходятся как минимум три ветви (проводника).
Контуром электрической цепи называют замкнутое соединение, которое могут входить несколько ветвей (рис. 3.46).
Ветви, содержащие источник электрической энергии, называйся активными, а ветви, не содержащие источников, называются пассивными.
Первый закон Кирхгофа. В разветвленной цепи ток в различных ветвях может иметь различное значение. Сумма токов, входящих узловую точку разветвленной цепи, должна быть равна сумме токов, выходящих из этой точки.
На рис. 3.4а показана узловая точка цепи А, для которой можно записать
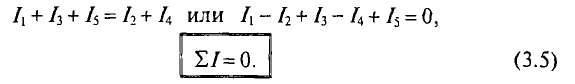
Выражение (3.5) представляет собой первого закона (правила) Кирхгофа.
Первый закон Кирхгофа формулируется так: алгебраическая сумма токов в ветвях, соединенных в один узел, равна нулю.
Токи, входящие в узел, принято считать положительными, а выходяшие из узла — отрицательными.
Второй закон Кирхгофа устанавливает зависимость между ЭДС и падением напряжения в замкнутом контуре любой электрической цепи.
Точки А, В, С и D являются узловыми точками (рис. 3.46), поскольку в каждой из них сходятся четыре проводника.
Определим потенциал каждой узловой точки, воспользовавшись выражением (3.4).
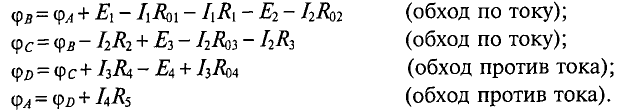
Сумма потенциалов всех узловых точек замкнутого контура равна
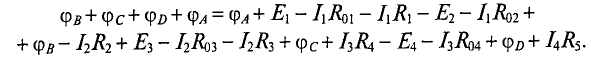
Сократив все потенциалы замкнутого контура, слева и справа от знака равенства, и перенеся все ЭДС замкнутого контура налево от знака равенства, а падения напряжения оставив справа, можно записать
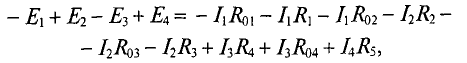
что и является вторым законом Кирхгофа, который формулируется так:
Алгебраическая сумма ЭДС в замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на всех участках этой цепи
(обход по току); (обход по току); (обход против тока); (обход против тока).

Выражение (3.6) представляет собой математическую запись второго закона (правила) Кирхгофа.
Для определения знаков в алгебраической сумме направление обхода контура выбирается произвольно: по часовой или против часовой стрелки.
ЭДС источника, совпадающая с выбранным направлением обхода контура, считается положительной, а не совпадающая — отрицательной.
Падение напряжения на сопротивлении R считается положительным, если ток, протекающий через него, совпадает с выбранным направлением обхода контура, или отрицательным — если не совпадает.
Для электрической цепи, изображенной на рис. 3.46, второй закон Кирхгофа записывается так:
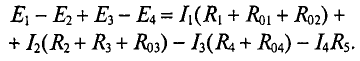
Направление обхода контура в приведенном расчете выбрано по часовой стрелке.
Последовательное соединение потребителей
Последовательным соединением участков электрической цепи называют соединение, при котором через все участки цепи проходит один и тот же ток (рис. 3.5).
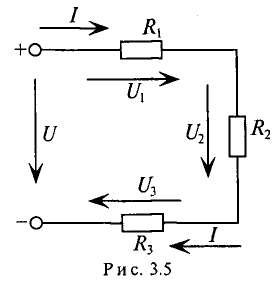
Напряжение на каждом последовательно включенном участке пропорционально величине сопротивления этого участка.
При последовательном соединении потребителей с сопротивлениями 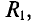
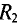 и
и 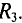 (рис. 3.5) напряжение на их замах равно
(рис. 3.5) напряжение на их замах равно
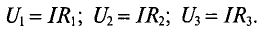
Воспользовавшись вторым законом Кирхгофа для рассматривали цепи (рис. 3.5), можно записать
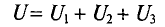
или

Откуда 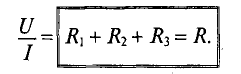 (3.8)
(3.8)
Таким образом, общее (эквивалентное) сопротивление R последовательно включенных сопротивлений (потребителей) равно сумме этих сопротивлений.
Ток в цепи последовательно включенных потребителей (рис. 3.5) определяется выражением
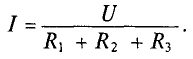
Нетрудно понять, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а следовательно, и режим работы (напряжение) всех последовательно включенных потребителей.
Поэтому последовательное соединение сопротивлений не нашло широкого практического применения.
Следует заметить, что при последовательном соединении резисторов на большем сопротивлении тратится большая мощность
Потенциометр
Распределение напряжений, пропорциональное сопротивлениям последовательно соединенных резисторов, используется в работе потенциометра (делителя напряжения). В качестве потенциометра можно использовать реостат с подвижным контактом, включенным как показано на рис. 3.6.
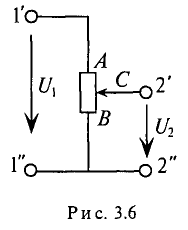
Изменяя сопротивление реостата, можно плавно изменять напряжение 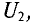 получаемое на потребителе: от величины входного напряжения
получаемое на потребителе: от величины входного напряжения 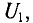 подведенного к клеммам
подведенного к клеммам 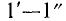 (движок реостата в точке А), до нуля (движок реостата в точке В). Потребитель подключается к клеммам
(движок реостата в точке А), до нуля (движок реостата в точке В). Потребитель подключается к клеммам 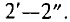
Делитель напряжения может состоять из нескольких резисторов с постоянными сопротивлениями, соединенными последовательно. Напряжение при этом можно снимать с каждого резистора или группы резисторов.
Потеря напряжения в проводах
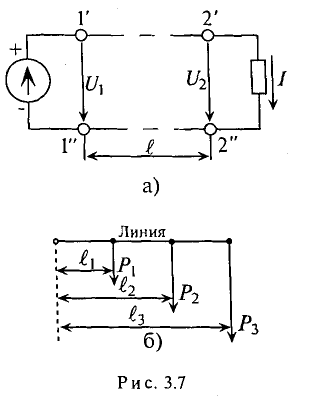
В линиях электропередачи (ЛЭП) электрической энергии соединительные провода включаются последовательно с потребителем (рис. 3.7а).
Так как провода обладают сопротивлением 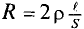 (двухпроводная линия), то при прохождении по ним тока происходит потеря напряжения на них. За счет этой потери напряжение в конце линии электропередачи
(двухпроводная линия), то при прохождении по ним тока происходит потеря напряжения на них. За счет этой потери напряжение в конце линии электропередачи 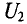 меньше, чем напряжение
меньше, чем напряжение 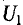 в начале. Величина потери напряжения в проводах:
в начале. Величина потери напряжения в проводах:
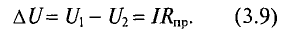
Из (3.9) следует, что потеря напряжения в проводах зависит от тока потребителя (нагрузки) I и составления проводов 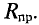
Для того чтобы увеличение тока линии не приводило к значительной потере напряжения и к уменьшению напряжения на потребителе 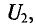 расчет течений проводов ЛЭП производят с учетом допустимой потери напряжения
расчет течений проводов ЛЭП производят с учетом допустимой потери напряжения
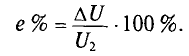
Допустимая потеря напряжения в многокилометровых ЛЭП не должна превышать 10%.
Расчет сечения проводов (двухпроводной линии) по допустимой потере напряжения производят по следующему выражению:
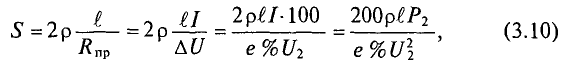
Где: S — сечение проводов ЛЭП, 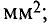 р — удельное сопротивление атериала провода,
р — удельное сопротивление атериала провода, 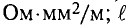 — длина ЛЭП, м;
— длина ЛЭП, м; 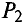 — мощность потребителя, Вт;
— мощность потребителя, Вт; 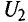 — напряжение на потребителе, В.
— напряжение на потребителе, В.
Выбранное по допустимым потерям напряжения сечение проводов ЛЭП должно быть проверено по допустимому току (Приложение 11).
Из (3.10) видно, что сечение проводов зависит от напряжения а потребителе 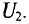 Поскольку эта зависимость квадратичная, то уменьшения сечения проводов рационально увеличивать напряжение ЛЭП. В настоящее время напряжение ЛЭП переменного тока достигает 1150 кВ, а постоянного тока 1500 кВ.
Поскольку эта зависимость квадратичная, то уменьшения сечения проводов рационально увеличивать напряжение ЛЭП. В настоящее время напряжение ЛЭП переменного тока достигает 1150 кВ, а постоянного тока 1500 кВ.
Выражение (3.10) справедливо для ЛЭП с нагрузкой в конце линии (рис. 3.7а).
Если же нагрузка распределена вдоль линии (рис. 3.76), то сечение проводов определяется выражением
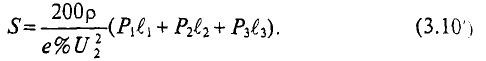
КПД линии электропередачи в процентах определяется выражением
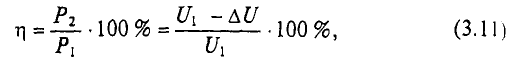
где 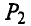 — мощность потребителя;
— мощность потребителя; 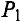 — мощность источника.
— мощность источника.
Как следует из (3.11), чем больше потеря напряжения 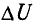 в про водах, тем меньше КПД линии электропередачи. КПД длинных линий электропередачи лежит в пределах (90—98) %.
в про водах, тем меньше КПД линии электропередачи. КПД длинных линий электропередачи лежит в пределах (90—98) %.
Параллельное соединение потребителей
Параллельным соединением участков электрической цепи называют соединение, при котором все участки цепи присоединяются к одной паре узлов, т. е. находятся под действием одного и того же напряжения (рис. 3.8). Токи параллельно включенных участков обратно пропорциональны сопротивлениям этих участков.
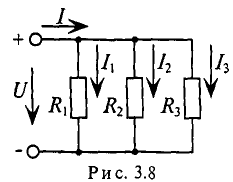
При параллельном соединении сопротивлений 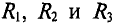 токи потребителей соответственно равны
токи потребителей соответственно равны
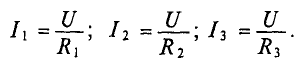
Воспользовавшись первым законом Кирхгофа, можно определить ток I в неразветвленной части цепи
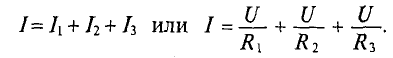
Тогда
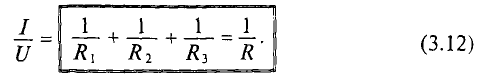
Таким образом, обратная величина общего (эквивалентного) сопротивления R параллельно включенных потребителей равна сумме обратных величин сопротивлений этих потребителей.
Величина, обратная сопротивлению, определяет проводимость потребителя g. Тогда общая (эквивалентная) проводимость цепи и параллельном соединении потребителей определяется суммой проводимостей потребителей

Если параллельно включены 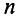 одинаковых потребителей с составлением
одинаковых потребителей с составлением 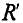 каждый, то эквивалентное сопротивление этих потребителей
каждый, то эквивалентное сопротивление этих потребителей 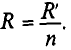 Если параллельно включены два потребителя с сопротивлениями
Если параллельно включены два потребителя с сопротивлениями 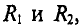 то их общее (эквивалентное) сопротивление в соответствии с (3.12) равно
то их общее (эквивалентное) сопротивление в соответствии с (3.12) равно
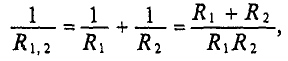
откуда
Если параллельно включены три потребителя с сопротивления 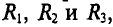 то общее их сопротивление (см. (3.12))
то общее их сопротивление (см. (3.12))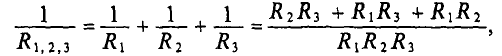
откуда
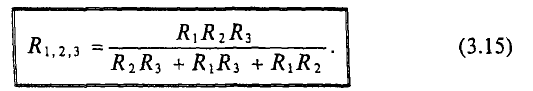
Изменение сопротивления какого-либо из параллельно соединенных потребителей не влияет на режим работы (напряжение) других потребителей, включая изменяемое. Поэтому параллельное соединение нашло широкое практическое применение.
При параллельном соединении потребителей на большем сопротивлении тратится меньшая мощность:
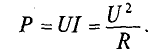
Анализ линейных электрических цепей с постоянными параметрами при гармоническом воздействии
Общие представления о методах формирования уравнений электрического равновесия сложных цепей:
До сих пор рассматривались только простейшие, одноконтурные и двухузловые цепи, а также цепи, которые приводятся к простейшим с помощью элементарных преобразований. Для анализа таких цепей использовалась основная система уравнений электрического равновесия, включающая в себя 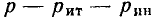 компонентных и р топологических уравнений, составленных на основании законов Кирхгофа. С помощью основной системы уравнений электрического равновесия, в принципе, можно производить анализ и сложных цепей, однако с ростом числа ветвей цепи анализ усложняется, так как для определения токов и напряжений цепи, содержащей р ветвей, приходится решать систему из
компонентных и р топологических уравнений, составленных на основании законов Кирхгофа. С помощью основной системы уравнений электрического равновесия, в принципе, можно производить анализ и сложных цепей, однако с ростом числа ветвей цепи анализ усложняется, так как для определения токов и напряжений цепи, содержащей р ветвей, приходится решать систему из 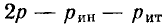 уравнений. Число одновременно решаемых уравнений может быть уменьшено, если учесть, что не все
уравнений. Число одновременно решаемых уравнений может быть уменьшено, если учесть, что не все 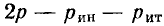 неизвестных токов и напряжений ветвей являются независимыми.
неизвестных токов и напряжений ветвей являются независимыми.
Для каждой электрической цепи можно выделить совокупность независимых токов и (или) напряжений ветвей, зная которые, можно определить все остальные (зависимые) токи и напряжения. Значения независимых токов и напряжений находят путем решения сокращенной системы уравнений электрического равновесия, содержащей меньшее, чем 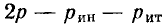 , число уравнений. В связи с тем что выбор независимых токов и напряжений неоднозначен, а число независимых токов и напряжений определяется тем, какие именно величины выбраны в качестве независимых, трудоемкость анализа цепи определяется рациональностью выбора системы независимых токов и напряжений.
, число уравнений. В связи с тем что выбор независимых токов и напряжений неоднозначен, а число независимых токов и напряжений определяется тем, какие именно величины выбраны в качестве независимых, трудоемкость анализа цепи определяется рациональностью выбора системы независимых токов и напряжений.
Методы, основанные на непосредственном применении законов Кирхгофа
К методам формирования уравнений электрического равновесия цепей, основанным на непосредственном применении законов Кирхгофа, относятся метод токов ветвей и метод напряжений ветвей. В методе токов ветвей в качестве независимых переменных, относительно которых составляется сокращенная система уравнений электрического равновесия, используют токи ветвей исследуемой цепи. Этот метод основан на том, что ток и напряжение каждой ветви, за исключением ветвей, содержащих идеализированные источники тока, а также ветвей, составленных только из идеализированных источников напряжения, связаны между собой однозначной зависимостью, которая определяется компонентным, уравнением. данной ветви. Таким образом, зная токи всех ветвей электрической цепи, можно определить напряжения этих ветвей.
Пусть линейная электрическая цепь состоит только из идеализированных двухполюсных пассивных элементов: сопротивлений, емкостей, индуктивностей, а также неуправляемых источников напряжения. Основная система уравнений электрического равновесия такой цепи будет содержать q — 1 уравнений баланса токов, р — q + 1 уравнений баланса напряжений и 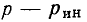 компонентных уравнений для определения р неизвестных токов и
компонентных уравнений для определения р неизвестных токов и 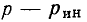 неизвестных напряжений ветвей (напряжения
неизвестных напряжений ветвей (напряжения 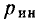 ветвей, состоящих только из источников напряжения, заданы). Если каким-либо образом определить токи всех ветвей, то неизвестные напряжения могут быть найдены с помощью
ветвей, состоящих только из источников напряжения, заданы). Если каким-либо образом определить токи всех ветвей, то неизвестные напряжения могут быть найдены с помощью 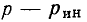 компонентных уравнений. Для определения р неизвестных токов ветвей можно воспользоваться q — 1 уравнениями баланса токов и р — q + 1 уравнениями баланса напряжений, выразив в последних напряжения ветвей через соответствующие токи.
компонентных уравнений. Для определения р неизвестных токов ветвей можно воспользоваться q — 1 уравнениями баланса токов и р — q + 1 уравнениями баланса напряжений, выразив в последних напряжения ветвей через соответствующие токи.
Таким образом, для цепи, не содержащей источников тока, применение метода тока ветвей позволяет уменьшить число уравнений, входящих в систему уравнений электрического равновесия от 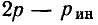 до р.
до р.
Пример №3
Составим систему уравнений электрического равновесия по методу токов ветвей для электрической цепи, схема которой приведена на рис. 4.1, а. Граф этой цепи, соответствующий сокращенному топологическому описанию, изображен на рис. 4.1, б. Как видно из рисунка, для данного топологического описания число ветвей р = 6, число узлов q = 4, причем ни одна из ветвей не содержит источников тока 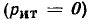 и не составлена только из источников напряжения
и не составлена только из источников напряжения 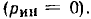 Выбирая дерево графа и систему независимых контуров в соответствии с рис. 4.1, в — д, составим основную систему уравнений электрического равновесия, которая будет включать в себя 12 уравнений, в том числе q — 1 = 3 уравнений баланса токов:
Выбирая дерево графа и систему независимых контуров в соответствии с рис. 4.1, в — д, составим основную систему уравнений электрического равновесия, которая будет включать в себя 12 уравнений, в том числе q — 1 = 3 уравнений баланса токов:

р - q + 1 = 3 уравнения баланса напряжений:

и р = 6 компонентных уравнений
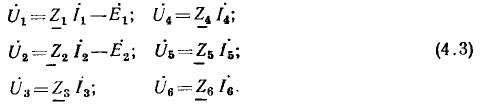
Подставляя уравнения (4.3) в (4.2), получим в сочетании с уравнениями (4.1) сокращенную систему уравнений электрического равновесия рассматриваемой цепи
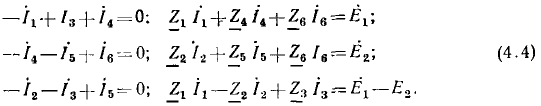
Таким образом, число одновременно решаемых уравнений уменьшилось от 12 до 6.
Рассмотрим более общий случай, когда исследуемая цепь помимо указанных ранее элементов включает в себя 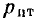 ветвей, содержащих неуправляемые источники тока (ток этих ветвей задан, а напряжение неизвестно).
ветвей, содержащих неуправляемые источники тока (ток этих ветвей задан, а напряжение неизвестно).
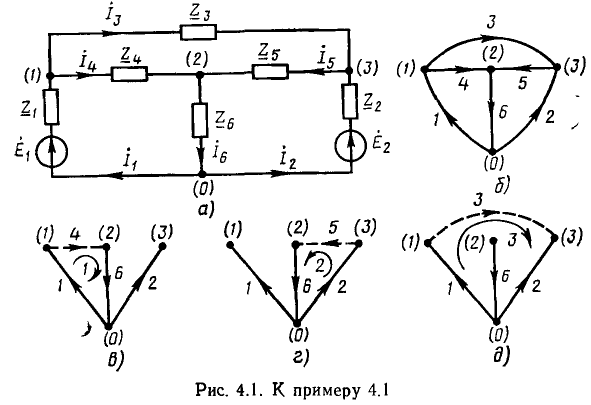
Выберем дерево графа цепи таким образом, чтобы ветви, содержащие источники тока, не входили бы в число ветвей дерева, т. е. являлись бы главными ветвями. Тогда напряжения этих ветвей будут фигурировать только в 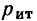 уравнениях баланса напряжений, составленных для главных контуров, замыкаемых ветвями, содержащими источники тока. Выражая в остальных
уравнениях баланса напряжений, составленных для главных контуров, замыкаемых ветвями, содержащими источники тока. Выражая в остальных 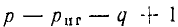 уравнениях, составленных на основании второго закона Кирхгофа, напряжения ветвей через токи этих же ветвей, получим в сочетании с q — 1 уравнениями, составленными на основании первого закона Кирхгофа,
уравнениях, составленных на основании второго закона Кирхгофа, напряжения ветвей через токи этих же ветвей, получим в сочетании с q — 1 уравнениями, составленными на основании первого закона Кирхгофа, 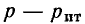 уравнений для определения
уравнений для определения 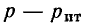 неизвестных токов ветвей.
неизвестных токов ветвей.
Пример №4
Используя метод токов ветвей, составим систему уравнений электрического равновесия цепи, эквивалентная схема которой для мгновенных значений приведена на рис. 1.39, а комплексная схема замещения — на рис. 4.2, а.
Как было показано в примере 1.7, основная система уравнений электрического равновесия этой цепи включает в себя 4 компонентных уравнения и 6 уравнений, составленных на основании законов Кирхгофа. Если дерево графа выбрано таким образом, что ветвь, содержащая источник тока, вошла в число главных ветвей (рис. 4.2, б), то напряжение этой ветви будет фигурировать только в одном уравнении, составленном на основании второго закона Кирхгофа.
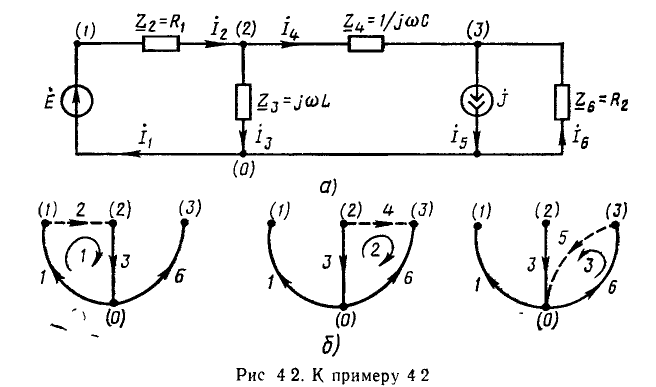
Это уравнение, после нахождения токов всех ветвей, можно использовать для определения неизвестного напряжения на источнике тока. Выражая в оставшихся уравнениях напряжения всех ветвей через соответствующие токи, получим систему уравнений для определения пяти неизвестных токов ветвей:
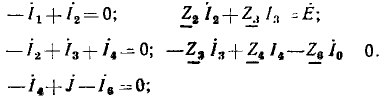
Далее будет показано, что число ветвей цепи, токи которых могут быть заданы независимо, не может превышать числа главных контуров цепи р — q + 1. Когда 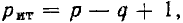 число неизвестных токов ветвей будет равно q — 1 и они могут быть определены из q — 1 уравнения баланса токов.
число неизвестных токов ветвей будет равно q — 1 и они могут быть определены из q — 1 уравнения баланса токов.
В связи с тем что напряжения на связанных индуктивностях выражаются через токи этих индуктивностей, метод токов ветвей может быть применен и для составления уравнений электрического равновесия цепей со связанными индуктивностями (см. пример 2.13).
Дуальным по отношению к методу токов ветвей является метод напряжений ветвей. При составлении системы уравнений электрического равновесия цепи с помощью этого метода в качестве независимых переменных используют неизвестные напряжения 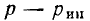 ветвей. Система уравнений электрического равновесия в этом случае включает в себя р — q +1 уравнений баланса напряжений и
ветвей. Система уравнений электрического равновесия в этом случае включает в себя р — q +1 уравнений баланса напряжений и 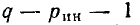 уравнений баланса токов, причем неизвестные токи всех ветвей, входящие в эти уравнения, должны быть выражены через напряжения этих же ветвей. Число ветвей, напряжения которых могут быть заданы независимо, не может превышать числа независимых узлов q— 1. Когда число ветвей, составленных только из независимых источников напряжения, равно числу независимых узлов
уравнений баланса токов, причем неизвестные токи всех ветвей, входящие в эти уравнения, должны быть выражены через напряжения этих же ветвей. Число ветвей, напряжения которых могут быть заданы независимо, не может превышать числа независимых узлов q— 1. Когда число ветвей, составленных только из независимых источников напряжения, равно числу независимых узлов 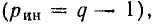 число неизвестных напряжений ветвей равно числу независимых контуров р — q + 1 и они могут быть определены из р — q + 1 уравнений баланса напряжений.
число неизвестных напряжений ветвей равно числу независимых контуров р — q + 1 и они могут быть определены из р — q + 1 уравнений баланса напряжений.
Метод напряжений ветвей в общем случае нельзя использовать для формирования уравнений электрического равновесия цепей со связанными индуктивностями. Это связано с тем, что токи таких индуктивностей могут быть выражены через соответствующие напряжения только при коэффициенте связи между индуктивностями, меныием единицы. Это следует из соотношений, полученных для токов связанных индуктивностей, выраженных через напряжения с использованием (2.165):
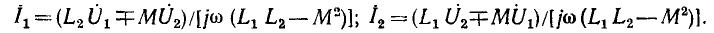
Полученные выражения имеют смысл только при 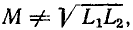 т. е. при
т. е. при 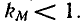 Таким образом, метод напряжений ветвей является менее общим, чем метод токов ветвей.
Таким образом, метод напряжений ветвей является менее общим, чем метод токов ветвей.
Итак, методы формирования уравнений электрического равновесия цепи, основанные на непосредственном применении законов Кирхгофа, позволяют уменьшить число одновременно решаемых уравнений от 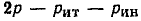 до
до  или
или 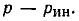
Метод контурных токов
Метод контурных токов основан на важной топологической особенности электрических цепей, вытекающей из первого закона Кирхгофа и заключающейся в том, что токи всех ветвей цепи могут быть выражены через токи главных ветвей. Для определения токов главных ветвей (контурных токов) составляют систему из 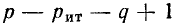 уравнений, называемых контурными уравнениями. Рассмотрим методику формирования контурных уравнений на примере простой цепи, не содержащей источников тока, схема которой приведена на рис. 4.1, а. Выбирая произвольно дерево графа этой цепи, убеждаемся, что токи ветвей дерева однозначно выражаются через токи главных ветвей. В частности, используя дерево графа и соответствующую ему систему контуров, изображенных на рис. 4.1, в—д, находим на основании первого закона Кирхгофа, что токи ветвей дерева
уравнений, называемых контурными уравнениями. Рассмотрим методику формирования контурных уравнений на примере простой цепи, не содержащей источников тока, схема которой приведена на рис. 4.1, а. Выбирая произвольно дерево графа этой цепи, убеждаемся, что токи ветвей дерева однозначно выражаются через токи главных ветвей. В частности, используя дерево графа и соответствующую ему систему контуров, изображенных на рис. 4.1, в—д, находим на основании первого закона Кирхгофа, что токи ветвей дерева 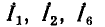 могут быть выражены через токи главных ветвей
могут быть выражены через токи главных ветвей 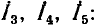
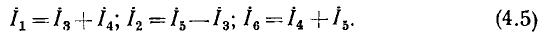
Таким образом, если каким-либо образом определить токи главных ветвей, то далее, используя соотношения (4.5), можно найти токи остальных ветвей цепи, а затем найти неизвестные напряжения ветвей. Следовательно, для полного описания процессов в цепи достаточно определить только токи главных ветвей исследуемой цепи. Из соотношения (4.5) также следует, что максимальное количество токов ветвей, которые могут быть заданы независимо, не может превышать числа главных ветвей.
Для определения токов главных ветвей цепи (см. рис. 4.1) воспользуемся уравнениями, составленными на основании второго закона Кирхгофа, выразив входящие в них напряжения ветвей через токи главных ветвей. Подставляя (4.3), (4.5) в уравнение (4.2), получаем
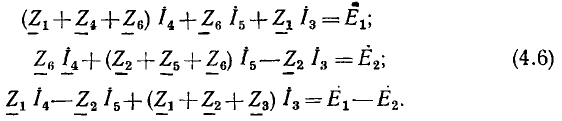
Разумеется, решить контурные уравнения (4.6), легче, чем основную систему уравнений электрического равновесия цепи (4.1)—(4.3) или систему уравнений (4.4).
На практике контурные уравнения формируют с помощью простого алгоритма, не прибегая к составлению основной системы уравнений электрического равновесия, поэтому применение этого метода позволяет упростить и составление, и решение уравнений электрического равновесия цепи. Для того чтобы сформулировать правила составления контурных уравнений, введем ряд новых понятий.
Собственным сопротивлением 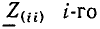 контура назовем сумму сопротивлений всех ветвей, входящих в этот контур. В цепи (см. рис. 4.1, а) выделено три независимых контура (см. рис. 4.1, в— д); их собственные сопротивления
контура назовем сумму сопротивлений всех ветвей, входящих в этот контур. В цепи (см. рис. 4.1, а) выделено три независимых контура (см. рис. 4.1, в— д); их собственные сопротивления
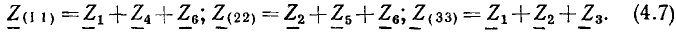
В каждом из уравнений (4.6) имеется член, равный произведению собственного сопротивления i-гo контура на ток главной ветви, входящей в данный контур. Этот член можно рассматривать как падение напряжения на собственном сопротивлении i-гo контура, вызванное током главной ветви, если бы он протекал через все ветви, входящие в данный контур, т. е. замыкался бы в i-м контуре. Такой ток называется контурным током. Таким образом, контурный ток i-гo контура 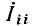 равен току главной ветви, входящей в данный контур. Направление контурного тока во всех элементах контура совпадает с направлением его обхода, т. е. с направлением соответствующей главной ветви. Для цепи, схема которой представлена на рис. 4.1, имеем
равен току главной ветви, входящей в данный контур. Направление контурного тока во всех элементах контура совпадает с направлением его обхода, т. е. с направлением соответствующей главной ветви. Для цепи, схема которой представлена на рис. 4.1, имеем
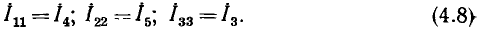
Как следует из (4.5) и (4.8), токи всех ветвей цепи могут быть выражены через контурные токи этой цепи.
Взаимным, или общим, сопротивлением i-гo и j-го контуров называется сопротивление 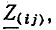 равное сумме сопротивлений ветвей, общих для этих контуров. Взаимное сопротивление
равное сумме сопротивлений ветвей, общих для этих контуров. Взаимное сопротивление 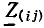 берется со знаком плюс, если контурные токи рассматриваемых контуров протекают через общие для этих контуров ветви в одинаковом направлении; если контурные токи в общих ветвях имеют противоположные направления, то взаимное сопротивление берут со знаком минус. Если рассматриваемые контуры не имеют общих ветвей, то их взаимное сопротивление равно нулю. Взаимные сопротивления контуров цепи (см. рис. 4.1)
берется со знаком плюс, если контурные токи рассматриваемых контуров протекают через общие для этих контуров ветви в одинаковом направлении; если контурные токи в общих ветвях имеют противоположные направления, то взаимное сопротивление берут со знаком минус. Если рассматриваемые контуры не имеют общих ветвей, то их взаимное сопротивление равно нулю. Взаимные сопротивления контуров цепи (см. рис. 4.1)
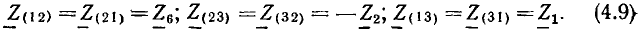
Контурной э. д. с. 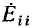 i-гo контура называется алгебраическая сумма э. д. с. всех идеализированных источников напряжения, входящих в данный контур. Если направление э. д. с. какого-либо источника, входящего в i-й контур, совпадает с направлением контурного тока этого контура, то соответствующая э. д.с. входит в
i-гo контура называется алгебраическая сумма э. д. с. всех идеализированных источников напряжения, входящих в данный контур. Если направление э. д. с. какого-либо источника, входящего в i-й контур, совпадает с направлением контурного тока этого контура, то соответствующая э. д.с. входит в 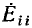 со знаком плюс, в противном случае— со знаком минус. Контурные э. д. с. рассматриваемой цепи
со знаком плюс, в противном случае— со знаком минус. Контурные э. д. с. рассматриваемой цепи
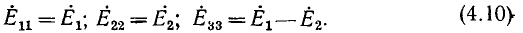
Используя обозначения (4.7)—(4.10), представим контурные уравнения (4.6) в канонической форме записи:
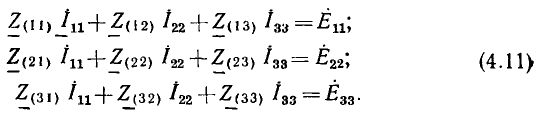
Анализируя (4.11), нетрудно установить, что все контурные уравнения имеют одинаковую структуру; левая часть контурного уравнения есть сумма членов, один из которых равен произведению контурного тока соответствующего контура на собственное сопротивление этого контура, а остальные — произведениям контурных токов других контуров на взаимные сопротивления этого контура и других контуров; правая часть контурного уравнения содержит только один член — контурную э.д.с. рассматриваемого контура.
Полученные результаты могут быть обобщены на случай произвольюй линейной цепи, составленной из сопротивлений, емкостей, индуктивностей и независимых источников напряжения:
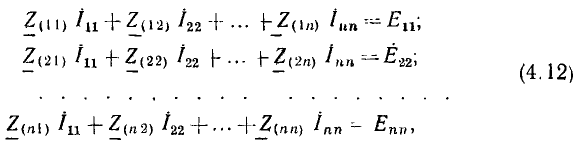
где n = р — q + 1 — число независимых контуров цепи. Итак, зная труктуру контурного уравнения, нетрудно сформировать систему онтурных уравнений любой цепи, не прибегая к составлению основой системы уравнений электрического равновесия.
Используя матричную форму, уравнения (4.12) можно переписать

Здесь
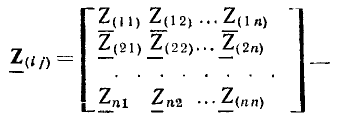
матрица контурных сопротивлений;
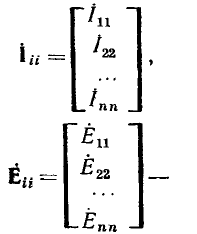
матрицы-столбцы контурных токов и контурных э. д. с.
Для линейных цепей, составленных только из сопротивлений, емкостей, индуктивностей и независимых источников напряжения, матрица контурных сопротивлений квадратная, причем вследствие того, что для таких цепей всегда выполняется условие 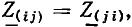 матрица
матрица 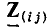 симметрична относительно главной диагонали.
симметрична относительно главной диагонали.
Решая систему уравнений (4.13) любым из методов, можно найти все неизвестные контурные токи цепи. Например, используя формулы Крамера, запишем выражение для контурного тока k-гo контура
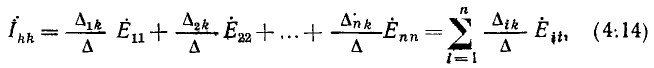
где 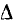 — определитель системы уравнений (4.13);
— определитель системы уравнений (4.13); 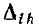 — алгебраическое дополнение элемента
— алгебраическое дополнение элемента 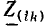 этого определителя. В аналогичной форме могут быть записаны выражения для контурных токов всех остальных контуров. Следует отметить, что формулы Крамера, позволяющие получить в явной форме аналитические выражения для контурных токов, нашли применение лишь при теоретическом исследовании свойств электрических цепей. Вычисление значений контурных токов при n > 3 с помощью формулы Крамера является весьма трудоемким. Поэтому на практике обычно используют более экономичные методы, такие, например, как метод исключения Гаусса или LU-пpeобразование [4, 5]
этого определителя. В аналогичной форме могут быть записаны выражения для контурных токов всех остальных контуров. Следует отметить, что формулы Крамера, позволяющие получить в явной форме аналитические выражения для контурных токов, нашли применение лишь при теоретическом исследовании свойств электрических цепей. Вычисление значений контурных токов при n > 3 с помощью формулы Крамера является весьма трудоемким. Поэтому на практике обычно используют более экономичные методы, такие, например, как метод исключения Гаусса или LU-пpeобразование [4, 5]
Если электрическая цепь помимо сопротивлений, емкостей, индуктивностей и независимых источников напряжения содержит также независимые источники тока, то последние с помощью рассмотренных в § 2.6 преобразований можно заменить независимыми источниками напряжения. Однако систему контурных уравнений такой цепи можно составить и не прибегая к преобразованию источников.
Пусть в состав исследуемой цепи входит 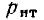 ветвей, включающих независимые источники тока. Выберем дерево цепи таким образом, Чтобы ветви с источниками тока вошли в состав главных ветвей. Очевидно, что контурные токи контуров, которые замыкаются главными ветвями, содержащими источники тока, равны токам соответствующих независимых источников. Эти токи заданы и не требуют определения. Таким образом, число неизвестных контурных токов меньше числа независимых контуров
ветвей, включающих независимые источники тока. Выберем дерево цепи таким образом, Чтобы ветви с источниками тока вошли в состав главных ветвей. Очевидно, что контурные токи контуров, которые замыкаются главными ветвями, содержащими источники тока, равны токам соответствующих независимых источников. Эти токи заданы и не требуют определения. Таким образом, число неизвестных контурных токов меньше числа независимых контуров  на
на 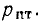 Для определения неизвестных контурных токов необходимо составить систему из р —
Для определения неизвестных контурных токов необходимо составить систему из р —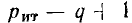 контурных уравнений для контуров, не содержащих ветвей с источниками тока. Контурные уравнения такой цепи могут быть записаны в такой же форме, как и контурные уравнения цепи, не содержащей источников тока (4.12), (4.13), Однако матрица контурных сопротивлений в этом случае будет не квадратной: число столбцов будет равно числу независимых контуров
контурных уравнений для контуров, не содержащих ветвей с источниками тока. Контурные уравнения такой цепи могут быть записаны в такой же форме, как и контурные уравнения цепи, не содержащей источников тока (4.12), (4.13), Однако матрица контурных сопротивлений в этом случае будет не квадратной: число столбцов будет равно числу независимых контуров 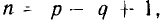 а число строк — числу неизвестных контурных токов
а число строк — числу неизвестных контурных токов 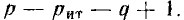 После формирования контурных уравнений в форме (4.12), (4.13) входящие в каждое уравнение члены, содержащие известные контурные токи, переносят в правую часть соответствующих уравнений.
После формирования контурных уравнений в форме (4.12), (4.13) входящие в каждое уравнение члены, содержащие известные контурные токи, переносят в правую часть соответствующих уравнений.
Пример №5
Составим систему контурных уравнений для цепи, схема которой приведена на рис. 4.2, а Число ветвей этой цепи р= 6, число узлов q = 4, число ветвей, содержащих источники тока, 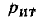 =1. Выберем дерево графа цепи таким образом, чтобы ветвь с источником тока вошла в число главных ветвей Соответствующая выбранному дереву система независимых контуров изображена на рис. 4.2, б. В связи с тем что число независимых контуров цепи равно
=1. Выберем дерево графа цепи таким образом, чтобы ветвь с источником тока вошла в число главных ветвей Соответствующая выбранному дереву система независимых контуров изображена на рис. 4.2, б. В связи с тем что число независимых контуров цепи равно 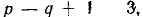 а число неизвестных контурных токов
а число неизвестных контурных токов 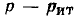
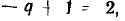 система контурных уравнений имеет вид
система контурных уравнений имеет вид
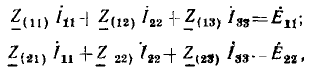
где 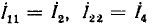 — неизвестные контурные токи первого и второго контуров;
— неизвестные контурные токи первого и второго контуров; 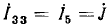 — известный контурный ток третьего контура;
— известный контурный ток третьего контура;
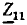
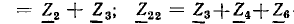 —собственные сопротивления первого и второго контуров;
—собственные сопротивления первого и второго контуров; 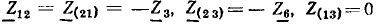 —взаимные сопротивления контуров;
—взаимные сопротивления контуров; 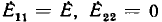 — контурные э.д.с. первого и второго контуров.
— контурные э.д.с. первого и второго контуров.
Перенося члены, содержащие известный контурный ток, в правую часть уравнений и выражая собственные и взаимные сопротивления контуров через параметры элементов рассматриваемой цепи, получаем окончательно
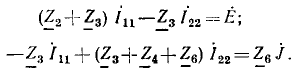
Таким образом, система контурных уравнений рассматриваемой цепи содержит два уравнения для определения двух неизвестных контурных токов.
Метод контурных токов можно использовать и для составления уравнений электрического равновесия цепей со связанными индуктивностями, однако алгоритм формирования матрицы контурных сопротивлений при этом усложняется. Поэтому при анализе цепей с взаимной индуктивностью целесообразно либо заменять связанные индуктивности участками цепей, не содержащими связанных индуктивностей, либо формировать уравнения электрического равновесия с помощью метода токов ветвей.
В ряде случаев при составлении контурных уравнений в качестве независимых удобно выбирать не главные контуры, а контуры, соответствующие ячейкам графа рассматриваемой цепи. Следует, однако, иметь в виду, что такой подход применим только к анализу цепей, граф которых является планарным.
Метод узловых напряжений
При составлении уравнений электрического равновесия цепи по методу напряжений ветвей в качестве независимых переменных были использованы  неизвестных напряжений. Принимая во внимание, что напряжения ветвей связаны
неизвестных напряжений. Принимая во внимание, что напряжения ветвей связаны 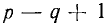 уравнениями баланса напряжений, количество независимых напряжений, относительно которых формируется система уравнений электрического равновесия цепи, может быть уменьшено до
уравнениями баланса напряжений, количество независимых напряжений, относительно которых формируется система уравнений электрического равновесия цепи, может быть уменьшено до 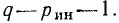 Если дерево графа цепй выбрано так, что ветви, содержащие только независимые источники напряжения, вошли в число ветвей дерева, то в качестве независимых переменных можно выбрать неизвестные
Если дерево графа цепй выбрано так, что ветви, содержащие только независимые источники напряжения, вошли в число ветвей дерева, то в качестве независимых переменных можно выбрать неизвестные 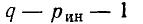 напряжения ветвей дерева. Такой метод формирования сокращенной системы уравнений электрического равновесия цепи называется методом напряжений ветвей дерева. Этот метод не получил широкого распространения.
напряжения ветвей дерева. Такой метод формирования сокращенной системы уравнений электрического равновесия цепи называется методом напряжений ветвей дерева. Этот метод не получил широкого распространения.
В качестве независимых переменных, относительно которых формируют уравнения электрического равновесия цепи, удобно использовать так называемые узловые напряжения, т. е. напряжения независимых узлов рассматриваемой цепи относительно базисного. Можно показать, что напряжения всех ветвей электрической цепи могут быть выражены через узловые напряжения этой цепи. Действительно, напряжение некоторой ветви, включенной между i-м и базисным узлами, равно узловому напряжению i-гo узла 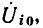 взятого со знаком плюс или минус в зависимости от направления напряжения этой ветви, а напряжение ветви, включенной между i-м и j-м узлами (рис. 4.3), — разности узловых напряжений этих узлов
взятого со знаком плюс или минус в зависимости от направления напряжения этой ветви, а напряжение ветви, включенной между i-м и j-м узлами (рис. 4.3), — разности узловых напряжений этих узлов 
Если исследуемая цепь не содержит независимых источников напряжения, то все q — 1 неизвестные узловые напряжения независимы. Если цепь содержит 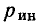 ветвей, составленных только из независимых
ветвей, составленных только из независимых
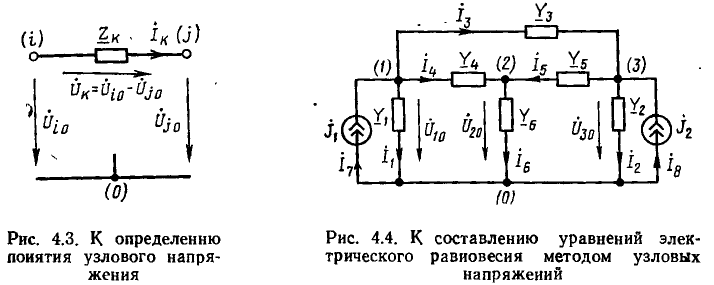
источников напряжения, то узловые напряжения 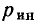 узлов могут быть выражены через
узлов могут быть выражены через  независимых узловых напряжения, для определения которых записывают
независимых узловых напряжения, для определения которых записывают  уравнений электрического равновесия цепи, называемых узловыми. Метод формирования уравнений электрического равновесия цепи,в котором в качестве независимых переменных используются неизвестные напряжения независимых узлов относительно базисного, называется методом узловых напряжений.
уравнений электрического равновесия цепи, называемых узловыми. Метод формирования уравнений электрического равновесия цепи,в котором в качестве независимых переменных используются неизвестные напряжения независимых узлов относительно базисного, называется методом узловых напряжений.
Рассмотрим метод формирования узловых уравнений на примере цепи, не содержащей источников напряжения (рис. 4.4). Рассматриваемая цепь получена из цепи, схема которой изображена на рис. 4.1, а, путем преобразования источников напряжения в источники тока и замены комплексных сопротивлений ветвей их комплексными проводимостями. Она имеет три независимых узла, для которых можно составить уравнения баланса токов
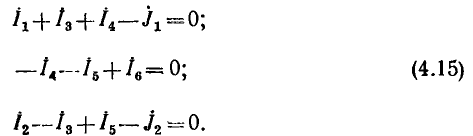
Выразим неизвестные токи ветвей цепи через напряжения этих ветвей, а напряжения ветвей — через соответствующие узловые напряжения:
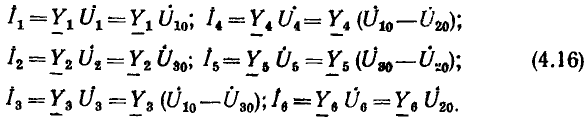
Подставляя выражения (4.16) в (4.15), получим систему уравнений для определения трех неизвестных узловых напряжений
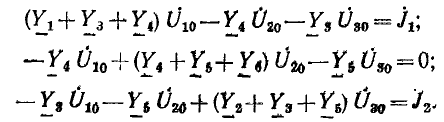
Введем ряд новых понятий. Собственной проводимостью  i-гo узла будем называть сумму проводимостей всей ветвей, подключенных к данному узлу. Для рассматриваемой цепи
i-гo узла будем называть сумму проводимостей всей ветвей, подключенных к данному узлу. Для рассматриваемой цепи
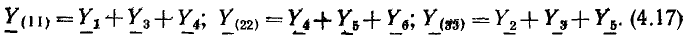
Взаимная проводимость i-го и j-гo узлов — это сумма проводимостей всех ветвей, включенных непосредственно между этими узлами, взятая с противоположным знаком. Если в цепи отсутствуют ветви, включенные непосредственно между i-м и /-м узлами, то 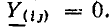 Для цепи, схема которой приведена на рис. 4.4:
Для цепи, схема которой приведена на рис. 4.4:
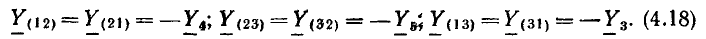
Узловым током  i-гo узла называется алгебраическая сумма токов всех источников тока, подключенных к данному узлу. Если ток какого-либо источника тока направлен к i-му узлу, То он входит в
i-гo узла называется алгебраическая сумма токов всех источников тока, подключенных к данному узлу. Если ток какого-либо источника тока направлен к i-му узлу, То он входит в 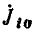 со знаком плюс, если тко направлен от i-го узла, то он входит в
со знаком плюс, если тко направлен от i-го узла, то он входит в 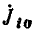 со знаком минус. Для рассматриваемой цепи
со знаком минус. Для рассматриваемой цепи
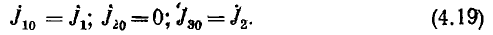
Используя обозначения (4.17)—(4.19), представим узловые уравнения исследуемой цепи в канонической форме записи
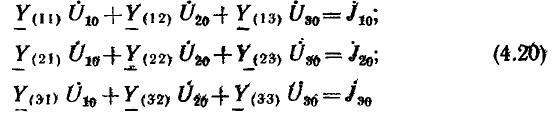
Итак, левая часть любого узлового уравнения, составленного для i-го независимого узла, есть сумма членов, один из которых равен произведению узлового напряжения i-гo узла на его собственную проводимость, а остальные — произведениям узловых напряжений других независимых узлов на взаимные проводимости i-го узла и этих узлов. Правая часть каждого уравнения равна узловому току соответствующего узла.
Таким образом, составить узловые уравнения, как и контурные, можно непосредственно по схеме электрической цепи. Написание уравнений электрического равновесия цепи по методу узловых напряжений упрощается еще за счет того, что не возникает необходимости определять систему независимых контуров и строить дерево графа.
Для линейной электрической цепи, имеющей m = q— 1 незавиcимых узлов и состоящей только из сопротивлений, емкостей, индуктивностей и независимых источников тока, система узловых уравнений может быть записана в виде
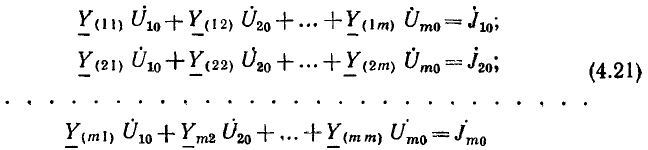
или

где
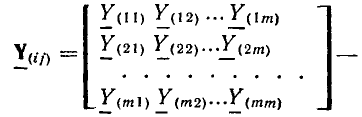
матрица узловых проводимостей цепи;
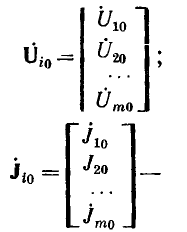
матрицы-столбцы узловых напряжений и узловых токов.
Можно убедиться, что для цепей рассматриваемого типа всегда выполняется условие 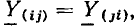 поэтому матрица узловых проводимостей таких цепей квадратная и симметричная относительно главной диагонали.
поэтому матрица узловых проводимостей таких цепей квадратная и симметричная относительно главной диагонали.
Решая систему узловых уравнений любым из способов, определяют все неизвестные узловые напряжения. Так, используя формулы Крамера, найдем узловое напряжение k-го узла:
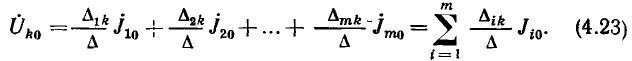
Здесь  — определитель системы уравнений (4.22);
— определитель системы уравнений (4.22); 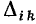 — алгебраическое дополнение элемента
— алгебраическое дополнение элемента 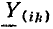 этого определителя.
этого определителя.
Если цепь содержит также независимые источники напряжения, то их можно либо заменить на источники тока, либо составить для цепи систему узловых уравнений без такой замены.
Пусть в рассматриваемой цепи имеется рия независимых источников напряжения. Очевидно, что узловые напряжения двух узлов, между которыми включен независимый источник напряжения, отличаются только на э. д. с. этого источника. Поэтому число независимых узловых напряжений цепи уменьшается от q— 1 до р — 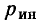 — 1, причем такие уравнения составляют только для узлов, напряжения которых выбраны в качестве независимых. Матрица узловых проводимостей цепи, содержащей независимые источники напряжения, будет не квадратной: число столбцов этой матрицы равно числу независимых узлов m = q— 1, а число строк — числу независимых узловых напряжений q—
— 1, причем такие уравнения составляют только для узлов, напряжения которых выбраны в качестве независимых. Матрица узловых проводимостей цепи, содержащей независимые источники напряжения, будет не квадратной: число столбцов этой матрицы равно числу независимых узлов m = q— 1, а число строк — числу независимых узловых напряжений q—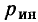 — 1. После формирования системы уравнений электрического равновесия цепи в виде (4.21), (4.22) члены, содержащие известные узловые напряжения, переносят в правую часть соответствующих уравнений.
— 1. После формирования системы уравнений электрического равновесия цепи в виде (4.21), (4.22) члены, содержащие известные узловые напряжения, переносят в правую часть соответствующих уравнений.
В простейшем случае исследуемая цепь может содержать 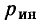 источников напряжения, имеющих общую точку. Выберем узел, к которому подключены все источники напряжения, в качестве базисного. Тогда узловые напряжения
источников напряжения, имеющих общую точку. Выберем узел, к которому подключены все источники напряжения, в качестве базисного. Тогда узловые напряжения 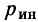 узлов, к которым подключены вторые полюсы источников напряжения, будут равны напряжениям этих источников, а систему узловых уравнений составляют только для узлов, к которым не подключены источники напряжения.
узлов, к которым подключены вторые полюсы источников напряжения, будут равны напряжениям этих источников, а систему узловых уравнений составляют только для узлов, к которым не подключены источники напряжения.
Пример №6
Используя метод узловых напряжений, составим уравнения электрического равновесия цепи, схема которой приведена на рис. 4.2, а. Эта цепь содержит q — 1=3 независимых узла и имеет один источник напряжения 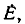 включенный между базисным узлом и узлом 1. Узловое напряжение этого узла
включенный между базисным узлом и узлом 1. Узловое напряжение этого узла 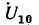 известно и равно
известно и равно 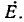 Для определения неизвестных узловых напряжений
Для определения неизвестных узловых напряжений 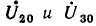 составляем два узловых уравнения
составляем два узловых уравнения
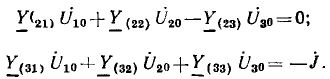
Здесь 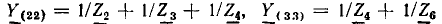 — собственные проводимости узлов 2 и 3;
— собственные проводимости узлов 2 и 3; 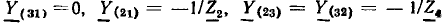 — взаимные проводимости узлов рассматриваемой цепи.
— взаимные проводимости узлов рассматриваемой цепи.
Перенося члены, содержащие известное узловое напряжение 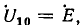 в правую часть уравнений и выражая собственные и взаимные проводимости узлов через параметры элементов цепи, получаем
в правую часть уравнений и выражая собственные и взаимные проводимости узлов через параметры элементов цепи, получаем
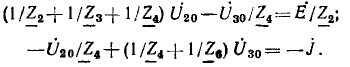
Аналогичная система уравнений электрического равновесия цепи получается и в том случае, когда источник напряжения 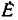 заменяют источником тока
заменяют источником тока 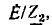 подключенным между узлом 2 и базисным (узел 1 в этом случае устраняется).
подключенным между узлом 2 и базисным (узел 1 в этом случае устраняется).
Метод узловых напряжений можно использовать и для анализа цепей с взаимной индуктивностью (при 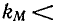 1), однако алгоритм формирования узловых уравнений в этом случае значительно усложняется.
1), однако алгоритм формирования узловых уравнений в этом случае значительно усложняется.
Формирование уравнений электрического равновесия цепей с зависимыми источниками
При формировании уравнений электрического равновесия цепей с зависимыми источниками следует различать источники, управляемые током или напряжением какой-либо невырожденной, т. е. не содержащей источников тока и не составленной только из источников напряжения, ветви и источники, у которых управляющее воздействие не является током или напряжением какой-либо невырожденной ветви. Наличие в исследуемой цепи управляемых источников первого типа не накладывает никаких ограничений, на применение ранее рассмотренных методов формирования уравнений электрического равновесия цепи. Включение в цепь управляемых источников второго типа может существенно усложнить анализ и сделать невозможным применение тех или иных методов формирования уравнений электрического равновесия.
Рассмотрим методику формирования уравнений электрического равновесия цепей, содержащих зависимые источники, управляемые током или напряжением какой-либо невырожденной ветви. Для таких цепей источники, управляемые напряжением, можно преобразовать в источники, управляемые током, и наоборот. Пусть в исследуемой цепи имеются источники напряжения и тока, управляемые напряжением а-й ветви:

где 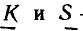 — коэффициенты управления источников.
— коэффициенты управления источников.
Используя компонентное уравнение а-й ветви, напряжение 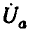 в соотношениях (4.24) можно выразить через ток этой ветви
в соотношениях (4.24) можно выразить через ток этой ветви 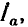 при этом источник, управляемый напряжением, преобразуется в источник, управляемый током. В простейшем случае связь напряжения и тока а-й ветви описывается законом Ома в комплексной форме
при этом источник, управляемый напряжением, преобразуется в источник, управляемый током. В простейшем случае связь напряжения и тока а-й ветви описывается законом Ома в комплексной форме

Подставляя (4.25) в (4.24), получаем
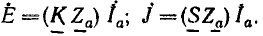
Аналогичным образом можно преобразовать источники, управляемые током какой-либо ветви, в источники, управляемые напряжением этой же ветви.
При составлении основной системы уравнений электрического равновесия цепей, содержащих зависимые источники напряжения или тока рассматриваемого типа, эти источники учитывают в уравнениях, составленных на основании законов Кирхгофа, наряду с независимыми источниками, а затем токи и э. д. с. зависимых источников выражают через соответствующие управляющие воздействия. В связи с тем что управляющие воздействия представляют собой токи и напряжения ветвей цепи, в основной системе уравнений электрического равновесия цепи не появится новых неизвестных токов или напряжений. При формировании уравнений электрического равновесия цепи по методу токов ветвей токи и э. д. с. управляемых источников должны быть выражены через неизвестные токи ветвей, а при формировании таких уравнений по методу напряжений ветвей — через неизвестные напряжения ветвей.
Пример №7
Используя метод токов ветвей, составим, уравнения злектрического равновесия цепи (см. рис. 4.2, а) при условии, что ток источника тока является функцией напряжения ветви, содержащей индуктивность: 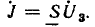
Задача решается в два этапа. На первом — формируют систему уравнений по методу токов ветвей, в которой ток источника j учитывается так же, как если бы это был ток независимого источника (см. пример 4.2):
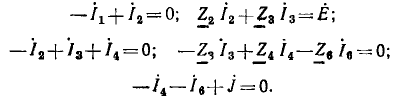
На втором — ток управляемого источника выражают через ток третьей ветви 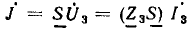 и подставляют в полученную систему уравнений:
и подставляют в полученную систему уравнений:
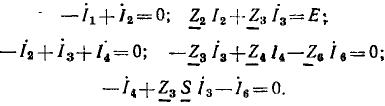
Таким образом получаем уравнения для определения пяти неизвестных токов ветвей, после решения которой и определения тока 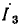 находят ток управляемого источника и напряжения всех ветвей.
находят ток управляемого источника и напряжения всех ветвей.
Методом контурных токов можно построить систему уравнений электрического равновесия цепи, содержащей зависимые источники напряжения, управляемые током. Если цепь содержит зависимые источники других типов, то они должны быть преобразованы в источники напряжения, управляемые током. При составлении контурных уравнений э. д. с. таких источников учитываются наравне с э. д. с. независимых источников, а затем переносятся в левую часть уравнений и выражаются через соответствующие контурные токи. Таким образом, наличие в исследуемой цепи источников э. д. с., управляемых током, приводит к изменению коэффициентов перед некоторыми из контурных токов и может обусловить несимметричность матрицы контурных сопротивлений относительно главной диагонали.
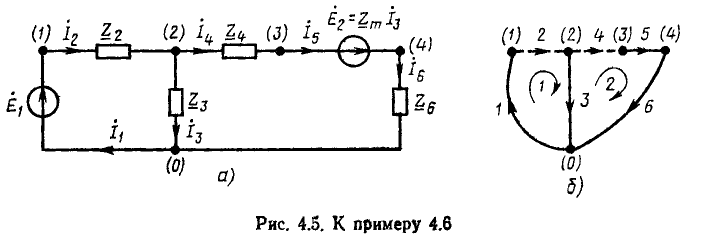
Пример №8
Составим систему контурных уравнений цепи (см. рис. 4.2) при условии, что ток источника тока является функцией напряжения на сопротивлении 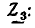
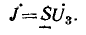
Преобразуем схему рассматриваемой цепи таким образом, чтобы управляемый напряжением источник тока был заменен на управляемый током источник напряжения (рис. 4.5, а):
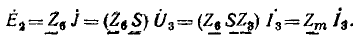
Выбрав систему независимых контуров (рис. 4.5, б), составим систему контурных уравнений цепи, в которой э. д. с. 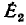 источника учтена так, как будто бы этот источник независимый:
источника учтена так, как будто бы этот источник независимый:
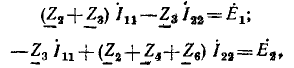
где 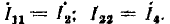
Далее перенося 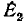 в левую часть контурных уравнений и выражая ее через контурные токи
в левую часть контурных уравнений и выражая ее через контурные токи 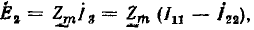 получаем
получаем
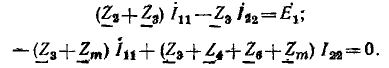
Матрица контурных сопротивлений рассматриваемой цепи несимметрична относительно главной диагонали:
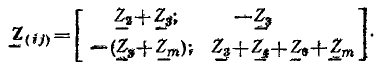
Методом узловых напряжений можно составить систему уравнений электрического равновесия цепей, содержащих управляемые напряжением источники тока. Если цепь содержит зависимые источники других типов, то они должны быть заменены на источники тока, управляемые напряжением. При составлении узловых уравнений токи таких источников учитывают наравне с токами независимых источников, а затем выражают через соответствующие узловые напряжения. Наличие в рассматриваемой цепи управляемых источников, как правило, приводит к тому, что матрица узловых проводимостей цепи становится несимметричной относительно главной диагонали.
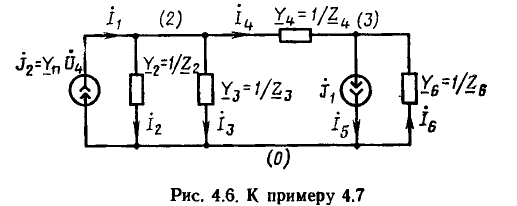
Пример №9
Составим узловые уравнения цепи (см. рис. 4.2, а) при условии, что э.д.с. источника напряжения является функцией тока 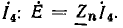
Преобразуем схему рассматриваемой цепи таким образом, чтобы управляемый током источник э.д.с. был заменен на управляемый напряжением источник тока 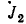 (рис. 4.6):
(рис. 4.6):
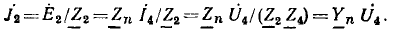
Составляем узловые уравнения преобразованной цепи, учитывая ток управляемого источника 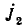 наравне с током независимого источника
наравне с током независимого источника 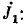
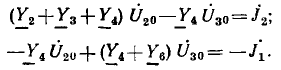
Перенося ток управляемого источника 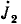 в левую часть узловых уравнений и выражая его через узловые напряжения:
в левую часть узловых уравнений и выражая его через узловые напряжения: 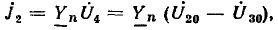 получаем
получаем
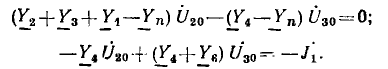
Из полученных уравнений видно, что матрица узловых проводимостей цепи несимметрична относительно главной диагонали:
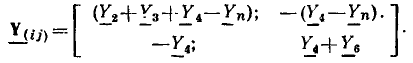
Рассмотрим особенности формирования уравнений электрического равновесия цепей, содержащих зависимые источники, у которых управляющее воздействие не является током или напряжением какой-либо невырожденной ветви. Для таких цепей, как правило, нельзя выполнить преобразования, связанные с изменением вида управляющего воздействия, а при составлении уравнений электрического равновесия могут появляться дополнительные неизвестные — управляющие токи или напряжения, не являющиеся токами или напряжениями ветвей.
Чтобы получить достаточное количество уравнений для определения всех неизвестных токов и напряжений, в состав рассматриваемых цепей обычно включают дополнительные вырожденные ветви, соответствующие управляющим воздействиям зависимых источников.
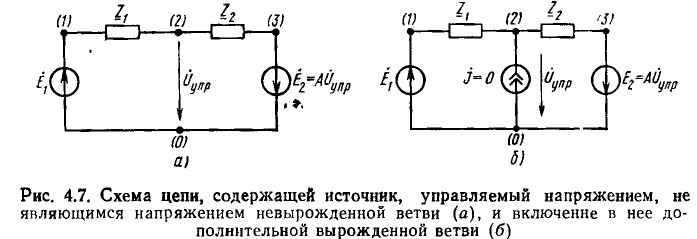
Так, если в цепи (рис. 4.7, а) имеется источник напряжения, э. д. с. которого зависит от напряжения 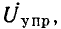 не являющегося напряжением какой-либо ветви, то для составления основной системы уравнений электрического равновесия эту цепь следует дополнить вырожденной
не являющегося напряжением какой-либо ветви, то для составления основной системы уравнений электрического равновесия эту цепь следует дополнить вырожденной
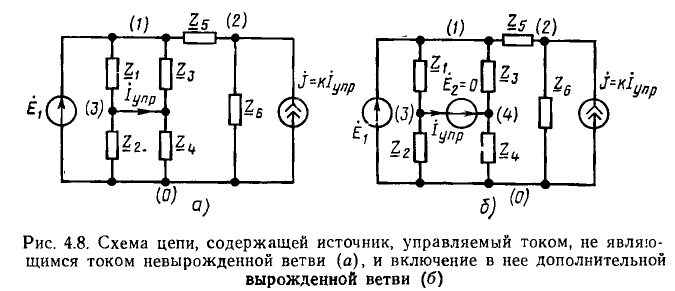
ветвью (рис. 4.7, б), содержащей независимый источник тока 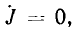 напряжение которого равном
напряжение которого равном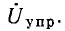 Если электрическая цепь содержит зависимый источник тока
Если электрическая цепь содержит зависимый источник тока 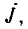 управляемый током
управляемый током 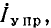 не являющимся током какой-либо ветви (рис. 4.8, а), то для составления основной системы уравнений электрического равновесия эту цепь следует дополнить вырожденной ветвью, содержащей независимый источник напряжения
не являющимся током какой-либо ветви (рис. 4.8, а), то для составления основной системы уравнений электрического равновесия эту цепь следует дополнить вырожденной ветвью, содержащей независимый источник напряжения 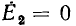 (рис. 4.8, б), ток которого равен
(рис. 4.8, б), ток которого равен 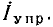 После введения дополнительных вырожденных ветвей основную систему урав нений электрического равновесия преобразованных цепей составляют по расммотренным ранее правилам.
После введения дополнительных вырожденных ветвей основную систему урав нений электрического равновесия преобразованных цепей составляют по расммотренным ранее правилам.
Если в цепи имеются источники, управляемые напряжением, которые не могут быть преобразованы в источники, управляемые током, то для составления уравнений электрического равновесия такой цепи нельзя воспользоваться методами токов ветвей и контурных токов; если в цепи имеются источники, управляемые током, которые не поддаются преобразованию в источники, управляемые напряжением, то для составления уравнений электрического равновесия оказываются неприменимыми методы напряжений ветвей и узловых напряжений.
На практике для формирования уравнений электрического равновесия используют тот из методов, в котором приходится определять меньшее количество независимых переменных. При 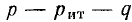
 рекомендуется применять метод узловых напряжений, в противном случае — метод контурных токов. Если количество решаемых уравнений окажется одинаковым, то предпочтение следует отдать методу узловых напряжений, в котором не требуется проведения трудоемкой (особенно для сложных, например непланарных, цепей) операции по выбору системы независимых контуров.
рекомендуется применять метод узловых напряжений, в противном случае — метод контурных токов. Если количество решаемых уравнений окажется одинаковым, то предпочтение следует отдать методу узловых напряжений, в котором не требуется проведения трудоемкой (особенно для сложных, например непланарных, цепей) операции по выбору системы независимых контуров.
Использование рассмотренных методов, как правило, является целесообразным только в тех случаях, когда в результате анализа требуется определить все или значительное количество неизвестных токов или напряжений. Если надо определить реакцию цепи (ток или напряжение) только одной или небольшого количества ветвей, то упростить анализ цепи можно путем использования методов, основанных на применении важнейших теорем теории цепей (см. далее).
Основные теоремы теории цепей
Сформулированный в гл. 1 принцип наложения (суперпозиции) отражает важнейшее свойство линейных электрических цепей.
Это свойство состоит в том, что реакция таких цепей на произвольное внешнее воздействие, представляющее собой линейную комбинацию более простых воздействий, равна линейной комбинации реакций, вызванных каждым из простых воздействий в отдельности.
Из принципа наложения следует, что ток или напряжение любой ветви линейной электрической цепи, содержащей наряду с пассивными элементами зависимые и независимые источники тока и напряжения, равны сумме частичных токов или напряжений, вызванных действием каждого независимого источника в отдельности.
Пусть цепь содержит независимые источники только одного типа, например источники напряжения. Контурный ток произвольного контура этой цепи может быть определен из выражения (4.14). Представляя все входящие в это выражение контурные э. д. с. 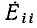 в виде алгебраической суммы э. д. с. входящих в контур источников напряжений
в виде алгебраической суммы э. д. с. входящих в контур источников напряжений 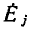 и приводя подобные члены, получаем
и приводя подобные члены, получаем
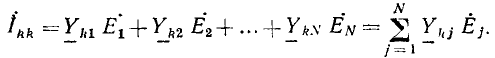
Здесь N — общее количество независимых источников э. д. с., входящих в состав цепи; 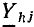 — коэффициенты, представляющие собой алгебраические суммы слагаемых вида
— коэффициенты, представляющие собой алгебраические суммы слагаемых вида 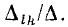
Так как 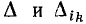 определяются только параметрами матрицы контурных сопротивлений, т. е. параметрами пассивных элементов цепи и коэффициентами управления зависимых источников, то значения
определяются только параметрами матрицы контурных сопротивлений, т. е. параметрами пассивных элементов цепи и коэффициентами управления зависимых источников, то значения 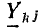 не зависят от э. д. с. независимых источников напряжения. Каждое из слагаемых вида
не зависят от э. д. с. независимых источников напряжения. Каждое из слагаемых вида 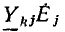 можно рассматривать как частичный ток k-го контура, вызванный действием источника э. д. с.
можно рассматривать как частичный ток k-го контура, вызванный действием источника э. д. с. 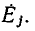
Действительно, если все входящие в цепь независимые источники э. д. с., кроме 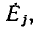 выключены (заменены короткозамыкающими перемычками), то ток k-го контура
выключены (заменены короткозамыкающими перемычками), то ток k-го контура

Следовательно, контурный ток любого контура линейной электрической цепи, содержащей независимые источники напряжения, равен сумме частичных токов, вызванных действием каждого из независимых источников по отдельности:
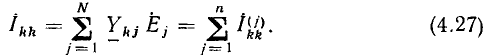
Из анализа выражений (4.26), (4.27) вытекает физический смысл коэффициентов 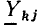 — они представляют собой комплексные передаточные проводимости цепи от зажимов
— они представляют собой комплексные передаточные проводимости цепи от зажимов 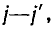 к которым подключен независимый источник напряжения м к зажимам k—k', к которым подключена ветвь с током
к которым подключен независимый источник напряжения м к зажимам k—k', к которым подключена ветвь с током 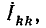 причем каждая из комплексных передаточных проводимостей определяется в режиме, когда все независимые источники напряжения, кроме
причем каждая из комплексных передаточных проводимостей определяется в режиме, когда все независимые источники напряжения, кроме 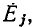 выключены.
выключены.
Если линейная электрическая цепь содержит независимые источники тока, то используя выражение (4.23), можно показать, что узловое напряжение каждого узла такой цепи равно сумме частичных узловых напряжений, вызванных каждым из источников тока в отдельности. При определении частичного узлового напряжения k-го узла, вызванного действием j-го источника тока, все остальные источники тока выключаются, т. е. ветви, содержащие эти источники, разрываются.
Пусть в рассматриваемой цепи имеется l независимых источников напряжения и m независимых источников тока. Присвоим ветвям, содержащим независимые источники напряжения, номера от 1 до l, а ветвям, содержащим независимые источники тока, от l + 1 до l + m. Составляя уравнения электрического равновесия такой цепи методами контурных токов или узловых напряжений и решая эти уравнение с помощью формул Крамера, находим ток и напряжение k-й ветви
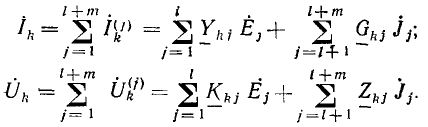
Здесь 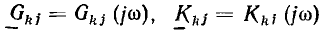 - комплексные коэффициенты передачи цепи по току и напряжению;
- комплексные коэффициенты передачи цепи по току и напряжению;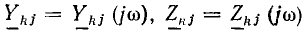 — комплексные передаточные проводимости и сопротивления. Каждая из величин
— комплексные передаточные проводимости и сопротивления. Каждая из величин 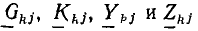 определяется в режиме, когда все независимые источники, кроме источника, находящегося в j-й ветви, выключены, т. е. представлены своими внутренними сопротивлениями.
определяется в режиме, когда все независимые источники, кроме источника, находящегося в j-й ветви, выключены, т. е. представлены своими внутренними сопротивлениями.
На принципе наложения основан широко используемый на практике метод анализа цепей — метод наложения. Его удобно применять в тех случаях, когда по условиям задачи требуется определить ток или напряжение одной из ветвей электрической цепи, в состав которой входит несколько независимых источников. В соответствии с принципом наложения искомый ток (напряжение) представляют в виде суммы частичных токов (напряжений). Для определения частичных токов (напряжений) используют эквивалентные схемы цепи, получаемые из исходной путем выключения всех независимых источников, кроме одного, вызывающего соответствующий частичный ток (напряжение). Таким образом, задача анализа сложной цепи, содержащей несколько независимых источников энергии, заменяется рядом более простых задач по исследованию цепей с одним независимым источником. Следует обратить внимание на то, что при определении частичных токов выключаются только независимые источники тока или напряжения. Параметры зависимых источников учитываются в матрице узловых проводимостей или контурных сопротивлений и при определении частичных токов (напряжений) эти источники не выключаются.
Пример №10
Используя метод наложения, определим ток  электрической цепи, комплексная схема замещения которой приведена на рис. 4.2, а. В соответствии с принципом наложения представим ток
электрической цепи, комплексная схема замещения которой приведена на рис. 4.2, а. В соответствии с принципом наложения представим ток 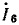 в виде суммы двух частичных токов
в виде суммы двух частичных токов 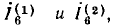 вызванных действием источника напряжения
вызванных действием источника напряжения 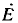 и источника тока
и источника тока 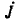 соответственно. Эквивалентные схемы для определения частичных токов приведены на рис. 4.9, а, б. Используя эквивалентные преобразования участков цепей со смешанным соединением элементов, определим частичные токи:
соответственно. Эквивалентные схемы для определения частичных токов приведены на рис. 4.9, а, б. Используя эквивалентные преобразования участков цепей со смешанным соединением элементов, определим частичные токи:
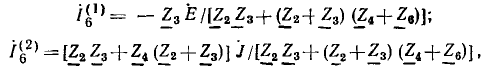
а затем, суммируя их, найдем искомый ток
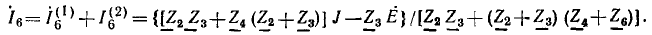
Из полученных выражений видно, что комплексный коэффициент передачи рассматриваемой цепи по току от зажимов 5—5' к зажимам 6—6’ и комплексная передаточная проводимость этой цепи от зажимов 1—1’ к зажимам 6—6' (номера зажимов совпадают с номерами ветвей) равны соответственно:
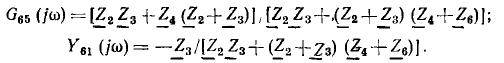
Метод наложения оказывается весьма эффективным и при анализе линейных цепей, находящихся под воздействием колебаний сложной формы. В этом случае сложное внешнее воздействие представляют в
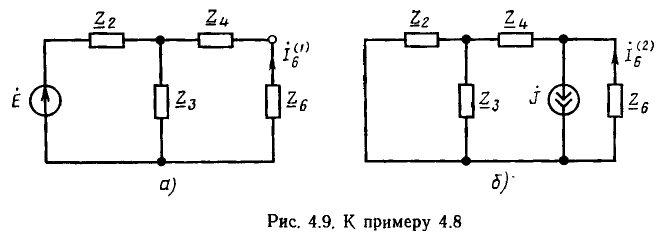
виде конечной или бесконечной суммы колебаний более простой формы, реакция цепи на воздействие которых может быть определена с помощью известных методов (подробнее см. гл. 6).
Необходимо отметить, что принцип наложения применим только для определения токов или напряжений линейной электрической цепи и не может быть использован для нахождения величин, которые не являются линейными функциями токов или напряжений. В частности, мощность, потребляемая каким-либо участком линейной электрической цепи, находящейся под воздействием нескольких независимых источников, не равна сумме мощностей, потребляемых этим же участком при воздействии каждого из независимых источников в отдельности .
Теорема взаимности
При изучении методов формирования уравнений электрического равновесия было установлено, что матрицы контурных сопротивлений и узловых проводимостей линейных цепей, составленных только из сопротивлений, емкостей, индуктивностей и независимых источников тока или напряжения, являются симметричными относительно главной диагонали. Можно показать, что симметричность этих матриц не нарушится и в том случае, когда в цепи имеется произвольное количество связанных индуктивностей. На симметричности матриц узловых проводимостей и контурных сопротивлений основано важное свойство линейных пассивных электрических цепей, которое формулируется в виде теоремы взаимности, или обратимости.
Рассмотрим линейную пассивную электрическую цепь, составленную из сопротивлений, емкостей и индуктивностей (в том числе и связанных).
В соответствии с теоремой взаимности контурный ток k-го контура цепи, вызванный действием единственного независимого источника напряжения, помещенного в i-й контур, равен контурному току i-гo контура, вызванному действием того же источника напряжения, перенесенного из i-гo контура в k-й.
Для доказательства теоремы выделим из рассматриваемой цепи главные ветви k-го и i-го контуров, а остальную часть цепи изобразим в виде четырехполюсника. Если независимый источник напряжения
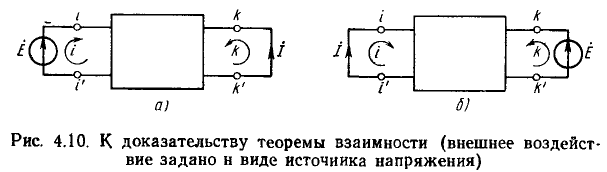
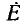 помещен в i-й контур (рис. 4.10, а), то в соответствии с выражением (4.14) контурный ток k-го контура
помещен в i-й контур (рис. 4.10, а), то в соответствии с выражением (4.14) контурный ток k-го контура
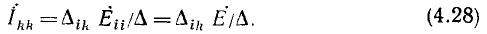
Аналогичным образом находим контурный ток i-го контура, вызванный действием того же источника напряжения 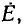 перенесенного из i-го контура в k-й (рис. 4.10,6):
перенесенного из i-го контура в k-й (рис. 4.10,6):
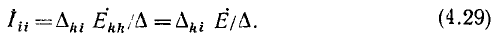
Выражения (4.28) и (4.29) отличаются только порядком индексов в алгебраических дополнениях 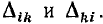 Учитывая симметричность матрицы контурных сопротивлений рассматриваемой цепи относительно главной диагонали, нетрудно прийти к выводу, что
Учитывая симметричность матрицы контурных сопротивлений рассматриваемой цепи относительно главной диагонали, нетрудно прийти к выводу, что 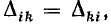 а следовательно,
а следовательно, 
Теорема взаимности для случая, когда внешнее воздействие на цепь задается в виде независимого источника тока, может быть сформулирована следующим образом.
Если независимый источник тока 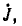 подключенный к какой-либо паре зажимов линейной пассивной цепи, вызывает на другой паре зажимов напряжение
подключенный к какой-либо паре зажимов линейной пассивной цепи, вызывает на другой паре зажимов напряжение 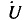 (рис. 4.11, а), то этот же источник тока, подключенный ко второй паре зажимов (рис. 4.11, б), вызовет на первой паре зажимов то же напряжение
(рис. 4.11, а), то этот же источник тока, подключенный ко второй паре зажимов (рис. 4.11, б), вызовет на первой паре зажимов то же напряжение 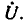
Доказательство этой теоремы взаимности производится гак же, как это было сделано при питании цепи от независимого источника напряжения.
Если электрическая цепь удовлетворяет теореме взаимности (в любой формулировке), то говорят, что она обладает взаимностью (обратимостью). Электрические цепи, обладающие взаимностью, называются взаимными (обратимыми). Если электрическая цепь не обладает взаимностью, то она является невзаимной (необратимой). К необратимым цепям относятся, в частности, нелинейные цепи (элементы матриц контурных сопротивлений и узловых проводимостей таких цепей зависят от токов или напряжений ветвей) и цепи, содержащие зависимые источники (матрицы контурных сопротивлений и узловых проводимостей таких цепей, как правило, несимметричны относительно главных диагоналей).
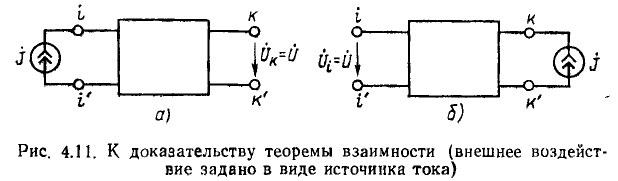
Применение теоремы взаимности в сочетании с принципом наложения позволяет в ряде случаев существенно упростить определение тока или напряжения какой-либо ветви электрической цепи, содержащей несколько независимых источников напряжения или тока.
Пример №11
Пусть, например, линейная электрическая цепь содержит Л/ независимых источников напряжения 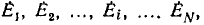 размещенных соответственно в ветвях 1, 2, ..., i, ..., N. Определим ток k-й ветви, не содержащей источников энергии. Найдем сначала токи
размещенных соответственно в ветвях 1, 2, ..., i, ..., N. Определим ток k-й ветви, не содержащей источников энергии. Найдем сначала токи 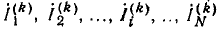 соответственно 1, 2, .... i, ..., N ветвей цепи, вызванные действием некоторого дополнительного источника э.д.с.
соответственно 1, 2, .... i, ..., N ветвей цепи, вызванные действием некоторого дополнительного источника э.д.с. 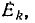 помещенного в k-ю ветвь, при выключенных источниках
помещенного в k-ю ветвь, при выключенных источниках 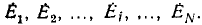 Далее, в соответствии с теоремой взаимности найдем частичные токи
Далее, в соответствии с теоремой взаимности найдем частичные токи 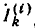 вызываемые в k-й ветви действием каждого из источников
вызываемые в k-й ветви действием каждого из источников 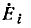 в отдельности. Если бы э.д.с. источника, расположенного в i-й ветви,
в отдельности. Если бы э.д.с. источника, расположенного в i-й ветви, 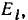 , была равна
, была равна 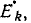 то согласно теореме взаимности частичный ток k-й ветви,
то согласно теореме взаимности частичный ток k-й ветви, 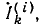 вызванный действием источника, расположенного в i-й ветви, был бы равен
вызванный действием источника, расположенного в i-й ветви, был бы равен 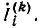 Если
Если 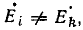 то частичный ток k-й ветви
то частичный ток k-й ветви 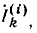 вызванный действием э.д.с.
вызванный действием э.д.с. 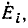 пропорционален
пропорционален 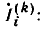
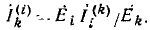
Суммируя частичные токи, вызванные действием всех независимых источников напряжения, находим
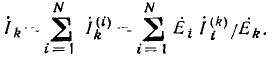
Таким образом, анализ сложной электрической цепи, содержащей N независимых источников напряжения, свелся к определению токов N ветвей более простой цепи, содержащей один независимый источник напряжения.
Теорема компенсации
Теорема компенсации формулируется следующим образом: токи и напряжения произвольной электрической цепи ие изменятся, если любую ветвь этой цепи заменить либо идеальным источником напряжения, э.д.с. которого равна напряжению данной ветви и направлена противоположно этому напряжению, либо идеальным источником тока, ток которого равен току рассматриваемой ветви и совпадает с иим по направлению.
Теорема компенсации базируется на общих свойствах основной системы уравнений электрического равновесия цепи и не накладывает ограничений на тип рассматриваемой цепи или характер внешнего воздействия. Рассмотрим, например, линейную электрическую цепь, находящуюся под гармоническим воздействием. Выделим в данной
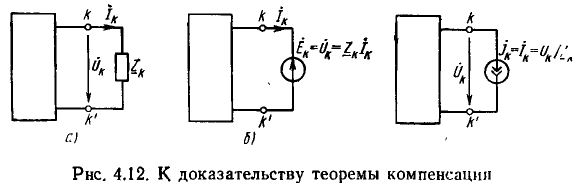
цепи произвольную ветвь, комплексное сопротивление которой равно 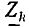 (рис. 4.12, а). Напряжение и ток этой ветви связаны уравнением, составленным на основании закона Ома в комплексной форме
(рис. 4.12, а). Напряжение и ток этой ветви связаны уравнением, составленным на основании закона Ома в комплексной форме 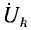
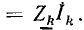 В соответствии с теоремой компенсации выделенную ветвь можно заменить либо идеальным источником напряжения, э. д. с: которого равна напряжению данной ветви
В соответствии с теоремой компенсации выделенную ветвь можно заменить либо идеальным источником напряжения, э. д. с: которого равна напряжению данной ветви 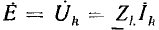 и направлена навстречу этому напряжению (рис. 4.12, б), либо идеальным источником тока, ток которого равен току рассматриваемой ветви
и направлена навстречу этому напряжению (рис. 4.12, б), либо идеальным источником тока, ток которого равен току рассматриваемой ветви 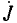
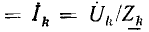 и совпадает с ним по направлению (рис. 4.12, в). Составляя основную систему уравнений электрического равновесия каждой из цепей (рис. 4.12, б, в), убедимся, что она совпадает с основной системой уравнений электрического равновесия исходной цепи. Действительно, при формировании уравнений электрического равновесия исходной цепи напряжение
и совпадает с ним по направлению (рис. 4.12, в). Составляя основную систему уравнений электрического равновесия каждой из цепей (рис. 4.12, б, в), убедимся, что она совпадает с основной системой уравнений электрического равновесия исходной цепи. Действительно, при формировании уравнений электрического равновесия исходной цепи напряжение 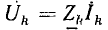 на выделенной ветви учитывается со знаком плюс в левой части уравнений баланса напряжений, составленных для контуров, содержащих рассматриваемую ветвь (предполагается, что направление обхода этих контуров совпадает с направлением тока
на выделенной ветви учитывается со знаком плюс в левой части уравнений баланса напряжений, составленных для контуров, содержащих рассматриваемую ветвь (предполагается, что направление обхода этих контуров совпадает с направлением тока 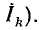 При составлении уравнений электрического равновесия цепи (рис. 4.12, б) член
При составлении уравнений электрического равновесия цепи (рис. 4.12, б) член 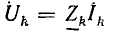 в левой части соответствующих уравнений отсутствует, однако в правой части этих уравнений появляется член
в левой части соответствующих уравнений отсутствует, однако в правой части этих уравнений появляется член 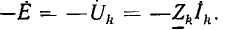 Следовательно, замена комплексного сопротивления
Следовательно, замена комплексного сопротивления 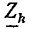 идеальным источником напряжения
идеальным источником напряжения 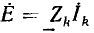 соответствует переносу члена
соответствует переносу члена 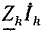 из левой части уравнений баланса напряжений в правую с соответствующим изменением знака.
из левой части уравнений баланса напряжений в правую с соответствующим изменением знака.
При составлении уравнений электрического равновесия исходной цепи (рис. 4.12, а) ток 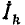 выделенной ветви учитывается в левой части уравнений баланса токов; соответствующие уравнения преобразованной цепи (рис. 4.12, в) вместо тока
выделенной ветви учитывается в левой части уравнений баланса токов; соответствующие уравнения преобразованной цепи (рис. 4.12, в) вместо тока 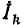 , протекающего через комплексное сопротивление
, протекающего через комплексное сопротивление 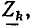 содержат равный ему ток
содержат равный ему ток 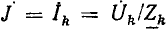 идеального источника тока. Таким образом, цепи, схемы которых приведены на рисунке, являются эквивалентными.
идеального источника тока. Таким образом, цепи, схемы которых приведены на рисунке, являются эквивалентными.
Необходимо отметить, что источники напряжения и тока, заменившие в соответствии с теоремой компенсации сопротивление ветви 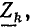 зависимые: э. д. с. источника напряжения
зависимые: э. д. с. источника напряжения 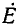 прямо пропорциональна току ветви, содержащей этот источник, а ток источника тока
прямо пропорциональна току ветви, содержащей этот источник, а ток источника тока 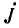 прямо пропорционален напряжению источника тока. Из эквивалентности испей следует, что идеальный источник напряжения, э. д. с. которого пропорциональна отдаваемому току
прямо пропорционален напряжению источника тока. Из эквивалентности испей следует, что идеальный источник напряжения, э. д. с. которого пропорциональна отдаваемому току 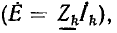 и идеальный источник тока, ток которого прямо пропорционален напряжению на зажимах источника
и идеальный источник тока, ток которого прямо пропорционален напряжению на зажимах источника 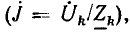 могут быть заменены комплексным сопротивлением
могут быть заменены комплексным сопротивлением
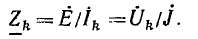
Теорема компенсации расширяет возможности эквивалентных преобразований электрических цепей.
Автономные и неавтономные двухполюсники
Рассмотрим произвольный линейный двухполюсник, содержащий наряду с идеализированными пассивными элементами управляемые и неуправляемые источники тока или напряжения. Представляют интерес два предельных режима работы такого двухполюсника: режим холостого хода, когда ток внешних выводов двухполюсника равен нулю, и режим короткого замыкания, при котором напряжение между внешними выводами двухполюсника равно нулю. Напряжение между выводами двухполюсника в режиме холостого хода называется напряжением холостого хода, а ток между выводами двухполюсника в режиме короткого замыкания — током короткого замыкания.
Двухполюсник, напряжение холостого хода или ток короткого замыкания которого не равны нулю, назовем автономным. Очевидно, что автономный двухполюсник должен содержать один или несколько нескомпенсированных независимых источников, т. е. таких источников, сумма частичных реакций на воздействие которых на внешних зажимах двухполюсника не равна тождественно нулю.
Если напряжение холостого хода в ток короткого замыкания двухполюсника тождественно равны нулю, то такой двухполюсник будем называть неавтономным. Неавтономный двухполюсник не может содержать нескомпенсированных независимых источников, т. е. в его состав могут входить только идеализированные пассивные элементы и управляемые источники тока или напряжения. Таким образом, активные двухполюсники могут быть автономными или неавтономными, а пассивные двухполюсники представляют собой частный случай неавтономных.
Комплексным входным сопротивлением 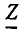 неавтономного двухполюсника называется отношение комплексной амплитуды напряжения на его зажимах к комплексной амплитуде тока (заметим, что данное ранее определение комплексного входного сопротивления пассивного двухполюсника естественным образом вытекает из этого определения). Если неавтономный двухполюсник не содержит управляемых источников, т. е. является пассивным, то его комплексное входное сопротивление может быть найдено, например, путем постепенного сворачивания схемы двухполюсника с использованием методов преобразования пассивных цепей. В общем случае комплексное входное сопротивление неавтономного двухполюсника находят методом пробного источника, в соответствии с которым к входу исследуемого двухполюсника подключают произвольный независимый источник напряжения или тока (пробный источник) и определяют отношение комплексных действующих значений напряжения и тока на внешних зажимах двухполюсника.
неавтономного двухполюсника называется отношение комплексной амплитуды напряжения на его зажимах к комплексной амплитуде тока (заметим, что данное ранее определение комплексного входного сопротивления пассивного двухполюсника естественным образом вытекает из этого определения). Если неавтономный двухполюсник не содержит управляемых источников, т. е. является пассивным, то его комплексное входное сопротивление может быть найдено, например, путем постепенного сворачивания схемы двухполюсника с использованием методов преобразования пассивных цепей. В общем случае комплексное входное сопротивление неавтономного двухполюсника находят методом пробного источника, в соответствии с которым к входу исследуемого двухполюсника подключают произвольный независимый источник напряжения или тока (пробный источник) и определяют отношение комплексных действующих значений напряжения и тока на внешних зажимах двухполюсника.
Пример №12
Определим комплексное входное сопротивление неавтономного двухполюсника, схема которого изображена на рис. 4.13, а (задачи такого типа часто встречаются на практике, например при определении комплексного входного сопротивления усилительного каскада на полевом транзисторе).
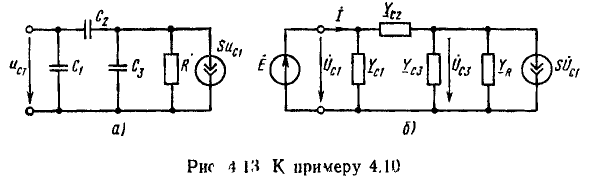
Подключим к входным зажимам исследуемой цепи пробный источник напряжения 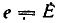 (рис. 4.13, б) и найдем комплексное действующее значение входного тока двухполюсника
(рис. 4.13, б) и найдем комплексное действующее значение входного тока двухполюсника
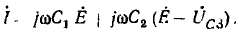
Для определения комплексного действующего значения напряжения на емкости 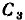 составим уравнение электрического равновесия цепи (рис. 4.13, б) по методу узловых напряжений
составим уравнение электрического равновесия цепи (рис. 4.13, б) по методу узловых напряжений
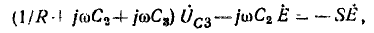
откуда
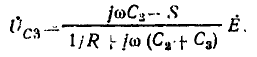
Таким образом, входной ток цепи прямо пропорционален э.д.с. пробного источника
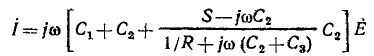
и, следовательно, комплексное входное сопротивление двухполюсника не зависит от этой э.д.с.
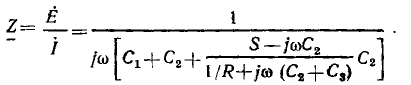
В области низких частот 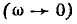 входное сопротивление двухполюсника имеет емкостной характер
входное сопротивление двухполюсника имеет емкостной характер
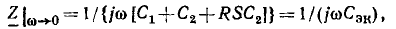
причем эквивалентная входная емкость двухполюсника
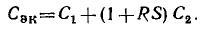
Аналогичный результат получается и в том случае, когда в качестве пробного используют произвольный независимый источник тока 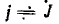
Каждому автономному двухполюснику можно поставить в соответствие некоторый неавтономный двухполюсник, который получается из исходного путем выключения всех входящих в него независимых источников тока и напряжения. Комплексным входным сопротивлением автономного двухполюсника называется комплексное входное сопротивление соответствующего ему неавтономного двухполюсника. Таким образом, комплексное входное сопротивление автономного двухполюсника может быть найдено как отношение комплексной амплитуды напряжения к комплексной амплитуде тока на зажимах неавтономного двухполюсника, который получается из заданного автономного двухполюсника путем выключения всех входящих в него независимых источников тока и напряжения. Комплексное входное сопротивление линейного автономного двухполюсника может быть также найдено как отношение комплексных изображений напряжения холостого хода и тока короткого замыкания этого двухполюсника.
Пример №13
Определим напряжение холостого хода 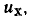 ток короткого замыкания
ток короткого замыкания 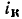 и комплексное входное сопротивление
и комплексное входное сопротивление 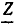 активного двухполюсника, схема которого приведена на рис. 4.14, а.
активного двухполюсника, схема которого приведена на рис. 4.14, а.
Для определения напряжения холостого хода двухполюсника  составим уравнение электрического равновесия рассматриваемой цепи по методу узловых напряжений
составим уравнение электрического равновесия рассматриваемой цепи по методу узловых напряжений
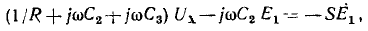
откуда
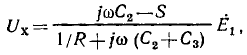
где 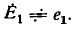
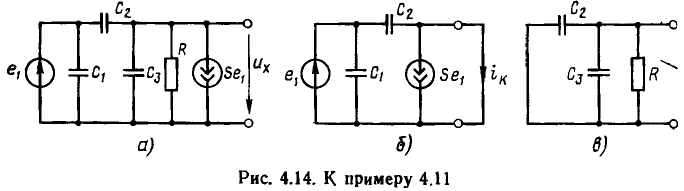
При коротком замыкании зажимов двухполюсника (рис. 4.14, б) выполняется соотношение
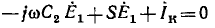
и, следовательно,
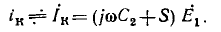
При выключении независимого источника э.д.с. 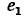 двухполюсник превращается в пассивный (рис. 4.14, в), поэтому его комплексное входное сопротивление
двухполюсник превращается в пассивный (рис. 4.14, в), поэтому его комплексное входное сопротивление 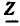 определяется выражением
определяется выражением
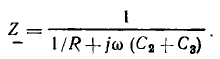
Аналогичный результат получается и в том случае, когда комплексное входное сопротивление рассматриваемого автономного двухполюсника определяется как отношение комплексных действующих значений напряжения холостого хода 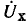 и тока короткого замыкания
и тока короткого замыкания 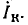
Теорема об эквивалентном источнике
Рассмотрим линейную электрическую цепь, которая наряду с идеялизированными пассивными элементами содержит управляемые и неуправляемые источники тока и напряжения. Выделим в этой цепи произвольную ветвь а—а' (рис. 4.15, а), а остальную часть цепи, к которой подключена эта ветвь, представим в виде автономного двухполюсника АД.
В соответствии с теоремой об эквивалентном источнике ток произвольной ветви линейной электрической цепи не изменится, если автономный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным линеаризованным источником энергии, который может быть представлен последовательной или параллельной схемой замещения. Э. д. с. идеального источника напряжения в последовательной схеме замещения равна напряжению холостого хода
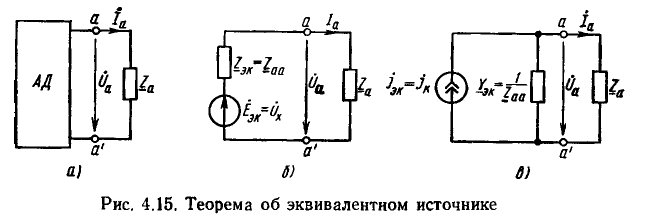
автономного двухполюсника (рис. 4.15, 6), ток идеального источника тока в параллельной схеме замещения равен току короткого замыкания автономного двухполюсника (рис. 4.15, в), а внутреннее сопротивление и внутренняя проводимость эквивалентного источника равны соответственно комплексному входному сопротивлению и комплексной входной проводимости автономного двухполюсника.
Для доказательства теоремы введем в выделенную ветвь а—а' два вспомогательных независимых источника напряжения 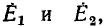 э. д. с. которых равны по значению, но противоположны по направлению (рис. 4.16, а). Очевидно, что введение двух скомпенсированных источников э. д. с. не нарушает режима работы цепи, поэтому ток ветви а—а' преобразованной цепи равен току
э. д. с. которых равны по значению, но противоположны по направлению (рис. 4.16, а). Очевидно, что введение двух скомпенсированных источников э. д. с. не нарушает режима работы цепи, поэтому ток ветви а—а' преобразованной цепи равен току 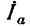 исходной цепи (см. рис. 4.15, а).
исходной цепи (см. рис. 4.15, а).
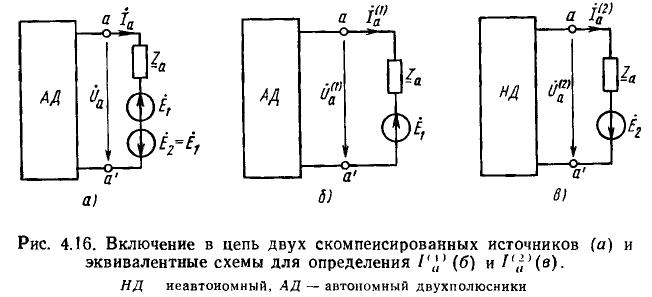
Далее, используя принцип наложения, представим ток рассматриваемой ветви преобразованной цепи в виде суммы двух составляющих 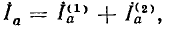 где
где 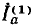 —частичный ток а-й ветви, создаваемый действием независимого источника напряжения
—частичный ток а-й ветви, создаваемый действием независимого источника напряжения 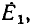 и всех независимых источников, входящих в состав автономного двухполюсника АД, а
и всех независимых источников, входящих в состав автономного двухполюсника АД, а 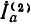 —частичный ток а-й ветви, вызываемый действием независимого источника напряжения
—частичный ток а-й ветви, вызываемый действием независимого источника напряжения 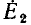 (рис. 4.16,6, в).
(рис. 4.16,6, в).
Из эквивалентной схемы, изображенной на рис. 4.16, б:

где 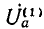 — напряжение на зажимах а—а’ автономного двухполюсника в режиме, когда отдаваемый им ток равен
— напряжение на зажимах а—а’ автономного двухполюсника в режиме, когда отдаваемый им ток равен 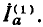 До сих пор не накладывалось никаких ограничений на э. д. с. вспомогательных источников напряжения. Выберем теперь
До сих пор не накладывалось никаких ограничений на э. д. с. вспомогательных источников напряжения. Выберем теперь 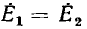 таким образом, чтобы
таким образом, чтобы 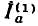 = 0. Очевидно, что в этом случае напряжение на внешних зажимах АД равно напряжению холостого хода автономного двухполюсника
= 0. Очевидно, что в этом случае напряжение на внешних зажимах АД равно напряжению холостого хода автономного двухполюсника 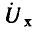 .
.
Используя выражение (4.30), найдем значение э. д. с. 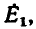 при котором частичный ток а-й ветви
при котором частичный ток а-й ветви 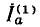 = 0:
= 0:

Таким образом, если э. д. с. вспомогательных источников выбрать равными напряжению холостого хода автономного двухполюсника 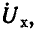 то ток ветви
то ток ветви 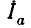 будет равен частичному току
будет равен частичному току 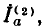 создаваемому действием источника напряжения
создаваемому действием источника напряжения 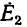 при выключении независимых источников, входящих в состав автономного двухполюсника, и выключении источника напряжения
при выключении независимых источников, входящих в состав автономного двухполюсника, и выключении источника напряжения 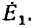
Используя эквивалентную схему для определения частичного тока 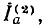 находим
находим
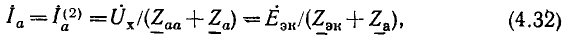
где 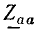 — комплексное входное сопротивление исходного автономного двухполюсника, равное комплексному входному сопротивлению приведенного на рис. 4.16, в неавтономного двухполюсника НД. Как видно из выражения (4.32), ток a-й ветви исходной цепи (см. рис. 4.15, а) равен току некоторой цепи, содержащей помимо сопротивления
— комплексное входное сопротивление исходного автономного двухполюсника, равное комплексному входному сопротивлению приведенного на рис. 4.16, в неавтономного двухполюсника НД. Как видно из выражения (4.32), ток a-й ветви исходной цепи (см. рис. 4.15, а) равен току некоторой цепи, содержащей помимо сопротивления 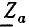 источник напряжения
источник напряжения 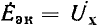 и комплексное сопротивление
и комплексное сопротивление  (см. рис. 4.15, б). Итак, ток выделенной ветви
(см. рис. 4.15, б). Итак, ток выделенной ветви 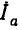 не изменился при замене автономного двухполюсника эквивалентным источником энергии, э. д. с. которого равна напряжению холостого хода автономного двухполюсника, а внутреннее сопротивление — его комплексному входному сопротивлению.
не изменился при замене автономного двухполюсника эквивалентным источником энергии, э. д. с. которого равна напряжению холостого хода автономного двухполюсника, а внутреннее сопротивление — его комплексному входному сопротивлению.
Переходя от последовательной схемы замещения эквивалентного источника к параллельной, можно показать, что значение тока 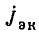 независимого источника тока (см. рис. 4.15, в) равно току короткого замыкания автономного двухполюсника, а внутренняя проводимость
независимого источника тока (см. рис. 4.15, в) равно току короткого замыкания автономного двухполюсника, а внутренняя проводимость 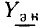 — его комплексной входной проводимости
— его комплексной входной проводимости 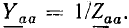
Воспользовавшись теоремой об эквивалентном источнике, можно найти последовательную или параллельную схемы замещения любого сколь угодно сложного линейного активного двухполюсника, поэтому данную теорему часто называют теоремой об активном двухполюснике. Эта теорема позволяет существенно упростить анализ цепей, особенно в тех случаях, когда требуется определить ток или напряжение только одной ветви сложной цепи, содержащей большое количество управляемых и неуправляемых источников тока и напряжения. В связи с тем что параметры элементов последовательной и параллельной схем замещения активного двухполюсника легко поддаются измерениям, выполняемым на внешних зажимах, теорему об эквивалентном источнике применяют и для построения эквивалентных схем активных двухполюсников по результатам их экспериментального исследования.
Пример №14
Используя теорему об эквивалентном источнике, определим ток 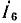 цепи, комплексная схема замещения которой приведена на рис. 4.2, а. Выделим из рассматриваемой цепи ветвь, содержащую сопротивление
цепи, комплексная схема замещения которой приведена на рис. 4.2, а. Выделим из рассматриваемой цепи ветвь, содержащую сопротивление 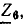 и представим остальную часть цепи, которую можно рассматривать как aetnoномный двухполюсник, последовательной схемой замещения (рис. 4.17, а). Э.д.с.
и представим остальную часть цепи, которую можно рассматривать как aetnoномный двухполюсник, последовательной схемой замещения (рис. 4.17, а). Э.д.с.
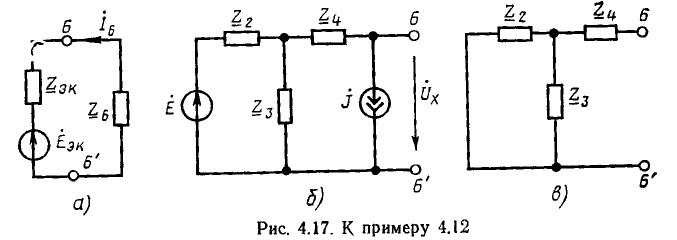
источника напряжения 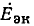 определяется как напряжение холостого хода на зажимах автономного двухполюсника, схема которого приведена на рис. 4.17, б:
определяется как напряжение холостого хода на зажимах автономного двухполюсника, схема которого приведена на рис. 4.17, б:
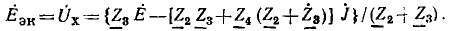
Внутреннее сопротивление эквивалентного источника равно входному сопротивлению неавтономного двухполюсника (рис. 4.17, в):
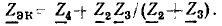
Наконец, используя преобразованную схему рассматриваемой цепи (рис. 4.17, а), находим искомый ток
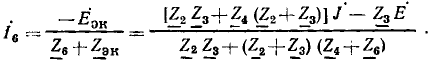
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |