
Линейные дифференциальные уравнения второго порядка с примерами решения
Содержание:
Общие свойства линейных однородных дифференциальных уравнений:
В этой лекции мы остановимся на изучении линейных дифференциальных уравнений второго порядка, которые представляют наиболее разработанную часть теории дифференциальных уравнений. Это объясняется тем, что линейные уравнения часто описывают реальные процессы, либо дают первое приближение изучаемого явления.
Определение 24.1.1. Дифференциальное уравнение линейное относительно искомой функции 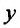
Это уравнение преобразуется к виду
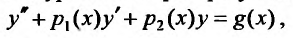 (24.1.1)
(24.1.1)
делением всех членов уравнения на коэффициент 
Предположим, что коэффициенты 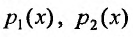 и правая часть
и правая часть 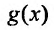 заданы и непрерывны при всех значениях
заданы и непрерывны при всех значениях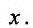 Если
Если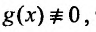 то уравнение называется линейным неоднородным, если же
то уравнение называется линейным неоднородным, если же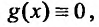 то уравнение принимает вид
то уравнение принимает вид
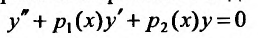 (24.1.2)
(24.1.2)
и называется линейным однородным.
Рассмотрим некоторые свойства однородных линейных дифференциальных уравнений (24.1.2).
Теорема 24.1.1. Если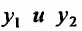 - два частных решения линейного однородного уравнения (2.2), то
- два частных решения линейного однородного уравнения (2.2), то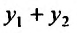 также является решение этого уравнения.
также является решение этого уравнения.
Доказательство. Так как 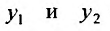 - решения уравнения (24.1.2), то, подставив решения в уравнение, получим тождества, которые образуют систему:
- решения уравнения (24.1.2), то, подставив решения в уравнение, получим тождества, которые образуют систему:
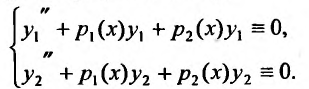 (24.1.3)
(24.1.3)
Подставляя в уравнение (24.1.2) сумму 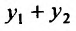 и принимая во внимание (24.1.3), получим:
и принимая во внимание (24.1.3), получим:
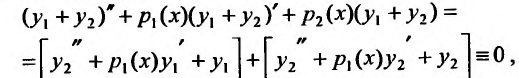
откуда и следует, что 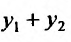 - решение уравнения (24.1.2).
- решение уравнения (24.1.2).
Теорема 24.1.2. Если у, - частное решение однородного уравнения (24.1.2). то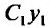 так же является частным решением уравнения (24.1.2).
так же является частным решением уравнения (24.1.2).
Доказательство. Так как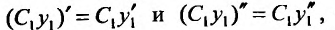 то
то 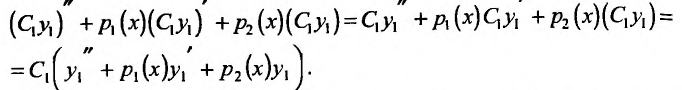
Из условия теоремы следует, что 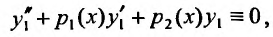 поэтому и (С,у,) + р,
поэтому и (С,у,) + р,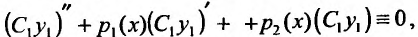 а это означает, что
а это означает, что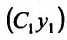 является частным решением уравнения (24.1.2).
является частным решением уравнения (24.1.2). 
Следствие 1. Если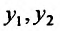 — частные решения линейного однородного уравнения (24.1.2), то
— частные решения линейного однородного уравнения (24.1.2), то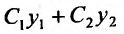 является частным решением уравнения (24.1.2).
является частным решением уравнения (24.1.2).
Доказательство. Действительно, 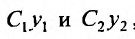 в силу теоремы 24.1.2.,- частные решения (24.1.2), а в силу теоремы 24.1.1 сумма
в силу теоремы 24.1.2.,- частные решения (24.1.2), а в силу теоремы 24.1.1 сумма 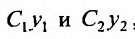 также является решением уравнения (24.1.2).
также является решением уравнения (24.1.2).
Заметим, что при сделанных предположениях относительно коэффициентов уравнения (24.1.2), оно имеет одно и только одно решение, проходящее через точку 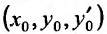 Кроме того, уравнение (24.1.2) имеет очевидное решение у = 0 - нулевое решение. В дальнейшем мы будем рассматривать ненулевые решения.
Кроме того, уравнение (24.1.2) имеет очевидное решение у = 0 - нулевое решение. В дальнейшем мы будем рассматривать ненулевые решения.
Определение 24.1.2. Определителем Вронского называется выражение 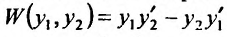 составленное из решений
составленное из решений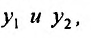 , и we производных
, и we производных 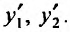
Теорема 24.1.3. Определитель Вронского вычисляется по формуле:

где С = const.
Доказательство. Для доказательства рассмотрим производную определителя
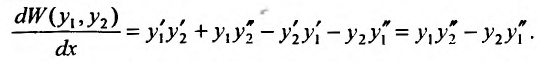
Так как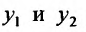 решения уравнения (24.1.2), то, подставив решения в уравнение (24.1.2), получим тождества:
решения уравнения (24.1.2), то, подставив решения в уравнение (24.1.2), получим тождества:
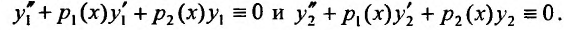
Умножая первое тождество на 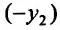 , а второе - на
, а второе - на 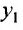 и складывая почленно, получим уравнение
и складывая почленно, получим уравнение
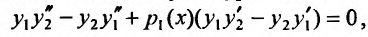 , в, котором два первых слагаемых - производная определителя Вронского, а выражение в скобках - определитель Вронского:
, в, котором два первых слагаемых - производная определителя Вронского, а выражение в скобках - определитель Вронского:
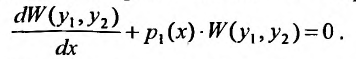
Умножив на dx, получим уравнение в дифференциальной форме: 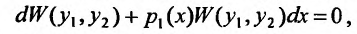 , которое является дифференциальным уравнением с разделяющимися переменными относительно определителя Вронского. Интегрируя его, получим формулу (24.1.4), называемой формулой Лиувиля.
, которое является дифференциальным уравнением с разделяющимися переменными относительно определителя Вронского. Интегрируя его, получим формулу (24.1.4), называемой формулой Лиувиля.
Выше мы рассматривали частные решения уравнения (24.1.2):  . Теперь возникает вопрос, какой формулой выражается общее решение линейного однородного уравнения второго порядка. Для получения формулы общего решения важную роль играет понятие линейной независимости решений.
. Теперь возникает вопрос, какой формулой выражается общее решение линейного однородного уравнения второго порядка. Для получения формулы общего решения важную роль играет понятие линейной независимости решений.
Определение 24.1.3. Два ненулевые решения,  , уравнения (24.1.2) называются линейно независимыми, если не существует отличных от нуля коэффициентов
, уравнения (24.1.2) называются линейно независимыми, если не существует отличных от нуля коэффициентов 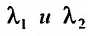 таких, что выполняется соотношение:
таких, что выполняется соотношение:
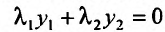 тождественное относительно х. Если же такие коэффициенты существуют, то
тождественное относительно х. Если же такие коэффициенты существуют, то 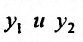 - линейно зависимы.
- линейно зависимы.
Таким образом, из определения 24.1.3 следует, что линейно зависимые (функции) решения отличаются на постоянный множитель.
Теорема 24.1.4. Если 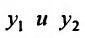 линейно зависимые на отрезке [a,b], то на этом отрезке определитель Вронского тождественно равен нулю.
линейно зависимые на отрезке [a,b], то на этом отрезке определитель Вронского тождественно равен нулю.
Доказательство. Действительно, если 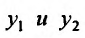 линейно зависимые решения, то они отличаются на постоянный множитель, т. е.
линейно зависимые решения, то они отличаются на постоянный множитель, т. е.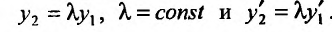 . Поэтому определитель Вронского равен нулю:
. Поэтому определитель Вронского равен нулю:
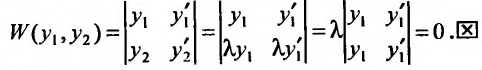
Теорема 24.1.5. Если ненулевые решения 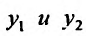 уравнения (2.2) линейно независимы на отрезке
уравнения (2.2) линейно независимы на отрезке 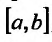 , то определитель Вронского, составленный для этих решений, не обращается в нуль ни в одной точке указанного отрезка.
, то определитель Вронского, составленный для этих решений, не обращается в нуль ни в одной точке указанного отрезка.
Доказательство. Предположим, что 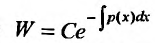 в некоторой точке х отрезка
в некоторой точке х отрезка 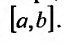 Тогда в силу теоремы 24.1.4 и формулы (24.1.4) он будет равен нулю во всех точках отрезка
Тогда в силу теоремы 24.1.4 и формулы (24.1.4) он будет равен нулю во всех точках отрезка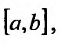 т.е.
т.е. 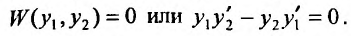
Так как 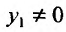 то, разделив равенство на
то, разделив равенство на 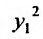 ,получим:
,получим: 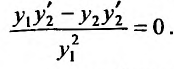
В левой части записано значение производной частного решения 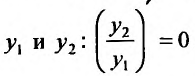 Тогда
Тогда 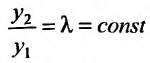 . Это означает, что решения
. Это означает, что решения 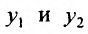 линейно зависимы, что противоречит их линейной независимости (по условию теоремы). Полученное противоречие и доказывает теорему.
линейно зависимы, что противоречит их линейной независимости (по условию теоремы). Полученное противоречие и доказывает теорему.
Теорема 24.1.6. Если 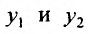 - два линейно независимых решения уравнения (24.1.2), то функция:
- два линейно независимых решения уравнения (24.1.2), то функция:
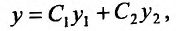 (24.1.5)
(24.1.5)
где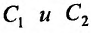 - произвольные постоянные, определяет его общее решение.
- произвольные постоянные, определяет его общее решение.
Доказательство. Из следствия 1 теоремы 24.1.2 следует, что функция 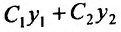 есть решение уравнения (24.1.2). Докажем теперь, что можно подобрать значения
есть решение уравнения (24.1.2). Докажем теперь, что можно подобрать значения 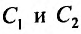 так, чтобы функция (24.1.5) удовлетворяла любым заданным начальным условиям.
так, чтобы функция (24.1.5) удовлетворяла любым заданным начальным условиям.
Пусть, при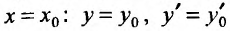 ( начальные условия). Подставляя их в равенство (24.1.5), получим систему линейных неоднородных уравнений, относительно
( начальные условия). Подставляя их в равенство (24.1.5), получим систему линейных неоднородных уравнений, относительно 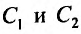 :
:

где 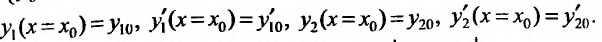
Так как определитель системы (24.1.6) , ,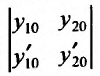 является определителем Вронского при
является определителем Вронского при 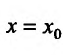 , и, следовательно, не равен нулю так как
, и, следовательно, не равен нулю так как 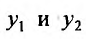 линейно независимы, то система (24.1.6) имеет решение, значит нужные
линейно независимы, то система (24.1.6) имеет решение, значит нужные 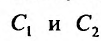 можно найти. Частное решение, которое получится из семейства (24.1.5), при найденных
можно найти. Частное решение, которое получится из семейства (24.1.5), при найденных 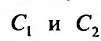 , удовлетворяет заданным начальным условиям. А это и означает, что функция (24.1.5) является общим решением уравнения (24.1.2). О
, удовлетворяет заданным начальным условиям. А это и означает, что функция (24.1.5) является общим решением уравнения (24.1.2). О
Заметим, что не существует методов для нахождения общего решения линейного однородного уравнения с переменными коэффициентами.
Однако, для уравнений с постоянными коэффициентами такой метод существует.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида:
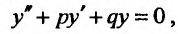 (24.2.1)
(24.2.1)
где р и q - постоянные числа. Нахождение общего решения уравнения (24.2.1) сводится к чисто алгебраическим операциям.
Вид уравнения (24.2.1) показывает, что частные решения этого уравнения следует искать, прежде всего, среди таких функций, которые в алгебраическом смысле подобны своим производным. Таким свойством обладает показательная функция. Поэтому будем искать частные решения в виде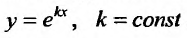 Так как
Так как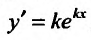 ,
, 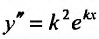 , то подставив в (24.2.1) значения
, то подставив в (24.2.1) значения 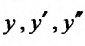 получим:
получим:
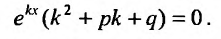
Множитель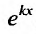 , не обращается в нуль ни при каких значениях х. Поэтому функция
, не обращается в нуль ни при каких значениях х. Поэтому функция 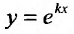 тогда и только тогда удовлетворяет линейному однородному уравнению с постоянными коэффициентами, когда число к является корнем уравнения:
тогда и только тогда удовлетворяет линейному однородному уравнению с постоянными коэффициентами, когда число к является корнем уравнения:
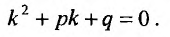 (24.2.2)
(24.2.2)
Алгебраическое квадратное уравнение (24.2.2) называют характеристическим уравнением данного дифференциального уравнения (24.2.1). Его корни находятся по формулам: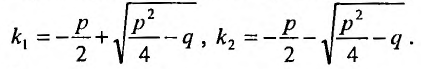
При этом могут представиться различные случаи, которые мы проанализируем подробнее.
1. Корчи характеристического уравнения действительны и различны: 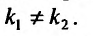
В этом случае частными решениями будут функции: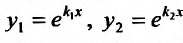
так как каждому из корней соответствует частное решение. Эти решения линейно независимы, потому что их отношение не равно постоянной величине:
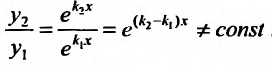
Тогда, в силу теоремы 24.1.6, общее решение уравнения (24.2.1) имеет вид:
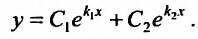
Пример:
Найти общее решение уравнения:
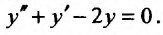
Решение:
В силу, изложенного выше, составляем характеристическое уравнение 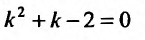 и находим его корни:
и находим его корни: 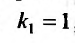
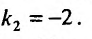
Так как корни характеристического уравнения различны, то общее решение задается функцией: 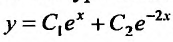
2. Корни характеристического уравнения комплексные.
Так как комплексные корни входят попарно сопряженными, то
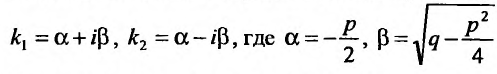
Частные решения можно записывать в виде: 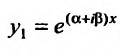 ,
,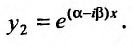
Это комплексные функции действительного аргумента, удовлетворяющие дифференциальному уравнению (24.2.1). Легко показать, что если какая-либо комплексная функция
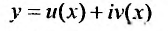 (24.2.3)
(24.2.3)
действительного аргумента удовлетворяет уравнению (24.2.1), то тгому уравнению удовлетворяют и функции 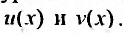 . Действительно, подставляя (24.2.3) в (24.2.1), получим:
. Действительно, подставляя (24.2.3) в (24.2.1), получим: 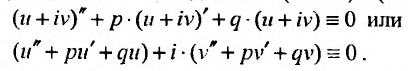
Комплексная функция равняется нулю, когда равны нулю ее действительная и мнимая части. Следовательно, 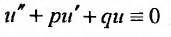 и
и 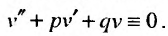
Это означает, что функции 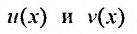 являются решениями уравнения (24.2.1), если функция
являются решениями уравнения (24.2.1), если функция 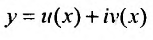 - решение уравнения (24.2.1).
- решение уравнения (24.2.1).
Перепишем теперь комплексные частные решения в виде суммы действительной и мнимой частей: 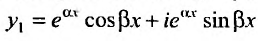 ,
,
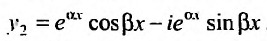
Тогда, частными решениями будут действительные функции: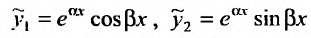 . Так как функции
. Так как функции 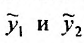 линейно независимы, то общее решение уравнения (24.2.1) в случае комплексных корней характеристического уравнения имеет вид:
линейно независимы, то общее решение уравнения (24.2.1) в случае комплексных корней характеристического уравнения имеет вид:
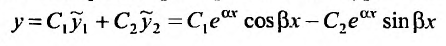
или

где 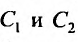 - произвольные постоянные.
- произвольные постоянные.
Заметим, что если в уравнении (24.2.2) р = 0,то характеристические корни чисто мнимые 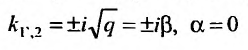 и решение
и решение
(24.2.4) имеет вид:
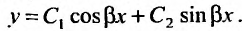
Пример:
Найти общее решение уравнения: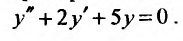
Решение:
Согласно изложенному выше, составляем характеристическое уравнение 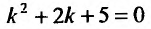 и находим его корни:
и находим его корни: 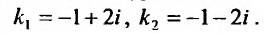
Следовательно, общее решение определяется функцией: 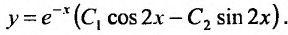
Пример:
Найти общее решение уравнения 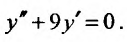
Решение:
Составим характеристическое уравнение 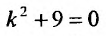 и найдем его корни
и найдем его корни 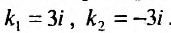 . Поэтому, обutec решение будет определяться функцией:
. Поэтому, обutec решение будет определяться функцией: 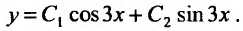
3. Корни характеристического уравнения действительные и равные: 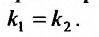 .
.
В этом случае, на основании случая 1, имеем одно частное решение 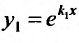 Нужно найти второе линейно независимое с первым. Будем его искать в виде
Нужно найти второе линейно независимое с первым. Будем его искать в виде 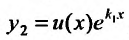 , где и(х) - неизвестная функция, подлежащая определению. Дифференцируя решение
, где и(х) - неизвестная функция, подлежащая определению. Дифференцируя решение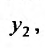 находим:
находим:
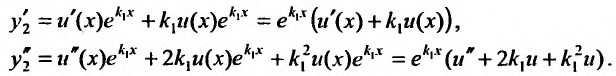
Подставляя функцию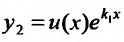 и се производные
и се производные 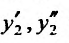 в уравнение (24.2.1), и выполняя элементарные преобразования, получаем
в уравнение (24.2.1), и выполняя элементарные преобразования, получаем
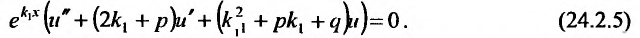
Так как 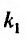 - кратный корень характеристического уравнения,
- кратный корень характеристического уравнения,
то 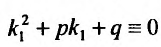 . Кроме того,
. Кроме того,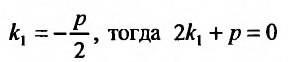 и поэтому в выражении (24.2.5) остается одно слагаемое, равное нулю:
и поэтому в выражении (24.2.5) остается одно слагаемое, равное нулю: 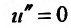 . Следовательно, для нахождения и(х) нужно решить уравнение
. Следовательно, для нахождения и(х) нужно решить уравнение 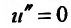 . Последовательно интегрируя уравнение
. Последовательно интегрируя уравнение 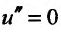 , получаем:
, получаем: 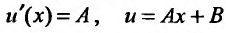 . В частности, можно положить
. В частности, можно положить 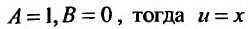 . Таким образом, в качестве второго частного решения можно взять функцию
. Таким образом, в качестве второго частного решения можно взять функцию 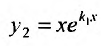 . Это решение линейно независимое с первым:
. Это решение линейно независимое с первым: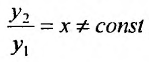 .
.
Поэтому общим решением будет функция:
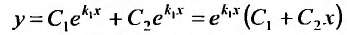
Пример:
Найти общее решение уравнения:
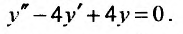
Решение:
Составляем характеристическое уравнение 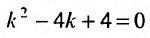 и находим его корни
и находим его корни 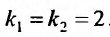 . Так как корни характеристического уравнения кратные действительные, то общее решение определяется функцией:
. Так как корни характеристического уравнения кратные действительные, то общее решение определяется функцией: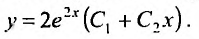
Структура общего решения линейного неоднородного уравнения второго порядка
В этом параграфе мы остановимся на изучении структуры общего решения линейного неоднородного уравнения второго порядка, т. с. уравнения вида:

Предположим, что уравнение (25.1.1) задано в области
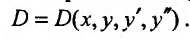
Функция 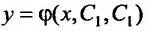 называется общим решением уравнения (25.1.1) в области D, если для любой точки области
называется общим решением уравнения (25.1.1) в области D, если для любой точки области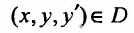 равенства
равенства

разрешимы относительно 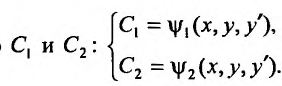
Иначе: функция 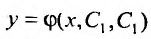 есть общее решение уравнения (25.1.1), если для любой точки из области D, можно указать такие значения постоянных
есть общее решение уравнения (25.1.1), если для любой точки из области D, можно указать такие значения постоянных 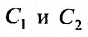 что выполняются равенства (25.1.2), н, при таких значениях постоянных, функция
что выполняются равенства (25.1.2), н, при таких значениях постоянных, функция 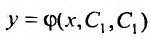 удовлетворяет уравнению (25.1.1).
удовлетворяет уравнению (25.1.1).
Структура общего решения уравнения (25.1.1) определяется следующей теоремой.
Теорема 25.1.1. Общее решение линейного неоднородного дифференциального уравнения (25.1.1) представляет сумму частного решения 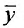 этого уравнения и общего решения Y соответствующего однородного уравнения (24.1.1).
этого уравнения и общего решения Y соответствующего однородного уравнения (24.1.1).
Доказательство. Пусть 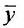 и Y соответственно частное решение уравнения (25.1.1) и общее решение соответствующего однородного уравнения (24.1.1). Нужно доказать, что произвольные постоянные, входящие в него, можно подобрать так, чтобы выполнялись начальные условия: при
и Y соответственно частное решение уравнения (25.1.1) и общее решение соответствующего однородного уравнения (24.1.1). Нужно доказать, что произвольные постоянные, входящие в него, можно подобрать так, чтобы выполнялись начальные условия: при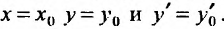
Так как 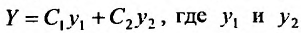 - линейно независимые решения уравнения (24.1.1), то нужно доказать, что функция:
- линейно независимые решения уравнения (24.1.1), то нужно доказать, что функция: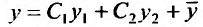 является общим решением уравнения (25.1.1), т.е. нужно доказать, что равенства:
является общим решением уравнения (25.1.1), т.е. нужно доказать, что равенства: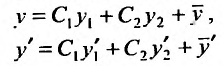 разрешимы относительно
разрешимы относительно 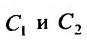
Подставляя в эти равенства начальные условия, получим систему относительно неизвестных 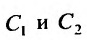
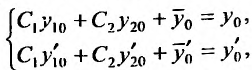
Эту систему можно переписать в виде:
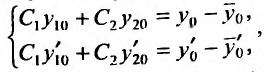
где 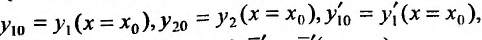
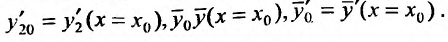
Определитель последней системы является определителем Вронского, для функций 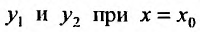 . И так как эти функции линейно независимы, то определитель Вронского не равен нулю. Следовательно, система имеет единственное решеннс. Определив
. И так как эти функции линейно независимы, то определитель Вронского не равен нулю. Следовательно, система имеет единственное решеннс. Определив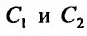 , найдем функцию
, найдем функцию 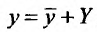 , которая определяет решение уравнения (25.1.1), удовлетворяющее данным начальным условиям.
, которая определяет решение уравнения (25.1.1), удовлетворяющее данным начальным условиям. 
Теорема 25.1.2. Если правая часть неоднородного уравнения (25.1.1) равна сумме двух функций:
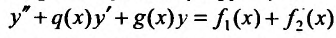 (25.1.3)
(25.1.3)
то частное решение такого уравнения можно получить как сумму частных решений аналогичных уравнений с правыми частями соответственно 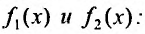

Доказательство. Пусть 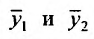 частные решения уравнений (25.1.4). Тогда при подстановке их в уравнение (25.1.3), получим тождества:
частные решения уравнений (25.1.4). Тогда при подстановке их в уравнение (25.1.3), получим тождества:
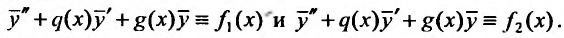
Складывая, правые и левые части тождеств, получаем:
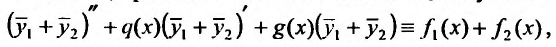
откуда следует, что сумма 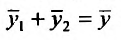 является решением уравнения (25.1.1).
является решением уравнения (25.1.1).
Таким образом, для решения неоднородного линейного уравнения необходимо найти общее решение соответствующего однородного и какое-либо частное решение исходного уравнения. Частное решение неоднородного линейного уравнения найти, вообще говоря, трудно Д1я уравнения (25.1.1). Мы остановимся на неоднородных линейных уравнениях с постоянными коэффициентами, т.е. уравнениях вида:
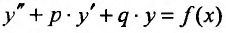 где р и q- постоянные коэффициенты, для которых существуют общие методы нахождения частных решений в зависимости от вида правой части.
где р и q- постоянные коэффициенты, для которых существуют общие методы нахождения частных решений в зависимости от вида правой части.
Способы нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и специальной правой частью
Пусть задано уравнение
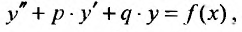 (25.2.1)
(25.2.1)
где р и q - действительные числа. Покажем, что частное решение уравнения (25.2.1) иногда можно найти, не прибегая к интегрированию, а методом неопределенных коэффициентов. Рассмотрим эти случаи.
1. Правая часть уравнения (25.1.1) представляет собой произведение показательной функции на многочлен: 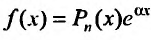 , где
, где 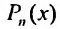 - многочлен n -ой степени.
- многочлен n -ой степени.
Если число а не является корнем характеристического уравнения 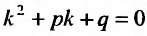 , составленного для соответствующего однородного уравнения
, составленного для соответствующего однородного уравнения 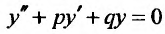 , то частное решение нужно искать в виде:
, то частное решение нужно искать в виде:
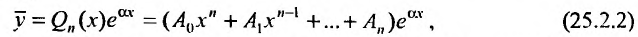
где 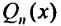 - многочлен степени n с неопределенными коэффициентами
- многочлен степени n с неопределенными коэффициентами 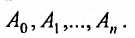
Действительно, подставляя 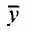 в уравнение (25.2.1) и сокращая все члены на
в уравнение (25.2.1) и сокращая все члены на 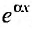 получаем:
получаем:
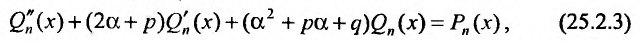
где 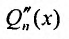 - многочлен степени
- многочлен степени 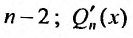 - многочлен степени
- многочлен степени 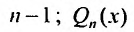 - многочлен степени n. Значит в левой и правой частях равенства (25.2.3) записаны многочлены степени n, которые будут равными, если равны коэффициенты при равных степенях х. Приравнивая коэффициенты при одинаковых степенях х, получим систему из n + 1 уравнений для определения коэффициентов
- многочлен степени n. Значит в левой и правой частях равенства (25.2.3) записаны многочлены степени n, которые будут равными, если равны коэффициенты при равных степенях х. Приравнивая коэффициенты при одинаковых степенях х, получим систему из n + 1 уравнений для определения коэффициентов 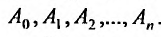
Если же число а простой корень характеристического уравнения, то частное решение следует искать в виде: 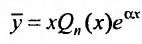 , где
, где
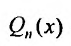 - многочлен степени п с неопределенными коэффициентами.
- многочлен степени п с неопределенными коэффициентами.
Действительно, если бы в этом случае стали искать частное решение в форме (25.2.2), то в равенстве (25.2.3) слева получили бы многочлен степени n-1, так как коэффициент при 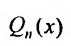 , т.е.
, т.е. 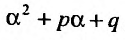 , равен нулю. Следовательно, ни при каких значениях
, равен нулю. Следовательно, ни при каких значениях 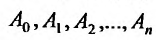 равенство (25.2.3) не было бы тождеством. Поэтому мы
равенство (25.2.3) не было бы тождеством. Поэтому мы 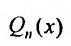 умножаем на х.
умножаем на х.
Если же число а двукратный корень характеристического уравнения, то частное решение следует искать в виде: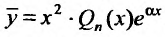 , так как кроме коэффициента при Q„(x), в равенстве (25.2.3), равен нулю и коэффициент при
, так как кроме коэффициента при Q„(x), в равенстве (25.2.3), равен нулю и коэффициент при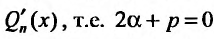 , и слева этого равенства будет стоять многочлен степени n - 2. При этом свободный член многочлена
, и слева этого равенства будет стоять многочлен степени n - 2. При этом свободный член многочлена 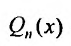 , в этом случае, и член первой степени исчезнут при дифференцировании и их можно не включать в частное решение.
, в этом случае, и член первой степени исчезнут при дифференцировании и их можно не включать в частное решение.
Замечание. Если правая часть уравнения (25.2.1) не содержит множителя 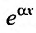 , то следует рассматривать а = 0 и частное решение искать в виде
, то следует рассматривать а = 0 и частное решение искать в виде 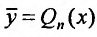 , учитывая при этом какой кратности нуль является корнем характеристического уравнения.
, учитывая при этом какой кратности нуль является корнем характеристического уравнения.
Пример №1
Найти общее решение уравнения:
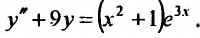
Решение:
Вначале находим общее решение соответствующего однородного уравнения 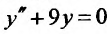 . Оно имеет вид:
. Оно имеет вид:
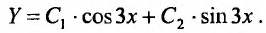
Далее ищем частное решение данного неоднородного уравнения. Так как правая часть заданного уравнения равна произведению многочлена на экспоненциальную функцию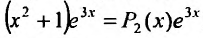 , и так как коэффициент 3 в показателе экспоненты не является корнем характеристического уравнения, то частное решение ищем в виде:
, и так как коэффициент 3 в показателе экспоненты не является корнем характеристического уравнения, то частное решение ищем в виде:
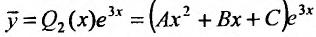
Вычисляя первую и вторую производные этого выражения и подставляя в дифференциальное уравнение, получим:
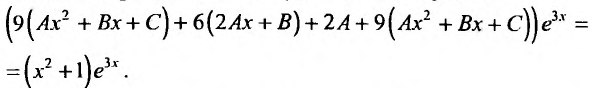
Сокращая на 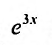 и приравнивая коэффициенты при одинаковых степенях х, будем иметь систему:
и приравнивая коэффициенты при одинаковых степенях х, будем иметь систему: 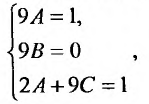
решая которую, находим: 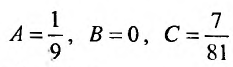 . Следовательно, частным решением является функция:
. Следовательно, частным решением является функция:
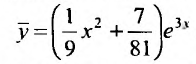
Общее решение заданного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного:
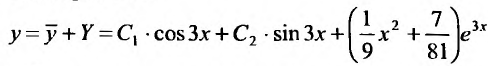
1. Пусть теперь правом часть уравнения (25.2.1) представляет собой произведение многочленов на тригонометрические функции и показательную функцию'.
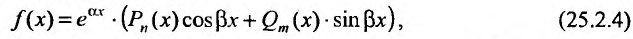
где 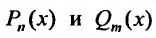 - многочлены степени n и m. Тогда частное решение определяется следующим образом:
- многочлены степени n и m. Тогда частное решение определяется следующим образом:
а) если число 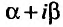 не является корнем характеристического уравнения, то частное решение следует искать в виде:
не является корнем характеристического уравнения, то частное решение следует искать в виде:
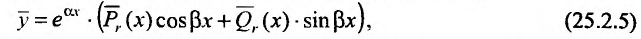
где 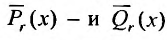 - многочлены с неопределенными коэффициентами, степень которых равна наивысшей степени многочленов
- многочлены с неопределенными коэффициентами, степень которых равна наивысшей степени многочленов 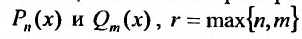 ;
;
б) если число 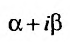 является корнем характеристического уравнения, то частное решение ищем в виде:
является корнем характеристического уравнения, то частное решение ищем в виде:
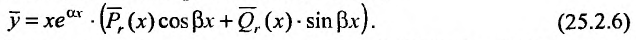
Заметим, что формы частных решений (25.2.5) и (25.2.6) сохраняются и в том случае, когда в правой части уравнения (25.2.1) один из многочленов 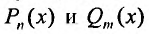 тождественно равен нулю, т.е. когда
тождественно равен нулю, т.е. когда
правая часть равна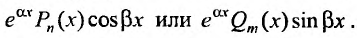
Кроме того, если правая часть уравнения (25.2.1) имеет вид: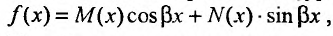 ,
,
где М и N - постоянные числа, то частное решение ищем в виде:
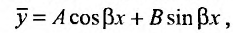 ,
,
где А и В постоянные, подлежащие определению, когда 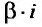 не являются корнем характеристического уравнения; если
не являются корнем характеристического уравнения; если 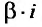 является корнем характеристического уравнения, то частное решение ищем в виде:
является корнем характеристического уравнения, то частное решение ищем в виде:
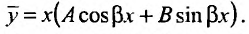
Пример №2
Найти общее решение линейного неоднородного уравнения 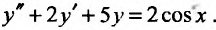
Решение:
Составим характеристическое уравнение соответствующего однородного уравнения: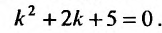 . Его корни
. Его корни 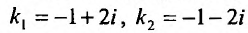
Поэтому общее решение соответствующего однородного уравнения определяется функцией: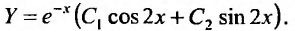
Согласно теории, изложенной выше, частное решение неоднородного уравнения ищем в виде: 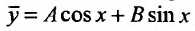 , где А и В -постоянные, подлежащие определению. Их определим, подставляя частное решение и его производные в заданное уравнение:
, где А и В -постоянные, подлежащие определению. Их определим, подставляя частное решение и его производные в заданное уравнение: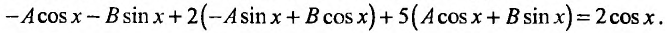
Приравнивая коэффициенты при одинаковых степенях cosx и sinx, получаем систему из двух уравнений:
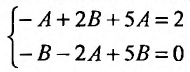
Решая эту систему, находим: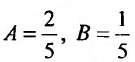 .
.
Следовательно, частное решение определяется функцией: 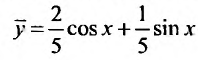 а общее — функцией:
а общее — функцией:
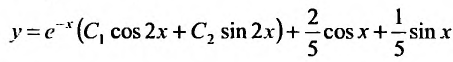
Способы решения дифференциальных уравнений второго порядка, допускающих понижение порядка
Рассмотрим дифференциальное уравнение второго порядка, разрешенное относительно производной 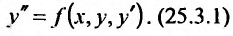
К простейшим интегрируемым дифференциальным уравнениям второго порядка вида (25.3.1) относятся уравнения, для которых функция, стоящая в правой части, зависит только от одного из трех аргументов 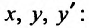

Рассмотрим также уравнения, допускающие понижение порядка, в которых функция зависит только от двух из трех аргументов: 
Общее решение уравнения (25.3.2) находится двукратным интегрированием. Рассмотрим соответствующий пример.
Пример №3
Проинтегрировать дифференциальное уравнение 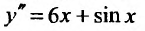
Решение:
Вычислим интегралы от обеих частей заданного уравнения, представив вторую производную в виде: 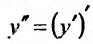 . Поскольку интеграл от производной функции равен самой функции, то, последовательно интегрируя, находим общее решение заданного уравнения:
. Поскольку интеграл от производной функции равен самой функции, то, последовательно интегрируя, находим общее решение заданного уравнения:
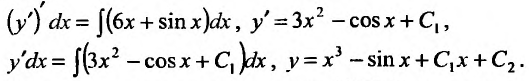
При интегрировании уравнения (25.3.3) вводится подстановка
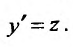 Тогда
Тогда 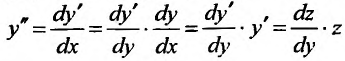 , и уравнение принимает вид
, и уравнение принимает вид 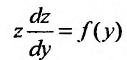 - Аналогично, подстановкой
- Аналогично, подстановкой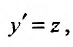
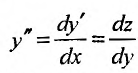 уравнение (25.3.4) приводится к виду
уравнение (25.3.4) приводится к виду 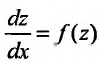
Преобразованные уравнения являются дифференциальными уравнениями первого порядка с разделяющимися переменными.
Пример №4
Найти частное решение дифференциального уравнения 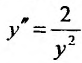 , удовлетворяющее условиям:
, удовлетворяющее условиям: 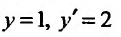 при х = 1.
при х = 1.
Решение:
Заданное уравнение относится к виду (25.3.3). Положим 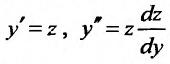 . Подставив, получим уравнение
. Подставив, получим уравнение 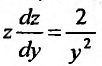 с разделяющимися переменными. Умножив на dy, и вычислив интегралы от обеих частей, последовательно находим:
с разделяющимися переменными. Умножив на dy, и вычислив интегралы от обеих частей, последовательно находим: 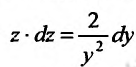
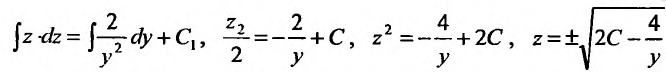
Выполним обратную подстановку 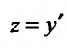 . Получим дифференциальное уравнение с разделяющимися переменными:
. Получим дифференциальное уравнение с разделяющимися переменными: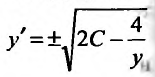 или
или 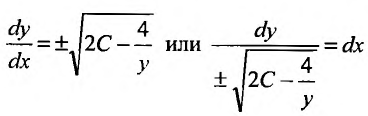 . Решение этого уравнения найдем, вычислив интегралы от обеих частей. Интеграл
. Решение этого уравнения найдем, вычислив интегралы от обеих частей. Интеграл 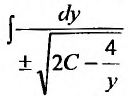 при помощи подстановки
при помощи подстановки 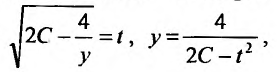
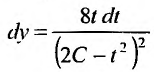 сводится к интегралу от рациональной дроби
сводится к интегралу от рациональной дроби 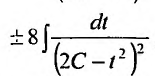 , который вычисляем, разложив рациональную дробь в сумму элементарных дробей:
, который вычисляем, разложив рациональную дробь в сумму элементарных дробей:
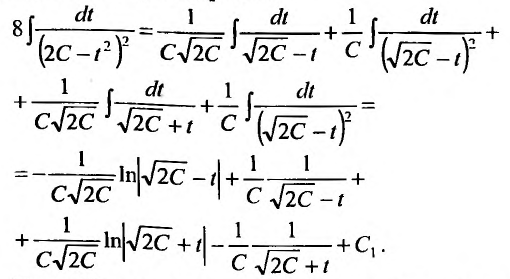
Тогда общее решение заданного уравнения будет иметь вид: 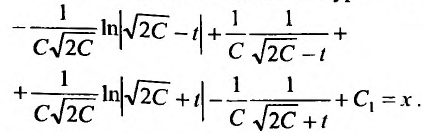
Уравнение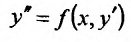 (25.3.5) подстановкой
(25.3.5) подстановкой 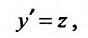
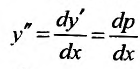 приводится к уравнению первого порядка
приводится к уравнению первого порядка
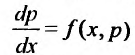 c неизвестной функцией p.
c неизвестной функцией p.
Пример №5
Проинтегрировать дифференциальное уравнение 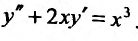
Решение:
Положим 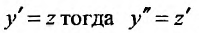 и заданное уравнение примет вид
и заданное уравнение примет вид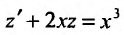 . Это линейное уравнение, которое интегрируем при помощи интегрирующего множителя
. Это линейное уравнение, которое интегрируем при помощи интегрирующего множителя
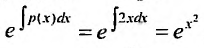 . Умножив на интегрирующим множитель, получим
. Умножив на интегрирующим множитель, получим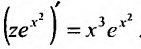 . Проинтегрировав обе части, последовательно находим z:
. Проинтегрировав обе части, последовательно находим z: 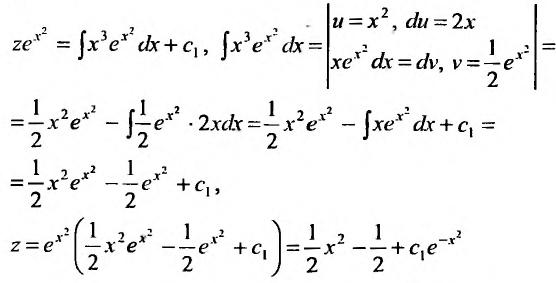 Подставив
Подставив 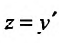 , получим:
, получим: 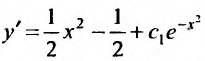
Вычислив интегралы левой и правой частей уравнения, находим общий интеграл:
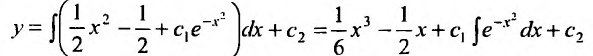
Уравнение (25.3.6), 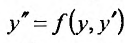 , подстановкой
, подстановкой 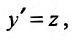
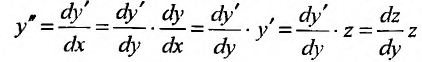 сводится к уравнению
сводится к уравнению
первого порядка: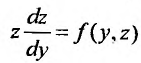 , в котором z функция, а у аргумент.
, в котором z функция, а у аргумент.
Пример №6
Проинтегрировать уравнение 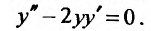
Решение:
Заданное уравнение имеет вид (25.3.6). Применим подстановку 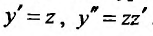 Тогда исходное уравнение преобразуются к уравнению с разделяющимися переменными:
Тогда исходное уравнение преобразуются к уравнению с разделяющимися переменными: 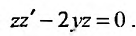 . Разделив переменные, последовательно находим:
. Разделив переменные, последовательно находим: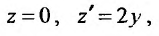
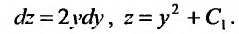
Выполнив обратную подстановку 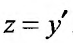 , получим два уравнения:
, получим два уравнения: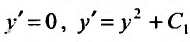 ,. Интегрируя эти уравнения, найдем:
,. Интегрируя эти уравнения, найдем: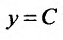
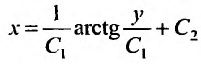
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |