
Линейные диаграммы
Содержание:
Линейные и круговые диаграммы:
Векторные уравнения
При изложении символического метода рассматривался расчет цепей с постоянными сопротивлениями или проводимостями. В этом случае поведение цепи иллюстрировалось векторными диаграммами сопротивлений, проводимостей, токов и напряжений, все векторы которых были постоянными и но величине и по направлению (фазе).
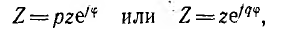
Однако часты случаи, когда сопротивление или проводимость участка цепи изменяется. Например, линия передачи имеет постоянное сопротивление, сопротивление же нагрузки может изменяться от бесконечности при холостом ходе до нуля при коротком замыкании Для практики наибольший интерес имеют случаи, когда изменяете модуль или аргумент сопротивления. В этих случаях переменное комплексное сопротивление может быть записано так:
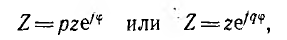
где р и q — безразмерные вещественные числа, в общем случае изменяющиеся в пределах
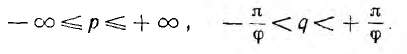
Векторы, изображающие эти переменные Рис. 10.1 сопротивления, будут также переменными.
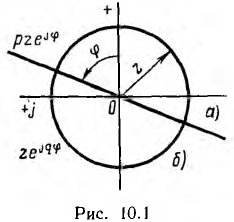
Начинаясь в начале координат комплексной плоскости, они своим концом будут перемещаться по тому или иному геометрическому месту точек (г. м. т.). Очевидно, что г. м. т. сопротивления 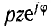 с переменным модулем рz будет прямая, проходящая через начало координат и образующая с осью вещественных угол
с переменным модулем рz будет прямая, проходящая через начало координат и образующая с осью вещественных угол 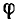 (рис. 10.1, а), а г. м. т. сопротивления
(рис. 10.1, а), а г. м. т. сопротивления 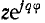 с переменным аргументом
с переменным аргументом 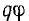 будет окружность радиуса z с центром в начале координат (рис. 10.1,6). Таким образом, в этих случаях г. м. т. получает вид линейной или круговой диаграмм.
будет окружность радиуса z с центром в начале координат (рис. 10.1,6). Таким образом, в этих случаях г. м. т. получает вид линейной или круговой диаграмм.
Если модуль сопротивления pz < 0 или абсолютное значение аргумента 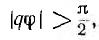 это сопротивление из потребителя энергии превращается в ее источник.
это сопротивление из потребителя энергии превращается в ее источник.
Если цепь содержит то или иное переменное сопротивление, то при заданном напряжении или токе всей цепи комплексы и векторы токов и напряжений ветвей будут также переменными.
Уравнения для комплексов искомых величин, содержащие постоянные и переменные величины, называются векторными уравнениями. Например, для цепи с параллельным соединением постоянной активной проводимости g и емкости С при переменной частоте со и неизменным током I всей цепи векторное уравнение для напряжения этой цени имеет вид:
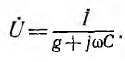
Из этого выражения видно, что для определения г. м. т. концов вектора U нужно сложить постоянный вектор g с г. м. т. 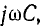 затем выполнить обращение, т. е. найти г. м. т. концов вектора
затем выполнить обращение, т. е. найти г. м. т. концов вектора 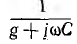 и результат умножить на постоянный вектор I. Из подобных oпераций состоит решение и более сложных задач. Поэтому далее общем виде рассматриваются эти основные операции, причем векторы обозначены большими буквами без точек.
и результат умножить на постоянный вектор I. Из подобных oпераций состоит решение и более сложных задач. Поэтому далее общем виде рассматриваются эти основные операции, причем векторы обозначены большими буквами без точек.
Действия над кривыми
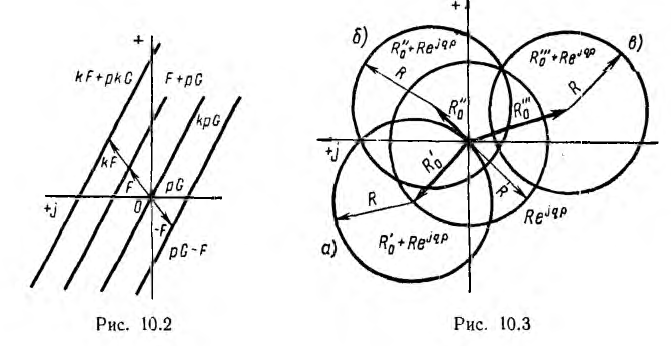
При суммировании г. м. т. с постоянным вектором г. м. т. сдвигается в направлении постоянного вектора на его величину. Например, сумма постоянного F и переменного pG векторов, т. е. векторное уравнение
V = F + pG,
в общем случае представляет собой прямую, не проходящую через начало координат (рис. 10.2).
Складывая постоянный вектор R0 с окружностью 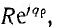 следует переместить центр окружности в конец постоянного вектора R0. Следовательно, векторное уравнение
следует переместить центр окружности в конец постоянного вектора R0. Следовательно, векторное уравнение
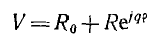
представляет собой также окружность, причем при абсолютных значениях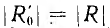 она, очевидно, проходит через начало координат (рис. 10.3, а); при
она, очевидно, проходит через начало координат (рис. 10.3, а); при  начало координат лежит внутри окружности (рис. 10.3,6), а при
начало координат лежит внутри окружности (рис. 10.3,6), а при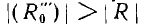 — вне этой окружности (рис. 10.3, в).
— вне этой окружности (рис. 10.3, в).
Вычитание из г. м. т. постоянного вектора сводится к сложению г. м. т. с комплексом вектора, у которого знак изменен на обратный (см. рис. 10.2).
При умножении г. м. т. на вещественное число k каждый вектор исходного г. м. т. удлиняется в k раз и дает подобное г. м. т. При умножении прямой pG на k
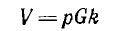
получается та же прямая, проходящая через начало координат. При умножении прямой F + pG на k
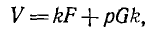
получается прямая, параллельная исходной и не проходящая чере начало координат (см. рис. 10.2).
При умножении окружности 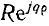 на вещественное число k
на вещественное число k
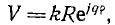
получается также окружность с центром в начале координат, но с радиусом, в к раз большим.
При умножении на k окружности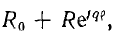 центр которой не расположен в начале координат,
центр которой не расположен в начале координат,
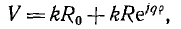
вектор центра окружности R0 и ее радиус R удлиняются в k раз (рис. 10.4). При этом обе окружности будут иметь общие касательные, исходящие из начала координат.
При умножении г. м. т. на постоянный комплекс 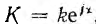 помимо умножения на модуль k, производится поворот вокруг начала координат на величину аргумента х в направлении, соответствующем знаку х; в результате получается подобное г. м. т.
помимо умножения на модуль k, производится поворот вокруг начала координат на величину аргумента х в направлении, соответствующем знаку х; в результате получается подобное г. м. т.
Деление г. м. т. на постоянный комплекс 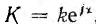 сводится, очевидно, к умножению на обратный комплекс
сводится, очевидно, к умножению на обратный комплекс
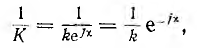
что означает деление на модуль k и поворот в обратную сторону на величину аргумента х.
Обращение вектора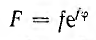 дает вектор
дает вектор
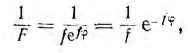
модуль которого обратен модулю исходного вектора, а аргумент противоположен по знаку, т. е. направление обращенного вектора совпаает с направлением вектора, сопряженного с исходным. Таким образом, операция обращения распадается на две, которые целесообразно выполнять в следующем порядке: нанести на график вектор Р, сопряженный с исходным вектором F, а затем в том же направлении отложить обратный вектор 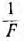 , величина которого равна
, величина которого равна 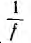 (рис. 10.5).
(рис. 10.5).
При обращении прямой 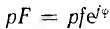 , проходящей через начало координат, получается векторное уравнение прямой, проходящей через начало координат и сопряженной с исходной прямой:
, проходящей через начало координат, получается векторное уравнение прямой, проходящей через начало координат и сопряженной с исходной прямой:
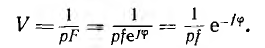
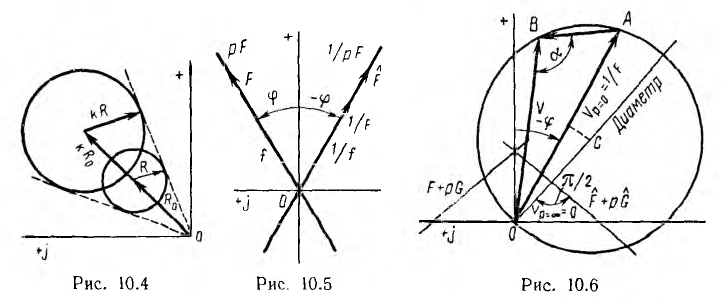
Обращение прямой F + pG, не проходящей через начало координат (рис. 10.6), дает векторное уравнение:
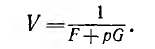
На диаграмме рис. 10.6 изображены частные значения векторов:
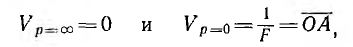
а также вектор V = 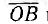 при каком-то значении р. Вектор
при каком-то значении р. Вектор 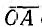 образует с осью вещественных угол —
образует с осью вещественных угол —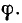
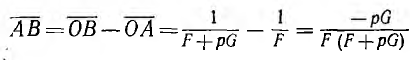
и при G = 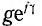 отношение
отношение
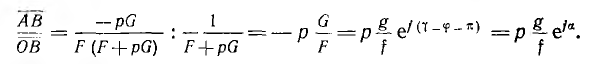
Аргумент 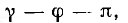 равный, очевидно, углу а между векторами
равный, очевидно, углу а между векторами 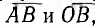 при изменении р сохраняет свою величину постоянной, а это значит, что г. м. т. вектора V есть окружность, хордой которой является вектор
при изменении р сохраняет свою величину постоянной, а это значит, что г. м. т. вектора V есть окружность, хордой которой является вектор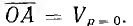 Так как
Так как 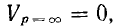 эта окружность проходит через начало координат.
эта окружность проходит через начало координат.
Если, согласно сказанному, нанести на график прямую 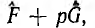 сопряженную с обращаемой прямой F + pG, то направление наибольшего обратного вектора, т. е. диаметра окружности, совпадает с наименьшим исходным вектором, т. е. с перпендикуляром к прямой
сопряженную с обращаемой прямой F + pG, то направление наибольшего обратного вектора, т. е. диаметра окружности, совпадает с наименьшим исходным вектором, т. е. с перпендикуляром к прямой 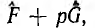
Следовательно, обращение прямой, не проходящей через начало координат, дает окружность, проходящую через начало координат, вектор центра которой перпендикулярен прямой, сопряженной с исходной.
Из только что доказанного вытекает обратная теорема — обращение окружности, проходящей через начало координат, дает прямую, не проходящую через начало координат и перпендикулярную направлению, сопряженному с вектором центра исходной окружности.
Можно сделать вывод, что векторное уравнение окружности, про ходящей через начало координат, может быть записано в двух видах
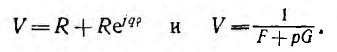
Если сдвинуть эту окружность путем сложения с каким-либо по стоянным вектором К, получается два вида уравнения окружности не проходящей через начало координат:
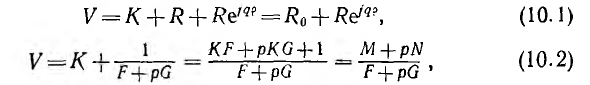
где
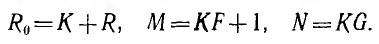
При обращении не проходящей через начало координат окружности, уравнение которой записано во второй форме, получается векторное уравнение
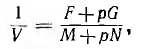
имеющее тот же вид, что и исходное уравнение и, следовательно, также представляющее окружность, не проходящую через начало координат.
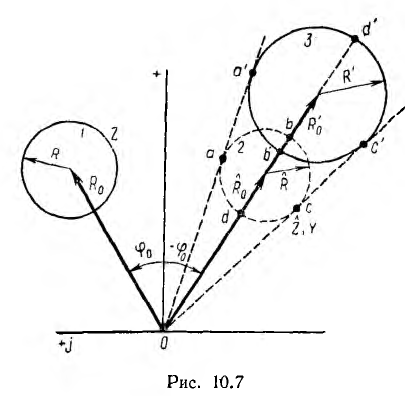
В соответствии со сказанным удобно на диаграмме (рис. 10.7) вместо исходной окружности 1 нанести окружность 2, сопряженную с исходной, т. е. имеющую сопряженный вектор центра, но такой же радиус. Затем осуществляется собственно обращение, дающее окружность 3. При этом взаимообратные точки а и а', b и b', с и с', d и d' будут находиться на тех же лучах, проведенных из начала координат, а исходная сопряженная 2 и обратная окружность 3 будут, очевидно, иметь общие касательные, проведенные из начала координат. Если обход исходных точек совершается по часовой стрелке (а, b, с, d), обход обратных точек (а', Ь', с', d') происходит в обратном направлении. Более длинному вектору, например 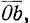 соответствует более короткий
соответствует более короткий 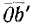 , а более короткому, например
, а более короткому, например 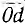 , соответствует длинный вектор
, соответствует длинный вектор 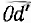 .
.
Выше шла речь o векторных уравнениях и диаграммах, связывающих отвлеченные величины, и, следовательно, изображаемых в одном масштабе. Применяя эти уравнения к цепям переменного тока, получают СВЯЗЬ между физически разнородными величинами — напряжениями, токами, сопротивлениями и проводимостями, масштабы которых при изображении на диаграмме не связаны друг с другом и могут выбираться совершенно произвольно. Так, например, если сопротивление Z какой-либо цепи изображается окружностью, не проходящей через начало координат, то обратная величина — проводимость Y изменяется также по окружности, не проходящей через начало координат и лежащей между теми же касательными, что и окружность Тогда выбором соответствующего масштаба можно совместить сопряженную окружность 1 с окружностью У.
При решении задач следует сначала составить векторные уравнения для искомых величин. Если необходимо знать все промежуточные величины, нужно строить г. м. т. для каждой из них поочередно, например так, как указано. Если необходимо знать лишь г. м. т. искомой величины, его строят по ее векторному уравнению. В рассмотренных далее примерах применены оба метода построения.
Диаграмма для линии передачи энергии к приемнику
В качестве примера применения линейных и круговых диаграмм рассматривается передача энергии от генератора с неизменным напряжением 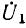 по линии с постоянным сопротивлением
по линии с постоянным сопротивлением 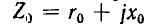
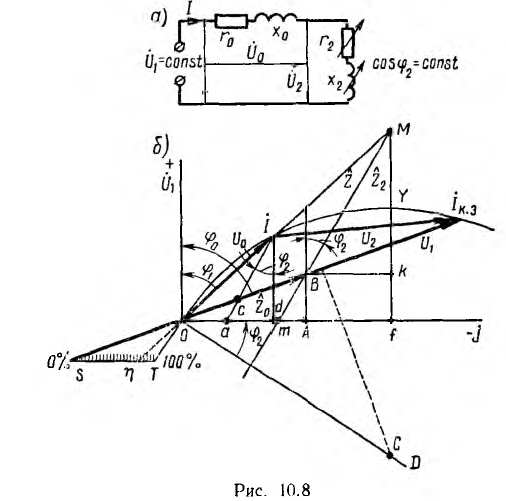
К приемнику с изменяющимся сопротивлением Z2, но при постоянном коэффициенте мощности 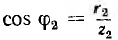 (рис. 10.8, а). Векторное уравнение тока цепи:
(рис. 10.8, а). Векторное уравнение тока цепи:
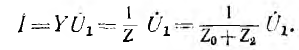
Следовательно, для нахождения г. м. т. концов вектора тока i надо: 1) найти сопряженное сопротивление Z всей цепи, сложив постоянное сопротивление линии с переменным сопротивлением Z0 приемника; 2) найти проводимость Y всей цепи, обратив сопротивление Z; 3) умножить Y на постоянную величину U1.
Построение показано на рис. 10.8, б. Напряжение U1 откладывается по оси вещественных вверх. Комплекс Z0 = r0 — jx0, сопряженный с комплексным полным сопротивлением линии Z0, изображен вектором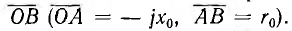 Этот вектор образует с осью вещественных угол
Этот вектор образует с осью вещественных угол 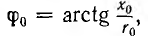 , откладываемый в данном случае по часовой стрелке.
, откладываемый в данном случае по часовой стрелке.
Так как угол сдвига 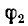 в приемнике остается постоянным, а изменяется только величина z2, то диаграммой Z2 будет прямая
в приемнике остается постоянным, а изменяется только величина z2, то диаграммой Z2 будет прямая 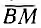 , проходящая через конец вектора
, проходящая через конец вектора 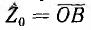 под углом
под углом 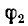 к оси вещественных. Эта же прямая будет диаграммой
к оси вещественных. Эта же прямая будет диаграммой 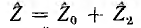 относительно начала координат. При обращении этой прямой получается диаграмма проводимости К всей цепи. Согласно доказанной теореме, это будет окружность, вектор центра
относительно начала координат. При обращении этой прямой получается диаграмма проводимости К всей цепи. Согласно доказанной теореме, это будет окружность, вектор центра 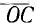 которой перпендикулярен прямой
которой перпендикулярен прямой 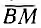 , т. е. образует угол
, т. е. образует угол 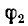 с осью мнимых величин. Умножая диаграмму Y на вещественное число U1 получают также окружность — диаграмму тока цепи I=YU1 чтобы окружности Y и I совпадали, надо выбрать для тока масштаб в U1 раз больший, чем масштаб для проводимости.
с осью мнимых величин. Умножая диаграмму Y на вещественное число U1 получают также окружность — диаграмму тока цепи I=YU1 чтобы окружности Y и I совпадали, надо выбрать для тока масштаб в U1 раз больший, чем масштаб для проводимости.
Таким образом, при изменении сопротивления приемника конец вектора тока перемещается по окружности тока, образуя с вектором напряжения U1 угол ϕ. При холостом ходе 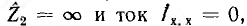 например при
например при 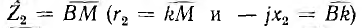 и сопротивлении всей цепи
и сопротивлении всей цепи 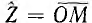 конец вектора тока I = 0I будет на пересечении вектора
конец вектора тока I = 0I будет на пересечении вектора 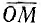 с окружностью тока. При коротком замыкании
с окружностью тока. При коротком замыкании 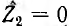 . сопротивление всей цепи
. сопротивление всей цепи 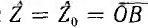 и конец вектора тока
и конец вектора тока 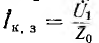 .
.
будет на пересечении луча 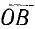 с окружностью тока:
с окружностью тока: 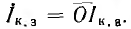 . Таким образом, вектор
. Таким образом, вектор 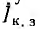 является хордой окружности тока и образует с вектором напряжения
является хордой окружности тока и образует с вектором напряжения 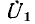 угол
угол 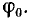
Окружность тока может быть построена сразу по вектору тока короткого замыкания 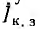 ; из его середины проводится перпендикуляр и центр С искомой окружности получается на пересечении перпендикуляра с прямой
; из его середины проводится перпендикуляр и центр С искомой окружности получается на пересечении перпендикуляра с прямой 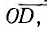 проходящей через начало координат и составляющей угол
проходящей через начало координат и составляющей угол 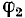 с осью мнимых.
с осью мнимых.
Векторное уравнение напряжения на линии
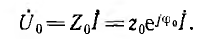
Следовательно, диаграмма напряжения на линии получится в результате умножения окружности тока на z0 и поворота на угол ϕ0, т. е. будет также окружностью. Если для напряжения взять масштаб в z0 раз больше масштаба тока, а вместо поворота диаграммы повернуть а угол ϕ0 в обратном направлении вектор напряжения U1 и то окружность напряжения U0 совпадает с окружностью тока, а вектор напряжения U1 — с вектором 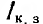 тока короткого замыкания; тогда напряжение на приемнике U2 может быть найдено на той же окружности, так как
тока короткого замыкания; тогда напряжение на приемнике U2 может быть найдено на той же окружности, так как 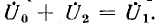 . Так, для случая холостого хода U0 = 0 и U2 =
. Так, для случая холостого хода U0 = 0 и U2 = 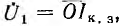 Для тока
Для тока 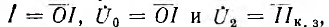 для коpоткого замыкания
для коpоткого замыкания 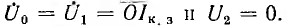
Средняя мощность 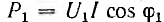 всей цепи может быть изображена перпендикуляром
всей цепи может быть изображена перпендикуляром 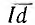 на ось мнимых из конца вектора тока I, так как U1 = const, а в масштабе тока
на ось мнимых из конца вектора тока I, так как U1 = const, а в масштабе тока 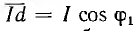 при этом если и есть масштаб для тока, масштаб для мощности будет равен nU1. Мощность всей цепи может быть изображена также отрезком Iа, составляющим постоянный угол
при этом если и есть масштаб для тока, масштаб для мощности будет равен nU1. Мощность всей цепи может быть изображена также отрезком Iа, составляющим постоянный угол 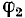 с перпендикуляром Id, но так как Id =
с перпендикуляром Id, но так как Id = 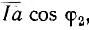 , то теперь масштаб мощности будет равен nU1 cos
, то теперь масштаб мощности будет равен nU1 cos 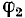 . Луч короткого замыкания
. Луч короткого замыкания 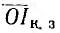 делит отрезок 1а на две части: Iс и Iса из рис. 10.8, б видно, что
делит отрезок 1а на две части: Iс и Iса из рис. 10.8, б видно, что
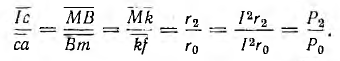
Следовательно, в том же масштабе отрезок Iс равен средней мощности Р2 приемника, отрезок са равен средней мощности Р0 потерь в линии передачи, а отрезок Ia равен средней мощности Р1 всей цепи, г. е. мощности генератора.
Из рис. 10.8, 6 видно, что Р2 = 0 при холостом ходе и: коротком смыкании и имеет максимум в одной из промежуточных точек; Р0 = 0 при холостом ходе и непрерывно растет по мере приближения к короткому замыканию; P1 = 0 при холостом ходе, проходит через максимум и равна Р0 при коротком замыкании.
Для непосредственного получения на диаграмме к. п. д. η =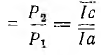 следует продолжить линии
следует продолжить линии 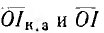 в обратную сторону, а также провести через начало координат прямую ОТ || Mm и разд< лить любую горизонтальную линию ST на 100 частей. Тогда из под< бия треугольников ОηТ и I0а, а также OST и сОа следует
в обратную сторону, а также провести через начало координат прямую ОТ || Mm и разд< лить любую горизонтальную линию ST на 100 частей. Тогда из под< бия треугольников ОηТ и I0а, а также OST и сОа следует
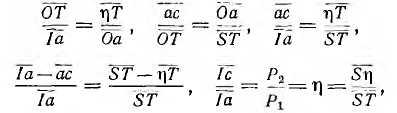
т. е. продолжение луча тока дает на прямой ST непосредственно величину к. п. д., соответствующего этому току.
На основании круговой диаграммы могут быть построены рабочиe характеристики в функции мощности приемника Р2 (рис. 10.9) и тока (рис. 10.10). На рис. 10.9 часть характеристик от холостого хода дo максимального значения Р2max показана сплошной линией, от максимального значения Р2max до короткого замыкания — пунктиром.
Диаграмма для четырехполюсника
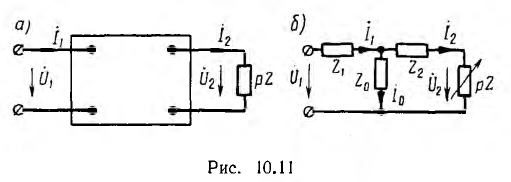
Пусть приемник с переменным сопротивлением 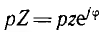 питается через пассивный четырехполюсник с параметрами А, В, С, D от источника неизменного напряжения U1 (рис. 10.11, а).
питается через пассивный четырехполюсник с параметрами А, В, С, D от источника неизменного напряжения U1 (рис. 10.11, а).
Тогда напряжение на выходе 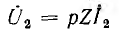 и уравнения четырехполюсника получают вид:
и уравнения четырехполюсника получают вид:
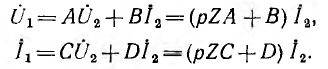
Ток на входе четырехполюсника определяется делением второй, уравнения на первое:
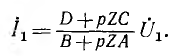
Это векторное уравнение является уравнением окружности, н проходящей через начало координат Если направить 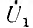 оси вещественных
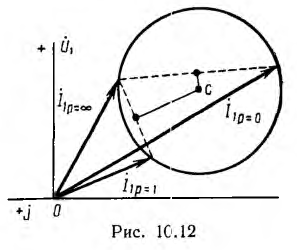
оси вещественных 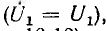 окружность токов можно построить п трем векторам (рис. 10.12):
окружность токов можно построить п трем векторам (рис. 10.12):
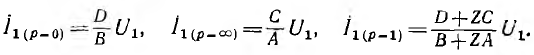
Первые два вектора являются соответственно векторами токов короткого замыкания и холостого хода, а третий — вектором тока для эдного из режимов нагрузки. Центр с окружности лежит на пересечении перпендикуляров к хордам в их средних точках, соединяющим •гонцы этих векторов.
Пусть четырехполюсник представляет собой Т-образную схему с сопротивлениями ветвей Z1, Z0, Z2 (см. рис. 10.11, б), и требуется найти диаграмму токов ветвей при переменном сопротивлении pZ нагрузки и постоянном напряжении U1 источника. Вычислив токи ветвей
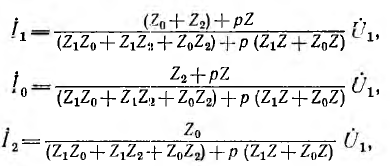
можно видеть, что г. м. т. концов векторов этих токов являются окружностями, причем окружности I1 и I0 не проходят через начало координат, а окружность I2 проходит через него. Все эти окружности могут быть также построены по трем точкам.
В случае питания сопротивления pZ через активный четырехполюсник его система уравнений может быть переписана следующим образом:
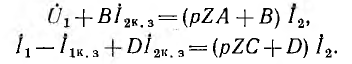
Ток I1 на входе активного четырехполюсника может быть определен делением второго уравнения на первое:
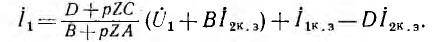
Дробь в правой части равенства является уравнением окружности, не проходящей через начало координат. Умножение этого г. м. т. на постоянный вектор 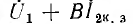 с последующим суммированием с постоянным вектором
с последующим суммированием с постоянным вектором 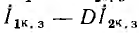 дает для г. м. т. I1 также уравнение окружности, в общем случае не проходящей через начало координат.
дает для г. м. т. I1 также уравнение окружности, в общем случае не проходящей через начало координат.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |