Квадрат и его свойства с определением и примерами решения

Квадратом называют прямоугольник, у которого все стороны равны.

На рисунке 57 изображен квадрат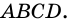

Сформулируем свойства квадрата.

1. Все углы квадрата прямые.

2. Периметр квадрата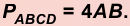

3. Диагонали квадрата равны (рис. 58).

4. Диагонали квадрата взаимно перпендикулярны и точкой пересечения делятся пополам (рис. 58).

5. Диагонали квадрата делят его углы пополам, то есть образуют углы по 45° со сторонами квадрата (рис. 58).

6. Точка пересечения диагоналей квадрата равноудалена от всех его вершин: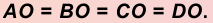

Пример:

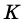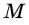Точки  и  принадлежат соответственно диагоналям 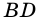и 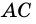квадрата  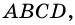причем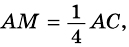  

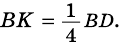
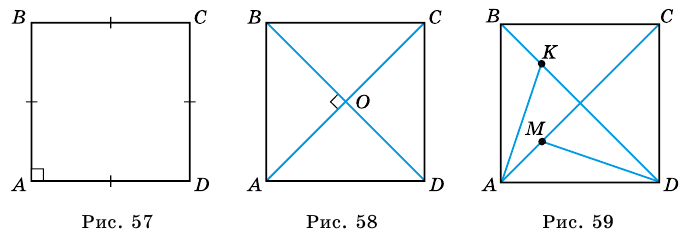
Докажите, что 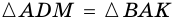 (рис. 59). 4

Доказательство:

1) 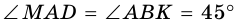(по свойству квадрата), 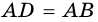(как стороны квадрата).

2) Так как 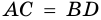(по свойству диагоналей квадрата) и

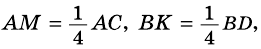то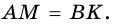

3) Тогда 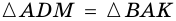(по двум сторонам и углу между ними). 

Рассмотрим признаки квадрата.

Теорема (признаки квадрата). 1) Если у прямоугольника диагонали взаимно перпендикулярны, то он является квадратом. 2) Если у ромба диагонали равны, то он является квадратом.

Доказательство:

1) Данный прямоугольник является параллелограммом, а параллелограмм со взаимно перпендикулярными диагоналями - ромбом. Следовательно, у данного прямоугольника все стороны равны, поэтому он является квадратом.

2) Данный ромб является параллелограммом, а параллелограмм с равными диагоналями - прямоугольником. Следовательно, у данного ромба все углы прямые, поэтому он является квадратом. 

Пример:

Докажите, что если в четырехугольнике все стороны равны и все углы равны, то этот четырехугольник - квадрат.

Доказательство:

1) Так как в четырехугольнике все углы равны, то, по признаку прямоугольника, он является прямоугольником.

2) Так как в прямоугольнике все стороны равны, то он является квадратом.

А еще раньше...

Термин «квадрат» происходит от латинского quadratum (quadrate -сделать четырехугольным).

Известный историк математики Д. Д. Мордухай-Болтовский (1876-1952) писал: «Первым четырехугольником, с которым познакомилась геометрия, был квадрат».