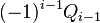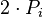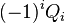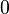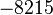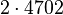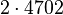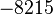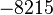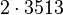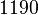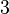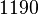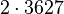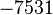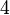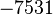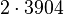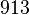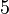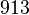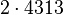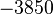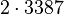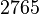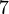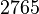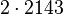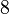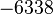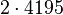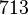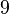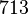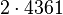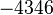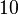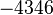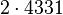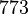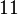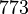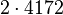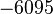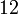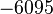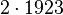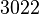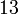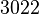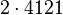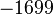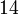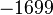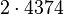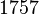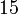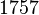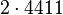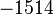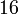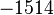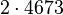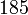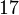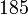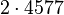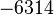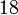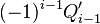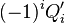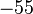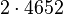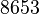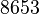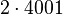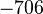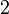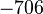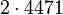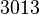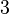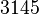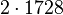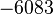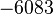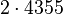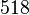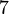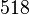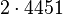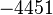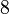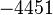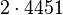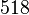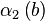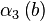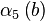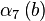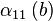Основные структуры алгоритмов: сравнительный анализ и примеры их использования (Ρ-алгоритм Полларда)
Содержание:
Введение
В настоящее время исследования в области построения быстрых алгоритмов факторизации интенсивно проводятся во всем мире. Ежегодно проводятся десятки конференций на эту тему, достигаются новые рекорды факторизации длинных чисел, исследуются известные проблемы алгоритмической теории чисел и ставятся новые задачи. Недавно (в конце 2009 года) группа европейских ученых во главе с Торстеном Кляйнджуном установила новый рекорд разложения 768-битного натурального числа с использованием сита поля чисел. Предыдущий 512-битный рекорд был установлен в 2000 году, то есть переход с 512-битных на 768-битные числа занял почти 10 лет. Поэтому следующую запись в 1024 бита при сохранении той же скорости роста исследования планируется завершить не ранее, чем в 2020 году.
При наличии измерения сложности алгоритмов и информационных структур я обычно говорю о 2 предметах: количестве действий, необходимых для завершения упражнения (вычисляемая сложность), и количестве ресурсов, в частности, памяти, которая необходима для метода ( пластическая сложность).
Алгоритм, который работает в 10 раз быстрее, но применяет в 10 раз больше зон, абсолютно способен приблизиться к назначению серверных машин с огромным объемом памяти.
Однако в интегрированных концепциях, где память уменьшается, этот тип метода не может быть применен.
В данных заметках я побеседуем о трудности вычислений, однако присутствие анализе алгоритмов сортировки я кроме того разберем проблема о ресурсах.
Наша страна практически полностью исключена из участия в этом конкурсе, что объясняется отсутствием источников финансирования таких проектов. Другой причиной является отсутствие в русской литературе самых передовых методов факторизации, таких как метод квадратичного сита и метод численного полевого сита. В отличие от проблемы распознавания простоты числа, факторизация, предположительно, является сложной вычислительной проблемой.
Вопрос о существовании алгоритма факторизации с полиномиальной сложностью на классическом компьютере является одной из важных открытых проблем современной теории .
В этот период имеется большое число алгоритмов сортировки информации. Зачастую подбор метода постановления вопросов находится в зависимости с текстуры сортируемых информации. В случае сортировки данное соответствие немаловажно, и способы сортировки как правило разделяются в 2 группы:
Сортировка массивов (внутренняя сортировка)
Сортировка последовательных файлов (внешняя сортировка)
Благодаря внутренней сортировке массивы расположены в основной памяти компьютера, что обеспечивает быстрый произвольный доступ к данным.
При внешней сортировке файлы хранятся в «более медленной», но более емкой внешней памяти, то есть на механических запоминающих устройствах (магнитных дисках и других носителях).
Критерии оценки методов сортировки:
количество операций сравнения пар ключей
количество перестановок элементов
экономное использование памяти
Целью написания работы является проведение сравнительного анализа методов факторизации натуральных чисел. В ходе работы были поставлены следующие задачи:
1. Рассмотреть алгоритмы факторизации натуральных чисел;
2. Провести сравнительное описание методов факторизации по группам сложности;
3. Рассмотреть выбранные методы факторизации на практических примерах;
Объектом исследования является выбор методов разложения натуральных чисел.
Предметом являются практические примеры применения метода. В данной работе были рассмотрены следующие методы факторизации натуральных чисел:
Экспоненциальные алгоритмы
- список возможных разделителей
- Метод факторизации фермы
Algorithm-алгоритм Полларда
- метод квадратичных форм Шенкса
- метод Лемана
Субэкспоненциальные алгоритмы
- алгоритм Диксона
Научная формулировка и разработка отдельных аспектов темы исследования отражена в трудах российских ученых и математиков. При написании работы использовалась периодическая учебная литература следующих авторов: Панчишкин А.А., Нестеренко Ю.В., Бухштаб А.А. и так далее.
1. Алгоритмы факторизации натуральных чисел
1.1 Факторизация натурального числа
Натуральное число называется простым, если оно делится только на себя и на 1. Число, не являющееся простым числом, называется составным. Очевидно, что любое простое число, не равное 2, нечетно.
Например, есть знаки деления целых чисел на разные простые числа, так что число в десятичной форме делится на 3 и 9, что достаточно для деления суммы его цифр на 3 и 9 соответственно. Чтобы разделить число на 5, достаточно, чтобы его последняя цифра была 0 или 5. Подобные выборочные свойства делимости возможно применять, в случае если для вас необходимо сократить комплект претендентов с целью контроля несложности либо обозначить сложные количества.
Другим методом извлечения обычных количеств считается ситечко Эратосфена, сваливаемое миксолидийскому научному работнику Эратосфену Киренскому, что проживал приблизительно 276 - 194 вплоть до н.э. Для того чтобы отыскать комплект обычных с целью заранее избранной верхней пределы B, сперва запишите очередность абсолютно всех непарный количеств с 3 вплоть до B. Далее подберите 1-ое количество в перечне, в таком случае имеется первоначальные 3, и забудьте его в list, зачеркните все без исключения сложные 3, включая с 6. Далее переведитесь к 2-ой количеству в перечне (верхняя пять) и зачеркните его многочисленные значимости, сохранив пять и т. д., до тех пока я никак не добьемся окончания перечня. Остальной перечень станет попросту.
Факторизация натурального числа называется его разложением в произведение простых факторов. Существование и единственность (с точностью до порядка факторов) такого разложения вытекает из основной теоремы арифметики.
Эта задача имеет большую вычислительную сложность. Один из самых популярных методов криптографии с открытым ключом, RSA, основан на сложности проблемы факторизации длинных целых чисел.
В данной работе были рассмотрены следующие методы факторизации натуральных чисел:
- экспоненциальные алгоритмы
- список возможных разделителей
- Метод факторизации фермы
Algorithm-алгоритм Полларда
- метод квадратичных форм Шенкса
- метод Лемана
Субэкспоненциальные алгоритмы
- алгоритм Диксона
- метод непрерывной дроби
- метод квадратичного сита
- метод эллиптической кривой
Ситовый номер поля
- метод числового поля специального сита
- Общее количество полей сита
- сложность факторизации
В зависимости от сложности алгоритмы факторизации можно разделить на две группы. Первая группа - это экспоненциальные алгоритмы, сложность которых экспоненциально зависит от длины входных параметров (то есть от длины самого числа в двоичном представлении). Чтобы указать их сложность, O-обозначение принимается. Это обозначение позволяет рассматривать только наиболее значимые элементы в функции f (n), исключая вторичные.
Например, в функции f (n) = 2n ^ 2-5n 1, если n достаточно велико, компонент n ^ 2 будет значительно превосходить другие члены, и, следовательно, характерное поведение этой функции определяется этим составная часть. Оставшиеся компоненты можно отбросить и условно записать, что эта функция имеет оценку поведения (в смысле скорости роста ее значений) вида O (n ^ 2).
Фраза «алгоритм факторинга с вычислительной сложностью O (N ^ (1⁄2))» означает, что при увеличении параметра N, характеризующего объем входной информации алгоритма, время алгоритма не может быть ограничено растущим значением медленнее, чем N ^ (1 ⁄2).
Вторая группа - это субэкспоненциальные алгоритмы, это алгоритмы, которые работают дольше, чем в полиномиальное время («суперполином»), но меньше, чем в экспоненциальном времени («субэкспоненциальный»). Для обозначения их сложности используется L-обозначение:
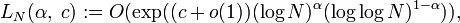
где N — число, подлежащее факторизации, 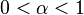 и c — некоторые константы.
и c — некоторые константы.
- Экспоненциальные алгоритмы
- Перебор возможных делителей — наиболее тривиальный алгоритм факторизации с вычислительной сложностью .
- ρ-алгоритм Полларда имеет сложность
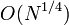 ;
; - метод квадратичных форм Шенкса имеет сложность
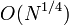 ;
; - метод Лемана имеет сложность
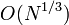
- Субэкспоненциальные алгоритмы
- алгоритм Диксона имеет сложность
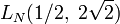 ;
; - метод непрерывных дробей имеет сложность
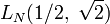 ;
; - метод квадратичного решета имеет сложность
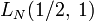 ;
; - метод эллиптических кривых имеет сложность
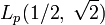 , где p — наименьшее простое, которое делит N.
, где p — наименьшее простое, которое делит N.
Поле номера сита
В настоящее время наиболее эффективными алгоритмами факторизации являются ситовые вариации числового поля:
- специальный метод просеивания числовых полей со сложностью (метод применим только для факторизации чисел специального типа);
- Общее число сит с полем сложности (метод применим ко всем числам).
Все без исключения информационные методы достаточно сложны, в соответствии с этим фактором они вызывают значительные расчетные ресурсы с целью длинных чисел. Однако теоретическое доказательство необходимой проблемы подобных вычислений или, другими словами, существования верхних границ буквы, а также никогда не было доказано, согласно этому фактору, наличия метода факторизации с полиномом. сложность в классическом ЭВМ с целью факторизации - единственные числа
Описание наиболее известных методов факторизации натуральных чисел.зац
ия натуральный число алгоритм
1.2 Перебор делителей
Разделительный перевод (экспериментальное разделение) - это заданный метод для уменьшения или контроля простоты величины посредством абсолютного перечисления абсолютно всех возможных делителей.
Описание алгоритма
Обычно перевод разделителей состоит в перечислении абсолютно всех полных (а также в версии: normal) значений от 2 до квадратного корня из факторизованного числа n и вычислении остатка с использованием d, члена в любой из этих величин. Если превышение деления на определенную величину m равно нулю, то m считается делителем числа n. В этом случае либо n объявляется трудным, и метод завершается (если рассматривается легкость n), либо n уменьшается на m, и процесс повторяется (если n факторизовано). Если квадратный позвоночник достигается с помощью n, и невозможно уменьшить n до 1-го числа с минимальными числами, n должно быть легко прочитано.
Практическое использование
В реальных задачах этот метод используется крайне редко из-за его огромной асимптотической сложности (в O-записи), но его использование целесообразно, если тестируемые величины относительно малы, поскольку этот метод довольно прост в реализации.
1.3 Метод факторизации Ферма
Метод факторизации Ферма - это алгоритм факторизации (факторинга) нечетного целого числа, предложенный Пьером Фармом (1601-1665) в 1643 году.
Этот метод основан на поиске таких целых чисел 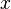 и
и 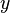 , которые удовлетворяют соотношению
, которые удовлетворяют соотношению 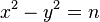 , что приводит к разложению
, что приводит к разложению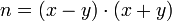 .
.
Обоснование
Метод Ферма основан на теореме о представлении числа в виде разности двух квадратов:
Если n>1 нечетно, то существует взаимно однозначное соответствие между разложениями на множители 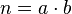 и представлениями в виде разности квадратов
и представлениями в виде разности квадратов 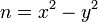 с
с 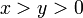 , задаваемое формулами
, задаваемое формулами 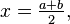
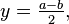
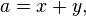
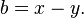
Доказательство
Если задана факторизация 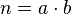 , то имеет место соотношение:
, то имеет место соотношение: 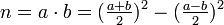 . Таким образом, получается представление в виде разности двух квадратов.
. Таким образом, получается представление в виде разности двух квадратов.
Обратно, если дано, что 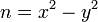 , то правую часть можно разложить на множители:
, то правую часть можно разложить на множители: 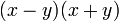 .
.
Описание алгоритма
Для разложения на множители нечётного числа 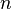 ищется пара чисел
ищется пара чисел 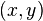 таких, что
таких, что 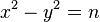 , или
, или 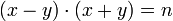 . При этом числа
. При этом числа 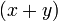 и
и 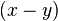 являются множителями
являются множителями 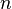 , возможно, тривиальными (то есть одно из них равно 1, а другое —
, возможно, тривиальными (то есть одно из них равно 1, а другое — 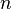 .)
.)
Равенство 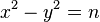 равносильно
равносильно 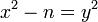 , то есть тому, что
, то есть тому, что 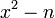 является квадратом.
является квадратом.
Начинается поиск такого квадрата с 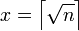 — наименьшего числа, при котором разность
— наименьшего числа, при котором разность 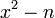 неотрицательна. Для каждого значения k€N начиная с k=1, вычисляют
неотрицательна. Для каждого значения k€N начиная с k=1, вычисляют 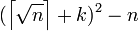 и проверьте, является ли это число точным квадратом. Если это не так, то k увеличивается на единицу и переходит к следующей итерации.
и проверьте, является ли это число точным квадратом. Если это не так, то k увеличивается на единицу и переходит к следующей итерации.
Если 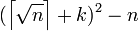 является точным квадратом, т.е.
является точным квадратом, т.е. 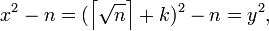 то получено разложение:
то получено разложение:
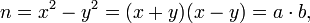 в котором
в котором 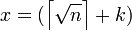
Если оно является тривиальным и единственным, то n — простое.
На практике значение выражения на 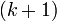 -ом шаге вычисляется с учетом значения на k-ом шаге:
-ом шаге вычисляется с учетом значения на k-ом шаге:
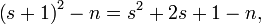 где
где 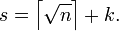
Таким образом, как и метод пробного деления, алгоритм Ферма имеет экспоненциальную оценку и не эффективен для разложения длинных чисел. Вы можете улучшить метод Ферма, сначала выполнив предварительное деление числа n на числа от 2 до некоторой константы B, тем самым исключив небольшие делители n на B включительно, а затем ищите Ферма.
1.4 Метод Крайчика-Ферма
Обобщение метода Ферма было предложено Морисом Крайчиком (1882-1957). Он предложил рассматривать вместо пар чисел 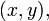 которые удовлетворяют соотношению
которые удовлетворяют соотношению 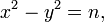 искать пары чисел, удовлетворяющих более общему уравнению
искать пары чисел, удовлетворяющих более общему уравнению 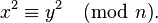 Крайчик заметил, что многие из чисел, получаемых по формуле
Крайчик заметил, что многие из чисел, получаемых по формуле 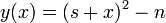 раскладываются на простые множители, т.е. числа
раскладываются на простые множители, т.е. числа 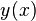 являются гладкими.
являются гладкими.
Последовательность действий по Крайчику
1. Найти множество пар 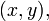 которые удовлетворяют соотношению
которые удовлетворяют соотношению 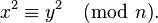
2. Определить полное или частное разложение чисел x и y на множители для каждой пары (x,y).
3. Выбрать пары ( x,y ), произведение которых удовлетворит соотношению 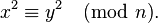
4. Разложить число n на множители.
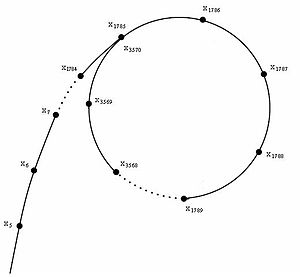
1.5 Ρ-алгоритм Полларда
Числовая последовательность зацикливается, начиная с некоторого n. Числовая последовательность зацикливается, начиная с некоторого n. Цикл можно представить в виде греческой буквы ρ.
Ρ-алгоритм Джона Полларда, предложенный им в 1975 году, используется для факторизации целых чисел. Он основан на алгоритме Флойда для определения длины цикла в последовательности и некоторых следствий из парадокса дней рождения. Алгоритм наиболее эффективен при расчете составных чисел с достаточно малыми множителями в разложении. Сложность алгоритма оценивается, как 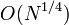 .
.
Во всех ρ-методах Полларда строится числовая последовательность, элементы которой образуют цикл, начиная с определенного числа n, что можно проиллюстрировать расположением чисел в виде греческой буквы ρ. Это было название семейства методов.
Описание алгоритма
Оригинальная версия
Рассмотрим последовательность целых чисел 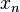 , такую что
, такую что 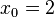 и
и 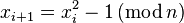 , где
, где 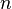 - число, которое нужно факторизовать. Оригинальный алгоритм выглядит следующим образом.
- число, которое нужно факторизовать. Оригинальный алгоритм выглядит следующим образом.
1. Будем вычислять тройки чисел
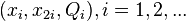 , где
, где 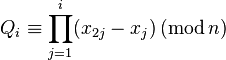 .
.
Причем каждая такая тройка получается из предыдущей.
2. Каждый раз, когда число 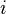 кратно числу
кратно числу 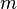 (скажем,
(скажем, 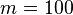 ), будем вычислять наибольший общий делитель
), будем вычислять наибольший общий делитель 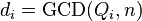 любым известным методом.
любым известным методом.
3. Если 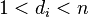 , то найдено частичное разложения числа
, то найдено частичное разложения числа 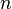 , причем
, причем 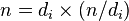 .
.
Найденный делитель 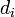 может быть составным, поэтому его также необходимо факторизовать. Если число
может быть составным, поэтому его также необходимо факторизовать. Если число 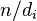 составное, то продолжаем алгоритм с модулем
составное, то продолжаем алгоритм с модулем 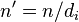 .
.
4. Вычисления повторяются S раз. Например, можно прекратить алгоритм при 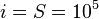 . Если при этом число не было до конца факторизовано, можно выбрать, например, другое начальное число
. Если при этом число не было до конца факторизовано, можно выбрать, например, другое начальное число 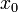 .
.
Современная версия
- Пусть n будет составным положительным целым числом, в которое вы хотите вложить. Алгоритм выглядит следующим образом:
- Выбираем небольшое число
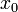 и строим последовательность
и строим последовательность 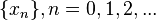 , определяя каждое следующее как
, определяя каждое следующее как 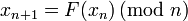 .
. - Одновременно на каждом i-ом шаге вычисляем
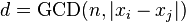 для каких-либо i, j таких, что j<i, например, i=2j.
для каких-либо i, j таких, что j<i, например, i=2j. - Если обнаружили, что d>1, , то вычисление заканчивается, и найденное на предыдущем шаге число d является делителем n. Если n/d не является простым числом, то процедуру поиска делителей можно продолжить, взяв в качестве n число n`=n/d.
Как на практике выбирать функцию F(x)? Функция должна быть не слишком сложной для вычисления, но в то же время не должна быть линейным многочленом, а также не должна порождать взаимно однозначное отображение. Обычно в качестве F(x) берут функцию 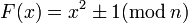 или
или 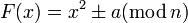 . Однако не следует использовать функции
. Однако не следует использовать функции 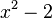 и
и 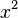 .
.
Если известно, что для делителя p числа n справедливо p=1(mod k) при некотором k>2 , то имеет смысл использовать 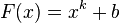 .
.
Существенным недостатком алгоритма в такой реализации является необходимость хранить большое число предыдущих значений 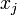 .
.
Улучшения алгоритма
Изначальная версия алгоритма обладает рядом недостатков. В настоящий момент существует несколько подходов к улучшению оригинального метода.
Пусть 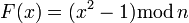 . Заметим, что если
. Заметим, что если 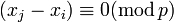 , то
, то 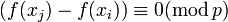 , поэтому, если пара
, поэтому, если пара 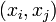 дает нам решение, то решение даст любая пара
дает нам решение, то решение даст любая пара 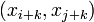 .
.
Поэтому, нет необходимости проверять все пары 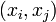 , а можно ограничиться парами вида
, а можно ограничиться парами вида 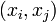 , где
, где 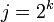 , и k пробегает набор последовательны значений 1, 2, 3, ..., а
, и k пробегает набор последовательны значений 1, 2, 3, ..., а 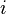 принимает значения из интервала
принимает значения из интервала ![[2^{k}+1; 2^{k+1}]](/evkovaupload/job/181728/93.png) . Например, k = 3,
. Например, k = 3, 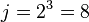 , а
, а ![i\in [9;16]](/evkovaupload/job/181728/95.png) .
.
Эта идея была предложена Ричардом Брентом в 1980 году и позволяет уменьшить количество выполняемых операций приблизительно на 25%.
Еще одна вариация P-метода Полларда была разработана Флойдом. Согласно Флойду, значение 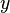 обновляется на каждом шаге по формуле
обновляется на каждом шаге по формуле 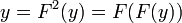 , поэтому на шаге i будут получены значения
, поэтому на шаге i будут получены значения 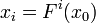 ,
, 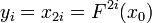 , и НОД на этом шаге вычисляется для
, и НОД на этом шаге вычисляется для 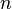 и
и 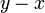 .
.
1.6 Метод квадратичных форм Шенкса
Это метод факторизации целых чисел, основанный на использовании квадратичных форм, разработанный Дэниелом Шенксом в 1975 году в качестве развития метода факторизации Ферма.
Для 32-разрядных компьютеров алгоритмы, основанные на этом методе, являются бесспорными лидерами алгоритмов факторизации для чисел между ними и, вероятно, останутся. Этот алгоритм может разбить почти любое составное 18-значное число менее чем за миллисекунду. Алгоритм чрезвычайно прост, красив и эффективен. Кроме того, методы, основанные на этом алгоритме, используются в качестве вспомогательных при разложении делителей больших чисел, таких как числа Ферма.
Вспомогательные определения
Чтобы понять, как реализован этот алгоритм, необходимо найти минимальную информацию о математических объектах, используемых в этом методе, а именно о квадратичных формах. Бинарная квадратичная форма является полиномом от двух переменных x и y:
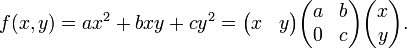
В методе Шенкса используются только неопределенные формы. Под 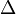 будем понимать дискриминант квадратичной формы. Будем говорить, что квадратичная форма
будем понимать дискриминант квадратичной формы. Будем говорить, что квадратичная форма 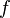 представляет целое число
представляет целое число 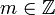 , если существуют такие целые числа
, если существуют такие целые числа 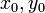 , что выполнено равенство:
, что выполнено равенство: 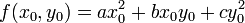 . В случае если выполнено равенство
. В случае если выполнено равенство 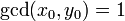 , то представление называется примитивным.
, то представление называется примитивным.
Для любой неопределенной квадратичной формы 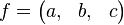 можно определить оператор редукции как:
можно определить оператор редукции как:
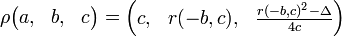 ,
,
Где r(-b,c) - определено, как целое число  , однозначно определяемое условиями:
, однозначно определяемое условиями:
r+b=0 mod (2c)
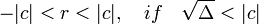
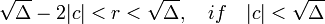
Результат применения оператора 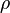 к форме
к форме 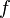
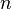 раз записывается в виде
раз записывается в виде 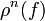 . Также определен оператор
. Также определен оператор 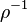 как:
как:
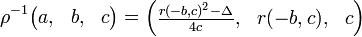 ,
,
где r(-b,c) определен так же, как и в прошлом случае. Заметим, что в результате применения операторов 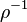 и
и 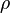 к квадратичной форме
к квадратичной форме 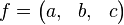 с дискриминантом
с дискриминантом 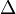 , полученные квадратичные формы так же будут иметь дискриминант
, полученные квадратичные формы так же будут иметь дискриминант 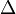 .
.
Метод получения редуцированной формы, эквивалентной данной, был найден еще Карлом Гауссом и состоит в последовательном применении оператора редукции g=p(f) , пока f не станет редуцированной.
Теорема.
Каждая форма f эквивалентна некоторой редуцированной форме, и любая редуцированная форма для f равна 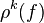 для некоторого положительного k. Если f - редуцирована, то
для некоторого положительного k. Если f - редуцирована, то 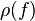 также редуцирована.
также редуцирована.
Также для ясности понимания всех операций с квадратичными формами нам нужны понятия квадратной, смежной и неоднозначной квадратичной формы.
Варианты
Идея метода Шенкса состоит в сопоставлении числу 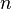 , которое надо разложить квадратичной бинарной формы
, которое надо разложить квадратичной бинарной формы 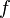 с дискриминантом D = 4n, с которой потом выполняется серия эквивалентных преобразований и переход от формы
с дискриминантом D = 4n, с которой потом выполняется серия эквивалентных преобразований и переход от формы 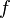 к неоднозначной форме
к неоднозначной форме 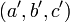 . Тогда,
. Тогда, 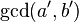 будет являться делителем n.
будет являться делителем n.
Первая версия работает с положительно определенными двоичными квадратичными формами заданного отрицательного дискриминанта, а в группе форм классов находит форму Ambigue, которая дает разложение дискриминанта на факторы.
Сложность первого варианта 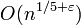 зависит от истинности расширенной гипотезы Римана.
зависит от истинности расширенной гипотезы Римана.
Второй вариант - SQUFOF, он использует группу классов бинарных квадратичных форм с положительным дискриминантом. Он также находит форму ambyg и разбивает дискриминант на факторы.
Сложность SQUFOF составляет 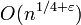 арифметических операций; при этом алгоритм работает с целыми числами, не превосходящими
арифметических операций; при этом алгоритм работает с целыми числами, не превосходящими 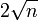 . Среди алгоритмов факторизации с экспоненциальной сложностью SQUFOF считается одним из самых эффективных.
. Среди алгоритмов факторизации с экспоненциальной сложностью SQUFOF считается одним из самых эффективных.
Описание алгоритма
Более подробно алгоритм может быть записан в следующем виде:
Вход: Нечетное составное число n, которое требуется факторизовать. Если n mod 4=1 заменим n на 2n. Теперь n mod 4=2;3 . Последнее свойство нужно, чтобы определитель квадратичной формы был фундаментальным, что обеспечивает сходимость метода.
Выход: Нетривиальный делитель n.
1. Определим исходную квадратичную форму 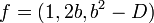 , с дискриминантом D=4n , где
, с дискриминантом D=4n , где 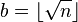 .
.
2. Выполним цикл редуцирований 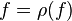 , пока форма
, пока форма 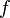 не станет квадратной.
не станет квадратной.
3. Вычислим квадратный корень из 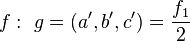 .
.
4. Выполним цикл редуцирований 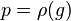 , пока значение второго коэффициента не стабилизируется
, пока значение второго коэффициента не стабилизируется 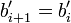 . Число итераций
. Число итераций 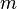 этого цикла должно быть примерно равно половине от числа итераций первого цикла. Последнее значение
этого цикла должно быть примерно равно половине от числа итераций первого цикла. Последнее значение 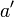 даст делитель числа
даст делитель числа 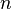 (возможно тривиальный).
(возможно тривиальный).
Алгоритм Лемана (или алгоритм Шермана Лемана) детерминировано раскладывает данное натуральное число 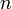 на множители за
на множители за 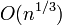 арифметических операций. Алгоритм был впервые предложен американским математиком Шерманом Леманом в 1974 году. Этот алгоритм был первым детерминированным алгоритмом факторизации для целых чисел, имеющих более низкую оценку, чем
арифметических операций. Алгоритм был впервые предложен американским математиком Шерманом Леманом в 1974 году. Этот алгоритм был первым детерминированным алгоритмом факторизации для целых чисел, имеющих более низкую оценку, чем 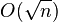 . В настоящий момент носит чисто исторический интерес и, как правило, не используется на практике.
. В настоящий момент носит чисто исторический интерес и, как правило, не используется на практике.
Алгоритм
Пусть n нечетно и n>8
Шаг 1. Для 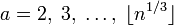 проверить условие a|n . Если на этом шаге мы не разложили
проверить условие a|n . Если на этом шаге мы не разложили 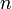 на множители, то переходим к шагу 2.
на множители, то переходим к шагу 2.
Шаг 2. Если на шаге 1 делитель не найден и n — составное, то n = pq, где p, q — простые числа, и 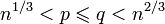 . Тогда для всех
. Тогда для всех 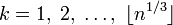 и всех
и всех  проверить, является ли число
проверить, является ли число 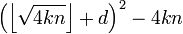 квадратом натурального числа. Если является, то для
квадратом натурального числа. Если является, то для 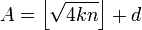 и
и 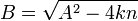 выполнено сравнение:
выполнено сравнение:
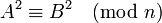 или (A-B)(A+B)=0 (mod n).
или (A-B)(A+B)=0 (mod n).
В этом случае для d*=( A-B, n ) проверяется неравенство 1< d*<n . Если оно выполнено, то n=d* . (n/d*) — разложение n на два множителя.
Если алгоритм не нашел разложение n на два множителя, то n — простое число.
Данный алгоритм в начале проверяет имеет ли 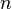 простые делители не превосходящие
простые делители не превосходящие 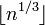 , а после устраивает перебор значений k и d для проверки выполнимости указанной ниже Теоремы. В случае, если искомые значения x и
, а после устраивает перебор значений k и d для проверки выполнимости указанной ниже Теоремы. В случае, если искомые значения x и 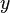 , не найдены, то мы получаем что число
, не найдены, то мы получаем что число 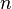 простое. Таким образом мы можем рассматривать данный алгоритм как тест числа
простое. Таким образом мы можем рассматривать данный алгоритм как тест числа 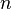 на простоту.
на простоту.
Трудоемкость
На первом шаге нам требуется произвести 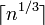 операций деления для поиска маленьких делителей числа
операций деления для поиска маленьких делителей числа 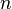 .
.
Трудоемкость второго шага оценивается в операциях тестирования числа 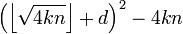 , на то, является ли оно полным квадратом. В начале заметим, что для всех
, на то, является ли оно полным квадратом. В начале заметим, что для всех 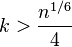 выполняется только две проверки: D=0 и D=1. Тогда, трудоемкость второго этапа оценивается сверху величиной
выполняется только две проверки: D=0 и D=1. Тогда, трудоемкость второго этапа оценивается сверху величиной
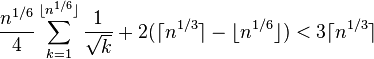 .
.
Таким образом трудоемкость всего есть величина 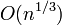 .
.
Глава 2. Примеры реализации алгоритмов натуральных чисел и оценка их эффективности
2.1 Примеры разложения натуральных чисел
2.1.1 Метод факторизации Ферма
Пример с малым числом итераций
Возьмем число n=10873. Вычислим 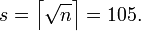 Для
Для 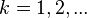 будем вычислять значения функции s+k . Для дальнейшей простоты построим таблицу, которая будет содержать значения y и
будем вычислять значения функции s+k . Для дальнейшей простоты построим таблицу, которая будет содержать значения y и 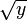 на каждом шаге итерации. Получим:
на каждом шаге итерации. Получим:
|
k |
y |
|
|
1 |
363 |
19,052 |
|
2 |
576 |
24 |
Как видно из таблицы, уже на втором шаге итерации было получено целое значение 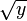 .
.
Таким образом имеет место следующее выражение: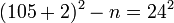 . Отсюда следует, что
. Отсюда следует, что 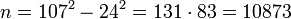
Пример с большим числом итераций
Пусть 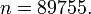 Тогда
Тогда 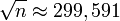 или
или 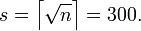
|
|
|
|
|
77 |
52374 |
228,854 |
|
78 |
53129 |
230,497 |
|
79 |
53886 |
232,134 |
|
80 |
54645 |
233,763 |
|
81 |
55406 |
235,385 |
|
82 |
56169 |
237 |
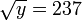
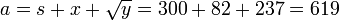
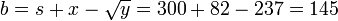
Данное разложение является не конечным, т.к., очевидно, что число 145 не является простым. Применив метод Ферма, получим145=29x5. В итоге, конечное разложение исходного числа n на произведение простых множителей 89755=5x29x619.
2.1.2 Метод Крайчика-Ферма
С помощью метода Крайчика-Ферма разложим число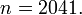 Число
Число 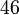 является первым, чей квадрат больше числа
является первым, чей квадрат больше числа 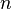 :
: 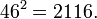
Вычислим значение функции 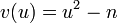 для всех
для всех 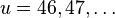 , получим
, получим 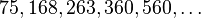
По методу Ферма, нужно было бы продолжать вычисления пока не был бы найден квадрат какого-либо числа. По методу Крайчика-Ферма далее нужно последовательно искать такие 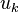 , для которых
, для которых 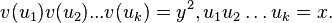 Тогда
Тогда
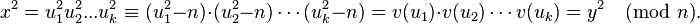
Из алгоритма Крайчика-Ферма следует, что все полученные числа 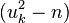 можно легко факторизовать.
можно легко факторизовать.
Действительно: 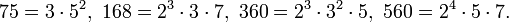
Очевидно, что произведение полученный четырех чисел будет квадратом: 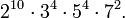 Тогда теперь можно вычислить
Тогда теперь можно вычислить 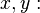
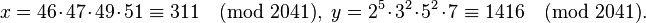
Далее с помощью алгоритма Евклида находим 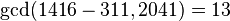 .
.
Таким образом, 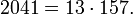
2.1.3 Ρ-алгоритм Полларда
Пусть n=8051, 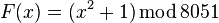 ,
, 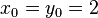 ,
, 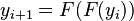 .
.
|
i |
xi |
yi |
НОД(|xi − yi|, 8051) |
|
1 |
5 |
26 |
1 |
|
2 |
26 |
7474 |
1 |
|
3 |
677 |
871 |
97 |
Таким образом, 97 - нетривиальный делитель числа 8051. Используя другие варианты полинома F (x) , можно также получить делитель 83.
2.1.4 Метод квадратичных форм Шенкса
Применим данный метод для факторизации числа N=22117019
|
Цикл №1 |
|||||||
|
Fi |
|||||||
|
i |
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
Цикл №2 |
|||||||
|
Gi |
|||||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
Теперь можно увидеть во втором цикле, что 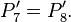 Следовательно число
Следовательно число 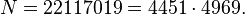
2.1.5 Алгоритм Лемана
Разберем пример с n=1387 , тогда для 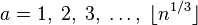 , где
, где 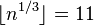 , проверяем является ли число
, проверяем является ли число 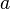 делителем числа
делителем числа 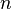 . Не трудно убедится, что таких нет, тогда переходим к следующему пункту.
. Не трудно убедится, что таких нет, тогда переходим к следующему пункту.
Для всех k=1,2,3,…, 11 и всех d = 0,1,…,4 проверяем, является ли число 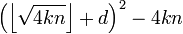 квадратом натурального числа. В нашем случае существуют такие k = 3 и d = 1 , что выражение
квадратом натурального числа. В нашем случае существуют такие k = 3 и d = 1 , что выражение 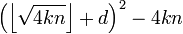 является полным квадратом и равно
является полным квадратом и равно 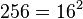 . Следовательно, A = 130 и
. Следовательно, A = 130 и
B = 16. Тогда d* = ( A-B; n ) =19 , удовлетворяет неравенству 1<d*<n и является делителем числа n. В итоге, мы разложили число 1387 на два множителя: 73 и 19.
2.1.6 Алгоритм Диксона
Факторизуем число n = 89755
L (18638) = 194,174…
M = 13,934…
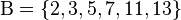
Все найденные числа b с соответствующими векторами 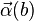 записываем в таблицу.
записываем в таблицу.
|
b |
a |
|
|
|
|
|
|
|
337 |
23814 |
1 |
5 |
0 |
2 |
0 |
0 |
|
430 |
5390 |
1 |
0 |
1 |
2 |
1 |
0 |
|
519 |
96 |
5 |
1 |
0 |
0 |
0 |
0 |
|
600 |
980 |
2 |
0 |
1 |
2 |
0 |
0 |
|
670 |
125 |
0 |
0 |
3 |
0 |
0 |
0 |
|
817 |
39204 |
2 |
4 |
0 |
0 |
2 |
0 |
|
860 |
21560 |
3 |
0 |
1 |
2 |
1 |
0 |
Решая линейную систему уравнений, получаем, что 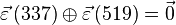 . Тогда
. Тогда
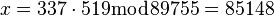
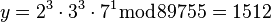
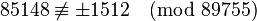
Следовательно,
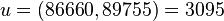
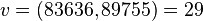 .
.
Получилось разложение 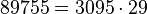
2.1.7 Факторизация с помощью эллиптических кривых
Допустим, нам нужно факторизовать число n = 455839.
Возьмем эллиптическую кривую и точку, лежащую на этой кривой
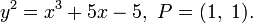
Попробуем вычислить 10!P:
- Для начала вычислим координаты точки
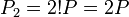 . Тангенс угла наклона касательной в точке P равен:
. Тангенс угла наклона касательной в точке P равен: 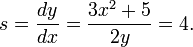
- Находим координаты точки
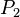 :
:
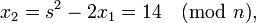
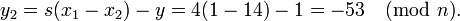 .
.
- Проверяем, что точка 2P действительно лежит на кривой:
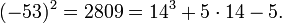
2. Теперь вычислим 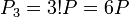 .
.
- Тангенс угла наклона касательной в точке 2P составляет
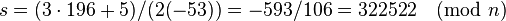 .
.
Для вычисления 593 / 106 по модулю n можно воспользоваться расширенным алгоритмом Евклида: 455839 = 4300·106 + 39, далее 106 = 2·39 + 28, далее 39 = 28 + 11, далее 28 = 2·11 + 6, далее 11 = 6 + 5, далее 6 = 5 + 1. Откуда получаем, что НОД(455839, 106) = 1, и в обратную сторону: 1 = 6 - 5 = 2·6 - 11 = 2·28 - 5·11 = 7·28 - 5·39 = 7·106 - 19·39 = 81707·106 - 19·455839. Откуда 1/106 = 81707 (mod 455839), таким образом, -593 / 106 = 322522 (mod 455839).
- Учитывая вычисленное s, мы можем вычислить координаты точки 2(2P), так же, как это было сделано выше: 4P = (259851, 116255). Проверяем, что точка действительно лежит на нашей эллиптической кривой.
- Суммируя 4P и 2P, находим
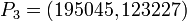 .
. - Аналогичным образом можно вычислить
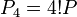 ,
, 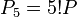 , и так далее. Когда дойдем до 8!P заметим, что требуется вычисление обратного элемента к 599 (mod 455839). Так как 455839 делится на 599, то мы нашли искомое разложение: 455839 = 599·761.
, и так далее. Когда дойдем до 8!P заметим, что требуется вычисление обратного элемента к 599 (mod 455839). Так как 455839 делится на 599, то мы нашли искомое разложение: 455839 = 599·761.
2.2 Факторизация в криптографии
Разложение (разложение) натуральных чисел на множители является сложной вычислительной задачей. Сложность решения этой проблемы лежит в основе одного из самых известных методов криптографии - метода RSA. Существует большое количество алгоритмов факторизации, среди которых наиболее быстрыми сегодня являются метод квадратичного сита и метод численного сита.
- RSA (сокращение от имен Rivest, Shamir и Adleman) - это криптографический алгоритм с открытым ключом, основанный на вычислительной сложности задачи факторизации больших целых чисел.
- Криптографические системы с открытым ключом используют так называемые односторонние функции, которые имеют следующее свойство:
- Если известно
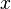 , то
, то 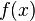 вычислить относительно просто
вычислить относительно просто - Если известно
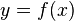 , то для вычисления
, то для вычисления 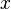 нет простого (эффективного) пути.
нет простого (эффективного) пути.
Односторонность понимается не как теоретическая однонаправленность, а как практическая невозможность вычисления обратного значения с использованием современных вычислительных средств в течение прогнозируемого интервала времени.
Криптографическая система с открытым ключом RSA основана на сложности проблемы факторизации произведения двух больших простых чисел. Для шифрования используется операция возведения в степень по модулю большого числа. Чтобы расшифровать за разумное время (обратная операция), необходимо уметь вычислять функцию Эйлера для данного большого числа, для которого необходимо знать разложение числа в простые множители.
В криптографической системе с открытым ключом каждый участник имеет как открытый ключ, так и закрытый ключ. В криптографической системе RSA каждый ключ состоит из пары целых чисел. Каждый участник самостоятельно создает свой открытый и закрытый ключи. Каждый из них хранит секретный ключ в секрете, а открытые ключи могут быть переданы кому угодно или даже опубликованы. Открытый и закрытый ключи каждого участника в обмене сообщениями криптосистемы RSA образуют «согласованную пару» в том смысле, что они являются взаимными, то есть:
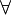 сообщения
сообщения 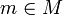 , где
, где 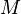 — множество допустимых сообщений
— множество допустимых сообщений
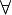 допустимых открытого и закрытого ключей
допустимых открытого и закрытого ключей 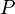 и
и 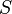
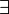 соответствующие функции шифрования
соответствующие функции шифрования 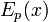 и расшифрования
и расшифрования 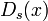 , такие что
, такие что
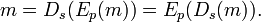
Алгоритм создания открытого и секретного ключей
RSA-ключи генерируются следующим образом:
- Выбираются два различных случайных простых числа
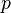 и
и 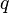 заданного размера.
заданного размера. - Вычисляется их произведение
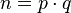 , которое называется модулем.
, которое называется модулем. - Вычисляется значение функции Эйлера от числа
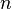 :
:
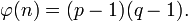
- Выбирается целое число

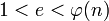 , взаимно простое со значением функции
, взаимно простое со значением функции 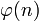 . Обычно в качестве
. Обычно в качестве  берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
берут простые числа, содержащие небольшое количество единичных бит в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
- Число
 называется открытой экспонентой.
называется открытой экспонентой. - Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в
 .
. - Слишком малые значения
 , например 3, потенциально могут ослабить безопасность схемы RSA.
, например 3, потенциально могут ослабить безопасность схемы RSA.
- Число
- Вычисляется число
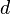 , мультипликативно обратное к числу
, мультипликативно обратное к числу  по модулю
по модулю 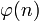 , то есть число, удовлетворяющее условию:
, то есть число, удовлетворяющее условию:
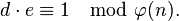
-
- Число d называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
- Пара
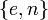 публикуется в качестве открытого ключа RSA.
публикуется в качестве открытого ключа RSA. - Пара
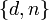 играет роль закрытого ключа RSA секрете.
играет роль закрытого ключа RSA секрете.
2.3 Примеры применения алгоритмов факторизации натуральных чисел в программной среде Maple
В программной среде maple реализован ряд алгоритмов факторизации, которые включают как отдельные алгоритмы, так и синтез нескольких алгоритмов для более продуктивной факторизации.
Ниже приведены списки методов, которые включены в различные версии Maple.
В Maple 6:
'squfof' - метод Квадратичных форм Шенкса;
'pollard' – алгоритм Полларда;
'lenstra' - метод эллиптических кривых Ленстры;
'easy' - без дальнейшей обработки.
В последних версиях Maple:
'mpqs' – множественный полиномиальный метод квадратичного решета;
'morrbril' – алгоритм Брилхарта-Моррисона;
'squfof' – метод квадратичных форм Шенкса;
'pollard' – алгоритм Полларда;
'lenstra' - метод эллиптических кривых Ленстры;
‘mpqsmixed' – ‘mpqs', ‘morrbril' и ‘pollard';
‘mixed' – 'morrbril' и 'pollard' (по умолчанию в версиях Maple 11 и более ранних)
‘easy' - без дальнейшей обработки;
‘Easy' – если данный вариант разложения будет выбран, результатом ifactor будет произведение чисел, которые легко было отделить, а также «_c.m._.n», которое обозначает m-значное составное число, которое не было разложено, где n – уникальный номер данного составного числа.
‘Pollard’ – метод Полларда, опционально требующий дополнительное целое k (ifactor(n,pollard,k)), которое повышает эффективность метода в том случае, если один из сомножителей имеет форму k*m+1.
- В процессе написания этой работы я использовал платформу Maple 6 для более детального рассмотрения различных алгоритмов факторизации натуральных чисел. Так как моей целью было проанализировать и сравнить некоторые алгоритмы, реализованные в среде Maple, и время их выполнения, я сделал следующее (см. Приложение, стр. 35)
n:=1225992214214988495889178222383575197953889910663283660941397211195293307578078718078619789346251171394591299026682300363349450174814676994019289743170166203329177516492641629553799863550875253574485611528087163760246308842411883285814684377331873414394475363668140223797216205606498904469268054423713940637910055764209685035
1. Проверить время выполнения алгоритмов для неструктурированного числа.
- сгенерировал два больших простых числа с использованием функций nextprime и prevprime;
- Умножил их и запустил процедуру ifactor для полученного числа без дополнительных параметров, с параметрами squifof, pollard и lenstra. Так как мне нужно время выполнения, я использовал функцию времени из ifactor;
- Получил значения для разных алгоритмов. Для алгоритма по умолчанию (алгоритм Моррисона-Брилхарта вместе с алгоритмом Полларда), получил значение 632,795 секунды.
- Для squifof это значение было «0», то есть малейшие доли секунды. Алгоритм Полларда пришлось остановить на 308ой тысяче секунд(3,56 суток), алгоритм Ленстры дал результат через 20311,795 секунды.
- Далее я применил алгоритмы для структурированного числа вида k*(2^t+1).
- Взял k равным простому числу 331, а t (степень двойки в выражении) равным 190. Нашёл значение выражения с этими данными;
- Применил ifactor и нашёл время выполнения ifactor от нашего числа. Время выполнения составило 47193,554 секунды;
- Далее я применил алгоритм squifof для числа той же структуры, но с большим показателем степени двойки, t = 9290. Данным алгоритмом число разложилось за 77.5 секунды;
- В третий раз я взял также структурированное число, но теперь это был факториал от данного числа t.
- Я положил t равным 1221 и получил очень крупное число в 2800 знаков;
- Воспользовавшись алгоритмом Ленстры, я получил время выполнения – всего 0,63 секунды.
Отсюда мы видим, что при изменении числовой структуры алгоритмы ведут себя по-разному. Используя тот же алгоритм, для разложения числа с 2800 символами требуется примерно в 32000 раз меньше времени, чем для разложения числа с 48 символами. Структура номера отличается. В первом случае в числе много маленьких делителей, а во втором случае их всего два, и оба являются большими простыми числами.
2.4 Оценка эффективности алгоритмов факторизации натуральных чисел
Получив результаты работы по разложению натуральных чисел различных структур, проведенной в Maple, мы на практике узнали, что ключевую роль во времени выполнения алгоритма, помимо размера числа, играет его структура.
На практике алгоритм Ленстры часто используется для идентификации (отбрасывания) небольших простых чисел. И мы увидели это, расширив 32000-значное число 1221! за 0,63 секунды. Как среди 1221! содержит все первые 1221 чисел, тогда не составит труда идентифицировать и отбросить все тривиальные делители.
Однако, если мы работаем с числом, которое содержит большие простые факторы, нам нужно увеличить число кривых, потому что с увеличением числа кривых шансы на нахождение простого делителя возрастают, но зависимость от ожидаемого числа на эллиптические кривые - число цифр в неизвестном делителе, экспоненциально. Метод Полларда очень быстро находит простые факторы малого и среднего размера, однако, сталкиваясь с большим простым фактором, он становится неэффективным.
Среди алгоритмов факторинга с экспоненциальной сложностью метод квадратичных форм Шенкса считается одним из наиболее эффективных. Этот алгоритм работает с целыми числами, не превышающими. Мы знаем, что для 32-битных компьютеров алгоритмы, основанные на этом методе, являются бесспорными лидерами алгоритмов факторизации для чисел между ранее и, вероятно, так и останутся. Этот алгоритм может разделить почти любое составное 18-значное число менее чем за миллисекунду.
Среди алгоритмов факторинга с экспоненциальной сложностью метод квадратичных форм Шенкса считается одним из наиболее эффективных. Этот алгоритм работает с целыми числами, не превышающими 2√n. Мы знаем, что для 32-битных компьютеров алгоритмы, основанные на этом методе, являются бесспорными лидерами алгоритмов факторизации для чисел между ранее и, вероятно, так и останутся. Этот алгоритм может разделить почти любое составное 18-значное число менее чем за миллисекунду. Алгоритм чрезвычайно прост, красив и эффективен. Кроме того, методы, основанные на этом алгоритме, используются в качестве вспомогательных при разложении делителей больших чисел.
Заключение
Факторизация натурального числа называется его разложением в произведение простых факторов. Эта задача имеет большую вычислительную сложность. Один из самых популярных методов криптографии с открытым ключом, метод RSA, основан на сложности задачи факторизации длинных целых чисел.
Вопрос о факторинге количеств возник не накануне, а тысячи лет назад. Можно только предположить, по какой причине в 1900 г. на Точном конгрессе Д. Гильберт вообще не внес его в свой список из 23 вопросов, а позже возлюбленная не оказалась в списке незавершенных точных вопросов С. Улама. Особый интерес и интерес математиков к этому вопросу стали проявляться только в последние десятилетия. Вероятно, катализатор для изобретения новейшего тренда - криптология с 2 ключами, появление шифров с не закрытым исходным кодом.
Можно предположить, что реальный интерес к проблеме факторизации величин продиктован определенной неопределенностью относительно абстрактного объяснения идентификации очень известного сегодня двухключевого кода (секретного источника) RSA, который, в убеждении, может быть взломан без понимания секретного ключа.
Самый простой и более сложный экспоненциальный метод, реализованный ручным методом. муравей. автоматический, считается выбор делителей. Кто-то ищет возможные делители количества от наибольшего количества до его квадрата. Кто-то абсолютно подходит для дезинтеграции в небольших количествах, поскольку его очень просто реализовать, но кто-то почти не работает с целью дезинтеграции в больших количествах.
Практическое использование различных методов для распада величин показало, что срок выполнения метода напрямую зависит от его типа и сложности расчетов.
В этой работе я проанализировал некоторые методы факторинга натуральных величин, а также провел их относительное представление в соответствии со строительными группами. Используя реальные образцы, я убедился в производительности и необходимости использовать 1 метод, который отличается, опять же, принимая во внимание текстуру заданного количества.
Аналогичным образом можно сделать следующие выводы: для факторизации натуральных величин существует достаточно большое количество методов, но эта цель далека от очевидного и довольно трудоемкого периода, демонстрирует анализ сложность факторинга алгоритмов. Некоторые методы имеют все шансы найти решение этой проблемы на протяжении веков. Чтобы сократить период надежды, следует выбрать метод факторинга, подходящий для текстуры величин.
Но решение этой задачи вообще не требуется в этой области, поскольку многочисленные крупные раскрытия и последние достижения в этой области появляются снова и снова. Эти достижения сочетаются не только с формированием расчетной силы.
Список литературы
- A. Heck. Introduction to Maple. Springer-Verlag, third edition, 2003.
- Бухштаб А.А. Теория чисел. — М.: Учпедгиз, 1960.
- Василенко О. Н. В19 Теоретико-числовые алгоритмы в криптографии. - М.:МЦНМО, 2003.—328 с. ISBN 5-94057-103-4.
- Ишмухаметов Ш.Т. Методы факторизации натуральных чисел: учебное пособие. Казань: Казан. Ун-т, 2011. 190 с.
- Д. Кнут Раздел 4.5.4. Разложение на простые множители // Искусство программирования = The Art of Computer Programming. — 3-е изд. — М.: Вильямс, 2007. — Т. 2. Получисленные алгоритмы. — С. 425—468. — 832 с.
- Макаренко А.В., Пыхтеев А.В., Ефимов С.С. Параллельная реализация и сравнительный анализ алгоритмов факторизации в системах с распределённой памятью.
- Манин Ю.И., Панчишкин А.А. Введение в современную теорию чисел. − М.: МЦНМО, 2009.
- Ю. И. Манин, А. А. Панчишкин. I.2.3. Разложение больших чисел на множители // Введение в теорию чисел.— М.: ВИНИТИ, 1990. — Т. 49. — С. 72—106. — 341 с.
- Молчанова Л.А. Введение в Maple. Учебно-методическое пособие. – Владивосток: Изд-во Дальневост. Ун-та, 2006. - 36 С.
- Ю. В. Нестеренко. Глава 4.7. Как раскладывают составные числа на множители // Введение в криптографию / Под ред. В. В. Ященко. — Питер, 2001. — 288 с.
- http://www.maplesoft.com – официальный сайт компании Maplesoft, производителя Maple.
- http://www.exponenta.ru – образовательный математический сайт.
- http://www.wikipedia.org/ - свободная энциклопедия.
> restart;
> p:=nextprime(476523189475631579423453); (23 знака)
q:=prevprime(957532186478621546879541); (23 знака)
p:= 476523189475631579423459
q:= 9575321864786215468879519
> n:=p*q;(48 знаков)
n:= 45628629152636796604667662309058697463550555236221
> time(ifactor(n));
632.795
> time(ifactor(n,squifof));
0.
> time(ifactor(n,pollard)); (остановлено на 308 тысяче секунд ожидания)
Warning, computation interrupted
> time(ifactor(n,lenstra));
20311.652
> restart;
> p: =nextprime(476523189475631579); (17 знаков)
q: =prevprime(957532186478621546879548756); (26 знака)
p: = 476523189475631647
q: =957532186478621546879548619
> n:=p*q;(45 знаков)

> time(ifactor(n));
294.891
> time(ifactor(n,squifof));
.016
> time(ifactor(n,lenstra));
3271.926
>
>
> restart;
> p: =nextprime(4765231894756315791);(19 знаков)
q: =prevprime(9575321869491284011);(19 знаков)
t:=nextprime(1112154682);(10 знаков)
> n:=p*q*t;(52 знака)




> time(ifactor(n));

> time(ifactor(n,squifof));

> time(ifactor(n,lenstra));

> restart;
k:=nextprime(320);t:=190;


> n:=k*(2^t)+1;(60 знаков)

> time(ifactor(n));

> k:=nextprime(320);t:=160;
n:=k*(2^t)+1; (52 знака)



> time(ifactor(n));

> k:=nextprime(320);t:=150;
n:=k*(2^t)+1;(48 знаков)



> time(ifactor(n));

> k:=nextprime(320);t:=9290;
n:=k*(2^t)+1;



Листинг программы
|
program kurs; uses crt; function pow (a,x: longint): longint; var t, i: longint; begin t: =a; for i: =1 to x-1 do t: =t*a; pow: =t; end; {pow} {----------------------------------------} procedure DelOstatok; var dd: array [1.200] of integer; R: integer; {размерность чисел} i: longint; {делитель} k: longint; {остаток} D,a,b: longint; {элементы заданного множества} SUM: longint; {кол-во эл-ов, удовл условию} S,T: byte; q: char; e,j,l,n: integer; maxa,minj,maxj: longint; begin repeat begin writeln ('введите ко-во чисел для нахождения НОК делителей'); readln (n); writeln ('введите ',n,' чисел: '); readln (dd [1]); maxa: =dd [1] ; for i: =2 to n do begin readln (dd [i]); if dd [i] >maxa then maxa: =dd [i] ; end; i: =1; while (dd [i] <>0) and (i<=n) do inc (i); if i<>n+1 then writeln ('НОК не сущ-ет') else begin e: =1; for i: =2 to maxa do begin maxj: =0; for l: =1 to n do begin j: =0; while (dd [l] mod i=0) do begin dd [l]: =dd [l] div i; inc (j); end; if (j>maxj) then maxj: =j; end; if (maxj<>0) then for l: =1 to maxj do e: =e*i; end; writeln ('НОК делителей=',e); end; end; i: =e; write ('введите остаток='); readln (k); if ( (i<=0) or (k<0)) then {проверка {вывод эл-ов на экран} end; writeln; end; writeln ('Повторить? (Y/N) '); q: =ReadKey; until q in ['N','n'] ; clrscr; end; {DelOstatok} {----------------------------------------} procedure Factor; var numb, powers: array [1. .100] of longint; c: longint; n: longint; n1,H: longint; i: longint; k,t: longint; q: char; begin repeat write ('Введите число='); readln (c); if c<=0 then {проверка на корр числа} begin writeln ('число должно быть>0'); readln; exit; end else {вывод мн-ва делителей} begin write ('мн-во делителей: D (num) ='); for H: = 1 to c do if c mod H=0 then write (H,' '); end; {конец вывода делителей} n: = 1; n1: = 0; while c <> 1 do begin i: = 2; while c mod i <> 0 do {проверка на делимостьс/без остатка} Inc (i); Inc (n1); if n1 = 1 then begin numb [n]: = i; powers [n]: = 1; end else if numb [n] = i then Inc (powers [n]) else begin Inc (n); {увеличение кол-ва простых множителей} numb [n]: = i; powers [n]: = 1; end; {while} c: = c div i; {деление числа на простой множитель} end; {while} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\} writeln; writeln ('кол-во простых множителей: ',n); write ('num = '); k: =1; t: =1; writeln ('НОД=',k); if k=1 then writeln ('числа взаимно простые'); end; begin i: =1; while (b [i] <>0) and (i<=n) do inc (i); if i<>n+1 then writeln ('НОК не сущ-ет') else begin d: =1; for i: =2 to maxa do begin maxj: =0; for l: =1 to n do begin j: =0; while (b [l] mod i=0) do begin b [l]: =b [l] div i; inc (j); end; if (j>maxj) then maxj: =j; end; if (maxj<>0) then for l: =1 to maxj do d: =d*i; end; writeln ('НОК=',d); end; end; end; writeln ('Повторить? (Y/N) '); q: =ReadKey; until q in ['N','n'] ; clrscr; end; {NodNok} {----------------------------------------} procedure SuperGorner; type vector= array [1. .11] of integer; rvector=array [1. .100] of real; var sum,suma: real; i,k,j,b,c,a,n: integer; vec: vector; vecb: rvector; veca: rvector; q: char; BEGIN Writeln ('Введите степень уравнения (max = 10) '); Readln (n); if n<=0 then writeln (‘степень не может быть<=0’) else begin Inc (n); writeln ('введите его коэффициенты: '); for i: = 1 to n do read (vec [i]); while vec [i] =0 do Begin i: =i-1; writeln ('ответ: 0'); End; k: =1; b: =vec [i] ; for j: =1 to abs (b) do begin if (b mod j) =0 then begin vecb [k]: =j; k: =k+1; procedure AntiExp; var s: array [1. .100] of integer; a,b, i,n,t: integer; q: char; begin repeat writeln ('введите кол-во эл-ов цепной дроби='); read (n); if n<=0 then writeln (‘кол-во эл-ов не может быть<=0’) else begin writeln ('введите значения этих эл-ов='); for i: =1 to n do read (s [i]); a: =1; b: =s [n] ; for i: = n downto 2 do begin t: =s [i-1] *b+a; a: =b; b: =t; end; writeln; writeln (b,'/',a); end; writeln ('Повторить? (Y/N) '); q: =ReadKey; until q in ['N','n'] ; clrscr; end; {AntiExp} {----------------------------------------} var k: integer; q: char; begin writeln ('Дискретная математика'); writeln ('Курсовая работа, группа 03-119, каф308'); writeln ('выполнил: Тузов И.И. '); writeln ('руководитель: Гридин А.Н. '); writeln; writeln ('Калькулятор с функциями, описанными ниже'); writeln; Writeln ('Нажмите Enter'); readln; clrscr; repeat writeln ('Какую выполнить операцию? '); writeln; writeln ('1-вычисление мн-ва N-значных чисел с заданным делителем и остатком '); writeln ('2-факторизация числа'); writeln ('3-нахождение НОД и НОК чисел'); writeln ('4-нахождение рационльных корней уравнения с целочисл коэфф'); writeln ('5-перевод рациональной дроби в цепную'); writeln ('6-перевод цепной дроби в рациональную'); read (k); |
делителя и остатка на отриц-сть} begin write ('делитель или остаток не могут быть<0 '); end else begin if i>k then {проверка на делитель>остатка} begin write ('введите размерность='); readln (R); if R<=0 then begin writeln ('некорректная размерность '); readln; end else begin if R=1 then begin a: =1; b: =9; end else begin a: =pow (10, (R-1)); {инициализация верх и нижн границ} b: =pow (10,R); b: =b-1; end; end; if b<i then {проверка на делимое>делителя} writeln ('делиоме не может быть < делителя ') else begin SUM: =0; {обнуление сумы кол-ва эл-ов} for D: = a to b do begin if (D mod i) =k then {проверка эл-ов на условие} begin SUM: =SUM+1; end; end; writeln; writeln ('кол-во эл-ов с делителем=', i: 3, ' и остатком=', k: 3, ' равно', SUM: 6); end; {b<i} end {if i>k} else write ('остаток не может быть > делителя '); end; {if otriz} {\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\} write ('вывести значения на экран? (1-да\0-нет) '); readln (S); if S=1 then if SUM=0 then writeln ('нет эл-ов, удовл. условию') else begin for D: = a to b do if (D mod i) =k then begin write (' ',D: 4); {вычисление кол-ва делителей и их мн-ва} for i: = 1 to n do begin write (numb [i], ' ^ ', powers [i]); k: =k* ( (pow (numb [i],powers [i] +1) - 1) div (numb [i] - 1)); t: =t* (powers [i] +1); {кол-во делителей} if i <> n then write (' * '); end; writeln; writeln ('кол-во множителей: tau (num) =',t); writeln ('сумма множителей: sigma (num) =',k); writeln ('Повторить? (Y/N) '); q: =ReadKey; until q in ['N','n'] ; clrscr; end; {Factor} {----------------------------------------} procedure NodNok; type TArray=array [1.200] of integer; var a,b: TArray; i,l,j,maxa,minj,maxj: longint; k,d: longint; n: integer; q: char; begin repeat clrscr; writeln ('введите ко-во чисел для нахождения НОД и НОК'); readln (n); writeln ('введите ',n,' чисел: '); if n<=0 then writeln (‘кол-во чисел не может быть<=0’) else begin readln (a [1]); b [1]: =a [1] ; maxa: =a [1] ; for i: =2 to n do begin readln (a [i]); b [i]: =a [i] ; if a [i] >maxa then maxa: =a [i] ; end; i: =1; while (a [i] =0) and (i<=n) do inc (i); if i=n+1 then writeln ('НОД - любое число') else begin for j: =1 to n do if a [j] =0 then a [j]: =a [i] ; k: =1; for i: =2 to maxa do begin minj: =1000; for l: =1 to n do begin j: =0; while (a [l] mod i=0) do begin a [l]: =a [l] div i; inc (j); end; if (j<minj) then minj: =j; end; if (minj<>0) then for l: =1 to minj do k: =k*i; end; vecb [k]: =-j; k: =k+1; end; end; a: =1; for j: =1 to abs (vec [1]) do begin if (vec [1] mod j) =0 then begin veca [a]: =j; a: =a+1; { veca [a]: =-j; a: =a+1; } End; end; b: =a; for j: =1 to k-1 do Begin for a: =1 to b-1 do Begin Begin c: =i; sum: =0; for i: =1 to c do Begin sum: =sum+vec [i] *pow1 (vecb [j] /veca [a],c-i); if (sum<0.00001) and (sum>-0.00001) then if vec [a] =1 then writeln ('ответ: ',round (vecb [j])) else writeln ('ответ: ',round (vecb [j]), '/',round (veca [a])); end; End; End; End; end; readln; end; {SuperGorner} {----------------------------------------} procedure Express; var a,b,t: integer; q: char; begin repeat writeln ('введите числитель='); readln (a); writeln ('введите знаменатель='); readln (b); if b=0 then writeln (‘знаменатель не может быть=0’) else begin write (' ['); while (a mod b>0) do begin write (a div b,','); a: =a mod b; t: =b; b: =a; a: =t; end; write (a div b, '] '); end; writeln (‘Повторить? (Y/N) '); q: =ReadKey; until q in ['N','n'] ; clrscr; end; {Express} {----------------------------------------} case k of 1: DelOstatok; 2: Factor; 3: NodNok; 4: SuperGorner; 5: Express; 6: AntiExp; else writeln ('нет операции'); end; {case} writeln ('Повторить выполнение калькулятора? (Y/N) '); q: =ReadKey; until q in ['N','n'] ; clrscr; readln; end. {prog} |
- Взаимосвязь права и государства (Анализ взаимосвязи государства и права)
- Кадровая стратегия в системе стратегического управления организацией
- Роль мотивации в поведении организации (Анализ персонала)
- Понятие и классификация функций государства (Характеристика внутренних функций государства, характеристика внешних функций государства)
- Законность и правопорядок (Основные принципы законности, законность и правопорядок)
- Менеджмент человеческих ресурсов (Кадровая политика на предприятии)
- Компоненты персонального компьютера
- Функции менеджмента
- Выбор стиля руководства в организации и профессионально выстроенной стратегии и логики руководства
- Устройство персонального компьютера (Съемные носители)
- Основы проектирования программ. Этапы создания программного обеспечения (Стандарты жизненного цикла)
- Понятие правонарушения (Социальное понятие правонарушения и его социологические признаки)