Круговые диаграммы

Содержание:

Круговые диаграммы

При проектировании электротехнических установок, например линий электропередачи, электрических двигателей и других устройств, представленных схемами замещения, возникает необходимость исследования режимов работы при изменении одного из параметров.

В таких случаях по данным расчетов строят графики изменения ряда электрических величин (тока, активной и реактивной мощностей, коэффициента мощности и т. д.) в зависимости от переменного параметра.

Применяя уже известные методы расчета цепей переменного тока, для построения графиков нужно много раз повторить решение одной и той же задачи. Трудоемкость и длительность такого способа очевидны.

В данном случае можно применить графический метод исследования электрических цепей переменного тока с помощью круговых диаграмм.

Круговая диаграмма неразветвленной цепи
с постоянным реактивным и переменным активным сопротивлениями

Обоснование метода, порядок построения круговой диаграммы и определение по ней ряда электрических величин рассмотрим сначала для одной из простых цепей.

Обоснование метода

При последовательном соединении индуктивного сопротивления X_L, и активного сопротивления R (рис. 19.1, а)

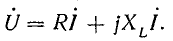
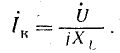
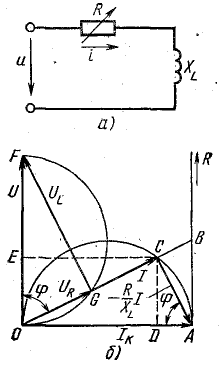
Рис. 19.1. Круговая диаграмма неразветвленной цепи с переменным активным сопротивлением

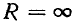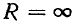Ток I_к при коротком замыкании участка с переменным сопротивлением называется током короткого замыкания, при  (разрыв цепи) Таким образом, при изменении активного сопротивления от до 0 ток в цепи изменяется от 0 до I_к.
Промежуточные величины тока можно найти, разделив уравнение напряжений на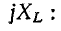

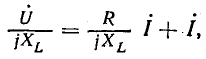
или

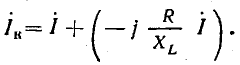
Из последнего уравнения видно, что сумма двух векторов — вектора тока I и отстающего от него на 90° вектора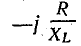 I постоянна и равна току короткого замыкания. Это соответствует случаю, когда конец вектора тока перемещается по окружности, проходящей через начало вектора тока и конец вектора 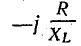, а вектор тока I_к является диаметром этой окружности (рис. 19.1, б).

Построение круговой диаграммы

Для построения окружности, которую называют круговой диаграммой токов, нужно определить ток короткого замыкания I_к, отложить на чертеже в определенном масштабе М_і отрезок 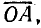соответствующий этому току, и построить на нем, как на диаметре, полуокружность. Ток короткого замыкания устанавливается в цепи при R = 0, поэтому является чисто индуктивным, отстает от напряжения на 90°. Исходя из этого, определяют направление вектора напряжения. Для выяснения зависимости тока и других величин от активного сопротивления нужно выполнить дополнительные построения — в некотором масштабе М_R по направлению вектора тока отложить индуктивное сопротивление Х_L .

Можно, в частности, сопротивление Х_L выразить тем же отрезком ОА; тогда масштаб сопротивлений М_R не будет произвольным:
  
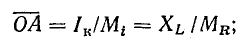
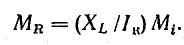
Из точки А в этом случае проводят прямую 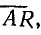перпендикулярную вектору I_к. На этой прямой от точки А в том же масштабе М_R откладывают величины активного сопротивления R. Отложив сопротивление R отрезком 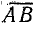и проведя прямую 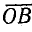, получим треугольник сопротивлений, гипотенуза которого 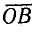выражает полное сопротивление цепи Z.

Определение величин по круговой диаграмме

В точке С пересечения прямой 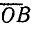с круговой диаграммой лежит конец вектора тока, проведенного из точки O. Численное значение тока находят умножением длины отрезка 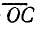на масштаб токов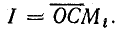
Аналогично находят токи при других сопротивлениях R от 0 до ∞.
Проекции отрезка 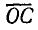на направления напряжения и тока короткого замыкания дают активную и реактивную составляющие тока в том же масштабе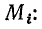
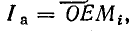
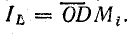
Отрезок 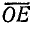 в масштабе мощности выражает активную мощность, а отрезок 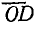— реактивную мощность цепи:


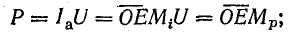
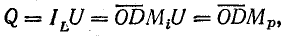
где 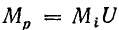 — масштаб мощности.

В масштабе мощности М_р отрезок 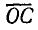выражает полную мощность цепи. Если на отрезке 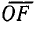выражающем в масштабе напряжений  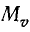полное напряжение цепи U, построить, как на диаметре, полуокружность, то можно определить активную и реактивную составляющие напряжения и коэффициент мощности 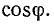Полуокружность OGP является круговой диаграммой напряжений. Отрезок 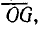совпадающий по направлению с вектором тока, в масштабе напряжений выражает активное напряжение U_R, а отрезок 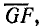перпендикулярный вектору тока, — реактивное напряжение U_L . Точка G, в которой совмещаются конец вектора U_R и начало вектора U_L, находится в пересечении линии тока 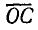с круговой диаграммой напряжений.
Этот вывод следует из подобия треугольников OGF и ОСА:
  
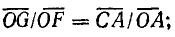
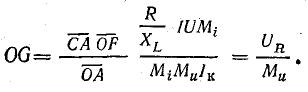
Из отношения

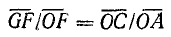
следует, что

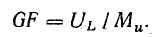
Отрезок 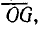одновременно выражает коэффициент мощности:


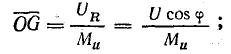
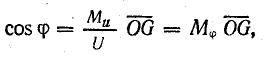
где 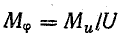— масштаб коэффициента мощности.

При увеличении R от 0 до ∞ 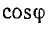 увеличивается от 0 до 1, причем отрезок 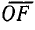в масштабе М_φ соответствует  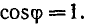Действительно, при R = ∞ направление вектора тока будет совпадать о направлением вектора напряжения (длина вектора тока в этом случае равна нулю). Круговая диаграмма напряжений пересечет направление вектора тока в точке F (точка G по диаграмме переместится и совпадет о точкой F).

Если отрезок ОF разделить на 100 частей, то, совмещая отрезок 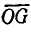с прямой 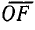, можно найти значения 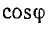точностью до 0,01.

В таком же порядке строится круговая диаграмма и определяются величины, характеризующие неразветвленную цепь с переменным активным сопротивлением и постоянной емкостью.

Ток в этой цепи опережает напряжение в общем случае на угол φ, а при R = 0 — на угол 90°. Поэтому круговая диаграмма располагается по другую сторону от вектора напряжения (на рис. 19.1, б круговую диаграмму нужно повернуть вокруг вектора напряжения на 180°).

Задача 19.1.

Построить графики изменения тока, активной, реактивной и полной мощностей, активного и реактивного напряжений, коэффициента мощности при изменении активного сопротивления от 0 до 20 Ом в цепи рис. 19.2, а, для которой известны Х_С = 10 Ом; U = 200 В.
Решение. Для решения задачи построим круговую диаграмму цепи и вычислим масштабы величин.
Ток короткого замыкания при R = 0

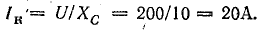
Выберем масштабы тока и напряжения: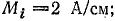  
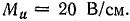
В этих масштабах рекомендуется построить на миллиметровой бумаге круговую диаграмму, подобную рис. 19.2, б.

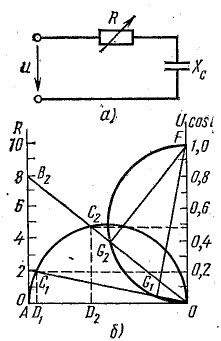
Рис. 19.2. К задаче 19.1

Отрезок ОА, выражающий ток I_к, имеет длину

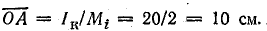
Отложим отрезк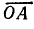и и 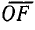и проведем окружности на этих отрезках, как на диаметрах.
Считая, что отрезок 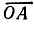выражает также емкостное сопротивление, определим масштаб сопротивлений:

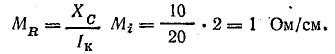
Масштаб мощности

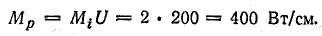
На рис. 19.2, б показано определение величин для двух значений активного сопротивления: R = 2,0 Ом и $ = 8,0 Ом. Результаты определения при этих и других значениях сопротивления записаны в табл. 19.1.

Таблица 19.1

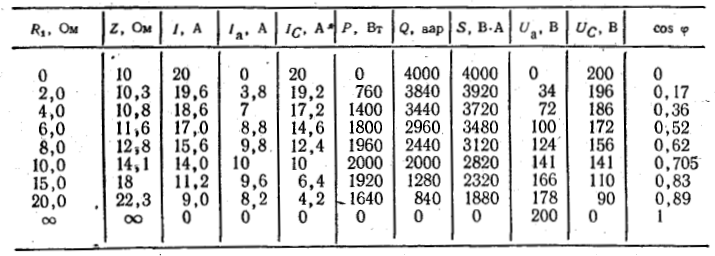
На рис. 19.3 построены кривые согласно условию задачи.

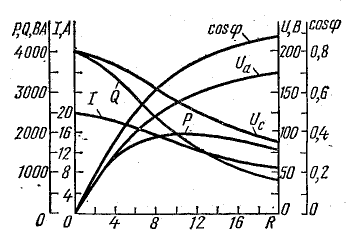
Рис. 19.3. К задаче 19.1

Круговая диаграмма неразветвленной цепи
с постоянным активным и переменным реактивным сопротивлениями

Особенность этой цепи по сравнению с предыдущей состоит в том, что переменным в ней является реактивное сопротивление — индуктивное или емкостное. Порядок рассмотрения вопроса остается таким же.

Обоснование метода

При последовательном соединении постоянного активного и переменного индуктивного сопротивлений (рис. 19.4, а) получается уравнение напряжений

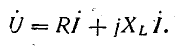
Ток короткого замыкания при Х_L = О

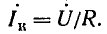
При X_L = ∞ ток в цепи I = 0.
Промежуточные величины токов найдем, разделив уравнение напряжений на R:

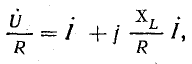
или

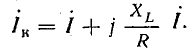
Из последнего уравнения видно, что сумма вектора тока и вектора 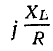I, опережающего ток на 90°, есть постоянная величина, равная току короткого замыкания.

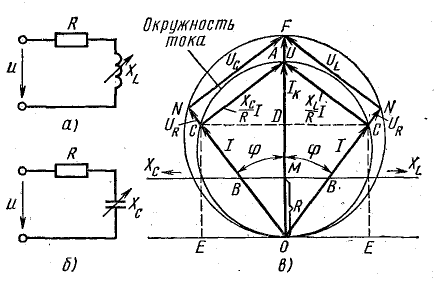
Рис. 19.4. Круговая диаграмма неразветвленной цепи с переменным реактивным сопротивлением

Если на отрезке 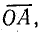выражающем в масштабе М_i ток короткого замыкания I_к, построить, как на диаметре, окружность, то сумму  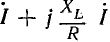можно выразить двумя хордами, пересекающимися на окружности под прямым углом (рис. 19.4, в).

Ток короткого замыкания является активным, поэтому с вектором тока совпадает по направлению вектор напряжения.

Построение круговой диаграммы

Построение круговой диаграммы целесообразно начать, отложив вектор напряжения, а затем вектор тока I_к (отрезок ).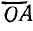

По линии тока I_к откладывают в произвольном масштабе М_R активное сопротивление R (отрезок 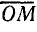), а из точки М, перпендикулярно 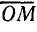проводят линию реактивного сопротивления Х_L.

Такой же порядок построения круговой диаграммы пригоден и для цепи с постоянным активным и переменным емкостным сопротивлениями (рис. 19.4, б). Ток в цепи с емкостью опережает напряжение, поэтому круговая диаграмма цепи R и С располагается слева от вектора напряжения.

Если цепи (рис. 19.4, а, б) будут иметь одинаковые активные сопротивления и напряжения, то при одинаковых масштабах круговые диаграммы обеих цепей являются двумя половинами одной окружности. Линия реактивных сопротивлений в обоих случаях одна и та же, но индуктивные сопротивления откладываются вправо, а емкостные — влево от вектора напряжения.

Определение величин по круговой диаграмме

Отложив реактивное сопротивление X в заданном масштабе отрезком 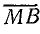 и проведя прямую  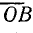до пересечения с круговой диаграммой в точке С, получим вектор тока 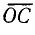. Отрезок 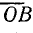в масштабе M_R равен полному сопротивлению цепи:   .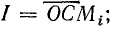

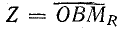Проекции отрезка 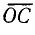 на направление напряжения (отрезок 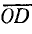) и на перпендикуляр к нему (линия 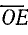) дают активную и реактивную составляющие тока в том же масштабе М_i. Отрезок 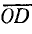в масштабе мощности выражает также активную мощность, а отрезок 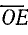— реактивную мощность. Отрезок 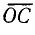в масштабе М_р равен полной мощности цепи.
Масштаб мощности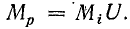

Для определения активного и реактивного напряжений и коэффициента мощности на отрезке 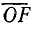, выражающем напряжение в цепи, как на диаметре, построим окружность. Отрезок 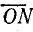в масштабе М_u дает активное напряжение, а отрезок 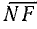— реактивное напряжение цепи. Это следует из подобия треугольников ONF и OMB:

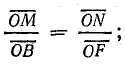
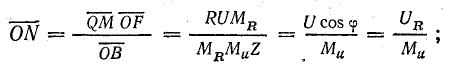
из соотношения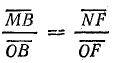 

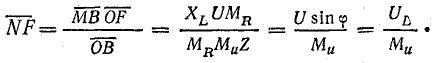
Отрезок 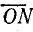одновременно выражает коэффициент мощности:
  
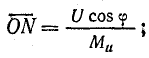
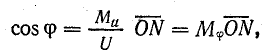
где 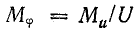— масштаб коэффициента мощности.
Отрезок ОF в масштабе Мφ соответствует 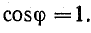Разделив этот отрезок на 100 частей и совмещая отрезок 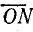с направлением 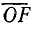, на шкале можно читать значения 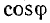с точностью до 0,01.

Если масштаб напряжения подобрать так, чтобы отрезок 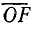был равен 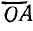, то круговая диаграмма напряжений совпадает с диаграммой токов. В этом случае не требуется проводить двух окружностей. Масштаб напряжения при заданном масштабе токов уже не может быть произвольным, а определяется из равенства
  

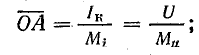
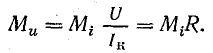
Задача 19.3. Построить круговую диаграмму цепи последовательного соединения катушки и резистора с переменным активным сопротивлением (рис. 19.5, а). Дано: R_к=3 Ом; Х_к=4 Ом; R изменяется от 0 до ∞. При сопротивлениях R = 1; 5; 9; 17 Ом определить по круговой диаграмме ток, активную, реактивную и полную мощности, коэффициент мощности катушки и всей цепи. Напряжение на зажимах цепи U = 160 В.
Решение. Отнеся сопротивление R_к к нагрузке, определим расчетный ток короткого замыкания при R_к + R = 0:

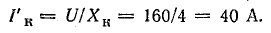
Круговую диаграмму рекомендуется построить на листе миллиметровой бумаги.

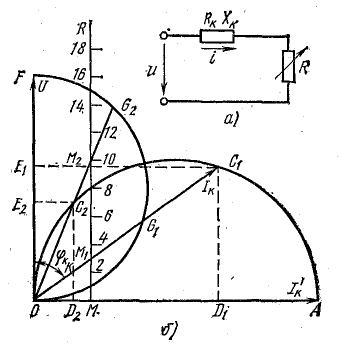
Рис. 19.5. К задаче 19.3

Выберем масштабы: тока М_i = 4 А/см; напряжения М_u = 20 В/см, сопротивления М_R = 2 Ом/см.

В этих масштабах отложим (рис. 19.5, б): ток I'_к — отрезок 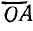, напряжение U — отрезок 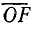, индуктивное сопротивление катушки Х_к—отрезок .
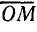Из точки М перпендикулярно току I'_к проведена прямая МR, по которой от точки М отложен отрезок 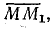 равный в масштабе М_R активному сопротивлению катушки R_к.

На отрезке 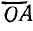, как на диаметре, построена круговая диаграмма токов (полуокружность ОС₂, С₁, А).

Прямая, проведенная из точки О через точку M₁ до пересечения с круговой диаграммой в точке С₁, дает величину тока в цепи при коротком замыкании участка с переменным активным сопротивлением .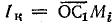
Дуга окружности между точками С₁ и О является геометрическим местом концов векторов тока при изменении сопротивления R от 0 до ∞. Искомые величины определены для двух значений сопротивления: R = 0; R = 7 Ом.
При R = 0 в цепь включена только катушка.
Ток в катушке

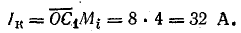
Активная мощность катушки при масштабе мощности

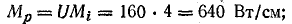
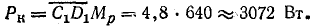
Реактивная мощность катушки

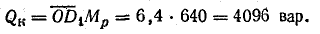
Полная мощность катушки

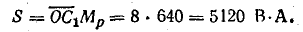
Коэффициент мощности катушки при масштабе


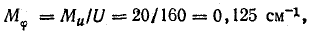
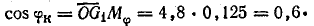
При R = 7 Ом ток

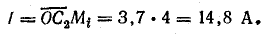
Активная, реактивная и полная мощности цепи:

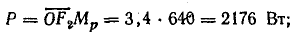
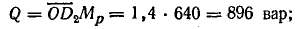
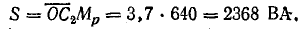
Коэффициент мощности цепи

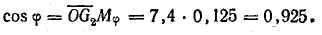
Активная мощность цепи делится на две части:

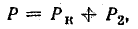
где Рк — мощность катушки; Р₂ — мощность в резисторе R.
Активная мощность катушки Р_к выражается отрезком 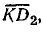а Р₂ — отрезком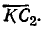 
Доказательство этого следует из подобия треугольников OMM₁ и OD₂K:
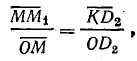, но
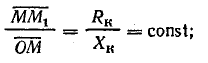
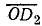в масштабе М_р есть реактивная мощность катушки при данном значении переменного сопротивления R. Поэтому

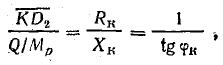
откуда

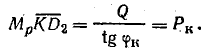
Отрезок 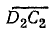в масштабе М_р равен активной мощности цепи, а мощность в резисторе R

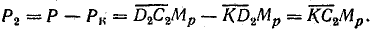
Отрезок 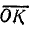. в масштабе М_р равен полной мощности катушки:

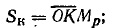
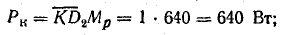
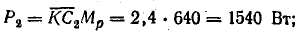
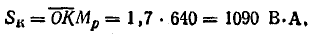
Определить по круговой диаграмме те же величины для других значений R, заданных в условии задачи.

Круговые диаграммы разветвленных цепей

С помощью круговых диаграмм можно исследовать и разветвленные цепи.

Разветвленная цепь с переменным активным сопротивлением

На рис. 19.6, а, б изображены схема разветвленной цепи с двумя ветвями и ее круговая диаграмма. Сопротивление первой ветви 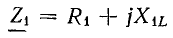постоянно.
Во второй ветви включены последовательно катушка 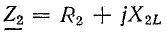 и резистор с переменным сопротивлением Я- При постоянном напряжении U режим первой ветви не меняется при изменении R. Вторая ветвь представляет собой неразветвленный участок, подобный схеме, рассмотренной при решении задачи 19.3.
Если рассмотреть эту ветвь отдельно, то построение круговой диаграммы можно считать известным. Особенность круговой lиаграммы всей цепи обусловлена наличием первой ветви.
Ток в первой ветви остается постоянным, поэтому при холостом ходе во второй ветви (R = ∞) I₂ = 0, а общий ток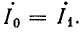
При коротком замыкании во второй ветви (R = 0) 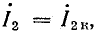а общий ток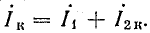 
Таким образом, при изменении сопротивления R от ∞ до 0 ток в цепи изменяется от I₁ до I_к, при этом конец вектора тока перемещается по дуге окружности, опирающейся на хорду I_2к (рис. 19.6, б).

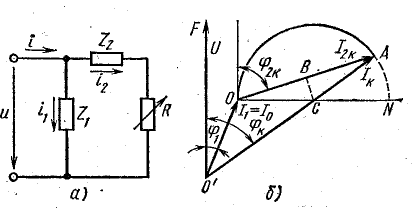
Рис. 19.6. Круговая диаграмма разветвленной цепи с переменным активным сопротивлением

Порядок построения круговой диаграммы следующий.
Определяют токи I₁ и I_2к. Выбирают масштабы напряжений и токов и проводят вектор общего напряжения U (отрезок 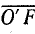) в произвольном направлении и вектор тока I₁ под углом  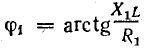к вектору напряжения. Из конца вектора I₁ проводят вектор I_2к (отрезок 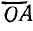) под углом 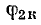к вектору напряжения:

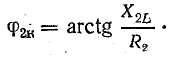
На отрезке 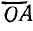, как на хорде, строят дугу окружности, центр которой С можно определить, проведя из середины хорды перпендикуляр 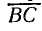до пересечения с линией  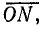перпендикулярной вектору напряжения. Линия  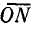является диаметром окружности, что было установлено при построении круговой диаграммы (см. рис. 19.1, б).
Отрезок 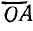в масштабе токов равен вектору общего тока при коротком замыкании сопротивления R.

Разветвленная цепь с переменным реактивным сопротивлением

Для схемы рис. 19.7, а, которая от предыдущей отличается тем, что во второй ветви есть переменное индуктивное сопротивление, а активное сопротивление постоянно, круговая диаграмма построена на рис. 19.7, б.

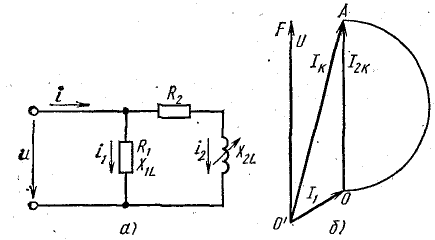
Рис. 19.7. Круговая диаграмма разветвленной цепи с переменным индуктивным сопротивлением

Порядок построения диаграммы такой же: определяют токи I₁ и I_2к (I_2к — ток во второй ветви при Х_2L = 0). После выбора масштабов тока и напряжения откладывают векторы токов I₁ и I_2к. Круговую диаграмму строят на векторе I_2k(отрезок 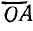), как на диаметре.

В этой части построение круговой диаграммы не отличается от рис. 19.4, в.
Определение по круговым диаграммам величин, характеризующих режимы разветвленных цепей, показано далее на конкретных примерах.

Задача 19.5.

Построить круговую диаграмму для цепи, схема которой показана на рис. 19.8, а, если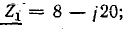     
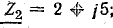
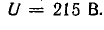
По круговой диаграмме определить токи в ветвях I₁, I₂, общий ток I, активные, реактивные и полные мощности второй ветви (Р₂, Q₂, S₂) и всей цепи (Р, Q, S), коэффициенты мощности второй ветви соsφ2 и всей цепи соsφ при трех величинах активного сопротивления R = 3; 5; 10 Ом. Определить сопротивление R, при котором в цепи наступит резонанс токов.
Решение. Ток в первой ветви

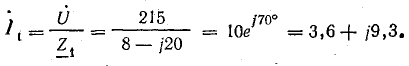
Ток во второй ветви при R = 0 (короткое замыкание)

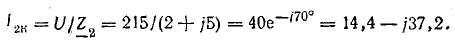
Круговую диаграмму рекомендуется построить на листе миллиметровой бумаги. Выберем масштабы: тока М_i = 4 А/см, напряжения М_u = 20 В/см. В комплексной плоскости отложим векторы напряжения и токов I₁ и I_2к (рис. 19.8, б).

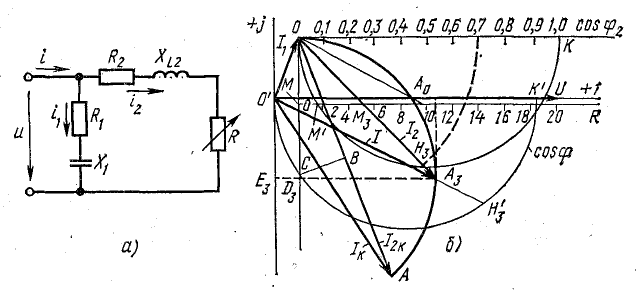
Рис. 19.8. К задаче 19.5

Круговая диаграмма токов — дуга окружности, опирающаяся на хорду 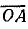 (вектор тока I_2к). Из середины хорды 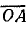(точка В) проведем перпендикуляр до пересечения в точке С с прямой, параллельной оси мнимых величин и проходящей через начало вектора I_2к (точка О). Дуга 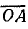, центр которой в точке С, является геометрическим местом концов векторов токов I₂ и I при любых величинах активного сопротивления R. Для определения величин по условию задачи на линии 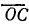от точки О отложим в масштабе сопротивлений величину Х₂. Выбираем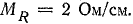
Отрезок 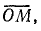выражающий сопротивление Х₂, имеет длину

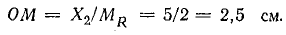
От точки М проводим прямую, параллельную действительной оси, с которой совпадает направление вектора напряжения.
На этой прямой наносим шкалу активных сопротивлений. Отрезок 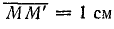в масштабе М_R равен сопротивлению R₂ = 2 Ом. От точки М' отсчитываются сопротивления R. При R = 3 Ом сумма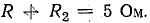
Отложив по шкале сопротивление 5 Ом, проведем через точку М₃ прямую 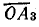до пересечения с круговой диаграммой в точке А₃, а из точки О' — прямую 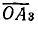  в масштабе М_i есть ток I₂, а 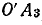— ток I.
Измерение этих отрезков дает:
    

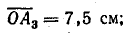
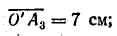
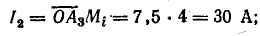
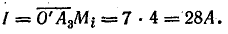
Полная мощность второй ветви (S₂) и всей цепи (S) при постоянном напряжении пропорциональна току, поэтому отрезк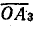и и 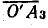 в масштабе мощностей равны соответственно S₂ и S.
Масштаб мощностей:

  
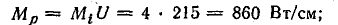
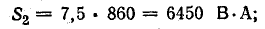
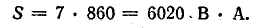
Проекции отрезков 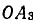 и 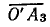на направление напряжения (действительная ось) в масштабе М_р равны активным мощностям:
 
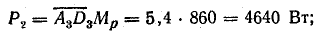
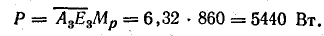
Проекции тех же отрезков на направление, перпендикулярное напряжению, в масштабе М_р равны реактивным мощностям:
 
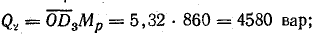
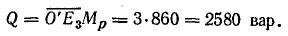
Для определения коэффициентов мощности выполнены дополнительные построения. Из точки О проведена прямая, параллельная вектору напряжения. На этой прямой отложен отрезок 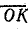, равный 10 произвольным единицам, например 10 см. На отрезке 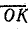, как на диаметре, построена полуокружность, которая пересекается с вектором тока I₂ (отрезок 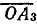) в точке Н₃. Отрезок  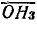в выбранных единицах на прямой 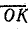дает значение 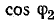. В данном случае масштаб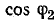
  
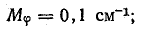
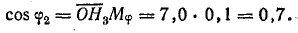
На отрезок 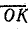 удобно нанести шкалу и повернуть отрезок  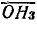вокруг точки О до совпадения с направлением 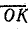. Значение 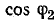можно прочитать на шкале косинусов.
Аналогично проводят полуокружность 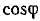. Диаметром этой полуокружности является отрезок, отложенный в том же масштабе из точки О' вдоль направления вектора напряжения (отрезок ).
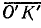Отрезок 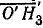 в масштабе M_φ дает значение .
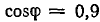При резонансе токов общий ток I совпадает по фазе с напряжением U. Поэтому точка пересечения круговой диаграммы токов с вектором напряжения U является концом вектора тока (точка A₀). Из точки О проведем отрезок 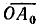до пересечения с линией сопротивлений. Искомое сопротивление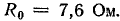
По круговой диаграмме определить величины, указанные в условии задачи при сопротивлениях R = 5 и 10 Ом.

Построение круговой диаграммы по результатам опытов холостого хода и короткого замыкания

Круговую диаграмму цепи можно построить по показаниям приборов, измерив те величины, которые являются исходными при построении.

Неразветвленная цепь

В неразветвленных цепях, изображенных на рис. 19.1, а; 19.4, а, б, достаточно измерить напряжение и ток I_к при коротком замыкании между точками 2 и 2' (рис. 19.9, а, б).

Величина постоянного сопротивления определяется по показаниям приборов, отношение напряжения к току равно Х_L в схеме рис. 19.9, а и R — в схеме рис. 19.9, б.

Рис. 19.9. К вопросу построения круговой диаграммы неразветвленной цепи по результатам опытов

В схеме рис. 19.5, а нужно дополнительно измерить активную мощность при коротком замыкании (рис. 19.9, в).
По показаниям приборов определяют параметры катушки:
  

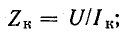
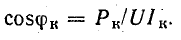
Разветвленная цепь

Для построения круговой диаграммы разветвленной цепи требуется провести опыты холостого хода и короткого замыкания (рис. 19.10).
При холостом ходе (разрыв цепи между точками 2 и 2') измеряют ток I₁, мощность Р₁ первой ветви и общее напряжение U. Определяют

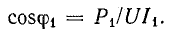
При коротком замыкании между точками 2 и 2' измеряют ток I_к, мощность Р_к всей цепи и общее напряжение U. Определяют

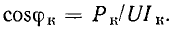
Этих данных достаточно для построения круговой диаграммы токов.

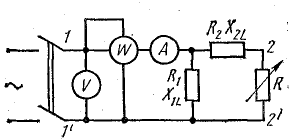
Рис. 19.10. К вопросу о построении круговой диаграммы разветвленной цепи по результатам опытов

Задача 19.7.

Построить круговую диаграмму цепи рис. 19.11, а по результатам опытов холостого хода и короткого замыкания:
        
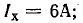
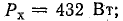
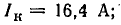
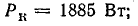
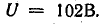
Пользуясь круговой диаграммой, построить кривые зависимости тока, активной, реактивной мощностей и 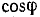 от сопротивления конденсатора Х_С.
Решение. По показаниям приборов определим коэффициенты мощности первой ветви (холостой ход) и всей цепи при коротком замыкании участка 2-2':
    
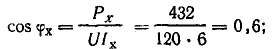
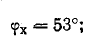
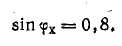
Для того чтобы не пользоваться транспортиром при построении круговой диаграммы, можно определить активную и реактивную составляющие тока:



  

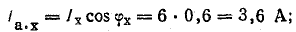
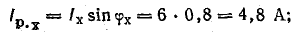
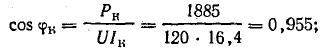
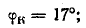
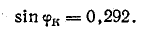
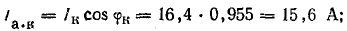
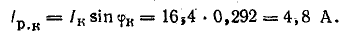
Круговую диаграмму (рис. 19.11, б) рекомендуется построить на листе миллиметровой бумаги в следующем порядке.

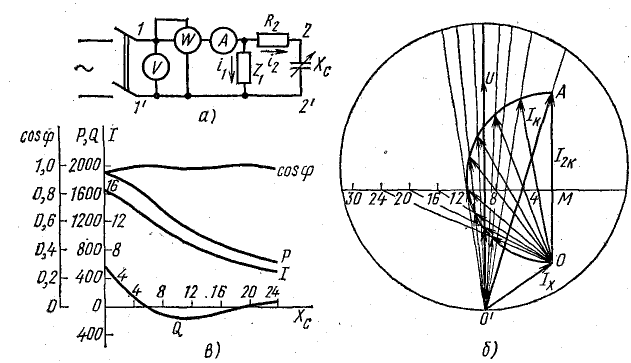
Рис. 19.11. К задаче 19.7

Выбрать масштабы тока и напряжения (например, 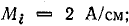; 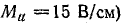) и отложить на чертеже векторы: U — в произвольном направлении, активные составляющие токов — вдоль вектора напряжения, реактивные — перпендикулярно ему, учитывая их индуктивный характер.
Построив векторы токов I_х и I_к, провести вектор I_2к так, чтобы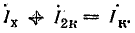
На векторе I_2к (отрезок 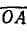), как на диаметре, построить полуокружность токов слева от диаметра 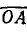, учитывая емкостный характер тока I₂. Из диаграммы следует, что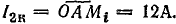
Активное сопротивление во второй ветви

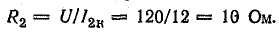
Далее надо выбрать масштаб сопротивлений {например, М_R = 4 Ом/см) и отложить от точки О по направлению вектора тока I_2к величину активного сопротивления R₂ (отрезок 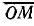). Через точку М провести линию реактивных сопротивлений и нанести шкалу.
Величины, определенные по круговой диаграмме согласно условию задачи, записаны в табл. 19.2.

Таблица 19.2

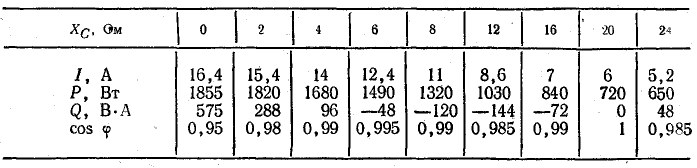
При Х_С = 5 Ом, Х_С = 20 Ом в цепи имеет место резонанс токов. Это видно из круговой диаграммы. Ток I совпадает по фазе с напряжением. На рис. 19.11, в построены графики согласно условию задачи.

Построение круговых диаграммы

Проектируя линии электропередачи, электрические двигатели и другие электротехнические установки, строят графики изменения тока, мощностей, коэффициента мощности и других величин от какого-либо переменного параметра, например сопротивления.

Для исследования режимов работы электрических цепей переменного тока при изменении одного из параметров цепи можно применить круговые диаграммы.

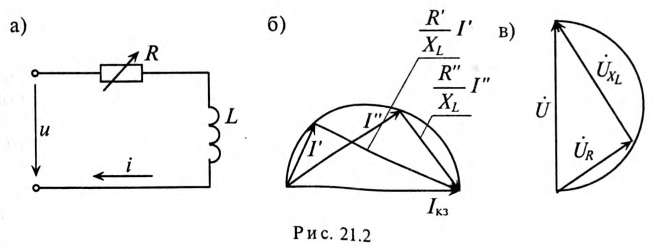
Обоснование метода, порядок построения круговых диаграмм и определение по ним электрических величин рассматриваются на примере неразветвленной цепи с переменным активным и постоянным реактивным (индуктивным) сопротивлением (рис. 21.2а).

Для этой цепи справедливо выражение (второй закон Кирхгофа)

Рассмотрим изменение тока в этой цепи при изменении сопротивления R от нуля до бесконечности.

При коротком замыкании (R = 0)

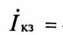
При холостом ходе (R =)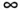

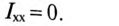
Для определения тока при любом сопротивлении R выражение (21.11) можно разделить на :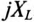

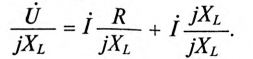
Тогда

Таким образом, геометрическая сумма двух векторов — вектора тока 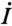и отстающего от него на 90° вектора 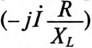— постоянна и равна току короткого замыкания. Следовательно, ток короткого замыкания 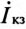— величина постоянная. Вектор тока короткого замыкания можно изобразить гипотенузой прямоугольного треугольника, катетами которого являются рассмотренные выше сдвинутые на угол 90° два вектора.

Для двух значений тока 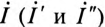при двух значениях сопротивления R (R' и R") построение треугольников показано на рис. 21.26. Следовательно, вектор тока короткого замыкания 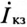можно рассматривать как диаметр полуокружности, по которой скользит конец вектора тока 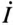при изменении сопротивления R (рис. 21.26).

При коротком замыкании рассматриваемая цепь имеет чисто индуктивный характер (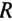 = 0). Следовательно, напряжение цепи U опережает ток 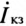на угол 90°. Напряжение цепи является результатом геометрической суммы двух напряжений, векторы которых сдвинуты на угол 90°, т. е. 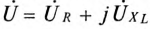. Таким образом, напряжение цепи U можно рассматривать как диаметр полуокружности, по которой вектор U_R скользит при изменении сопротивления R (рис. 21.2в).

Для построения круговой диаграммы рассматриваемой цепи необходимо задаться масштабом тока 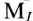и масштабом напряжения 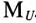. В соответствующих масштабах строят вектор 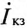и опережающий его на угол 90° вектор напряжения U. На этих векторах проводят полуокружности (рис. 21.3).

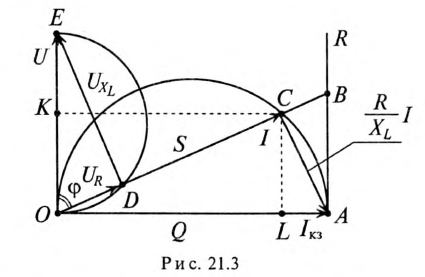
Для выяснения зависимости тока и других величин от сопротивления R необходимо выполнить дополнительные построения. В масштабе сопротивлений 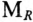по направлению вектора тока 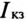откладывают индуктивное сопротивление X_L. Сопротивление X_L можно выразить тем же отрезком OA, что и ток 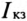, тогда масштаб сопротивлений 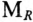определяют из отношения

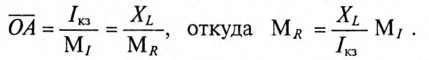
В этом масштабе на прямой 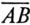перпендикулярно 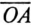откладывают величину активного сопротивления R (отрезок 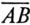), тогда отрезок 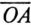выражает полное сопротивление Z рассматриваемой цепи (рис. 21.3). Очевидно, отрезок 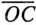в масштабе тока 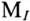и является вектором тока 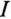при соответствующем значении сопротивления R, а отрезок - вектор 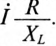 Отрезок 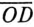в масштабе напряжения 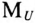является вектором напряжения 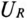(совпадает по фазе с током 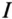), а отрезок 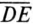— вектором напряжения 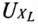(на угол 90° опережает ток ).

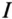Проекция вектора тока 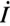 на вектор напряжения 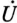(отрезок 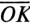) является активным током 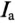, а проекция тока 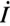на вектор тока короткого замыкания 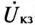(отрезок 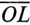) — реактивным током /р, т. е. h=OKM,\ Ip=OL M,.    _

Очевидно, тот же отрезок 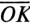, но в масштабе мощности М/> является активной мощностью цепи Р, а отрезок 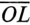- реактивной мощностью цепи Q, т.е. 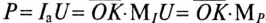, а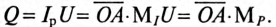

Отсюда следует, что масштаб мощности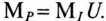

Тогда отрезок 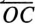в масштабе мощности 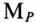— полная, или кажущаяся, мощность цепи S. Следовательно, на круговой диаграмме (рис. 21.3) видны изменения токов, напряжений, мощностей, сопротивлений и угла сдвига фаз <р между током и напряжением в зависимости от изменяющейся величины активного сопротивления R.

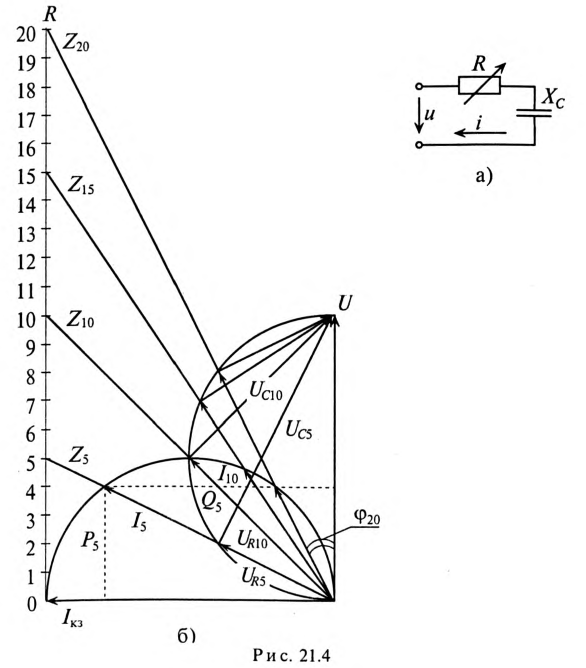
В таком же порядке строится круговая диаграмма для неразветвленной цепи с переменным активным и постоянным емкостным сопротивлениями. Однако ток в этой цепи опережает напряжение на угол ф, а при коротком замыкании (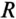 = 0) — на угол 90° (см. рис. 21.4).

Пример 21.1

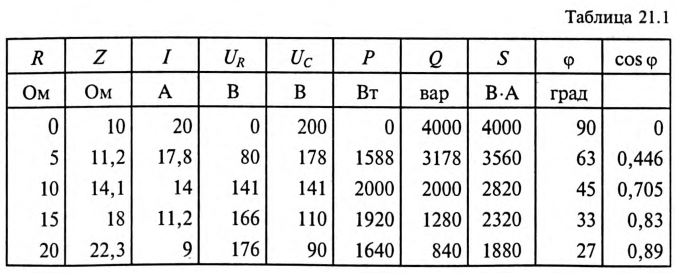
Построить круговую диаграмму неразветвленной цепи с постоянным емкостным и переменным активным сопротивлениями (рис. 21.4а) и определить по ней значения тока, активного и реактивного напряжений, активной, реактивной и полной мощностей, а также полного сопротивления, угла ф и коэффициента мощности для переменных активных сопротивлений: R = 0; 5; 10; 15; 20 Ом, если к цепи приложено напряжение U= 200 В, а емкостное сопротивление Х_с= 10 Ом.

Решение

Определяем ток короткого замыкания цепи (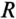=0)

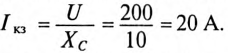
Выбираем масштабы тока 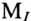=2 А/см и напряжения 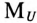= 20 В/см. Тогда масштаб сопротивлений можно определить 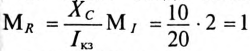Ом/см, а масштаб мощности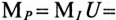 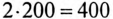Вт/см.

В этих масштабах строим круговую диаграмму (рис. 21.46), по которой определяем все искомые величины для цепи (рис. 21.4а) при указанных сопротивлениях R и заносим их в таблицу 21.1.

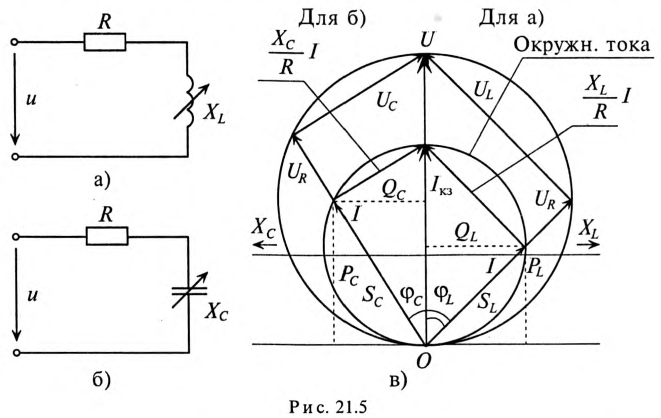
Если в неразветвленной цепи (рис. 21.5а, б) переменным является реактивное сопротивление (индуктивное или емкостное), то при коротком замыкании (Х= 0) 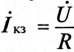, цепь чисто активная и напряжение цепи совпадает по фазе с током .

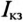Для построения круговой диаграммы цепей (рис. 21.5а, б) учитывают, что диаметрами полуокружностей являются ток 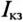и напряжение цепи U.

Построение круговых диаграмм производится аналогично предыдущим (рис. 21.3 и 21.46). Особенностью построения круговых диаграмм с переменным реактивным сопротивлением является то, что векторы 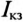 и U совпадают по фазе.

Масштабы выбирают и рассчитывают как указано выше.

Построение круговых диаграмм для неразветвленных цепей с переменными реактивными сопротивлениями X_L и Х_с показано на рис. 21.5в.