
Кривые поверхности в начертательной геометрии с примерами
Содержание:
В архитектурно-строительной практике широко применяются пространственные криволинейные формы, основу которых представляют различные кривые поверхности в их "чистом" геометрическом виде или составленные из нескольких поверхностей. При выборе исходной поверхности архитектор должен в совершенстве знать геометрию этих поверхностей: их основные характеристики, свойства, принципы образования и изображения и др.
Классификация поверхностей на протяжении длительного периода была предметом научных исследований, но пока не удалось установить единую систему, так как за ее основу могут быть взяты разные критерии: характер образующей, признак развертывания и прочее.
В данной лекции приводится один из примеров классификации.
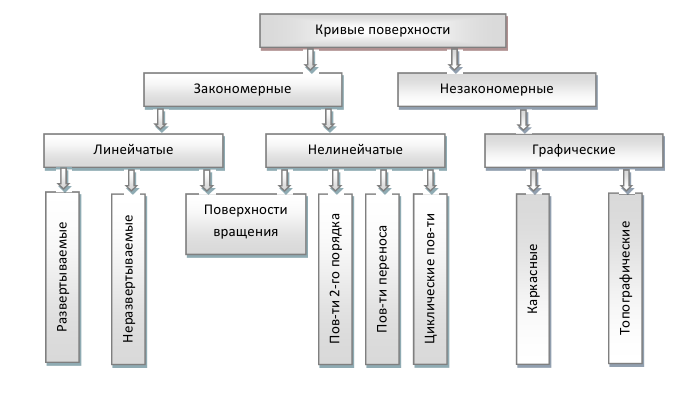
Кривые поверхности
Кривые поверхности широко применяются в различных областях техники, архитектуры, строительства и т.д. Начертательная геометрия изучает кривые поверхности, способы их образования, позиционные, метрические и другие их свойства.
Под поверхностью подразумевают непрерывное множество точек, если между координатами точек может быть установлена зависимость, определяемая уравнением вида F (х, у, z) = 0, где F (х, у, z) - многочлен п-ой степени или в форме какой-либо трансцендентной функции. В первом случае поверхности называются алгебраическими, во втором -трансцендентными.
Порядок поверхности равняется степени её уравнения. Порядок поверхности может быть определен также числом точек пересечения произвольной прямой с поверхностью, при этом считаются и мнимые и действительные точки. Порядок линии пересечения двух поверхностей равняется произведению порядков пересекающихся поверхностей.
Иногда поверхность трактуют как непрерывное двупараметрическое множество точек.
В начертательной геометрии поверхность рассматривается как совокупность последовательных положений перемещающейся в пространстве линии. Линия, которая перемещается, называется образующей. Линия, по которой перемещается образующая, называется направляющей. При своем перемещении образующая может оставаться параллельной какому-либо направлению, какой-либо плоскости или перемещаться по двум, трем направляющим. Общий случай образования поверхности путем поступательного перемещения образующей в соответствии с наложенными на неё условиями показан на рисунке 9.1 а.
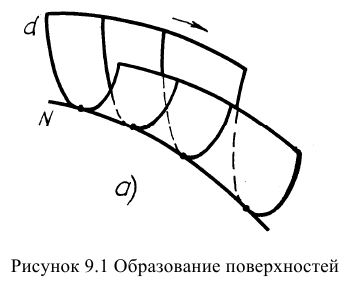
Линейчатые поверхности
Поверхность можно представить образованной перемещением какой-либо линии (образующей) по второй линии (направляющей). Если образующая прямая линия, то поверхность называется линейчатой, в противном случае - нелинейчатой или кривой.
Линейчатые поверхности делятся на развертываемые и не развертываемые. Развертываемые линейчатые поверхности.
К развертываемым линейчатым поверхностям относятся: цилиндрическая, коническая и поверхность с ребром возврата
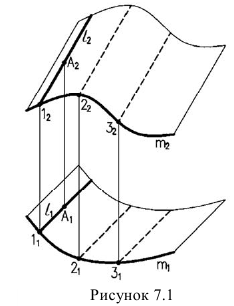
Цилиндрическая поверхность образуется параллельным перемещением прямой - образующей по какой-либо криволинейной направляющей (рисунок 7.1).
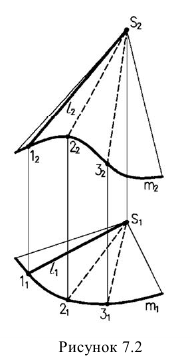
Если направляющая - замкнутая линия, поверхность называется замкнутой. Линия пересечения плоскостью, перпендикулярной образующим, называется нормальным сечением. Все виды нормального сечения уточняют название поверхности: круговая, эллиптическая, параболическая и др. Коническая поверхность образуется перемещением прямой (образующей), проходящей через одну неподвижную точку - вершину, по криволинейной направляющей (рисунок 7.2).
Неподвижная точка делит образующую на две полупрямые и поэтому поверхность образует две полости.
Коническая поверхность, как и цилиндрическая, может быть замкнутой. Если направляющая является окружностью, а вершина расположена на перпендикуляре, восстановленном в центре окружности, то поверхность называется прямым круговым конусом или поверхностью вращения. В противном случае коническая поверхность называется поверхностью второго порядка.
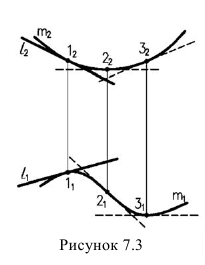
Поверхность с ребром возврата (торc) образуется при перемещении прямой линии в пространстве, которая все время остается касательной к некоторой пространственной кривой линии, называемой ребром возврата (рисунок 7.3). Эта поверхность двупольная, так как точка касания образует две полупрямые
Неразвертываемые линейчатые поверхности
К неразвертываемым линейчатым поверхностям относятся поверхности с плоскостью параллелизма: цилиндроиды, коноиды и гиперболические параболы и др.
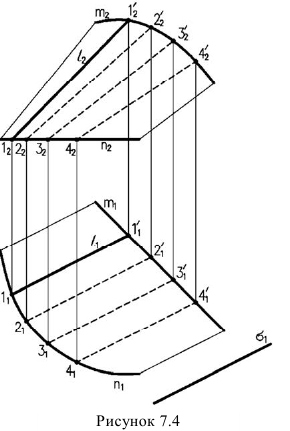
Цилиндроид - поверхность, полученная перемещением прямой образующей, которая все время остается параллельной определенной плоскости, называемой плоскостью параллелизма, по двум кривым направляющим (рисунок 7.4).
l - образующая; m, n - направляющие; 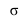 - плоскость параллелизма.
- плоскость параллелизма.
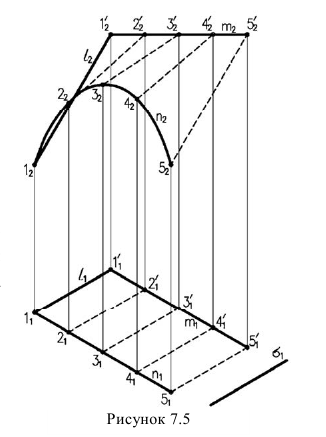
Коноид - поверхность, полученная перемещением прямой образующей, которая все время остается параллельной плоскости параллелизма, по двум направляющим, одна из которых прямая, вторая кривая (рисунок 7.5).
l - образующая;
m, n - направляющие;
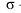 - плоскость параллелизма.
- плоскость параллелизма.
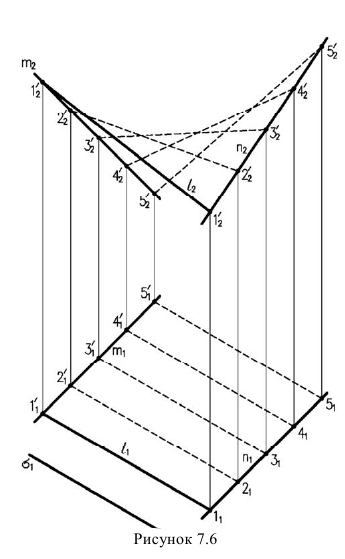
Гиперболический параболоид - поверхность, полученная перемещением прямолинейной образующей, которая все время остается параллельной плоскости параллелизма по двум прямым направляющим (рисунок 7.6)
1 - образующая;
m, n - направляющие;
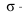 - плоскость параллелизма. Поверхности вращении.
- плоскость параллелизма. Поверхности вращении.
Поверхности вращении образующей вращением какой-либо линии вокруг примой, называемой осью вращения.
Поверхности вращения делятся на линейчатые, когда образующая прямая и нелинейчатые, когда образующая кривая. Точки образующей при вращении дают окружности, называемые параллелями, из которых наибольшая - экватор, наименьшая - горловина. Плоскости, проходящие через ось вращения, пересекают поверхность по меридианам. Меридиан, лежащий в плоскости параллельной плоскости проекций называется главным.
Линейчатые поверхности вращении
В зависимости от положения прямой образующей по отношению к оси вращения, линейчатые поверхности делятся на цилиндрическую, коническую и однополостный гиперболоид вращения.
Цилиндрическая поверхность образуется вращением вокруг оси прямой - образующей, параллельной оси вращения (рисунок 7.7). Коническая поверхность образуется которая пересекает ось вращением вокруг оси (рисунок 7.8).
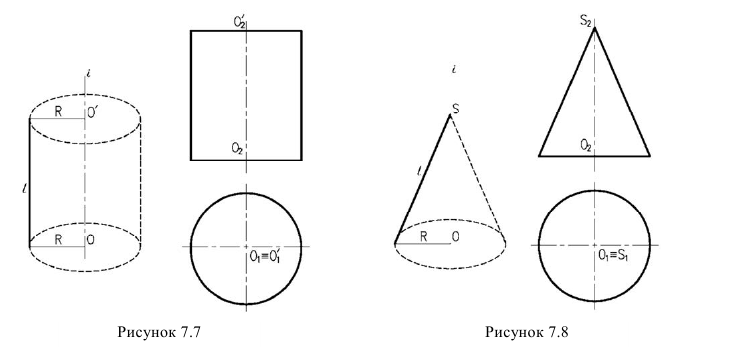
Однополоеcный гиперболоид вращения образуется вращением прямой - образующей, скрещивающейся с осью вращения. На рисунке 7.9 построен однополостный гиперболоид вращения. Для построения этой поверхности изображено двенадцать положений образующей. Главным меридианом гиперболоида вращения будет гипербола. Поэтому если гиперболу вращать вокруг оси, также получим гиперболоид вращения.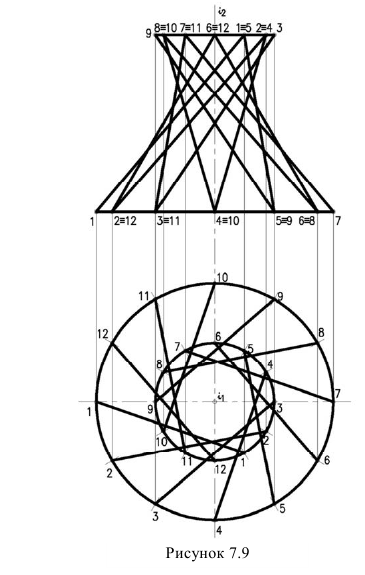
Нелинейчатые поверхности вращения (криволинейные)
В зависимости от формы образующей и положения оси вращения получается тот или иной вид поверхности: сфера (рисунок 7.10а), тор (рисунок 7.106), эллипсоид (рисунок 7.1 Ов) и т.н. 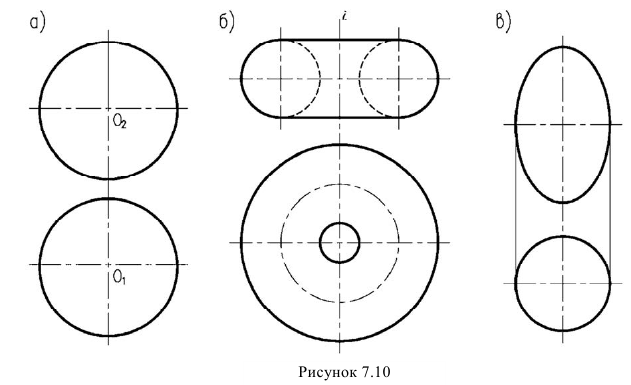
Винтовые поверхности
Винтовые поверхности образуются винтовым движением прямой или кривой линии. В первом случае поверхность будет линейчатой, во втором - криволинейной.
Рассмотрим построение некоторых из них.
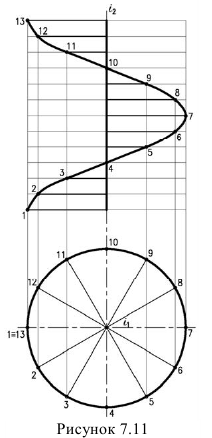
Винтовой коноид (примой геликоид) - образуется перемещением прямой - образующей но двум направляющим оси и винтовой линии. Плоскостью параллелизма в этом случае является плоскостью проекций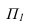 (рисунок 7.11). Для построения взято двенадцать положений образующей.
(рисунок 7.11). Для построения взято двенадцать положений образующей.
Винтовой коноид является основой для построения винтовой лестницы.
Развертывающийся геликоид (эвольвентный геликоид) - относится к поверхностям с ребром возврата. Ребром возврата является винтовая линия. Прямая-образующая перемещается по винтовой линии, оставаясь к ней касательной. Рисунок 7.12.
Известно, что если соединить следы касательных к винтовой линии на плоскости перпендикулярной оси, получим эвольвенту окружности. Поэтому, определив фронтальное положение этих следов мы можем построить фронтальные проекции касательных к винтовой линии (рисунок 7.12).
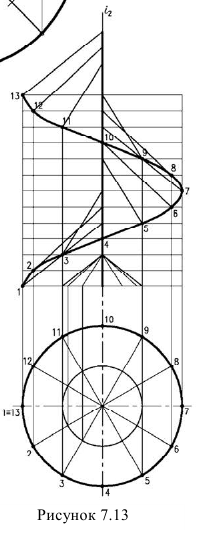
Наклонный геликоид - образуется перемещением прямой образующей, которая все время остается параллельной направляющему конусу, но двум направляющим - винтовой линии и оси (рисунок 7.13).
Для построения поверхности наклонного геликоида сначала строим направляющий конус с образующими, а затем уже строим ряд образующих поверхностей, параллельных образующим конуса.
Поверхности переноса
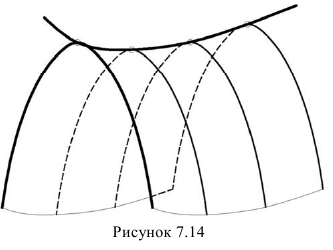
Поверхности переноса образуются поступательным переносом одной кривой линии вдоль другой (рисунок 7.14).
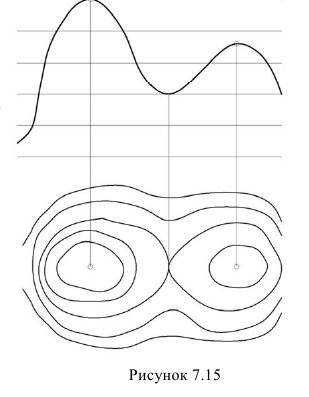
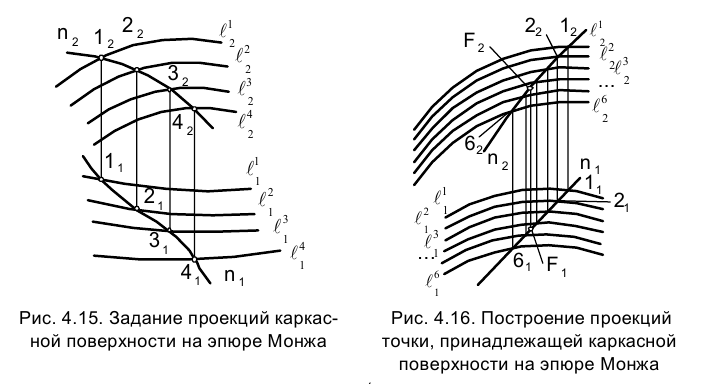
Каркасные поверхности, задаются некоторым числом дискретных каркасов. Примером, является обшивка автомобилей, самолетов, кораблей и т.п. Топографическая поверхность представляется рядом горизонталей поверхности (рисунок 7.15).
Плоские и пространственные кривые
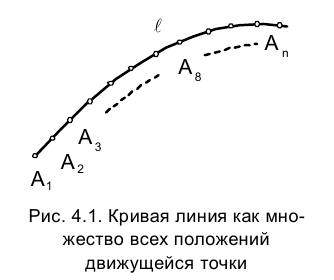
Как математическая абстракция кривая линия - это множеcтво всех положений движущейся точки (рис. 4.1), изменяющей направление своего перемещения.
На практике кривыми линиями представляются очертания многих инженерных конструкций и сооружений, деталей механизмов и машин, траектории движущихся объектов, автострад и т.д. Кривые линии являются широко используемым инструментом при построении математических моделей сложных пространственных конфигураций, интерпретируют графически сложные процессы и явления.
По своей ориентации в пространстве кривые линии делятся два класса: плоские и пространственные. Как плоские, так пространственные кривые могут быть алгебраическими, трансцендентными и графическими. Алгебраическими кривыми называются линии, которые могут быть заданы алгебраическими уравнениями, т.е. полиномом n-й степени, определяющей порядок кривой. Геометрически порядок плоской алгебраической кривой определяется числом точек ее пересечения с прямой линией, а пространственной алгебраической кривой - наибольшим числом точек ее пересечения с плоскостью общего положения.
Трансцендентные кривые определяются неалгебраическим уравнением. Большинство их пересекается с прямой и с плоскостью в бесконечном числе точек.
Графические линии обычно задаются своими проекциями на чертеже. Их примером являются линии теоретического чертежа корпуса
судна.
Плоские кривые
Кривые линии, все точки которых принадлежат плоскости, называются плоскими.
Рассмотрим элемент кривой ℓ, принадлежащей плоскости 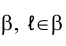 (рис. 4.2).
(рис. 4.2).
Возьмем на кривой ℓ произвольную точку 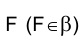 и проведем через нее секущую FК. При перемещении точки К по кривой ℓ в направлении точки F секущая поворачивается вокруг точки F. Когда точка К совпадает с точкой F, секущая FК займет некоторое предельное положение t. Назовем ее касательной к кривой ℓ в точке F.
и проведем через нее секущую FК. При перемещении точки К по кривой ℓ в направлении точки F секущая поворачивается вокруг точки F. Когда точка К совпадает с точкой F, секущая FК займет некоторое предельное положение t. Назовем ее касательной к кривой ℓ в точке F.
Прямая, проведенная в плоскости кривой в точке F перпендикулярно касательной, называется нормалью (рис. 4.3).
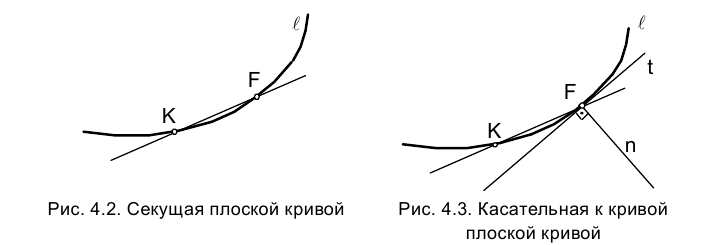
Рассмотрим несколько способов построения касательных и нормалей к кривым линиям.
На рис. 4.4 показано построение касательной к кривой линии ℓ, проходящей через не принадлежащую кривой точку Е. Через эту точку проведен пучок прямых, пересекающих кривую ℓ. Стягивающие дуги кривой хорды обозначены цифрами 11, 22, 33. Проведенная через середины хорд кривая m называется кривой ошибок.
Точка Р пересечения заданной кривой ℓ c кривой ошибок m и определяет точку касания прямой, проведенной к кривой ℓ через точку 
Также с использованием кривой ошибок строится касательная к кривой, параллельная заданному направлению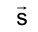 в точке Р (рис. 4.5).
в точке Р (рис. 4.5).
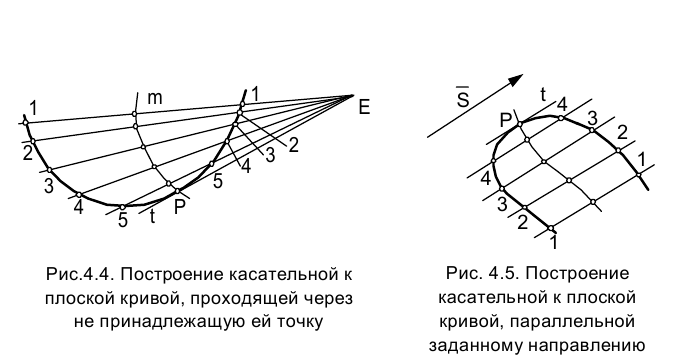
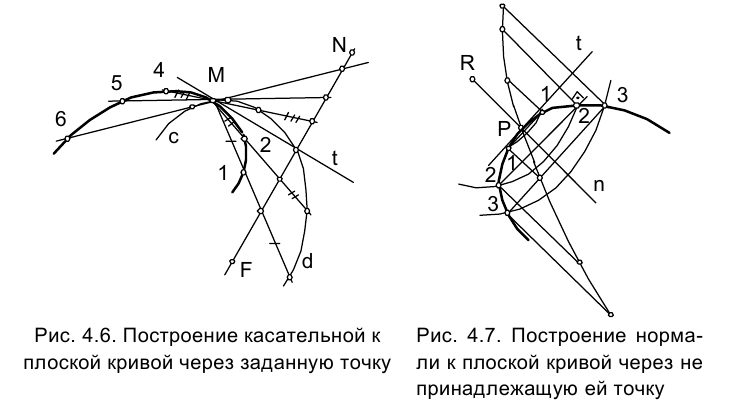
На рис. 4.6 приведен пример построения касательной к кривой ℓ через заданную ее точку.
Рассмотрим пример построения нормали к кривой линии ℓ, проходящей через заданную точку R, не принадлежащую (рис. 4.7). Из точки R как из центра проводим дуги концентрических окружностей произвольных радиусов, пересекающих кривую ℓ. Обозначим концы хорд, стягивающих соответствующие дуги. В концах хорд восставляем противоположно направленные перпендикуляры и откладываем на них отрезки, равные длинам этих хорд. Линия ошибок m, соединяющая концы хорд, пересекает кривую ℓ в точке Р. Прямая n является искомой нормалью к кривой ℓ, проходящей через точку R.
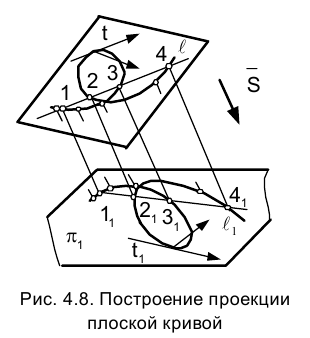
Проанализируем поведение проекций плоских кривых линий. На рис. 4.8. задана плоская кривая ℓ, направление проецирования 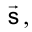
r , плоскость проекций 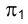 . При данном (стрелкой) направлении проецирования кривая проецируется на плоскость
. При данном (стрелкой) направлении проецирования кривая проецируется на плоскость 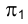 в кривую
в кривую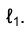 . При этом
. При этом
заданная секущая кривой ℓ, проецируется в секущую проекции кривой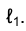
Точки 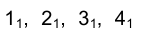 пересечения проекции секущей с проекцией кривой являются проекциями точек пересечения кривой ℓ с ее секущей и
пересечения проекции секущей с проекцией кривой являются проекциями точек пересечения кривой ℓ с ее секущей и
их количество одинаково.
При параллельном проецировании порядок плоской алгебраической кривой не меняется. При стремлении перемещающейся по кривой точки к бесконечности проекция этой точки также стремится к бесконечности, т.е. несобственные точки кривой проецируются в несобственные точки проекции кривой.
При перемещении точки К секущей по кривой ℓ по направлению к точке F секущая будет стремиться занять некоторое предельное положение, в котором она превратится в касательную к кривой ℓ в точке F. Аналогично проекция касательной в точке 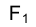 к кривой
к кривой 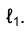 - предельное положение проекции секущей.
- предельное положение проекции секущей.
Итак, касательная к кривой проецируется в касательную к проекции кривой.
В частном случае, когда плоскость, которой принадлежит кривая, параллельна плоскости проекций, кривая и ее проекция конгруэнтны.
Наиболее наглядным является представление кривой как траектории движущейся точки. При этом в каждый момент времени направление движения точки определяется вектором касательной к кривой.
Движение точки связано с непрерывным изменением двух величин: расстояниям 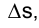 , на которое точка удалилась от своего начального положения, и угла
, на которое точка удалилась от своего начального положения, и угла 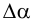 - поворота касательной относительно начального положения (рис. 4.9). Угол между касательными в двух бесконечно близких точках кривой, называемый углом смежности, отнесенный к единице длины дуги, определяет степень искривленности
- поворота касательной относительно начального положения (рис. 4.9). Угол между касательными в двух бесконечно близких точках кривой, называемый углом смежности, отнесенный к единице длины дуги, определяет степень искривленности
кривой. Характеристикой формы кривой в каждой ее точке является ее кривизна.
Кривизной (K) кривой в данной точке называется предел отношения угла смежности 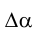 между касательными в точках А и B к длине дуги
между касательными в точках А и B к длине дуги 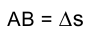 при стремлении
при стремлении 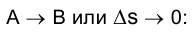
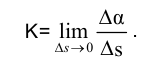
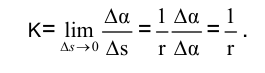
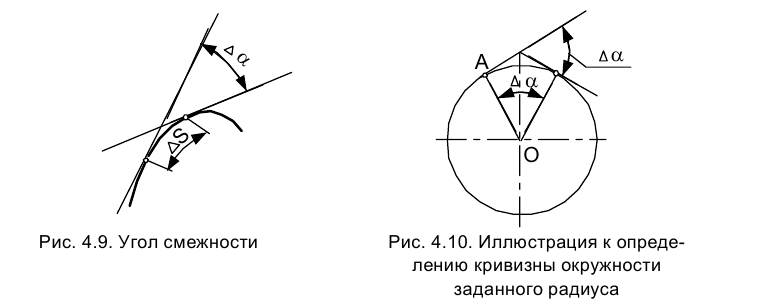
Из приведенных рассуждений следует, что кривизна окружности в любой ее точке не зависит от выбора этой точки и равна 1/r.
В общем случае кривизна в произвольных точках плоской кривой различна и определяется посредством так называемой соприкасающейся окружности, т.е. окружности, проходящей через заданную и две бесконечно близкие к ней точки.
Центр соприкасающейся окружности называют центром кривизны кривой в данной точке. Радиус R соприкасающейся окружности называют радиусом кривизны кривой в данной точке. Кривизна же K кривой в данной точке определяется отношением 1/R
Пространственные кривые
Пространственными кривыми, или линиями двойной кривизны, называются линии, все точки которых не принадлежат одной плоскости (рис. 4.11). На чертеже пространственную кривую задают последовательностью ее точек.
Определение касательной к пространственной кривой совпадает с аналогичным определением касательной к плоской кривой, а именно: касательной прямой t в точке F пространственной кривой ℓ. называется предельное положение секущей КF, когда точка К, оставаясь на линии ℓ, стремится к точке F (рис. 4.11).
Корректность построения проекций пространственных кривых определяется следующей теоремой: касательная t к пространственной кривой ℓ, проецируется в касательную 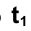 к ее проекции ℓ1, если t не проецируется в точку.
к ее проекции ℓ1, если t не проецируется в точку.
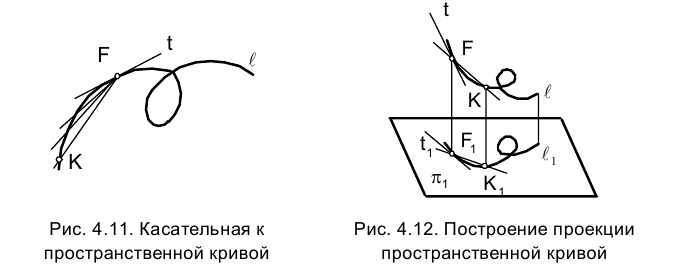
Рассмотрим некоторую пространственную кривую ℓ, проекция которой на горизонтальной плоскости проекций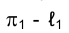 (рис. 4.12). Построим на кривой ℓ секущую КF, ортогональная проекция которой на плоскость
(рис. 4.12). Построим на кривой ℓ секущую КF, ортогональная проекция которой на плоскость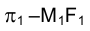 - секущая кривой
- секущая кривой 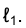 . При перемещении точки К по кривой ℓ к точке F секущая КF, поворачиваясь вокруг неподвижной точки F, стремится к своему предельному положению - положению касательной t к кривой ℓ. В то время, когда точка К движется по кривой ℓ, ее проекция
. При перемещении точки К по кривой ℓ к точке F секущая КF, поворачиваясь вокруг неподвижной точки F, стремится к своему предельному положению - положению касательной t к кривой ℓ. В то время, когда точка К движется по кривой ℓ, ее проекция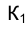 перемещается по кривой
перемещается по кривой 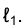 , стремясь к своему предельному положению - точке
, стремясь к своему предельному положению - точке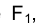 , а секущая
, а секущая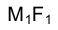 к своему предельному положению - положению касательной
к своему предельному положению - положению касательной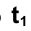 к кривой
к кривой 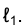 . В тот момент, когда точка К совпадет с точкой F и секущая КF станет касательной t к кривой ℓ, точка
. В тот момент, когда точка К совпадет с точкой F и секущая КF станет касательной t к кривой ℓ, точка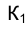 с точкой
с точкой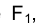 и секущая
и секущая 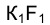 станет касательной
станет касательной 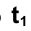 к кривой ℓ.
к кривой ℓ.
Поскольку проекционная связь между прямыми КF и 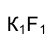 сохраняется в любой момент движения, она не нарушится и при совпадении точек
сохраняется в любой момент движения, она не нарушится и при совпадении точек 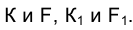 Следовательно, касательная t к кривой ℓ спроецируется на плоскость
Следовательно, касательная t к кривой ℓ спроецируется на плоскость 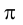 в касательную
в касательную 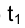 к кривой
к кривой 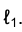
Утверждение, обратное доказанному, неверно. Прямая лишь тогда будет касательной к пространственной кривой в некоторой точке А, когда обе ее проекции будут касательными к соответствующим проекциям кривой в точках, являющихся проекциями точки А.
В отличие от плоской кривой, для определения характера которой достаточно одной ее проекции, в случае пространственной кривой необходимо располагать ее проекциями на плоскости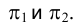
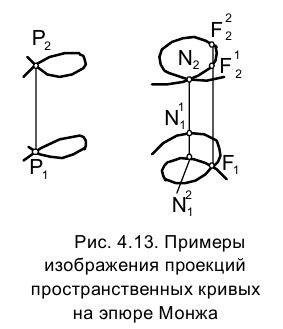
На рис. 4.13 приведены примеры изображения на эпюре Монжа двух пространственных кривых ℓ и m.
Каркасные поверхности
Каркасом поверхности называется множество точек и линий, определяющих поверхность. В свою очередь, поверхности, заданные некоторым непрерывным каркасом, называются каркасными поверхностями.
Место, занимаемое каркасными поверхностями в приведенной выше классификации поверхностей, также условно, как условна и сама классификация поверхностей. Действительно, линейчатую поверхность, поверхность вращения или циклическую поверхность можно задать некоторым каркасом. С другой стороны, целый ряд каркасных поверхностей может быть отнесен к другим классам поверхностей.
В зависимости от способа задания каркасные поверхности подразделяются на поверхности с точечным, линейным или смешанным каркасом. Под точечным каркасом понимается совокупность точек, принадлежащих поверхности. Линейчатый каркас определяется совокупностью принадлежащих поверхности линий, а смешанный - совокупностью линий и точек.
Назначение каркаса поверхности состоит в том, чтобы дать достаточно полное представление о форме поверхности и возможность построить ее подробное изображение на эпюре Монжа.
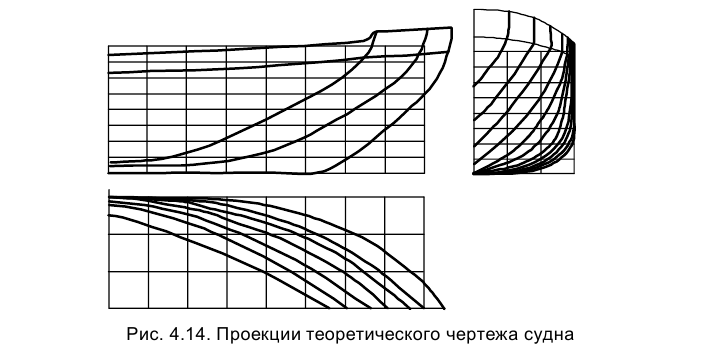
Каркасные способы задания поверхностей, как правило, используются в тех случаях, когда необходимо определить поверхность, образование которой не подчинено никакому геометрическому закону. Характерным примером каркасного задания поверхности является теоретический чертеж судна или летательного аппарата (рис. 4.14).
Построение проекций точек и линий, принадлежащих каркасной поверхности, осуществляется теми же методами, что и при построении точек и линий, принадлежащих плоскости.
Рассмотрим несколько типовых задач на определение элементов каркасных поверхностей.
Задача 1. Предположим, что каркасная поверхность задана семейством линий 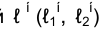 (рис.205). Если задана фронтальная проекция линии n, которая пересекает элементы задания поверхности
(рис.205). Если задана фронтальная проекция линии n, которая пересекает элементы задания поверхности 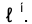 то ее горизонтальная проекция может быть легко построена по проекциям точек пересечения n с
то ее горизонтальная проекция может быть легко построена по проекциям точек пересечения n с 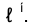 . При этом следует отметить, что положение проекций точек линий на чертеже каркасной поверхности определяется с меньшей точностью, чем на плоскости, так как горизонтальные проекции линий типа n интерполируются по точкам пересечения ее с элементами задания поверхности.
. При этом следует отметить, что положение проекций точек линий на чертеже каркасной поверхности определяется с меньшей точностью, чем на плоскости, так как горизонтальные проекции линий типа n интерполируются по точкам пересечения ее с элементами задания поверхности.
Степень точности решения задач с каркасными поверхностями зависит от частоты задания ее обводов.
Задача 2. Дана горизонтальная проекция точки 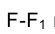 на каркасе
на каркасе 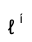 поверхности. Построить фронтальную проекцию точки
поверхности. Построить фронтальную проекцию точки 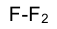 (рис. 4.16).
(рис. 4.16).
Решение.
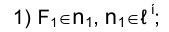
2) строим проекции точек пересечения 
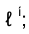
3) по точкам 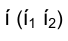 интерполируем фронтальную проекцию линии
интерполируем фронтальную проекцию линии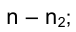 ;
;
4) строим фронтальную проекцию точки  как точки, принадлежащей линии n.
как точки, принадлежащей линии n.
Задача 3. На чертеже каркаса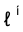 поверхности по горизонтальной проекции кривой
поверхности по горизонтальной проекции кривой  , построить ее фронтальную проекцию
, построить ее фронтальную проекцию 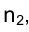 , зная, что эта линия принадлежит поверхности (рис. 4.17).
, зная, что эта линия принадлежит поверхности (рис. 4.17).
Решение.
1) через точку 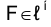 строят пучок линий
строят пучок линий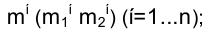
2) определяются горизонтальные проекции точек пересечения пучка линий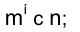 ;
;
3) по горизонтальным проекциям точек пересечения 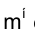 с n строится
с n строится 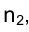 .
.
Задача 4. Построить проекции линий пересечения n горизонтально проецирующей поверхности a каркасной поверхностью 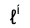 (рис. 4.18). Решение этой задачи сводится к определению второй проекции линии, принадлежащей каркасу поверхности, по заданному
(рис. 4.18). Решение этой задачи сводится к определению второй проекции линии, принадлежащей каркасу поверхности, по заданному
положению ее первой проекции (см. задачу 1).
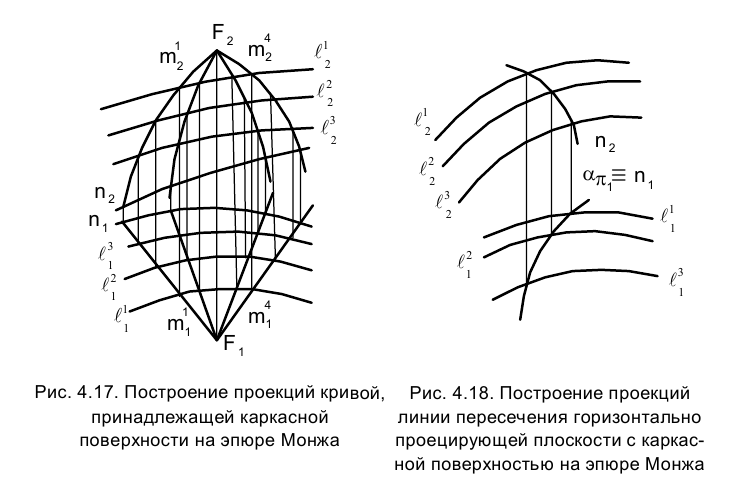
Задача 5. Построить точку F пересечения поверхности 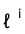 с кривой линией n (рис. 4.19).
с кривой линией n (рис. 4.19).
Решение этой задачи осуществляется с помощью вспомогательной проецирующей поверхности, которую надо подобрать таким образом,
чтобы она пересекала элементы 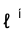 , задающие каркас исходной поверхности.
, задающие каркас исходной поверхности.
Последовательность решения задачи:
1) заключаем кривую n в проецирующую поверхность a;
2) строим кривую m, по которой a пересекает поверхность 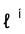 ;
;
3) строим точку F пересечения кривых m и n.
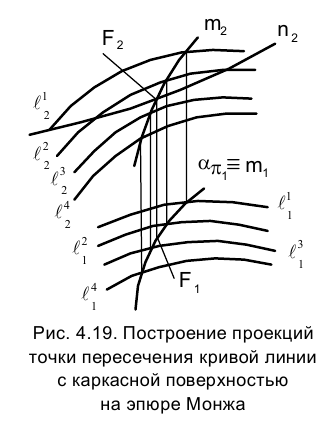
Схема решения этой задачи совпадает со схемой решения задачи на пересечение прямой с плоскостью.
Позиционные задачи на поверхности
Построение проекций точки, принадлежащей кривой поверхности, в принципе аналогично построению точки, принадлежащей поверхности многогранника (см. разд. 3.). Для линейчатой поверхности эта задача решается построением образующей, на которой находится данная точка.
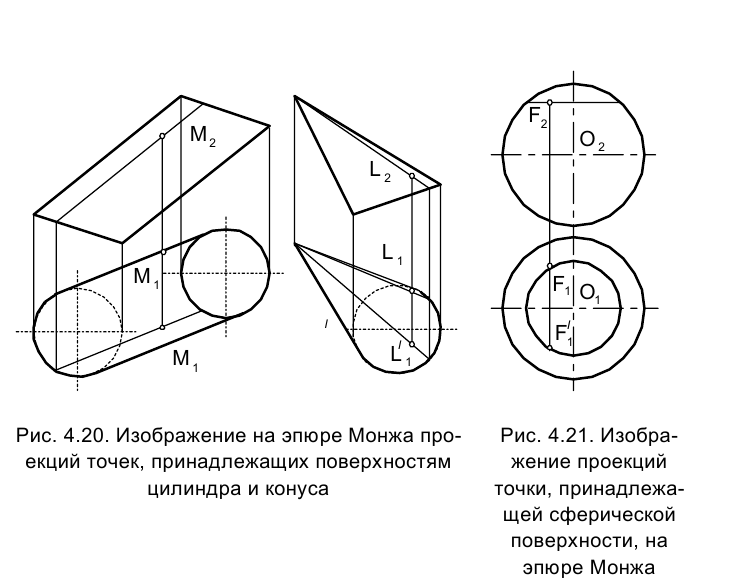
Так, если задана фронтальная проекция точки 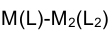 на поверхности цилиндра или конуса, то, построив проекции образующих, проходящих в пространстве через точку М(L), можно определить горизонтальные проекции
на поверхности цилиндра или конуса, то, построив проекции образующих, проходящих в пространстве через точку М(L), можно определить горизонтальные проекции 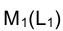 этой точки (рис. 4.20). Следует заметить, что фронтальной проекции точки
этой точки (рис. 4.20). Следует заметить, что фронтальной проекции точки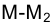 в пространстве соответствуют две точки, лежащие на двух образующих, фронтальные проекции которых совпадают с фронтальной проекцией образующей, проведенной через точку M. Горизонтальные же проекции этих образующих на эпюре не совпадают.
в пространстве соответствуют две точки, лежащие на двух образующих, фронтальные проекции которых совпадают с фронтальной проекцией образующей, проведенной через точку M. Горизонтальные же проекции этих образующих на эпюре не совпадают.
Построение точки на сферической поверхности требует построения вспомогательной кривой, в качестве которой воспользоваться параллелью, т.е. кривой на поверхности сферы, параллельной плоскости 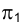 (рис. 4.21).
(рис. 4.21).
На плоскости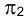 параллель изобразится отрезком прямой, перпендикулярной направлению проецирования, а на плоскости
параллель изобразится отрезком прямой, перпендикулярной направлению проецирования, а на плоскости 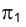 - в истинную величину - окружностью с диаметром, равным указанному выше отрезку, и центром, совпадающим с центром окружности большого круга, определяющей горизонтальную проекцию сферы.
- в истинную величину - окружностью с диаметром, равным указанному выше отрезку, и центром, совпадающим с центром окружности большого круга, определяющей горизонтальную проекцию сферы.
Итак, если на поверхности сферы задана фронтальная проекция принадлежащей ей точки 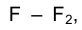 то построив параллель, проходящую через эту точку, определим ее горизонтальные проекции.
то построив параллель, проходящую через эту точку, определим ее горизонтальные проекции.
Вновь, как и в рассмотренном выше случае линейчатых поверхностей, следует внести коррективы, связанные с тем, что в действительности в пространстве точка F является фронтальной проекцией двух принадлежащих поверхности сферы точек, расположенных на прямой, перпендикулярной плоскости 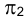 . Поэтому следует иметь в виду, что, задавая точку, принадлежащую поверхности сферы на эпюре Монжа, ее фронтальной или горизонтальной проекцией мы, по сути дела, строим проекции двух различных точек сферы.
. Поэтому следует иметь в виду, что, задавая точку, принадлежащую поверхности сферы на эпюре Монжа, ее фронтальной или горизонтальной проекцией мы, по сути дела, строим проекции двух различных точек сферы.
Значительный интерес с точки зрения использования в инженерной практике полученных результатов представляют решения задач по определению истинной формы сечений, получающихся при пересечении плоскостью конической поверхности. В зависимости от взаимной ориентации в пространстве конической поверхности и пересекающей ее плоскости в сечении могут получиться различные линии:
эллипс, парабола, гипербола, окружность, пересекающиеся прямые, а также точка.
Для иллюстрации вышесказанного рассмотрим конус вращения, пересекаемый проецирующей плоскостью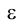 (рис. 4.22).
(рис. 4.22).
1. Если фронтально проецирующая плоскость 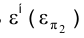 пересекает все образующие конуса, то в сечении в общем случае получается эллипс (рис. 4.22а). Поскольку плоскость e при этом не параллельна ни одной из образующих конуса, то она пересекается с каждой из них в конечной точке и, следовательно, эллипс представляет собой кривую, не имеющую бесконечно удаленных (несобственных) точек. В частных случаях вместо эллипса в сечении может получиться окружность или даже точка (рис. 4.22а).
пересекает все образующие конуса, то в сечении в общем случае получается эллипс (рис. 4.22а). Поскольку плоскость e при этом не параллельна ни одной из образующих конуса, то она пересекается с каждой из них в конечной точке и, следовательно, эллипс представляет собой кривую, не имеющую бесконечно удаленных (несобственных) точек. В частных случаях вместо эллипса в сечении может получиться окружность или даже точка (рис. 4.22а).
2. Если секущая плоскость e параллельна одной из образующих конуса, то в сечении получается парабола (рис. 4.22б). Секущая плоскость e пересекает все образующие, кроме одной - той, которой она параллельна. Следовательно, парабола имеет одну бесконечно удаленную точку. В частном случае вместо параболы может получиться прямая (см. рис. 4.22б), что соответствует случаю, когда секущая плоскость становится касательной к поверхности конуса. В этом случае плоскость называют предельной секущей плоскостью.
3. Если секущая плоскость e параллельна двум образующим конуса, то в сечении получается гипербола (рис. 4.22в). Рассуждая аналогично вышесказанному, можно прийти к выводу, что гипербола имеет две бесконечно удаленные точки. Частным случаем является параллельность секущей плоскости оси конуса. В этом случае она параллельна двум образующим, проекции которых совпадают с проекциями оси. Получающаяся в сечении кривая линия также является гиперболой.
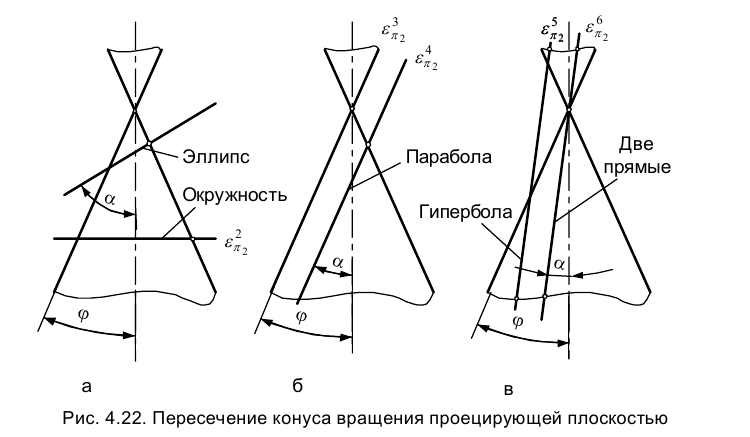
Анализируя три упомянутые выше кривые, можно различать их по числу бесконечно удаленных точек. Эллипс их не имеет, парабола имеет одну, гипербола - две.
То или иное конкретное коническое сечение можно определить, сравнивая величину половины угла при вершине конуса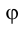 и величину угла наклона секущей плоскости к оси конуса a.
и величину угла наклона секущей плоскости к оси конуса a.
Если:
- 1)
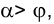 , то сечение - эллипс;
, то сечение - эллипс; - 2)
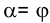 , то сечение - парабола;
, то сечение - парабола; - 3)
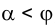 , то сечение - гипербола.
, то сечение - гипербола.
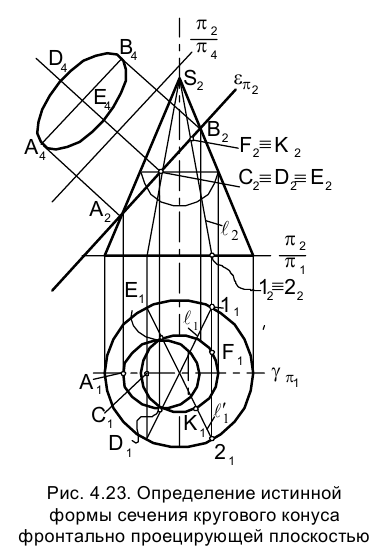
В заключение рассмотрим задачу об определении истинной величины эллипса, полученного при пересечении прямого кругового конуса фронтально проецирующей плоскостью на эпюре Монжа (рис. 4.23).
Следы плоскости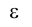 на фронтальной плоскости проекций -
на фронтальной плоскости проекций -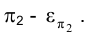 . Так как заданный конус Ф (S,L) и плоскость имеют в качестве общей плоскости симметрии горизонтально проецирующую плоскость
. Так как заданный конус Ф (S,L) и плоскость имеют в качестве общей плоскости симметрии горизонтально проецирующую плоскость 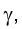 , проходящую через вершину конуса S, то сам эллипс сечения и его горизонтальная проекция симметричны относительно этой плоскости. Горизонтальная проекция эллипса сечения симметрична относительно следа плоскости на горизонтальной плоскости проекций
, проходящую через вершину конуса S, то сам эллипс сечения и его горизонтальная проекция симметричны относительно этой плоскости. Горизонтальная проекция эллипса сечения симметрична относительно следа плоскости на горизонтальной плоскости проекций 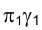 и также является эллипсом.
и также является эллипсом.
Отрезок 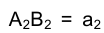 большая ось эллипса; малая же ось эллипса определяется хордой окружности, лежащей в плоскости, параллельной
большая ось эллипса; малая же ось эллипса определяется хордой окружности, лежащей в плоскости, параллельной 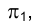 , и проходящей через точку С - середину отрезка
, и проходящей через точку С - середину отрезка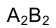 большой оси эллипса. Направление указанной хорды совпадает с направлением проецирования точек.
большой оси эллипса. Направление указанной хорды совпадает с направлением проецирования точек.
Итак, концами большой оси эллипса являются точки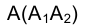 и
и 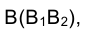 , а малой - точки .
, а малой - точки .
Построение проекций произвольной точки, принадлежащей эллипсу сечения, например точки 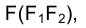 , осуществляется построением проекций проходящей через эту точку образующей. Так, через фронтальную проекцию вершины
, осуществляется построением проекций проходящей через эту точку образующей. Так, через фронтальную проекцию вершины 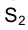 конуса и фронтальную проекцию точки
конуса и фронтальную проекцию точки 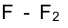 строится фронтальная проекция
строится фронтальная проекция 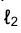 образующей ℓ конуса. Прямая
образующей ℓ конуса. Прямая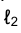 пересекает фронтальную проекцию основания конуса в точке
пересекает фронтальную проекцию основания конуса в точке 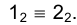 Соответствующие горизонтальные проекции точек 1 и 2 –
Соответствующие горизонтальные проекции точек 1 и 2 – 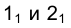 - найдутся как точки пересечения направления проецирования, проведенного через точку
- найдутся как точки пересечения направления проецирования, проведенного через точку 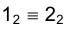 с окружностью основания конуса.
с окружностью основания конуса.
Прямые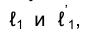 , проведенные через горизонтальную проекцию вершины конуса и точки
, проведенные через горизонтальную проекцию вершины конуса и точки 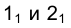 соответственно, определяют на эпюре горизонтальные проекции образующих, проходящих в пространстве через точки F и К эллипса сечения, фронтальные проекции которых совпадают с точкой
соответственно, определяют на эпюре горизонтальные проекции образующих, проходящих в пространстве через точки F и К эллипса сечения, фронтальные проекции которых совпадают с точкой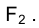 .
.
Горизонтальные проекции точек F и К –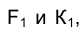 принадлежащие горизонтальной проекции эллипса сечения, находятся в пересечении направления проецирования, проведенного через точку
принадлежащие горизонтальной проекции эллипса сечения, находятся в пересечении направления проецирования, проведенного через точку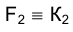 с прямыми
с прямыми 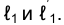
1. Приведенным выше способом можно построить горизонтальные проекции любого числа точек эллипса сечения. По существу, мы воспользовались решением задачи 4 раздела 1.5 о нахождении точек встречи прямой (образующей конуса) с проецирующей плоскостью.
Для построения истинной величины эллипса сечения можно воспользоваться, например, способом замены плоскостей проекций. Так на рис. 4.23 плоскость 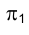 в старой системе плоскостей
в старой системе плоскостей 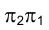 проекций заменена плоскостью
проекций заменена плоскостью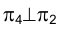 и параллельной плоскости e в новой системе плоскостей проекций
и параллельной плоскости e в новой системе плоскостей проекций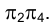 .
.
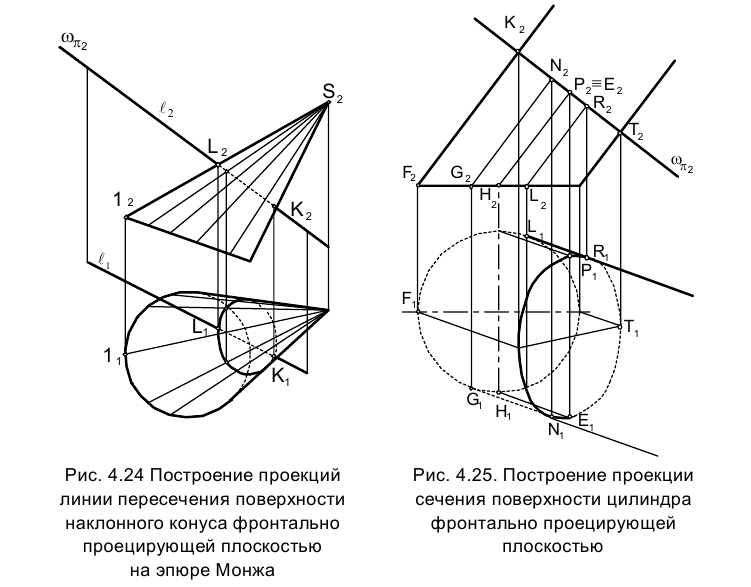
Построим линию пересечения фронтально проецирующей плоскости c с поверхностью наклонного конуса (рис. 4.24).
Для построения эллипса, который, как видно из рисунка, является линией пересечения плоскости c с поверхностью конуса, воспользуемся хорошо известным решением задачи о нахождении точки встречи прямой с проецирующей плоскостью (раздел 1.5, задача 4).
При этом в качестве заданной прямой в пространстве последовательно выбираются образующие конуса, а на эпюре их проекции.
Аналогично решается задача о пересечении фронтально проецирующей плоскостью цилиндрической поверхности (рис. 4.25).
На рис. 4.26 приведено решение задачи о пересечении горизонтально проецирующей плоскостью сферической поверхности. Видно, что находящийся внутри контура горизонтальной проекции сферы отрезок следа горизонтально проецирующей плоскости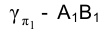 и представляет собой горизонтальную проекцию сечения.
и представляет собой горизонтальную проекцию сечения.
Фронтальная проекция получающегося сечения представляет собой эллипс, большая ось которого 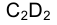 равна длине отрезка А1В1.
равна длине отрезка А1В1.
На эпюре Монжа она по направлению совпадает с направлением проецирования точек, проведенным через точку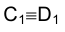 - середину отрезка
- середину отрезка 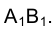
Для определения видимости элементов эллипса сечения на фронтальной плоскости проекций следует провести горизонтально проецирующую плоскость 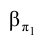 , параллельную плоскости
, параллельную плоскости 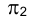 через центр сферы O. Сечение поверхности сферы плоскостью b - окружность большого круга, пересекающая в пространстве окружность, получающуюся в сечении сферы плоскостью c в точках Р и R, горизонтальные проекции которых
через центр сферы O. Сечение поверхности сферы плоскостью b - окружность большого круга, пересекающая в пространстве окружность, получающуюся в сечении сферы плоскостью c в точках Р и R, горизонтальные проекции которых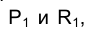 , совпадают друг с другом и с точкой пересечения следов проецирующих плоскостей
, совпадают друг с другом и с точкой пересечения следов проецирующих плоскостей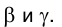
Фронтальные проекции точек Р и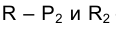 - определяются как точки пересечения направления проецирования, проходящего через точку Р1ºR1, с окружностью большого круга и определяют границы видимости эллипса сечения сферы плоскостью
- определяются как точки пересечения направления проецирования, проходящего через точку Р1ºR1, с окружностью большого круга и определяют границы видимости эллипса сечения сферы плоскостью 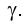 .
.
Для нахождения точек, при надлежащих эллипсу сечения и не лежащих на его осях, можно пересечь сферу несколькими горизонтально проецирующими плоскостями, параллельными плоскости 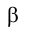 Фронтальные проекции точек пера сечения окружностей, получающихся в
Фронтальные проекции точек пера сечения окружностей, получающихся в
сечениях этими плоскостями сферической поверхности с окружностью, полученной при пересечении сферы плоскостью 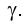 и являются дополнительными точками, необходимыми для построения эллипса.
и являются дополнительными точками, необходимыми для построения эллипса.
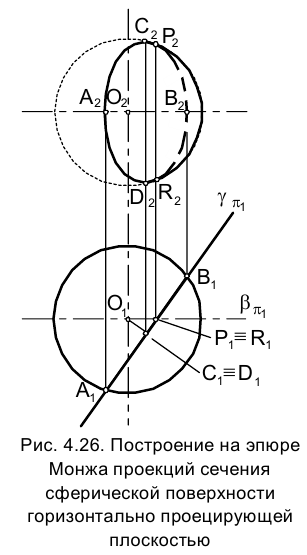
Пересечение поверхности с прямой линией
Алгоритм решения данного класса задач является основой для нахождения решения более сложных задач о взаимном пересечении поверхностей. В общем случае он формулируется следующим образом
- через прямую следует провести вспомогательную плоскость;
- найти линию пересечения этой плоскости с данной поверхностью;
- определить точки пересечения полученной линии с данной прямой.
Как видно, приведенный алгоритм решения напоминает алгоритм решения задачи о нахождении точки встречи прямой с плоскостью общего положения. В данном случае через прямую можно, аналогично упомянутому случаю, провести бесчисленное множество различных плоскостей, однако для упрощения решения задачи следует выбрать вспомогательную плоскость так, чтобы можно было наиболее просто построить линию ее пересечения с поверхностью.
Рассмотрим задачу об определении точек пересечения прямой ℓ 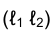 с конической поверхностью (рис. 4.27).
с конической поверхностью (рис. 4.27).
Проведем через прямую ℓ фронтально проецирующую плоскость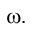 и построим аналогично решению предыдущей задачи (см. рис. 4.24)
и построим аналогично решению предыдущей задачи (см. рис. 4.24)
проекцию эллипса сечения плоскостью 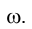 . Найденная горизонтальная проекция эллипса сечения представляет собой, в соответствии со сформулированным выше общим алгоритмом решения, горизонтальную проекцию линии пересечения плоскости
. Найденная горизонтальная проекция эллипса сечения представляет собой, в соответствии со сформулированным выше общим алгоритмом решения, горизонтальную проекцию линии пересечения плоскости 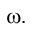 с поверхностью конуса.
с поверхностью конуса.
Точки пересечения горизонтальной проекций прямой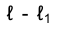 с горизонтальной проекцией построенной линии являются горизонтальными проекциями
с горизонтальной проекцией построенной линии являются горизонтальными проекциями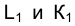 точек К и L пересечения прямой ℓ с поверхностью конуса. Фронтальные проекции этих точек
точек К и L пересечения прямой ℓ с поверхностью конуса. Фронтальные проекции этих точек 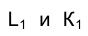 найдутся в пересечении фронтальной проекции прямой ℓ - ℓ2 с направлениями проецирования, проведенными через точки
найдутся в пересечении фронтальной проекции прямой ℓ - ℓ2 с направлениями проецирования, проведенными через точки 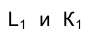
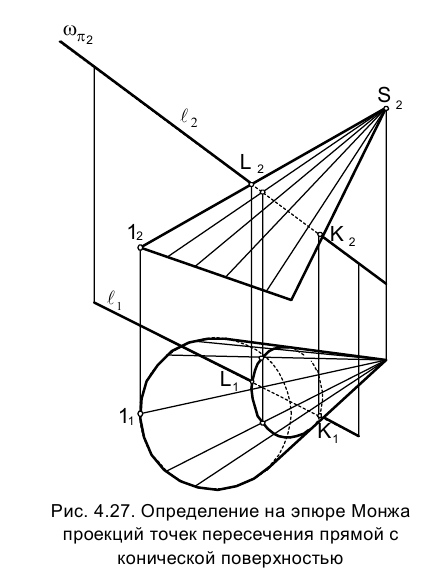
Следует заметить, что указанное решение не обладает достаточной точностью из-за необходимости строить кривую линию пересечения вспомогательной плоскости с кривой поверхностью с помощью лекал. Поэтому часто бывает целесообразнее применить другой более точный и изящный способ.
Найдем точки пересечения прямой общего положения ℓ с конусом произвольного вида.
Рассмотрим сначала пространственную интерпретацию решения. Проведем через прямую ℓ и вершину конуса S вспомогательную плоскость 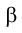 (рис. 4.28). Плоскость
(рис. 4.28). Плоскость 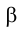 - одна из зачисленного множества плоскостей, содержащих прямую ℓ, пересекает конус по образующим.
- одна из зачисленного множества плоскостей, содержащих прямую ℓ, пересекает конус по образующим.
Найдем линию пересечения плоскости  с плоскостью основания конуса
с плоскостью основания конуса 
Плоскость основания конуса g может быть произвольно расположена в пространстве. На рис. 4.28 след плоскости 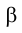 на плоскости g определяется точками F и М, где F - точка пересечения прямой ℓ с плоскостью
на плоскости g определяется точками F и М, где F - точка пересечения прямой ℓ с плоскостью 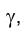 , а М - точка пересечения с плоскостью g произвольной прямой, проходящей через вершину конуса S и пересекающей прямую ℓ в точке К.
, а М - точка пересечения с плоскостью g произвольной прямой, проходящей через вершину конуса S и пересекающей прямую ℓ в точке К.
Через точки пересечения следа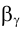 - F и М с контуром основания конуса А и В и вершину конуса S проходят образующие АS и ВS, по которым вспомогательная плоскость
- F и М с контуром основания конуса А и В и вершину конуса S проходят образующие АS и ВS, по которым вспомогательная плоскость 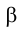 пересекает поверхность конуса. Точки G и H пересечения образующих АS и ВS с прямой ℓ и являются точками встречи прямой ℓ, с поверхностью конуса. Рис. 4.29 иллюстрирует решение задачи в соответствии с рассмотренным алгоритмом на эпюре Монжа. Отметим лишь, что плоскость
пересекает поверхность конуса. Точки G и H пересечения образующих АS и ВS с прямой ℓ и являются точками встречи прямой ℓ, с поверхностью конуса. Рис. 4.29 иллюстрирует решение задачи в соответствии с рассмотренным алгоритмом на эпюре Монжа. Отметим лишь, что плоскость 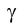 - фронтально проецирующая.
- фронтально проецирующая.
Ознакомившись на примере конической поверхности с общим алгоритмом решения, рассмотрим теперь еще один конкретный пример.
На рис. 4.30 приведено решение задачи об определении точек пересечения отрезка прямой АВ с поверхностью цилиндра. В основу решения положено построение вспомогательной плоскости a, содержащей отрезок прямой АВ и заданной отрезками пересекающихся прямых 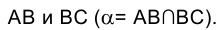
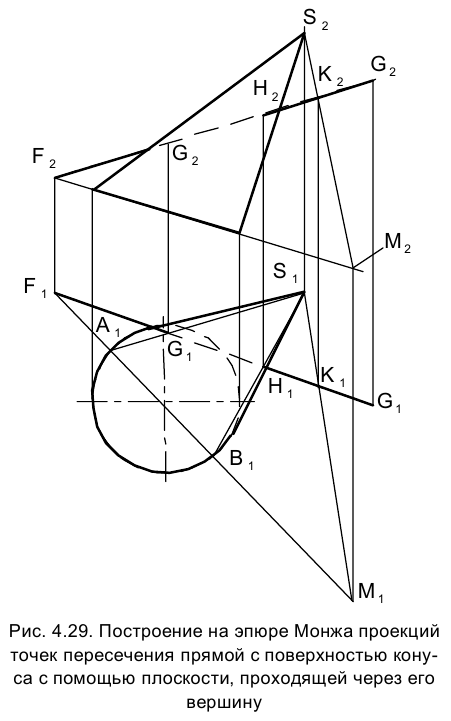
Плоскость a пересекает плоскость нижнего основания цилиндра. Поскольку отрезок ВС параллелен образующим цилиндра, плоскость a пересекает его боковую поверхность по образующим, проведенным через точки N и Р его основания.
Построив горизонтальные проекции этих образующих 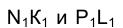 и определив точки их пересечения с горизонтальной проекцией прямой
и определив точки их пересечения с горизонтальной проекцией прямой 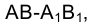 находим горизонтальные проекции точек пересечения отрезка прямой АВ с поверхностью цилиндра
находим горизонтальные проекции точек пересечения отрезка прямой АВ с поверхностью цилиндра 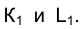 . Построение затем фронтальных проекций точек К и L -
. Построение затем фронтальных проекций точек К и L - 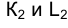 - очевидно.
- очевидно.
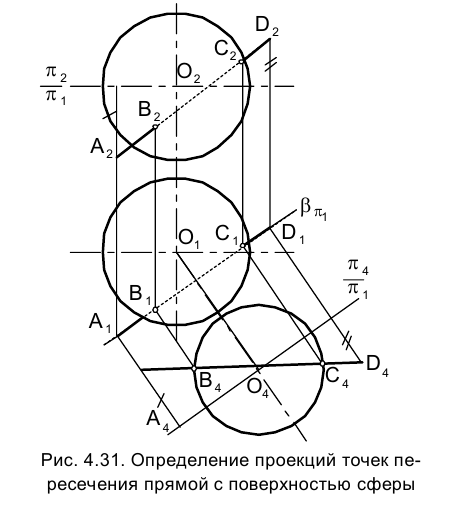
Для определения точек пересечения прямой линии со сферической поверхностью можно использовать способ замены плоскостей проекций. На рис. 4.31 приведено изображение на эпюре Монжа проекций сферы с центром в точке 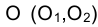 и отрезка прямой
и отрезка прямой 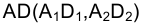 . Заменим фронтальную плоскость
. Заменим фронтальную плоскость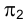 в старой
в старой 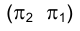 системе плоскостей проекций плоскостью
системе плоскостей проекций плоскостью 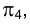 , содержащей отрезок АВ и перпендикулярной плоскости
, содержащей отрезок АВ и перпендикулярной плоскости 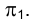 .
.
Новая система плоскостей проекций - (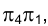 ). Ортогональная проекция отрезка АD на плоскость
). Ортогональная проекция отрезка АD на плоскость 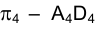 – определяет его истинную величину, направление проецирования точек в системе плоскостей проекций
– определяет его истинную величину, направление проецирования точек в системе плоскостей проекций 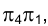 , естественно, перпендикулярно горизонтальной проекции отрезка АD –
, естественно, перпендикулярно горизонтальной проекции отрезка АD – 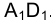 . B качестве линии отсчета
. B качестве линии отсчета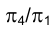 в системе плоскостей проекций
в системе плоскостей проекций 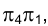 выбирается прямая, параллельная направлению оси проекций
выбирается прямая, параллельная направлению оси проекций 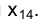
Поскольку в системе плоскостей проекций 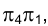 , фронтальная проекция центра сферы
, фронтальная проекция центра сферы 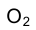 принадлежит линии отсчета , очевидно, что проекция центра сферы
принадлежит линии отсчета , очевидно, что проекция центра сферы 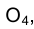 , как и проекция центра окружности, получающейся в сечении сферы плоскостью
, как и проекция центра окружности, получающейся в сечении сферы плоскостью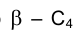 на плоскость
на плоскость 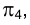 , должны находиться на линии отсчета
, должны находиться на линии отсчета 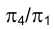
Из точки 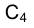 как из центра проведем окружность - изображение истинной величины сечения поверхности сферы плоскостью b радиусом, равным половине длины части отрезка
как из центра проведем окружность - изображение истинной величины сечения поверхности сферы плоскостью b радиусом, равным половине длины части отрезка 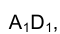 , заключенного внутри горизонтальной проекции сферы.
, заключенного внутри горизонтальной проекции сферы.
Точки пересечения построенной окружности с отрезком 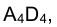 , определяют положение проекций точек пересечения отрезка AD с поверхностью сферы на плоскости
, определяют положение проекций точек пересечения отрезка AD с поверхностью сферы на плоскости 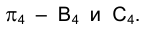 Положение проекций точек В и С в старой системе плоскостей проекций
Положение проекций точек В и С в старой системе плоскостей проекций 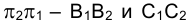 определяется проведением соответствующих направлений проецирования.
определяется проведением соответствующих направлений проецирования.
Классификация поверхностей
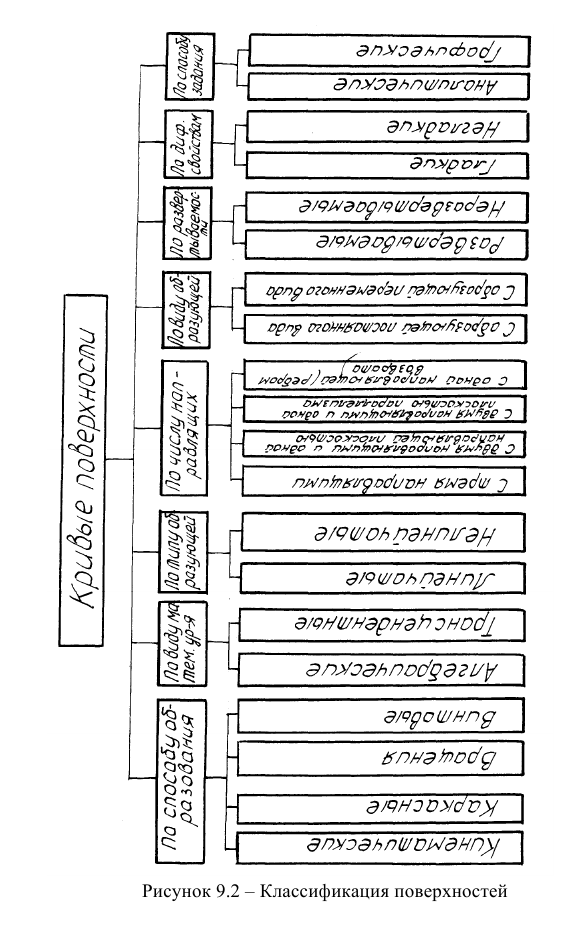
На рисунке 9.2 приведена общая приближенная схема классификации кривых поверхностей по различным признакам. При этом следует сказать, что систематизация поверхностей при их величайшем многообразии является сложной математической и геометрической задачей.
Тот факт, что одна и та же поверхность может быть образована различными способами, превносит в любую схему классификации относительную приблизительность.
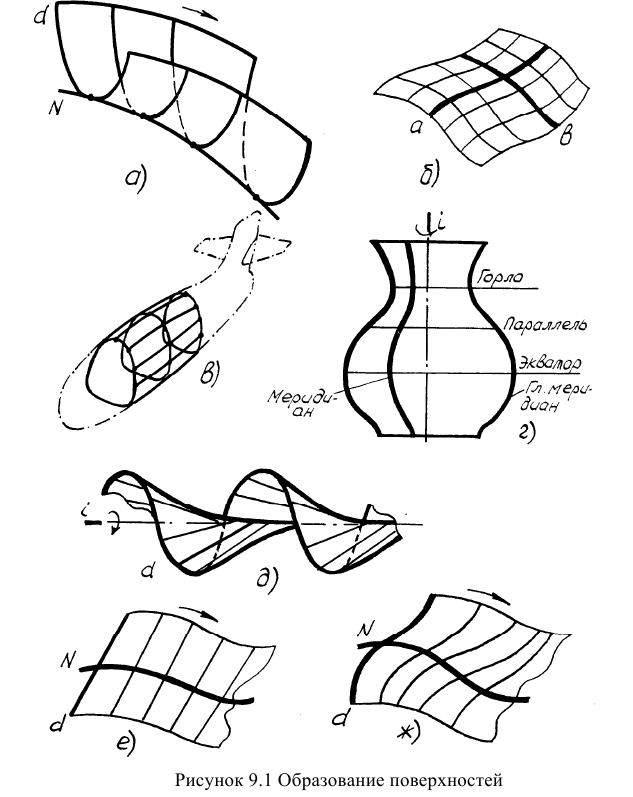
Поверхности в общем случае могут быть образованы путем поступательного перемещения в пространстве образующей (кинематический способ), путем задания её каркасом (каркасный способ), путем особого винтового перемещения образующей (винтовой способ), Поверхности в соответствии с конкретным способом образования могут называться кинематическими, каркасными, поверхностями вращения, винтовыми поверхностями. Однако некоторые виды поверхностей могут быть образованы как теми, так и другими способами.
Каркасный способ образования и задания поверхностей осуществляется множеством точек или линий, принадлежащих поверхности. Множество точек или линий, определяющих поверхность, называется каркасом. Каркасы подразделяются на точечные и линейные. Наиболее распространены линейные каркасы. На рисунке 9.16 показан каркас поверхности, состоящий из двух ортогонально расположенных семейств линий. На рисунке 9.1 в показан каркас фюзеляжа самолета. Поверхности вращения - это поверхности, которые образуются какой-либо образующей при вращении её вокруг неподвижной оси в соответствии с рисунком 9.1г. Каждая точка образующей при вращении вокруг оси описывает окружность с центром на оси вращения. Эти окружности называются параллелями. Наибольшую и наименьшую параллели называют соответственно экватором и горлом.
Плоскости, проходящие через ось вращения, называют
меридиональными, а линии, по которым они пересекают поверхности, -меридианами. Меридиан в плоскости, параллельной фронтальной плоскости проекций, называется главным меридианом или очерковой образующей.
Винтовые поверхности - это поверхности, которые образуются винтовым перемещением образующей в соответствии с рисунком 9.1д. Винтовые поверхности могут быть образованы как криволинейной, так и прямолинейной образующей. Непременным условием образования винтовой поверхности является условие перемещения образующей по винтовой линии.
В качестве образующих поверхности используются прямые и кривые линии. Если образующей является прямая, то поверхность называется линейчатой, если кривая линия - нелинейчатой (рисунок 9.1е, ж).
Поверхности можно классифицировать по числу направляющих. Линейчатая поверхность в общем случае однозначно определяется тремя направляющими линиями. Следовательно, чтобы задать линейчатую поверхность на эпюре Монжа, достаточно указать проекции трех её направляющих. Третью направляющую при этом необходимо задать так,чтобы она находилась внутри конгруэнции прямых, определяемой двумя уже взятыми направляющими.
Поверхность может быть образована двумя направляющими и одной направляющей плоскостью, при этом образующая составляет с направляющей плоскостью какой-либо угол, сохраняемый при перемещении образующей. Если образующая всегда будет параллельна направляющей плоскости, то в этом случае направляющая плоскость называется плоскостью параллелизма.
Линейчатые поверхности, образованные одной направляющей, называются торсами. Торсом называют линейчатую поверхность, которую можно совместить всеми её точками с плоскостью без складок и разрывов.
Это свойство линейчатых поверхностей характеризует их возможность развертываться в плоскость.
Образующая кривой поверхности может быть постоянной и переменной. Переменная образующая может менять свои размеры и форму в процессе перемещения. По этому признаку поверхности делятся на поверхности с постоянной и поверхности с переменной образующей.
Поверхности, в каждой точке которых можно провести одну касательную плоскость, называются гладкими поверхностями. Если в некоторых точках поверхности можно провести несколько касательных плоскостей или, если в этих точках меняется направление касательной плоскости, то такие поверхности называются негладкими.
Поверхности, которые подчиняются какому-либо уравнению, называются аналитическими или закономерными. Поверхности, которые нельзя описать уравнениями, можно задать только графически. Такие поверхности называются графическими или конструкторскими.
Приведем примеры поверхностей, приведенных в схеме классификации. К поверхностям, полученным тремя направляющими, можно отнести косой цилиндр, дважды косой цилиндроид, однополостный гиперболоид и др. Представителями нелинейчатых поверхностей с переменной образующей являются каналовые и циклические поверхности. Среди нелинейчатых поверхностей с постоянной образующей можно отметить трубчатые поверхности.
К линейчатым поверхностям с двумя направляющими и одной направляющей плоскостью относятся косой цилиндроид, косой коноид. Если образующая параллельна плоскости параллелизма, то образуется прямой цилиндроид, прямой коноид, косая плоскость.
К линейчатым поверхностям с одной направляющей относятся поверхность с ребром возврата, цилиндрическая и коническая поверхности.
Линейчатые поверхности
Линейчатая поверхность в общем случае однозначно определяется тремя направляющими линиями. 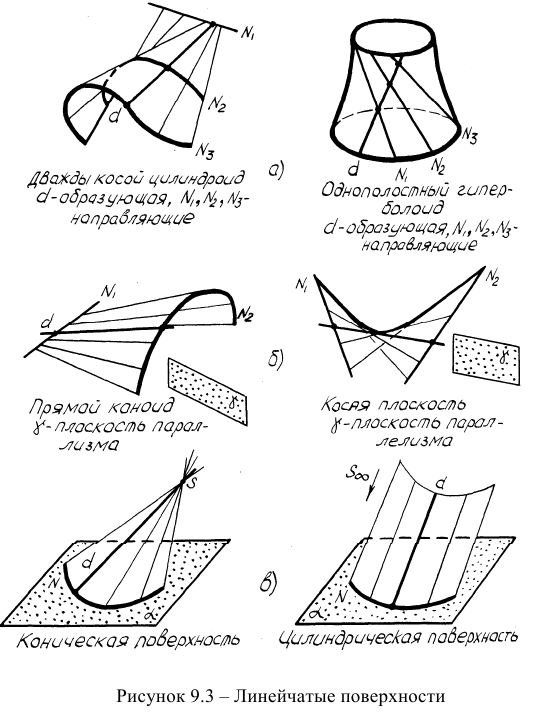
Поверхность дважды косого цилиндроида (рисунок 9.3а) образуется в том случае, когда две из трех направляющих - кривые линии, в третья -прямая линия. Поверхность однополостного гиперболоида может быть получена при движении прямолинейной образующей по трем скрещивающимся прямым, не параллельным одной плоскости. Очерковой образующей такой поверхности будет являться гипербола. Примером практического использования гиперболоидов в технике является башня инженера Шухова.
Поверхность прямого коноида (рисунок 9.36) может быть получена в том случае, когда из двух направляющих одна является прямой линией. Для задания на эпюре прямого коноида необходимо указать проекции кривой и прямой направляющих и плоскости параллелизма. Косая плоскость или гиперболический параболоид может быть получен при скольжении прямой по двум скрещивающимся прямолинейным направляющим, при этом образующая все время остается параллельной плоскости параллелизма в соответствие с рисунком 9.36.
Линейчатые поверхности с одной направляющей (торсы) образуются, когда образующая (прямая линия) движется по кривой направляющей. Если образующая параллельна какому-либо направлению или пересекается с другими положениями образующей в несобственной точке, то образуются цилиндрические поверхности (рисунок 9.3в). Если все прямолинейные образующие пересекаются в собственной точке S, то образуются конические поверхности (рисунок 9.3в).
Нелинейчатые поверхности
Как было указано, нелинейчатыми поверхностями называются поверхности с криволинейными образующими. Она может быть постоянной или переменной.
Среди поверхностей с переменной образующей можно выделить каналовые поверхности (рисунок 9.4а). Каналовая поверхность образована непрерывным каркасом замкнутых плоских сечений, определенным образом ориентированных в пространстве. Площади этих сечений монотонно изменяются в процессе их перемещения по направляющей. Плоскости образующих могут быть параллельны какой-либо плоскости параллелизма или перпендикулярны к направляющей линии (прямые каналовые поверхности). Каналовые поверхности используются при создании переходных участков трубопроводов от одного диаметра и сечения к другим. 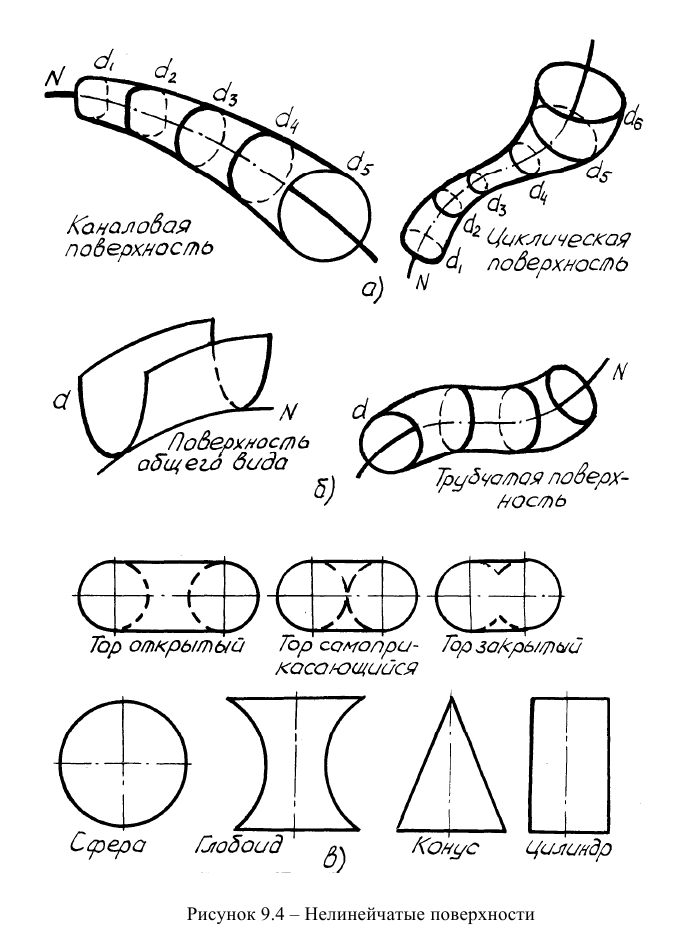
Циклические поверхности образуются с помощью окружностей разного диаметра, центр которых перемещается по криволинейной направляющей в соответствии с рисунком 9.4а.
При постоянной криволинейной образующей могут быть образованы поверхности общего вида и трубчатые поверхности (рисунок 9.46).
Поверхность общего вида образуется произвольной кривой линией, характер перемещения которой определяется формой и положением направляющей и дополнительными условиями, составляющими содержание.
Трубчатая поверхность является частным случаем циклической и каналовой поверхностей. Диаметр образующей окружности при перемещении по криволинейной направляющей не изменяется.
Поверхности вращения
Широкое применение в технике нашли поверхности вращения. Среди поверхностей вращения можно особо выделить торы, сферу, глобоид, конусы вращения, цилиндры вращения, эллипсоид вращения, параболоид вращения, однополостный и двухполостный гиперболоиды (рисунки 9.4в и 9.5а).
Тор - поверхность вращения, образованная вращением окружности (дуги окружности) вокруг компланарной с ней прямой (оси тора). Ось вращения тора не совпадает с центром окружности. Если центр окружности принадлежит оси вращения, то образуется сферическая поверхность.
Торы характеризуются большим многообразием форм. На рисунке 9.4в приведены лишь торы, образуемые вращением полной окружности вокруг оси, не совпадающей с её центром (открытый, самоприкасающийся и закрытый торы).
Глобоид является частным случаем тора. Конические и цилиндрические поверхности вращения образуются при вращении прямой линии вокруг оси. Если образующая пересекается с осью, то образуется прямой круговой конус, если она параллельна оси, то образуется прямой круговой цилиндр. При вращении эллипса, параболы и гиперболы вокруг осей образуются соответственно эллипсоид, параболоид, одно- и двухполостный гиперболоиды вращения. 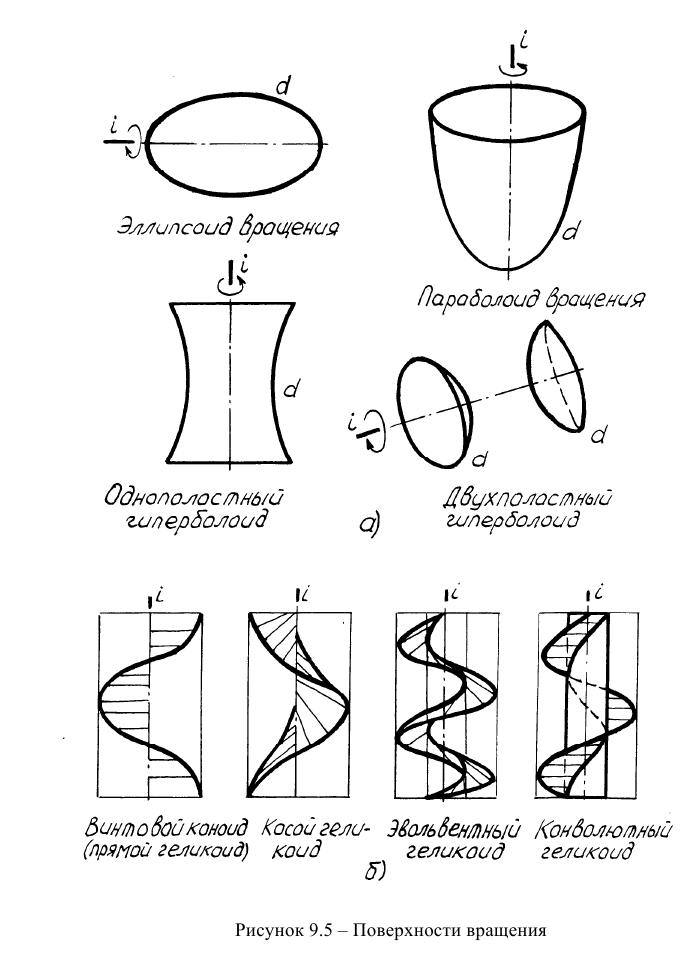
Винтовые поверхности
Среди винтовых поверхностей можно выделить винтовой коноид (прямой геликоид), косой геликоид, эвольвентный геликоид и конволютный геликоид в соответствии с рисунком 9.56. Принцип образования упомянутых винтовых поверхностей ясен из приведенных рисунков.
Прямой геликоид получается в результате движения прямой образующей, которая, пересекая ось под прямым углом, вращается вокруг оси по винтовой линии. Косой геликоид (Архимедов геликоид) получается в результате движения образующей, которая пересекает ось под углом, не равным 90 градусов.
Эвольвентный геликоид образуется, когда образующая во всех своих положениях остается касательной к цилиндрической винтовой линии. Угол наклона образующей к плоскости Н равен углу подъема винтовой линии.
Конволютный геликоид образуется, когда образующая скользит по винтовой линии, оставаясь касательной к цилиндру. Угол наклона образующей к плоскости Н не равен углу подъема винтовой линии.
9.7 Точка на поверхности В связи с тем, что в технике поверхности вращения широко применяются, то дальнейшие геометрические операции целесообразно производить применительно к поверхностям вращения.
Аналогично условию принадлежности точки плоскости можно утверждать, что точка принадлежит поверхности, если она принадлежит прямой или кривой линии, находящейся на этой поверхности. На рисунке 9.6а точка С принадлежит поверхности, так как принадлежит одной из образующих поверхности. В другом примере точка А принадлежит поверхности вращения Ф, так как принадлежит окружности, находящейся на поверхности.
На этом же рисунке представлены различные положения точки на поверхности прямого кругового конуса. Построение проекций точек производится с учетом следующих правил:
1) Если фронтальная проекция точка совпадает с осью, то по крайней мере одна из других проекций точки находится на образующей. В этом случае точка 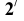 находится по свойству эпюра Монжа: ордината точки на профильной проекции равна ординате точки на горизонтальной проекции;
находится по свойству эпюра Монжа: ордината точки на профильной проекции равна ординате точки на горизонтальной проекции;
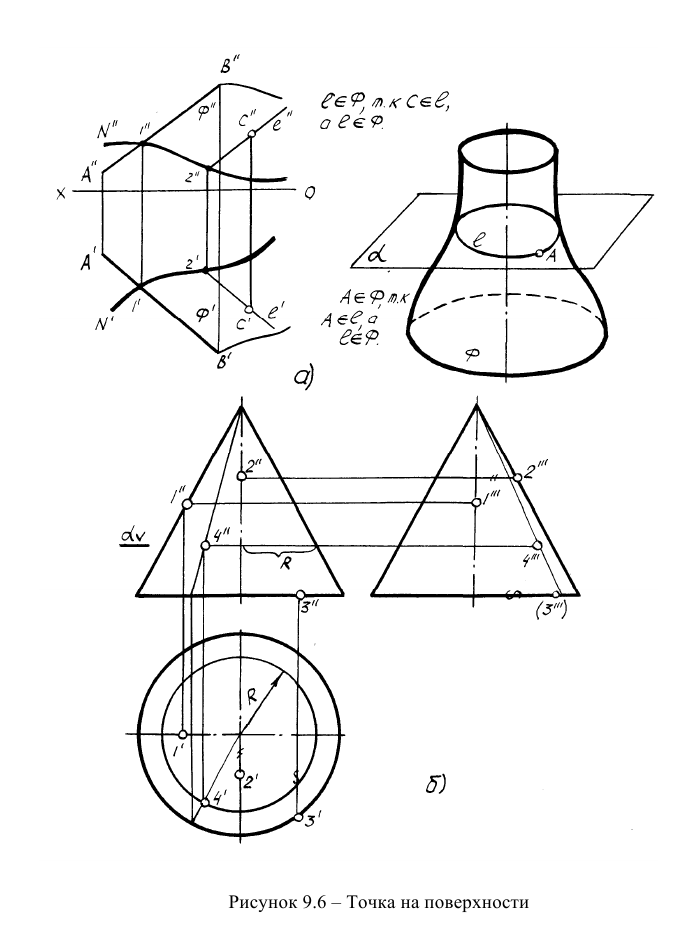
2) Если фронтальная проекция точки находится на образующей, то две другие проекции точки будут находиться на осях;
3) Точки, не находящиеся на оси или образующей, могут быть построены с помощью образующих или методом секущих вспомогательных плоскостей. Метод заключается в следующем. Через точку 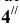 проведем секущую вспомогательную плоскость частного положения (например, горизонтальную плоскость а). В качестве вспомогательной плоскости берут такую плоскость, которая давала бы в сечении исходной поверхности простую фигуру (прямые линии, окружность известного радиуса и т.д.).
проведем секущую вспомогательную плоскость частного положения (например, горизонтальную плоскость а). В качестве вспомогательной плоскости берут такую плоскость, которая давала бы в сечении исходной поверхности простую фигуру (прямые линии, окружность известного радиуса и т.д.).
В сечении конуса вспомогательной плоскостью будет окружность радиуса R. На горизонтальной проекции конуса строим окружность сечения и на ней находим точку 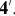 . Точку
. Точку 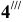 находим по упомянутому свойству эпюра Монжа.
находим по упомянутому свойству эпюра Монжа.
Точки 1, 2, 3 на рисунке 9.6 называются характерными. Построение проекций этих точек не вызывает затруднений.
Сечение поверхностей плоскостями
Сечение поверхностей плоскостями частного и общего положения является одной из главных тем начертательной геометрии. Основой этой темы являются конические, цилиндрические, сферические и торовые сечения. Наглядное изображение сечений упомянутых поверхностей представлено на рисунке 9.7.
Самой интересной поверхностью, с точки зрения разнообразия сечений, является поверхность прямого кругового конуса.
Если секущая плоскость проходит параллельно основанию, то в сечении получается окружность, радиус которой равен расстоянию от оси конуса до образующей вдоль следа секущей плоскости.
Если секущая плоскость не параллельна основанию и пересекает обе очерковые образующие, то в сечении получается эллипс. Плоскость, параллельная оси конуса, в сечении образует гиперболу.
Если секущая плоскость пересекает одну из образующих и угол её наклона равен углу наклона образующей, то в сечении образуется парабола.
Плоскость, проходящая через вершину конуса, в сечении образует треугольник. 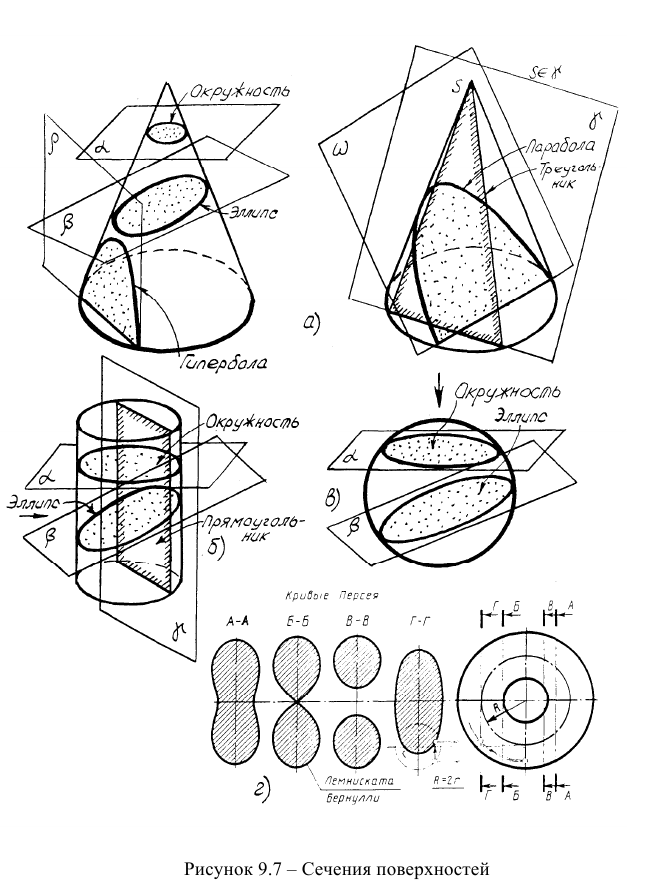
Цилиндрические сечения менее разнообразны. Наклонное сечение цилиндра является эллипсом, сечение плоскостью, параллельной оси,
представляет из себя прямоугольник. В сечении цилиндра плоскостью, перпендикулярной оси, образуется окружность.
Всякое сечение сферы есть окружность, если проецирование происходит в направлении, перпендикулярном плоскости сечения, и эллипс, если это не соблюдается.
Возможные сечения открытого тора представлены на рисунке 9.7г. Одно из сечений является лемнискатой Бернулли (сечение Б-Б), другие кривые линии являются графическими линиями и называются кривыми Персея.
Сечение поверхностей вращения плоскостью частного положения на примере сферы представлено на рисунке 9.8. Построение сечения начнем с поиска характерных точек. Это точки 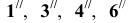 на фронтальной проекции. Остальные проекции точек находим по методике, рассмотренной ранее (см. тему "Точка на поверхности"). Далее намечаем промежуточные точки
на фронтальной проекции. Остальные проекции точек находим по методике, рассмотренной ранее (см. тему "Точка на поверхности"). Далее намечаем промежуточные точки 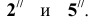 Проводим через указанные точки вспомогательные плоскости
Проводим через указанные точки вспомогательные плоскости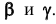 На горизонтальной проекции строим окружности сечений радиусами
На горизонтальной проекции строим окружности сечений радиусами 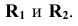 Там, где линии связи точек 2 и 5 пересекают контуры сечений получаем горизонтальные проекции точек
Там, где линии связи точек 2 и 5 пересекают контуры сечений получаем горизонтальные проекции точек 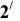 и
и 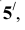 а затем строим их профильные проекции. Полученные точки соединяем плавной линией.
а затем строим их профильные проекции. Полученные точки соединяем плавной линией.
На рисунке 9.86 представлено построение сечения конуса плоскостью общего положения, заданной следами. Характерными точками являются точки 1 и 8, в которых горизонтальный след плоскости пересекает окружность основания конуса, так как они лежат в одной плоскости проекций Н. Далее задача по построению сечения заключается в нахождении следующих точек: наивысшей точки на фронтальной проекции, точки касания кривой линии сечения с очерковой образующей конуса, промежуточных точек.
Наивысшую точку найдем с помощью вспомогательной горизонтально-проецирующей плоскости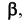 , перпендикулярной заданной плоскости и проходящей через вершину конуса. Сначала найдем линию пересечения заданной и вспомогательной плоскостей, затем построим сечение конуса вспомогательной плоскостью (треугольник) и там, где указанные элементы пересекаются, найдем точку
, перпендикулярной заданной плоскости и проходящей через вершину конуса. Сначала найдем линию пересечения заданной и вспомогательной плоскостей, затем построим сечение конуса вспомогательной плоскостью (треугольник) и там, где указанные элементы пересекаются, найдем точку 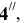 , которая и будет наивысшей.
, которая и будет наивысшей.
Точку касания будущего сечения конуса с очерковой образующей найдем с помощью вспомогательной фронтальной плоскости 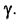 . Точка касания 5 находится в месте пересечения линии пересечения плоскостей а и
. Точка касания 5 находится в месте пересечения линии пересечения плоскостей а и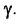 и очерковой образующей конуса.
и очерковой образующей конуса.
Промежуточные точки 2, 3, 6, 7 найдем методом секущих вспомогательных плоскостей, для чего используем горизонтальные плоскости 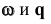 . Полученные точки соединяем плавной линией.
. Полученные точки соединяем плавной линией.
Пересечение прямой с поверхностью
Задача пересечения прямой с поверхностью решается аналогично задаче о пересечении прямой с поверхностью многогранников. Отличие состоит в том, что в сечении кривой поверхности вспомогательной плоскостью в большинстве случаев образуются кривые линии. Общая методика решения задачи представлена на рисунке 9.9а. 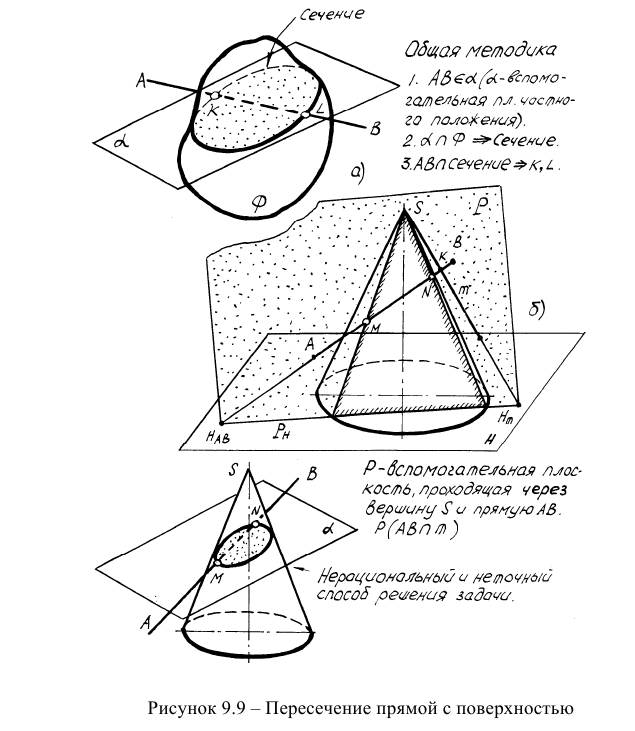
Если прямая находится в частном положении, то задача значительно упрощается. В некоторых случаях для упрощения решения применяют методы преобразования с тем, чтобы получить в сечении более удобные для построения кривые линии, например, окружность известного радиуса.
В случае пересечения прямой общего положения с конусом в качестве вспомогательной плоскости используют плоскость общего положения, проходящую через вершину конуса. Вспомогательную плоскость задают двумя пересекающимися прямыми АВ и m. В сечении конуса такой вспомогательной плоскостью образуется треугольник. Использование в качестве вспомогательных плоскостей горизонтально-или фронтально-проецирующих плоскостей нерационально, так как они в сечениях образуют эллипс и гиперболу, построение которых связано с большой трудоемкостью и неточностью (рисунок 9.96).
Пример: Найти точки встречи прямой частного (а) и общего (б) положения с поверхностью конуса.
Решение: На рисунке 9.10 представлено решение задач.
В первой задаче прямая является горизонталью. Проведем через прямую горизонтальную вспомогательную плоскость  . В сечении конуса на горизонтальной проекции будет окружность радиуса R. Там, где прямая пересекается с окружностью найдем точки встречи прямой с поверхностью (точки 1 и 2).
. В сечении конуса на горизонтальной проекции будет окружность радиуса R. Там, где прямая пересекается с окружностью найдем точки встречи прямой с поверхностью (точки 1 и 2).
Вторую задачу решим с помощью вспомогательной плоскости, проходящей через вершину конуса S. Возьмем на прямой АВ любую точку К и соединим её с вершиной конуса S. Две прямые АВ и m являются пересекающимися прямыми и, следовательно, задают плоскость, проходящую через прямую АВ и вершину S. В сечении конуса этой плоскостью получится треугольник. Чтобы треугольник построить, необходимо найти горизонтальный след вспомогательной плоскости.
Находим горизонтальные следы прямых АВ и m и, соединив их, получим горизонтальный след плоскости. След пересекается с основанием конуса в точках 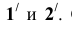 Соединив точки с вершиной S, получим сечение конуса в виде треугольника
Соединив точки с вершиной S, получим сечение конуса в виде треугольника 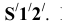 В местах пересечения прямой АВ с контуром треугольника находим искомые точки М и N.
В местах пересечения прямой АВ с контуром треугольника находим искомые точки М и N.
Пример: Построить точки встречи прямой АВ с поверхностью сферы (Рис.9.11).
Решение: Прямая АВ является прямой общего положения. Применение проецирующих вспомогательных плоскостей частного положения в этой задаче нецелесообразно, так как в сечениях сферы образуются эллипсы. 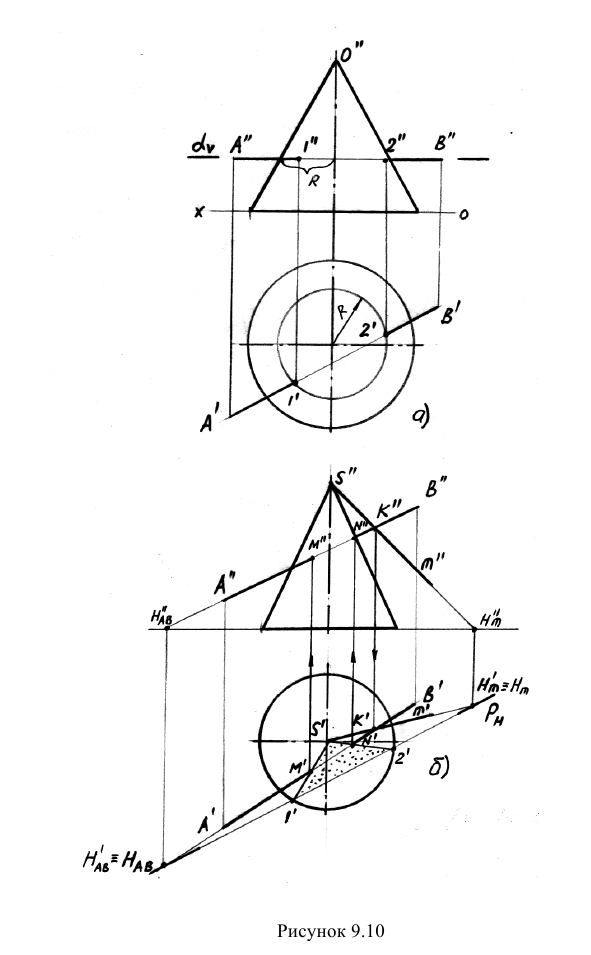
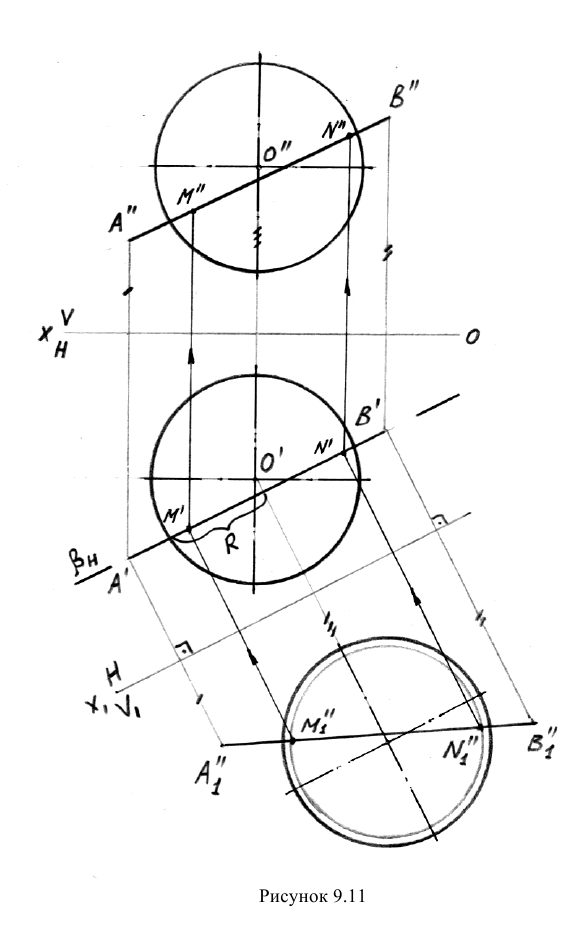
Решим задачу с использованием метода замены плоскостей проекций. Заменой фронтальной плоскости проекций переведем прямую АВ из общего положения в частное (в положение фронтали). После построений в образованной новой системе плоскостей проекций через прямую проведем вспомогательную фронтальную плоскость 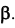 В сечении сферы вспомогательной плоскостью будет окружность радиуса R. Там, где прямая пересекается с контуром окружности, получаем искомые точки М и N.
В сечении сферы вспомогательной плоскостью будет окружность радиуса R. Там, где прямая пересекается с контуром окружности, получаем искомые точки М и N.
Пересечение поверхностей
Задача о пересечении поверхностей является наиболее значительной в курсе начертательной геометрии как с теоретической, так и с практической точек зрения. Основные методики решения упомянутой задачи широко используются в различных отраслях промышленности.
Линия, общая для обеих пересекающихся поверхностей, называется линией пересечения. Построение линий пересечения и их разметка на различных металлоконструкциях является одной из главных и сложных инженерных задач.
Существуют различные частные случаи пересечения поверхностей, обусловленные геометрическими и математическими закономерностями (рисунок 9.12а).
Две цилиндрические поверхности с параллельными осями пересекаются по прямым линиям, соединяющим точки пересечения оснований цилиндров. Две конические поверхности с общей вершиной пересекаются по прямым линиям, соединяющим вершину и точки пересечения оснований. Соосные поверхности вращения второго порядка пересекаются по окружностям, фронтальная проекция которых является прямыми линиями.
Соосные со сферой тела вращения пересекаются по окружностям, фронтальная или горизонтальная проекции которых являются прямыми линиями.
Если две поверхности второго порядка описаны вокруг одной и той же сферы, то линия их пересечения распадается на две кривые линии второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания (теорема Монжа). Сказанное означает, что на одной из проекций линии пересечения являются прямыми линиями, соединяющими противоположные характерные точки. Характерными точками являются точки пересечения образующих линий поверхностей. 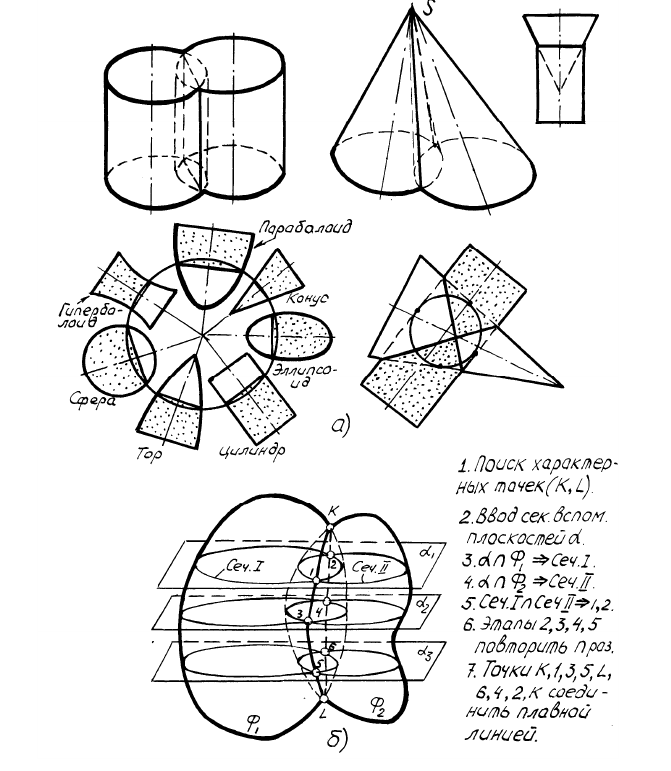
Рисунок 9.12 - Частные случаи пересечения поверхностей (а) и построение линии пересечения методом секущих вспомогательных плоскостей (б)
В начертательной геометрии разработано множество методов построения линий пересечения поверхностей. Самыми распространенными методами являются метод секущих вспомогательных плоскостей и метод концентрических сфер.
Сущность метода вспомогательных секущих плоскостей заключается в том, что при помощи секущих плоскостей находятся общие точки, принадлежащие пересекающимся поверхностям. Наглядно суть метода представлена на рисунке 9.126. Он содержит общий порядок решения:
- Поиск характерных точек и построение их проекций (точки К и L);
- Ввод секущей вспомогательной плоскости. В качестве вспомогательных плоскостей берут плоскости частного положения, которые образуют в сечениях поверхностей простые фигуры (принцип простых сечений);
- Строят сечения поверхностей вспомогательной плоскостью (Сеч.1 и Сеч.И);
- Находят общие точки обоих сечений (точки 1 и 2);
- Пункты 2, 3, 4 повторяют несколько раз (в учебных чертежах 5-7 раз) с новыми вспомогательными плоскостями;
- Полученные точки соединяют плавной линией с учетом видимости проекций.
Метод концентрических сфер основан на частном случае пересечения поверхностей (пересечение тел вращения со сферой, когда ось тел проходит через центр сферы) (рисунок 9.12а). Сущность метода сфер заключается в том, что поверхности пересекают не плоскостями, а сферами. Это объясняется тем, что всякая сфера с центром на оси поверхности вращения пересекает любую поверхность вращения по окружности, т.е. по линии, построение которой не вызывает затруднений. Далее находят линии пересечения поверхностей с проведенной сферой, после чего находят общие точки линий пересечения. Полученные точки являются точками линии пересечения поверхностей.
Центр сфер, как правило, выбирают в точке пересечения осей поверхностей (рисунок 9.13). Максимальный радиус сфер равен расстоянию от центра сфер до наиболее удаленной характерной точки. Минимальный радиус сфер равен максимальной нормали, проведенной из центра сфер на боковую поверхность пересекающихся объектов. 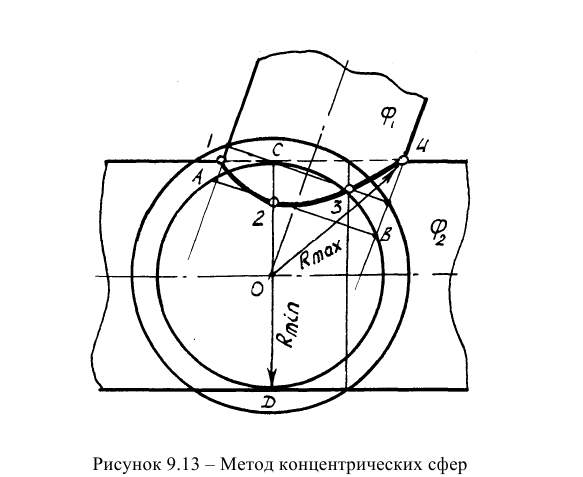
Прикладные методы разметки линии пересечения
Сочленение двух поверхностей или технических форм является сложной инженерной задачей. Традиционно задача о разметке линии пересечения технических форм и обрезке форм перед стыковкой решается поэтапно следующим образом:
- Разработка чертежей с построением линии пересечения соединения технических форм (желательно в масштабе 1:1);
- Выполнение разверток пересекающихся технических форм и нанесение линии пересечения на развертки;
- Изготовление шаблонов по полученным разверткам;
- Нанесение линии пересечения на обе пересекающиеся технические формы и обрезка перед стыковкой;
- Стыковка технических форм и сварка изделия.
Традиционный метод разметки соединения технических форм отличается большой трудоемкостью и неточностью. 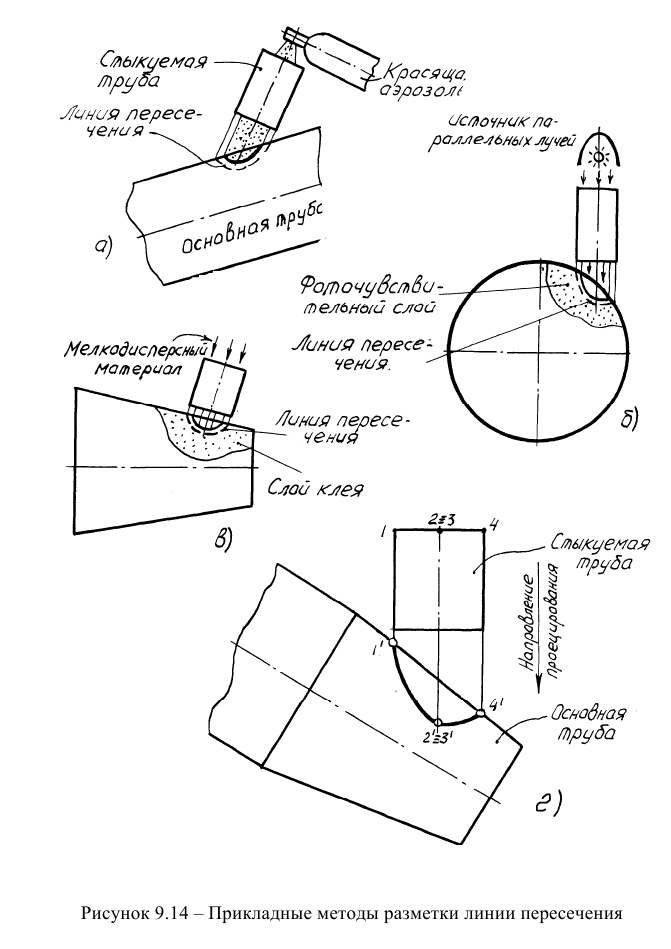
Профессором Кириным Е.М.А разработано несколько прикладных методов разметки линии пересечения непосредственно на деталях, минуя стадию разработки чертежей и изготовления шаблонов (способы разметки защищены авторскими свидетельствами и патентами).
Новая технология разметочных работ при изготовлении трубного соединения основана на том, что линия пересечения двух поверхностей, одна из которых является цилиндрической или призматической, является параллельной проекцией цилиндра или призмы на поверхность другого объекта, входящего в состав соединения (рисунок 9.14г). Из этого следует: для того, чтобы построить линию пересечения, например, трубного соединения, необходимо стыкуемую трубу параллельно спроецировать на основную трубу в направлении оси стыкуемой трубы. Вопрос состоит лишь в том, как получить проекцию стыкуемой трубы на основную непосредственно на трубах. Автором предложено несколько технических решений.
В одном из них (рисунок 9.14а) линия пересечения получается путем нанесения на основную трубу красящей аэрозоли, распыляемой через стыкуемую трубу. На основной трубе образуется разметочная зона в виде окрашенного пятна. По этой зоне с припуском на толщину стыкуемой трубы размечается линия пересечения, эквидистантная разметочной зоне. По линии пересечения в основной трубе вырезается отверстие, в которое вставляется стыкуемая труба. Затем стыкуемая труба размечается по контуру отверстия и обрезается. Затем трубы свариваются. Трудоемкость разметки трубного соединения уменьшается в несколько раз, соединение получается точным, плотным и герметичным.
По другому способу в соответствии с рисунком 9.146 разметочная зона образуется за счет взаимодействия пучка параллельных лучей с фоточувствительным слоем, нанесенным на основную трубу. На рисунке 9.14в показано получение разметочной зоны за счет прилипания мелкодисперсного материала к клеевому слою на основной трубе.
Развертки кривых поверхностей
Общие сведения о развертках были даны в разделе 7.14 "Развертки многогранников". Развертки развертываемых кривых поверхностей также могут производиться методом нормального сечения и методом раскатки.
По возможности развертываться в плоскость кривые поверхности делятся на развертываемые и условно-развертываемые. Развертки условно развертываемых поверхностей могут быть произведены только приближенно.
Разверткой прямого кругового конуса является сектор окружности с радиусом, равным длине образующей конуса и углом при вершине конуса.
Разверткой прямого кругового цилиндра является прямоугольник шириной, равной высоте цилиндра и длиной, равной длине окружности основания. В примерах к данной теме показано построение разверток некоторых поверхностей. 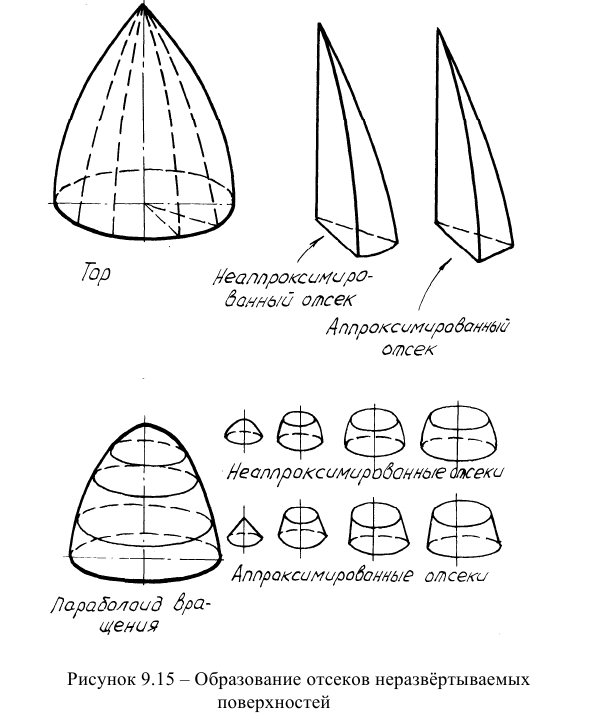
Развертки неразвертываемых (условно-развертываемых)
поверхностей могут быть осуществлены путем аппроксимации отсеков поверхностей. Аппроксимация - это приближенная замена отсеков неразвертываемой поверхности отсеками развертывемой поверхности. В качестве аппроксимирующих поверхностей используют плоскости, конические и цилиндрические поверхности. На рисунке 9.15 представлена аппроксимация поверхности тора и параболоида вращения цилиндрическими и коническими поверхностями.
Пример условно-приближенной развертки торовой поверхности представлен на рисунке 10.16. Решение задачи заключается в том, что поверхность тора делят на несколько равных отсеков (например, на 12 отсеков) и неразвертываемую поверхность отсека заменяют развертываемой цилиндрической поверхностью. Далее поверхность элементарного отсека развертывают в плоскость. 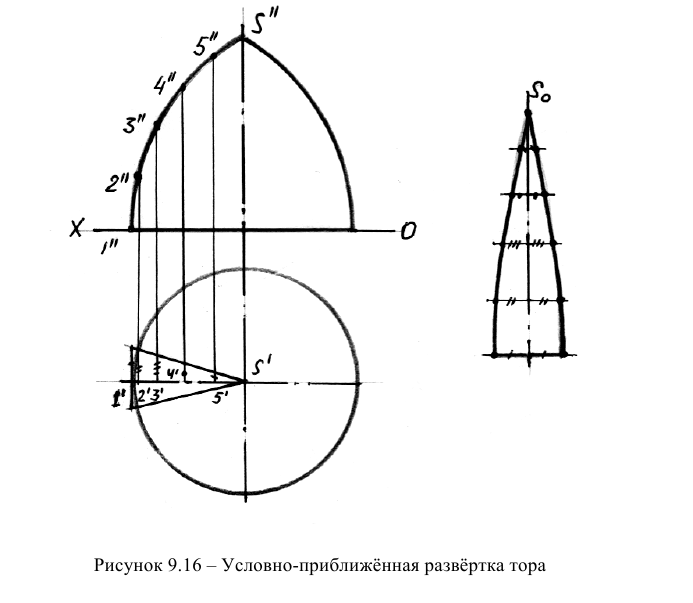
Пример: Построить проекции усеченного конуса, натуральную величину сечения и развертку усеченной части конуса с нанесением на ней линии сечения (рисунок 9.17). 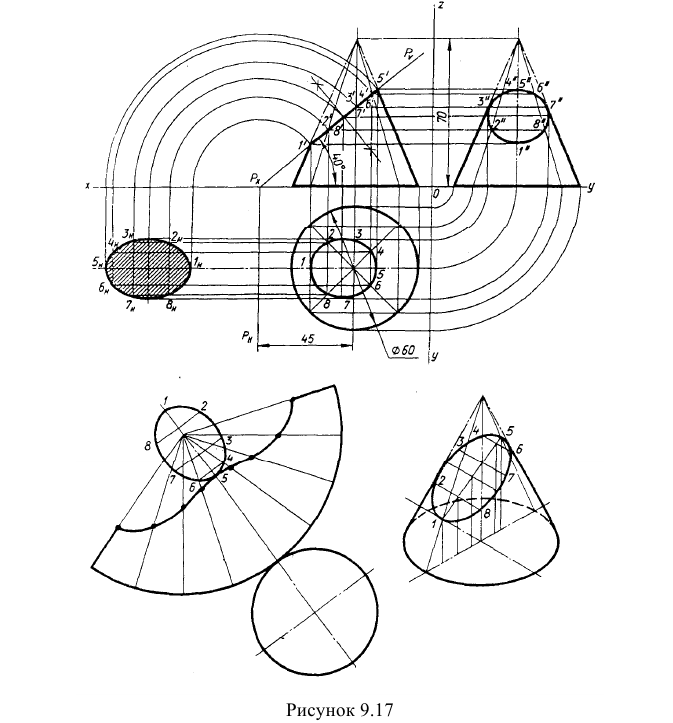
Решение: Точки сечения 1, 3, 5 построим как характерные точки. Промежуточные точки 4, 6 и 2, 8 построим с помощью образующих. Натуральную величину сечения построим методом совмещения (см. тему "Метод совмещения").
Развертку поверхности усеченного конуса построим методом раскатки, разделив основание конуса на восемь частей.
Пример: Построить линию пересечения конуса с цилиндром и развертку конуса с нанесением на неё линии пересечения (Рис.9.18). 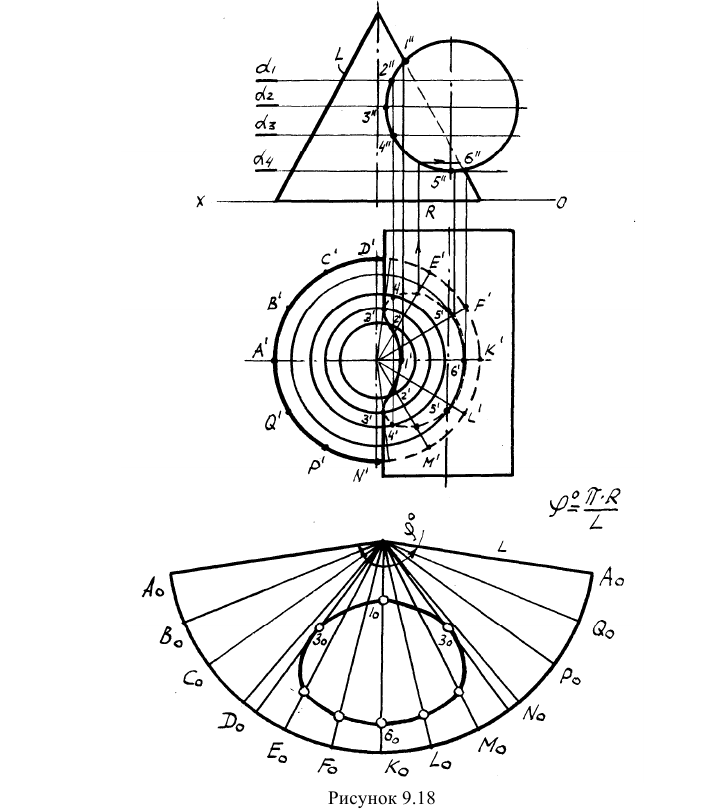
Решение: Линию пересечения конуса с цилиндром построим методом секущих вспомогательных плоскостей. В качестве вспомогательных плоскостей используем горизонтальные плоскости. Развертку конуса построим методом раскатки (см. тему "Развертка пирамиды").
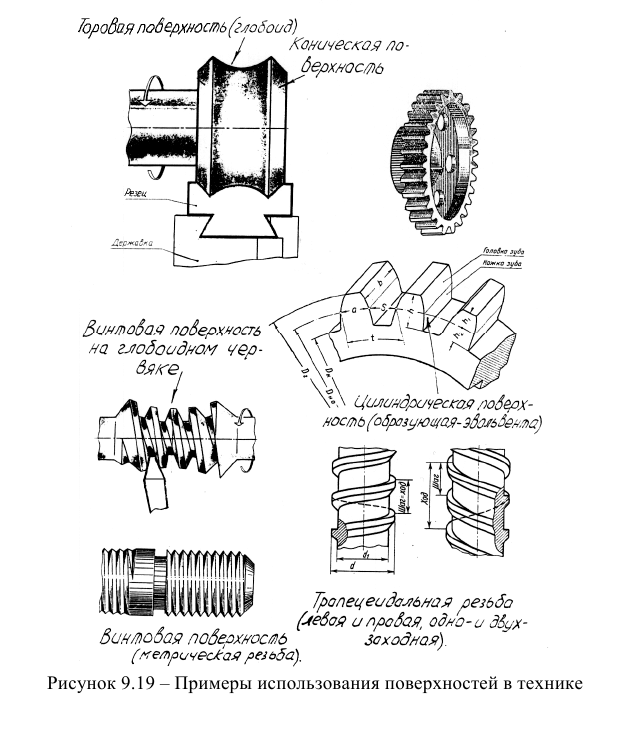
В заключении темы "Кривые поверхности" отметим, что кривые поверхности находят широкое использование в технике, архитектуре и строительстве. На рисунке 9.19 представлены примеры их использования в технике.
Определение кривой поверхности
В начертательной геометрии поверхность определяется как след движущейся в пространстве линии, называемой образующей [12]. Такое представление об образовании поверхности удобно для графических построений.
Представление об образовании поверхности непрерывным движением линии позволяет такие поверхности называть кинематическими. При этом линия, образующая поверхность, может во время движения деформироваться. Тогда говорят о поверхности с «переменной образующей».
Образующая линия может быть прямой или кривой.
Закон движения образующей может быть задан другими линиями, называемыми направляющими поверхности. По ним образующая в процессе своего движения скользит.
Поверхность, которая образована движением прямой линии, называют линейчатой поверхностью. Таким образом, линейчатая поверхность представляет собой геометрическое место прямых линий.
Поверхность, которая образована движением кривой линии, называют нелинейчатой поверхностью. Примерами такой поверхности является сфера, тор и др.
Одна и та же поверхность может быть образована перемещением различных линий и согласно различным условиям движения, то есть законы образования поверхности в ряде случаев могут быть разнообразными. Для решения геометрических задач, как правило, используют наиболее простой или удобный закон задания поверхности.
Некоторые кривые поверхности могут быть развернуты так, что совместятся все своим точками с плоскостью без разрывов, складок, или растяжений. Такие поверхности называют развертываемыми. К ним относятся только линейчатые поверхности, причем такие, у которых смежные прямолинейные образующие параллельны, или пересекаются между собой, или являются касательными к некоторой пространственной кривой.
Все кривые нелинейчатые поверхности и те линейчатые, которые не могут быть развернуты в плоскость, называются неразвертывающимися (или косыми).
Задать поверхность на чертеже – значит указать условия, позволяющие построить каждую точку этой поверхности. Для задания поверхности достаточно иметь проекции направляющих линий (одной или нескольких) и указать, как строится образующая линия. Для придания же изображениям поверхности наглядности вычерчивают еще и ее очерк, показывают несколько промежуточных положений образующих поверхности, отображая, таким образом, поверхность в виде каркаса.
Обзор некоторых кривых поверхностей, их изображение на чертеже
1. Поверхности линейчатые развертываемые.
1.1. Цилиндрическая поверхность. Образуется движением прямой линии l по криволинейной направляющей n и остающейся во всех своих положениях параллельной некоторой заданной прямой линии S (рис. 11.9).
1.2. Коническая поверхность. Образуется движением прямой линии l по криволинейной направляющей и проходящей во всех своих положениях через некоторую неподвижную точку S, называемую вершиной конической поверхности (рис. 11.10).
Линия, получаемая при пересечении цилиндрической или конической поверхностей с плоскостью, называется следом поверхности. На рис. 11.9, а и рис. 11.10, а показаны следы этих поверхностей в пространстве.
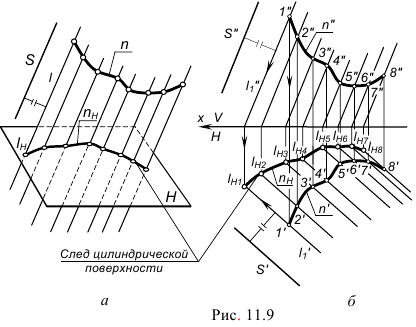
На рис. 11.9, б показано построение на чертеже горизонтального следа nH цилиндрической поверхности посредством семейства произвольно задаваемых образующих l, параллельных прямой S, определяющей их направление. След nH построен по точкам lH1, lH2, lH3, … , lH8, являющимся горизонтальными следами образующих.
Для построения недостающих проекций точек, принадлежащих цилиндрической или конической поверхности, также используют их образующие.
На рис. 11.10, б показано построение недостающей фронтальной A" проекции точки A(A') посредством промежуточной образующей l(l',l"). Вначале строят ту проекцию образующей l, на которой находится заданная проекция A' точки, то есть в данном случае – горизонтальную проекцию l'. Затем, используя точку пересечения 1(1',1") этой образующей с направляющей кривой линией n(n',n"), строят фронтальную проекцию l" образующей, и посредством линии связи находят искомую недостающую проекцию точки A".
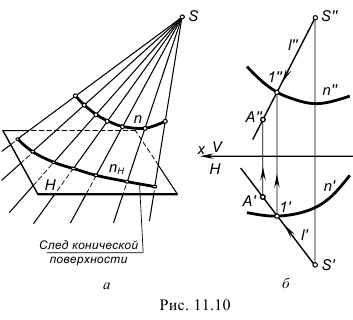
1.3. Поверхность с ребром возврата (торсовая). Образуется непрерывным движением прямолинейной образующей l, во всех своих положениях касающихся некоторой пространственной кривой n. Эта пространственная кривая является для данного типа поверхностей направляющей. Ее называют ребро возврата.
На рис. 11.11, а торсовая поверхность показана в пространстве и показан ее след nH как линия пересечения поверхности с некоторой горизонтальной плоскостью H. На рис. рис. 11.11, б приведен чертеж торсовой поверхности и показано построение недостающей горизонтальной проекции A' принадлежащей ей точки A(A"). Для построения использовалась образующая l(l',l"), задаваемая через заданную проекцию точки A" касательно к ребру возврата поверхности в точке 1(1',1").
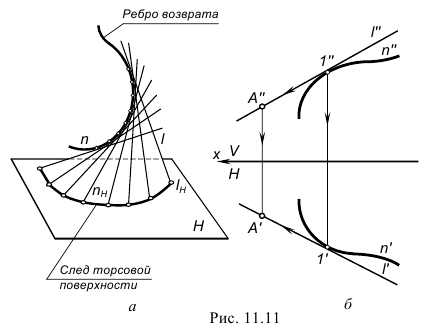
2. Поверхности линейчатые неразвертываемые.
2.1. Поверхности с плоскостью параллелизма.
Цилиндроид и коноид – это поверхности, образованные движением прямолинейной образующей по двум направляющим, и остающейся во всех своих положениях параллельной некоторой заданной плоскости, называемой плоскостью параллелизма. В качестве плоскости параллелизма может задаваться некоторая проецирующая плоскость (ее след указывается на чертеже, рис. 11.12) или оговаривается, что плоскостью параллелизма является одна из плоскостей проекций (рис. 11.13).
Всякая плоскость, параллельная плоскости параллелизма, пересекает цилиндроид или коноид по прямой линии – по образующей. Это свойство используется при решении задач.
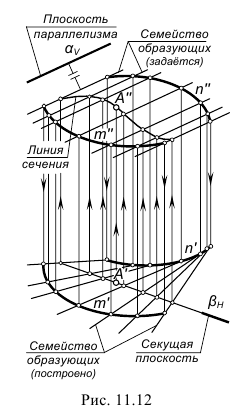
На рис. 11.12 показано построение недостающей фронтальной проекции точки A(A') на поверхности цилиндроида, заданного двумя направляющими n(n',n") и m(m',m") и фронтально-проецирующей плоскость αV в качестве параллелизма. Поскольку применить вышерассмотренный алгоритм, когда было достаточно воспользоваться одной из образующих, в данном случае не представляется возможным (не известно, как будет направлена образующая через заданную проекцию A' точки), необходимо вначале построить семейство образующих, задавая их фронтальные проекции параллельно следу плоскости параллелизма αV (согласно закону образования поверхности цилиндроида). Построив обе проекции каркаса цилиндроида из образующих, выполняют его сечение произвольной горизонтально-проецирующей плоскостью, проходящей через заданную проекцию A' точки. Затем строят фронтальную проекцию линии сечения и на ней посредством линии связи находят искомую проекцию A" точки.
На рис. 11.13 показано построение недостающей горизонтальной проекции точки A, принадлежащей поверхности коноида, заданного кривой n(n',n") и прямой m(m',m") направляющими и плоскостью параллелизма, в качестве которой служит горизонтальная плоскость проекций H. Для этого через ее заданную проекцию A" построена фронтальная проекция образующей l(l") коноида, занимающая горизонтальное положение. Затем по точкам пересечения 1(1") и 2(2") образующей с направляющими n(n',n") и m(m',m") построена горизонтальная проекция l' образующей и на ней посредством линии связи найдена искомая горизонтальная проекция A' точки.
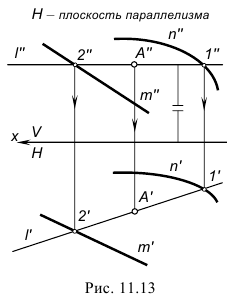
Гиперболический параболоид (косая плоскость) образуется движением прямолинейной образующей по двум скрещивающимся прямым направляющим параллельно некоторой плоскости параллелизма. Эту поверхность называют также линейчатым параболоидом.
На рис. 11.14 приведен чертеж рассматриваемой поверхности в виде каркаса из образующих. Поверхность задана двумя скрещивающимися в параллельных плоскостях прямыми направляющими n(n',n") и m(m',m") и горизонтально проецирующей плоскостью параллелизма αH. Там же показано построение недостающей фронтальной проекции A" точки A(A'), принадлежащей поверхности. Построение выполнено посредством образующей l(l'), для чего через заданную проекцию A' вначале построена горизонтальная проекция l' образующей. Затем по точкам 1(1') и 2(2') ее пересечения с направляющими строят фронтальную проекцию образующей и отмечают на ней посредством линии связи искомую проекцию A" точки.
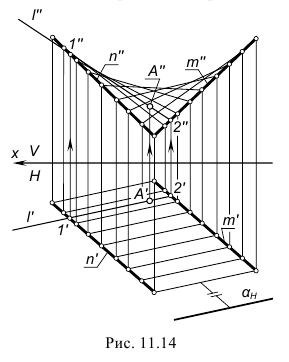
Название рассмотренной поверхности «гиперболический параболоид» связано с тем, что ее фронтальный очерк (касательная кривая к фронтальным проекциям образующих) представляет собой параболу (рис. 11.6). Такую же форму имеет и профильный очерк данной поверхности. Кроме того, линия сечения данной поверхности горизонтальной плоскостью имеет форму гиперболы (форму гиперболы имеет также горизонтальный след поверхности, который можно построить, если найти горизонтальные следы ее образующих).
2.2. Поверхность с тремя направляющими – однополостный гиперболоид.
Эта линейчатая поверхность образуется при перемещении прямой образующей по трем скрещивающимся прямым направляющим, не параллельным одной плоскости. В частном случае линейчатая поверхность с тремя направляющими пересекается плоскостью по гиперболе; отсюда и произошло ее название – однополостный гиперболоид [23] (однополостный гиперболоид вращения, как частный случай поверхности, может быть получен вращением гиперболы вокруг ее мнимой оси или вращением прямой линии вокруг скрещивающей с ней оси).
На рис. 11.15 приведен чертеж фрагмента линейчатой поверхности с тремя направляющими n(n',n"), k(k',k") и m(m',m"). Там же показаны построения для определения положения недостающей проекции A' точки A(A"). Воспользоваться для этого одной из образующих в данном примере не представляется возможным, так как неизвестно положение ее фронтальной проекции, проходящей через заданную проекцию A" точки. Зато благодаря проецирующему положению направляющей k(k',k") можно задать горизонтальные проекции любых образующих. Воспользуемся этим и построим горизонтальную проекцию каркаса поверхности из семейства образующих l(l'). Затем по точкам их пересечения с горизонтальными проекциями n' и m' направляющих построим фронтальные проекции l" этих образующих. Далее выполним сечение поверхности фронтально-проецирующей плоскостью αV. По фронтальным проекциям точек ее пересечения с образующими построим горизонтальную проекцию кривой линии этого сечения и на ней посредством линии связи определим положение искомой проекции A' точки.
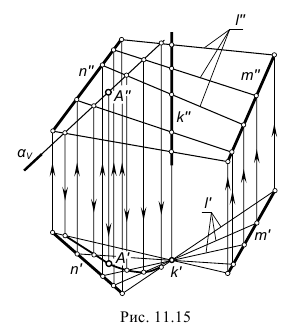
Структуризация материала одиннадцатой лекции в рассмотренном объеме схематически представлена на рис. 11.16 (лист 1). На последующих листах 2 и 3 приведены иллюстрации к этой схеме, компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении (рис. 11.17 и 11.18).
Кривые поверхности:
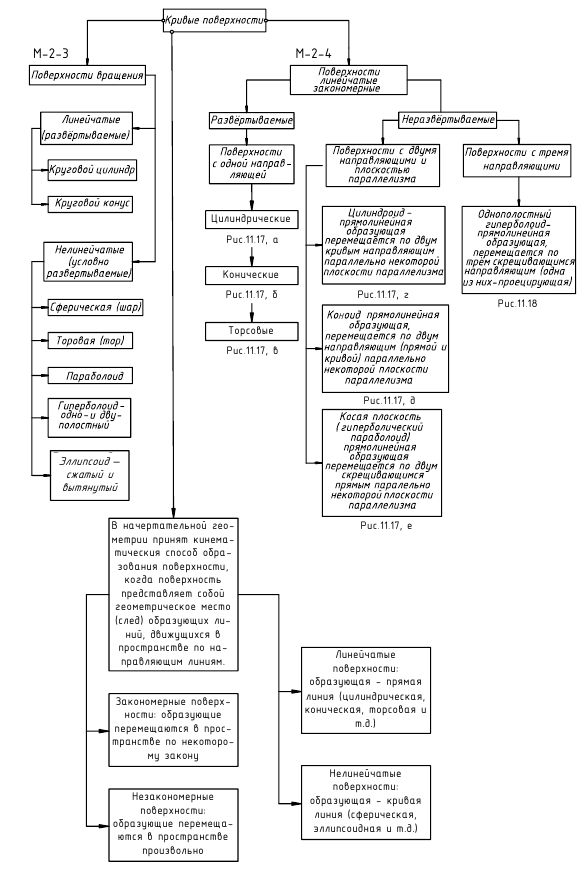
Поверхности с одной направляющей (закономерные, развёртываемые)
Цилиндрические
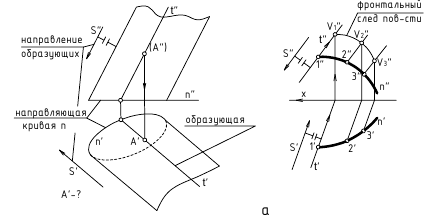
Конические
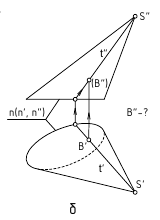
Торс - поверхность с ребром возврата
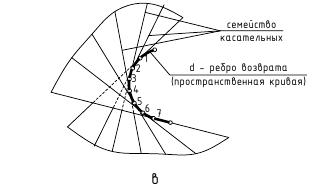
Поверхности с двумя направляющими и плоскостью параллелизма
(закономерные, развертываемые)
Цилиндроид (ф(m,n,α(αV))
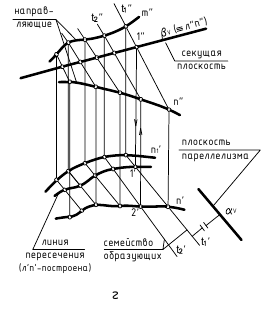
Коноид (ф(m,n,α(αV))
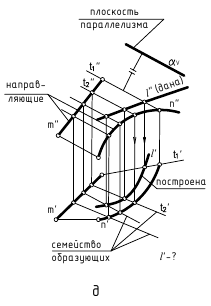
Косая плоскость - гиперболический параболоид (ф(m,n,α(αV))
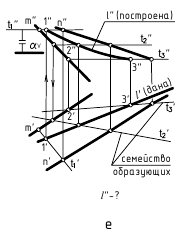
Поверхности с тремя скрещивающимися направляющими - однополостный гиперболоид (ф(a, b, c))
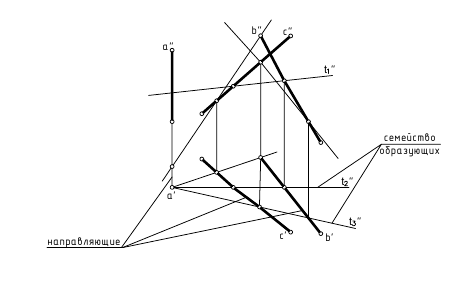
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |