
Кривые линии в начертательной геометрии с примерами
Содержание:
Кривую линию можно рассматривать как множество последовательных положений точки, непрерывно перемещающейся в пространстве. Кривая линия может являться результатом пересечения между собой поверхностей или поверхности и плоскости.
Различают плоские и пространственные линии. Кривая линия называется плоской, если все точки линии лежат в одной плоскости, и пространственной, если ее точки нс лежат в одной плоскости. Плоскими линиями являются, например, окружность, эллипс, овал. Примером пространственной линии может служить винтовая линия.
Проекциями пространственной кривой являются плоские линии. Плоская кривая проецируется в виде плоской линии или в виде прямой линии, если кривая находится в проецирующей плоскости.
В общем случае секущая АВ кривой проецируется секущей се проекции, а касательная CD к кривой проецируется касательной к ее проекции (рис. 5.1). 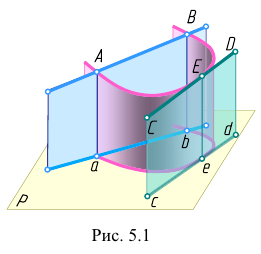
Линия считается закономерной, если в своем образовании она подчинена какому-либо геометрическому закону. Закономерные линии подразделяют на алгебраические и трансцендентные. В первом случае линию можно описать алгебраическим уравнением, а во втором - трансцендентным (например, тригонометрическим). Порядок алгебраической кривой равен степени ее уравнения или максимальному числу точек ее возможного пересечения с плоскостью или прямой.
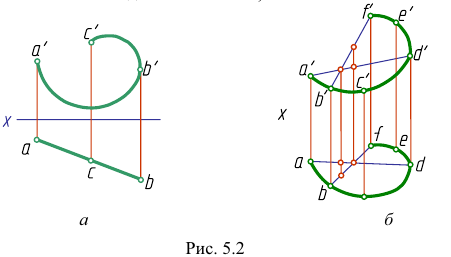
На комплексном чертеже кривая линия задается своими проекциями, которые строят по проекциям точек, принадлежащих этой линии. Если плоскость плоской кривой занимает проецирующее положение (рис. 5.2, а), то одна проекция этой кривой имеет форму прямой. У пространственной кривой все проекции - кривые линии (рис. 5.2, б).
Чтобы определить по чертежу, какая задана кривая (плоская или пространственная), необходимо выяснить, принадлежат ли все точки кривой одной плоскости. Заданная на рис. 5.2, б кривая является пространственной, так как прямые AD и BF не пересекаются, а скрещиваются (то есть не лежат в одной плоскости).
В начертательной геометрии кривая часто строится как линия, последовательно проходящая через задающие ее точки. Упорядоченное множество точек, определяющих линию, составляет се точечный каркас. Точки каркаса подразделяют на опорные и промежуточные. Промежуточные точки должны обеспечить необходимую и достаточную плотность каркаса, то есть обеспечивают количественную характеристику кривой. Наиболее важны опорные точки, которые отражают качественную характеристику кривой. Рассмотрим некоторые из опорных точек.
Экстремальные точки это точки, которые удалены от плоскостей проекций на максимальное или минимальное расстояние (верхняя и нижняя, крайние правая и левая точки).
Точки видимости. Если кривую рассматривать как линию на какой-то непрозрачной поверхности, то те точки, в которых меняется видимость кривой, называют точками видимости (обычно они расположены на контурных линиях поверхности).
К опорным относят и точки, в которых кривая пересекает свою ось или плоскость симметрии (если таковые имеются).
Кривые второго порядка:
Уравнениям второй степени соответствуют кривые второго порядка. К ним относятся эллипс, гипербола и парабола. Окружность является частным случаем эллипса; точка, две пересекающиеся, параллельные и две совпавшие прямые есть вырожденные случаи кривых второго порядка. Все эти линии (кроме двух параллельных прямых) можно встретить на конической поверхности вращения, поэтому часто их называют кониками.
Кривые линии
Кривую линию можно рассматривать как непрерывное множество последовательных положений точки, движущейся в пространстве, то есть как траекторию движущейся точки. На протяжении кривой линии не должно быть прямолинейных участков. Кривая линия определяется положениями составляющих ее точек, точки кривой определяются их координатами. Если координаты любой точки кривой удовлетворяют некоторому уравнению, то такие кривые называются закономерными. Закономерные кривые линии образуются по определенному закону и могут быть заданы графически и аналитически.
Аналитически кривую линию на плоскости можно задать уравнением
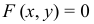
(может оказаться, что данному уравнению 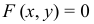 не удовлетворяют координаты ни одной действительной точки на плоскости. Тогда условно говорят, что данные уравнения изображаются мнимой кривой), в пространстве - двумя уравнениями (как линию пересечения двух поверхностей)
не удовлетворяют координаты ни одной действительной точки на плоскости. Тогда условно говорят, что данные уравнения изображаются мнимой кривой), в пространстве - двумя уравнениями (как линию пересечения двух поверхностей)
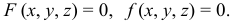
Существуют также незакономерные кривые, образование которых носит эмпирический характер. Незакономерные кривые линии задаются только графически на чертеже.
Одна и та же кривая линия может быть образована разными способами:
- движением точки в пространстве;
- пересечением кривой поверхности с плоскостью;
- взаимным пересечением двух поверхностей, из которых хотя бы одна кривая.
Кривые линии подразделяют на плоские и пространственные. У плоских кривых все точки принадлежат плоскости, у пространственных кривых точки не принадлежат одной плоскости. Пространственные прямые называются также линиями двоякой кривизны. Наиболее известными из плоских и пространственных кривых линий являются соответственно окружность и цилиндрическая винтовая линия.
Закономерные кривые, определяемые в декартовой системе координат алгебраическим уравнением вида 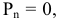 где
где 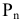 - многочлен
- многочлен 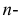 й степени от одного или нескольких переменных
й степени от одного или нескольких переменных 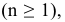 называются алгебраическими.
называются алгебраическими.
Порядком алгебраической кривой линии называется степень ее уравнения. Геометрически порядок плоской алгебраической кривой линии характеризуется наибольшим числом точек ее пересечения с прямой линией. Порядок пространственной алгебраической кривой линии определяется наибольшим числом точек ее пересечения с плоскостью общего положения.
К линиям первого порядка относятся прямые линии, рассмотренные ранее.
Линии второго порядка - это эллипс, гипербола и парабола.
Из линий третьего порядка наиболее известны Аньези локон, декартов лист, полукубическая парабола, строфоида.
Из линий четвертого порядка - улитка Паскаля, конхоида Никомеда, лемниската Бернулли.
Из линий высших порядков - кривая Ламе, синусоидальная спираль.
Если закономерная кривая определяется неалгебраическим уравнением, то она относится к числу трансцендентных. Среди трансцендентных кривых выделяют графики тригонометрических функций, показательной и логарифмической функции, класс циклоидальных кривых, спирали.
Локальные элементы кривой
Локальные свойства характеризуют кривую и относятся к весьма малым частям ее. Каждая из кривых линий обладает большей или меньшей степенью искривленности. Эта искривленность задается некоторым числом и называется кривизной. Кривизна 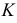 в точке
в точке 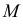 - это число, характеризующее отклонение кривой (в малой ее части, заключающей точку
- это число, характеризующее отклонение кривой (в малой ее части, заключающей точку 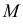 ) от прямой линии.
) от прямой линии.
Радиусом кривизны 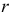 в точке
в точке 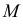 кривой называется величина, обратная кривизне
кривой называется величина, обратная кривизне 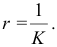 Чем больше искривлена кривая вблизи заданной точки, тем больше
Чем больше искривлена кривая вблизи заданной точки, тем больше 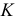 и меньше
и меньше 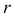 в этой точке. В общем случае для любой точки
в этой точке. В общем случае для любой точки 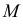 кривизна и радиус кривизны различны, они характеризуют кривую на бесконечно малом участке, составляющем окрестность точки
кривизна и радиус кривизны различны, они характеризуют кривую на бесконечно малом участке, составляющем окрестность точки 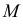 .
.
Секущей называется прямая, пересекающая кривую в одной, двух или более точках.
Касательная к кривой в точке 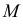 определяется как предельное положение секущей, проходящей через
определяется как предельное положение секущей, проходящей через 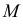 и соседнюю точку
и соседнюю точку 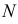 кривой, при условии, что
кривой, при условии, что 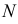 стремится к
стремится к 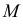 (рис. 135). Касательная указывает направление движения точки.
(рис. 135). Касательная указывает направление движения точки.
Нормаль для плоских кривых - это прямая, перпендикулярная касательной в точке касания 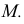
Для пространственных кривых линий в каждой точке 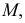 в общем случае, определяются три прямые и три плоскости, взаимно пересекающиеся в
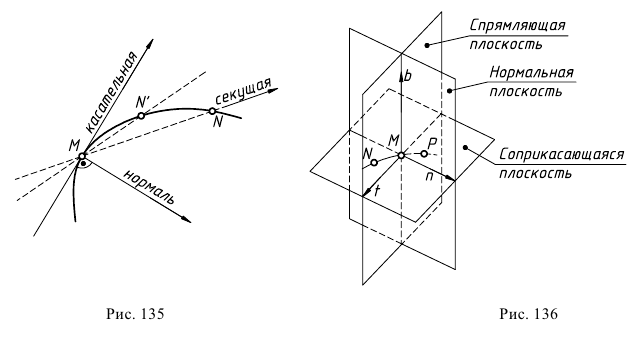
в общем случае, определяются три прямые и три плоскости, взаимно пересекающиеся в 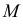 под прямыми углами и образующие сопровождающий трехгранник (рис. 136). На рисунке видно, что касательная
под прямыми углами и образующие сопровождающий трехгранник (рис. 136). На рисунке видно, что касательная 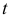 к кривой в точке
к кривой в точке 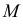 перпендикулярна нормальной плоскости. Все прямые, проходящие через
перпендикулярна нормальной плоскости. Все прямые, проходящие через 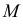 и лежащие в этой плоскости, называются нормалями пространственной кривой в точке
и лежащие в этой плоскости, называются нормалями пространственной кривой в точке 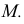
Соприкасающаяся плоскость - это предельное положение плоскости, проходящей через три близкие точки кривой 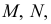 и
и 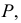 когда
когда 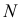 и
и 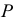 стремятся к
стремятся к 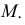 Соприкасающаяся плоскость содержит в себе касательную.
Соприкасающаяся плоскость содержит в себе касательную.
Главная нормаль 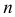 - это линия пересечения нормальной и соприкасающейся плоскостей (та из нормалей, которая лежит в соприкасающейся плоскости).
- это линия пересечения нормальной и соприкасающейся плоскостей (та из нормалей, которая лежит в соприкасающейся плоскости).
Бинормаль 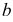 - прямая, перпендикулярная соприкасающейся плоскости.
- прямая, перпендикулярная соприкасающейся плоскости.
Спрямляющая плоскость - проходит через касательную и бинормаль.
Длина отрезка кривой (плоской или пространственной) определяется в общем случае приближенно путем замены кривой линии вписанной в нее ломаной линией с максимально большим числом ее сторон, достаточно хорошо передающей форму кривой.
Свойства проекций кривой линии
Из всех инвариантных свойств проецирования для кривой линии можно выделить следующие:
- - проекции кривой в общем случае есть кривые. В частном случае плоская кривая проецируется в прямую, если она принадлежит проецирующей плоскости;
- - если точка лежит на кривой, то ее проекции лежат на одноименных проекциях этой кривой;
- - если прямая касается кривой в пространстве, то проекции этой прямой касаются одноименных проекций кривой. Секущая кривой проецируется как секущая проекции кривой;
- - кривая, представляющая собой проекцию кривой некоторого порядка, сохраняет тот же порядок или оказывается кривой более низкого порядка.
Плоские кривые линии
При построении проекций плоской кривой линии необходимо указывать на их так называемые характерные точки, к которым относятся особые точки кривой, а также точки, наиболее удаленные от плоскости проекций и наиболее близкие к ним. Плоская кривая, к каждой точке которой можно провести касательную, называется плавной. Однако на кривой могут существовать точки, в которых имеются две касательные, общая касательная для двух ветвей или нескольких витков кривой. Кривая в таких точках не является плавной.
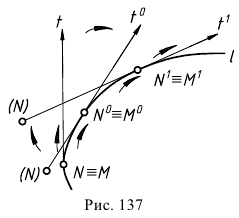
Пусть касательная 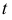 перекатывается по кривой
перекатывается по кривой 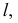 при этом переменная точка касания
при этом переменная точка касания 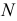 совершает поступательное движение по касательной (рис. 137). В каждом своем положении переменная точка касания
совершает поступательное движение по касательной (рис. 137). В каждом своем положении переменная точка касания 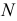 совпадает с произвольной точкой
совпадает с произвольной точкой 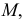 перемещающейся по кривой
перемещающейся по кривой 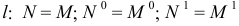 и т.д.
и т.д.
Если в некоторой точке 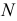 изменяется направление поступательного движения ее по касательной, то она называется особой точкой.
изменяется направление поступательного движения ее по касательной, то она называется особой точкой.
Если в некотором положении изменяется направление поворота касательной 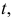 то она называется особой касательной.
то она называется особой касательной.
Если таких изменений не происходит, то точка 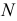 и касательная
и касательная 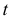 называются обыкновенными. Соответствующая точка
называются обыкновенными. Соответствующая точка 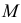 кривой также называется обыкновенной (рис. 138, а).
кривой также называется обыкновенной (рис. 138, а).
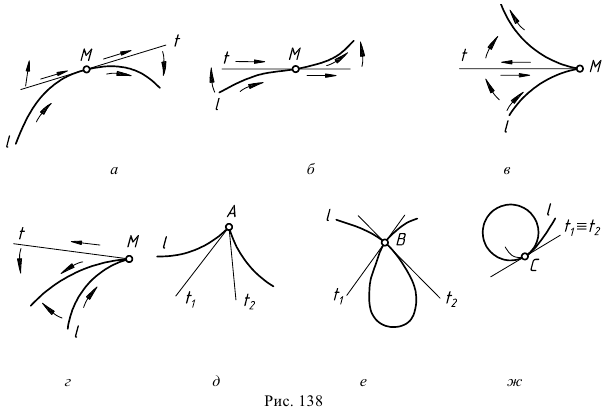
На рис. 138 представлены некоторые особые точки кривых:
- - точка перегиба (с особой касательной) (см. рис. 138, б);
- - точка возврата первого рода или заострения (особая точка) (см. рис. 138, в);
- - точка возврата второго рода, или «клюв» (особая точка с особой касательной) (см. рис. 138, г);
- - точка излома
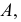 в которой имеются две касательные (см. рис.138, д);
в которой имеются две касательные (см. рис.138, д); - - узловая точка
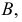 в которой кривая пересекает себя и имеет две касательные (см. рис. 138, е);
в которой кривая пересекает себя и имеет две касательные (см. рис. 138, е); - - точка самоприкосновения
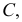 в которой кривая встречает самое себя, но обе касательные совпадают (см. рис. 138, ж).
в которой кривая встречает самое себя, но обе касательные совпадают (см. рис. 138, ж).
На комплексном чертеже задаются проекции нескольких обыкновенных и всех особых точек кривой линии. Касательные и нормали к кривым линиям строят или графически, или пользуясь специальными приборами.
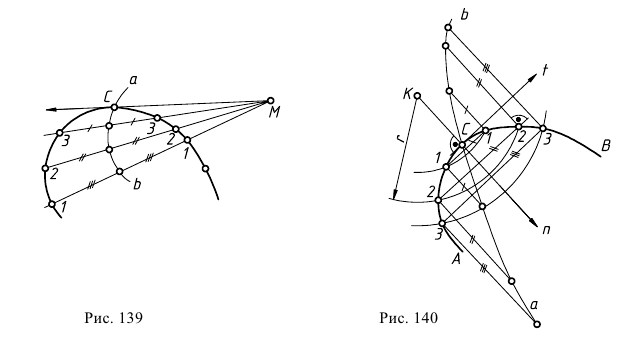
На рис. 139 показано построение касательной к кривой линии, проходящей через заданную вне кривой точку 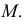 Через точку
Через точку 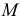 проводят пучок прямых, пересекающих кривую по хордам 11, 22, 33, ... . Через середины хорд проводят кривую
проводят пучок прямых, пересекающих кривую по хордам 11, 22, 33, ... . Через середины хорд проводят кривую 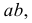 которая называется кривой ошибок. Эта вспомогательная кривая пересекает данную кривую в точке
которая называется кривой ошибок. Эта вспомогательная кривая пересекает данную кривую в точке 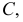 являющейся точкой касания. Прямая
являющейся точкой касания. Прямая 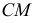 есть касательная к данной кривой линии.
есть касательная к данной кривой линии.
Построение нормали к кривой линии, проходящей через заданную точку 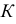 вне кривой, показано на рис. 140. Принимая точку
вне кривой, показано на рис. 140. Принимая точку 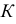 за центр, проводят ряд окружностей, пересекающих кривую по хордам 11, 22, 33 и т.д. Из концов хорд проводят разносторонне направленные перпендикуляры к ним, на которых откладывают отрезки, равные длинам соответствующих хорд. Концы отрезков этих перпендикуляров намечают кривую ошибок - линию
за центр, проводят ряд окружностей, пересекающих кривую по хордам 11, 22, 33 и т.д. Из концов хорд проводят разносторонне направленные перпендикуляры к ним, на которых откладывают отрезки, равные длинам соответствующих хорд. Концы отрезков этих перпендикуляров намечают кривую ошибок - линию 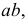 пересекающую данную кривую в точке
пересекающую данную кривую в точке 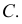 Прямая
Прямая 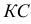 задает направление искомой нормали
задает направление искомой нормали 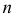 к данной кривой.
к данной кривой.
Кривые линии называются соприкасающимися. если в общей их точке 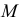 они имеют общую касательную. Нормали кривых линий в точке соприкасания лежат на одной прямой.
они имеют общую касательную. Нормали кривых линий в точке соприкасания лежат на одной прямой.
Соприкасание называется внутренним, если в точке соприкасания нормали кривых совпадают (рис. 141, а). Если нормали направлены в разные стороны, то кривые линии имеют внешние соприкасания (рис. 141,б).
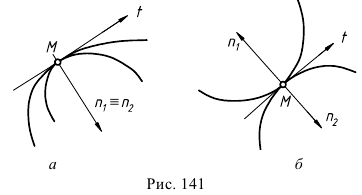
Соприкасающаяся окружность в данной точке кривой определяет кривизну плоской кривой в этой точке. Соприкасающейся окружностью или кругом кривизны кривой называют предельное положение окружности, когда она проходит через данную точку и две бесконечно близкие к ней точки кривой. Радиус этой окружности 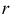 есть радиус кривизны, а центр
есть радиус кривизны, а центр 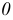 - центр кривизны кривой линии в данной точке (рис. 142).
- центр кривизны кривой линии в данной точке (рис. 142).
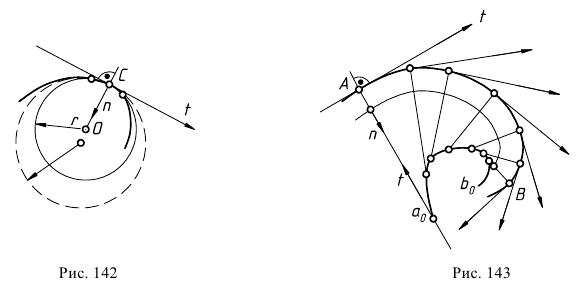
Геометрическое место центров кривизны 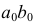 для всех точек данной кривой
для всех точек данной кривой 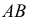 есть кривая, называемая эволютой (рис. 143).Она является огибающей нормалей данной кривой.
есть кривая, называемая эволютой (рис. 143).Она является огибающей нормалей данной кривой.
Рассматриваемую кривую линию 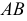 по отношению к своей эволюте называют эвольвентой. Касательные эволюты являются нормалями эвольвенты. Через каждую точку касательной к эволюте проходит одна и только одна эвольвента. Всякая плоская кривая линия есть геометрическое место центров кривизны бесчисленного множества эвольвент.
по отношению к своей эволюте называют эвольвентой. Касательные эволюты являются нормалями эвольвенты. Через каждую точку касательной к эволюте проходит одна и только одна эвольвента. Всякая плоская кривая линия есть геометрическое место центров кривизны бесчисленного множества эвольвент.
Плоские кривые линии второго порядка и их проекции
Алгебраическую кривую линию, которая описывается в системе декартовых координат уравнением второй степени относительно текущих координат, называют линией второго порядка.
Общее уравнение второй степени с двумя переменными имеет вид
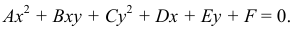
После приведения уравнения кривой к каноническому виду кривые могут быть квалифицированы следующим образом:
- кривые эллиптического типа. Это эллипс (в частном случае окружность, одна точка или мнимое место точек);
- кривые гиперболического типа. Это гипербола или пара пересекающихся прямых;
- кривые линии параболического типа - парабола, пара параллельных прямых (в частном случае совпадающих) или мнимое место точек.
Кривые линии второго порядка называют кониками или линиями конических сечений, так как они могут быть получены при пересечении прямого кругового конуса с плоскостью. Конические сечения будут рассмотрены далее (Раздел VII. 1.). Кривую второго порядка однозначно определяют заданием пяти точек общего положения: через заданные пять точек проходит одна и только одна кривая второго порядка. Если хотя бы три точки лежат на одной прямой, то получается распадающееся коническое сечение.
Эллипс представляет собой геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная. Каноническое уравнение эллипса имеет вид
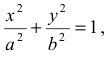 где
где 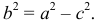
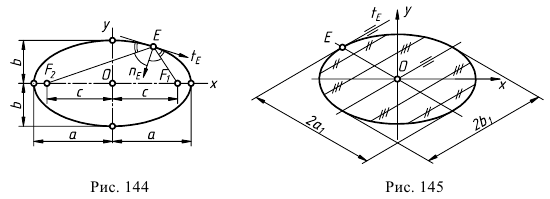
Оси координат являются осями симметрии эллипса (рис. 144). Точка 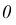 пересечения осей симметрии называется центром эллипса, точки пересечения эллипса осями симметрии - вершинами эллипса. Отрезки, соединяющие противоположные вершины эллипса, равные
пересечения осей симметрии называется центром эллипса, точки пересечения эллипса осями симметрии - вершинами эллипса. Отрезки, соединяющие противоположные вершины эллипса, равные 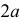 и
и 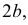 называют соответственно большой и малой осями эллипса. Два фокуса эллипса - точки
называют соответственно большой и малой осями эллипса. Два фокуса эллипса - точки 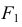 и
и 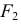 расположены на расстоянии
расположены на расстоянии 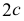 друг от друга. Величину
друг от друга. Величину 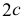 называют фокусным расстоянием. Любая точка
называют фокусным расстоянием. Любая точка 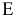 плоскости принадлежит эллипсу, если соблюдается условие
плоскости принадлежит эллипсу, если соблюдается условие 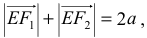 где
где 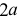 - большая ось эллипса.
- большая ось эллипса.
Диаметры эллипса - это отрезки прямых, проходящие через центр эллипса. Геометрическим местом середин хорд, параллельных одному из диаметров эллипса, является диаметр, сопряженный заданному. На рис.145 диаметры 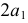 и
и 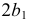 является сопряженными. Большая и малая оси эллипса являются сопряженными взаимно перпендикулярными диаметрами.
является сопряженными. Большая и малая оси эллипса являются сопряженными взаимно перпендикулярными диаметрами.
Касательные, проведенные к эллипсу в концах какого-либо диаметра, параллельны другому диаметру, сопряженному с первым. Касательная 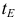 к эллипсу составляет равные углы с фокальными радиусами-векторами точки касания. Нормаль
к эллипсу составляет равные углы с фокальными радиусами-векторами точки касания. Нормаль 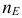 эллипса в заданной точке является биссектрисой угла между фокальными радиусами-векторами этой точки (см. рис. 144).
эллипса в заданной точке является биссектрисой угла между фокальными радиусами-векторами этой точки (см. рис. 144).
Частным видом эллипса является окружность. Если фокусы 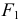 и
и 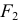 совпадают, то из условия
совпадают, то из условия 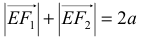 имеем
имеем 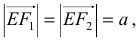 получается геометрическое место точек, равноудаленных от одной данной точки, т.е. окружность. Эллипс есть кривая, родственная окружности. На родстве двух фигур основан ряд способов построения эллипса.
получается геометрическое место точек, равноудаленных от одной данной точки, т.е. окружность. Эллипс есть кривая, родственная окружности. На родстве двух фигур основан ряд способов построения эллипса.
На рис. 146 представлен один из способов построения эллипса по его сопряженным диаметрам. Этот способ используют в случае, когда эллипс проецируется на плоскости проекций в виде эллипсов.
Пусть заданы проекции двух произвольно выбранных и делящихся пополам отрезков - 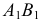 и
и 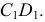 Эти отрезки можно рассматривать как сопряженные диаметры эллипса. Один из отрезков, например
Эти отрезки можно рассматривать как сопряженные диаметры эллипса. Один из отрезков, например 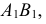 примем за диаметр окружности, родственной эллипсу. Здесь диаметр окружности
примем за диаметр окружности, родственной эллипсу. Здесь диаметр окружности 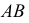 совпадает с диаметром
совпадает с диаметром 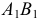 эллипса. Диаметры
эллипса. Диаметры 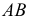 и
и 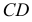 родственной эллипсу окружности являются взаимно сопряженными, т.е. взаимно перпендикулярными. Построив окружность и наметив на ней ряд точек
родственной эллипсу окружности являются взаимно сопряженными, т.е. взаимно перпендикулярными. Построив окружность и наметив на ней ряд точек 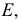 можно определить соответствующий им ряд точек
можно определить соответствующий им ряд точек 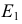 эллипса.
эллипса.
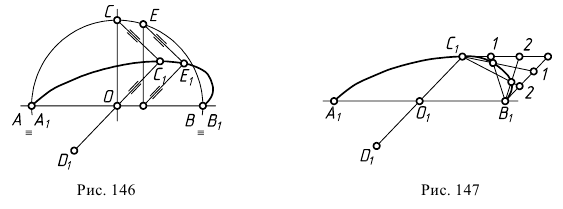
Другой способ построения эллипса по его сопряженным диаметрам показан на рис. 147. На полудиаметрах эллипса 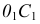 и
и 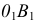 строят параллелограмм. Стороны параллелограмма делят соответственно на одинаковое число равных отрезков. Лучи, проведенные из точек
строят параллелограмм. Стороны параллелограмма делят соответственно на одинаковое число равных отрезков. Лучи, проведенные из точек 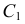 и
и 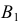 - концов полудиаметров через одинаково нумерованные точки сторон параллелограмма, пересекаются в точках эллипса.
- концов полудиаметров через одинаково нумерованные точки сторон параллелограмма, пересекаются в точках эллипса.
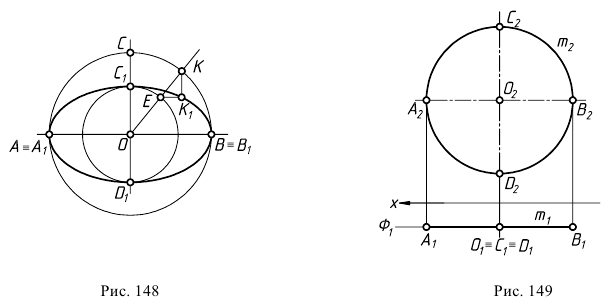
На рис. 148 показан способ построения эллипса по заданным осям. Для построения точек эллипса из центра 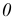 проводят две окружности, диаметрами которых являются большая
проводят две окружности, диаметрами которых являются большая 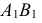 и малая
и малая 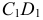 оси эллипса. Из центра
оси эллипса. Из центра 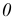 произвольно проводят луч, который пересекает окружности в точках
произвольно проводят луч, который пересекает окружности в точках 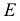 и
и 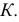 Из этих точек проводят прямые, параллельные соответственно осям
Из этих точек проводят прямые, параллельные соответственно осям 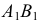 и
и 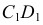 эллипса. Точка
эллипса. Точка 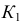 их пересечения является точкой эллипса. Выбирая другие лучи и помечая точки на окружностях, строят соответствующие точки эллипса.
их пересечения является точкой эллипса. Выбирая другие лучи и помечая точки на окружностях, строят соответствующие точки эллипса.
В начертательной геометрии эллипсы чаще всего рассматривают как проекции окружности. При ортогональном параллельном проецировании окружность может проецироваться на плоскости проекций в виде отрезка прямой, окружности (частные случаи) или в виде эллипса (общий случай).
Окружность проецируется на плоскость проекций без искажения, если ее плоскость параллельна плоскости проекций. Пусть окружность лежит во фронтальной плоскости уровня, тогда ее фронтальная проекция есть окружность, а горизонтальная - отрезок, равный диаметру и параллельный оси проекций 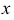 (рис. 149).
(рис. 149).
Если окружность принадлежит проецирующей плоскости, то одна из ее проекций совпадает со следом плоскости и равна диаметру окружности, а другая есть эллипс.
Пусть окружность данного диаметра принадлежит заданной горизонтально-проецирующей плоскости 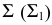 (рис. 150). Горизонтальная проекция окружности
(рис. 150). Горизонтальная проекция окружности 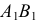 равна диаметру и совпадает со следом плоскости
равна диаметру и совпадает со следом плоскости 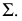 Фронтальная проекция окружности есть эллипс, большая ось которого а есть проекция вертикального диаметра
Фронтальная проекция окружности есть эллипс, большая ось которого а есть проекция вертикального диаметра 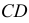 окружности. Большая ось эллипса является горизонтально-проецирующей прямой и на
окружности. Большая ось эллипса является горизонтально-проецирующей прямой и на 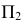 изображается в истинную величину, равную диаметру окружности. Малая ось эллипса
изображается в истинную величину, равную диаметру окружности. Малая ось эллипса 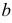 перпендикулярна большой оси и параллельна оси
перпендикулярна большой оси и параллельна оси 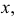 она является горизонталью. Таким образом, фронтальная проекция горизонтального диаметра окружности есть малая ось эллипса.
она является горизонталью. Таким образом, фронтальная проекция горизонтального диаметра окружности есть малая ось эллипса.
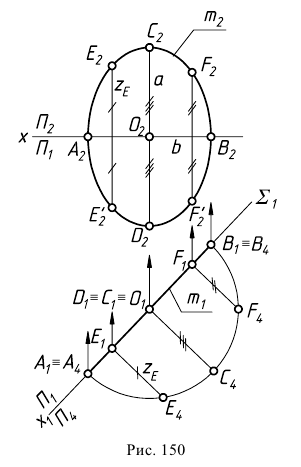
Построение других точек эллипса выполняют способом хорд. Хорды параллельны вертикальному диаметру и на 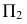 проецируются в натуральную величину. Для более точного построения на чертеже ось проекций
проецируются в натуральную величину. Для более точного построения на чертеже ось проекций 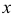 проводят через фронтальную проекцию центра эллипса - точку
проводят через фронтальную проекцию центра эллипса - точку 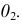 Вводят дополнительную плоскость проекций
Вводят дополнительную плоскость проекций 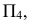 которая совпадает с плоскостью
которая совпадает с плоскостью 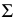 (на чертеже новая ось
(на чертеже новая ось 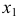 совпадает со следом
совпадает со следом 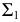 ). На плоскости проекций
). На плоскости проекций 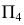 изобразится только половина окружности с положительными координатами
изобразится только половина окружности с положительными координатами 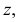 равными половине хорд. Величину координаты
равными половине хорд. Величину координаты 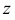 откладывают от оси
откладывают от оси 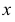 по линиям связи вверх и вниз. Получаются две точки эллипса
по линиям связи вверх и вниз. Получаются две точки эллипса 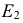 и
и 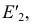 симметричные относительно малой оси. Аналогично строят другие точки эллипса.
симметричные относительно малой оси. Аналогично строят другие точки эллипса.
Если окружность принадлежит плоскости общего положения, то ортогональными проекциями ее являются эллипсы. Большая ось эллипса равна и параллельна тому диаметру окружности, который параллелен данной плоскости проекций. Малая ось эллипса равна проекции диаметра окружности, являющегося линией наибольшего ската плоскости этой окружности.
Пусть окружность лежит в плоскости общего положения, заданной горизонталью и фронталью 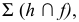 точка пересечения которых принимается за центр окружности
точка пересечения которых принимается за центр окружности 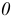 (рис. 151). Диаметр окружности 12 совпадает с горизонталью, а диаметр 34 совпадает с фронталью. На горизонтальной плоскости проекций большая ось эллипса совпадает с проекцией горизонтали
(рис. 151). Диаметр окружности 12 совпадает с горизонталью, а диаметр 34 совпадает с фронталью. На горизонтальной плоскости проекций большая ось эллипса совпадает с проекцией горизонтали 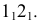 Малую ось эллипса
Малую ось эллипса 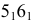 определяют с помощью дополнительной плоскости проекций
определяют с помощью дополнительной плоскости проекций 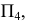 перпендикулярной заданной плоскости
перпендикулярной заданной плоскости 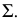
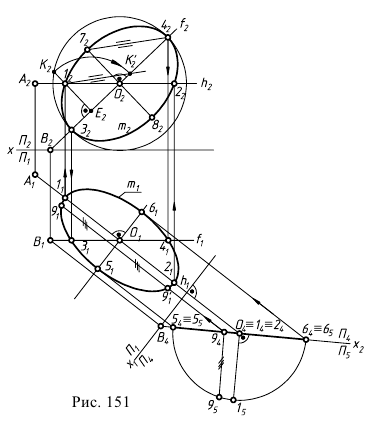
На 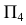 окружность проецируется в отрезок, равный диаметру. В системе плоскостей
окружность проецируется в отрезок, равный диаметру. В системе плоскостей 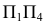 решаем ранее рассмотренную задачу построения эллипса как проекции окружности, лежащей в проецирующей плоскости. Аналогично можно построить большую и малую оси эллипса - фронтальной проекции окружности. Однако здесь приведен другой способ построения эллипса. На фронтальной плоскости проекций большая ось эллипса совпадает с направлением фронтали плоскости и равна диаметру 34 окружности. Для построения малой оси эллипса проводят окружность с диаметром, равным большой оси эллипса. Через точку
решаем ранее рассмотренную задачу построения эллипса как проекции окружности, лежащей в проецирующей плоскости. Аналогично можно построить большую и малую оси эллипса - фронтальной проекции окружности. Однако здесь приведен другой способ построения эллипса. На фронтальной плоскости проекций большая ось эллипса совпадает с направлением фронтали плоскости и равна диаметру 34 окружности. Для построения малой оси эллипса проводят окружность с диаметром, равным большой оси эллипса. Через точку 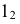 перпендикулярно большой оси строят соответственно полухорды
перпендикулярно большой оси строят соответственно полухорды 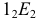 и
и 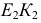 эллипса и окружности. Полухорду
эллипса и окружности. Полухорду 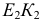 вращением вокруг точки
вращением вокруг точки 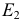 совмещают с большой осью.
совмещают с большой осью.
Точки 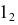 и
и 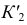 соединяют прямой линией, параллельно которой из точки
соединяют прямой линией, параллельно которой из точки 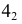 проводят прямую до пересечения в точке
проводят прямую до пересечения в точке 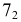 с направлением малой оси эллипса. Отрезок
с направлением малой оси эллипса. Отрезок 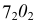 определяет величину малой полуоси эллипса - фронтальной проекции окружности.
определяет величину малой полуоси эллипса - фронтальной проекции окружности.
По заданным осям можно построить другие точки эллипса рассмотренным выше способом (см. рис. 148).
Гипербола - это геометрическое место точек, для которых абсолютная величина разности расстояний до двух заданных фиксированных точек (фокусов) есть величина постоянная.
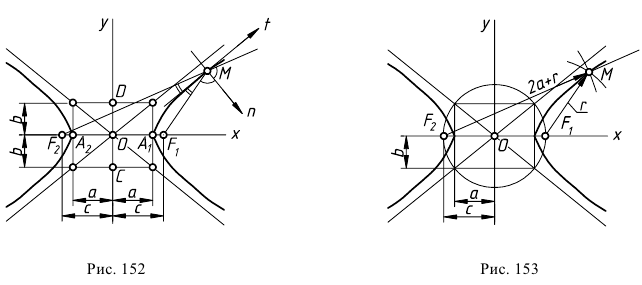
На рис. 152 точки 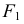 и
и 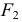 являются фокусами гиперболы. Расстояние между ними
являются фокусами гиперболы. Расстояние между ними 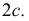 Точка пересечения координатных осей
Точка пересечения координатных осей 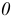 является центром симметрии. Точки
является центром симметрии. Точки 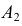 и
и 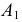 - вершины гиперболы, расстояние между ними
- вершины гиперболы, расстояние между ними 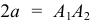 называют действительной осью гиперболы. Ось симметрии
называют действительной осью гиперболы. Ось симметрии 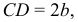 которая не пересекает гиперболу, называют мнимой осью.
которая не пересекает гиперболу, называют мнимой осью.
Асимптоты гиперболы - прямые, к которым ветви гиперболы неограниченно приближаются при удалении в бесконечность. Асимптоты гиперболы направлены по диагоналям прямоугольника со сторонами 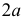 и
и 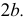
Каноническое уравнение гиперболы (оси координат совпадают с осями гиперболы) имеет вид
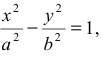 где
где 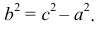
Любая точка 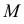 плоскости принадлежит правой ветви гиперболы, если соблюдается условие
плоскости принадлежит правой ветви гиперболы, если соблюдается условие 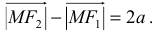 Точки, для которых
Точки, для которых 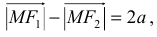 принадлежат левой ветви. Касательная
принадлежат левой ветви. Касательная 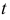 и нормаль
и нормаль 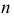 к гиперболе являются биссектрисами соответственно внутреннего и внешнего углов, образованных радиусами-векторами, проведенными из фокусов в точку касания.
к гиперболе являются биссектрисами соответственно внутреннего и внешнего углов, образованных радиусами-векторами, проведенными из фокусов в точку касания.
На рис. 153 показано построение гиперболы по точкам, если известны величины ее полуосей 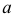 и
и 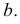 Из точки
Из точки 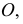 как из центра, проводят окружность радиусом
как из центра, проводят окружность радиусом 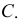 Окружность пересекает ось
Окружность пересекает ось 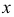 в точках
в точках 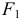 и
и 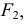 являющихся фокусами гиперболы. Из фокусов, как из центров, проводят дуги окружностей соответственно радиусами
являющихся фокусами гиперболы. Из фокусов, как из центров, проводят дуги окружностей соответственно радиусами 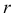 и
и 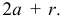 Точки их пересечения являются точками гиперболы, так как разность расстояний от каждой точки до фокусов равна
Точки их пересечения являются точками гиперболы, так как разность расстояний от каждой точки до фокусов равна 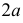 и есть величина постоянная. Изменяя
и есть величина постоянная. Изменяя 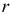 и повторяя построения, находят новые точки гиперболы.
и повторяя построения, находят новые точки гиперболы.
Парабола - это геометрическое место точек, равноудаленных от фиксированной точки (фокуса) и от заданной прямой (директрисы).
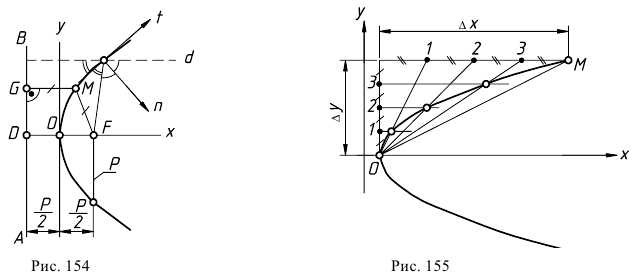
На рис. 154 точка 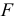 есть фокус параболы, а прямая
есть фокус параболы, а прямая 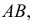 перпендикулярная оси
перпендикулярная оси 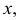 - ее директриса. Ось
- ее директриса. Ось 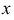 совпадает с осью симметрии параболы, точка
совпадает с осью симметрии параболы, точка 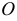 является вершиной параболы. Расстояние от фокуса до вершины параболы равно
является вершиной параболы. Расстояние от фокуса до вершины параболы равно 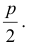 Величина
Величина 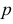 называется фокальным параметром и равна расстоянию от фокуса до директрисы или половине хорды, проходящей через фокус перпендикулярно оси
называется фокальным параметром и равна расстоянию от фокуса до директрисы или половине хорды, проходящей через фокус перпендикулярно оси 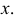
Каноническое уравнение параболы: 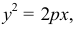 где
где 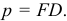 Любая точка
Любая точка 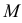 плоскости принадлежит параболе, если
плоскости принадлежит параболе, если 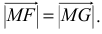
Касательная 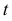 и нормаль
и нормаль 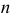 к параболе являются биссектрисами углов между фокальным радиусом-вектором точки параболы и диаметром, проходящим через эту же точку. Под диаметром
к параболе являются биссектрисами углов между фокальным радиусом-вектором точки параболы и диаметром, проходящим через эту же точку. Под диаметром 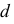 параболы понимают прямую, параллельную оси параболы. На рис. 155 показан способ построения параболы, если известна ее вершина - точка
параболы понимают прямую, параллельную оси параболы. На рис. 155 показан способ построения параболы, если известна ее вершина - точка 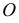 и одна из точек - точка
и одна из точек - точка 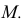 Соединив вершину
Соединив вершину 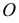 с точкой
с точкой 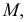 определяют разности координат
определяют разности координат 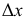 и
и 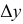 между этими точками. Расстояния
между этими точками. Расстояния 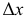 и
и 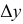 делят на одинаковое количество равных частей, точки деления обозначают. Через точки деления с одинаковыми номерами проводят линии построения, на пересечении которых определяют искомые точки параболы.
делят на одинаковое количество равных частей, точки деления обозначают. Через точки деления с одинаковыми номерами проводят линии построения, на пересечении которых определяют искомые точки параболы.
Пространственные кривые линии и их проекции
Пространственную кривую линию на чертеже задают последовательным рядом ее точек. Чтобы установить особые точки пространственной кривой, необходимо наличие двух ее проекций, в отличие от плоской кривой, для определения особых точек которой достаточно одной проекции. Сопоставление горизонтальной и фронтальной проекций на рис. 156 показывает, что хотя на горизонтальной проекции имеется двойная точка, но на самой кривой двойной точки нет.
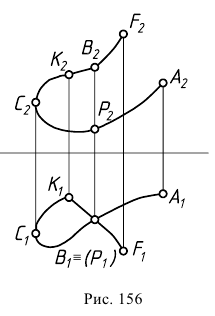
Так же, как и для плоской кривой, касательная к кривой в пространстве проецируется в касательную к проекции этой кривой. Проецирующая плоскость, проведенная через касательную к проекции кривой, касается кривой в пространстве.
Но если для плоской кривой можно было провести только один перпендикуляр к касательной в точке 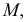 то для пространственной кривой таких перпендикуляров в точке касания можно провести бесчисленное множество, что приводит к понятию нормальной плоскости.
то для пространственной кривой таких перпендикуляров в точке касания можно провести бесчисленное множество, что приводит к понятию нормальной плоскости.
Тремя плоскостями - спрямляющей, соприкасающейся и нормальной (см. рис.136), образующими трехгранник, пользуются как координатными при рассмотрении кривой в данной ее точке. Положение трехгранника зависит от положения точки на кривой.
Если касательные к пространственной кривой линии во всех ее точках одинаково наклонны к какой-либо плоскости, то такие линии называются линиями одинакового уклона.
Цилиндрические винтовые линии одинакового уклона широко применяются в технике. Моделью такой линии может служить цилиндрическая пружина.
Цилиндрическая винтовая линия - гелиса - есть траектория сложного движения точки, равномерно перемещающейся по образующей и равномерно вращающейся вместе с этой образующей вокруг оси цилиндра.
Винтовая линия имеет три параметра: диаметр цилиндра, шаг и направление. Шаг - это смещение точки вдоль образующей за один оборот. Различают два направления винтовой линии: правое - при движение точки вверх против часовой стрелки и левое - при движении точки вверх по часовой стрелке.
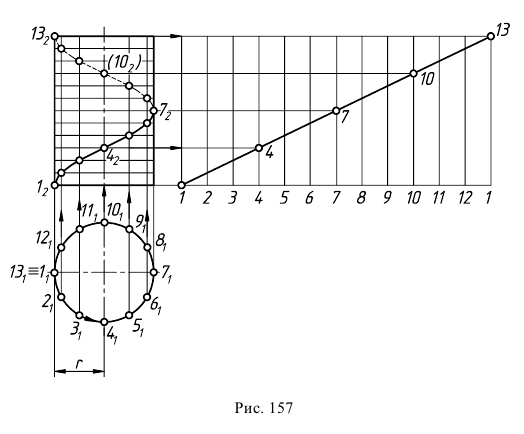
На рис. 157 построена гелиса заданного радиуса 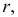 правого направления и с шагом, равным высоте цилиндра. Для построения проекций такой линии длина окружности (горизонтальная проекция цилиндра) и высота прямоугольника (фронтальная проекция цилиндра) делятся на 12 равных частей. Через точки деления окружности проводят вертикальные линии связи.
правого направления и с шагом, равным высоте цилиндра. Для построения проекций такой линии длина окружности (горизонтальная проекция цилиндра) и высота прямоугольника (фронтальная проекция цилиндра) делятся на 12 равных частей. Через точки деления окружности проводят вертикальные линии связи.
На фронтальной плоскости проекций через точки деления прямоугольника проводят прямые, параллельные основанию. Точки пересечения линий связи с соответствующей горизонтальной прямой определяют фронтальную проекцию цилиндрической винтовой линии. На видимой части цилиндра гелиса будет видимой, на невидимой - нет. Направление винтовой линии на чертеже определяет стрелка, поставленная на горизонтальной проекции. Итак, горизонтальная проекция винтовой линии есть окружность, а фронтальная - синусоида.
При построении развертки цилиндрическая поверхность развертывается в прямоугольник со сторонами, равными длине окружности основания и высоте цилиндра. Винтовая линия на развертке преобразуется в прямую - диагональ прямоугольника, так как для каждой точки этой прямой существует пропорциональная зависимость между отрезками длины окружности и высоты цилиндра.
Что такое поверхности
В существующем мире нас окружает неограниченное количество разнообразных поверхностей. Некоторые могут быть математически описаны, другие настолько сложны, что не поддаются математическому описанию.
В математике под поверхностью подразумевается непрерывное множество точек, если между координатами точек этого множества может быть установлена зависимость, определяемая уравнением вида 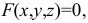 где
где 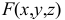 - многочлен
- многочлен 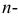 й степени, или в форме какой-либо трансцендентной функции. В первом случае поверхности называются алгебраическими, во втором - трансцендентными.
й степени, или в форме какой-либо трансцендентной функции. В первом случае поверхности называются алгебраическими, во втором - трансцендентными.
Если алгебраическая поверхность описывается уравнением 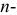 й степени, то поверхность считается
й степени, то поверхность считается 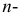 го порядка.
го порядка.
Любая произвольно расположенная секущая плоскость пересекает поверхность по кривой того же порядка (иногда распадающейся или мнимой), какой имеет сама поверхность.
Порядок поверхности может быть определен также числом точек ее пересечения с произвольной прямой, считая все точки (действительные и мнимые).
Что такое кривые линии
Кривой линией называется траектория точки, перемещающейся в пространстве по какому-либо закону. Однако, имеются кривые линии, не описываемые какой-либо закономерностью (незакономерные кривые линии). Кривая линия может быть также определена как однопараметрическое множество точек.
На рисунке 8.1 представлена классификация кривых линий. 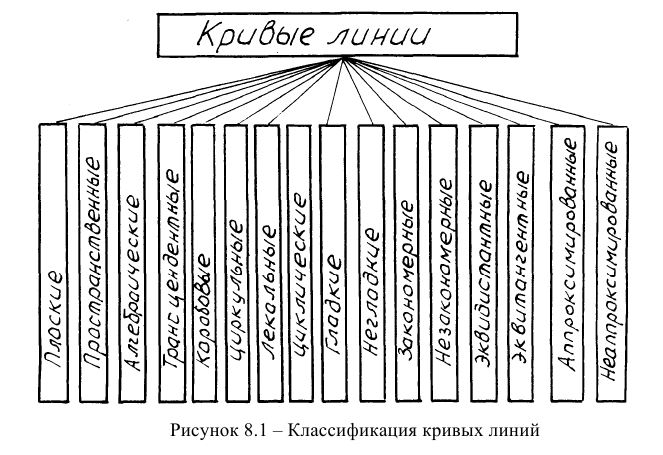
Плоской кривой линией называется линия, каждая точка которой принадлежит одной плоскости. В противном случае кривая линия называется пространственной (винтовая линия, линии пересечения двух поверхностей, из которых хотя бы одна является кривой поверхностью).
Закономерные линии описываются уравнениями и делятся на алгебраические второго и высшего порядков и трансцендентные, описываемые тригонометрическими функциями. Порядок кривой линии -это степень её уравнения или количество точек пересечения кривой линии с прямой линией (для плоских кривых) или количество точек пересечения с плоскостью (для пространственных линий). Кривые второго порядка иногда называются кониками. 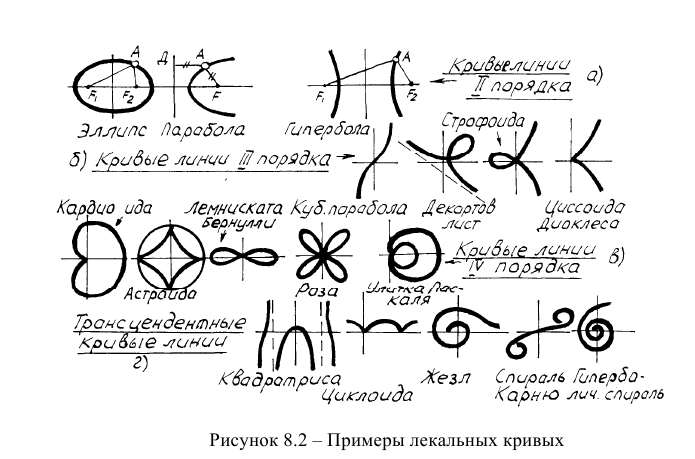
Коробовыми линиями (или обводами) называются составные кривые линии, дуги которых последовательно определены парами точек обвода. Если на стыках можно построить общую касательную, то обвод называется гладким. Циркульными линиями называются линии, построение которых можно осуществить циркулем (овал, овоид, завиток и др.).
Лекальными кривыми называются плоские закономерные линии, при вычерчивании которых используются лекала (эллипс, парабола, гипербола и др.). Циклические кривые линии - это линии, повторяющиеся в процессе образования (циклоида, эпициклоида, гипоциклоида и др.).
Гладкие кривые линии состоят из обыкновенных точек. Обыкновенные точки кривой линии - это точки, в которых можно построить только одну касательную к кривой линии. Если кривая линия содержит особые точки (см. далее), то линия называется негладкой.
Эквидистантные и эквитангентные линии - это линии, равноудаленные от некоей кривой линии и повторяющие её форму. Аппроксимированные линии - это линии, приближенно замененные другими более удобными для вычерчивания линиями (например, эллипс иногда заменяют овалом).
Кривые линии могут быть образованы движением точки в пространстве, пересечением кривой поверхности плоскостью (кривые Персея), взаимным пересечением двух поверхностей. Кривые Персея, например, образуются при пересечения торовых поверхностей плоскостью.
На рисунке 8.2 представлены некоторые алгебраические кривые линии второго, третьего и четвертого порядков, а также трансцендентные кривые линии.
Наиболее часто в технике применяются лекальные кривые линии, которые могут быть плоскими и пространственными. К ним относятся эллипс, парабола, гипербола, эвольвента, циклоида, винтовая линия и другие, примеры которых приведены на рисунке 8.3. Способы построения лекальных кривых обычно рассматривается в курсе технического черчения.
Эвольвента - траектория точки касательной, перекатываемой без скольжения по окружности. Иногда её неправильно называют разверткой окружности.
Синусоида - кривая линия, описываемая уравнением 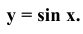
Гипербола - геометрическое место точек, разность расстояний которых от двух точек, называемых фокусами, есть величина постоянная.
Винтовая линия - траектория точки, перемещающейся по образующей цилиндра, конуса или тора, в то время как сама образующая равномерно вращается вокруг оси упомянутых поверхностей.
Эллипс - геометрическое место точек, сумма расстояний которых до двух точек, называемых фокусами, есть величина постоянная.
Парабола - геометрическое место точек, равноудаленных от некоторой точки, называемой фокусом, и некоторой прямой, называемой директрисой.
Циклоида - траектория точки окружности, перекатываемой без скольжения по прямой линии. При построении эпи- и гипоциклоиды окружность перекатывают по окружности.
На рисунке 8.4 представлены особые точки кривых линий. Особыми точками называются точки, в которых можно провести не одну, а две и более касательных или в которых изменяется направление движения точки или вращения касательной.
На эпюре кривые линии задаются множеством точек, принадлежащих линии (рисунок 8.5). Возможны табличный и аналитический способы задания. 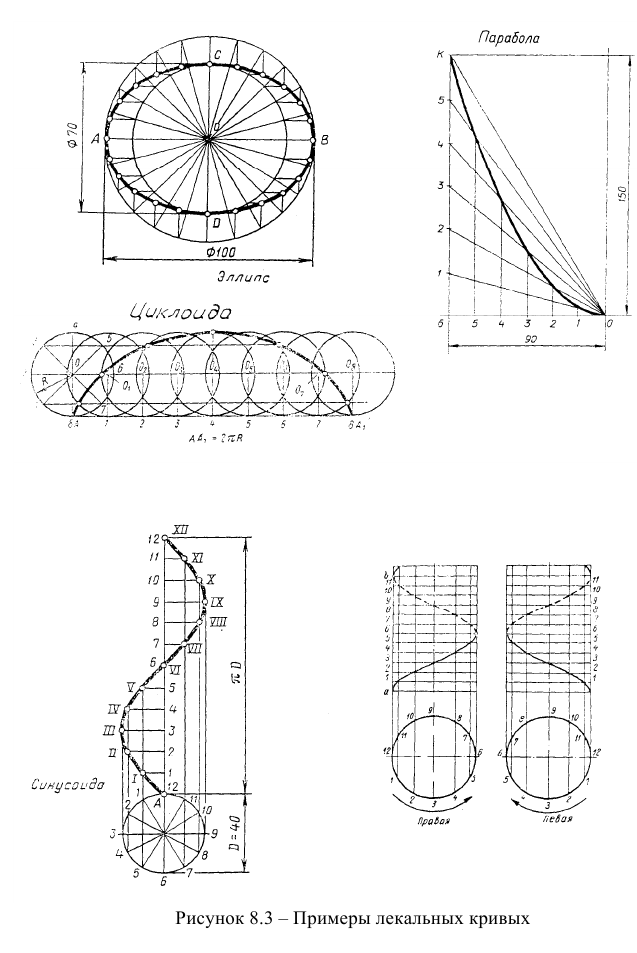

Проекции кривой линии имеют следующие свойства:
- В общем случае проекция кривой линии есть кривая линия;
- Если точка принадлежит кривой линии, то её проекции принадлежат одноименным проекциям кривой;
- Касательная к кривой линии проецируется в касательную к проекциям кривой линии.
Пример: Построить проекции правой цилиндрической винтовой линии, проходящей через точку поверхности цилиндра. 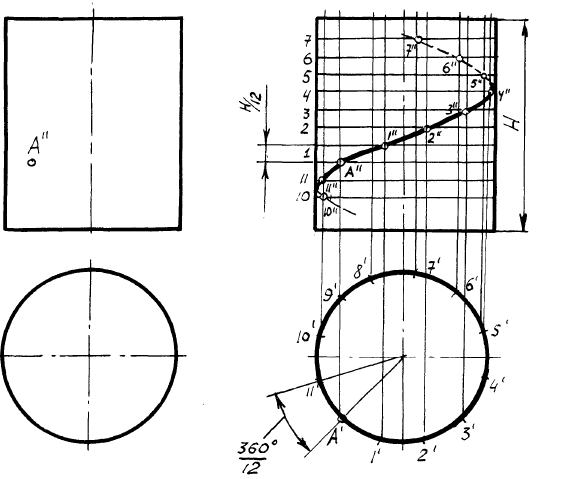
Решение: Находим точку 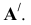 Начиная с точки
Начиная с точки 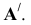 , делим окружность основания цилиндра на 12 частей. Высоту цилиндра Н делим на 12 частей, начиная с точки
, делим окружность основания цилиндра на 12 частей. Высоту цилиндра Н делим на 12 частей, начиная с точки 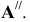 На пересечении вертикальных и горизонтальных одноименных линий находим точки винтовой линии, которые плавно соединяем (рисунок 8.6).
На пересечении вертикальных и горизонтальных одноименных линий находим точки винтовой линии, которые плавно соединяем (рисунок 8.6).
Кривые линии и кривые поверхности
Линию можно рассматривать как множество последовательных положений движущейся точки – траекторию точки.
Кривая – разновидность линии, которая получается, когда движущая точка изменяет направление своего движения. Кривая линия может являться результатом пересечения кривой поверхности плоскостью или кривых поверхностей между собой.
В начертательной геометрии кривые линии изучаются по их проекциям. Если все точки кривой лежат в одной плоскости, кривую называют плоской, в противном случае – пространственной.
Кривая - это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по разному. В начертательной геометрии кривую рассматривают как траекторию, описанную движущей точкой, как проекцию другой кривой, как линию пересечения двух поверхностей (рисунок 7.1), как множество точек, обладающих каким-либо общим для всех их свойством и т.д.
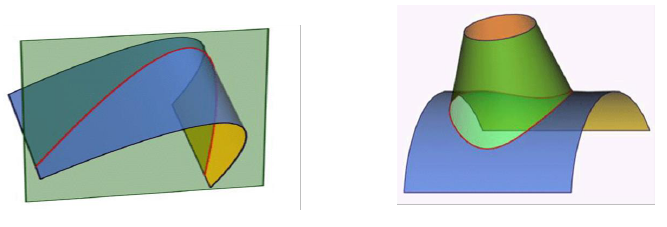 Рисунок 7.1 – Кривая, как линия пересечения двух поверхностей
Рисунок 7.1 – Кривая, как линия пересечения двух поверхностей
Способы задания кривых. Каждая кривая включает в себя геометрические элементы, которые составляют её определитель, т.е. совокупность независимых условий, однозначно определяющих эту кривую.
Различны и способы задания кривых:
- Аналитический – кривая задана математическим уравнением;
- Графический – кривая задана визуально на носителе графической информации;
- Табличный – кривая задана координатами последовательного ряда точек.
Кривые линии делятся на плоские и пространственные.
Об этом можно узнать по наличию конкурирующих точек на двух ее проекциях. Изображения пространственных кривых могут и не иметь конкурирующих точек. В таком случае, если требуется, кривую проверяют на плоскостность. Для этого соединяют попарно четыре произвольные точки кривой прямыми. Если прямые пересекаются, то исследуемая кривая плоская, а если скрещиваются - пространственная.
Из пространственных кривых более всего применяются гелисы -цилиндрические винтовые линии. Обычно их ориентируют относительно плоскостей проекций так, чтобы ось была перпендикулярна к одной из них. Тогда проекции гелисы - окружность и синусоида.
Такую линию в пространстве описывает точка, которая движется по какой-либо образующей прямого кругового цилиндра, вращающегося вокруг своей оси так, что путь проходимый точкой по образующей пропорционален углу поворота цилиндра.
Все плоские кривые разделяются на циркульные, состоящие из сопряженных дуг окружностей (их проводят при помощи циркуля), и лекальные, вычерчивающиеся с помощью лекала по предварительно построенным точкам.
Некоторые кривые, часто встречающиеся в практике
Рассмотрим построение некоторых плоских кривых (эллипса, синусоиды, спирали Архимеда), а также пространственных винтовых линий [5].
Эллипс (рис 7.2.) – плоская замкнутая кривая, у которой сумма расстояний от любой ее точки (например, от точки М) до двух заданных точек F1 и F2 (фокус эллипса) есть величина постоянная, равная большой оси эллипса АВ (F1M+F2M=AB).
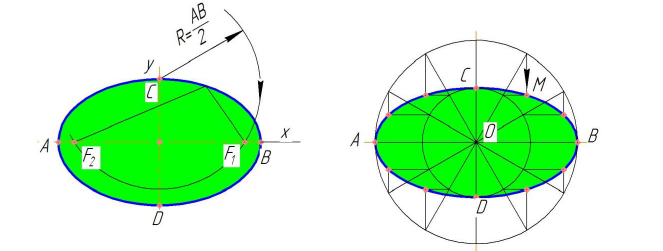
Рисунок 7.2 - Эллипс Рисунок 7.3 - Построение эллипса
Отрезок CD – малая ось эллипса, точка О – центр эллипса. Точка F1 и F2 расположены на большой оси АВ симметрично относительно точки О и удалены от концов малой оси (точек С и D) на расстояние, равное половине большой оси эллипса.
Существует ряд способов построения эллипса. Наиболее просто построить эллипс по двум его осям при помощи вспомогательных окружностей (рис. 7.3).
Синусоида- кривая, характеризующая изменение синуса угла в зависимости от величины центрального угла (рис.7.4).
Расстояние между крайними точками синусоиды по высоте, равное диаметру производящей окружности, называется амплитудой. Расстояние 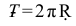 - шаг синусоиды. Построение точек синусоиды
- шаг синусоиды. Построение точек синусоиды 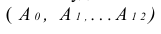 показано на рисунке 7.4.
показано на рисунке 7.4.
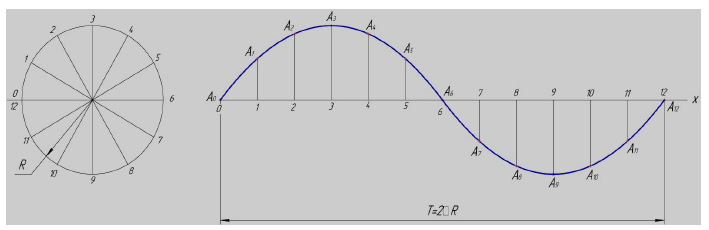
Рисунок 7.4 - Построение точек синусоиды
Спираль Архимеда (рис. 7.5 ) – кривая , которую описывает точка, равномерно вращающаяся вокруг неподвижной точки (полюса О) и одновременно равномерно удаляющаяся от него. Расстояние ОА, пройденное точкой от полюса О при повороте на 360 º - шаг спирали.
Точки, принадлежащие спирали Архимеда, строят, исходя из определения кривой, задаваясь шагом ОА и направлением вращения.
Полученный отрезок и окружность делят на одинаковое число частей (12) и через точки деления окружности проводят в одном направлении касательные к ней. По каждой касательной откладываем отрезки 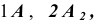
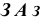 и т.д.,равные соответственно
и т.д.,равные соответственно 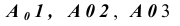 и т.д. Полученные точки соединяем плавной кривой.
и т.д. Полученные точки соединяем плавной кривой.
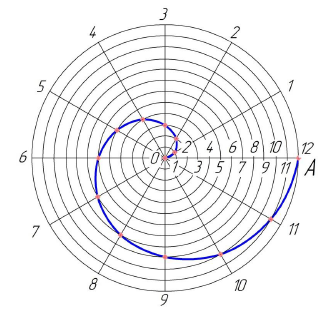 Рисунок 7.5 - Спираль Архимеда
Рисунок 7.5 - Спираль Архимеда
Цилиндрическая винтовая линия (гелиса) – пространственная кривая, которая образуется на поверхности цилиндра вращения в результате двойного равномерного движения точки – вращение вокруг оси цилиндра и поступательного движения вдоль образующей цилиндра (рис. 7.6).
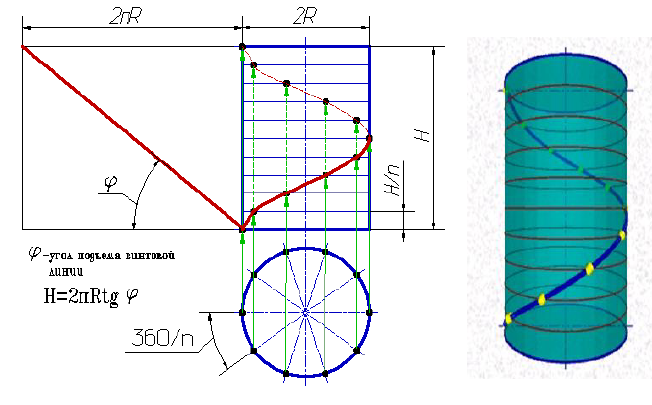 Рисунок 7.6 - Цилиндрическая винтовая линия
Рисунок 7.6 - Цилиндрическая винтовая линия
Шаг винтовой линии (Н) – расстояние между двумя ее соседними витками в направлении параллельности. Для построения цилиндрической винтовой линии делим окружность основания цилиндра и шаг Н винтовой линии на ровное число частей (12). Определим соответствующие фронтальные проекции перемещаемой точки и соединим их плавной кривой.
Горизонтальная проекция цилиндрической винтовой линии – окружность, а фронтальная синусоида. Разверткой цилиндрической винтовой линии является прямая.
Угол α – угол подъема винтовой линии: 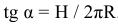 . Различают правые и левые винтовые линии. У правой подъем слева вверх направо, у левой – справа вверх налево.
. Различают правые и левые винтовые линии. У правой подъем слева вверх направо, у левой – справа вверх налево.
Коническая винтовая линия – пространственная кривая, которая образуется на поверхности конуса вращения в результате двойного равномерного движения точки – вращения вокруг оси конуса и поступательного движения вдоль образующей конуса (рис. 7.7) .
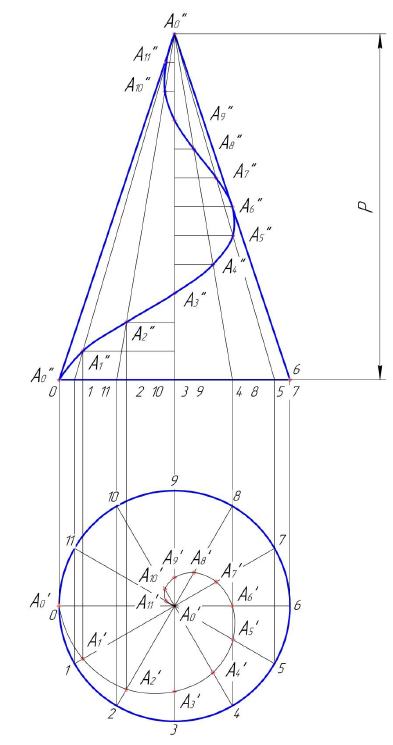
Рисунок 7.7 - Коническая винтовая линия
Шаг конической винтовой линии Р - величина прямолинейного перемещения точки в направлении оси конуса при полном обороте вокруг оси.
Для построения проекций конической винтовой линии разделим окружность основания конуса и шаг Р на равное число частей (12). Проводим проекции образующих конуса и определим на них положение соответствующих проекций точек 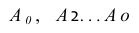 и соединим их плавной кривой.
и соединим их плавной кривой.
Горизонтальная проекция винтовой линии – спираль Архимеда, а фронтальная – затухающая синусоида (синусоида с уменьшающейся амплитудой).
Образование и классификация поверхностей
Перемещающаяся в пространстве линия или поверхность называется образующей, которая при движении может сохранять или изменять свою форму.
Закон перемещения образующей обычно определяется другими линиями (иногда точками), называемыми направляющими, по которым скользит образующая при своем движении, а также условием движения образующей.
Различают три основных способа задания поверхности:
- - аналитический (поверхность задается уравнением);
- - каркасный (поверхность задается совокупностью точек или линий);
- - кинематический (поверхность образуется непрерывным перемещением в пространстве какой–либо линии поверхности).
В начертательной геометрии пользуются, главным образом, кинематическим способом образования поверхностей (Рисунок 7.8) [1]. При этом способе поверхность рассматривается как совокупность всех последовательных положений линии, перемещающейся в пространстве по определенному закону.
Линия, производящая поверхность в каждом ее положении, называется образующей (L). Образующая может быть как прямой, так и и любой кривой, постоянной или менять свою форму в процессе перемещения.
Неподвижная линия, по которой скользит образующая, называется направляющей (М).
Совокупность нескольких последовательных положений образующей и направляющих создает каркас поверхности. Не трудно убедиться (рис. 7.8), что образующие L и направляющие М можно менять местами. При этом поверхность получается одна и та же.
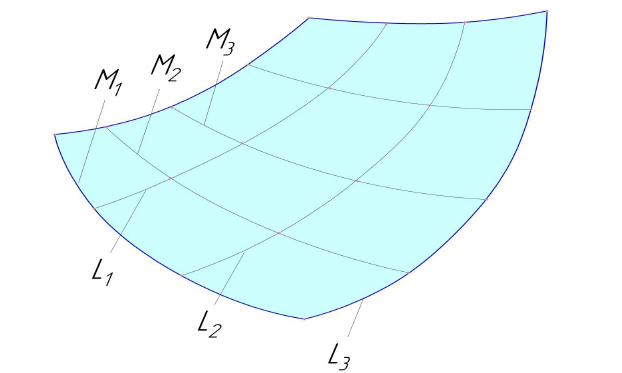
Рисунок 7.8 - Образование поверхности
Поверхность на чертеже считается заданной полностью, когда по одной проекции точки, принадлежащей поверхности, можно построить вторую ее проекцию. Точка принадлежит поверхности, если принадлежит какой-либо линии, лежащей на этой поверхности.
Чтобы задать поверхность на комплексном чертеже достаточно иметь на нем такие элементы поверхности, которые позволят построить каждую ее точку. Совокупность элементов поверхности, позволяющих построить каждую ее точку, называется определителем поверхности (Ф). Определитель состоит из 2-х частей: Ф(Г), /А/:(Г) – геометрической, в которую входят основные геометрические элементы и соотношения между ними и [А] -алгоритмической, содержащей закон построения отдельных точек и линий данной поверхности. Условно геометрическую часть заключают в круглые скобки, а алгоритмическую – в квадратные. Для придания чертежу поверхности наглядности наряду с проекцией определителя в большинстве случаев дается еще и очертание её.
Очерком поверхности называется след (линия) на плоскости проекций проецирующей поверхности, который огибает заданную поверхность. Это, как правило, контурная линия, которую называют линией видимости.
В зависимости от формы образующей и закона ее перемещения в пространстве поверхности условно можно разделить на следующие классы [1]:
- Линейчатые поверхности;
- Поверхности вращения;
- Винтовые поверхности;
- Поверхности второго порядка;
- Циклические поверхности;
- Топографические поверхности.
Следует отметить, что отдельные поверхности могут быть отнесены не к одному, а к нескольким классам.
Линейчатой поверхностью называется поверхность, образованная перемещением в пространстве прямолинейной образующей, закон движения которой может быть различным.
В общем случае линейчатые поверхности однозначно определяется тремя направляющими линиями.
В зависимости от вида направляющих и закона движения образующей получаются различные типы линейчатых поверхностей.
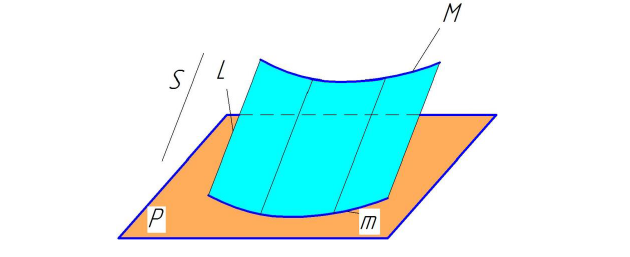
Рисунок 7.9 - Образование цилиндрической поверхности
Рассмотрим некоторые линейчатые поверхности с одной направляющей. Цилиндрическая поверхность образуется движением прямой линии L по некоторой кривой линии М и имеющей постоянное направление S. На рис. 7.9 показана цилиндрическая поверхность, у которой L - прямолинейная образующая, М – криволинейная направляющая, S – заданное направление перемещения образующей.
Следует отметить, что одна и та же поверхность может быть получена различными способами. Например, цилиндрическая поверхность может быть получена в результате перемещения прямолинейной образующей по кривой направляющей, или движением кривой образующей по прямолинейной направляющей.
Для большей наглядности изображения поверхностей в ряде случаев используют ее очерк – границы видимости на плоскостях проекций. Очерк проекции получается при пересечении с плоскостью проекций проецирующей поверхности, обертывающей данную. Например, очерком сферы является окружность радиуса, равного радиусу сферы.
В зависимости от формы образующей поверхности разделяются на линейчатые (образующая – прямая линия) и нелинейчатые (криволинейная образующая). Линейчатые поверхности называются развертывающимися, если их можно совместить с плоскостью без разрывов и складок. Не развертывающиеся поверхности не могут быть совмещены с плоскостью без наличия разрывов и складок.
Поверхности с постоянной образующей – поверхности, образующая которых не имеет своей формы при образовании поверхности. Поверхности с переменной образующей – поверхности, образующая которых изменяется при образовании поверхности.
Винтовые поверхности
Винтовые поверхности образуются винтовым движением некоторой линии – образующей.
Под винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси, и вращательного, вокруг той же оси.
При этом поступательное и угловое перемещение находятся в определенной зависимости 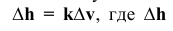 – линейное перемещение за время
– линейное перемещение за время 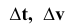 – угловое перемещение за то же время, k – коэффициент пропорциональности. Если k = Const, то шаг поверхности постоянный.
– угловое перемещение за то же время, k – коэффициент пропорциональности. Если k = Const, то шаг поверхности постоянный.
Линейчатые винтовые поверхности (образующая - прямая линия) называются геликоидами.
Прямой геликоид (рис. 7.10) образуется движением прямой, которая пересекает винтовую линию, а также ось винтовой линии i под прямым углом [5].
Поскольку образующая перпендикулярна оси винтовой линии, то она параллельна плоскости проекций Н. Поэтому другое название прямого геликоида - винтовой коноид.
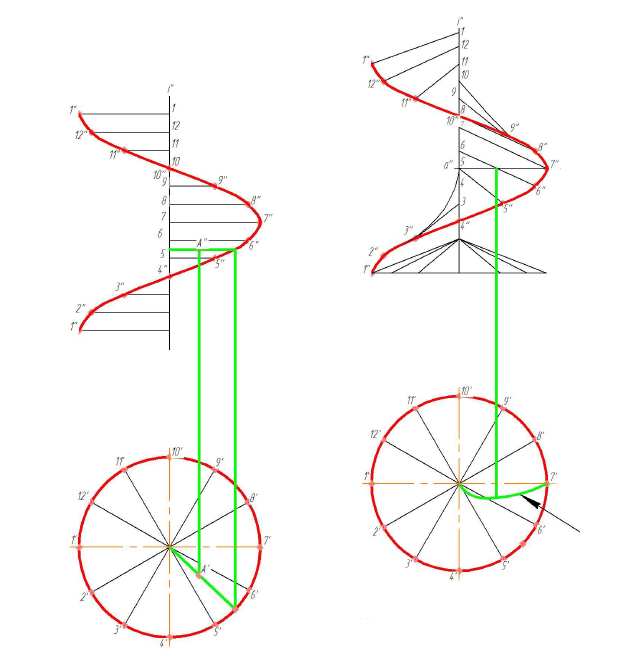
Рисунок 7.10 - Прямой геликоид Рисунок 7.11 - Косой геликоид
Косой геликоид (рис. 7.11) образуется движением прямой, которая пересекает винтовую линию и ось винтовой линии i под постоянным углом не равным 90° [5].
Особое место занимают такие нелинейные поверхности, образование которых, не подчинено ни какому закону. Оптимальную форму таких поверхностей определяют теми физическими условиями, в которых они работают и устанавливают ее форму экспериментально (поверхности лопастей турбин, обшивка каркасов морских судов и самолетов).
Поверхности вращения
Поверхности вращения – это поверхности созданные при вращении образующей m вокруг оси i (рис. 7.12).
Геометрическая часть определителя состоит из двух линий: образующей m и оси i .
Алгоритмическая часть включает две операции:
- На образующей m выделяют ряд точек A, B, C, …F;
- Каждую точку вращают вокруг оси i.
Так создается каркас поверхности, состоящей из множества окружностей), плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором.
Из закона образования поверхности вращения вытекают два основных свойства:
- Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.
- Плоскость, проходящая через ось вращения, пересекает поверхность по двум симметричным относительно оси линиям – меридианам.
Плоскость проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.
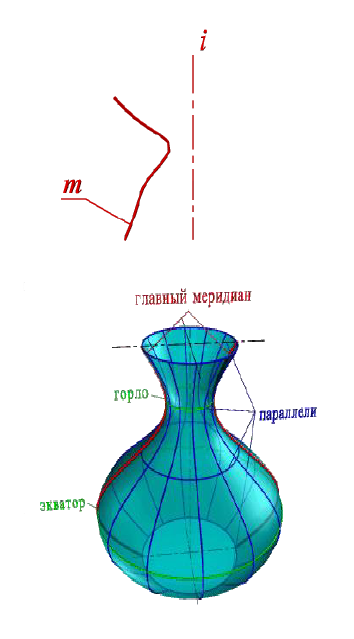
Рисунок 7.12 - Поверхность вращения
Замкнутую область пространства вместе с ее границей (поверхностью) называют геометрическим телом.
Рассмотрим наиболее распространенные поверхности вращения с прямолинейными и криволинейными образующими.
Цилиндр вращения (рис. 7.12) образуется вращением прямой вокруг параллельной ей оси i. Все точки образующей (например, точка А) описывают окружности (параллели) равные окружностям оснований цилиндра.
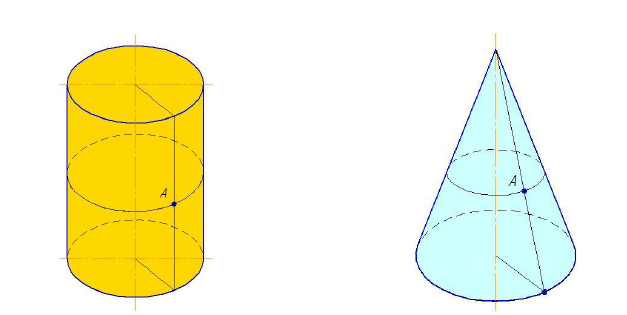
Рисунок 7.12 - Цилиндр вращения Рисунок 7. 13 - Конус вращения
Конус вращения (рис. 7.13) образуется вращением прямой вокруг пересекающейся с ней оси i. Все точки образующей описывают окружности различных радиусов. Величина радиуса изменяется от нуля до радиуса окружности основания конуса.
Однополостный гиперболоид вращения (рис. 7.14) образуется вращением образующей линии ℓ вокруг скрещивающейся с ней оси i. Точки образующей ℓ описывают окружности переменных радиусов. Радиус параллели наименьшего радиуса (горла) равен кратчайшему расстоянию между образующей ℓ и осью i.
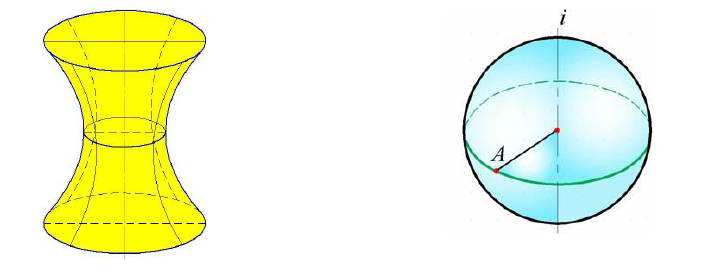
Рисунок 7.14 - Однополостный
Рисунок 7.15 - Сфера гиперболоид вращения
Сфера (рис. 7.15) образуется вращением окружности вокруг ее диаметра. Точки образующей окружности описывают окружности переменных радиусов. Точка А описывает параллель наибольшего радиуса (экватор). Для сферы экватор и меридианы - равные между собой окружности.
Эллипсоид вращения образуется вращением эллипса вокруг его оси. При вращении эллипса вокруг его большой оси получается вытянутый эллипсоид, при вращении вокруг малой - сжатый эллипсоид. Для эллипсоида вращения меридианом является эллипс.
 Рисунок 7.16 – Тор
Рисунок 7.16 – Тор
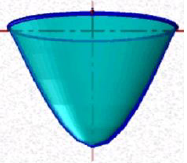
Рисунок 7.17 – Однополостный гиперболоид
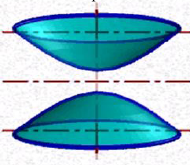
Рисунок 7.18 – Двуполостный гиперболоид
Тор (рис. 7.16) образуется вращением окружности вокруг оси i, лежащей в плоскости окружности, но не проходящей через ее центр.
В зависимости от взаимного расположения образующей окружности и оси вращения различают: открытый тор (круговое кольцо), замкнутый, самопересекающийся.
Внутреннюю часть открытого тора в технике называют глобоидом.
Пример применения - глобоидная червячная передача.
Однополостный гиперболоид вращения (рис.7.17) образуется вращением гиперболы вокруг ее мнимой оси.
Двуполостный гиперболоид вращения (рис. 7.18) образуется вращением гиперболы вокруг ее действительной оси.
Меридианами гиперболоидов вращения являются гиперболы.
Параболоид вращения (рис. 7.19) образуется вращением параболы вокруг ее оси.
Меридианом параболоида вращения является парабола.
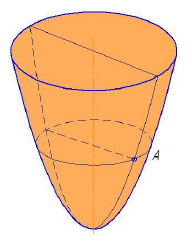
Рисунок 7.19 –Параболоид вращения
Поверхности вращения: цилиндр, конус, однополостный гиперболоид — являются также и линейчатыми поверхностями.
Тор является поверхностью четвертого порядка, что соответствует максимальному числу точек пересечения поверхности с прямой линией. Все остальные перечисленные выше поверхности вращения являются поверхностью второго порядка.
Поверхности циклические, каркасные и с плоскостью параллелизма
Циклическая поверхность образуется окружностью постоянного или переменного радиуса при ее произвольном движении.
Каналовая поверхность (рис. 7.20) образуется движением окружности переменного радиуса вдоль кривой направляющей, причем плоскость образующей окружности остается перпендикулярной к заданной направляющей, по которой движется центр окружности. Если радиус об-разующей окружности постоянен, то такая каналовая поверхность называется трубчатой.
Когда направляющей кривой является цилиндрическая винтовая линия, образуется трубчатая винтовая поверхность. Она может быть получена и движением сферы постоянного диаметра, центр которой перемещается по цилиндрической винтовой линии. Примером такой поверхности является поверхность цилиндрической пружины с круглым сечением витков.
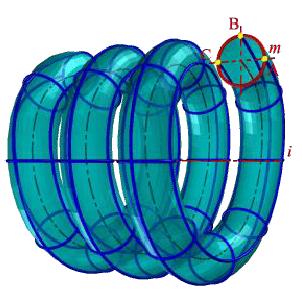
Рисунок 7.20 – Каналовая поверхность
Каркасными называют поверхности, заданные некоторым числом линий - каркас поверхности может быть получен линиями пересечения ее плоскостями параллельными плоскостям проекций.
Примером каркасных поверхностей могут служить поверхности корпусов судов, самолетов, автомобилей. К разряду каркасных поверхностей относится и топографическая поверхность. Эта изображается совокупностью горизонталей, т.е. линий, получаемых в сечении земной поверхности поверхность горизонтальными плоскостями.
Поверхности с плоскостью параллелизма (поверхности Каталана) представляют собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n.
Поверхности с плоскостью параллелизма имеют применение в архитектуре, строительстве, в конструировании технических форм.
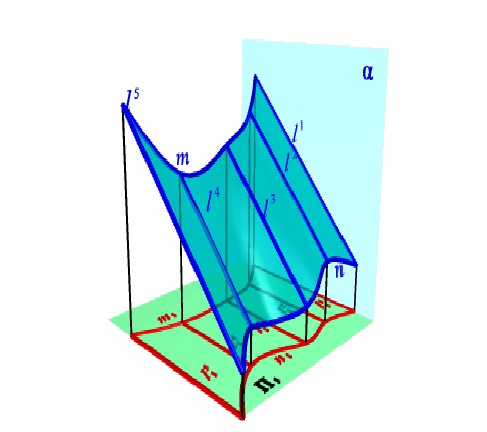
Рисунок 7.15 – Поверхности с плоскостью параллелизма
Точка и линия на поверхности
Точка принадлежит поверхности в том случае, если она находится на линии лежащей на этой поверхности. В качестве таких линий могут быть выбраны образующие, параллели, меридианы и др.
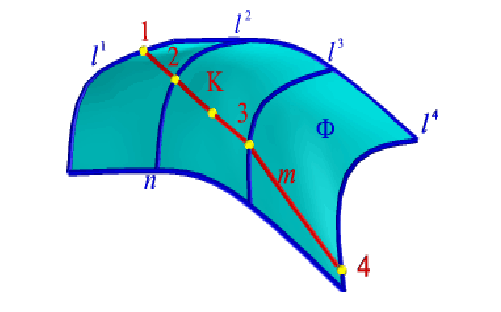
Рисунок 7.16 – Точка и линия на поверхности
Рассмотрим построение точек, лежащих на геометрических телах и поверхностях.
Точка на поверхности цилиндра
Поверхности цилиндра вращения (рис. 7.17) является горизонтально проецирующей, образующие цилиндра перпендикулярны горизонтальной плоскости проекций, вследствие чего поверхность цилиндра проецируется на эту плоскость окружностью [5].
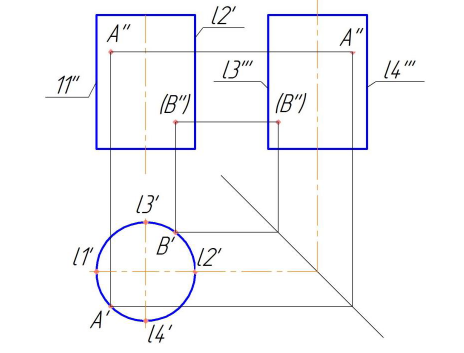
Рисунок 7.17 - Точка на поверхности цилиндра
Горизонтальные проекции точек А и В (А' и В') лежат на окружности.
Профильные проекции этих точек А"' и В "' находятся при помощи линий.
Очерковые образующие цилиндра разделяют фронтальную и профильные проекции на видимую и невидимые части. Так образующие L1 и L2 делят цилиндрическую поверхность на видимую спереди и невидимую, образующие L3 и L4 на видимую слева и невидимую. Невидимые проекции точек указаны в скобках.
Точка на поверхности конуса
Конус вращения является также и линейной поверхностью, поэтому для построения точек на его поверхности можно использовать и образующие и параллели.
На рис. 7.18а показано построение горизонтальной А' и профильной А"' проекций точки А по заданной фронтальной проекции А" при помощи образующей [5].
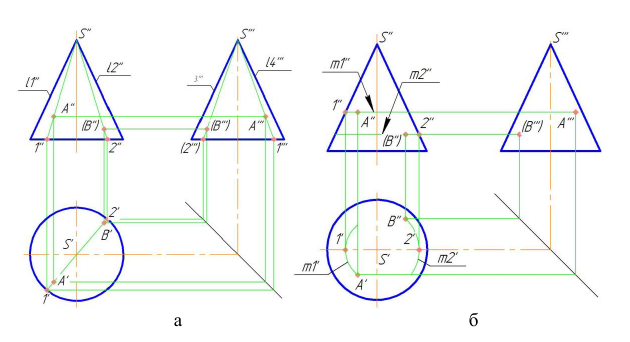
Рисунок 7.18 - Точка на поверхности конуса
Если задана горизонтальная проекция В' точки В, то построение начинается с проведения горизонтальной проекции S '2' образующей S2, на которой находится точка В. Определить фронтальную проекцию S" 2" этой образующей, по линиям связи находим фронтальную проекцию - В" точки В, а затем и профильную В”'.
Образующие L1 и L2 разделяют коническую поверхность на видимую спереди и невидимую, а образующие L3 и L4 на видимую слева и невидимую.
Проекции B" и В"' находятся на невидимой части конуса. Горизонтальная проекция поверхности конуса является видимой.
На рис. 7.18 б показано построение недостающих проекций точек A и В при помощи параллелей. Через заданные проекции А'' и В' проводятся проекции m''1 и m' 2 параллелей m1 и m2 Используя т.1 и 2, лежащие на очерковых образующих, определим положение проекций m'1 и m''2 проведенных параллелей. По линиям связи определим положение проекций А' и А '' точки А и проекций В'' и В''' точки В.
Точка на поверхности сферы
На рис. 7.19 приведены проекции сферы, которые ограничены экватором К, фронтальным меридианом m и профильным n [5]. Каждый из них проецируется на соответствующую плоскость проекций в натуральную величину (окружность), на остальные - в виде отрезков прямых длиной, равной диаметру сферы. На этом же рисунке показано построение недостающих проекций точек А, В и С по заданным фронтальным проекциям этих точек. Точка А находится на экваторе К, точка В — на фронтальном меридиане m, точка С — на профильном меридиане n. Недостающие проекции определяются при помощи линий связи (проведение линий связи на рисунке показано стрелками).
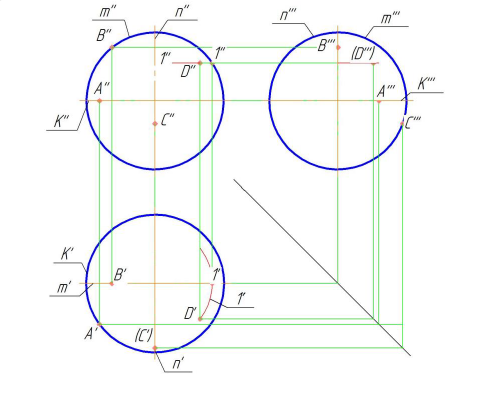
Рисунок 7.19 - Точка на поверхности сферы
Экватор К разделяет сферу на видимую (верхняя половина) на горизонтальной проекции невидимую части. Фронтальный меридиан m разделяет сферу на видимую (ближняя половина) и невидимую части на фронтальной проекции.
Профильный меридиан n разделяет сферу на видимую (левая половина) и невидимую части на профильной проекции.
Так на рис. 7.19 горизонтальная проекция С' точки С невидимая (взята в скобки), т.к. находится на нижней (невидимой) половине сферы.
На поверхности сферы можно провести множество параллелей, соответственно параллельных плоскостям проекций. Эти параллели используются для построения проекций точек на сфере.
По данной фронтальной проекции А" точки А, найдена горизонтальная А' как принадлежащая горизонтальной параллели L1. Для построения горизонтальной проекции L'2 использована точка 1, принадлежащая фронтальному меридиану. Профильная проекция А'" точки А построена при помощи линий связи и находится на невидимой (правой половине) части сферы.
Точка на поверхности тора
На рисунке 7.20 представлены проекции открытого тора (кругового кольца), полученного вращением окружности радиуса r вокруг оси i.
Проекции экватора обозначены k, горла - m, крайних параллелей n1 (верхняя) и n2 (нижняя).
Стрелками на рисунке показано построение фронтальных проекций точек А, В, С по заданным горизонтальным, расположенных соответственно на экваторе k, горле - m, и крайней (верхней) параллели п1.
Для построения горизонтальной проекции D' точки D, через фронтальную проекцию D" проведена фронтальная проекция L"1 параллели L1. Горизонтальная проекция L'1 параллели L1 построена при помощи точки 1, лежащей на образующей окружности.
Горизонтальная проекция точки В найдена при помощи линий связи, как принадлежащая параллели L1.
Для построения фронтальной проекции точки Е (по заданной гори-зонтальной), лежащей на внутренней части тора, использована параллель L2. Фронтальная проекция этой параллели строится при помощи точки 2, принадлежащей образующей окружности.
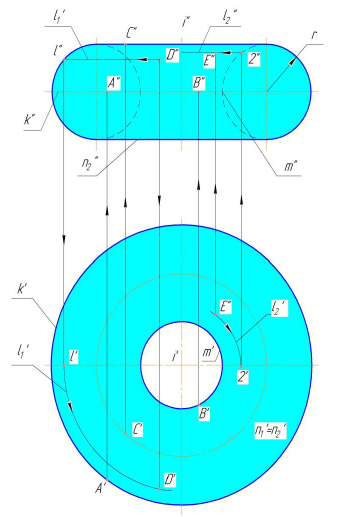
Рисунок 7.20 - Точка на поверхности тора
Экватор k разделяет тор на видимую (верхняя половина) и невидимую части на горизонтальной проекции. На фронтальной проекции видимой является ближняя наружная часть открытого тора.
Определение кривых линий
Проектирование обводов сложных технических форм напрямую связано с вопросом конструирования кривых по наперед заданным условиям. Последнее в большой степени обусловлено способом задания и формирования кривых.
Принято рассматривать кривые по отношению их к трехмерному пространству. Если кривые полностью принадлежат гиперпространству (двумерной плоскости) расширенного Евклидова пространства 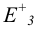 ,то такие кривые называет плоскими. Все остальные относят к пространственным кривым.
,то такие кривые называет плоскими. Все остальные относят к пространственным кривым.
В общем случае кривые рассматриваются как результат пересечения поверхностей. В этом смысле плоские кривые являются результатом пересечения поверхности с плоскостью.
Все кривые на чертеже задаются проекциями, которые являются плоскими кривыми, поэтому большая честь раздела и посвящена конструированию плоских кривых.
В практической работе проектировщику приходится иметь дело с двумя большими классами кривых, представляющих дуги простых кривых (графиков функций) и составных (сложных). Составные кривые, получившие в технике название обводов, конструируются из ряда дуг простых с соблюдением заданных условий на стыках.
Дифференциальные характеристики кривой
Форма и характер поведения плоской кривой в окрестности любой точки определяется ее дифференциальными характеристиками.
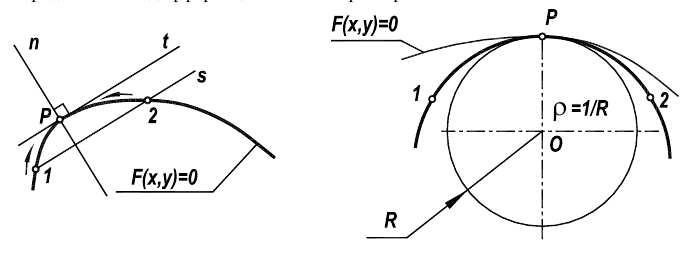
Рисунок 7.1 - Характеристики кривой линии F(x,y)=0
К основным характеристикам плоской кривой относят касательную t, нормаль т и кривизну р (рисунок 7.1).
Касательная (в точке Р) — предельное положение секущей 12 при бесконечном приближении точек У и 2 к точке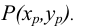
Уравнение касательной имеет вид:
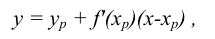
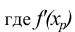 — первая производная в точке
— первая производная в точке 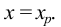
Нормаль — линия, перпендикулярная касательной в фиксированной точке кривой.
Кривизна — величина, обратная значению радиуса круга кривизны кривой p=l/R в фиксированной точке Р, определится уравнением:
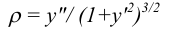
где штрихи означают дифференцирование по X .
Круг кривизны — предельное положение соприкасающейся окружности 1Р2 при бесконечном приближении точек 1 и 2 к точке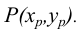
Приведенные уравнения показывают, что касательная и кривизна не являются полными аналогами первой и второй производной (такая аналогия принята в вычислительной математике), хотя и связаны с ними.
Особые точки кривых
"Поведение кривой" можно оценить и по типу точек, которые она несет на себе (рисунок 7.2).
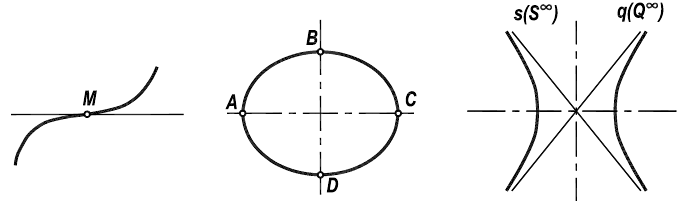
Рисунок 7.2 — Точки кривой
Точка кривой, в которой определена единственная касательная, называется обыкновенной (регулярной). Если в обыкновенной точке (А, В, С, D) кривизна достигает экстремального значения (например, ноль), то такая точка называется специальной. К специальным точкам относятся точки перегиба М, точки экстремума (вершины кривой В, D) и несобственные точки 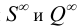 (рисунок 7.2). В точке перегиба ветви кривой расположены по разные стороны от касательной, кривизна в ней равна нулю (радиус кривизны стремится к бесконечности). Несобственная точка — это точка пересечения кривой с несобственной прямой плоскости. Такие точки на чертеже задаются асимптотами.
(рисунок 7.2). В точке перегиба ветви кривой расположены по разные стороны от касательной, кривизна в ней равна нулю (радиус кривизны стремится к бесконечности). Несобственная точка — это точка пересечения кривой с несобственной прямой плоскости. Такие точки на чертеже задаются асимптотами.
Точка кривой, в которой не определено положение касательной, получила название особой. К таким точкам относят (рисунок 7.3) узловые точки
А, точки возврата С и D , излома K, прекращения L, точки изолированные В, асимптотические M и точки самоприкосновения E.
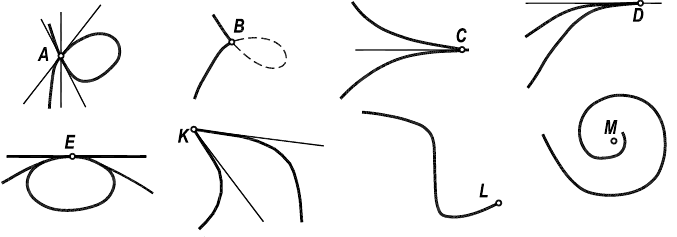
Рисунок 7.3 - Особые точки кривых
При проектировании технических форм следует избегать работы с дугами, несущими на себе особые точки.
Алгебраические кривые
Кривые могут быть классифицированы по виду их уравнения. Кривые, определяемые уравнениями в виде полиномов типа:
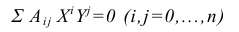
или отношения полиномов, получили название алгебраических. Все прочие кривые называют трансцендентными.
Для алгебраических кривых существует специальная характеристика -порядок кривой. Она совпадает по значению с максимальной степенью полинома. Геометрически порядок определяется числом точек пересечения алгебраической кривой с произвольной прямой линией. Эти точки могут быть: действительными (А и В), или мнимыми (D) (в соответствии с рисунком 7.4). Еще одна существенная характеристика - жанр (род) кривой.
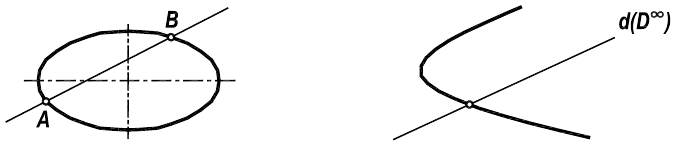
Рисунок 7.4 - Точки пересечения кривой линии с прямой
Жанр (род) кривой определяется как разность между возможными для данного порядка и существующими количествами двойных (совпавших) точек. Кривые нулевого жанра называют рациональными. Эти кривые нашли широкое применение для описания гидро - и аэродинамических профилей.
Конические сечения
Кривые, получающиеся при пересечении прямого кругового конуса плоскостью, называются кониками или коническими сечениями (рисунок 7.5).
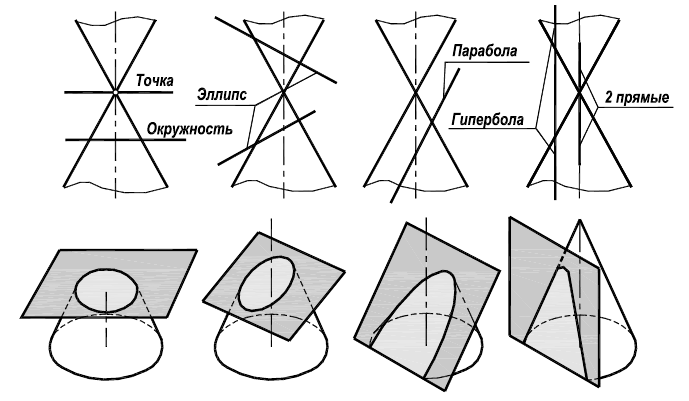
Рисунок 7.5 - Коники
Если секущая плоскость перпендикулярна оси вращения, то в сечении (в общем случае) получается окружность. При прохождении такой плоскости через вершину конуса окружность вырождается в точку.
Плоскость, пересекающая конус одновременно по всем образующим, позволяет получить эллипс.
Плоскость, параллельная образующей, отсекает параболу. В частном случае, когда секущая плоскость касается образующей, парабола вырождается в две совпавшие прямые.
Плоскость, параллельная оси вращения, отсекает гиперболу. В частном случае, при прохождении плоскости через саму ось, получаются две пересекающиеся прямые.
Наиболее употребительные графические способы построения дуг кривых второго порядка основаны на методах проективной геометрии. В соответствии с рисунком 7.6 дуга кривой второго порядка может быть определена тремя точками и касательными в двух точках. Например, точки А, В, С и касательные 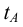
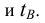
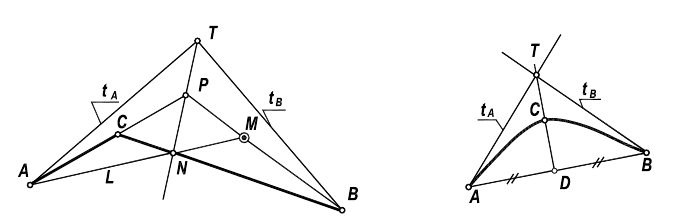
Рисунок 7.6 - Построение коник
Порядок построения точек дуги коники следующий: строится треугольник АТВ, где 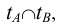 а затем внутри этого треугольника - точки
а затем внутри этого треугольника - точки 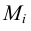 кривой второго порядка.
кривой второго порядка.
Для построения текущей точки дуги объединяются точки А, В и С. Проводится произвольная прямая l, которая в пересечении с прямой ВС определит положение точки N. Точки N и Т (пересечение касательных) соединяются прямой. Пересечение прямых NT и АС позволяет получить точку Р. Положение текущей точки дуги коники 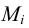 - найдется в пересечении прямых ВР и AN.
- найдется в пересечении прямых ВР и AN.
Меняя положение точки N, можно получить множество точек дуги кривой второго порядка.
Изменение положения точки С приведет получению другой формы коники. Такая возможность управления формой кривой широко используется в инженерной практике, для чего введено понятие инженерного дискриминанта.
В этом случае точка С задается на медиане DT 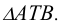 . Инженерный дискриминант f определяется из отношения f = CD/TD. Он характеризует тип коники:при f< 0.5 — это дуга эллипса, при f=0 дуга параболы, при f>0.5 — дуга гиперболы.
. Инженерный дискриминант f определяется из отношения f = CD/TD. Он характеризует тип коники:при f< 0.5 — это дуга эллипса, при f=0 дуга параболы, при f>0.5 — дуга гиперболы.
В отдельных случаях, если известен тип коники, построение кривой может быть значительно упрощено. Например, парабола может быть построена, как пропорциональная кривая (рисунок 7.7).
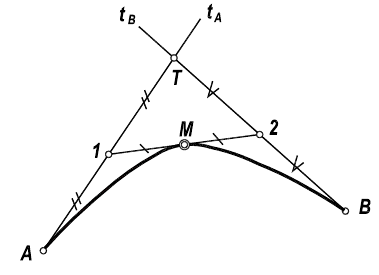
Рисунок 7.7 - Парабола
Исходная информация для построения дуги параболы: граничные точки А, В и точка пересечения касательных Т.
Отрезки АТ и ВТ делятся точками 1 и 2 пополам. Прямая 12 также делится пополам. Точка М — точка параболы.
Затем процесс повторяется (в обе стороны): граничные точки А, М и точка пересечения касательных 1 и т.д.
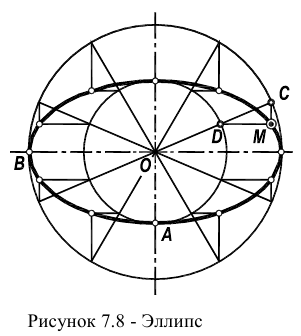
Эллипс удобнее стоить по его полуосям (большой ОВ и малой ОА).
Для построения эллипса проводятся две соосные окружности радиусами ОВ и ОА (рисунок 7.8). Проведение произвольной прямой ОС и дальнейшее построение "ключа” (треугольника СDM со сторонами параллельными осям эллипса) позволяет определить положение текущей точки эллипса М.
Плоские обводы
Решение практических задач по формированию сложных технических контуров наталкивается на такую проблему, как невозможность представления всего контура единственной кривой. Это и породило необходимость конструирования составных кривых (кривых, сформированных из дуг простых).
В технике такие кривые получили название обводов, в математике они более известны как сплайны (spline). Основной характеристикой обвода является гладкость. Под гладкостью понимают число совпавших производных (уравнений стыкующихся кривых) в точках стыка.
Наиболее простой вариант построения составной кривой - из дуг окружностей.
Окружности могут сопрягаться таким образом, что в точках стыка будут располагаться общие касательные. Такой стык соответствует первому порядку гладкости (совпадают только первые производные).
Для построения этого обвода используется идея радиусо - графического сопряжения дуг окружностей. Исходной информацией является точечный ряд (1,2,3,...,n) и касательная на одном из концов этого ряда (например, 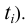
Вследствие того, что окружность трехпараметрическая кривая, для её построения кроме точки i нужно определить еще одну, например (i+1) или (i-1). He нарушая общности рассуждений, рассмотрим вариант с (i+1)-ой точкой (рисунок 7.9).
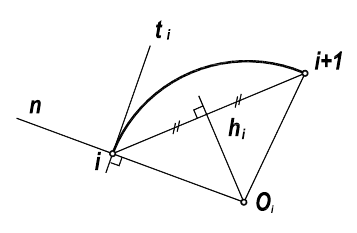
Рисунок 7.9 - Дуга окружности с заданными параметрами
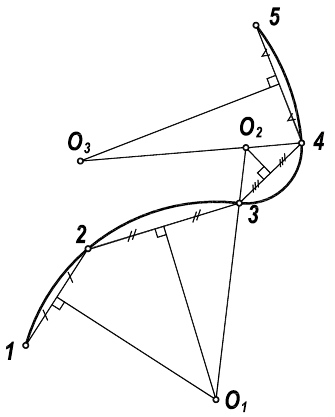
Рисунок 7.10 - Обвод первого порядка гладкости
Графическое решение выглядит следующим образом: через точку i проводится нормаль n . Конечные точки i и (i+1) соединяются хордой. В средней точке хорды строится перпендикуляр h . Пересечение нормали п и перпендикуляра h и определит положение центра искомой окружности. Радиус окружности совпадает с отрезками [o-i] и [o-(i+ Касательная к построенной окружности будет перпендикулярна радиусу, проведенному в (i+1)-ю точку.
Касательная к построенной окружности будет перпендикулярна радиусу, проведенному в (i+1)-ю точку.
Центры соприкасающихся окружностей лежат на одной прямой, проходящей через точку касания. Таким образом, определение центра окружности сопрягающейся с i-той найдется на пересечении линии 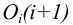 с перпендикуляром к середине хорды (i+l)(i+2) (рисунок 7.10).
с перпендикуляром к середине хорды (i+l)(i+2) (рисунок 7.10).
Пространственные кривые
В отличие от плоских кривых, пространственные кривые (линии двоякой кривизны) не лежат всеми своими точками в одной плоскости.
Общие свойства пространственной кривой, ее проекции связаны со свойствами проецирования и справедливы для проекций плоских кривых:
- несобственная точка кривой проецируется в несобственную точку ее
- проекции;
- касательная к кривой проецируется в касательную к ее проекции;
- порядок проекции алгебраической кривой равен порядку самой кривой. В частных случаях проекция может распадаться и иметь меньший, чем у кривой, порядок. Например, кривая второго порядка, лежащая в проецирующей плоскости, проецируется в «двойную» прямую.
Исследование свойств кривой в окрестности ее точки, так называемых дифференциальных (локальных) свойств, производится путем построения проекций кривой на гранях сопровождающего трехгранника (рисунок 7.11).
Сопровождающий трехгранник (трехгранник Френе) состоит из трех ребер — касательной t, нормали n и бинормали b и из трех граней — соприкасающейся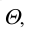 нормальной Г, спрямляющей
нормальной Г, спрямляющей 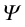 плоскостей.
плоскостей.
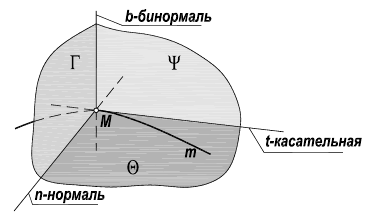
Рисунок 7.11 - Оснащение пространственной кривой
Рассмотрим наиболее часто встречающуюся на практике пространственную кривую — цилиндрическую винтовую линию (рисунок 7.12.)
Цилиндрическая винтовая линия представляет собой траекторию точки, совершающей равномерное движение вдоль некоторой прямой, которая в свою очередь равномерно вращается вокруг параллельной ей оси.
Расстояние h, на которое точка М перемещается вдоль образующей за один ее оборот, называется шагом винтовой линии. Описываемая при этом точкой М дуга называется витком.
Число р = h/2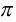 называется параметром винтовой линии и определяет перемещение z точки М вдоль прямой m за время поворота последней на угол <;р, равный одному радиану.
называется параметром винтовой линии и определяет перемещение z точки М вдоль прямой m за время поворота последней на угол <;р, равный одному радиану.
Радиус г цилиндрической поверхности, описываемой прямой т вращением вокруг оси i параллельнойm, называется радиусом винтовой линии, а ось / — осью винтовой линии.
Очевидно, что винтовая линия однозначно определяется своей осью i, шагом h и радиусом r. Поэтому для построения проекций винтовой линии 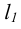 и
и 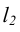 на чертеже задается цилиндрическая поверхность вращения с осью i, радиусом r. На оси i откладывается отрезок, равный шагу h.
на чертеже задается цилиндрическая поверхность вращения с осью i, радиусом r. На оси i откладывается отрезок, равный шагу h.
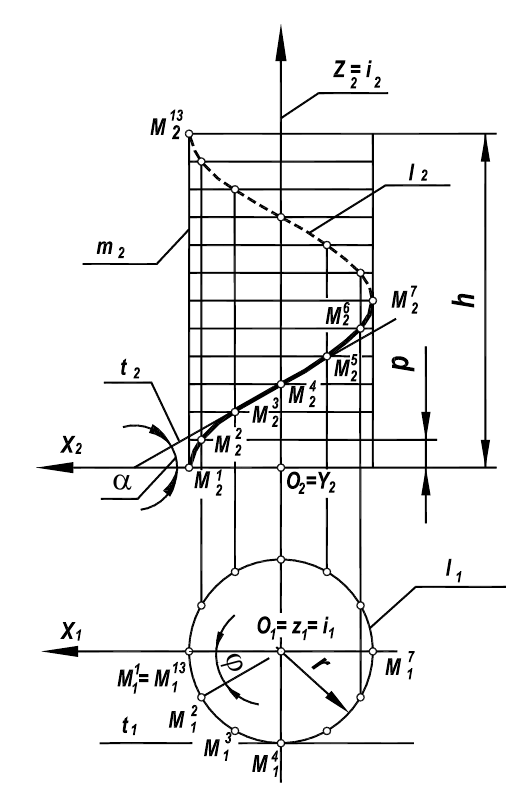
Рисунок 7.12 - Цилиндрическая винтовая линия
Вырожденная проекция цилиндрической поверхности есть горизонтальная проекция 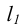 данной винтовой линии. Для построения фронтальной проекций линии
данной винтовой линии. Для построения фронтальной проекций линии 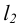 окружность делится на равное число частей (в соответствии с рисунком 7.12). Фронтальные проекции точек винтовой линии находятся как точки пересечения одноименных горизонтальных и вертикальных прямых, проведенных через точки деления.
окружность делится на равное число частей (в соответствии с рисунком 7.12). Фронтальные проекции точек винтовой линии находятся как точки пересечения одноименных горизонтальных и вертикальных прямых, проведенных через точки деления.
Винтовая линия может быть правой или левой в зависимости от направления закручивания. Угол а между касательной к винтовой линии и плоскостью 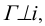 , постоянен для любой ее точки и называется углом подъема винтовой линии.
, постоянен для любой ее точки и называется углом подъема винтовой линии.
Нетрудно показать, что на поверхности цилиндра некоторая кратчайшая линия, соединяющая две точки поверхности, будет винтовой линией.
В технике также встречаются винтовые линии, принадлежащие коническим поверхностям и некоторым поверхностям вращения.
Кривые линии и поверхности
Кривую линию можно представить как траекторию движущейся точки в пространстве. Примером служат, например, спираль Архимеда, цилиндрическая или коническая винтовая линия (рис. 11.7, а и б и рис. 11.8, а).
Кривая линия может быть получена в результате пересечения поверхностей между собой или пересечения кривой поверхности плоскостью. На поверхности конуса в зависимости от положения секущей плоскости образуется ряд кривых линий – эллипс, гипербола, парабола, окружность (см. рис. 7.11–7.15). Эллипс или окружность получаются также в сечениях плоскостью цилиндра (см. рис. 7.7 и 7.8) и кругового однополостного гиперболоида. Осевыми сечениями однополостного гиперболоида являются гиперболы (см. рис. 7.29, а), а параболоида – параболы (см. рис. 7.29, а).
Кривые линии могут быть плоскими и пространственными (линиями двоякой кривизны). Примерами плоских кривых линий являются окружность, эллипс, парабола, спираль Архимеда, пространственных – винтовые линии, линии пересечения кривых поверхностей.
Пространственная линия всегда проецируется в виде кривой, а плоская – только при условии, что ее плоскость не перпендикулярна плоскости проекций (если перпендикулярна – проецируются в виде прямой).
Линия считается закономерной, если в своем образовании она подчинена какому-либо геометрическому закону, а если при этом она определяется в декартовых координатах алгебраическим уравнением, ее называют алгебраической. Степень уравнения определяет «порядок» кривой. Так, например, эллипс – кривая второго порядка. Проекция кривой сохраняет ее порядок или оказывается кривой более низкого порядка.
Если кривая не определяется алгебраическим уравнением, то она относится к числу трансцендентных.
Касательная прямая к кривой линии в общем случае проецируется в виде касательной к проекции этой кривой. Так, например, касательная к окружности в некоторой точке проецируется в касательную к эллипсу, являющемуся проекцией этой окружности.
Если в каждой точке кривой можно построить только одну касательную прямую линию, то кривая называется плавной или монотонной.
Такая плоская кривая в каждой ее точке имеет только одну нормаль – прямую, перпендикулярную к соответствующей касательной в каждой точке кривой и принадлежащую плоскости.
Составные кривые линии – классификация точек стыка
Кривая линия может быть составной, если на ней есть точка стыка, называемая вершиной, в которой соединяются две кривые линии (рис. 11.1 и 11.2) [23]. Существует понятие обыкновенная вершина кривой. Это точка A на рис. 11.1. В ней соединяются (соприкасаются) две монотонные плоские кривые линии l1 и l2, касательные t1 и t2, к которым в этой точке противоположно направлены по одной линии, а нормали n1 и n2 и центры кривизны O1 и O2 совпадают (рис. 11.1, а).
Если хотя бы одно из указанных условий не выполняется, то речь ведут об особой точке на составной кривой. Двойной называют особую точку B стыка (вершину) составной кривой, если касательные направлены в разные стороны, нормали совпадают по направлению, а вот центры кривизны различны (рис. 11.1, б). Точка перегиба получается в том случае, когда в ней противоположные направления имеют и касательные, и нормали к составной кривой. Это особая точка стыка C (рис. 11.1, в).
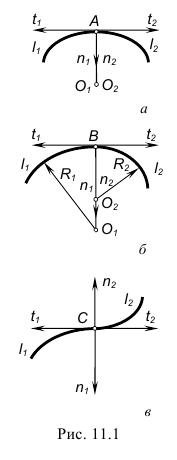
Из всего многообразия точек стыка следует уделить внимание и так называемым точкам возврата 1-го и 2-го рода и точке излома (рис. 11.2) [23].
На рис. 11.2, а изображена точка D возврата 1-го рода, в которой касательные t1 и t2 к каждой кривой совпадают по направлению, а нормали n1 и n2 имеют противоположные направления.
На рис. 11.2, б изображена точка E возврата 2-го рода, в которой и касательные t1 и t2 к каждой кривой, и нормали n1 и n2 попарно совпадают по направлению.
На рис. 11.2, в и г изображены точки К и L излома, в которых касательные t1 и t2 не принадлежат одной прямой.
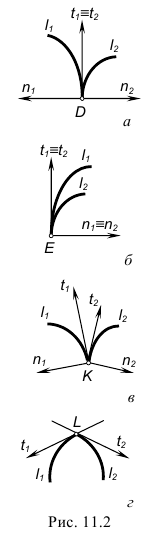
Плоские и пространственные кривые линии
Для построения ортогональных проекций кривой необходимо построить проекции ряда точек, принадлежащих этой кривой, и через них провести под лекала плавные кривые. Следует иметь в виду, что по двум проекциям нельзя без дополнительных построений определить, является линия пространственной или плоской кривой.
На рис. 11.3 показаны эти дополнительные построения, которые позволяют сказать: вверху приведен чертеж плоской кривой k(k',k"), а под ним – пространственной l(l',l"). Суть дополнительных построений сводится к соединению попарно четырех точек A(A',A") и B(B',B"), C(C',C") и D(D',D"), произвольно взятых на кривой, прямыми линиями.
Поскольку на рис. 11.3, а эти прямые являются пересекающими, о чем свидетельствует расположение проекций 1' и 1" точки их пересечения на одной линии связи, то все указанные точки A(A',A"), B(B',B"), C(C',C") и D(D',D") лежат в одной плоскости. В силу этого линия k(k',k"), которой принадлежат эти точки, является плоской кривой (у плоской кривой все принадлежащие ей точки должны лежать в одной плоскости).
Внизу на рис. 11.3, б отмеченное условие не выполняется – точки пересечения проекций прямых, попарно соединяющих проекции четырех точек A(A',A") и B(B',B"), C(C',C") и D(D',D"), принадлежащих кривой l(l',l"), лежат на разных линиях связи. Следовательно, эти прямые не лежат в одной плоскости, являясь скрещивающимися. Поэтому не лежат в ней и соединяемые ими точки кривой, свидетельствуя о том, что эта линия – пространственная кривая.
Цилиндрические и конические винтовые линии
Из пространственных кривых в технике находят широкое применение винтовые линии и поверхности. Винтовую линию можно рассматривать как результат перемещения точки по поверхности вращения.
Гелисой называют винтовую линию, которая образуется в результате равномерного вращения точки вокруг оси и одновременного перемещения с постоянной скоростью вдоль нее.
Величину P перемещения точки вдоль направления оси, соответствующем одному ее обороту вокруг оси, называют шагом винтовой линии.
Для построения проекции винтовой линии, в частности гелисы, предварительно строят проекции прямого кругового цилиндра (рис. 11.7, б).
Окружность основания цилиндра (горизонтальная проекция гелисы) делят на равное количество равных частей (например, на 12, так как это можно сделать тем же раствором циркуля, которым была вычерчена окружность). На такое же количество частей делят цилиндр по высоте, равной шагу винтовой линии, на фронтальной проекции. Из точек, отмеченных на окружности, проводят вертикальные линии связи до их пересечения с горизонтальными линиями, проведенными из соответствующих точек деления шага. Соединив полученные точки плавной кривой линией, получают фронтальную проекцию винтовой линии (линия изображена с учетом ее видимости на поверхности цилиндра, рис. 11.7, б).
Различают правые и левые винтовые линии. Изображенная на рис. 11.7, б цилиндрическая винтовая линия является правой. Она характеризуется тем, что при вращении по часовой стрелке точка удаляется от наблюдателя, а при вращении против часовой стрелки – приближается. Если эти условия не соблюдаются, винтовая линия называется левой.
На рис. 11.7, б справа показано построение развертки винтовой линии. Там же приведена формула для определения крутизны винтовой линии.
На рис. 11.8, а приведена коническая винтовая линия, которая образуется в результате движения точки по поверхности конуса при условии, что она равномерно вращается вокруг оси конуса и движется вдоль нее с постоянной скоростью. Судя по направлениям этих ее движений – это также правая винтовая линия. Для построения ее проекций горизонтальные проекцию окружностей оснований приведенного усеченного конуса делят на 12 равных частей и, соединяя их, строят горизонтальные проекции образующих конуса. Определив фронтальные проекции полученных точек посредством линий связей, строят фронтальные проекции образующих. Затем делят конус по высоте (равна шагу винтовой линии) на то же количество частей горизонтальными линиями и отмечают точки их пересечения с фронтальными проекциями образующих. Соединив найденные точки плавной кривой линией, получают фронтальную проекцию конической винтовой линии (линия изображена с учетом видимости ее на поверхности конуса, рис. 11.8, а). Далее, опуская из этих точек линии связи, отмечают на пересечениях с горизонтальными проекциями соответствующих образующих точки, через которые пройдет горизонтальная проекция конической винтовой линии. По форме она представляет собой спираль Архимеда. Там же, на рис. 11.8, а, показаны дополнительные построения по определению горизонтальных проекций 3' и 9' точек винтовой линии на образующих, не пересекаемых линиями связи, а сливающихся с ними. Графически показано, как поделены горизонтальные проекции этих образующих на отрезки в том же отношении, в котором поделены их фронтальные проекции винтовой линией (для уменьшения количества построений указанное деление обоих отрезков совмещено в одном построении).
Винтовые поверхности – прямой и косой геликоиды
При винтовом движении отрезка линии образуются винтовые поверхности. В зависимости от формы образующей линии, винтовые поверхности могут быть линейчатыми и нелинейчатыми. Они находят большое применение в технике, особенно в машиностроении и поэтому заслуживают отдельного внимания.
Все точки образующей при винтовом движении описывают винтовые линии (за исключением точки, находящейся на оси вращения поверхности), каждая из которых может служить направляющей поверхности. Линейчатые винтовые поверхности называют геликоидами. В зависимости от положения образующей относительно оси вращения геликоиды могут быть прямыми (образующая перпендикулярна оси) и косыми (образующая наклонена к оси).
Чертеж прямого геликоида приведен на рис. 11.8, б. Построение его проекций вначале повторяет построения цилиндрической винтовой линии, приведенные на рис. 11.7, б. Но вместо фронтального очерка цилиндра необходимо показать фронтальные проекции образующих винтовой поверхности. Эти проекции представляют собой горизонтальные отрезки, расположенные между осью вращения поверхности и фронтальной проекцией винтовой линии. Фронтальный очерк прямого геликоида образуют указанная винтовая линия, являющаяся проекцией траектории движения внешнего конца образующей, и проекция траектории движения ее внутреннего конца, совпадающая с фронтальной проекцией оси вращения образующей. Направление геликоида определяют так же, как и винтовой линии.
При построении проекций косого геликоида необходимо знать угол наклона его образующей к оси вращения. Эта поверхность имеет более сложный очерк (рис. 11.4).
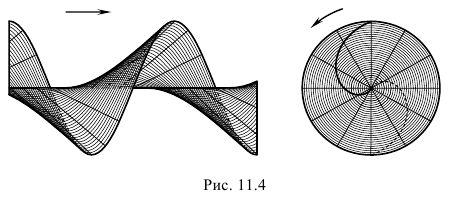
Чертеж косого геликоида, образованного наклонной прямолинейной образующей за 1,5 оборота винтового движения, приведен на рис. 11.5 и повторен на рис. 11.8, в.
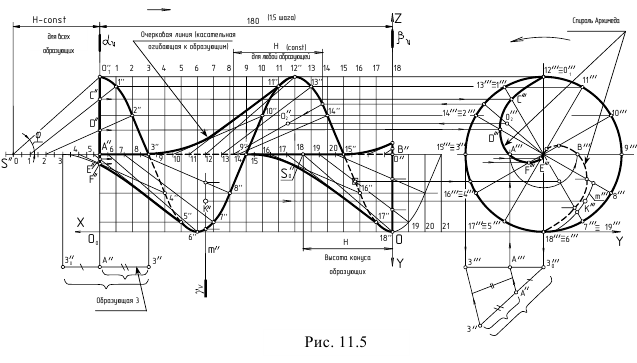
Исходным условием для построений его чертежа является шаг винтового движения образующей и ее начальное положение под углом φ к оси вращения (рис. 11.5). В процессе движения образующая должна оставаться параллельной поверхности направляющего конуса высотой H. Для построения 18 фронтальных проекций образующей, равномерно расположенных на протяжении 1,5 шага поверхности, используют вспомогательную сетку. При этом расстояние H между концами каждой образующей, измеренное вдоль оси вращения, должно быть постоянным. Затем проводят огибающие кривые очерковые линии, касательные к проекциям образующих, и строят торцевые срезы рассматриваемого участка косого геликоида профильными плоскостями. Профильные проекции этих срезов представляют собой спирали Архимеда. Проекции A"' и B"' точек, принадлежащих образующей в ее третьем и девятом положениях, могут быть определены путем дополнительных построений, основанных на графическом делении отрезков в заданном отношении.
Построение недостающей профильной проекции K"' и недостающей фронтальной проекции O2" точек K"(K"') и O(O2"'), принадлежащих винтовой поверхности, показано на том же чертеже (рис. 11.5). В первом случае использовалась линия m сечения поверхности профильной плоскостью γ(γV), во втором – промежуточная образующая.
Структуризация материала данной лекции схематически представлена на рис. 11.6 (лист 1). На последующих листах 2 и 3 (рис. 11.7 и 11.8) компактно приведены иллюстрации к этой схеме для визуального закрепления основной части изученного материала при повторении.
Кривые линии. Кривые поверхности – винтовые
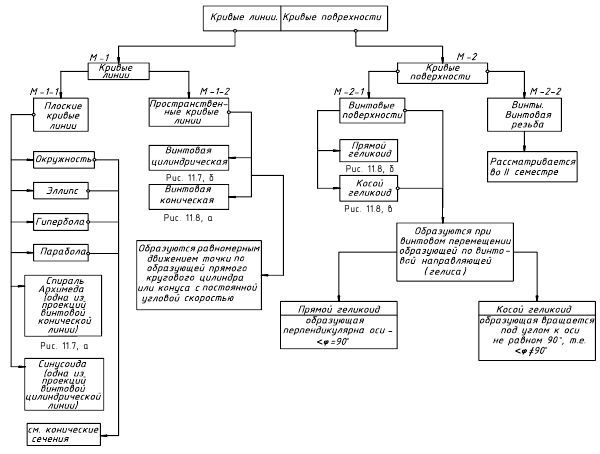
Плоская кривая – все точки линии лежат в одной плоскости.
Пространственная кривая – все точки линии не принадлежат одной плоскости.
Плоские кривые. Спираль Архимеда
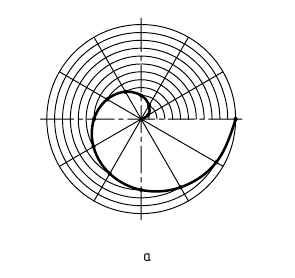
Пространственные кривые
Цилиндрическая винтовая пространственная линия.
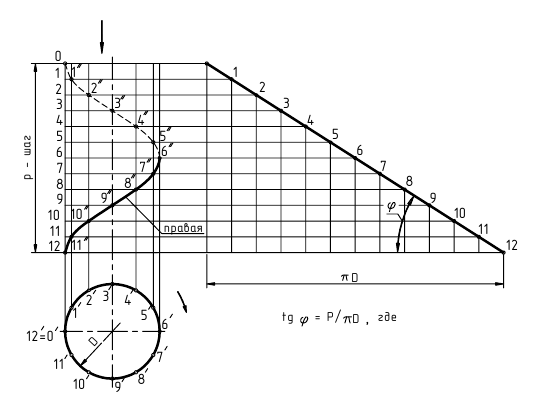
Характеризуется:
- - углом подъема φ;
- - шагом - Р;
- - направлением хода.
- φ- угол подъема винтовой линии;
- Р - шаг: расстояние, на которое перемещается точка по образующей вдоль оси за один оборот;
- πD - длина окружности.
Правая винтовая линия - точка удаляется от наблюдателя, вращаясь по часовой стрелке.
Левая винтовая линия - точка удаляется от наблюдателя, вращаясь против часовой стрелки.
Коническая пространственная винтовая линия
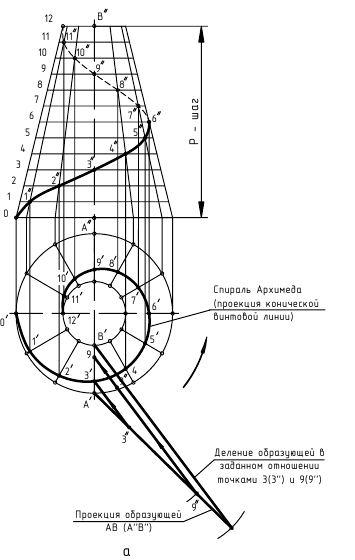
Винтовая поверхность - прямой геликоид
(образующие перпендикулярны оси)
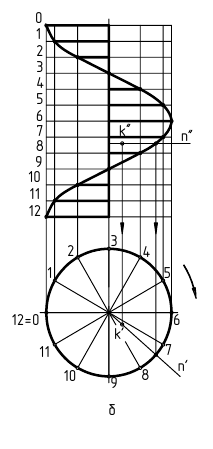
Винтовая поверхность – косой геликоид
(образующие не перпендикулярны оси, φ≠90°)
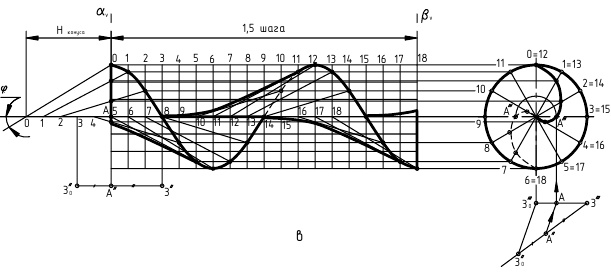
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Образование и задание поверхности на чертеже
- Пересечение поверхности плоскостью и прямой
- Развертки поверхностей
- Способы преобразования проекций
- Способы преобразования чертежа
- Ортогональное проецирование: точка, прямая, плоскость
- Взаимное расположение геометрических образов и фигур
- Преобразование чертежа